当前位置：文档之家 › 材科基考点强化(第5讲扩散)

材科基考点强化(第5讲扩散)

  • 格式：doc
  • 大小：139.50 KB
  • 文档页数：4

下载文档原格式

  / 4

合集下载

石德珂《材料科学基础》考点精讲5

石德珂《材料科学基础》考点精讲5

瓶内 Ｃ ＝ｋ槡ｐ０，瓶外 Ｃ′＝０
因此，Ｊ＝－ＤｄＣ ＝－Ｄｃ－ｃ′＝－Ｄｋ槡ｐ０
ｄｘ
ｈ
ｈ
措施：改变容器材料，减小 Ｄ和 ｋ；降低容器内储存氢气压力 ｐ０；增加壁厚 ｈ。 二、扩散第二定律（菲克）（非稳态扩散，ｄＣ／ｄｔ≠０） １．Ｃｔ＝ｘ（ＤＣｘ） ＝Ｄ２ｘＣ２
— １４９—
Ｃ— ｔ
浓度随时间的变化率，ｋｇ／（ｍ３·ｓ）
［解］详见视频。 ［例 ４］ 钢的渗碳有时在 ８７０℃而不是在 ９２７℃下进行，为什么？已知碳在 γ－Ｆｅ中的扩散常数 为 ２．０×１０－５ｍ２ｓ－１，扩散激活能 Ｑ＝１．４×１０５Ｊ／ｍｏｌ（Ｒ＝８．３１Ｊ／ｍｏｌ·Ｋ），请问在 ８７０℃下渗碳要多少 小时才能得到相当于在 ９２７℃下 １０小时的渗碳深度？ ［解］详见视频。
— １５２—
硝酸酒精 ５００Ｋ ２０钢 渗碳后空冷 表层全脱碳，白亮部分为铁素体 次表层为部分脱碳层，即珠光体 ＋少量铁素体 过渡区为珠光体 ＋铁素体（白色网块）
［例 ３］ 菲克第二定律的解之一是误差函数解，可用于铁的渗碳过程。若温度固定，不同时间碳 的浓度分布如图所示。已知渗碳 １小时后达到某一特定浓度的渗碳层厚度为 ０．５ｍｍ，问再继续渗碳 ８ 小时后，相同浓度的渗碳层厚度是多少？
－
互扩散系数—由 Ａ和 Ｂ组元构成的扩散偶中，Ｄ ＝ｘＢＤＡ ＋ｘＡＤＢ 代表两组元的综合扩散系数，称 为互扩散系数或化学扩散系数。
— １４８—
调幅分解 — 是指过饱和固溶体在一定温度下分解成结构相同、成分不同的两个相的过程。 ［例题］ 名词解释 上坡扩散 反应扩散 柯肯达尔效应……．
第五章 扩散与固态相变
本章考研要求 一、扩散定律 二、扩散的微观机制 三、扩散的驱动力 四、反应扩散 五、扩散的影响因素

扩散现象的知识点总结

扩散现象的知识点总结

扩散现象的知识点总结一、定义扩散是指分子、离子或其他微观粒子由高浓度向低浓度扩散的过程。

在这一过程中，物质会在不同浓度区域间发生自发性的热运动，最终达到浓度均匀的状态。

二、扩散的原理1. 布朗运动：布朗运动是扩散现象最基本的原理之一。

物质在水平方向上不断做无规则的运动，这种无规则的运动导致了物质的扩散。

2. 浓度差驱动：扩散是由高浓度区域向低浓度区域自发性的运动。

浓度差是扩散的驱动力。

3. 气体分子的扩散：气体分子在容器内由高浓度区域向低浓度区域自发性地运动，从而实现了扩散。

这个过程是由气体分子的不断热运动所驱动的。

三、扩散的影响因素1. 温度：温度升高会加快分子的热运动速度，从而促进扩散的发生。

2. 浓度差：浓度差越大，扩散越快。

3. 扩散系数：扩散系数是评价某种物质在给定条件下的扩散速率的因素。

四、扩散的应用1. 生物学：细胞能够通过扩散的方式从细胞外部获取氧气和营养物质，排除废物。

2. 化学工业：化学反应中许多反应物和产物都需要通过扩散来实现。

3. 材料科学：扩散对于材料的热处理和表面处理具有重要意义。

五、扩散的研究方法1. 扩散试验：扩散试验是通过对实验条件的控制，通过测定扩散系数等参数来研究扩散现象。

2. 模拟计算：计算机模拟可以通过数值计算模拟扩散过程，进一步深入研究扩散现象。

3. 实验观察：通过显微镜等仪器观察扩散现象，了解扩散的过程和规律。

六、扩散的发展趋势1. 理论研究：扩散现象的理论研究将进一步深化，更精确的模型将被建立。

2. 技术应用：扩散技术将被应用到更多的领域，包括新材料的生产和表面处理等。

3. 环境保护：在环境保护领域，扩散技术将有望用于污染物的清除和处理。

综上所述，扩散现象是自然界中一种普遍存在的物理现象，它在生物学、化学工业、材料科学等领域都有重要的应用和研究价值。

通过对扩散现象的深入研究，可以更好地认识自然界的规律，推动科学技术的发展。

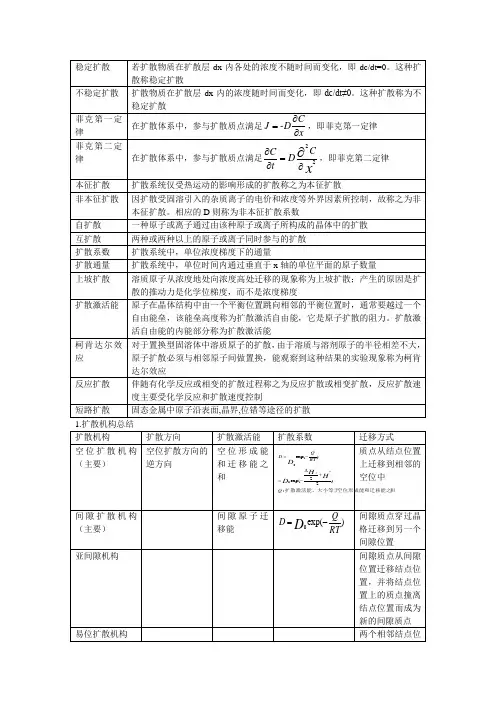
材料科学基础-扩散

材料科学基础-扩散

稳定扩散 若扩散物质在扩散层dx 内各处的浓度不随时间而变化，即dc/dt=0。

这种扩散称稳定扩散不稳定扩散 扩散物质在扩散层dx 内的浓度随时间而变化，即dc/dt≠0。

这种扩散称为不稳定扩散菲克第一定律在扩散体系中，参与扩散质点满足xC-DJ ∂∂=，即菲克第一定律 菲克第二定律 在扩散体系中，参与扩散质点满足xC D t C22∂=∂∂∂，即菲克第二定律 本征扩散 扩散系统仅受热运动的影响形成的扩散称之为本征扩散非本征扩散 因扩散受固溶引入的杂质离子的电价和浓度等外界因素所控制，故称之为非本征扩散。

相应的D 则称为非本征扩散系数自扩散 一种原子或离子通过由该种原子或离子所构成的晶体中的扩散 互扩散 两种或两种以上的原子或离子同时参与的扩散 扩散系数 扩散系统中，单位浓度梯度下的通量扩散通量 扩散系统中，单位时间内通过垂直于x 轴的单位平面的原子数量上坡扩散 溶质原子从浓度地处向浓度高处迁移的现象称为上坡扩散；产生的原因是扩散的推动力是化学位梯度，而不是浓度梯度扩散激活能原子在晶体结构中由一个平衡位置跳向相邻的平衡位置时，通常要越过一个自由能垒，该能垒高度称为扩散激活自由能，它是原子扩散的阻力。

扩散激活自由能的内能部分称为扩散激活能柯肯达尔效应 对于置换型固溶体中溶质原子的扩散，由于溶质与溶剂原子的半径相差不大，原子扩散必须与相邻原子间做置换，能观察到这种结果的实验现象称为柯肯达尔效应反应扩散 伴随有化学反应或相变的扩散过程称之为反应扩散或相变扩散，反应扩散速度主要受化学反应和扩散速度控制短路扩散 固态金属中原子沿表面,晶界,位错等途径的扩散1.扩散机构总结扩散机构扩散方向 扩散激活能 扩散系数迁移方式 空位扩散机构（主要）空位扩散方向的逆方向空位形成能和迁移能之和和空位形成能和迁移能之扩散激活能，大小等于:)22exp()(exp *00Q RTQ D HHD Df+∆-=-=质点从结点位置上迁移到相邻的空位中间隙扩散机构（主要）间隙原子迁移能 )(exp 0RT Q D D -=间隙质点穿过晶格迁移到另一个间隙位置 亚间隙机构间隙质点从间隙位置迁移结点位置，并将结点位置上的质点撞离结点位置而成为新的间隙质点 易位扩散机构两个相邻结点位置上的质点直接交换位置进行迁移环易位机构几个结点位置上的质点以封闭的环形依次交换位置进行迁移1.空位机构和间隙机构是金属体系和离子化合物体系中质点扩散的主要形式2.空位机构比间隙机构的扩散激活能大，但是扩散系数小3.固态金属中扩散方向是化学位梯度降低方向 2.扩散中常用公式)(exp 0RT Q D D -=δ261D Γ=(频率,自由程)xC -D J ∂∂=(适用于稳定扩散和非稳定扩散)x C D t C 22∂=∂∂∂（不稳定扩散） dxdc -DA JA dt dm == Dt K x =(实验测得的浓度已知) DtA t x x4),(lnI 2-=（A ：图像的截距，Dt41-为斜率；）3.扩散的结果都是使不均匀体系均匀化，不平衡逐渐达到平衡4.非稳定扩散类型①扩散质在晶体表面浓度恒定情况：)2(),(C 0Dtx erfc t x C =②定量扩散质由晶体表面向内部扩散（示踪扩散法原理）：)4exp(2),(C 221)(DtM t x xDt -=π5.本征扩散一般处于高温处，非本征扩散一般处于低温处；由杂质扩散转变为本征扩散，其T1-ln D r 曲线上会出现转折点;置换型固溶体扩散一般只能在高温进行;杂质浓度升高,转折点升高6.扩散系数测定一般使用示踪扩散方法7.扩散动力学方程式（能斯特-爱因斯坦方程）)ln ln 1)((D 211221~γγ∂∂++=D N D N①(γγ21ln ln 1∂∂+)>0:扩散系数大于0,正常扩散,高浓度向低浓度迁移,溶质趋于均匀②(γγ21ln ln 1∂∂+)<0:扩散系数小于0,反常扩散,低浓度向高浓度迁移,溶质偏聚或分相8.影响扩散系数因素①温度:影响扩散激活能和改变物质结构 ②杂质 ③气氛 ④固溶体类型:间隙性固溶体比置换型固溶体更容易扩散;在置换型固溶体中,原子间尺寸差别越小,电负性越大,亲和力越强,扩散越困难 ⑤扩散物质性质和结构 ⑥化学键类型和强度 ⑦扩散介质结构:体心立方结构大于面心立方结构的扩散系数 ⑧结构缺陷:结构缺陷活化能小,容易扩散 9.激活能越大,扩散速率对温度的敏感性越大 10.反应扩散对扩散层深度的影响过程实际上反应扩散起初由于新相层较浅,原子扩散不是主要矛盾,过程由表面扩散所支配,新相层的增加服从直线关系;随新相层深度增加,原子扩散逐步称为主要矛盾,新相层的增加服从抛物线规律。

材科-第五章-扩散共69页文档

材科-第五章-扩散共69页文档

反应扩散：由之导致形成一种新相的扩散。
3 固态扩散的条件
（1）温度足够高；
（2）时间足够长；
基
（3）扩散原子能固溶；
本 概
（4）具有驱动力：化学位梯度。
念
第 五
第一节 扩散定律及其应用
章
1 菲克第一定律
（1）第一定律描述：单位时间内通过垂直于扩 散方向的单位截面积的扩散物质流量（扩散通量J） 与该截面处的浓度梯度成正比。
律 (2)扩散过程中空位浓度保持不变；
及 (3)扩散驱动力为浓度梯度
其
应
用
J* ( D D ) ci D ~ ci
i
x 2 1 1 2
x
D1、D2:偏扩散系数或本征扩散系数
~
D ：互扩散系数
~
D = Di的情况: (1)自扩散；(2)稀固溶体
第 五
第一节 扩散定律及其应用
(1) 扩散速率取决于 外界条件 C/ x 扩散体系的性质 D
(2) D是一个很重要的参数: 单位浓度梯度、单位截面、单 位时间通过的流量。
D取决于 传送的质点本身的性质： 半径、电荷、极化性 能等
三维表达式：
J＝ iJx
jJy
kJz
D(iC j CkC) x y z
（2）Kirkendall实验
l
在Cu－30%Zn的合金两边焊上纯铜， 并在焊缝处加入一些细的Mo丝作标
记。
Cu
Cu-Zn
测定标记之间的距离 在785℃下保温 Cu
一天(24hr)后再测量
Cu
Cu-Zn
Cu 标记之间的距离缩短了0.0015cm
Cu
Cu-Zn
56天后
Cu

陆佩文版无机材料科学基础习题及解答第五章扩散

陆佩文版无机材料科学基础习题及解答第五章扩散

第五章扩散7-1解释并区分下列概念：（1）稳定扩散与不稳定扩散；（2）本征扩散与非本征扩散；（3）自扩散与互扩散；（4）扩散系数与扩散通量。

解：略7-2 浓度差会引起扩散，扩散是否总是从高浓度处向低浓度处进行?为什么?解：扩散是由于梯度差所引起的，而浓度差只是梯度差的一种。

当另外一种梯度差，比如应力差的影响大于浓度差，扩散则会从低浓度向高浓度进行。

7-3 欲使Ca2＋在CaO中的扩散直至CaO的熔点（2600℃）时都是非本质扩散，要求三价离子有什么样的浓度？试对你在计算中所做的各种特性值的估计作充分说明。

已知CaO肖特基缺陷形成能为6eV。

解：掺杂M3+引起V’’Ca的缺陷反应如下：当CaO在熔点时，肖特基缺陷的浓度为：所以欲使Ca2＋在CaO中的扩散直至CaO的熔点（2600℃）时都是非本质扩散，M3+的浓度为，即7-4 试根据图7-32查取：（1）CaO在1145℃和1650℃的扩散系数值；（2）Al2O3在1393℃和1716℃的扩散系数值；并计算CaO和Al2O3中Ca2＋和Al3＋的扩散活化能和D0值。

解：由图可知CaO在1145℃和1650℃的扩散系数值分别为，Al2O3在1393℃和1716℃的扩散系数值分别为根据可得到CaO在1145℃和1650℃的扩散系数的比值为：，将值代入后可得，Al2O3的计算类推。

7-5已知氢和镍在面心立方铁中的扩散数据为cm2/s和cm2/s，试计算1000℃的扩散系数，并对其差别进行解释。

解：将T=1000℃代入上述方程中可得，同理可知。

原因：与镍原子相比氢原子小得多，更容易在面心立方的铁中通过空隙扩散。

7-6 在制造硅半导体器体中，常使硼扩散到硅单晶中，若在1600K温度下，保持硼在硅单晶表面的浓度恒定（恒定源半无限扩散），要求距表面10－3cm深度处硼的浓度是表面浓度的一半，问需要多长时间（已知D1600℃＝8×10－12cm2/s；当时，）？解：此模型可以看作是半无限棒的一维扩散问题，可用高斯误差函数求解。

山大材料科学基础考研第五章

山大材料科学基础考研第五章
第五章 材料中的扩散—概述
扩散: 由于热运动而导致原子(分子)在介 质中迁移的现象.
微观: 热激活的原子通过自身热振动克服 束缚而迁移它处的过程.
宏观: 原子无序跃迁的统计结果.
主要研究内容:
扩散速率及其宏观规律; 扩散微观机理—扩散中原子的具体迁移方式.
2020/1/19
第五章 材料中的扩散
c t0
c0
x
c( x, t ) c0 (cs c0 )[1 erf ( 2
)] Dt
—扩散第二方程特解,式中:
erf ( x ) 2 Dt
—误差函数
适用条件: 半无限长棒
2020/1/19
第五章 材料中的扩散
12
§5.1 扩散定律及其应用
设为渗碳层深度(表面至给定浓度c*的距离),
设: 原子振动频率为; 具有跃迁条件的原子几率为
exp(-Gm/kT); 原子发生跃迁跳到邻近位置的几率 为z; 邻近位置中可接收扩散原子的位置的几率为
则原P子; 跃迁频率为:
zP exp( Gm )
kT
a. 间隙扩散: P≈1
2020/1/19
D 1 fa2 1 fa2 z exp( Sm )exp( Hm )
式中:
2020/1/19

M 0 cdx
第五章 材料中的扩散
样品表面单位面积 上Au198涂覆量.
11
§5.1 扩散定律及其应用
3) 恒定源扩散—扩散过程中工件表面浓度始 终为恒定值cs菲克第二定律(一维)
扩散方程在渗碳过程中的应用误差函数解
边界条件: c x0 cs
初始条件:
2020/1/19
第五章 材料中的扩散

物理冶金原理：5-扩散

物理冶金原理：5-扩散
D = Do × e-Q/RT Ln D = ln Do－Q/RT
Ln Do 斜率 k = Q/R 求出Q
Ln D
1/T
几种典型扩散现象
• 下坡扩散Down-Hill Diffusion ： • 上坡扩散 Up-Hill Diffusion:
•Down-Hill Diffusion
DA, DB
Vacancy Mechanism:
Diffusion of Substitutional Solute Atoms
空位机制：置换式溶质原子
（置换式原子的扩散就是空位的反向运动）
空位机制：置换式溶质原子
（置换式原子的扩散就是空位的反向运动）
间隙机制：间隙溶质原子 Interstitial Mechanism:
元素原子自扩散激活能与元素熔点的关系 Q = k . Tm
元素原子自扩散激活能与元素熔点的关系 Q = k . Tm
晶 体 结 构 的 影 响
影响扩散的因素
• 晶体缺陷密度： 空位浓度: 过饱和空位（固溶后不能停留太长时间） 位错及层错密度：是扩散的快速通道 晶界（晶粒尺寸）: 纳米材料（表面纳米化－渗氮） 相界:
• 温度足够高：能量起伏、热激活 • 时间足够长：大量原子微观上无规
则跃迁、物质的定向传输 • 存在驱动力（浓度梯度、化学位梯
度、应变能梯度、表面能梯度）
扩散对材料科学与工程的意义
材料合成、制备、加工、使用过程都是控制 扩散的过程：
• 固态相变与热处理过程： • 凝固加工（铸造、焊接、…….) • 成形热加工（热锻、热轧、热挤压, ……) • 高温力学行为及氧化、腐蚀等性能： • 粉末冶金烧结： • 表面化学热处理与表面渗工艺， • 扩散连接, …….

5 第五章 材料中的扩散

5 第五章 材料中的扩散

Ⅱ 壁厚为d的管的扩散
内壁半径为r1，外壁半径为r2。管长为L。 扩散物质从管内向管外扩散，稳定后，内壁浓度为C1， 外壁浓度为C2，显然扩散是轴对称，浓度仅和r有关。 由扩散第一定律，有：
c 2c 因为 0且 D 2 0 t x 2c 2c 则 D（ 2 ＋ 2 ) 0 x y c c c c c 且 (D ) (D ) 0 t x x y y 化为简单式为 2C＝0 d dc 化为柱坐标，则： （r ) 0 dr dr
根据以上情况，有初始条件为：t＝0，x<0，则C=C2 x>0，则C=C1 边界条件： t≥0，x＝－∞，则C=C2 x＝+∞，则C=C1
x , 将C＝f（x，t）换为C＝f（）单变量函数关系。 2 Dt c dc dc x dc 根据拉氏变换： ( ) t d t d 4t Dt 2t d 令＝
2. 扩散第二定律 ☻描 述
绝大多数扩散过程是非稳态扩散，在第一章图中，棒 中各处浓度梯度随扩散时间不断发生变化，因此，这种情 况下第一定律就不能应用了。
第二定律就是针对浓度梯度随时间变化的情况的。
☻ 推导过程
dx J1 J2
见左图，阴影部分的微小体积。 J1和J2分别为流入小体积和从小体积 中流出的扩散物质通量。两平面面积 均为A。
柱坐标方程的通解为 C=A+Blnr 当r、c分别为r1、c1及r2、c2时 c1＝A+Blnr1 c2 =A+Blnr2 c -c c -c 其中A＝c1－ 2 1 lnr1 B= 2 1 ln( r2 r ) ln( r2 r ) 1 1 r2 )+c ln( r ) c ln( 1 2 （c -c ） r r1 c=c1 + 2 1 ln( r r )= 1 ln( r2 r ) ln( r2 r ) 1 1 dc 1（c2 -c1） 管壁各处的浓度梯度为： = dt r ln( r2 ) r1 1（c2 -c1） 因为J＝D r ln( r2 ) r1 则扩散t时刻后，单位长度管子扩散的物质总量为： （c -c ） M＝2πrtJ=2πtD 2 1 ln( r2 r ) 1 实验测出M后（通过收集气体中C的减少量），可计算D。

材科基考点精讲(第5讲 扩散)

材科基考点精讲(第5讲 扩散)

扩散方程：
网学天地（） 版权所有
真题
1．简述柯肯达尔效应及物理本质。 答：柯肯达尔效应：在置换式固溶体的扩散过程中，放置在 原始界面上的标志物的位置发生了移动，移动速率与时间成 抛物线关系，这是由于两种组元不等量的原子交换造成的。 物理本质：对于置换型溶质原子的扩散，由于溶剂与溶质原 子的半径相差不会很大，原子扩散时必须与相邻原子间作置 换，两者的可动性大致趋于同一数量级，因此，必须考虑溶 质和溶剂原子不同的扩散速率。因此最终导致的结果就是， 原始界面的标志物会向扩散速率大的一侧移动。
网学天地（） 版权所有
（1）菲克第二定律 引出 如图所示设为单位面积A上取dx的单 元体，体积为Adx，在dt的时间内通 过截面1流入的物质量为j(x)·A·dt。
而通过截面2流出的物质量为：
在dt时间内，单元体中的积有量为：
网学天地（） 版权所有
《材料科学基础》考点精讲系列
扩散
主讲人：王 准
网学天地
主要内容 一、菲克定律 二、代位扩散 三、扩散中的热力学 四、扩散的微观机制 五、影响扩散系数的因素 六、反应扩散
网学天地（） 版权所有
扩散：由构成物质的微粒(离子、原子、分子)的热运动而产 生的物质迁移现象称为扩散。扩散的宏观表现是物质的定向 输送。 在固体材料中也存在扩散，并且它是固体中物质传输的唯一 方式。因为固体不能象气体或液体那样通过流动来进行物质 传输。即使在纯金属中也同样发生扩散，用参入放射性同位 素可以证明。 扩散在材料的生产和使用中的物理过程有密切关系，例如： 凝固、偏析、均匀化退火、冷变形后的回复和再结晶、固态 相变、化学热处理、烧结、氧化、蠕变等。
由高斯解求扩散7×107s后，表面（x＝0）硼浓度为：

扩散知识点总结

扩散知识点总结

扩散知识点总结一、什么是扩散扩散是一种物质在其他物质中自发迁移的现象。

在自然界中，物质的扩散现象无处不在，它在化学、生物、物理等领域都有着广泛的应用。

对于一个系统而言，如果某种物质在不同位置的浓度是不一样的，那么这种物质就会通过扩散的方式来达到平衡状态。

扩散的速率受到多种因素的影响，比如温度、浓度梯度、表面积等。

二、扩散的类型1. 质量扩散质量扩散是指物质在另一种物质中的自发迁移和分布的现象。

在化学反应的过程中，往往需要通过质量扩散来实现反应的进行。

质量扩散可以通过一系列的数学模型来描述，比如弥散方程等。

2. 热量扩散热量扩散是指热能在物质之间的自发传输。

在物体温度不均匀的情况下，热能会通过热传导的方式来达到热平衡。

热量扩散也是一种重要的物理现象，它对于热力学的研究具有重要的意义。

3. 动量扩散动量扩散是指流体中物质在横向方向上的自发传播。

在气体或液体中，由于分子热运动的不规则性，会导致物质在横向方向上的不均匀分布。

这种不均匀性通常会通过动量扩散来进行调整。

三、扩散的影响因素1. 温度温度对于扩散速率的影响非常显著。

温度升高会导致分子的热运动增加，从而促进扩散的发生。

因此，温度越高，扩散速率就越快。

2. 浓度梯度浓度梯度指的是物质在不同位置上的浓度差异。

当浓度差异越大时，分子之间的碰撞频率就会增加，从而促进扩散的进行。

因此，浓度梯度越大，扩散速率也就越快。

3. 界面界面的特性对于扩散也有着重要的影响。

比如，界面的面积越大，扩散速率就越快。

在固体表面或者气液界面上，扩散速率通常会更快。

4. 扩散介质的性质扩散介质的性质对于扩散速率也有着显著的影响。

比如，一些材料可能具有不同的扩散系数，这会导致它们在相同条件下的扩散速率不同。

四、扩散的应用1. 化学反应在化学反应的过程中，往往需要通过扩散来实现反应的进行。

比如，在两种反应物中需要通过扩散来实现相互碰撞，从而进行反应。

2. 材料工程在材料工程中，扩散是一个非常重要的现象。

材科基考点强化(第5讲 扩散)

材科基考点强化(第5讲 扩散)

主要考点考点1：菲克第一定律考点2：菲克第二定律考点3：影响扩散速率的因素考点4：扩散机制考点5：上坡扩散考点6：反应扩散考点7：柯肯达尔效应考点8：综合考点1：菲克第一定律例1（名词解释）：稳态扩散。

例2：写出菲克第一定律的数学表达式，并注明表达式中各参量的含义及单位。

例3：扩散第一定律的应用条件是什么对于浓度梯度随时间变化的情况，能否应用用扩散第一定律 答：扩散第一定律应用条件为稳态扩散，即质量浓度不随时间而变化。

非稳态扩散情况下通常也可应用扩散第一定律，但必须进行修正使之大致符合直线的情况下才可使用。

考点2：菲克第二定律…例1：考虑扩散系数为常量的半无限的一维扩散，保持扩散源的浓度为2C 不变；保持扩散介质中扩散物质的初始浓度为1C ，且均匀分布。

这时扩散介质中扩散物质的浓度随扩散时间和扩散距离的变化可用下式来表示（ ）。

A ．()2,1exp2C C x t ⎡⎤=-⎢⎥⎣⎦B ．()112,()1exp C x t C C C ⎡⎤=+--⎢⎥⎣⎦C ．()1212,1exp22C C C C C x t ⎡⎤--=+-⎢⎥⎣⎦例2：已知碳在γ-Fe 中的扩散常数50 2.010D -=⨯ 2m /s ，扩散激活能314010J/mol Q =⨯，要想得到与在927℃时渗碳10h 的相同厚度，则在870℃渗碳需要多长时间（忽略不同温度下碳在γ-Fe 中溶解度的不同）例3：生产中，在930℃对20号钢零件进行气体渗碳，渗碳碳势为%，零件的技术要求是渗碳层含碳量不低于%。

（1）渗碳2h 后，估算渗碳层的深度（2）若要求渗碳层的深度达到0.5mm ，渗碳时间应为多少小时（930℃时碳在γ-Fe 中的扩散系数为1221610m /s -⨯）C C 1.0%w =，并将工件中碳浓度为C 0.4%w =处至表面的距离x 定义为渗碳层深度。

已知渗碳1h 后，渗碳层深度为0.12mm ，若要求渗碳层深度达到0.48mm ，计算共需渗碳多长时间。

材料科学基础-扩散

材料科学基础-扩散

交换机制
环形机制
空位机制
松弛机制
简单间隙机制
推填子间隙机制
非共线推填子
哑铃间隙扩散
挤列扩散机制
哑铃转位扩散
三、固态金属扩散的条件 ① 存在扩散驱动力——化学位梯度（不是浓度梯 度）；此外，化学位梯度、温度梯度、应力梯度、 电场梯度、磁场梯度等也可以引起扩散(热力学) ② 扩散原子与基体固溶——（前提条件） ③ 温度足够高——温度越高，跃迁几率大（动力学） ④ 足够长时间——扩散1mm距离，必须跃迁亿万次 （宏观迁移的动力学条件）
四、固态扩散的分类
通常扩散伴随浓度变化, 且高浓度→低浓度，但 实际上：并非一定如此
例如： 纯金属以及均匀固溶体中晶粒的长大(晶界的 迁移)——扩散中无浓度变化； 又如： 奥氏体转变为珠光体时： 奥氏体转变为渗碳体时碳由低浓度的奥氏体向 高浓度的渗碳体扩散 ——扩散的种类（类型）不同
根据扩散中是否发生浓度变化分类
固态扩散是大量原子无序跃迁的统计结果
若晶体周期场的势能曲线是倾斜的，导致向右跳跃 的原子数大于反向跳回的原子数，大量原子无序迁跃 的统计结果，即造成了物质的定向输送——扩散
设存在纯金属8列原子，中间四列原子含有4个同位素原子，每 个原子平均跃迁一次后出现的同位素原子分布情况。
二、扩散机制 扩散不仅由原子热运动所控制，而且还要受具体的 晶体结构所制约；即扩散机制随晶体结构不同而变化 两种主要机制： (1) 空位扩散—主要机制 如：自扩散，置换扩散 (2) 间隙扩散—小原子 如：碳在奥氏体中扩散
第八章
扩散
扩散是物质中原子（分子）的迁移现象，是物质 传输的一种方式。例如：熔炼，偏析，均匀化，氧 化等过程 气、液 态——对流、扩散、（带电粒子迁移） 固态 ——扩散（唯一机制）

第五章材料中的扩散ppt

第五章材料中的扩散ppt

The Fundamental of Materials Science
Chapter 5 Diffusion
Dr. R.S. Yang 2019/7/22
菲克第二定律
当扩散过程是非稳态扩散，即扩散过程中各点的浓度随时间 变化，则菲克第一定律将不适用，此时需要菲克第二定律。
dx
沿扩散方向取一个小的体积元，其厚度为
dx，截面积为A。设dt时间内流入、流出此
J1
J2
A
小体积元的扩散通量分别为J1和J2，则：
流入体积元内物质的量为： J 1 A d t
流出体积元内物质的量为： J 2 A d t
∴体积元内浓度的改变为： CJ1AdtJ2Adt
Adx
C J1 J2 t dx
dx很 小 ， J2J1 J xdx
互扩散：原子通过进入对方元素晶体点阵而导致的扩散。有浓度 变化。
（2）根据扩散方向
下坡扩散：原子由高浓度处向低浓度处进行的扩散。 上坡扩散：原子由低浓度处向高浓度处进行的扩散。
（3）根据是否出现新相
原子扩散：扩散过程中不出现新相。 反应扩散：由此导致形成一种新相的扩散。
The Fundamental of Materials Science
Chapter 5 Diffusion
Dr. R.S. Yang 2019/7/22
§5.0 概述
扩散机制：
间隙原子的扩散：← 间隙式扩散机制 置换式固溶体中的扩散：← 空位扩散机制
扩散问题的研究方法：
表象理论：通过一些宏观测量参数来描述扩散过程； 原子理论：通过研究扩散的微观机制来研究扩散过程。
0
x 易知：erf()erf()(奇函数)
erf()1

5材料导论第五扩散

5材料导论第五扩散
Diffusion is a process of the transfer of mass. The
phenomenon of material transport by atomic motion.
From an atomic perspective, diffusion more, there are more empty interstitial positions than vacancies; hence, the probability of interstitial atomic movement is greater than for vacancy diffusion.
Comparing interstitial diffusion with vacancy diffusion in metal alloys
In most metal alloys, interstitial diffusion occurs much more rapidly than diffusion by the vacancy mode, since the interstitial atoms are smaller, and thus more mobile.
金属中单个原子的运动时毫无规则的，若
从大量原子统计来看，可能存在定向的原子扩
散流。
1). Diffusion flux (J)扩散通量
The rate of mass transfer is frequently expressed as a diffusion flux (J) , defined as the mass (or, equivalently the number of atoms) M diffusing through and perpendicular to a unit cross sectional area of solid per unit of time.

材料科学基础5 材料中的扩散

材料科学基础5 材料中的扩散

• 令某种复合缺陷的浓度为cf，则： • cf=n/N=exp(ΔGf/2kT) • =exp(ΔSf/2k)exp(-ΔHf/2kT) • 如果扩散以空位机制进行，则本征扩散系数可表 示为： • D=fα2νzexp[(ΔSf+2ΔSm)/2k]· • exp[(ΔHf+2ΔHm)/2kT]/6 • =D0exp[(ΔHf+2ΔHm)/2kT]
• 空位扩散 • 设空位浓度为cν，由统计热力学知： • cν=exp(-ΔGf/kT)=exp(ΔHf/kT)exp(ΔSf/k) • 式中ΔGf为空位形成自由能；ΔSf为空位形 成熵；ΔHf为空位形成焓。 D=fα2νzexp[(ΔSf+ΔSm)/k]exp[(ΔHf+ • ΔHm)/kT]=D0exp[(ΔHf+ΔHm)/kT]
• 非晶态固体中的扩散 • 非晶态固体的扩散能力与原子排列紧密 程度相关。通常非晶态固体中的原子排 列没有晶态的致密，跃迁频率相对较高， 因此迁移率更大，扩散激活能较低，扩 散系数较高。
• 在聚合物中，小分子，原子或离子可在 大分子链的间隙中扩散。与晶态聚合物 相比，玻璃态聚合物中更容易发生扩散。 某些聚合物还具有选择性扩散特性。被 用于各种膜分离技术，如稀有元素富集 和海水淡化。
（3）扩散激活能（总结） 间隙扩散扩散激活能与扩散系数的关系 D=D0exp(-Q/RT) D0：扩散常数。 空位扩散激活能与扩散系数的关系 D=D0exp(-△E/kT) △E=△Ef(空位形成功)+△Em（空位迁 移激活能）。
3 扩散的驱动力与上坡扩散 （1）扩散的驱动力 对于多元体系，设n为组元i的原子数， 则在等温等压条件下，组元i原子的自由能可 用化学位表示：
• 即：δ/2Dt=const, 或： • δ=αDt 这里是与cs和c*有关的常数。 • 渗碳层深度与Dt成正比是制定渗碳工艺 的理论依据。

第5章《材料科学》 扩散讲解

第5章《材料科学》 扩散讲解

§5.1.1 扩散定律
第一定律推导：
如右图所示，设有一金属棒，沿x轴方向存在着浓度梯度，并设： (1)有两个垂直于X轴方向的单位面积的原子平面l和2，其面间距离 为dx。 (2)当温度和浓度恒定时，每一扩散原子的平均跃迁领率为f。 (3)C1和C2分别代表平面l和平面2的扩散原子体积浓度．
由假设可知：
§5.1.2 扩散定律的应用
② 扩散的抛物线规律：由式（3.11）和（3.12）看出，如果要求距 焊接面为x处的浓度达到C，则所需要的扩散时间可由下式计算
x K Dt
（3.13）
式中，K是与晶体结构有关的常数。此关系式表明，原子的扩散距离与时间呈 抛物线关系，许多扩散型相变的生长过程也满足这种关系。
c
x
Cp:平均成分；A0：振幅Cmax- Cp；λ:晶粒间距的一半。 例：对于均匀化退火，若要求晶粒中心成分偏析振幅降低 到1/100,则：
[C(λ／2,t)- Cp]/( Cmax- Cp)=exp(-π2Dt/λ2)=1/100。 （4）高斯解(薄膜解） Cx=(M/√πDT)exp(-x2/4Dt) 适用条件：限定扩散源、衰减薄膜源（扩散物质总量M不变；t=0,c=0) 例：半导体Si中P的掺杂。
令
1 1 1 1 dC f (n1 n2 ) f (C1 C2 )dx (C2 C1)dx f (dx)2 2 2 2 2 dx dC 1 2 J D ( ) D f (dx) 并代入上式，有： dx 2 J
同时可写出y、z方向的菲克第一定律表达式。
§5.1.1 扩散定律

2
A1 A2
解出积分常数
A1
C1 C 2

, A2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

主要考点
考点1：菲克第一定律
考点2：菲克第二定律
考点3：影响扩散速率的因素
考点4：扩散机制
考点5：上坡扩散
考点6：反应扩散
考点7：柯肯达尔效应
考点8：综合
考点1：菲克第一定律
例1（名词解释）：稳态扩散。

例2：写出菲克第一定律的数学表达式，并注明表达式中各参量的含义及单位。

例3：扩散第一定律的应用条件是什么？对于浓度梯度随时间变化的情况，能否应用用扩散第一定律？
答：扩散第一定律应用条件为稳态扩散，即质量浓度不随时间而变化。

非稳态扩散情况下通常也可应用扩散第一定律，但必须进行修正使之大致符合直线的情况下才可使用。

考点2：菲克第二定律
例1：考虑扩散系数为常量的半无限的一维扩散，保持扩散源的浓度为2C 不变；保持扩散介质中扩
散物质的初始浓度为1C ，且均匀分布。

这时扩散介质中扩散物质的浓度随扩散时间和扩散距离的变
化可用下式来表示（ ）。

A ．(
)2,1exp 2C C x t ⎡⎤=-⎢⎥⎣⎦
B ．(
)112,()1exp C x t C C C ⎡⎤=+--⎢⎥⎣
⎦ C ．(
)1212,1exp 22C C C C C x t ⎡⎤--=+-⎢⎥⎣⎦
例2：已知碳在γ-Fe 中的扩散常数50 2.010D -=⨯ 2m /s ，扩散激活能314010J/mol Q =⨯，要想得到与在927℃时渗碳10h 的相同厚度，则在870℃渗碳需要多长时间？（忽略不同温度下碳在γ-Fe 中溶解度的不同）
例3：生产中，在930℃对20号钢零件进行气体渗碳，渗碳碳势为1.2%，零件的技术要求是渗碳层含碳量不低于0.6%。

（1）渗碳2h 后，估算渗碳层的深度？（2）若要求渗碳层的深度达到0.5mm ，渗碳时间应为多少小时？（930℃时碳在γ-Fe 中的扩散系数为1221610m /s -⨯）
C
C 1.0%w =，并将工件中碳浓度为C 0.4%w =处至表面的距离x 定义为渗碳层深度。

已知渗碳1h 后，
渗碳层深度为0.12mm ，若要求渗碳层深度达到0.48mm ，计算共需渗碳多长时间。

例5：为改善钛合金的切削加工性能，研制了一种新加工工艺：渗氢处理+机械加工+脱氢处理。

已知某钛合金构件在800℃真空脱氢1小时其距表面0.05mm 处的性能符合规定要求。

为进一步降低该构件的热处理变形，拟将该合金构件在700℃处理，问处理多少时间在距表面0.1mm 处将达到上述相同规定要求？并分析氢在钛合金中的扩散能力。

设氢在该钛合金的扩散激活能为16.62KJ/mol ，扩散常数D 0=12810cm /s -⨯。

考点3：影响扩散速率的因素
例1（名词解释）：扩散激活能。

例2（解释名词）：扩散系数。

例3：“升高温度将加快原子的扩散，其原因主要是温度的升高降低了扩散激活能。

”试问此判断正确与否，为什么？
例4：杂质掺杂从哪几个方面影响扩散系数？
例5：固态金属中原子扩散的最快路径是（ ）。

A ．晶内扩散
B ．晶界扩散
C ．位错扩散
D ．表面扩散
例6：扩散系数与温度的关系式是_________。

在高温阶段和低温阶段，扩散系数较大的是_________。

例7：碳在铁素体及奥氏体中的扩散系数为什么存在很大的区别？
例8：常通过向钢的表层深入某些原子来改善钢的表面性能，试问若分别向钢的表层渗入碳原子和铬原子，在相同的试渗工艺下，哪一种原子的渗入深度更大，为什么？
例9：有两块化学成分相同的固溶体合金，一块未经塑性变形，一块经过了冷塑性变形。

试问溶质原子在那一块合金中的扩散更为容易，为什么？
例10：（1）已知Zn 在Cu 中扩散时，扩散系数522.110m /s D -=⨯，激活能51.710J/mol Q =⨯，求820℃时在中的扩散系数；（2）讨论影响金属材料扩散的因素。

考点4：扩散机制
例：在铁的晶体中固溶有碳原子和镍原子，问在同一温度下，碳原子和镍原子各以什么机制进行扩散，为什么？其中哪一种原子具有更大的扩散系数，为什么？
考点5：上坡扩散
例1（名词解释）：上坡扩散。

例2：上坡扩散产生的原因分析。

考点6：反应扩散
例1（名词解释）：反应扩散。

例2：碳质量分数为0.1%的低碳钢工件，置于碳质量分数为1.2%的渗碳气氛中，在920℃下进行渗碳，通常渗碳数小时后即可达到工艺要求。

（1）画出：①渗碳结束时；②渗碳结束后缓慢冷却至室温时，这两种情况下工件表层至心部平衡组织示意图；（2）试说明在渗碳温度不变的前提下，要使工件达到相同的渗碳层深度，可采取哪些措施减少渗碳时间？
例3：纯铁在950℃渗碳，表面浓度达到0.9%C ，缓慢冷却后，重新加热到800℃继续渗碳，试列出：
（1）达到800℃时，工件表面到心部的组织分布区域示意图；（2）在800℃长时间渗碳后（碳气氛为1.5%C ），工件表面到心部的组织分布区域示意图，并解释组织形成的原因；（3）在800℃长时间渗碳后缓慢冷却至室温的组织分布区域示意图。

例4：纯铁试样在800℃进行气体渗碳，已知表层已出现新相γ，设与α相平衡的γ相的碳浓度为
C 2，与Fe 3C 平衡的γ相的碳浓度为C 3，与γ相平衡的α相的碳浓度为C 1，若渗碳t 小时，试画出渗碳温度下的碳浓度分布曲线及试样由表面至心部的组织示意图；若渗碳后缓冷，请画出室温下的组织示意图。

考点7：柯肯达尔效应
例1：置换扩散与间隙扩散的扩散系数有何不同？在扩散偶中，如果是间隙扩散，是否会发生柯肯达尔效应？为什么？
例2：在柯肯达尔扩散实验中，一个二元系统，A 组元的原子百分比浓度为0.4，两个组元的实际扩散系数分别为72A 10cm /s D -=和82B 910cm /s D -=⨯，在标志界面处A 组元的成份随距离的变化率为2.0cm -1，则互扩散系数及标志移动速度分布为（ ）。

A ．829.610cm /s -⨯和8210cm/s -⨯
B ．829.610cm /s -⨯和8110cm/s -⨯
C ．829.410cm /s -⨯和8210cm/s -⨯
例3：如图所示，由A 组元棒和B 组元棒焊接成的扩散偶，并在焊缝处用Mo 丝做标记，在773K 扩散足够的时间，试问：（1）标记在焊接面何侧？（2）扩散中的空位最终聚集在何侧？已知A 组元在B 组元构成的晶体中的扩散常数（D 0）和激活能（Q ）分别为522.110m /s -⨯，51.710J/mol ⨯；而B 组元在A 组元构成的晶体中的扩散常数（D 0）和激活能（Q ）分别为520.810m /s -⨯，51.410J/mol ⨯。

考点8：综合
例1：下列有关固体中扩散的说法中，正确的是（ ）。

A ．原子扩散的驱动力是存在着浓度梯度
B ．空位扩散是指间隙固溶体中的溶质原子从一个间隙跳到另一个间隙
C ．晶界上点阵畸变较大，因而原子迁移阻力较大，所以比晶内的扩散系数要小
D ．成分均匀的材料中也存在着扩散
解析：A 中驱动力应为化学势梯队，因此错。

B 中的解释是间隙扩散机制，不是空位扩散机制，因此错。

C 中晶界上扩散系数要比晶内更大，因此错。

例2：在870℃下渗碳比927℃渗碳淬火变形小，可得到较细的晶粒。

碳在γ-Fe 中的扩散系数520 2.010m /s D -=⨯，激活能140kJ/mol Q =，8.314J/K.mol R =。

请计算：（1）870℃下和927℃下碳在γ-Fe 中的扩散系数；（2）在870℃得到与927℃渗碳10h 相同结果所需时间？（3）若规定0.3%C 作为渗碳层厚度的量度，在927℃渗碳10h ，其渗碳层厚度为870℃渗碳10h 的多少倍？
例3：对含有0.1%C 的钢进行表面渗碳增强处理，渗碳时将钢置于浓度为1.2%C 的气氛中，在高温下通过扩散达到进入钢材体内的目的。

为了获得最佳应用性能，在钢表面以下0.2cm 处必须达到浓度为0.45%C ，扩散激活能为32900cal/mole ，气体常数 1.987cal/(mol K)R =⋅。

若该钢材的扩散常数D 0为0.115cm 2/s 。

试求：（1）1100℃时的扩散系数；（2）扩散所需时间与扩散温度的函数关系；（3）分解计算800℃、900℃、1000℃、1100℃和1200℃温度下所需的扩散时间并以此作出扩散时间与温度之间的关系简图。

β 0 1 2 3 4 5 6 7 8 9 0.7 0.6778 0.6847 0.6914 0.6981 0.7047 0.7112 0.7175 0.7238 0.7300 0.7361
（注：文档可能无法思考全面，请浏览后下载，供参考。

可复制、编制，期待你的好评与关注）。