连续系统零极点分布与频响特性的关系

增加零极点以及零极点分布对系统的影响一般说来，系统的极点决定系统的固有特性，而零点对于系统的暂态响应和频率响应会造成很大影响。

以下对于零极点的分布研究均是对于开环传递函数。

零点一般是使得稳定性增加，但是会使调节时间变长，极点会使调节时间变短，是系统反应更快，但是也会使系统的稳定性变差。

在波特图上反应为，增加一个零点会在幅频特性曲线上增加一个+20db/10倍频的曲线，幅频曲线上移，增加一个极点，会在幅频特性曲线上增加一个-20db/10倍频的曲线，幅频曲线下移。

在s左半平面增加零点时，会增加系统响应的超调量，带宽增大，能够减小系统的调节时间，增快反应速度，当零点离虚轴越近，对系统影响越大，当零点实部远大于原二阶系统阻尼系数ξ时，附加零点对系统的影响减小，所以当零点远离虚轴时，可以忽略零点对系统的影响。

从波特图上来看，增加一个零点相当于增加一个+20db/10倍频的斜率，可以使的系统的相角裕度变大，增强系统的稳定性。

在s右半平面增加零点，也就是非最小相位系统，非最小相位系统的相位变化范围较大，其过大的相位滞后使得输出响应变得缓慢。

因此，若控制对象是非最小相位系统，其控制效果特别是快速性一般比较差，而且校正也困难。

对于非最小相位系统而言，当频率从零变化到无穷大时，相位角的便变化范围总是大于最小相位系统的相角范围，当ω等于无穷大时，其相位角不等于-（n-m）×90º。

非最小相位系统存在着过大的相位滞后，影响系统的稳定性和响应的快速性。

在s左半平面增加极点时，系统超调量%pσ减小，调整时间st(s)增大，从波特图上看，s左半平面增加一个极点时，会在幅频特性曲线上增加一个-20db/10倍频的曲线，也就意味着幅频特性曲线会整体下移，导致相角域度减小，从而使得稳定性下降。

当极点离原点越近，就会增大系统的过渡时间，使得调节时间增加，稳定性下降，当系统影响越大当极点实部远大于原二阶系统阻尼系数ξ时，附加极点对系统的影响减小，所以当极点远离虚轴时可以忽略极点对系统的影响。

实验名称：连续系统的零极点及频率响应特性报告人：姓名班级学号一、实验目的1、掌握系统函数零极点的定义；2、用MA TLAB实现部分分式展开；3、掌握零极点与频率响应的关系；4、掌握极点与系统稳定性的关系。

二、实验内容及运行结果1、已知下列系统函数H（s）或状态方程，求及其零极点，并且画出零极点图，试判断系统是否稳定，根据零极点位置推导单位冲激响应的形式，求解系统的冲激响应h(t)和频率响应H（w）。

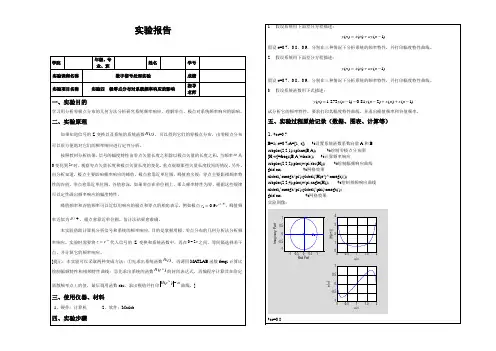
(1)num=[1 0 1]; %分子系数，按降幂顺序排列den=[1 2 5]; %分母系数，按降幂顺序排列[z,p]=tf2zp(num,den); %求零点z和极点pfigure(1)zplane(z,p) %作出零极点图sys=tf(num,den);poles=roots(den)figure(2);pzmap(sys)t=0:0.02:10;h=impulse(num,den,t); %绘制冲激响应曲线figure(3);plot(t,h)title('Impulse Respone')[H,w]=freqs(num,den); %绘制频率响应曲线figure(4);plot(w,abs(H))xlabel('\omega')title('Magnitude Respone')poles =-1.0000 + 2.0000i-1.0000 - 2.0000i系统的稳定性和频响特点：由于系统函数的极点位于s虚轴，故系统稳定；并且单位冲激响应是等幅振荡（单位阶跃）信号。

(2)num=[3 -9 6]; %分子系数，按降幂顺序排列den=[1 2 2]; %分母系数，按降幂顺序排列[z,p]=tf2zp(num,den); %求零点z和极点pfigure(1)zplane(z,p) %作出零极点图sys=tf(num,den);poles=roots(den)figure(2);pzmap(sys)t=0:0.02:10;h=impulse(num,den,t); %绘制冲激响应曲线figure(3);plot(t,h)title('Impulse Respone')[H,w]=freqs(num,den); %绘制频率响应曲线figure(4);plot(w,abs(H))xlabel('\omega')title('Magnitude Respone')poles =-1.0000 + 1.0000i-1.0000 - 1.0000i系统的稳定性：由于系统函数的极点位于s右半平面，故系统不稳定；单位冲激响应是随时间增长的信号。

连续系统零极点分布与频响特性的关系（答案在下方）1. 连续系统零极点图的画法pzplot()函数可用来绘制连续系统的零极点图，具体用法如下：pzplot(SYS) 计算LTI 模型SYS 的零点和极点并绘制零、极点图。

其中SYS 的产生可以采用传递函数法：SYS=tf(b,a)，b 和a 分别为系统函数的分子多项式和分母多项式系数矩阵。

例1：系统函数为()232251241420s s H s s s s ++=+++，完成一幅适当标注的零极点图。

解：MATLAB 代码如下：b=[2 5 12]; a=([1 4 14 20]); SYS=tf(b,a); pzplot(SYS);系统的零极点图如图1所示。

图1 例1系统的零极点图P ole-Zero MapReal AxisI m a g i n a r y A x i s2. 由系统的零极点分布决定系统的频率响应特性稳定的连续时间系统的频率响应特性可以由系统函数得到()()()()()()11j j 11j j j mmjjj j s ωs ωnniii i s z ωz H ωH s KKs p ωp ======--===--∏∏∏∏ (1)令分子中每一项j j ejψj j ωz N -=,分母中每一项j j e iθi i ωp M -=，则 ()1212j j j 12j j j 12e e e j e e e mnψψψm θθθn N N N H ωKM M M =L L (2) ()1212j mnN N N H ωKM M M =L L (3)()()()1212m n ωψψψθθθφ=++-++L L (4)分析频率响应特性的方法： 1.()()j j s ωH ωH s ==，带入数值，得到()j H ωω～的分布；2.根据零极点图中零极点的分布，用几何的方法定性判断系统的频率响应特性；3.对模拟系统，MATLAB 信号处理工具箱提供了freqs()函数是用来求取模拟滤波器的频率响应。

连续系统零极点分布与频响特性的关系1. 连续系统的表示()()()()()()()12121212b b a a n n b n n a b s b s b n H s a s a s a n ----+++=+++通过下面例子，说明B, A 矩阵的写法：(a) ()20.532s H s s s +=++ [1,0.5];B = [1,3,2];A = (b) ()2132H s s s =++ [1];B = [1,3,2];A =(c) ()232sH s s s =++ [1 ];0B = [1,3,2];A =注意：(c)的B 矩阵由于缺少常数项，故补了一个0。

2.连续系统零极点图的画法pzplot()函数可用来绘制连续系统的零极点图，具体用法如下：pzplot(SYS) 计算LTI 模型SYS 的零点和极点并绘制零、极点图。

其中SYS 的产生可以采用传递函数法：SYS=tf(b,a)，b 和a 分别为系统函数的分子多项式和分母多项式系数矩阵。

例1：系统函数为()232251241420s s H s s s s ++=+++，完成一幅适当标注的零极点图。

解：MATLAB 代码如下：b=[2 5 12]; a=([1 4 14 20]); % 创建系统模型 SYS=tf(b,a); % 绘制零极点图 pzplot(SYS);系统的零极点图如图1所示。

图1 例1系统的零极点图3. 由系统的零极点分布决定系统的频率响应特性MATLAB 信号处理工具箱提供了freqs()函数是用来求取连续系统的频率响应。

具体函数的用法是：H=freqs(B, A, W) 返回模拟滤波器的频率响应()j H ω，即复数频率响应矩阵H ，其中的B 、A 是已知系统的传递函数模型，W 为已选定的频率点。

如果直接使用freqs(B, A, W)，则直接绘制幅度响应和相位响应曲线，不返回任何值。

如果缺省频率范围W ，函数将自动选用一组200个频率点范围。