常量与变量练习题

20.1常量和变量练习题一．选择题1．某人要在规定的时间内加工100个零件，如果用n表示工作效率，用t表示规定的时间，下列说法正确的是（）A．数100和n，t都是常量B．数100和n都是变量C．n和t都是变量D．数100和t都是变量2．一本笔记本3元，买x本需要y元，在这一问题中，自变量是（）A．笔记本B．3C．X D．y3．李师傅到单位附近的加油站加油，如图是所用的加油机上的数据显示牌，则其中的常量是（）A．金额B．数量C．单价D．金额和数量4．在圆的面积公式S＝πR2中，常量与变量分别是（）A．2是常量，S、π、R是变量B．π是常量，S、R是变量C．2是常量，R是变量D．2是常量，S、R是变量5．将一个底面直径是10厘米，高为36厘米的圆柱体锻压成底面直径为20厘米的圆柱体，在这个过程中不改变的是（）A．圆柱的高B．圆柱的侧面积C．圆柱的体积D．圆柱的底面积6．如果用总长为60m的篱笆围成一个长方形场地，设长方形的面积为S（m2），周长为p（m），一边长为a（m），那么S，p，a中是变量的是（）A．S和p B．S和a C．p和a D．S，p，a7．某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据（如下表）：温度/℃﹣20﹣100102030声速/m/s318324330336342348下列说法错误的是（）A．在这个变化中，自变量是温度，因变量是声速B．温度越高，声速越快C．当空气温度为20℃时，声音5s可以传播1740m D．当温度每升高10℃，声速增加6m/s8．一辆汽车以50km/h的速度行驶，行驶的路程s（km）与行驶的时间t（h）之间的关系式为s＝50t，其中变量是（）A．速度与路程B．速度与时间C．路程与时间D．三者均为变量9．2005年第一期国债存期3年，年利率规定为p%，不计复利，若购买x元这一期国债，三年后可得利息y＝3px%元．在这里，y，p，x中，变量有（）A．0个B．1个C．2个D．3个10.骆驼被称为“沙漠之舟”，它的体温是随时间的变化而变化的，在这一问题中，因变量是（）A．沙漠B．体温C．时间D．骆驼11．下列说法正确的是（）A．内错角相等B．一个角的补角一定大于它本身C．任何数的0次方都等于1 D．对于圆的周长公式C＝2πR，R是自变量，C是因变量12．以固定的速度v0（米/秒）向上抛一个小球，小球的高度h（米）与小球的运动的时间t（秒）之间的关系式是h＝v0t﹣4.9t2，在这个关系式中，常量、变量分别为（）A．4.9是常量，t、h是变量B．v0是常量，t、h是变量C．v0、﹣4.9是常量，t、h是变量D．4.9是常量，v0、t、h是变量13．世纪花园居民小区收取电费的标准是0.6元/千瓦时，当用电量为x（单位：千瓦时）时，收取电费为y（单位：元）．在这个问题中，下列说法中正确的是（）A．x是自变量，0.6元/千瓦时是因变量B．y是自变量，x是因变量C．0.6元/千瓦时是自变量，y是因变量D．x是自变量，y是因变量14．一个长方形的面积是10cm2，其长是acm，宽是bcm，下列判断错误的是（）A．10是常量B．10是变量C．b是变量D．a是变量15．某款贴图的成本价为1.5元，销售商对其销量与定价的关系进行了调查，结果如下：定价/元 1.8 2 2.3 2.5 2.8 3销量/个2025 3026 2218你认为其因变量为（）A．成本价B．定价C．销量D．以上说法都不正确16．以下是关于常量和变量的说法：（1）在一个变化过程中，允许出现多个变量和常量；（2）变量就是变量，它不可以转化为常量；（3）变量和常量是相对而言的，在一定条件下可以相互转化；（4）在一个变化过程中，变量只有2个，常量可以没有，也可能有多个．其中正确的说法有（）A．1个B．2个C．3个D．4个二．填空题17．某种树木的分枝生长规律如图所示，则预计到第6年时，树木的分枝数为，其中自变量是，因变量是．年份第一年第二年第三年第四年第五年分枝数1123518．完成以下问题：（1）某人持续以a米/分钟的速度t分钟内跑了s米，其中常量是，变量是；（2）在t分钟内，不同的人以不同的速度a米/分钟跑了s米，其中常量是，变量是；（3）s米的路程不同的人以不同的速度a米/分钟各需跑t分钟，其中常量是，变量是；19．汽车行驶的路程s、行驶时间t和行驶速度v之间有下列关系：s＝vt．如果汽车以每时60km的速度行驶，那么在s＝vt中，变量是，常量是；如果汽车行驶的时间t规定为1小时，那么在s＝vt中，变量是，常量是；如果甲乙两地的路程s为200km，汽车从甲地开往乙地，那么在s＝vt中，变量是，常量是．三．解答题20．在一次实验中，小强把一根弹簧的上端固定，在其下端悬挂物体．下面是他测得的弹簧的长度y与所挂物体的质量x的一组对应值：所挂物体的质量x/kg012345弹簧的长度y/cm202224262830（1）上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？（2）填空：①当所挂的物体为3kg时，弹簧长是．不挂重物时，弹簧长是．②当所挂物体的质量为8kg（在弹簧的弹性限度范围内）时，弹簧长度是．。

《20.1常量与变量》同步练习1.学校计划买100个乒乓球，买乒乓球的总费用W(元）与单价n(元/个）的关系式W=100n 中（ ）A.100是常量，W ，n 是变量B.100，W 是常量，n 是变量C.100，n 是常量，W 是变量D.无法确定2.一长方体的宽为b(定值），长为x(x>b ），高为h ，体积为V ，则V=bxh ，其中变量是 ( ）A.xB.hC.VD.x ，h ，V3.下列说法正确的是 ( ）A.常量是指永远不变的量B.具体的数一定是常量C.字母一定表示变量D.球的体积公式334r V π=中，变量是π，r 4.下表是某报纸公布的世界人口数据情况，表中的变量 ( ）A.仅有一个，是时间(年份）B.仅有一个，是人口数C.有两个，一个是人口数，另一个是时间(年份）D.一个也没有5.完成以下问题：(1）某人持续以a 米/分的速度t 分钟内跑了s 米，其中常量是 ，变量是 ；(2）在t 分钟内，不同的人以不同的速度a 米/分跑了s 米，其中常量是 ，变量是 ；(3）s 米的路程，不同的人以不同的速度a 米/分各需跑t 分钟，其中常量是 ，变量是 ；(4）根据以上叙述，写一句关于常量与变量的结论： 。

6.我国是一个严重缺水的国家，我们都应该倍加珍惜水资源，节约用水。

据测试，拧不紧的水龙头每秒会滴下2滴水，每滴水约0.5毫升。

小燕子同学在洗手时，没有拧紧水龙头，当小燕子离开x(时）后水龙头滴了y(毫升）水。

在这段文字涉及的量中，哪些是常量，哪些是变量？7.按如图所示的方式摆放餐桌和椅子。

用x 来表示餐桌的张数，用y 来表示可坐人数.(1）题中有几个变量？(2）你能写出两个变量之间的关系吗？8.分析并指出下列关系中的变量与常量。

(1）球的表面积S cm 2与球的半径R cm 的关系式是S=4πR 2；(2）以固定的速度v 0米/秒向上抛一个小球，小球的高度h 米与小球运动的时间t 秒之间的关系式是h=v 0t-4.9t 2；(3）一物体自高处自由落下，这个物体运动的距离h m 与它下落的时间t s 的关系式是221gt h (其中g 取9.8 m/s 2）； (4）已知橙子每千克的售价是 1.8元，则购买数量w 千克与所付款x 元之间的关系式是x=1.8w 。

5.1 常量与变量1.在圆的周长计算公式C=2πR 中，常量与变量分别是( ).A.2是常量,C,π,R 是变量B.2π是常量,C,R是变量C. C,2是常量,R 是变量D.2是常量,C,R 是变量2.某人要在规定的时间内加工100个零件，则关于工作效率η与时间t之间的关系，下列说法中正确的是( ).A.数100 和η,t都是变量B.数100 和η都是常量C.η和t是变量D.数100 和t都是常量3.一期国债期限规定为3年，年利率规定为p%，不计复利.若购买x元这一期国债，三年后可得利息y=3px%元.在y,p,x中,变量有( ).A.0个B.1个C.2个D.3个4.甲、乙两地相距50km，若一辆汽车以50km/h的速度从甲地开往乙地，则汽车距乙地的路程s(km)关于行驶的时间t(h)的关系式s=50-50t(0≤t≤1)中,常量有( ).A.1个B.2个C.3个D.4个5.直角三角形两个锐角的度数分别为x，y，其关系式为y=90°−x,其中变量为，常量为.6.多边形内角和α关于边数n的关系式为α=(n--2)×180°,其中变量为，常量为7.阅读并完成下列各题：(1)某人持续以a(m/ min)的速度经t(min)跑了s(m),其中常量为,变量为(2)在t(min)内,不同的人以不同的速度a(m/ min)跑了s(m),其中常量为,变量为.(3)s(m)的路程，不同的人以不同的速度a(m/ min)各需跑的时间为t(min)，其中常量为,变量为.(4)根据以上三句叙述，写出一句关于常量与变量的结论：.8.齿轮每分钟转120转，如果n 表示转数，t表示转动时间.(1)用含n的代数式表示t.(2)说出其中的变量与常量.9.以21m/s的速度向上抛一个小球，小球的高度h(m)关于小球运动的时间t(s)的函数关系式为ℎ=21t−4.9t².下列说法中，正确的是( ).A.-4.9 是常量,21,t,h是变量B.21,-4.9是常量,t,h是变量C. t,h 是常量,21,-4.9是变量D. t,h 是常量,-4.9 是变量10.设路程s，速度v，时间t，有函数关系式s= vt.下列说法中，正确的是( ).A.当s一定时，v是常量，t是变量B.当v一定时，t是常量，s是变量C.当t一定时，t是常量，s，v是变量D.当t一定时，s是常量，v是变量11.如图所示，圆柱的高是3cm，当圆柱的底面半径由小到大变化时，圆柱的体积也随之发生了变化.(1)在这个变化中，变量为.(2)当底面半径由1cm变化到10cm时，圆柱的体积增加了cm³.12.下表为小华做观察水的沸腾实验时所记录的数据：时间(min)0123456789101112温度(℃)6065707580859095100100100100100(1)时间是8min时,水的温度为.(2)此表反映了变量和之间的关系.(3)当时，温度随时间增加而增加；当时，水的温度不再变化.13.行驶中的汽车，在刹车后由于惯性，还将继续向前滑行一段距离才能停止，这段距离称为“刹车距离”.为了测定某种型号汽车的刹车性能(车速不超过140km/h)，对这种汽车进行测试，测得数据如下表：刹车时车速(km/h)20406080100120刹车距离(m) 1.0 3.67.813.62130请解答下列问题：(1)上表反映了哪两个变量之间的关系?(2)如果刹车时车速为60km/h，那么刹车距离是多少米?14.某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表)：温度(℃)-20-100102030声速(m/s)318324330336342348下列说法中，错误的是( ).A.在这个变化中，自变量是温度，因变量是声速B.温度越高，声速越快C.当空气温度为20℃时，声音5s可以传播1740mD.当温度每升高10℃，声速增加6m/s(F−32),则其中的变量是,常量是.15.已知摄氏温度C 与华氏温度F 之间的对应关系为C=5916.如图所示，等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10，AC与MN在同一条直线上，开始时点A 与点M 重合，让△ABC向右运动，最后点A 与点N 重合.试写出重叠部分的面积y关于MA 的长度x的关系式，并指出其中的常量与变量.5.1 常量与变量1. B2. C3. C4. B5. x,y - 1,90°6. n,α - 2,180°7.(1)a t,s (2)t a,s (3)s a,t(4)常量和变量在一个过程中是相对存在的8.(1)t=n120.(2)变量:t,n;常量: 1120.9. B 10. C 11.(1)半径、体积(2)297π12.(1)100℃(2)温度时间(3)0~8min8~12min13.(1)刹车时车速和刹车距离之间的关系.(2)7.8m.14. C 15. C,F 59,-3216.由题意知,开始时点A 与点M 重合,让△ABC向右运动，两图形重合的长度为AM=x，∵∠BAC=45∘,∴S阴影=12×AM×ℎ=12AM2=12x2⋅∴y=12x2.常量：12；变量：重叠部分的面积y与MA的长度x.。

解：（1）80千帕；45千帕 （2）大气压，海拔
（3）大气压随着海拔的升高而下降
1.空中一个物体由静止自由下落，它下落的距离与时间之间有下 面的关系：
时间t/秒 距离h/米 1 4.9×1 2 4.9×4 3 4.9×9 4 4.9×16 … …
（1）当物体下落5秒时，它下落的距离是多少？下落2.5秒时呢？ （2）将下落的距离h用关于时间t的代数式表示； （3）在这个问题中哪些量是变量？哪些量是常量？
解：（1）当物体下落5秒时，下落的距离是4.9×25； 下落2.52 （3）h，t是变量，4.9是常量
2.地球周围被厚厚的大气层所包围，大 气对物体会产生一定的压强.在不同的高 度，由于空气稀薄程度不同，所产生的 大气压也不同.右图表示的是不同海拔的 大气压. （1）海拔为2千米时，大气压大约是多 少？海拔为6.5千米时呢？ （2）图中反映了哪两个量之间的关系？ （3）你从图中能得到什么信息？

20.1常量和变量补充习题（一）基础练习1．齿轮每分钟转120转，如果用n表示转数，t表示时间(分)，那么用t表示n的关系式是，其中常量是，变量是。

2．正方体体积V和棱长a之间的关系是，其中的变量是．3．某种商品的单价是每只5元，它的销售额y(元)与所售商品数量x(只)之间的关系式是，其中是变量，是常量．4．若某一汽车速度为每小时100千米，则行驶路程s(千米)与所用时间t(小时)的关系式是，其中是常量，是变量．5．下列命题中错误的是()A．在等速运动公式s＝vt中，v是常量B．在用公式C＝2πR计算不同的半径所对应的周长C时，C,R是变量，2π是常量C．练习本定价0．5元／个，买x个本子付款y元，它们的关系可以表示成y＝0．5x，这里的x为自然数D．今有360本图书借给学生阅读，每人9本，则余下书数y(本)与学生数x(个)间的关系为y=360－9x，其自变量x的取值范围是0≤x<406．某商店在售货时，其售货数量x(千克)与所得金额y(元)如下表所示．(1)写出y与x之间的关系式．(2)当售货量为12．5千克时，所得金额为多少元?7．为了测量一种皮球的弹起高度与下落高度之间关系，通过试验，测得下列一组数据：(单位：厘米)试根据两组数据的关系写出下落高度H与弹跳高度h之间的关系式．能力提高8．某城市出租车收费按路程计算．3km之内(包括3km)收费6元，超过3km每增加1km 加收1．6元，则路程x≥3km时，车费y(元)与路程x(km)之间的关系式为。

9．某商店进一批货，每件10元，售出时，每件加利润2元，如售出x件，应收货款y 元，则y与x之间的关系式为，其中是常量，是变量．当x＝12时，y＝。

答案1．n=120t120n、t2．v=a3v、a3．y＝5xy、x54．s＝100t100s、t5．D6．(1)y=8.4x(2)1057.h=34H8.y=6+1.6(x－3) 9．y=12x12y、x144元。

VB常量、变量及表达式练习题一、判断题1.ST$、B001、ASC都是合法的变量名。

（）2.表达式5*7\3与7\3*5的值相等。

（）3.”A”大于”a”。

（）二、写出VB的运算符，按优先级别写。

1.算术运算符：2.关系运算符：3.逻辑运算符：三、填空题1.表达式4+15 Mod 8的值是_____。

2.“a”,”T”,”Z”,”9”这四个字符中，______的ASCII码值最大。

3.表达式3\3*3/3 mod 3的值是_______.4.当X=-19,Y=8,F=100,NUM=-12时，求下列表达式的逻辑值（用True和False回答）（1）X>0 OR X<=0 逻辑值为______（2）NOT (X>Y) 逻辑值为_______（3）X+Y<=NUM逻辑值为______（4）X－Y<NUM AND NOT(Y>0) OR NUM >＝－25 逻辑值为______（5）X MOD 2=0 逻辑值为____5."7 mod 3+3^3/4\5"的值为____6.True or False 的值为_____7.X,Y均小于Z的表达式为________8.表达式“4<5 and 7=5“的值为______9.若a的值为True，则表达式“a=(4=3)“的值为______10.字符串常量必须用_____括起来。

11.闰年的条件是:年份(Y)能被4整除,但不能被100整除;或者Y能被400整除.表示该条件的逻辑表达式是:12.表示条件"变量X 为能被5整除的偶数"的逻辑表达式是:13.一元二次方程ax 2+bx+c=0有实根的条件是a ≠0,并且b 2-4ac ≥0,表示该条件的逻辑表达式是:四、选择题1.下面四个VB 关系表达式中结果为“真“的是（ ）A. “A”>”A ”B. “THAT ”>”THE ”C. ”H ”D. “b ”>”B ” 2.下面四个表达式中其值为0的是（ ）A. 4/5B. 5 mod 4C. 4\5D. 4 mod 53.下面表达式的值为真的是（ ）A. “ABC ”>”Aba ”B. “3+2”>”4”C. “ABC ”>”ABC ”D.“ABC ”>”ABB ”4、求一个三位正整数N 的十位数的正确方法是（ ）A.Int(N/10)-Int(N/100)*10B.Int(N/10)-Int(N/100)C.N-Int(N/100)*100D.Int(N-Int(N/100)*100)5、若x 是大于零的偶数，则下列关系表达式值一定为真的是（ ）A ． x Mod 2 = 1B ．x\2 = 0C ． x\2 = x/2D ．Int(x/2) <> x/26、设a=2,b=3,c=4,d=5,表达式 a>b And c<=d Or 2*a>c 的值是 （ ）A ．TrueB ．FalseC ．-1D ．1六、写出下列数学式的VB 表达式 1.xy n n n )2)(1(-- 3.4131211+++2.311xy + 4.yx xy x 133++函数练习1.写出下列函数的值(1)INT(-3.5)+INT(4.8)(2)SIN(0) (3)SQR(ABS(-10)+15) (4)LOG(EXP(12)) (5)10\5/32.X=-8.55，下列函数表达式的值各是什么(1)ABS(X)+INT(X)(2)SIN(X)+SIN(-X) (3)INT(SQR(-X)) (4)FIX(X)+INT(X)(5)FIX(2*X)*10 3.写出下列数学表达式的VB 表达式(1))2(cos 2π (2)aac b b 242-+- (3)2ln 8x e (4)322)lg(x b a + (5)033sin lg +x (6)||sin 2x x e x-+ (7)|sin |ln 3yx x e ++π 4.把VB 表达式写成数学表达式(1)(SIN(X)+COS(X)+ABS(X))*(LOG(9)/LOG(10)+TAN(X))(2)(EXP(X)+EXP(Y))/(A+B)5.选择题(1)X=-9.8，表达式INT(X)+FIX(－X)的值是( ) A.1 B.17 C.0 D.－1(2)执行A ＝9\4后，A 的值为( ) A.9/4 B.3 C.2 D.2.25(3)表达式SQR(2^3^2) MOD 7的值为( )A.0B.1C.2D.3(4)下列逻辑表达式中正确的是( )A.X>Y AND Y>ZB.X>Y>ZC.X>Y AND >ZD.X>Y .AND. Y>Z(5)表达式INT(17.8)+FIX(-17.8)的值是( )A.0B.－1C.1D.－16 (6)X+Y 小于10且X-Y 大于0的逻辑表达式是( )A.x+y<10 or x-y>0B.(x+y<10): (x-y)>0C.x+y<10 .and. x-y>0D.x+y<10 and x-y>0(7)表达式16/4-2^5*8/4 MOD 5\2的值为________。

《常量和变量》练习题
【巩固提升】
1.指出下列各表述关系中的常量和变量.
（1）匀速运动公式s =vt （v 表示速度，t 表示时间，s 表示路程). （2）边长为xcm 的正方体，它的表面积为S ．
2.函数
中，其中变量是_____、_____，常量是_____．
3.若球体的体积为V ，半径为R,则.其中变量______，常量是______.
4.一根蜡烛原长a 厘米，点燃后燃烧时间为t （分），所剩余蜡烛的长为y （厘
米），其中的变量是（ ）
A.a 、y
B.t
C.t 、y
D.a
5.声音在空气中传播的速度y(m/s)与气温x(℃)有如下表所示的关系： (1)当气温是35 ℃时，音速是多少？
(2)这一变化过程中，反映了哪两个变量之间的
关系？写出这个关系的关系式．
6.观察图，根据图中的数据回答问题：
(1)设图形的周长为l ，梯形的个数为n ，试写出l 与 n 的关系式；
(2) 在上述变化过程中，变量、常量分别是什么？
2
cm 8y x =-34
3
V R π=。

常温和变温的题目
一、以下哪个是常量的例子？
A. 今天的日期
B. 明天的天气
C. 圆周率π的值
D. 用户输入的年龄
（答案）C
二、在编程中，变量通常用于存储什么？
A. 固定不变的数据
B. 临时或可变的数据
C. 程序的指令
D. 程序的注释
（答案）B
三、下列哪个选项描述的是变量？
A. 地球的自转周期
B. 水的沸点温度
C. 用户在网站上输入的密码
D. 光速在真空中的速度
（答案）C
四、在物理公式中，哪些符号通常代表常量？
A. v（速度）
B. m（质量）
C. G（万有引力常数）
D. t（时间）
（答案）C
五、下列哪个不是变量在程序中的常见用途？
A. 存储计算结果
B. 记录用户输入
C. 控制循环次数
D. 定义程序的语言
（答案）D
六、在化学实验中，哪个量可以被视为常量？
A. 反应物的初始质量
B. 实验室的室温
C. 反应过程中产生的气体体积
D. 加入催化剂的量（假设催化剂不消耗）
（答案）D
七、下列哪个是程序设计中，变量命名的不推荐做法？
A. 使用有意义的名称
B. 使用简短的名称以提高编码速度
C. 避免使用保留字作为变量名
D. 遵循一致的命名规范
（答案）B
八、在经济学中，哪个变量通常随着市场条件的变化而变化？
A. 货币的面值
B. 国家的GDP增长率
C. 物理学中的光速
D. 公司的注册资本
（答案）B。

《5.1 常量与变量》课时同步练习2020-2021年数学浙教新版八（上）一．选择题（共9小题）1．在行进路程s、速度v和时间t的相关计算中，若保持行驶的路程不变，则下列说法正确的是（）A．变量只有速度vB．变量只有时间tC．速度v和时间t都是变量D．速度v、时间t、路程s都是常量2．在进行路程s、速度v和时间t的相关计算中，若保持行驶的路程不变，则下列说法正确的是（）A．s、v是变量B．s、t是变量C．v、t是变量D．s、v、t都是变量3．小丽的微信红包原有100元钱，她在新年一周里抢红包，红包里的钱随着时间的变化而变化，在上述过程中，自变量是（）A．时间B．小丽C．100元D．红包里的钱4．李师傅到单位附近的加油站加油，如图是所用的加油机上的数据显示牌，则其中的常量是（）A．金额B．数量C．单价D．金额和数量5．在圆周长的计算公式C＝2πr中，变量有（）A．C，πB．C，r C．π，r D．C，2π6．在球的体积公式VπR3中，下列说法正确的是（）A．V、π、R是变量，为常量B．V、π是变量，R为常量C．V、R是变量，、π为常量D．以上都不对7．小明的微信红包原有80元钱，他在新年一周里抢红包，红包里的钱随着时间的变化而变化，在上述过程中，自变量是（）A．时间B．小明C．80元D．红包里的钱8．某人要在规定的时间内加工100个零件，如果用n表示工作效率，用t表示规定的时间，下列说法正确的是（）A．数100和n，t都是常量B．数100和n都是变量C．n和t都是变量D．数100和t都是变量9．地表以下岩层的温度随着所处深度的变化而变化，在这一问题中因变量是（）A．地表B．岩层的温度C．所处深度D．时间二．填空题（共9小题）10．自变量x与因变量y的关系如图，当x每增加1时，y增加．11．圆的面积S与半径R之间的关系是S＝πR2．请指出公式S＝πR2中常量是．12．李师傅到单位附近的加油站加油，如图是所用的加油机上的数据显示牌，则其中的常量是．13．圆的面积计算公式S＝πR2中是自变量．14．骆驼被称为“沙漠之舟”，它的体温随时间的变化而变化，在这一变量关系中，因变量是．15．长方形的周长为10，长为x，宽为y，则y与x的关系式为．16．我们知道，地面有一定的温度，高空也有一定的温度，且高空中的温度是随着距地面高度的变化而变化的，如果t表示某高空中的温度，h表示距地面的高度，则是自变量．17．“早穿皮袄，午穿纱，围着火炉吃西瓜．”这句谚语反映了我国新疆地区一天中，随变化而变化，其中自变量是，因变量是．18．一辆汽车以一定的速度匀速行驶，行驶的路程随时间的变化而变化，在这一变化过程中，自变量是．三．解答题（共4小题）19．如图是一位病人的体温记录图，看图回答下列问题：（1）自变量是，因变量是；（2）护士每隔小时给病人量一次体温；（3）这位病人的最高体温是摄氏度，最低体温是摄氏度；（4）他在4月8日12时的体温是摄氏度；（5）图中的横虚线表示；20．植物呼吸作用受温度影响很大，观察如图，回答问题：（1）此图反映的自变量和因变量分别是什么？（2）温度在什么范围内时豌豆苗的呼吸强度逐渐变强？在什么范围内逐渐减弱？（3）要使豌豆呼吸作用最强，应控制在什么温度左右？要抑制豌豆的呼吸应控制在什么温度左右？21．在一次实验中，小强把一根弹簧的上端固定，在其下端悬挂物体．下面是他测得的弹簧的长度y与所挂物体的质量x的一组对应值：所挂物体的质量x/kg012345弹簧的长度y/cm202224262830（1）上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？（2）填空：①当所挂的物体为3kg时，弹簧长是．不挂重物时，弹簧长是．②当所挂物体的质量为8kg（在弹簧的弹性限度范围内）时，弹簧长度是．22．指出下列变化过程中，哪个变量随着另一个变量的变化而变化？（1）一辆汽车以80km/h的速度匀速行驶，行驶的路程s（km）与行驶时间t（h）（2）圆的半径r和圆面积S满足：S＝πr2．（3）银行的存款利率P与存期t．参考答案一．选择题（共9小题）1．解：在行进路程s、速度v和时间t的相关计算中，若保持行驶的路程不变，则速度v和时间t是变量，行进路程s是常量，故选：C．2．解：在进行路程s、速度v和时间t的相关计算中，若保持行驶的路程不变，则v、t是变量，s是常量，故选：C．3．解：小丽的微信红包原有100元钱，她在新年一周里抢红包，红包里的钱随着时间的变化而变化，在上述过程中，自变量是时间，故选：A．4．解：常量是固定不变的量，变量是变化的量，单价是不变的量，而金额是随着数量的变化而变化，故选：C．5．解：在圆周长的计算公式C＝2πr中，变量有C和r，故选：B．6．解：在球的体积公式VπR3中，V，R是变量，，π是常量，故选：C．7．解：小明的微信红包原有80元钱，他在新年一周里抢红包，红包里的钱随着时间的变化而变化，在上述过程中，自变量是时间．故选：A．8．解：n，其中n、t为变量，100为常量．故选：C．9．解：∵地表以下岩层的温度随着所处深度的变化而变化，∴自变量是深度，因变量是岩层的温度．故选：B．二．填空题（共9小题）10．解：当x增加1变为x+1，则y变为y1＝2（x+1）+10＝2x+2+10＝2x+12，∴y1﹣y＝2x+12﹣（2x+10）＝2x+12﹣2x﹣10＝2，故答案为：2．11．解：公式S＝πR2中常量是π，故答案为：π．12．解：常量是固定不变的量，变量是变化的量，单价6.48是不变的量，而金额是随着数量的变化而变化，故常量是：6.48．故答案为：6.48．13．解：圆的面积计算公式S＝πR2中R是自变量．故答案为：R．14．解：∵骆驼的体温随时间的变化而变化，∴自变量是时间，因变量是体温，故答案为：体温15．解：由题意可得，2（x+y）＝10，整理可得，y＝﹣x+5．故答案为：y＝﹣x+5．16．解：∵高空中的温度t是随着距地面高度h的变化而变化的，∴自变量是h，因变量是t，故答案为：h．17．解：“早穿皮袄，午穿纱，围着火炉吃西瓜．”这句谚语反映了我国新疆地区一天中，温度随时间变化而变化，其中自变量是：时间，因变量是：温度．故答案是：温度、时间、时间、温度．18．解：由题意得：在这一变化过程中，自变量是时间，故答案为：时间．三．解答题（共4小题）19．解：（1）自变量是时间，因变量是体温；（2）护士每隔6小时给病人量一次体温；（3）这位病人的最高体温是39.5摄氏度，最低体温是36.8摄氏度；（4）他在4月8日12时的体温是37.5摄氏度；（5）图中的横虚线表示人的正常体温；故答案为：时间；体温；6；39.5；36.8；37.5；人的正常体温．20．解：（1）此图反映的自变量是温度，因变量是呼吸作用强度；（2）由图象知，温度在0℃到35℃范围内时豌豆苗的呼吸强度逐渐变强；在35℃到50℃范围内逐渐减弱；（3）由图象知，要使豌豆呼吸作用最强，应控制在35℃左右；要抑制豌豆的呼吸应控制在0℃左右．21．解：（1）反映了弹簧长度y与所挂物体质量x之间的关系，所挂物体的质量是自变量，弹簧的长度是因变量；（2）①根据表格可知：当所挂物体重量为3千克时，弹簧长度为26cm；不挂重物时，弹簧长度为10cm；故答案为：26cm20cm．②根据表格可知：所挂重物每增加1千克，弹簧增长2cm，根据弹簧的长度＝弹簧原来的长度+弹簧伸长的长度可知当所挂物体的重量为x千克时，弹簧长度y＝2x+20，将x＝8代入得y＝2×8+20＝36．故答案为：36cm．22．解：（1）s＝80t，s随着t的变化而变化；（2）圆的半径r和圆面积S关系式S＝πr2，其中S随着r的变化而变化；（3）银行的存款利率P随着存期t的变化而变化。

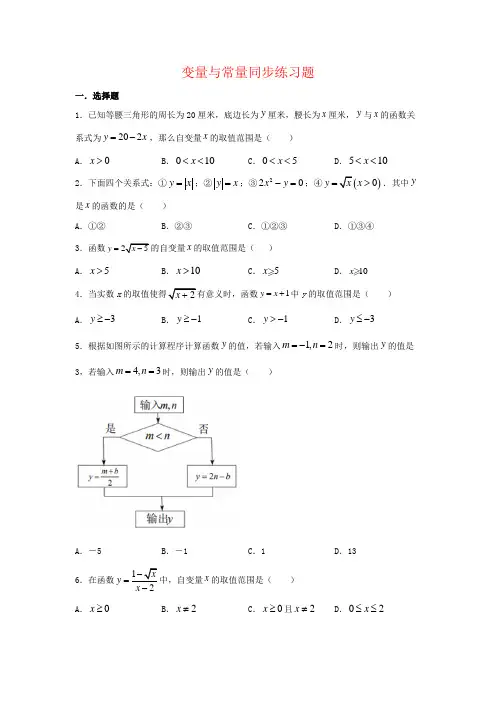
变量与常量同步练习题一．选择题1．已知等腰三角形的周长为20厘米，底边长为y 厘米，腰长为x 厘米，y 与x 的函数关系式为202y x =-，那么自变量x 的取值范围是（ ） A ．0x >B ．010x <<C ．05x <<D ．510x <<2．下面四个关系式：①y x =；②y x =；③220x y -=；④)0y x =>．其中y是x 的函数的是（ ） A ．①②B ．②③C ．①②③D ．①③④3．函数y =的自变量x 的取值范围是（ ） A ．5x >B ．10x >C ．5xD ．10x4．当实数x 1y x =+中y 的取值范围是（ ） A ．3y ≥-B ．1y ≥-C ．1y >-D ．3y ≤-5．根据如图所示的计算程序计算函数y 的值，若输入1,2m n =-=时，则输出y 的值是3，若输入4,3m n ==时，则输出y 的值是（ ）A ．－5B ．－1C ．1D ．136．在函数y =x 的取值范围是（ ） A ．0x ≥B ．2x ≠C ．0x ≥且2x ≠D ．02x ≤≤7．函数y x 的取值范围是（ ） A ．x ≠3B ．x ≤5C ．x ≤5且x ≠3D ．x ＜5且x ≠38．下列曲线中表示y 是x 的函数的是( )A ．B ．C ．D ．9．在地球某地，地表以下岩层的温度y （℃）与所处深度x （km ）之间的关系可以近似地用表达式y=35x+20来表示，当自变量x 每增加1km 时，因变量y 的变化情况是（ ） A ．减少35°CB ．增加35°CC ．减少55°CD ．增加55°C10．下列各曲线中不能表示y 是x 的函数的是（ ）A ．B ．C ．D ．11．下列函数中，自变量x 的取值范围是2021x ≥的函数是（ ）A ．12021y x =-B ．y =．y =．12021y x =-12．变量x ，y 的一些对应值如下表：根据表格中的数据规律，当5x =-时，y 的值是（ ） A ．75 B ．-29 C ．41 D ．75二．填空题 11．在函数y ＝中，自变量x 的取值范围是．12．变量x ，y 有如下关系：①y ＝3x 2；②y 2＝8x ．其中y 是x 的函数的是 ．（填序号） 13．已知函数，那么f （2）＝ ．15．一辆车的油箱有80升汽油，该车行驶时每1小时耗油4升，则油箱的剩余油量y（升）与该车行驶时间x（小时）（0≤x≤20）之间的函数关系式为．三、解答题13．求出下列函数中自变量x的取值范围．①y= 1x−2②y= √2+x．14．已知菱形的两条对角线长分别为y与x，且菱形的面积为10，请求出y与x的函数关系式并计算当x＝5时，y的值．。

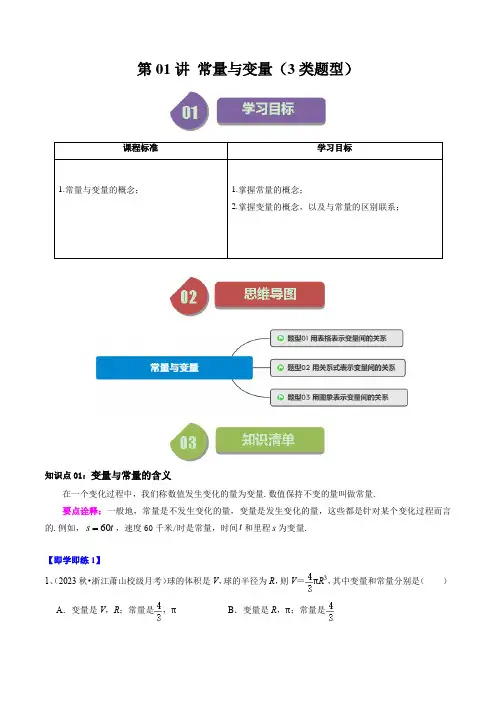
课程标准学习目标知识点01：变量与常量的含义要点诠释：一般地，常量是不发生变化的量，变量是发生变化的量，这些都是针对某个变化过程而言的.例如，60s t ，速度60千米/时是常量，时间t 和里程s 为变量.【即学即练1】1、（2023秋•浙江萧山校级月考）球的体积是V ，球的半径为R ，则V ＝πR 3，其中变量和常量分别是（ ）A ．变量是V ，R ；常量是，πB ．变量是R ，π；常量是C．变量是V，R，π；常量是D．变量是V，R3；常量是π题型01 用表格表示变量间的关系A．金额B．单价C．数量D．金额和数量根据以上信息，可以得到y与x之间的关系式为．4．（2023春·河南周口·七年级校考阶段练习）用一根长26cm的铁丝首尾相连围成一个长方形，长方形的长A．B．C．D．2．（2023秋·陕西榆林·八年级校考开学考试）骑自行车是一种健康自然的运动旅游方式，长期坚持骑自行车可增强心血管功能，提高人体新陈代谢和免疫力.如图是骑行爱好者老刘某天骑自行车行驶路程（km）与时间（h）的关系图象，观察图象得到下列信息，其中错误．．的是（）A．点P表示老刘出发5h，他一共骑行80km B．老刘实际骑行时间为5hC．0~2h老刘的骑行速度为15km/h D．老刘的骑行在0~2h的速度比3~5h的速度慢3．（2023春·辽宁锦州·七年级统考期中）如图是小乐从学校到家里行进的路程s（米）与时间t（分）之间关系的图象．观察图象，从中得到如下信息：①学校离小乐家1000米；②小乐用了20分钟到家；③小乐前10分钟走了路程的一半；④小乐后10分钟比前10分钟走得快，其中正确的有（填序号）．4．（2024春·六年级课时练习）一港口受潮汐的影响，某天24小时港内的水深大致如图，港口规定：为了保证航行安全，只有当船底与水底间的距离不少于4米时，才能进出该港．一艘吃水深度（即船底与水面的距离）为2米的轮船进出该港的时间最多为（单位：时）小时．5．（2023春·甘肃张掖·七年级校考期末）如图中的折线ABC是甲地向乙地打长途所需要付的费y（元）与通话时间t（分钟）之间的关系的图像．(1)通话1分钟，要付 费多少元？通话5分钟要付多少 费？(2)如果通话3分钟以上， 费y （元）与时间t （分钟）的关系式是()2.53y t =+-，那么通话4分钟的 费是多少元？A 夯实基础1．（2023春·云南·七年级统考期中）在圆面积公式2πS r =中，常量与变量分别是（ ）A ．常量是π，变量是S ，rB ．常量是2，变量是S ，π，rC ．常量是S ，变量是π，rD ．常量是r ，变量是S ，π2．（2023秋·广东广州·九年级广州大学附属中学校考开学考试）下列各图象中，y 不是x 的函数的是（ ）A ．B ．C ．D ．3．（2023春·陕西榆林·七年级校考期中）一个长方体的底面是边长为8cm 的正方形，当高为()cm h 时，体积为()3cm v ，则v 与h 的关系式是 ． 4．（2023春·贵州毕节·七年级校联考期中）宋代词人蒋捷曾在《一剪梅·舟过吴江》中提到：“流光容易把人抛．红了樱桃，绿了芭蕉”．昭通鲁甸樱桃上市后，每千克樱桃16元，则购买樱桃的费用y （元）与樱桃重A ．31y n =+B ．31y n =-C ．21y n =+D ．21y n =-根据以上信息，可以得到y与x之间的关系式为．5（2023秋·浙江宁波·七年级统考开学考试）一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同(1)甲、乙两地之间的距离是___________千米．(1)在这个关系式中，因变量、常量分别是什么？5．（2023春·陕西榆林·七年级校考期中）按如图所示的方式摆放餐桌和椅子，1张餐桌摆6把椅子，2张餐桌摆10把椅子，3张餐桌摆14把椅子…，其中餐桌的数量用x（张）表示，椅子的数量用y（把）表示，椅子的数量随着餐桌数量的变化而变化．(1)题中反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？(2)请写出椅子的数量y（把）和餐桌的数量x（张）之间的关系式；(3)按如图所示的方式摆放餐桌和椅子，能否刚好坐80人？请说明理由．6．（2023春·四川达州·七年级校考期中）如图，已知自行车与摩托车从甲地开往乙地，OA与BC分别表示它们与甲地距离，（千米）与时间t（小时）的关系，则：(1)摩托车每小时走________千米，自行车每小时走_________千米；(2)摩托车出发后多少小时，它们相遇？(3)摩托车出发后多少小时，他们相距20千米？。

c语言常量和变量练习题常量和变量练习题1、以下选项中可作为 C 语言合法常量的是A)-80 B)-080 C)-8e1.0 D)-80.0e2、以下选项中可作为 C 语言合法整数的是A) -034 B) 0386C) 0XffaD) x2a23、以下选项中可作为 C 语言合法常量的是A) e5 B) -3.0e5C) 5e0.5D)0xaa4、以下选项中可作为 C 语言合法常量的是A) -0xa B) -037 C) ox3a D) .1235、下列变量定义中合法的是A) short _a=1.le-1; B) double b=1+5e2.5;C) long double=0xfdaL; D) float 2_and=1-e-3;6、下列变量定义中不合法的是A) int a=b=1; B) int a=5.8;C) double x=5; D) char c=100; 7．（）是构成 C 语言程序的基本单位。

A、函数B、过程C、子程序D、子例程8．C 语言程序从A) 程序中第一条可执行语句 B) 程序中第一个函数C) 程序中的 main 函数 D) 包含文件中的第一个函数9、以下说法中正确的是（）。

A、C 语言程序总是从第一个定义的函数开始执行B、在 C 语言程序中，要调用的函数必须在 main( )函数中定义C、C 语言程序总是从 main( )函数开始执行D、C 语言程序中的 main( )函数必须放在程序的开始部分10.下列关于 C 语言的说法错误的是（）。

A) C 程序的工作过程是编辑、编译、连接、运行B) C 语言不区分大小写。

C) C 程序的三种基本结构是顺序、选择、循环D) C 程序从 main 函数开始执行11.下列正确的标识符是（）。

A.-a1B.a[i]C.a2_iD.int t12．下列 C 语言用户标识符中合法的是（）。

A)3ax B)x C)case D)-e2 E)union13．下列四组选项中，正确的 C 语言标识符是（）。

八年级数学：常量和变量练习（含解析）1．在△ABC中，它的底边为a，底边上的高为h，则面积S＝12ah，若h是定长，则此式中( A )A．S，a是变量B．S，h，a是变量C．a，h是变量D．以上都不对解析：S与a可以取不同的数值．故选A.2．小军用50元钱去买单价是8元的笔记本，则他剩余的钱Q(元)与他买这种笔记本的本数x之间的关系是( C )A．Q＝8xB．Q＝8x－50C．Q＝50－8xD．Q＝8x＋50解析：剩余的钱＝原有的钱－x个笔记本的钱．故选C.3．明明从广州给远在上海的爷爷打电话，电话费随着时间的变化而变化，在这个过程中，变量是( B )A．明明、电话费B．电话费、时间C．时间、明明D．爷爷、电话费解析：电话费和时间可以取不同的数值．故选B.4．三角形的一个内角的度数为x，与它相邻的外角的度数为y，则y与x之间的关系式是( D )A．y＝xB．y＝2xC．y＝90°－xD．y＝180°－x解析：∵x＋y＝180°，∴y＝180°－x.故选D.5．林老师骑摩托车到加油站加油，发现每个加油器都有三个量，其中一个量的单位是“元/升”，其数值固定不变，另外两个量分别表示“数量”“金额”，数值一直在变化，在这三个量中，“元/升”是常量，“数量”与“金额”是变量． 6．如图所示，△ABC 的底边BC 上的高是6 cm ，当三角形的顶点C 沿底边所在直线向点B 运动时，三角形的面积发生了变化．在这个变化过程中，变量是BC 和三角形的面积，常量是6_cm.7．如图所示，圆柱的高是3 cm ，当圆柱的底面半径由小到大变化时，圆柱的体积也随之发生变化．(1)在这个变化中，变量是圆柱的底面半径与圆柱的体积，其中，圆柱的体积随着圆柱的底面半径的变化而变化；(2)当底面半径由1 cm 变化到10 cm 时，圆柱的体积增加了多少？解：根据圆柱的体积＝圆柱的底面积×高，得π×102×3－π×12×3＝(102－12)×3π＝297π(cm 3)．答：当底面半径由1 cm 变化到10 cm 时，圆柱的体积增加了297π cm 3.8．某公司提供了一种移动通讯服务的收费标准，如下表：项目月基本服务费 月免费通话时间 超出后每分收费 标准 40元 150分 0.6元则每月话费y (元)与每月通话时间x (分)之间有关系式y ＝⎩⎨⎧ 400≤x ≤150，0.6x －50x >150，在这个关系式中，常量是什么？变量是什么？解：当0≤x≤150时，y,40是常量，x是变量；当x>150时，0.6，－50是常量，x，y是变量．9．某电影院观众席的座位按下列方式设置：(1)(2)根据表格分析，第5排、第6排各有多少个座位？(3)请你用式子表示座位数n与排数N之间的关系．解：(1)该表格表示了座位数与排数之间的关系，它们都是变量．(2)第5排有62个座位，第6排有65个座位．(3)n＝50＋3(N－1)＝47＋3N.。

常量与变量课后练习（含答案）1．在△ABC中，它的底边是a，底边上的高是h，则三角形面积S＝ah，当a为定长时，在此式中（）A．S，h是变量，，a是常量B．S，h，a是变量，是常量C．S，h是变量，，S是常量D．S是变量，，a，h是常量2．在圆的周长C＝2πR中，常量与变量分别是（）A．2是常量，C、π、R是变量B．2π是常量，C、R是变量C．C、2是常量，R是变量D．2是常量，C、R是变量3．李师傅到单位附近的加油站加油，如图是所用的加油机上的数据显示牌，则其中的常量是（）A．金额B．数量C．单价D．金额和数量4．骆驼被称为“沙漠之舟”，它的体温是随时间的变化而变化的，在这一问题中，因变量是（）A．沙漠B．体温C．时间D．骆驼5．在利用太阳能热水器来加热水的过程中，热水器里的水温随所晒时间的长短而变化，这个问题中因变量是（）A．太阳光强弱B．水的温度C．所晒时间D．热水器6．以固定的速度v0（米/秒）向上抛一个小球，小球的高度h（米）与小球的运动的时间t （秒）之间的关系式是h＝v0t﹣4.9t2，在这个关系式中，常量、变量分别为（）A．4.9是常量，t、h是变量B．v0是常量，t、h是变量C．v0、﹣4.9是常量，t、h是变量D．4.9是常量，v0、t、h是变量7．“早穿皮袄，午穿纱，围着火炉吃西瓜．”这句谚语反映了我国新疆地区一天中，随变化而变化，其中自变量是，因变量是．8．如果用总长为60m的篱笆围成一个长方形场地，设长方形的面积为S（m2），周长为p （m），一边长为a（m），那么S，p，a中是变量的是（）A．S和p B．S和a C．p和a D．S，p，a9．弹簧挂上物体后会伸长，测得一弹簧的长度y（cm）与所挂的物体的质量x（kg）之间有下面的关系，下列说法不正确的是（）x/kg012345y/cm2020.52121.52222.5A．弹簧不挂重物时的长度为0cmB．x与y都是变量，且x是自变量，y是因变量C．物体质量每增加1 kg，弹簧长度y增加0.5cmD．所挂物体质量为7 kg时，弹簧长度为23.5cm10．某人要在规定的时间内加工100个零件，则工作效率η与时间t之间的关系中，下列说法正确的是（）A．数100和η，t都是变量B．数100和η都是常量C．η和t是变量D．数100和t都是常量11．对于圆的周长公式C＝2πR，下列说法正确的是（）A．π、R是变量，2是常量B．R是变量，π是常量C．C是变量，π、R是常量D．C、R是变量，2、π是常量12．明明从广州给远在上海的爷爷打电话，电话费随着时间的变化而变化，在这个过程中，因变量是（）A．明明B．电话费C．时间D．爷爷13．在圆的周长公式C＝2πR中，是变量的是（）A．C B．R C．π和R D．C和R14．在利用太阳能热水器来加热水的过程中，热水器里的水温随所晒时间的长短而变化，这个问题中因变量是（）A．太阳光强弱B．水的温度C．所晒时间D．热水器的容积15．世纪花园居民小区收取电费的标准是0.6元/千瓦时，当用电量为x（单位：千瓦时）时，收取电费为y（单位：元）．在这个问题中，下列说法中正确的是（）A．x是自变量，0.6元/千瓦时是因变量B．y是自变量，x是因变量C．0.6元/千瓦时是自变量，y是因变量D．x是自变量，y是因变量16．一本笔记本5元，买x本共付y元，则5和y分别是（）A．常量，常量B．变量，变量C．常量，变量D．变量，常量参考答案及解析1．在△ABC中，它的底边是a，底边上的高是h，则三角形面积S＝ah，当a为定长时，在此式中（）A．S，h是变量，，a是常量B．S，h，a是变量，是常量C．S，h是变量，，S是常量D．S是变量，，a，h是常量【考点】常量与变量．【分析】根据函数的定义：对于函数中的每个值x，变量y按照一定的法则有一个确定的值y与之对应；来解答即可．【解答】解：∵三角形面积S＝ah，∴当a为定长时，在此式中S、h是变量，，a是常量；故选：A．【点评】函数的定义：设x和y是两个变量，D是实数集的某个子集，若对于D中的每个值x，变量y按照一定的法则有一个确定的值y与之对应，称变量y为变量x的函数，记作y＝f（x）；变量是指在程序的运行过程中随时可以发生变化的量．2．在圆的周长C＝2πR中，常量与变量分别是（）A．2是常量，C、π、R是变量B．2π是常量，C、R是变量C．C、2是常量，R是变量D．2是常量，C、R是变量【考点】常量与变量．【分析】根据在一个变化的过程中，数值发生变化的量称为变量；数值始终不变的量称为常量，即可答题．【解答】解：∵在圆的周长公式C＝2πr中，C与r是改变的，π是不变的；∴变量是C，r，常量是2π．故选：B．【点评】本题考查了常量与变量的知识，属于基础题，变量是指在程序的运行过程中随时可以发生变化的量．3．李师傅到单位附近的加油站加油，如图是所用的加油机上的数据显示牌，则其中的常量是（）A．金额B．数量C．单价D．金额和数量【考点】常量与变量．【分析】根据常量与变量的定义即可判断．【解答】解：常量是固定不变的量，变量是变化的量，单价是不变的量，而金额是随着数量的变化而变化，故选：C．【点评】本题考查常量与变量，解题的关键是正确理解常量与变量，本题属于基础题型．4．骆驼被称为“沙漠之舟”，它的体温是随时间的变化而变化的，在这一问题中，因变量是（）A．沙漠B．体温C．时间D．骆驼【考点】常量与变量．【分析】因为骆驼的体温随时间的变化而变化，符合“对于一个变化过程中的两个量x 和y，对于每一个x的值，y都有唯一的值和它相对应”的函数定义，自变量是时间，因变量是体温．【解答】解：∵骆驼的体温随时间的变化而变化，∴自变量是时间，因变量是体温，故选：B．【点评】考查了函数的定义：设x和y是两个变量，D是实数集的某个子集，若对于D 中的每个值x，变量y按照一定的法则有一个确定的值y与之对应，称变量y为变量x的函数．5．在利用太阳能热水器来加热水的过程中，热水器里的水温随所晒时间的长短而变化，这个问题中因变量是（）A．太阳光强弱B．水的温度C．所晒时间D．热水器【考点】常量与变量．【分析】函数的定义：设在某变化过程中有两个变量x、y，如果对于x在某一范围内的每一个确定的值，y都有唯一的值与它对应，那么称y是x的函数，x叫自变量．函数关系式中，某特定的数会随另一个（或另几个）会变动的数的变动而变动，就称为因变量．【解答】解：根据函数的定义可知，水温是随着所晒时间的长短而变化，可知水温是因变量，所晒时间为自变量．故选：B．【点评】本题主要考查常量与变量的知识，解题的关键是对函数的定义以及对自变量和因变量的认识和理解，难度不大．6．以固定的速度v0（米/秒）向上抛一个小球，小球的高度h（米）与小球的运动的时间t （秒）之间的关系式是h＝v0t﹣4.9t2，在这个关系式中，常量、变量分别为（）A．4.9是常量，t、h是变量B．v0是常量，t、h是变量C．v0、﹣4.9是常量，t、h是变量D．4.9是常量，v0、t、h是变量【考点】常量与变量．【分析】根据在一个变化的过程中，数值发生变化的量称为变量；数值始终不变的量称为常量，即可答题．【解答】解：h＝v0t﹣4.9t2中的v0（米/秒）是固定的速度，﹣4.9是定值，故v0和﹣4.9是常量，t、h是变量，故选：C．【点评】本题考查了常量与变量的知识，属于基础题，变量是指在程序的运行过程中随时可以发生变化的量．7．“早穿皮袄，午穿纱，围着火炉吃西瓜．”这句谚语反映了我国新疆地区一天中，温度随时间变化而变化，其中自变量是时间，因变量是温度．【考点】常量与变量．【分析】根据函数的定义：对于函数中的每个值x，变量y按照一定的法则有一个确定的值y与之对应；来解答即可．【解答】解：“早穿皮袄，午穿纱，围着火炉吃西瓜．”这句谚语反映了我国新疆地区一天中，温度随时间变化而变化，其中自变量是：时间，因变量是：温度．故答案是：温度、时间、时间、温度．【点评】函数的定义：设x和y是两个变量，D是实数集的某个子集，若对于D中的每个值x，变量y按照一定的法则有一个确定的值y与之对应，称变量y为变量x的函数，记作y＝f（x）；变量是指在程序的运行过程中随时可以发生变化的量．8．如果用总长为60m的篱笆围成一个长方形场地，设长方形的面积为S（m2），周长为p （m），一边长为a（m），那么S，p，a中是变量的是（）A．S和p B．S和a C．p和a D．S，p，a【考点】常量与变量．【分析】根据篱笆的总长确定，即可得到周长、一边长及面积中的变量．【解答】解：∵篱笆的总长为60米，∴周长P是定值，而面积S和一边长a是变量，故选：B．【点评】本题考查了常量与变量的知识，解题的关键是能够根据篱笆总长不变确定定值，然后确定变量．9．弹簧挂上物体后会伸长，测得一弹簧的长度y（cm）与所挂的物体的质量x（kg）之间有下面的关系，下列说法不正确的是（）x/kg012345y/cm2020.52121.52222.5A．弹簧不挂重物时的长度为0cmB．x与y都是变量，且x是自变量，y是因变量C．物体质量每增加1 kg，弹簧长度y增加0.5cmD．所挂物体质量为7 kg时，弹簧长度为23.5cm【考点】常量与变量．【分析】根据自变量、因变量的含义，以及弹簧的长度y（cm）与所挂的物体的质量x （kg）之间的关系逐一判断即可．【解答】解：∵弹簧不挂重物时的长度为20cm，∴选项A不正确；∵x与y都是变量，且x是自变量，y是因变量，∴选项B正确；∵20.5﹣20＝0.5（cm），21﹣20.5＝0.5（cm），21.5﹣21＝0.5（cm），22﹣21.5＝0.5（cm），22.5﹣22＝0.5（cm），∴物体质量每增加1 kg，弹簧长度y增加0.5cm，∴选项C正确；∵22.5+0.5×（7﹣5）＝22.5+1＝23.5（cm）∴所挂物体质量为7kg时，弹簧长度为23.5cm，∴选项D正确．故选：A．【点评】此题主要考查了函数的定义：在一个变化过程中，有两个变量x，y，对于x的每一个取值，y都有唯一确定的值与之对应，则x叫自变量，y叫因变量．10．某人要在规定的时间内加工100个零件，则工作效率η与时间t之间的关系中，下列说法正确的是（）A．数100和η，t都是变量B．数100和η都是常量C．η和t是变量D．数100和t都是常量【考点】常量与变量．【分析】常量是在某个过程中不变的量，变量就是在某个过程中可以取到不同的数值，变化的量．根据定义即可判断．【解答】解：某人要在规定的时间内加工100个零件，则工作效率η与时间t之间的关系中：η和t是变量，零件的个数100是常量．故选：C．【点评】本题考查了常量与变量的概念，是一个基础题．11．对于圆的周长公式C＝2πR，下列说法正确的是（）A．π、R是变量，2是常量B．R是变量，π是常量C．C是变量，π、R是常量D．C、R是变量，2、π是常量【考点】常量与变量．【分析】常量就是在变化过程中不变的量，变量是指在变化过程中随时可以发生变化的量．【解答】解：C、R是变量，2、π是常量．故选：D．【点评】本题主要考查了常量，变量的定义，是需要识记的内容．12．明明从广州给远在上海的爷爷打电话，电话费随着时间的变化而变化，在这个过程中，因变量是（）A．明明B．电话费C．时间D．爷爷【考点】常量与变量．【分析】根据函数的定义：对于函数中的每个值x，变量y按照一定的法则有一个确定的值y与之对应．【解答】解：∵电话费随着时间的变化而变化，∴自变量是时间，因变量是电话费；故选：B．【点评】函数的定义：设x和y是两个变量，D是实数集的某个子集，若对于D中的每个值x，变量y按照一定的法则有一个确定的值y与之对应，称变量y为变量x的函数，其中x叫自变量，y叫x的函数．13．在圆的周长公式C＝2πR中，是变量的是（）A．C B．R C．π和R D．C和R【考点】常量与变量．【分析】根据变量是改变的量，据此即可确定周长公式中的变量．【解答】解：圆的周长公式C＝2πR中，变量是C和R，故选：D．【点评】本题考查了常量和变量的定义，明确变量是改变的量，常量是不变的量．14．在利用太阳能热水器来加热水的过程中，热水器里的水温随所晒时间的长短而变化，这个问题中因变量是（）A．太阳光强弱B．水的温度C．所晒时间D．热水器的容积【考点】常量与变量．【分析】函数的定义：设在某变化过程中有两个变量x、y，如果对于x在某一范围内的每一个确定的值，y都有唯一的值与它对应，那么称y是x的函数，x叫自变量．函数关系式中，某特定的数会随另一个（或另几个）会变动的数的变动而变动，就称为因变量．【解答】解：根据函数的定义可知，水温是随着所晒时间的长短而变化，可知水温是因变量，所晒时间为自变量．故选：B．【点评】本题主要考查的是对函数的定义以及对自变量和因变量的认识和理解．15．世纪花园居民小区收取电费的标准是0.6元/千瓦时，当用电量为x（单位：千瓦时）时，收取电费为y（单位：元）．在这个问题中，下列说法中正确的是（）A．x是自变量，0.6元/千瓦时是因变量B．y是自变量，x是因变量C．0.6元/千瓦时是自变量，y是因变量D．x是自变量，y是因变量【考点】常量与变量．【分析】根据函数的定义：对于函数中的每个值x，变量y按照一定的法则有一个确定的值y与之对应；来解答即可．【解答】解：在这个问题中，x是自变量，y是因变量，0.6元/千瓦时是常数．故选：D．【点评】函数的定义：设x和y是两个变量，D是实数集的某个子集，若对于D中的每个值x，变量y按照一定的法则有一个确定的值y与之对应，称变量y为变量x的函数，记作y＝f（x）；变量是指在程序的运行过程中随时可以发生变化的量．16．一本笔记本5元，买x本共付y元，则5和y分别是（）A．常量，常量B．变量，变量C．常量，变量D．变量，常量【考点】常量与变量．【分析】在一个变化的过程中，数值发生变化的量称为变量，数值始终不变的量称为常量，所以5和y分别是常量，变量，据此判断即可．【解答】解：一本笔记本5元，买x本共付y元，则5和y分别是常量，变量．故选：C．【点评】此题主要考查了常量与边量问题，要熟练掌握，解答此题的关键是要明确：常量与变量必须存在于同一个变化过程中，判断一个量是常量还是变量，需要看两个方面：一是它是否在一个变化过程中；二是看它在这个变化过程中的取值情况是否发生变化．。

一、选择题1. 以下不是C语言的特点的是（B）。

A、语言简洁紧凑B、能够编制出功能复杂的程序C、C语言可以直接对硬件操作D、C语言移植性好2. 下列字符序列中，不可用作C语言标识符的是（B ）。

A．abc123 B．no.1 C．_123_ D．_ok3. 正确的C语言标识符是（A）。

A．_buy_2 B．2_buy C．?_buy D．buy?4. 请选出可用作C语言用户标识符的一组标识符（B ）。

A．void B．a3_b3 C．For D．2adefine _123 -abc DOWORD IF Case sizeof5. 下列符号中，不属于转义字符的是（B）。

A．\\ B．\0xAA C．\t D．\06. 不属于C语言关键字的是（D ）。

A．int B．break C．while D．character7. 是C语言提供的合法关键字的是（B）。

A．Float B．signed C．integer D．Char8. 以下能定义为用户标示符的是（C）。

A．scanf B．Void C．_3com_ D．int9. 一个C程序是由（B ）。

A、一个主程序和若干子程序组成B、一个或多个函数组成C、若干过程组成D、若干子程序组成10. C语言程序的基本单位是（C ）。

A．程序行B．语句C．函数D．字符11. 下列说法中，错误的是（A）。

A．每个语句必须独占一行，语句的最后可以是一个分号，也可以是一个回车换行符号B．每个函数都有一个函数头和一个函数体，主函数也不例外C．主函数只能调用用户函数或系统函数，用户函数可以相互调用D．程序是由若干个函数组成的，但是必须有、而且只能有一个主函数12. 以下说法中正确的是（C）。

A．C语言程序总是从第一个定义的函数开始执行B．在C语言程序中，要调用的函数必须在main( )函数中定义C．C语言程序总是从main( )函数开始执行D．C语言程序中的main( )函数必须放在程序的开始部分13. C编译程序是（C ）。

补充知识：一、变量的声明变量声明就是将变量的名称和数据类型事先通知给应用程序，也叫做变量定义。

分为隐式声明和显式声明两种。

1、隐式声明：就是在使用一个变量之前并不专门声明这个变量而直接使用。

这种方式下，往往由于用户输入不细心而把变量名拼错，导致程序出现错误。

2、显式声明：为了避免写错变量名引起的麻烦，可以规定，只要遇到一个未经明确声明就当成变量的名字，Visual Basic 都发出错误警告。

要显式声明变量，需在类模块、窗体模块或标准模块的声明段中加入语句：Option Explicit也可以在“工具”菜单中选取“选项”，单击“编辑器”选项卡，再复选“要求变量声明”选项。

这样就在任何新模块中自动插入 Option Explicit 语句，但不会在已经建立起来的模块中自动插入；所以在工程内部，只能用手工方法向现有模块添加 Option Explicit。

显式声明变量的语法格式：Dim | Static | Public | Private <变量名> [<类型符> | AS <类型词>] 功能：显式声明变量及其类型、作用域，以及该变量是动态变量，还是静态变量。

说明：Dim用在标准模块（Module)、窗体模块(Form)或过程(Procedure)中定义变量。

Static 用于在过程中定义静态变量。

静态变量在每次引用后，其值继续保留。

Public用来在标准模块中定义全局变量。

Private用在窗体模块或过程中声明变量为私有变量。

二、用户自定义数据类型用户自定义数据类型又叫记录类型，它是由若干个基本类型的数据项组成，可描述同一对象的不同属性。

比如：一个学生的记录可包含考号（KH），姓名（XM），年龄（NL），成绩（CJ）等信息，把这些信息集中在一起就形成一个记录类型。

语法：Type 数据类型名数据项AS 数据类型数据项AS 数据类型……End Type上例就可以定义如下：Type sturecKh as String * 10Xm as String * 8Nl as IntegerCj as SingleEnd Type这样就形成了一个自定义类型sturec。