下载文档原格式
BGP是一个路径矢量路由协议，它的工作就是在自主系统间交换路由信息，以便发现访问互联网某处数据的最有效路径。
如何选择最佳路径进行路由?思科无边界网络为我们揭示了BGP的14条选路原则：BGP的选路原则:前提(路由的下一跳可达、关闭同步、路由没有被惩罚、前缀没有被入境路由策略拒绝)，具体原则如下：1:weight先比较管理权重(越大越优先)，这个参数本地有效。
虽然Weight属性是Cisco 私有的,但是很多厂商也是内置该属性(但无法显示及修改),这样就保证了本地始发的路由是最优先的,因为本地始发路由的Weight为32768,从其他BGP Peer学习过来的路由的Weight为0.2:local-pref本地首选项(越大越优先)，这个参数在本AS内传递。
Local Preference 属性只能在IBGP Peer之间传递,如果在EBGP Peer之间收到的路由的路径属性中携带了Local Preference,则会触发Notifacation报文,造成会话中断。
3：路由器本地始发的路径优先。
本地始发的路径特点是next-hop为0.0.0.0，weight 为32768。
可以使用不同的方式比如network或redistribute等，那么这些方式之间是存在优先顺序的原则：network>redistribute>aggregate，但该原则是不会作为BGP路由选路策略的。
4:具有最短AS-path路径(就是AS-PATH中AS最少的优先)的路由优先。
但是可以配置bgp bestpath as-path ignore来忽略这一步。
注意：在做聚合路由时，使用as-set后产生的AS-Path列表中的{}里的AS号长度只算一个AS号的长度;而在联盟内的AS-Path列表中的()的AS号长度不做计算依据!不同方向的route-map对于插入的AS号的位置是不同的。
5：比较origin属性，具有最低origin源码。
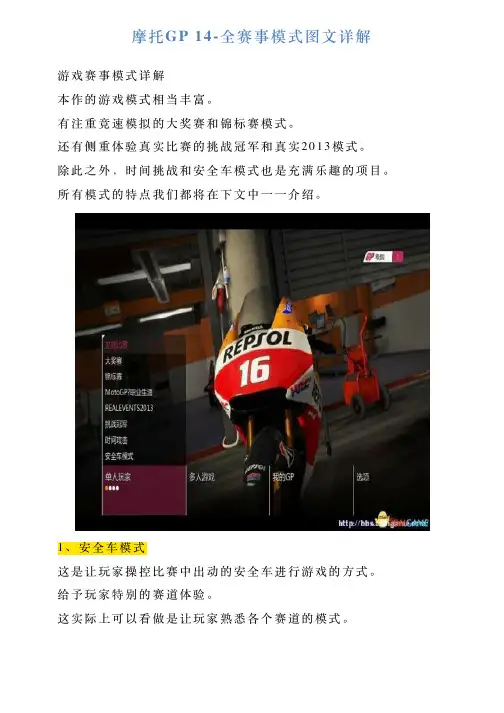
摩托GP 14-全赛事模式图⽂详解 游戏赛事模式详解 本作的游戏模式相当丰富。
有注重竞速模拟的⼤奖赛和锦标赛模式。
还有侧重体验真实⽐赛的挑战冠军和真实2013模式。
除此之外，时间挑战和安全车模式也是充满乐趣的项⽬。
所有模式的特点我们都将在下⽂中⼀⼀介绍。
1、安全车模式 这是让玩家操控⽐赛中出动的安全车进⾏游戏的⽅式。
给予玩家特别的赛道体验。
这实际上可以看做是让玩家熟悉各个赛道的模式。
⼤家可以选择游戏中的所有赛道。
著名的银⽯赛道、雪邦赛道都是榜上有名。
在开始赛道前，还会涉及到诸多的⽐赛选项。
这是在很多游戏模式中都会进⾏的个性化选择。
可以选择牵引⼒控制的强度，还可以开关⾃动刹车选项。
%{p a g e-b r e a k|安全车模式（1）|p a g e-b r e a k}% 同时，天⽓条件也对赛道产⽣⼀定的影响。
下⾬会导致赛道湿滑，抓地⼒不⾜。
适应不同天⽓并合理应对才能取得好的成绩。
最后是驾驶辅助选项。
玩家可以在这⾥选择是否开启最佳路径指引。
将变速器设置为⾃动、半⾃动或者⼿动模式。
还能够设置倒回的时间长度。
不开启路径指引，⼿动变速，不使⽤倒回，关闭⾃动刹车。
是的，这是最为困难的模式，但确实操作感最强的模式。
多样的选择给予了玩家各取所需的乐趣。
%{p a g e-b r e a k|安全车模式（2）|p a g e-b r e a k}% 2、时间挑战 时间挑战模式类似于⼀个单圈计时赛。
玩家将不断在选定的跑道上奔驰。
⼀次次刷新⾃⼰的单圈最快成绩，直到⾃⼰的极限! 玩家可以选择不同组别的赛车进⾏挑战。
从250c c到1000c c速度会越来越快。
当然，玩家在时间挑战中除了使⽤⾃⼰的代理车⼿外，还能使⽤真实车⼿。
各个著名车队的优秀车⼿任君挑选。
操控⾃⼰的偶像驾车驰骋也是⼀种别样的乐趣。
时间挑战模式中最短⽤时和当前⽤时会显⽰在右上⾓。
多次挑战后，⾃然会找到合理的节奏。
最佳路径问题的极大值原理求解方法The maximum value principle is an important concept in mathematics that can be applied to solve a variety of optimization problems, including the best path problem. In essence, the principle states that when trying to find the best path between two points, one should look for the path that maximizes a certain value, such as profit, efficiency, or safety. By applying this principle, one can make informed decisions that lead to optimal outcomes.极大值原理是数学中的一个重要概念，可以应用于解决各种优化问题，包括最佳路径问题。
其本质上是指在寻找两点之间的最佳路径时，应该寻找能最大化某种价值的路径，比如利润、效率或安全性。
通过应用这一原理，人们可以做出明智的决策，达到最优结果。
When it comes to solving the best path problem using the maximum value principle, it is important to consider all relevant factors that contribute to the overall value of the path. This may include factors such as distance, cost, time, and any constraints that need to be taken into account. By carefully analyzing these factors anddetermining how they impact the value of different paths, one can identify the path that maximizes the desired value.在使用极大值原理解决最佳路径问题时，重要的是要考虑所有影响路径整体价值的相关因素。
最佳路径的概念最佳路径是一种优化问题的解决方案，它在众多路径中寻找最优或最佳的路径。
这个概念在多个领域有着广泛的应用，如交通路线规划，物流运输，电子电路设计，网络传输等等。
最佳路径的目标可以是最短路径、最快路径、最省资源路径或其他特定需求下的最优路径。
在实际应用中，最佳路径的求解通常涉及到多个变量和约束条件。
这些变量和约束条件可以是路程、时间、成本、资源消耗、风险等。
根据不同的求解目标，我们可以使用不同的算法和技术来寻找最佳路径。
下面将介绍一些常见的最佳路径求解方法。
1.最短路径算法：最短路径算法是最常见也是最简单的求解最佳路径问题的方法之一。
其中，迪杰斯特拉算法和弗洛伊德算法是最短路径问题的典型算法。
迪杰斯特拉算法用于求解单源点到其他所有点的最短路径，而弗洛伊德算法则可以求解任意两点之间的最短路径。
这些算法的基本思想是通过遍历路径图的所有可能路径，并更新最短路径值，最终找到最佳路径。
2.最快路径算法：最快路径算法是用于求解最佳路径问题中的另一类常见方法。
在交通运输、航空航天和电子电路设计等领域，求解最快路径是十分重要和实际的问题。
迪杰斯特拉算法也可以用来求解最快路径，只需要将路径权重定义为时间或其他类似的指标。
3.约束条件下的最佳路径算法：在一些实际问题中，我们可能需要在一定的约束条件下求解最佳路径。
例如，在物流运输中，货物可能受到资源限制、时间窗口限制、交通限制等约束条件的影响，这就需要求解在这些约束条件下的最优路径。
针对这些问题，可以使用动态规划、线性规划、模拟退火等算法来求解。
4.多目标最佳路径算法：在许多应用场景中，最佳路径问题不仅涉及到单一目标，还可能涉及多个目标。
例如，在交通路线规划中，我们可能同时考虑路程和时间的优化。
这时，我们需要使用多目标最佳路径算法来寻找平衡的解。
常见的多目标求解方法有多目标遗传算法、帕累托优化等。
总结来说，最佳路径是指在众多路径中求解最优或最佳的路径。
根据不同的求解目标和约束条件，我们可以使用不同的算法和技术来寻找最佳路径。
《最佳路径》课件完整版一、教学内容本节课我们将学习《最佳路径》这一主题，内容涉及教材第六章第二节。
详细内容包括路径选择的原则、路径规划的算法、实际生活中的路径应用等。
通过学习，学生将掌握路径规划的基本原理和常用算法，并能将其应用于解决实际问题。
二、教学目标1. 理解路径选择的原则，掌握路径规划的算法。
2. 能够运用所学知识解决实际生活中的路径问题。
3. 培养学生的逻辑思维能力和问题解决能力。
三、教学难点与重点教学难点：路径规划算法的理解与运用。
教学重点：路径选择原则的掌握，路径规划算法的讲解。
四、教具与学具准备1. 教具：PPT课件、黑板、粉笔。
2. 学具：学生用书、练习册、计算器。
五、教学过程1. 实践情景引入（5分钟）利用PPT展示现实生活中的路径问题，如：如何从学校到商场购物最快捷？引导学生思考并讨论。
2. 理论知识讲解（15分钟）介绍路径选择的原则，讲解路径规划的算法，如：最短路径算法、最小树算法等。
3. 例题讲解（15分钟）结合教材例题，详细讲解解题思路，让学生掌握路径规划的方法。
4. 随堂练习（10分钟）学生独立完成练习册上的题目，巩固所学知识。
5. 小组讨论（10分钟）学生分组讨论实际生活中的路径问题，分享解题思路。
六、板书设计1. 路径选择原则2. 路径规划算法3. 例题解析4. 小组讨论成果展示七、作业设计1. 作业题目：（1）从家到学校有几种不同的路径，哪种路径最短？（2）如果要在城市中规划一条公交线路，如何选择路径？2. 答案：（1）最短路径可以通过Dijkstra算法或Floyd算法计算得出。
（2）公交线路的规划可以考虑最小树算法。
八、课后反思及拓展延伸2. 拓展延伸：（1）了解其他路径规划算法，如A算法、遗传算法等。
（2）研究路径规划在交通、物流等领域的应用。
重点和难点解析1. 教学难点与重点的确定2. 例题讲解的深度和广度4. 作业设计的生活实际应用一、教学难点与重点的确定1. 详细介绍算法的原理，以直观的方式呈现算法的步骤。
《最佳路径》课件一、引言在日常生活和工作中，我们经常需要从一个地方出发，到达另一个地方。
如何选择一条最佳路径，既能够节省时间，又能够减少能源消耗，是摆在我们面前的一个实际问题。
本课件旨在介绍最佳路径的相关概念、算法以及实际应用，帮助大家更好地理解和应用最佳路径知识。
二、最佳路径的概念1.路径：路径是指从一个地点到另一个地点所经过的路线。
在数学中，路径通常用图来表示，图由节点和边组成，节点代表地点，边代表路径。
2.距离：距离是指从一个地点到另一个地点所经过的实际路程。
在图论中，边上的权值通常表示距离。
3.最佳路径：最佳路径是指在所有可能的路径中，距离最短或者代价最小的路径。
在现实生活中，最佳路径可能还需要考虑其他因素，如时间、费用、路况等。
三、最佳路径的算法1.暴力法：暴力法是最简单的最佳路径算法，它尝试所有可能的路径组合，然后找出其中距离最短或代价最小的路径。
但是，当节点数量较多时，暴力法的计算量会急剧增加，不适用于大规模问题。
2.Dijkstra算法：Dijkstra算法是一种贪心算法，用于求解单源最短路径问题。
它从起点开始，逐步向外扩展，直到找到目标点的最短路径。
Dijkstra算法的时间复杂度为O(n^2)，适用于稠密图。
3.A算法：A算法是一种启发式搜索算法，用于求解单源最短路径问题。
它结合了Dijkstra算法和最佳优先搜索算法的优点，通过启发式函数评估每个节点的潜在代价，从而更快地找到最佳路径。
A算法的时间复杂度取决于启发式函数的质量，适用于稀疏图。
4.Floyd算法：Floyd算法是一种动态规划算法，用于求解多源最短路径问题。
它通过迭代更新任意两点之间的最短路径，最终得到所有节点之间的最短路径。
Floyd算法的时间复杂度为O(n^3)，适用于中等规模的问题。
四、最佳路径的应用1.路径规划：在地图导航、自动驾驶等领域，最佳路径算法被用于计算从起点到终点的最佳行驶路线。
这有助于提高出行效率，减少能源消耗。
2024年教学课件《最佳路径》.一、教学内容本节课选自教材《信息技术》第八章第二节“最佳路径”，详细内容包括图论基本概念，最短路径算法——迪杰斯特拉算法，以及实际应用案例分析。
二、教学目标1. 理解图论的基本概念，掌握图的表示方法。
2. 学会运用迪杰斯特拉算法求解最短路径问题。
3. 能够运用所学知识解决实际生活中的路径优化问题。
三、教学难点与重点重点：图论基本概念，迪杰斯特拉算法。
难点：迪杰斯特拉算法的理解与运用。
四、教具与学具准备1. 教师准备：多媒体教学设备，PPT课件。
2. 学生准备：计算机，教材，《信息技术》软件。
五、教学过程1. 实践情景引入（5分钟）利用PPT展示地图导航、快递配送等生活中的路径优化问题，引发学生对最佳路径求解的兴趣。
2. 知识讲解（15分钟）讲解图论基本概念，包括图的定义、表示方法等；介绍迪杰斯特拉算法的基本原理。
3. 例题讲解（10分钟）结合教材例题，详细讲解迪杰斯特拉算法的求解过程。
4. 随堂练习（15分钟）布置两道课堂练习题，要求学生在《信息技术》软件中完成，教师巡回指导。
5. 应用案例分析（10分钟）分析生活中的路径优化问题，引导学生运用所学知识解决实际问题。
6. 课堂小结（5分钟）七、作业设计1. 作业题目：（1）教材课后习题2.3.1、2.3.2；2. 答案：（1）教材课后习题答案；（2）最优配送路径：A→B→C→D→E，总距离最短。
八、课后反思及拓展延伸1. 课后反思：本节课学生对图论基本概念和迪杰斯特拉算法的理解程度，以及对实际问题的解决能力。
2. 拓展延伸：引导学生了解其他最短路径算法，如贝尔曼福特算法、A算法等，并尝试运用到实际生活中。
通过本节课的学习，希望学生能够掌握图论基本概念和迪杰斯特拉算法，提高解决实际生活中路径优化问题的能力。
同时，通过课后反思和拓展延伸，培养学生的自主学习能力和创新精神。
重点和难点解析1. 教学难点与重点的确定；2. 例题讲解的详细程度；3. 作业设计的合理性和答案的准确性；4. 课后反思及拓展延伸的实际效果。
最佳路径课件 (.zip一、教学内容本节课我们将探讨《最佳路径》这一主题，内容涵盖教材第四章第三节：基本路径搜索算法及其应用。
详细内容包括图的表示方法、深度优先搜索（DFS）与广度优先搜索（BFS）算法原理，以及最短路径算法如迪杰斯特拉（Dijkstra）和贝尔曼福特（BellmanFord）算法。
二、教学目标1. 理解图的表示方法，掌握深度优先搜索和广度优先搜索算法的应用。
2. 学习并掌握最短路径算法，能够运用算法解决实际问题。
3. 培养学生的逻辑思维能力和问题解决能力。
三、教学难点与重点重点：图的表示方法、路径搜索算法原理及其应用。
难点：最短路径算法的推导和应用，特别是迪杰斯特拉算法和贝尔曼福特算法的实现。
四、教具与学具准备1. 教具：PPT课件、黑板、粉笔。
2. 学具：笔记本电脑、教材、草稿纸、笔。
五、教学过程1. 引入实践情景（5分钟）：通过展示地图导航系统的实际应用，让学生体会最佳路径搜索在生活中的重要性。
2. 图的表示方法讲解（10分钟）：介绍邻接矩阵和邻接表两种表示方法，并通过例题讲解其应用。
3. 深度优先搜索和广度优先搜索算法讲解（15分钟）：阐述算法原理，给出示例，并进行随堂练习。
4. 最短路径算法讲解（20分钟）：分别讲解迪杰斯特拉算法和贝尔曼福特算法，结合例题进行讲解。
5. 课堂互动（15分钟）：让学生分组讨论，解决实际问题，如给定一个城市地图，运用所学算法寻找最短路径。
六、板书设计1. 图的表示方法2. 深度优先搜索和广度优先搜索算法3. 最短路径算法迪杰斯特拉算法贝尔曼福特算法七、作业设计1. 作业题目：（1）给定一个无向图，运用深度优先搜索和广度优先搜索算法找出所有连通分量。
（2）给定一个有向图，使用迪杰斯特拉算法和贝尔曼福特算法找出图中两个顶点间的最短路径。
2. 答案：见附件。
八、课后反思及拓展延伸1. 反思：本节课学生对图的表示方法和路径搜索算法的掌握程度，以及课堂互动环节的参与度。
最佳路径格罗培斯的思维过程格罗培斯的思维是指数学家格罗培斯在解决图论中的最佳路径问题中所采用的思考过程。
这个问题是指如何在给定的图中找到从一个顶点到另一个顶点的最短路径。
格罗培斯的解决方法被称为“最佳路径格罗培斯的思维过程（Dijkstra's algorithm）”。
下面将详细介绍最佳路径格罗培斯的思维过程。
格罗培斯的思维过程可以分为以下几个步骤：1.初始化：首先，格罗培斯将图中的所有顶点分为两个集合：已知最短路径的集合和未知最短路径的集合。
对于起始顶点，将其标记为已知最短路径集合，其他顶点标记为未知最短路径集合。
然后，格罗培斯将起始顶点到其余各顶点的距离初始化为无穷大，表示这些顶点距离起始顶点的距离是未知的。
2.遍历邻居顶点：选择起始顶点的邻居顶点中距离最短的一个，将其加入已知最短路径集合中，并更新与该顶点相邻的未知最短路径顶点的距离。
具体而言，对于与已知最短路径顶点相邻的未知最短路径顶点，格罗培斯会计算通过已知最短路径顶点到达该未知顶点的距离，并与之前设置的距离进行比较。
如果通过已知最短路径顶点到达该未知顶点的距离更短，则更新该未知顶点的距离。
3.重复步骤2：重复执行步骤2，直到所有顶点都被加入已知最短路径集合中。
4.最短路径计算：最后，根据格罗培斯的思维过程，可以得到从起始顶点到其他各顶点的最短路径。
其中，通过每个顶点所经过的那些已知最短路径顶点，可以构建出最短路径。
格罗培斯的思维过程的关键是通过逐步遍历邻居顶点来不断更新顶点的最短路径。
格罗培斯的思维过程保证了每个节点都能以最短路径加入已知最短路径集合中，并且每个节点的最短路径在加入已知最短路径集合之后都会得到更新。
最终，通过这样的迭代和更新，可以确定每个节点的最短路径。
《最佳路径》优质课件一、教学内容本节课选自教材《计算机科学导论》第六章“图论”的第二节“最佳路径”，主要内容包括图的基本概念，图的表示方法，以及最佳路径的算法实现。
详细内容涉及图的定义、顶点和边的关系、邻接矩阵和邻接表的表示方法，重点探讨Dijkstra算法和Floyd算法的计算过程及其在实际问题中的应用。
二、教学目标1. 理解图的基本概念，掌握图的表示方法。
2. 学会使用Dijkstra算法和Floyd算法求解最佳路径问题。
3. 能够将图论知识应用于实际问题的解决。
三、教学难点与重点教学难点：Dijkstra算法和Floyd算法的理解和实现。
教学重点：图的表示方法，以及最佳路径的算法实现。
四、教具与学具准备1. PPT课件：展示图的基本概念、算法流程等关键知识点。
2. 计算机及投影仪：演示算法的实现过程和实例。
3. 课堂练习材料：发放相关习题，供学生随堂练习。
五、教学过程1. 导入：通过现实生活中最佳路径的选择问题，引出本节课的主题。
2. 知识讲解：a. 介绍图的基本概念，如顶点、边、度等。
b. 讲解图的表示方法，如邻接矩阵和邻接表。
c. 详细讲解Dijkstra算法和Floyd算法的原理和计算过程。
3. 例题讲解：a. 结合具体例题，演示Dijkstra算法和Floyd算法的计算过程。
b. 分析算法的时间复杂度和空间复杂度。
4. 随堂练习：a. 发放习题，让学生独立完成。
b. 讲解习题，分析解题思路和关键步骤。
六、板书设计1. 图的基本概念2. 图的表示方法a. 邻接矩阵b. 邻接表3. 最佳路径算法a. Dijkstra算法b. Floyd算法4. 例题及解题思路七、作业设计1. 作业题目：123| | |456123| | |4562. 答案：a. 最佳路径为：145，路径长度为8。
b. 任意顶点间的最佳路径如下：1236：路径长度为111456：路径长度为121256：路径长度为13八、课后反思及拓展延伸1. 反思：本节课学生对图的基本概念和表示方法的掌握程度较好，但对Dijkstra算法和Floyd算法的理解仍有不足，需要在课后加强练习。
《最佳路径》语文一等奖说课稿1、《最佳路径》语文一等奖说课稿一、课程标准指出：“阅读教学是学生、教师、文本之间对话的过程。
”我以为在这三者中，教师首先要与文本对话，才能引导学生与文本进行对话。
所以，我觉得上好一节的前提是反复钻研教材。
我在钻研教材的时候，起先只认识到这篇课文是以平白朴素的语言向我们讲述了世界建筑大师格罗培斯为设计迪斯尼乐园的路径而大伤脑筋，后来从一位年老的葡萄园主身上得受到启发，最终他设计的路径被评为世界最佳设计。
这堂课的重点和难点就是要让学生弄清楚格罗培斯的设计与法国南部农民卖葡萄有什么联系。
而这个联系就是从老太太卖葡萄的方法上得到了“给人自由任其选择”的设计灵感。
但当我继续深读下去，我觉得这联系不仅仅如此。
其实许多园主卖葡萄的方法是给顾客摘好葡萄，这正和格罗培斯前50次的设计一样，是在为游客设计他认为最佳的路径。
而老太太卖葡萄的方法却是让顾客自己去摘葡萄，让顾客挑选自己认为最好的葡萄。
从老太太的卖葡萄的方法上，格罗培斯受到启发，于是他的设计观念有了转变，从原来为游人设计转变为让游人自己设计。
而最佳设计的获得这“以人为本”的`设计理念是不可或缺的。
我认为这篇课文不仅仅让我们懂得“给人自由任其选择”的人文思想，还让我们懂得在遇到困难时，要学会多角度、多层次地思考。
纵观整篇课文，我觉得文章有着“苦思——启发——决定”这样一条文路。
因为苦思，因为借地中海海滨清理思绪，所以看到南部农民卖葡萄，才会突发灵感，于是做了决定。
我这堂课的设计就是以“苦思——启发——决定”为我的教学线索，紧扣课后问题“格罗培斯的迪斯尼乐园路径设计为什么被评为世界最佳设计？它与法国南部农民卖葡萄有什么联系？”展开教学。
教学目标：1.引导学生在读、思、议中明白格罗培斯的迪斯尼乐园路径设计为什么被评为世界最佳设计以及它与法国南部农民卖葡萄之间的联系。
2.懂得尊重他人，相信他人，给人自由与选择的机会，其中蕴含着巨大的价值。
最佳路径教案引言本教案将介绍最佳路径问题，即在给定的网络图中找到起点到终点的最短路径。
这个问题在现实生活中有很多应用场景，如导航系统中的路线规划、电信网络中数据包传输的最优路径选择等。
本教案将围绕以下几个主题展开：1.最佳路径问题的定义和概念2.最佳路径算法的常见方法及其原理3.实际应用中的最佳路径问题案例4.最佳路径问题的扩展和拓展一、最佳路径问题的定义和概念最佳路径问题，又称为最短路径问题，是指在给定的网络图中，找到从起点到终点的最短路径。
最佳路径可以根据不同的度量标准进行评估，如路径长度、路径耗时、路径费用等。
最佳路径问题的解决过程可以抽象为在网络图中找到一条从起点到终点的路径，使得该路径在各种度量标准下达到最优。
这个问题可以用图论和图算法来解决。
二、最佳路径算法的常见方法及其原理1. Dijkstra算法Dijkstra算法是解决最佳路径问题的经典算法之一。
它以贪心策略进行，逐步确定起点到其他顶点的最短路径长度。
Dijkstra算法的基本思想是，首先将起点的最短路径长度设为0，然后逐步更新其他节点的最短路径长度。
Dijkstra算法的基本步骤如下：•初始化起点到其他节点的距离为无穷大，起点到自身的距离为0。
•选择距离起点最近的节点作为当前节点，更新与当前节点相邻节点的最短路径长度。
•重复以上步骤，直到所有节点的最短路径长度确定。
2. Bellman-Ford算法Bellman-Ford算法也是解决最佳路径问题的常见算法之一。
与Dijkstra算法不同的是，Bellman-Ford算法可以处理带有负权边的图。
Bellman-Ford算法的基本思想是，通过迭代更新节点的最短路径估计，直到找到最优解或发现负权环。
Bellman-Ford算法的基本步骤如下：•初始化起点到其他节点的距离为无穷大，起点到自身的距离为0。
•重复以下步骤，直到所有节点的最短路径长度确定。
–对所有边进行松弛操作，更新节点的最短路径估计。
最佳路径教案简介最佳路径是指在一定条件下，使得从起点到终点经过的总距离或总权值最小的路径。
本教案将介绍最佳路径的概念、算法以及应用。
内容什么是最佳路径？在地图中，我们经常需要找出最短或最快的路线。
这就是最佳路径问题。
最佳路径问题可以抽象为图论中的一类问题，主要包括单源最短路径问题、多源最短路径问题、最小生成树问题等。
最短路径算法Dijkstra算法Dijkstra算法是一种单源最短路径算法，适用于权值为非负数的图。
算法思路如下：1.将起点到所有点的最短距离初始化为无穷大。
2.从起点开始，遍历所有邻居节点，更新它们与起点的距离。
3.选择距离最小的节点作为下一个起点，并标记为已访问。
4.重复2-3步，直到到达终点或所有可达节点都已访问。
Bellman-Ford算法Bellman-Ford算法是一种单源最短路径算法，适用于权值为负数的图。
算法思路如下：1.将起点到所有点的最短距离初始化为无穷大，并将起点到自身的距离初始化为0。
2.对每条边进行松弛操作（即如果从当前节点可达的某个节点路径距离比目前已知的路径距离短，则更新该节点的路径距离）。
3.重复2步|V|-1次，其中|V|为节点数。
4.检查是否存在负环，如果存在，则说明图中不存在最短路径。
Floyd算法Floyd算法是一种多源最短路径算法，适用于任意权值的图。
算法思路如下：1.将每对节点之间的距离初始化为无穷大。
2.对于每个节点，将它连接的节点之间的距离赋为权值。
3.对于每一对节点，尝试通过一个中间节点缩短两点之间的距离。
4.重复3步，直到所有节点之间的距离不再缩小。
最佳路径应用最佳路径算法在生活中有许多应用。
例如，我们可以用最短路径算法计算出打车或自驾时的最佳路线；用最小生成树算法构建城市的公路系统；用最佳路径算法进行物流规划等等。
总结在本教案中，我们介绍了最佳路径的概念和算法，包括Dijkstra算法、Bellman-Ford算法、以及Floyd算法。
最佳路径教案教案概述：本教案旨在介绍最佳路径问题的基本概念和解决方法，通过引导学生学习最短路径算法，培养学生解决实际问题的能力。
本教案适用于中学信息技术、数学或物理课程。
教学目标：1. 了解最佳路径问题的背景和重要性；2. 掌握迪杰斯特拉算法和弗洛伊德算法；3. 能够应用最短路径算法解决实际问题；4. 培养学生合作、分析和解决问题的能力。
教学准备：1. 教师准备一台电脑和投影设备，用于展示教学材料；2. 确保每个学生都有一台计算机，并安装图形编辑软件。
教学步骤：引入：最佳路径在我们的日常生活中无处不在，比如找到最短驾驶路径、最快的公交路线等。
那么，怎样在计算机系统中找到最佳路径呢？今天，我们将学习如何解决最佳路径问题。
1. 讲解最佳路径概念和背景（10分钟）最佳路径问题是指在具有多个节点和路径的图中，找到一条路径使得起始节点到目标节点的总权重最小。
这在我们的生活和工作中有很多应用，比如导航系统。
接下来，我们将学习两种最短路径算法。
2. 迪杰斯特拉算法讲解和演示（25分钟）迪杰斯特拉算法是一种常用的解决最佳路径问题的算法。
让我来向大家介绍迪杰斯特拉算法的基本原理和步骤：1) 创建两个集合：一个用于存储已确定最短路径的节点，一个用于存储未确定最短路径的节点；2) 将起始节点加入已确定最短路径的节点集合中；3) 对于未确定最短路径的节点，计算其与起始节点的距离，并更新最短路径和距离；4) 重复以上步骤，直到目标节点被添加到已确定最短路径的节点集合中。
接下来，我将通过演示迪杰斯特拉算法的应用来帮助大家更好地理解。
3. 学生实践探究（30分钟）现在，让我们来进行一些实践探究，以加深对迪杰斯特拉算法的理解。
请你们在计算机上打开图形编辑软件，创建一个简单的图形，并使用迪杰斯特拉算法找到最佳路径。
4. 弗洛伊德算法讲解和实践（25分钟）除迪杰斯特拉算法外，我们还有另一种解决最佳路径问题的算法，那就是弗洛伊德算法。
14、最佳的路径、教学目标:1.利用已有的识字方法，自主学习本课生字，并能正确美观地书写。
联系上下文和自己已有的积累，理解生字词在文中的意思。
体会重点词语在表情达意上的作用。
2.了解迪斯尼乐园景点间路径的产生过程，从中理解来自生活的灵感与伟大建筑设计之间的联系。
3.正确、流利、有感情地朗读课文，积累美词佳句。
二、教学重点：品读课文，了解迪斯尼乐园景点间路径的产生过程，从而了解来自生活中的灵感与伟大建筑设计之间的联系。
三、教学难点: 理解重点词句，体会其表情达意上的作用。
四、课前准备:1.教师搜集有关格罗培斯的故事和生平的资料。
2.学生搜集迪斯尼乐园的资料。
五、教学课时: 2课时第一课时1课时、激趣导入，揭示课题1、同学们，你们喜欢看动画片么？大家一定对“米老鼠”“唐老鸭”这样的动画人物不陌生。
知道他们是谁创造的么？（美国动画片大师沃尔特.迪斯尼）2、（格罗培斯：美国哈佛大学建筑学院院长，现代主义大师和景观建筑方面的专家，他从事建筑研究40多年，攻克过无数个建筑方面的难题，在世界各地留下70多处精美的杰作。
）3、迪斯尼公司的创始人不但创造出了这么多个性鲜明、活泼可爱的动画人物，对于全世界热爱动画片的人来说，他还有一个巨大的贡献，那就是迪斯尼乐园。
迪斯尼乐园备受全世界男女老少的喜爱，这里可以说是每个人梦的故乡，好像来到了用梦和幻想编织的殿堂。
3、揭示课题，质疑。
今天我们要学习的课文，就是和迪斯尼乐园有关的。
【板书课题：6、最佳路径】（最佳路径：就是最好的路线。
）看到这个题目，你们脑中产生了哪些问题?（为什么迪斯尼乐园的路径是最佳路径？这条最佳路径是如何设计出来的？这是一条怎样的路径？）、初读课文，理解大意1、请同学们带着这些问题，自由朗读课文，要求读准字音。
2、检查读书情况。
指名分节通读全文，正音：滨、窄、踩，多音字：吆喝（h e）、看k①）管、调转（di GO zhu也）。
理解词语微不足道：非常渺小，不值得一提。
迎刃而解：，劈竹子时,头上几节一破开，下面的顺着刀口自己就裂开了.比喻处理事情、解决问题很顺利4、交流初步阅读后能解答的问题，也可提出新的问题。
5、理清课文层次你能按照事情的发生、发展、高潮、结果来给课文分分段吗?第一段1―― 2）写格罗培斯为迪斯尼乐园的路径设计大伤脑筋，决定前往地中海海滨（遇到难题）第二段（3）写一位年迈的葡萄园主卖葡萄的办法让格罗培斯从中受到启发。
（获得启示）第三段（4―― 5）,格罗培斯让人按照人们在草地上踩出的痕迹铺设人行道，这样的设计最终被评为世界最佳设计。
（完成设计获得最佳）6、能说说课文主要讲了一件什么事吗?（▲世界建筑大师格罗培斯为迪斯尼乐园的路径设计大伤脑筋，前往地中海海滨清理思绪, 后来从一位年老的葡萄园主卖葡萄的方法上受到启发，格罗培斯让人按照人们在草地上踩出的痕迹铺设人行道，这样的设计最终被评为世界最佳设计。
）（2课时）教学目标:1、有感情地朗读课文。
2、理解课文内容。
3 、懂得尊重他人，相信他人，给人自由与选择的机会，其中蕴含着巨大的价值。
教学准备：多媒体课件教学过程:、复习引入课文讲了一件什么事情?、感悟路径的最佳。
1演示课件，教师介绍：这就是迪斯尼乐园，小草……游客们，乐园提前开放，快来参观吧! 、（4节内容）你想参观哪里？（学生自由说）2一批又一批游客来了又走了，在迪斯尼乐园的草坪上留下了无数的小道，这些小道是怎样、的呢？为什么有宽有窄呢?一年之后，格罗培斯按照你们踩出的小道铺设了路径，游客们，再到迪斯尼乐园的草坪上, 3、你仿佛看到了怎样的小道?（我看到了有的小路宽，有的小路窄。
我看到草地上有很多的小脚印。
我看到小道像丝绸一样弯弯曲曲。
）4、走在这样大小路上，有怎样的感受？（无拘无束，自由）5、划一划课文，迅速找出最佳路径是怎样的一条路径?6、能用一句话来说吗?7、能用词语来说吗？（有窄有宽，优雅自然）现在再让我们再次读一读这八个浓缩的词语。
8走在这样大小路上，你想对格罗培斯说什么?（高超的设计、创意、尊重、无拘无束）小结：、鲁迅说世上本没有路，走的人多了，也就成了路”，自然是最美，人性是最美的。
这条小路让我们感受到了设计师对人们的尊重，高超的设计，感受到了设计的魅力。
三、读懂两种卖葡萄的方法1、过渡：世界建筑大师格罗培斯真是太高明了，不用自己绞尽脑汁去设计，而让游客自己走出来。
他怎么会想到这一招的呢？（从法国著名葡萄产区卖葡萄的方式中受到启发）2、自读课文，练说卖葡萄的方式。
3、让学生说说自己喜欢到哪去买葡萄，并说说自己的理由。
（板书：给人自由信任他人）4、自己用个词语概括一下不同的卖葡萄方法产生的不同结果。
（教师先出世一组，另一组让学生说）冷清 5、他得到的启发究竟是什么?6、。
哎呀，这个司机有点糊涂了，想一想，上车后他们会说些什么？想象他们的动作、神态、 语言，同桌进行对话，每对至少两次，联系上下文，说出设计方案，了解这一最佳路径的诞生与农民买葡萄之间的联系。
（教师参与学生讨论，时机点拨）格罗培斯 说：“格罗培斯 说：“ 总结：同学们刚才说得很好，把自己对课文的理解都说出来了，从中也学到了不少。
假如此时格罗培斯现在就在我们得眼前，你会对他说些什么呢？（格罗培斯他有了灵感能马 上抓住）（善于从成功者的做法中获得启示。
） 6、最佳路径的设计与法国南部农民卖葡萄有什么联系?（因为格罗培斯是受当地农民卖葡萄的方法而产生路径设计方案的，两者之间有一些共同点，都把选择的权利交给了大家，让大家去寻找最适合最佳的东西，都是顺其自然的，都 包含着对人们的信任、尊重••… 四、感受设计之难。
1创造这样一个最佳路径来，容易吗？（学生在书上批注）40多年——工作时间长经验丰富 无数个一一攻克难题多 经验丰富无人问津人流如潮 门可罗雀 门庭若市红火 司机问：“ ?”司机问：“ ?”2、 在交流中，主要紧扣2两小节中的一些词句:最微不足道一一设计路径不难3.交流后学生整理，补充批注。
（对路径设计的要求之高，总是力求完美，追求最佳，并为之付出艰辛的劳动。
对工作严谨一丝不苟、精益求精）4、小结：正是因为格罗培斯的细致严谨，追求完美，。
他追求的不是设计出”而是最佳” 才使他的设计成为了最佳路径。
如果没有他先前的一丝不苟，也不可能在这瞬间找到灵感，设计出最佳路径。
创造力，往小处说，就是要先努力，先进行认真的思考，然后才能抓住灵感。
五、写颁奖词一一深化“最佳路径”，进一步认识大师。
1同学们，假如你是伦敦国际园林建筑艺术研讨会上的专家、评委，你能说说为什么把迪斯尼乐园的路径设计评为最佳路径？迪斯尼乐园的路径设计之所以评为最佳路径，理由一:理由二:理由三▲这样的设计给了游人以权利，是把游人放在了第一位的；▲这样的设计是顺其自然的，看来在没有办法的时候，顺其自然是一种最佳的选择;▲道路的设计不是用脑子挖空心思想出来的，而是用脚走出来的▲它是众多的人自由选择的结果，符合众多人的心愿……专家们，那么多的理由让我们相信：读题。
2、、你觉得他是大师吗?总结：同学们，假如你是伦敦国际园林建筑艺术研讨会上的专家、评委，你能为他写颁奖词吗?3、创设情境：伦敦国际园林建筑艺术评比大赛颁奖典礼现场师：我宣布世界最佳路径设计奖获得者是迪斯尼乐园。
让我们以热烈的掌声欢迎格罗培斯先生上台领奖。
师：下面我们请评委会宣读颁奖词。
格罗培斯追求完美，先后修改了50多次，还不满意，最后让大家共同来创造，这样的路径已不是哪一个人的设计，而是给予我们每个人自由，任其选择，它把游人放在了第一位。
这许多小道不仅“有宽有窄”，而且“优雅自然”。
道路的设计不是挖空心思想出来的，而是用脚走出来的。
铺设的人行道没有刻板的模式，富有艺术性。
世界建筑大师之所以伟大，不仅因为他有精湛的艺术，创新的思维。
还因为他那种精益求精的精神，更表现在他尊重他人，为人着想的人本思想。
我们感谢格罗培斯，他送给了我们一个道理：有的时候，不知怎么办时，给人自由，任其选择，也许就是最佳路径。
3、专家们，那么多的理由让我们相信：读题。
六、拓展11.大师的设计给了我们什么启发?学了这篇课文，我们知道这最佳路径不光是指迪斯尼乐园的路径设计被评为最佳，也指这种这种设计路径的方法是最佳的，更是指让同学们学习格罗培斯这种在生活中留意观察，细心琢磨的方法。
这样每个人能找到属于自己的通往成功的最佳路径。
创新的思维，还在于精益求精的精神，更在于他尊重他人，为人着想的人本思想。
善于从成功者的做法中获得启示。
创造力，往小处说，就是要先努力，先进行认真的思考，然后才能抓住灵感。
2.生活中的哪些做法也体现出了最佳路径呢?自助餐厅里，食客可以自由挑选自己喜欢的食物。
购物超市里，顾客可以任意选购自己需要的商品。
游乐场里，游客可以随意选择自己喜欢的游艺项目。
3 ．总结：同学们，我们感谢格罗培斯，他送给我们一个道理：有的时候，不知怎么办的时候，给人自由，任其选择，也许是最佳路径。
在这里，老师真诚祝愿我们每一位同学能以格罗培斯为榜样，不断争取，创造“最佳”。
4、课外阅读《不要放过偶然的现象》板书设计：6、最佳路径自然天成优雅自然给人自由信任他人。
