五年级奥数--图形的面积(二)

不规则图形面积计算我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形，一般称为基本图形或规则图形.我们的面积及周长都有相应的公式直接计算.如下表：实际问题中，有些图形不是以基本图形的形状出现，而是由一些基本图形组合、拼凑成的，它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规则图形。

那么，不规则图形的面积及周长怎样去计算呢？我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系，问题就能解决了。

一、例题与方法指导例1 如右图，甲、乙两图形都是正方形，它们的边长分别是10厘米和12厘米.求阴影部分的面积。

思路导航：阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形（△ABG、△BDE、△EFG）的面积之和。

例2 如右图，正方形ABCD的边长为6厘米，△ABE、△ADF 与四边形AECF的面积彼此相等，求三角形AEF的面积.思路导航：∵△ABE 、△ADF 与四边形AECF 的面积彼此相等，∴四边形 AECF 的面积与△ABE 、△ADF 的面积都等于正方形ABCD 的13。

在△ABE 中，因为AB=6.所以BE=4，同理DF=4，因此CE=CF=2， ∴△ECF 的面积为2×2÷2=2。

所以S △AEF=S 四边形AECF-S △ECF=12-2=10（平方厘米）。

例3 两块等腰直角三角形的三角板，直角边分别是10厘米和6厘米。

如右图那样重合.求重合部分（阴影部分）的面积。

思路导航：在等腰直角三角形ABC 中∵AB=10∵EF=BF=AB-AF=10-6=4，∴阴影部分面积=S △ABG-S △BEF=25-8=17（平方厘米）。

例4 如右图，A 为△CDE 的DE 边上中点，BC=CD ，若△ABC （阴影部分）面积为5平方厘米.求△ABD 及△ACE 的面积.B C思路导航：取BD中点F，连结AF.因为△ADF、△ABF和△ABC等底、等高，所以它们的面积相等，都等于5平方厘米.∴△ACD的面积等于15平方厘米，△ABD的面积等于10平方厘米。

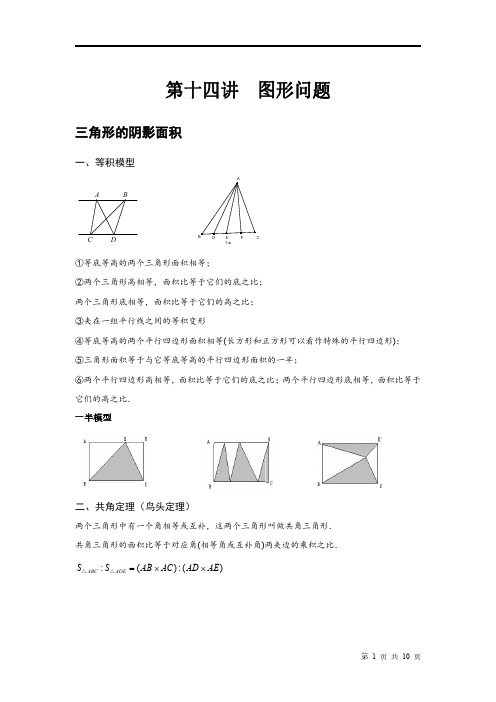
第十四讲图形问题三角形的阴影面积一、等积模型D C BA 1-a ①等底等高的两个三角形面积相等；②两个三角形高相等，面积比等于它们的底之比；两个三角形底相等，面积比等于它们的高之比；③夹在一组平行线之间的等积变形④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形)；⑤三角形面积等于与它等底等高的平行四边形面积的一半；⑥两个平行四边形高相等，面积比等于它们的底之比；两个平行四边形底相等，面积比等于它们的高之比．一半模型二、共角定理（鸟头定理）两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形．共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比．:():()ABC ADE S S AB AC AD AE =⨯⨯△△三、蝴蝶定理任意四边形中的比例关系(“蝴蝶定理”)：①1243::S S S S=或者1324S S S S⨯=⨯②()()1243::AO OC S S S S=++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径．通过构造模型，一方面可以使不规则四边形的面积关系与四边形内的三角形相联系；另一方面，也可以得到与面积对应的对角线的比例关系．S4S3S2S1ODCBA梯形中比例关系(“梯形蝴蝶定理”)：①2213::S S a b=②221324::::::S S S S a b ab ab=；③S的对应份数为()2a b+．例一、图是由两个完全一样的直角三角形重叠在一起，求阴影部分的面积。

AB CDOaS3S2S1S4练习一、图是两个完全一样的直角三角形重叠在一起，按图中的已知条件求阴影部分的面积。

（单位：厘米）练习二、图是正方形ABCD是有三个长方形拼成。

长方形EFGH的宽式正方形的一半，甲阴影部分的面积是30平方厘米。

求阴影部分的总面积。

例二、图是梯形的上底AB长20厘米，下底DC长30厘米，高15厘米，求阴影部分的面积。

练习一、图中，梯形的下底为8厘米，高为4厘米。

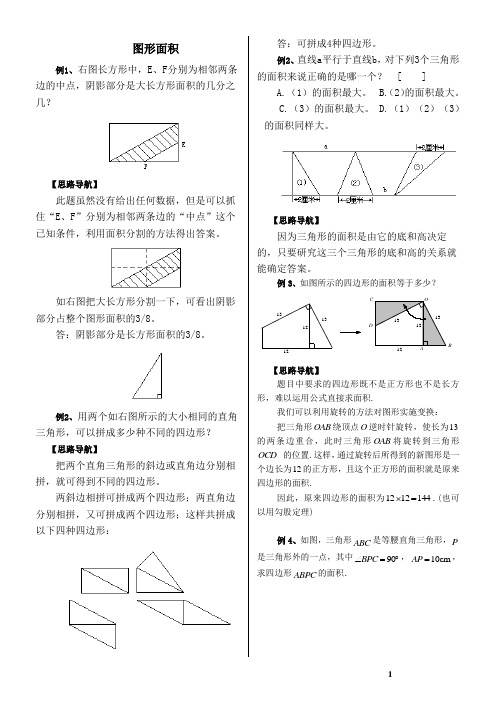
图形面积例1、右图长方形中，E、F分别为相邻两条边的中点，阴影部分是大长方形面积的几分之几？【思路导航】此题虽然没有给出任何数据，但是可以抓住“E、F”分别为相邻两条边的“中点”这个已知条件，利用面积分割的方法得出答案。

如右图把大长方形分割一下，可看出阴影部分占整个图形面积的3/8。

答：阴影部分是长方形面积的3/8。

例2、用两个如右图所示的大小相同的直角三角形，可以拼成多少种不同的四边形？【思路导航】把两个直角三角形的斜边或直角边分别相拼，就可得到不同的四边形。

两斜边相拼可拼成两个四边形；两直角边分别相拼，又可拼成两个四边形；这样共拼成以下四种四边形：答：可拼成4种四边形。

例2、直线a平行于直线b，对下列3个三角形的面积来说正确的是哪一个？[ ]A.（1）的面积最大。

B.（2）的面积最大。

C.（3）的面积最大。

D.（1）（2）（3）的面积同样大。

【思路导航】因为三角形的面积是由它的底和高决定的，只要研究这三个三角形的底和高的关系就能确定答案。

例3、如图所示的四边形的面积等于多少？ODBA13131213131212【思路导航】题目中要求的四边形既不是正方形也不是长方形，难以运用公式直接求面积.我们可以利用旋转的方法对图形实施变换：把三角形OAB绕顶点O逆时针旋转，使长为13的两条边重合，此时三角形OAB将旋转到三角形OCD的位置.这样，通过旋转后所得到的新图形是一个边长为12的正方形，且这个正方形的面积就是原来四边形的面积.因此，原来四边形的面积为1212144⨯=.(也可以用勾股定理)例4、如图，三角形ABC是等腰直角三角形，P 是三角形外的一点，其中90BPC∠=︒，10cmAP=，求四边形ABPC的面积．12 PDCBAP'PDCBA【思路导航】因为BAC ∠和BPC ∠都是直角，和为180︒，所以ABP ∠和ACP ∠的和也为180︒，可以旋转三角形APC ，使AC 和AB 重合，则四边形的面积转化为等腰直角三角形'AP P ，面积为1010250⨯÷=平方厘米．【随堂练习】1、边长是15厘米的3个正方形拼成一个长方形，这个长方形的周长是多少？2、用一块长8分米，宽4分米的长方形纸板与两块边长4分米的正方形纸板拼成一个正方形．拼成的正方形的周长是多少分米？3、两个大小相同的正方形拼成了一个长方形，长方形的周长比原来的两个正方形周长的和减少了6厘米，原来一个正方形的周长是多少厘米？4、(2007年”希望杯”第一试)右图中的阴影部分BCGF 是正方形，线段FH 长18厘米，线段AC 长24厘米，则长方形ADHE 的周长是 厘米．A CB5、如图，在长方形ABCD 中，EFGH 是正方形．已知10cm AF =，7cm HC =，求长方形ABCD 的周长．HGFE DCBA6、如右图所示，在一个正方形内画中、小两个正方形，使三个正方形具有公共顶点，这样大正方形被分割成了正方形区域甲，和L 形区域乙和丙．甲的周长为4厘米，乙的边长是甲的周长的1.5倍，丙的周长是乙的周长的1.5倍，那么丙的周长为多少厘米？EF 长多少厘米？F E A7、有9个小长方形，它们的长和宽分别相等，用这9个小长方形拼成的大长方形(如图)的面积是45平方厘米，求这个大长方形的周长．8、右图的长方形被分割成5个正方形，已知原长方形的面积为120平方厘米，求原长方形的长与宽．9、冯大叔给儿子做玩具用8个一样大的小长方形拼图，拼出了如图甲、乙的两种图案：图案甲是一个正方形，图案乙是一个大的长方形；图案甲的中间留下了边长是2cm的正方形小洞．求小长方形的长和宽？10、用同样的长方形条砖，在一个盆的周围砌成一个正方形边框，如右图所示．已知外面大正方形的周长是264厘米，里面小正方形的面积是900平方厘米，每块长方形条砖的长是_________厘米，宽是______厘米．11、如图所示。

1 / 4五年级奥数第六讲———平面图形面积的计算一、知识重点1. 基本平面图形特点及面积公式特点面积公式① 四条边都相等。

正方形② 四个角都是直角。

S=aa③ 有四条对称轴。

①对边相等。

长方形②四个角都是直角。

S=ab③有二条对称轴。

平行四边形三角形梯形① 两组对边平行且相等。

② 对角相等，相邻的两个角之和为180°③ 平行四边形简单变形。

①两边之和大于第三条边。

②两边之差小于第三条边。

③三个角的内角和是④有三条边和三个角，拥有稳固性。

① 只有一组对边平行。

② 中位线等于上下底和的一半。

S=ahS=ah ÷ 2S=(a+b)h ÷22. 基本解题方法：由两个或多个简单的基本几何图形组合成的组合图形，要计算这样的组合图形面积，先依据图形的基本关系，再运用分解、组合、平移、割补、添协助线等几种方法将图形变为基本图形分别计算。

【典型例题】【例 1】 已知平行四边表的面积是28 平方厘米，【练一练】假如用铁丝围成以下列图同样的求暗影部分的面积。

平行四边形，需要用多少厘米铁丝？（单位：厘米）1 / 4180°。

【例 2】求图中暗影部分的面积。

【练一练】下列图中甲和乙都是正方形，求暗影部分（单位：厘米）的面积。

（单位：厘米）【例 3】以下图，甲三角形的面积比【练一练】平行四边形ABCD 的边长乙三角形的面积大 6 平方厘米，求CE 的长度。

BC=10 厘米，直角三角形 BCE 的直角边 EC 长 8 厘米，已知暗影部分的面积比三角形 EFG 的面积大10 平方厘米。

求 CF 的长。

【例 4】两条对角线把梯形 ABCD 切割成四个三角形。

【练一练】下边的梯形 ABCD 中，下底是已知两个三角形的面积（以下图），求另两个三角形上底的 2 倍， E 是 AB 的中点，求梯形 ABCD 的面积各是多少？（单位：厘米）的面积是三角形EDB 面积的多少倍？B【练一练】【练一练】计算下边图形的面积。

22B A 302432P N M F E D C B A 五年级奥数训练——长方形、正方形的面积姓名：例1 已知大正方形比小正方形边长多2厘米，大正方形比小正方形的面积大40平方厘米.求大、小正方形的面积各是多少平方厘米？练 习 一 有一块长方形草地，长20米，宽15米。

在它的四周向外筑一条宽2米的小路,求小路的面积.例 2 一个大长方形被两条平行于它的两条边的线段分成四个较小的长方形，其中三个长方形的面积如下图所求,求第四个长方形的面积.练 习 二 下图一个长方形被分成四个小长方形，其中三个长方形的面积分别是24平方厘米、30平方厘米和32平方厘米,求阴影部分的面积。

例3 把20分米长的线段分成两段,并且在每一段上作一正方形，已知两个正方形的面积相差40平方分米，大正方形的面积是多少平方分米？一块正方形，一边划出15米，另一边划出10米搞绿化，剩下的面积比原来减少了1350平方米。

这块地原来的面积是多少平方米?例4 有一个正方形ABCD如下图，请把这个正方形的面积扩大1倍，并画出来。

练习四四个完全一样的长方形和一个小正方形组成了一个大正方形，如果大、小正方形的面积分别是49平方米和4平方米，求其中一个长方形的宽.例5 有一个周长是72厘米的长方形，它是由三个大小相等的正方形拼成的.一个正方形的面积是多少平方厘米？练习五五个同样大小的正方形拼成一个长方形,这个长方形的周长是36厘米，求每个正方形的面积是多少平方厘米?588881、把一个长方形的长增加5分米，宽增加8分米后,得到一个面积比原长方形多181平方分米的正方形。

求这个正方形的边长是多少分米？2、下图中阴影部分是边长5厘米的正方形，四块完全一样的长方形的宽是8厘米,求整个图形的面积.3、有一个正方形草坪，沿草坪四周向外修建一米宽的小路，路面面积是80平方米。

求草坪的面积。

4、下图中，正方形ABCD的边长4厘米,求长方形EFGD的面积。

5、有一个小长方形，它和一个正方形拼成了一个大长方形ABCD(如下图）,已知大长方形的面积是35平方厘米,且周长比原来小长方形的周长多10厘米。

组合图形的面积【2 】1.根本平面图形特点及面积公式特点面积公式正方形①四条边都相等.②四个角都是直角.③有四条对称轴.S=a2长方形①对边相等.②四个角都是直角.③有二条对称轴.S=ab平行四边形①两组对边平行且相等.②对角相等,相邻的两个角之和为180°③平行四边形轻易变形.S=ah三角形①双方之和大于第三条边.②双方之差小于第三条边.③三个角的内角和是180°.④有三条边和三个角,具有稳固性.S=ah÷2梯形①只有一组对边平行.②中位线等于高低底和的一半.S=(a+b)h÷22.根本解题办法：由两个或多个简略的根本几何图形组合成的组合图形,要盘算如许的组合图形面积,先依据图形的根本关系,再应用分化.组合.平移.割补.添帮助线等几种办法将图形变成根本图形分离盘算.1.已知右面的两个正方形边长分离为6分米和4分米,求图中暗影部分的面积.2.右图是两个雷同的直角三角形叠在一路,求暗影部分的面积.（单位：厘米）3.如图,这个长方形的长是9厘米,宽是8厘米,A和B是宽的中点,求长方形内暗影部分的面积.4.在右图中,三角形EDF的面积比三角形ABE的面积大6平方厘米,已知长方形ABDC的长和宽分离为6厘米.4厘米,DF的长是若干厘米？5.正方形ABCD的面积是100平方厘米,AE=8厘米,CF=6厘米,求暗影部分的面积.6.右图是一块长方形公园绿地,绿地长24米,宽16米,中央有一条宽为2米的道路,求草地（暗影部分）的面积.7.如图,三角形ABC的面积是24平方厘米,且DC=2AD,E.F分离是AF.BC的中点,那么暗影部分的面积是若干？8.如下图,是一块长方形草地,长方形的长是16米,宽是10米,中央有两条宽2米的道路,一条是长方形,一条是平行四边形,那么有草部分（暗影部分）的面积有多大？9.如图,一个三角形的底长5米,假如底延伸1米,那么面积就增长2平方米.问本来的三角形的面积是若干平方米?1米组合图形的面积功课1.在右图中,三角形EDF的面积比三角形ABE的面积大75平方厘米,已知正方形ABCD的边长为15厘米,DF的长是若干厘米？2.如图,ABCD是一个长12厘米,宽5厘米的长方形,求暗影部分三角形ACE的面积.3.已知正方形乙的边长是8厘米,正方形甲的面积是36平方厘米,那么图中暗影部分的面积是若干？4.如图,A.B两点是长方形长和宽的中点,那么暗影部分占长方形的面积是若干？5.如图,在平行四边形ABCD中,E.F分离是AC.BC的三等分点,且平行四边形的.面积为54平方厘米,求S△BEF6.盘算右边图形的面积.（至罕用3种办法）（单位：米）。

组合图形的面积姓名知识、规律、方法1、常见的几种规则图形。

（1）三角形：有三条线段首位相接围成的图形。

分类：（2）四边形2、面积计算公式。

三角形：S=ah÷2 长方形：S=ab正方形：S=a2 平行四边形：S=ah梯形：S=（a+b）h÷2【例题1】正图正方形中套着一个长方形，正方形的边长是12厘米，长方形的四个角的顶点把正方形的四条边各分成两段，其中长的一段是短的2倍。

求中间长方形的面积。

【例题2】四边形ABCD和四边形DEFG都是正方形，已知三角形AFH的面积是7平方厘米。

三角形CDH的面积是多少平方厘米？【例题3】下图中正方形的边长为8厘米，CE为20厘米，梯形BCDF的面积是多少平方厘米？【例题4】图中ABCD是长方形，三角形EFD的面积比三角形ABF的面积大6平方厘米，求ED的长。

练习：一、已知右面的两个正方形边长分别为6分米和4分米，求图中阴影部分的面积。

二、右图是两个相同的直角三角形叠在一起，求阴影部分的面积。

（单位：厘米）三、如图，这个长方形的长是9厘米，宽是8厘米，A和B是宽的中点，求长方形内阴影部分的面积。

四、右图是一块长方形公园绿地，绿地长24米，宽16米，中间有一条宽为2米的道路，求草地（阴影部分）的面积。

五、如图，三角形ABC的面积是90平方厘米，EF平行于BC，AB=3AE，那么三角形甲、乙、丙的面积各是多少平方厘米？六、在等腰梯形ABCD中，AD=12厘米，高DF=10厘米。

三角形CDE的面积是24平方厘米。

求梯形面积。

七、在右图中，三角形EDF的面积比三角形ABE的面积大75平方厘米，已知正方形ABCD的边长为15厘米，DF的长是多少厘米？八、如图，ABCD是一个长12厘米，宽5厘米的长方形，求阴影部分三角形ACE的面积。

九、如图，A、B两点是长方形长和宽的中点，长为8，宽为6，那么阴影部分占长方形的面积是多少？十、在正方形ABCD中，AB是4厘米，三角形BCF比三角形DEF的面积多2平方厘米，求DE的长。

完整版)五年级奥数平面图形面积计算五年级奥数第六讲——平面图形面积的计算一、知识要点1.基本平面图形特征及面积公式正方形：特征：四条边相等，四个角都是直角，有四条对称轴。

面积公式：S=边长的平方长方形：特征：对边相等，四个角都是直角，有二条对称轴。

面积公式：S=长×宽平行四边形：特征：两组对边平行且相等，对角相等，相邻的两个角之和为180°，容易变形。

面积公式：S=底边×高三角形：特征：两边之和大于第三条边，两边之差小于第三条边，三个角的内角和是180°，具有稳定性。

面积公式：S=底边×XXX÷2梯形：特征：只有一组对边平行，中位线等于上下底和的一半。

面积公式：S=(上底+下底)×高÷22.基本解题方法：由两个或多个简单的基本几何图形组合成的组合图形，要计算这样的组合图形面积，先根据图形的基本关系，再运用分解、组合、平移、割补、添辅助线等几种方法将图形变成基本图形分别计算。

典型例题】例1】已知平行四边形的面积是28平方厘米，求阴影部分的面积。

例2】求图中阴影部分的面积。

例3】如图所示，甲三角形的面积比乙三角形的面积大6平方厘米，求CE的长度。

例4】两条对角线把梯形ABCD分割成四个三角形。

已知两个三角形的面积（如图所示），求另两个三角形的面积各是多少？练与拓展】1.计算下面图形的面积。

2.下面的梯形中，阴影部分面积是150平方厘米，求梯形的面积。

3.正方形ABCD的边长是12厘米，已知DE是EC长度的2倍，求三角形DEF的面积和CF的长。

4.平行四边形ABCD的边长BC=10厘米，直角三角形BCE的直角边EC长8厘米，已知阴影部分的面积比三角形EFG的面积大10平方厘米，求CF的长。

5.正方形ABCD的面积是100平方厘米，AE=8厘米，请计算以下图形的面积。

1.在一块长80米、宽30米的长方形地上，修了宽为2米和3米的两条小路，求草地的面积。

长方形、正方形的周长［知识要点］同学们都知道，长方形的周长=（长＋宽）×2，正方形的周长=边长×4。

长方形、正方形的周长公式只能用来计算标准的长方形和正方形的周长。

如何应用所学知识巧求表面上看起来不是长方形或正方形的图形的周长，还需同学们灵活应用已学知识，掌握转化的思考方法，把复杂的问题转化为标准的图形，以便计算它们的周长。

［范例解析］例1有5张同样大小的纸如下图（a）重叠着，每张纸都是边长6厘米的正方形，重叠的部分为边长的一半，求重叠后图形的周长。

思路与导航根据题意，我们可以把每个正方形的边长的一半同时向左、右、上、下平移（如图b），转化成一个大正方形，这个大正方形的周长和原来5个小正方形重叠后的图形的周长相等。

因此，所求周长是18×4=72厘米。

例2 一块长方形木板，沿着它的长度不同的两条边各截去4厘米，截掉的面积为192平方厘米。

现在这块木板的周长是多少厘米？思路导航把截掉的192平方厘米分成A、B、C三块（如图），其中AB的面积是192－4×4=176（平方厘米）。

把A和B移到一起拼成一个宽4厘米的长方形，而此长方形的长就是这块木板剩下部分的周长的一半。

176÷4=44（厘米），现在这块木板的周长是44×2=88（厘米）。

例3求下列图形的周长。

（单位：厘米）思路导航：从图中可以看出，整个图形的周长由八条线段围成，其中四条横着，四条竖着。

其中上面三条横着的线段和是10厘米，那么这样四条横着的线段和是10+10=20（厘米），四条竖着的线段和是8×2+2×2=20（厘米）。

所以，整个图形的周长是20+20=40（厘米）。

例4下图是边长为4厘米的正方形，求正方形中阴影部分的周长。

例5 如下图，阴影部分是正方形，DF=6厘米，AB=9厘米，求最大的长方形的周长。

分析根据题意可知，最大长方形的宽就是正方形的边长。

因为BC=EF，CF=DE，所以，AB＋BC＋CF=AB＋FE＋ED=9＋6=15（厘米），这正好是最大长方形周长的一半。