椭圆与双曲线的标准方程共21页

椭圆双曲线的准线方程
1、椭圆：
(x^2/a^2)+(y^2/b^2)=1（a>b>0）
准线方程为：x=±a^2/c
2、双曲线
双曲线：(x^2/a^2)-(y^2/b^2)=1
准线方程为：x=±a^2/c
圆锥曲线上任意一点到一焦点的距离与其对应的准线（同在Y轴一侧的焦点与准线）对应的距离比为离心率。

椭圆上任意一点到焦点距离与该点到相应准线距离的比等于离心率e。

扩展资料
几何性质：
准线到顶点的距离为Rn/e，准线到焦点的距离为P = Rn(1+e)/e = L0/e 。

当离心率e大于零时，则P为有限量，准线到焦点的距离为P = Rn(1+e)/e = L0/e 。

当离心率e等于零时，则P为无限大，P是非普适量。

用无限远来定义圆锥曲线是不符合常理的。

教科书中定义局限性的原因是不了解准线的几何性质，当e等于零时则准线为无限远，准线是非普适量，是局限性的量。

教科书中用准线来定义圆锥曲线不包含圆的原因。

右焦点对应右准线,左焦点对应左准线
返回
5
椭圆的标准方程：
y
F1
O F2
x
双曲线的标准方程:
y
F2
O
x
F1
返回6
两种标准方程的椭圆性质的比较
方程 图形
y
O
F1
F2 x
A2 y
F2 B2
B1 O x F1
范围 对称性
顶点 离心率
-a≤x≤a,-b ≤y≤b
A1
-b ≤x≤b, -a≤y≤a
关于x轴、y轴、原点对称 A1(-a,0), A2(a,0) A1(0,-a), A2(0,a)
B1(0,-b), B2(0,b) B1(-b,0), B2(b,0)
7
双曲线
性 质 图象
范围
对称 性
顶点
渐近 线
离心 率
y
ox 或
y
或
ox
关于 坐标 轴和 原点 都对 称
返回8
求椭圆或双曲线的标准方程方法步骤:
(1)焦点明确直接设题,再求出a,b
(2)焦点不明确设题技巧:椭圆可设为
双曲线可设为: 等轴双曲线可设为:
(3)已知双曲线
的两个焦点分别
为F1,F2,点P在双曲线上且满足∠F1PF2=90°, 求△F1PF2的面积
13
例4:焦半径公式的应用
在双曲线
上求一
点P,使它到左焦点的距离是它
到右焦点的距离的两倍
14
椭圆与 双曲线
(复习课)
1
复习流程
知识回顾 典例再现
2
知识网络
定义
标准方程
性质 常用结论
3
椭圆的第一定义:平面上到两个定点的距离的和（2a）等 于常数（大于|F1F2 |）的点的轨迹叫椭圆。

04
椭圆与双曲线在生活 中的应用
建筑学：拱形结构设计与优化
椭圆型拱门
椭圆型拱门在建筑设计中常用来 增加空间感和美观度，其优雅的 曲线形状能够分散压力，提高结
构的稳定性。
椭圆型穹顶
大型公共建筑中，椭圆型穹顶不 仅具有视觉冲击力，还能有效地 分散重力，提高建筑的承重能力
。
双曲线型结构
双曲线在建筑设计中可用于创造 独特的空间效果，如双曲线型楼 梯、走廊等，增加建筑的动感和
几何意义
离心率反映了焦点到椭圆中心的距离与长轴半径的比例关系，也决定了椭圆形 状的变化。
椭圆上任意一点性质
到两焦点的距离之和
椭圆上任意一点到两个焦点的距离之 和等于长轴的长度，即 (2a)。
中点性质
任意弦的中点轨迹是以椭圆中心为中 心、以短轴为直径的圆。
切线性质
过椭圆上任意一点的切线与通过该点 且与长轴平行的直线交于一点，该点 位于与焦点连线上的中垂线上。
THANKS
感谢观看
综合运用各种技巧
在解题过程中，可以综合运用代数、几何、三角等多种数学知识和 技巧，提高解题效率。
06
总结回顾与拓展延伸
关键知识点总结回顾
椭圆的定义与性质
双曲线的定义与性质
椭圆是平面上所有满足到两个定点（焦点 ）距离之和为常数的点的集合；其性质包 括对称性、离心率、长轴和短轴等。
双曲线是平面上所有满足到两个定点（焦 点）距离之差为常数的点的集合；其性质 包括对称性、离心率、实轴和虚轴等。
椭圆与双曲线在现实生活中的应用
介绍椭圆和双曲线在物理学、工程学、经济学等领域的应用，以及其 在解决实际问题中的重要作用。
著名数学家的贡献
介绍对椭圆和双曲线研究做出重要贡献的数学家，如阿波罗尼乌斯、 开普勒等，以及他们的主要成就和思想方法。

椭圆的定义、性质及标准方程1. 椭圆的定义：⑴第一定义：平面内与两个定点12F F 、的距离之和等于常数（大于12F F ）的点的轨迹叫做椭圆。

这两个定点叫做椭圆的焦点，两焦点的距离叫做椭圆的焦距。

⑵第二定义：动点M 到定点F 的距离和它到定直线l 的距离之比等于常数)10(<<e e ，则动点M 的轨迹叫做椭圆。

定点F 是椭圆的焦点，定直线l 叫做椭圆的准线，常数e 叫做椭圆的离心率。

说明：①若常数2a 等于2c ，则动点轨迹是线段12F F 。

②若常数2a 小于2c ，则动点轨迹不存在。

2.3. 椭圆上的任一点和焦点连结的线段长称为焦半径。

焦半径公式：椭圆焦点在x 轴上时，设12F F 、分别是椭圆的左、右焦点，()00P x y ，是椭圆上任一点，则10PF a ex =+，20PF a ex =-。

推导过程：由第二定义得11PF e d =（1d 为点P 到左准线的距离）， 则211000a PF ed e x ex a a ex c ⎛⎫==+=+=+ ⎪⎝⎭；同理得20PF a ex =-。

简记为：左“＋”右“－”。

由此可见，过焦点的弦的弦长是一个仅与它的中点的横坐标有关的数。

22221x y a b +=；若焦点在y 轴上，则为22221y x a b+=。

有时为了运算方便，设),0(122n m m ny mx ≠>=+。

双曲线的定义、方程和性质1． 定义（1）第一定义：平面内到两定点F 1、F 2的距离之差的绝对值等于定长2a （小于|F 1F 2|）的点的轨迹叫双曲线。

说明：①||PF 1|-|PF 2||=2a （2a <|F 1F 2|）是双曲线；若2a=|F 1F 2|，轨迹是以F 1、F 2为端点的射线；2a >|F 1F 2|时无轨迹。

②设M 是双曲线上任意一点，若M 点在双曲线右边一支上，则|MF 1|>|MF 2|，|MF 1|-|MF 2|=2a ；若M 在双曲线的左支上，则|MF 1|<|MF 2|，|MF 1|-|MF 2|=-2a ，故|MF 1|-|MF 2|=±2a ，这是与椭圆不同的地方。

椭圆和双曲线公式
椭圆的标准方程共分两种情况：
当焦点在x轴时，椭圆的标准方程是：x^2/a^2+y^2/b^2=1，(a>b>0)；当焦点在y轴时，椭圆的标准方程是：y^2/a^2+x^2/b^2=1，(a>b>0)；其中a^2-c^2=b^2。

推导:PF1+PF2>F1F2(P为椭圆上的点F为焦点)。

双曲线的标准方程分两种情况：
焦点在X轴上时为：x^2/a^2-y^2/b^2=1，（a>0，b>0）。

焦点在Y轴上时为：y^2/a^2-x^2/b^2=1，（a>0，b>0）。

双曲线的离心率为：e=c/a
双曲线的焦点在y轴上的双曲线的渐近线为：y=+-（a/b）*x。

扩展资料
设椭圆的两个焦点分别为F1，F2，它们之间的距离为2c，椭圆上任意一点到F1，F2的距离和为2a（2a>2c）。

以F1，F2所在直线为x轴，线段F1F2的垂直平分线为y轴，建立直角坐标系xOy，则F1,F2的坐标分别为（-c,0)，（c,0)。

等轴双曲线：一双曲线的实轴与虚轴长相等即：2a=2b且e=√2、这时渐近线方程为：y=±x（无论焦点在x轴还是y轴）。

例1
已知点P(x,y)到定点F(c,0)的距离与它到定直
a2 c 线l:x= 的距离的比是常数 (a>c>0),求点P的轨迹. c a
y
P
· F
l
O
x
若(a>c>0)变为(c>a>0)呢?
解 :根据题意可得
化简得
(a2 c2 ) x2 a2 y 2 a2 (a2 c2 )
( x c) 2 y 2 c 2 a a | x| c
可知，椭圆、双曲线、抛物线有共同性质为:
平面内到一定点F 与到一条定直线l 的距离之比为常数 e 的点的轨迹: ( 点F 不在直线l 上） 当 0< e <1 时, 点的轨迹是椭圆. 当 e >1 时, 点的轨迹是双曲线. 当 e = 1 时, 点的轨迹是抛物线.
其中e是圆锥曲线的离心率, 定点F是圆锥曲线的焦点, 定直线l是圆锥曲线的准线.
x2 y2 1 4 3
1 2
3. 动点P( x, y)到定点A(3,0)的距离比它到定直线 x=-5的距离小2,则动点P的轨迹方程是 y 2 12 x
例3 的距离.
已知双曲线
x2 y2 1 64 36
上一点P到左焦点的距离为14，求P点到右准线
法一:由已知可得a=8，b=6，c=10.
圆锥曲线的共同性质
复习回顾
1、 椭圆的定义：
表达式 |PF1|+|PF2|=2a(2a>|F1F2|）
平面内到两定点 F1、F2 距离之和等于常数 2a (2a>|F1F2|）的点的轨迹
2 、双曲线的定义：
平面内到两定点F1、F2 距离之差的绝对值等于常数2a (2a< |F1F2| )的点的轨迹 表达式||PF1|-|PF2||=2a (2a<|F1F2|)

||MF1|－|MF2||=2a
x2 y2 a2 b2 1(a 0,b 0)
y2 a2
x2 b2
1(a
0,b
0)
F（±c，0） F（0，±c）
F（±c，0） F（0，±c）
a>b>0，a2=b2+c2
a>0，b>0，但a不一 定大于b，c2=a2+b2
y
P
F1 O F2 x
双曲线的更多秘密， 等着我们一起探索！
绘制距离之差为定值 的点的运动轨迹
设︱FF2︱=2a
-6-
运动过程中，平面上动点M到两定点距离的差为常数
特点观察
-7-
绘制距离之差为定值的 点的运动轨迹过程中
①如图(A)， |MF1|-|MF2|=|F2F|=2a
②如图(B)，
|MF2||MF1|=|F1F|=2a
由①②综合可得：
| |MF1|-|MF2| | = 2a
焦点在X轴上的双曲线标准方程
c2=a2+b2
-12-
焦点位置改变，标准方程如何变化？
y
M
F1 O F2 x
y M
F2 x
O
F1
x2 a2
F2(c,0)
c2=a2+b2
(a 0，b 0)
y2 x2 a2 b2 1
F1(0,-c),F2(0,c)
-13-
根据标准方程判断焦点位置
2.3 双曲线及其标准方程
生活中的双曲线
发电厂冷却塔外形线
-2-
巴西利亚大教堂
花瓶轮廓线
反比例函数图像
-3-
数学中的双曲线
F1 o F2
双曲线及其标准方程

椭圆、双曲线、抛物线的标准方程与几何性质
椭圆 1．到两定点 F1,F2 的距离之 和为定值 2a(2a>|F1F2|)的点 的轨迹 2．与定点和直线的距离之 比为定值 e 的点的轨迹. （0<e<1） 双曲线 1．到两定点 F1,F2 的距 离之差的绝对值为定值 2a(0<2a<|F1F2|)的点的 轨迹 2．与定点和直线的距离 之比为定值 e 的点的轨 迹.（e>1） 抛物线
|x| a，yR 原点 O（0，0） (a,0), (─a,0) x 轴，y 轴; 实轴长 2a, 虚轴长 2b. F1(c,0), F2(─c,0) 2c （c= a 2 b 2 ）
e c (e 1) a
x0 (0,0) x轴
p F ( ,0 ) 2
对称轴 焦点 焦距 离心率 准线
定
义
与定点和直线的距离相 等的点的轨迹. （e=1）
图 形
方
标准 方程 参数 方程 范围 中心 顶点
x2 y2 1 ( a b >0) a2 b2
x2 y2 1 (a>0,b>0) a2 b2
y2=2px
x 2 pt 2 y 2 pt (t 为参数)
程
x a cos y b sin (参数为离心角）
─axa，─byb 原点 O（0，0） (a,0), (─a,0), (0,b) , (0,─b) x 轴，y 轴； 长轴长 2a,短轴长 2b F1(c,0), F2(─c,0) 2c （c= a 2 b 2 ）
e c (0 e 1) a
x a sec y b tan (参数为离心角）
e=1
x p 2

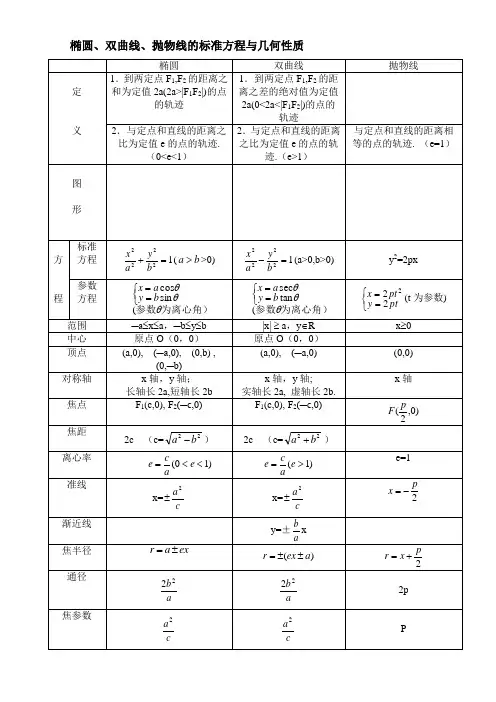
椭圆_双曲线_知识点
椭圆与双曲线是以二次曲线为基础的曲线，这两种曲线同属于双曲线族。

椭圆曲线的
二次方程如下：
$$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$$
其中，a,b代表椭圆的两个半径；同时，双曲线的标准二次方程为：
$$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$$
可以看出，两者只有被除数和方向不同，同是都为常数。

从表面上看，椭圆是左右对称，而双曲线则形式各不相同，收放自如，具有左右对称性以及上下对称性。

这两种曲线均为二次曲线，但两者间仍有明显区别：对于同一点，椭圆曲线的切线是
弧形的，而双曲线的切线是折线的。

而且，椭圆的极点的横纵坐标都有实数值，而双曲线
的极点的横坐标为实数，纵坐标都是无穷小。

另外，椭圆、双曲线等二次曲线的性质有共同之处，比如可以到达任一点的过渡性、
经过原点的轨迹是完美的圆周、经过任一点的二阶导数值为0 。

椭圆曲线在数学中被广泛用于实际应用，比如加密技术中的椭圆曲线加密，常用于方
便快捷的现代加密算法；双曲线方程式是高等数学中重要的内容，可用于证明费马小定理。

▪
26、要使整个人生都过得舒适、愉快，这是不可能的，因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情，化为上进的力量，才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者，好之者不如乐之者。——孔子
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人，倚靠在明眼的跛子肩上。——叔本华
谢谢！
21
要冒一次险!整个生命就是一场冒险。走得最远的人，常是愿意 去做，并愿意去冒险的人。“稳妥”之船，从未能从岸边走远。-戴尔．卡耐基。
梦 境
3、人生就像一杯没有加糖的咖啡，喝起来是苦涩的，回味起来却有 久久不会退去的余香。
椭圆与双曲线的标准方程 4、守业的最好办法就是不断的发展。 5、当爱不能完美，我宁愿选择无悔，不管来生多么美丽，我不愿失 去今生对你的记忆，我不求天长地久的美景，我只要生生世世的轮 回里有你。

共焦点的椭圆与双曲线方程的设法1. 概述共焦点的椭圆与双曲线方程是数学中一个重要且常见的问题。

通过研究共焦点椭圆与双曲线的方程，可以深入理解数学中椭圆和双曲线的性质，对于解决实际问题具有重要的理论和实际意义。

本文将探讨共焦点的椭圆与双曲线方程的推导及其相关性质。

2. 共焦点椭圆与双曲线的定义共焦点椭圆与双曲线是指在同一平面上，有两个不同的集合（椭圆和双曲线），它们的焦点相同。

椭圆是指平面上到两定点的距离之和等于常数的动点轨迹，而双曲线是指平面上到一对定点的距离之差等于常数的动点轨迹。

共焦点椭圆与双曲线即是这样两种集合的焦点相同，并且这两种集合存在一定关系的情况。

3. 共焦点椭圆与双曲线的方程共焦点椭圆与双曲线的方程可以通过公式推导得到。

对于椭圆而言，其标准方程为：\[ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \]对于双曲线而言，其标准方程为：\[ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \]当两者具有相同焦点时，在同一坐标系中，椭圆的焦点坐标为F(ae, 0)和F'(-ae, 0)，双曲线的焦点坐标为F(ae, 0)和F'(-ae, 0)。

根据这一特性，可以得到共焦点椭圆与双曲线的方程。

4. 共焦点椭圆与双曲线的性质共焦点椭圆与双曲线有许多重要的性质，这些性质对于理解椭圆和双曲线的特点具有重要意义。

4.1 共焦点椭圆与双曲线的焦点性质：由于共焦点椭圆与双曲线具有相同的焦点，因此它们的焦点性质是相似的。

椭圆的焦点性质是指动点到两焦点的距离之和是常数，而双曲线的焦点性质是指动点到两焦点的距离之差是常数。

在共焦点曲线中，这一性质是相互关联的，体现了它们具有共同的焦点。

4.2 共焦点椭圆与双曲线的几何性质：共焦点椭圆与双曲线在几何性质上也有一些相似之处。

它们都可以通过离心率、焦距和半长轴等参数进行描述，而这些参数与焦点密切相关，从而展现出共焦点曲线的特殊性质。

拉动拉链（M），思考拉链头（M）运动的轨迹是什么图形？
双曲线的定义
①如图(A)， |MF1|-|MF2|=2a
②如图(B)，|MF2|-|MF1|=2a
由①②可得： | |MF1|-|MF2| | = 2a （差的绝对值）上面 两条
曲线合起来叫做双曲线,每一条叫做双曲线的一支.
双曲线的定义
（2）定义
北师大版选择性必修一
2.2.1 双曲线的标准方程
复习
复习 平面内到两个定点F1,F2的距离之和等于常数(大于|F1F2|)的点
的集合（或轨迹）叫做椭圆.
问题1 如果平面内到两个定点F1,F2的距离之差也是一个常数，这
样的点的轨迹是什么图形呢？
双曲线的定义
模型试验：取一条拉链，如图，把它固定在板上的F1、F2两点，

tan
2
中2可以直接使用此公式求双曲线焦点三角形的面积．
双曲线的焦点三角形
例3
2
F1，F2是双曲线
4
−
2
9
= 1的两个焦点，点P在双曲线右支
上，∠F1PF2＝90°.求△F1PF2的面积．
双曲线的轨迹方程
例4 在△ABC中,已知||＝4 2,且三个内角A,B,C满足2sin A＋
sin C＝2sin B．建立适当的坐标系，求顶点C的轨迹方程．
点的轨迹是什么？
2、若常数2a=0,轨迹是什么?
双曲线的定义
3、若常数2a=|F1F2|轨迹是什么？
4、若常数2a＞|F1F2|轨迹是什么？
双曲线的标准方程
双曲线标准方程的推导
(1)建立直角坐标系.
y
(2)设点的坐标
M
(3)根据定义推导出双曲线的标准方程

椭圆与双曲线椭圆与双曲线是数学中的重要曲线，它们在几何学、物理学和工程学中起着重要的作用。

本文将对椭圆与双曲线进行详细介绍，并讨论它们的性质和应用。

一、椭圆的定义和性质椭圆可以通过以下定义得到：给定一个固定点F（焦点）和一条不经过焦点F的定长线段2a，所有与焦点F的距离之和等于定长线段2a 的点P的轨迹，就构成一个椭圆。

椭圆的性质如下：1. 焦点到椭圆上任意一点的距离之和等于定长线段2a；2. 如果椭圆的长轴长度为2a，短轴长度为2b，且a>b，则椭圆的离心率e的计算公式为e=c/a，其中c为焦点到中心的距离；3. 椭圆的离心率e满足0<e<1，当e=0时，椭圆是一个圆；4. 椭圆的焦点、长轴、短轴都是对称的。

二、椭圆的应用椭圆在现实生活和科学研究中有广泛的应用。

以下是一些椭圆的应用：1. 天体运动：行星围绕太阳的轨道是椭圆；2. 高速公路设计：高速公路的水平曲线通常采用椭圆形状，以保证驾驶员的安全视距；3. 弦乐器：弦乐器中的琴弦振动生成椭圆形的波形；4. 通信：卫星轨道常采用椭圆形状。

三、双曲线的定义和性质双曲线可以通过以下定义得到：给定一个固定点F（焦点）和一条且不经过焦点F的定长线段2a，所有与焦点F的距离之差等于定长线段2a的点P的轨迹，就构成一个双曲线。

双曲线的性质如下：1. 焦点到双曲线上任意一点的距离之差等于定长线段2a；2. 双曲线的离心率e的计算公式为e=c/a，其中c为焦点到中心的距离；3. 双曲线的离心率e满足e>1，当e=1时，双曲线是一个抛物线；4. 双曲线的对称轴、焦点、顶点等都有特定的性质。

四、双曲线的应用双曲线在不同领域有广泛的应用。

以下是一些双曲线的应用：1. 物理学：双曲线是物理学中许多运动的轨迹，如陀螺、行星运动等；2. 工程学：双曲线广泛应用于工程设计，如天桥、隧道和大坝的拱形结构等；3. 电磁学：电场和磁场分布呈现出双曲线形状，双曲线方程用于描述电磁波的传播；4. 统计学：双曲线函数可用于描述分布函数。

性质应用
双曲线的性质在许多领域中都有应用。例如，在声学中，声音的传播路径可以用 双曲线来描述。在光学中，双曲线用于描述光的折射和反射。此外，双曲线还用 于描述电子的运动轨迹以及某些化学反应的动力学。
图像与性质应用的比较
相同点
椭圆和双曲线都是二次曲线，具有一些共同的性质。例如，它们都具有两个焦点，且都满足特定的数学方程。
双曲线的焦点与离心率
焦点
双曲线有两个焦点，位于双曲线 的两侧，与双曲线相切。
离心率
双曲线的离心率是衡量双曲线开 口程度的指标，其值大于1。离心 率越大，双曲线的开口程度越大 。
焦点与离心率比较
焦点数量
焦点位置
离心率范围
几何特性
椭圆和双曲线都有两个焦点。
椭圆的焦点位于椭圆中心两侧 ，而双曲线的焦点位于双曲线 的两侧。
椭圆的参数 $a$、$b$ 和 $c$ 之间满足 $a^2 = b^2 + c^2$。
双曲线的标准方程与几何特性
标准方程
双曲线的标准方程为 $frac{x^2}{a^2} - frac{y^2}{b^2} = 1$，其中 $a$ 和 $b$ 是双曲线的半实轴和半虚轴。
焦点位置
双曲线的两个焦点位于副轴上，距离 原点的距离分别为 $c$ 和 $-c$，其 中 $c = sqrt{a^2 + b^2}$。
02
标准方程与几何特性
椭圆的标准方程与几何特性
标准方程
几何特性
椭圆的标准方程为 $frac{x^2}{a^2} + frac{y^2}{b^2} = 1$，其中 $a$ 和 $b$ 是 椭圆的半长轴和半短轴。
椭圆是一个封闭的曲线，它有两个焦点， 并且有一个主轴和一条副轴。

双曲线(1) 若焦点在x轴上的椭圆2212x ym+=的离心率为12，则m= ( )Ｂ32Ｃ83Ｄ23(2) 若方程x2+ky2=2表示焦点在y轴上的椭圆, 那么实数k的取值范围是 ( )A (0, +∞)B (0, 2)C (1, +∞)D (0, 1)(3) 设P是双曲线19222=-yax上一点，双曲线的一条渐近线方程为023=-yx,F1、F2分别是双曲线的左、右焦点，若3||1=PF，则=||2PF ( )A 1或5B 6C 7D 9(4) 已知双曲线1222=-yx的焦点为F1、F2，点M在双曲线上且120,MF MF⋅=则点M到x轴的距离为 ( ) A43B53(5) 设椭圆的两个焦点分别为F1、、F2，过F2作椭圆长轴的垂线交椭圆于点P，若△F1PF2为等腰直角三角形，则椭圆的离心率是( )C 216若双曲线的渐近线方程为xy3±=，它的一个焦点是()0,10，则双曲线的方程是__________.8、过双曲线22221x ya b-=(a＞0，b＞0)的左焦点且垂直于x轴的直线与双曲线相交于M、N两点，以MN为直径的圆恰好过双曲线的右顶点，则双曲线的离心率等于_________．9、点A 、B 分别是椭圆1203622=+y x 长轴的左、右端点，点F 是椭圆的右焦点，点P 在椭圆上，且位于x 轴上方，PF PA ⊥.求点P 的坐标；10 ．设1F ,2F 是椭圆E :2222x y a b +=1(a >b >0)的左、右焦点,P 为直线32ax =上一点,△21F PF 是底角为030的等腰三角形,则E 的离心率为 （ ）A ．12B ．23C ．34D ．4511．椭圆22221(0)x y a b a b+=>>的左、右顶点分别是A,B,左、右焦点分别是F 1,F 2.若|AF 1|,|F 1F 2|,|F 1B|成等比数列,则此椭圆的离心率为 （ ）A ．14B C ．12D12、已知双曲线C :22x a -22y b=1的焦距为10 ,点P (2,1)在C 的渐近线上,则C 的方程为（ ）A ．220x -25y =1B ．25x -220y =1C ．280x -220y =1D ．220x -280y =113、已知双曲线22x a-25y =1的右焦点为(3,0),则该双曲线的离心率等于A14B ．4C ．32D ．4314已知12,F F 为双曲线222x y -=的左,右焦点,点P 在C 上,12||2||PF PF =,则12cos F PF ∠=（ ）A ．14 B ．35C ．34 D ．4515、椭圆的中心在原点,焦距为4,一条准线为4x =-,则该椭圆的方程为（ ）A ．2211612x y += B ．221128x y += C ．22184x y += D ．221124x y += 16设P 为直线3by x a=与双曲线22221(0,0)x y a b a b -=>> 左支的交点,1F 是左焦点,1PF 垂直于x 轴,则双曲线的离心率e =___17已知双曲线)0,0(1:22221>>=-b a by a x C 与双曲线1164:222=-y x C 有相同的渐近线,且1C 的右焦点为F ,则a =______,b =_______.18、设双曲线以椭圆192522=+y x 长轴的两个端点为焦点，其准线过椭圆的焦点，则双曲线的渐近线的斜率为（ ） A ．2± B ．34±C ．21± D ．43±19椭圆1422=+y x 的两个焦点为F 1、F 2，过F 1作垂直于x 轴的直线与椭圆相交，一个交点为P ，则||2PF =（ ）A ．23B ．3C ．27D ．420．中心在原点，准线方程是4±=x ，离心率是21的椭圆方程为 （ ）A ．1422=+y xB ．14322=+y xC ．13422=+y xD ．1422=+y x ２1、双曲线224x y -=的两条渐近线与直线3x =围成一个三角形区域,表示该区域的不等式组是（ ）(A)0003x y x y x -≥⎧⎪+≥⎨⎪≤≤⎩ (B)0003x y x y x -≥⎧⎪+≤⎨⎪≤≤⎩ (C) 0003x y x y x -≤⎧⎪+≤⎨⎪≤≤⎩ (D) 0003x y x y x -≤⎧⎪+≥⎨⎪≤≤⎩22双曲线与椭圆1522=+y x 共焦点，且一条渐近线方程是03=-y x ，则此双曲线方程为 （ ）A ．1322=-x yB ．1322=-x yC ．1322=-y xD ．1322=-y x23若椭圆x k y e 2289112++==的离心率,则实数k 的值是；24、双曲线的一个顶点把焦点之间的线段分成长短两段比是3 ：1，则双曲线的离心率e=（ ）（A ）2 （B ） 3 （C ）4 （D ）525、双曲线mx 2+y 2=1的虚轴长是实轴长的2倍，则m =（ ） （A ）14-（B ）14（C ）4 （D ）4-26、已知双曲线ny n x --1222=1的离心率为3,则n =（ ） （A ）2 （B ） 3 （C ）4 （D ）527、双曲线1366422=-y x上一点M 到它的右焦点的距离是8，则点M 到右准线的距离为（ ）（A ） 10 （B ）7732 （C ）27（D ）53228、双曲线191622=-y x 上一点P 对两焦点F 1、F 2的视角为60°，则△F 1PF 2的面积为（ ） （A ） 23（B ）33（C ）63（D ）93。