位移法解题步骤例题2(精)
- 格式:doc
- 大小:322.00 KB
- 文档页数:2

三根杆的位移法例题
摘要:
1.介绍三根杆的位移法例题
2.详解三根杆的位移法例题的解法
3.总结三根杆的位移法例题的解法及注意事项
正文:
一、介绍三根杆的位移法例题
三根杆的位移法例题是力学中的一种经典问题,主要涉及到杆的弯曲和应力分布等方面的知识。
这个问题通常描述为:有三根杆固定在一点,并承受一定的力,求杆的位移或应力分布。
这个问题在实际工程中有着广泛的应用,如建筑结构、桥梁设计等。
二、详解三根杆的位移法例题的解法
解三根杆的位移法例题,一般可以分为以下几个步骤:
1.建立模型:首先,根据题目描述,建立三根杆的模型,明确杆的材料、截面形状、边界条件等。
2.列方程:根据力学原理,如力矩平衡、静力平衡等原理,列出方程组。
3.解方程:通过数学方法,如代入法、消元法等,解出方程组中的未知量。
4.计算结果:根据解出的方程,计算出杆的位移或应力分布。
三、总结三根杆的位移法例题的解法及注意事项
解三根杆的位移法例题,需要掌握力学基础知识,熟悉杆的弯曲和应力分
布规律,同时具备一定的数学运算能力。
在解题过程中,要注意以下几点:
1.准确理解题意,明确杆的边界条件和受力情况。
2.在列方程时,要注意单位的统一,保证计算的准确性。
3.在解方程时,要根据方程的特性选择合适的解法,避免盲目尝试。
4.在计算结果时,要注意单位的转换和有效数字的保留。
通过以上步骤和注意事项,可以较好地解决三根杆的位移法例题。




高中物理位移公式大全总结及例题位移是描述物体位置变化的物理量,是矢量,既有大小又有方向。
在高中物理中,我们主要学习匀速直线运动和匀变速直线运动中的位移公式。
1.匀速直线运动•位移公式:o s = vto其中:▪s:位移(m)▪v:速度(m/s)▪t:时间(s)这个公式表示,在匀速直线运动中,物体在单位时间内通过的距离(即速度)乘以运动时间,就等于物体的位移。
2.匀变速直线运动•位移公式:o s = v₀t + 1/2at²o其中:▪s:位移(m)▪v₀:初速度(m/s)▪t:时间(s)▪a:加速度(m/s²)这个公式表示,在匀变速直线运动中,物体的位移等于初速度乘以时间加上1/2乘以加速度乘以时间的平方。
•其他常用公式:o末速度公式:v = v₀ + ato平均速度公式:v̄= (v₀ + v) / 2o中间时刻速度公式:vₘ = v₀ + 1/2at3.公式的应用这些公式在解决匀速直线运动和匀变速直线运动的问题中非常重要。
我们可以利用这些公式,结合已知条件,求解未知的物理量,如位移、速度、时间、加速度等。
4.注意:•在使用这些公式时,一定要注意单位的统一,一般采用国际单位制。
•对于不同的运动情况,可能需要选择不同的公式进行计算。
•在解决实际问题时,要仔细分析题意,找出已知量和未知量,然后选择合适的公式进行求解。
5.例题一个物体以2m/s的速度匀速运动了5s,求物体的位移。
解:•已知:v = 2m/s,t = 5s•求:s•根据公式s = vt,代入数据得:s = 2m/s × 5s = 10m•答:物体的位移为10m。
6.总结位移公式是高中物理中非常基础且重要的公式。
掌握这些公式,并能灵活运用,对于解决力学问题具有重要意义。
7.温馨提示:•多做练习:通过大量的练习,可以加深对公式的理解和记忆。
•画示意图:在解题过程中,画示意图可以帮助我们更好地理解题意,找出解题思路。


高中物理运动题解题思路及示例一、速度与位移的计算在物理学中,速度和位移是最基本的运动量,它们的计算方法也是解决物理运动题的关键。
下面通过几个具体的例子来说明解题思路。
例题1:一个小球从静止开始沿直线运动,经过2秒后速度为4 m/s,求此时小球的位移。
解析:根据速度的定义,速度等于位移与时间的比值。
所以,我们可以用速度乘以时间来计算位移,即位移等于速度乘以时间。
在本题中,速度为4 m/s,时间为2秒,所以位移等于4 m/s ×2 s = 8 m。
因此,小球在经过2秒后的位移为8米。
例题2:一个物体以10 m/s的速度匀速运动了5秒,求此时物体的位移。
解析:根据速度的定义,速度等于位移与时间的比值。
所以,我们可以用速度乘以时间来计算位移,即位移等于速度乘以时间。
在本题中,速度为10 m/s,时间为5秒,所以位移等于10 m/s × 5 s = 50 m。
因此,物体在经过5秒后的位移为50米。
二、加速度与速度的计算当物体在运动过程中受到外力的作用时,它的速度就会发生变化,这时我们需要考虑加速度的概念。
下面通过几个具体的例子来说明解题思路。
例题3:一个物体以5 m/s^2的加速度匀加速运动了10秒,求此时物体的速度。
解析:根据加速度的定义,加速度等于速度的变化量与时间的比值。
所以,我们可以用加速度乘以时间来计算速度的变化量,即速度的变化量等于加速度乘以时间。
在本题中,加速度为5 m/s^2,时间为10秒,所以速度的变化量等于5 m/s^2× 10 s = 50 m/s。
由于物体是匀加速运动,所以它的初始速度为0 m/s,即物体的速度等于初始速度加上速度的变化量,即速度等于0 m/s + 50 m/s = 50 m/s。
因此,物体在经过10秒后的速度为50 m/s。
例题4:一个物体以2 m/s的速度匀加速运动了5秒,求此时物体的加速度。
解析:根据加速度的定义,加速度等于速度的变化量与时间的比值。

位移可以这样求先看题,一辆汽车以20m/s 的速度行驶,现因故刹车,并最终停止运动,已知汽车刹车过程的加速度大小是5m/s 2。
则汽车的刹车距离是多少?汽车做匀减速直线运动,刹车距离就是汽车在刹车过程发生的位移的大小,你可以先来想一想?或者动手试一试!1. 利用位移公式来求先算出刹车过程所用的时间t ,因刹车过程汽车做减速运动,所以加速度a 应该取负值,即a=-5m/s 2,时间s 4m/s 5-m/s 20--020===a v t ,经4s 汽车停止。
当然也可以口算,加速度大小是5m/s 2,也就是说汽车的速度每秒减小5m/s ,初速度为20m/s ,所以汽车速度经4s即可减为0,到停止时间s 4=t 。
接下来,再代入位移公式,即可求出刹车距离,即:m 40s)4()m/s 5(21s 420m/s 212220=⨯-⨯+⨯=+=at t v x 2. 利用速度-位移公式可求利用匀变速直线运动的速度-位移公式也可以解出来,什么是速度-位移公式?末速初速平方差,2ax 等于它,即:ax v v 2-202=,所以,0m 4m/s 5-2m/s 20-2-02220=⨯==)()(a v x 3. 利用汽车运动的逆过程求解我们来个逆向思维,什么意思?就是将整个过程倒过来进行,或者说假如时光可以倒流,我们这个过程将变成初速度为0的反方向的匀加速直线运动。
这样理解,位移大小就等于m 404s)(5m/s 2121222=⨯⨯==at x 。
看看,是不是很简单。
(当然先得算出刹车过程所用的时间t =4s )。
4. 利用t v =x 求解以上我们介绍了三种解法,想想哪一种最简单?我们认为都不是太简单,最简单的是现在介绍的第4种,利用平均速度乘时间求位移,即:t v =x 。
时间前面算过了t =4s, 而平均速度就等于初速度加末速度除以2,即:0m/s 12020m/s 20=+=+=v v v ,所以,40m s 4m/s 10x =⨯==t v ,希望同学们不要小看这个公式,解起题来很快的。
位移法习题与答案位移法是结构力学中常用的一种分析方法,通过计算结构在外力作用下的位移,来求解结构的应力、应变和变形等问题。
在学习位移法时,习题与答案的练习是非常重要的,可以帮助我们加深对位移法的理解和掌握。
下面将给大家介绍一些位移法习题及其答案。
习题一:求解简支梁的弯矩分布已知一根长度为L的简支梁,受到均布载荷q作用,求解弯矩分布。
解答:首先,我们需要根据受力分析确定梁的反力。
对于简支梁,两个支座处的反力相等,且为qL/2。
接下来,我们可以利用位移法求解弯矩分布。
假设梁的弯矩分布为M(x),则根据位移法的基本原理,可以得到以下方程:d2M(x)/dx2 = -q对该方程进行两次积分,得到:M(x) = -q*x^2/2 + C1*x + C2由于梁两端是简支条件,即位移和转角为零,可以得到边界条件:M(0) = 0M(L) = 0代入上述方程,解得C1 = qL/2,C2 = -qL^2/2。
因此,弯矩分布为:M(x) = -q*x^2/2 + qL/2*x - qL^2/2习题二:求解悬臂梁的挠度已知一根长度为L的悬臂梁,受到集中力F作用在悬臂端点,求解梁的挠度。
解答:首先,我们需要根据受力分析确定梁的反力。
对于悬臂梁,端点处的反力只有一个,即为F。
接下来,我们可以利用位移法求解梁的挠度。
假设梁的挠度为δ(x),则根据位移法的基本原理,可以得到以下方程:d2δ(x)/dx2 = -F/(EI)对该方程进行两次积分,得到:δ(x) = -F*x^2/(2EI) + C1*x + C2由于梁端点处的位移为零,可以得到边界条件:δ(0) = 0dδ(x)/dx|_(x=L) = 0代入上述方程,解得C1 = 0,C2 = 0。
因此,梁的挠度为:δ(x) = -F*x^2/(2EI)习题三:求解悬臂梁的最大挠度已知一根长度为L的悬臂梁,受到均布载荷q作用,求解梁的最大挠度。
解答:首先,我们需要根据受力分析确定梁的反力。
位移法解题步骤
例题2
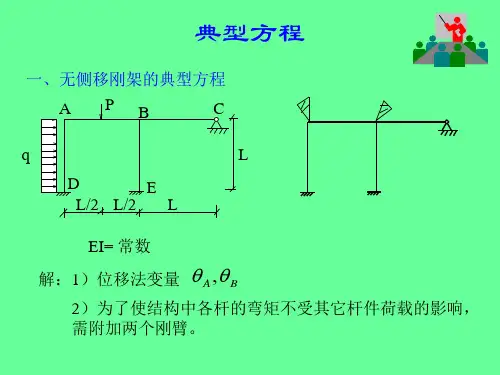
用位移法作例题2图(a )所示对称刚架的弯矩图(EI 为常数)。
解:⑴取半刚架。
此结构为一对称刚架,且承受对称荷载,故可取半刚架计算,半刚架计算简图如例题2图(b )所示。
⑵作位移法基本体系图。
半刚架只有一个刚结点C ,只有一个角位移,无线位移。
位移法基本体系如例题2图(c )所示。
⑶列位移法基本方程。
01111=+P R Z r
⑷求系数和自由项。
令 16===EI i i CE AC ,23
==EI i CK 。
根据载常数和形常数作1M 、P M 图[例题2图(d)、(e)]。
由1M 图及公式可得
1024411=++=r
由P M 图及公式可得
)(1545301m kN R P ⋅-=-=
⑸解算方程。
将系数和自由项代入位移法基本方程中,得
015101=-Z
解方程,得 5.111
11=-=r R Z P ⑹根据叠加法作弯矩图。
计算杆端弯矩。
)(273025.1m kN M AC ⋅-=-⨯=
)(363045.1m kN M CA ⋅=+⨯=
)(424525.1m kN M CK ⋅-=-⨯=
())(5.255.2225.1m kN M KC ⋅-=--⨯=
)(645.1m kN M CE ⋅=⨯=
)(325.1m kN M EC ⋅=⨯=
例题2图。