计算机图形学实验报告实验2

淮阴工学院计算机科学系实验报告书课程名：《计算机图形学》题目：实验2圆或椭圆的绘制班级：学号：姓名：1、实验内容或题目1、通过实验，进一步理解和掌握DDA和中点算法；2、掌握以上算法生成直线段、椭圆或圆的基本过程；3、通过编程，会在TC环境下完成用DDA或中点算法实现直线段、椭圆或圆的绘制。

2、实验目的与要求用DDA算法或中点（Besenham）算法实现直线段、椭圆或圆的绘制。

3、实验步骤与源程序⑴实验步骤1、算法、原理清晰，有详细的设计步骤；2、依据算法、步骤或程序流程图，用C语言编写源程序；3、编辑源程序并进行调试；4、进行运行测试，并结合情况进行调整；5、对运行结果进行保存与分析；6、打印源程序或把源程序以文件的形式提交；7、按格式书写实验报告。

⑵源代码#include "stdio.h"#include "conio.h"#include "graphics.h"#include<time.h>#include<math.h>void ellipsepoint(long x0,long y0,long x,long y,long color){putpixel((int)(x0+x),(int)(y0+y),(int)color);putpixel((int)(x0-x),(int)(y0+y),(int)color);putpixel((int)(x0+x),(int)(y0-y),(int)color);putpixel((int)(x0-x),(int)(y0-y),(int)color);}void midpointellipse(long x0,long y0,long a,long b,long color) {long x,y,d,sa,sb,xp,yp;sa=a*a,sb=b*b;xp=(long)((float)sa/(float)sqrt((float)(sa+sb)));yp=(long)((float)sb/(float)sqrt((float)(sa+sb)));x=0,y=b,d=sa+4*sb-4*sa*b;while(x<xp){if(d<0){d=d+4*sb*(2*x+3);x++;}else{d=d+4*sb*(2*x+3)+4*sa*(2-2*y);x++;y--;}ellipsepoint(x0,y0,x,y,color);}x=a,y=0,d=4*sa+sb-4*a*sb;while(y<yp){if(d<0){d=d+4*sa*(2*y+3);y++;}else{d=d+4*sa*(2*y+3)+4*sb*(2-2*x);y++;x--;}ellipsepoint(x0,y0,x,y,color);}}main(){clock_tstart=clock(),end,t;intgraphdriver=VGA,graphmode=VGAHI;initgraph(&graphdriver,&graphmode,"");midpointellipse(300,200,300,180,RED);end=clock();t=end-start;printf("%d\n",t);getch();closegraph();}4、测试数据与实验结果（可以抓图粘贴）5、结果分析与实验体会在这次实验中，我们遇到了很多困难，刚开始我们在实现圆的绘制时，调试后，要么就是没有图形，要么就是在左上角有个四分之一的圆，在其过程中，代码也改了好多次。

实验二: 直线的生成算法的实现班级 08信计2班学号 20080502055 姓名分数一、实验目的和要求:1.理解直线生成的原理；2.掌握几种常用的直线生成算法；3.利用C实现直线生成的DDA算法。

二、实验内容:1.了解直线的生成原理2、掌握几种基本的直线生成算法: DDA画线法、中点画线法、Bresenham画线法。

3、仿照教材关于直线生成的DDA算法, 编译程序。

4.调试、编译、运行程序。

三、实验过程及结果分析1.直线DDA算法:算法原理：已知过端点P0（x0,y0）, P1（x1,y1）的直线段L(P0,P1), 斜率为k=(y1-y0)/(x1-x0), 画线过程从x的左端点x0开始, 向x右端点步进, 步长为1个像素, 计算相应的y坐标为y=kx+B。

计算y i+1 = kx i+B=kx i +B+kx=y i +kx当x=1,yi+1=yi+k, 即当x每递增1, y递增k。

由计算过程可知, y与k可能为浮点数, 需要取y整数, 源程序中round(y）=(int)(y+0.5)表示y四舍五入所得的整数值。

（1）程序代码:#include"stdio.h"#include"graphics.h"void linedda(int x0,int y0,int x1,int y1,int color){int x,dy,dx,y;float m;dx=x1-x0;dy=y1-y0;m=dy/dx;y=y0;for(x=x0;x<=x1;x++){putpixel(x,(int)(y+0.5),color);y+=m;setbkcolor(7);}}main(){int a,b,c,d,e;int graphdriver=DETECT;int graphmode=0;initgraph(&graphdriver,&graphmode,"");a=100;b=100;c=200;d=300;e=5;linedda(a,b,c,d,e);getch();closegraph();}运行结果:2.中点画线算法:假定所画直线的斜率为k∈[0,1], 如果在x方向上增量为1, 则y方向上的增量只能在0~1之间。

《计算机图形学》实验报告(实验二：图形填充算法)一、实验目的及要求用两种方法做图形的填充算法！二、理论基础1.边填充算法对于每一条扫描线和每条多边形的交点（x1,y1），将该扫描线上的交点右方的所有像素取补。

2.种子填充算法利用栈来实现种子填充算法。

种子像素入栈，当栈非空时重复执行如下步骤：将栈顶像素出栈，将出栈像素置成多边形色，按左，上，右，下顺序检查与出栈像素相邻的四个像素，若其中某个像素不再边界且未置成多边形，则把该像素入栈！三、算法设计与分析1、边填充算法void CEdge_mark_fillView::OnDraw(CDC* pDC){CEdge_mark_fillDoc* pDoc = GetDocument();ASSERT_V ALID(pDoc);int d[500][500]={0};int inside;int x,y;Bresenham(80,101,100,400,d);Bresenham(100,300,290,400,d);Bresenham(292,400,382,50,d);Bresenham(380,50,202,150,d);Bresenham(200,150,82,101,d);for(y=0;y<500;y++){inside=0;for(x=0;x<500;x++){if(d[x][y]==1)if(d[x+1][y]!=1){inside=!(inside);}if(inside!=0)pDC->SetPixel(x,y,12);}}}2、种子填充int x=299,y=51;COLORREF oldcolor;COLORREF newcolor;oldcolor=RGB(256,256,256);newcolor=RGB(123,123,123);pDC->MoveTo (40,40);pDC->LineTo (80,40);pDC->LineTo (70,80);pDC->LineTo (40,40);FloodFill(51,51,RGB(255,255,255),RGB(0,0,255));pDC->LineTo (40,40);void CMyView::FloodFill(int x,int y,COLORREF oldcolor,COLORREF newcolor) {CDC* pDC;pDC=GetDC();if(pDC->GetPixel(x,y)==oldcolor){pDC->SetPixel(x,y,newcolor);FloodFill(x,y-1,oldcolor,newcolor);FloodFill(x,y+1,oldcolor,newcolor);FloodFill(x-1,y,oldcolor,newcolor);FloodFill(x+1,y,oldcolor,newcolor);}四、程序调试及结果的分析1、2、四、实验心得及建议由于很多不会，所以这次没能按时当堂完成，下来花了不少时间才弄出来，第二种尤其比较麻烦，在同学的帮助下才做出来了。

《计算机图形学》实验报告班级计算机科学与技术姓名学号2014 年6 月2 日实验一基本图形生成算法一、实验目的：1、掌握中点Bresenham绘制直线的原理；2、设计中点Bresenham算法；3、掌握八分法中点Bresenham算法绘制圆的原理；4、设计八分法绘制圆的中点Bresenham算法；5、掌握绘制1/4椭圆弧的上半部分和下半部分的中点Bresenham算法原理；6、掌握下半部分椭圆偏差判别式的初始值计算方法；7、设计顺时针四分法绘制椭圆的中点Bresenham算法。

二、实验过程：1、实验描述实验1：使用中点Bresenham算法绘制斜率为0<=k<=1的直线。

实验2：使用中点Bresenham算法绘制圆心位于屏幕客户区中心的圆。

实验3：使用中点Bresenham算法绘制圆心位于屏幕客户区中心的椭圆。

2、实验过程1）用MFC(exe)建立一个单文档工程；2）编写对话框，生成相应对象，设置相应变量；3）在类CLineView中声明相应函数，并在相关的cpp文件中实现；4）在OnDraw（）函数里调用函数实现绘制直线、圆、椭圆；5）运行程序，输入相应值，绘制出图形。

三、源代码实验1：直线中点Bresenham算法1.// cline.cpp : implementation file// cline dialogcline::cline(CWnd* pParent /*=NULL*/): CDialog(cline::IDD, pParent){//{{AFX_DATA_INIT(cline)m_x0 = 0;m_y0 = 0;m_x1 = 0;m_y1 = 0;//}}AFX_DATA_INIT}void cline::DoDataExchange(CDataExchange* pDX){CDialog::DoDataExchange(pDX);//{{AFX_DATA_MAP(cline)DDX_Text(pDX, IDC_x0, m_x0);DDX_Text(pDX, IDC_y0, m_y0);DDX_Text(pDX, IDC_x1, m_x1);DDX_Text(pDX, IDC_y1, m_y1);//}}AFX_DATA_MAP}BEGIN_MESSAGE_MAP(cline, CDialog)//{{AFX_MSG_MAP(cline)//}}AFX_MSG_MAPEND_MESSAGE_MAP()2、// LineView.hclass CLineView : public CView{public:CLineDoc* GetDocument();..........void Mbline(double,double,double,double); //直线中点Bresenham函数.......}3、// Line.cpp//*******************直线中点Bresenham函数*********************/void CLineView::Mbline(double x0, double y0, double x1, double y1) {CClientDC dc(this);COLORREF rgb=RGB(0,0,255); //定义直线颜色为蓝色double x,y,d,k;x=x0; y=y0; k=(y1-y0)/(x1-x0); d=0.5-k;for(x=x0;x<=x1;x++){dc.SetPixel((int)x,(int)y,rgb);if(d<0){y++;d+=1-k;}elsed-=k;}}4、//LineView.cppvoid CLineView::OnDraw(CDC* pDC){CLineDoc* pDoc = GetDocument();ASSERT_VALID(pDoc);// TODO: add draw code for native data herecline a;a.DoModal();//初始化CLineView::Mbline(a.m_x0,a.m_y0,a.m_x1,a.m_y1); }实验2：圆中点Bresenham算法1、//cricle.cpp// Ccricle dialogCcricle::Ccricle(CWnd* pParent /*=NULL*/): CDialog(Ccricle::IDD, pParent){//{{AFX_DATA_INIT(Ccricle)m_r = 0;//}}AFX_DATA_INIT}void Ccricle::DoDataExchange(CDataExchange* pDX) {CDialog::DoDataExchange(pDX);//{{AFX_DATA_MAP(Ccricle)DDX_Text(pDX, r_EDIT, m_r);//}}AFX_DATA_MAP}2、//CcircleView.hclass CCcircleView : public CView{.......public:CCcircleDoc* GetDocument();void CirclePoint(double,double); //八分法画圆函数void Mbcircle(double); //圆中点Bresenham函数........}3、//CcircleView.cppvoid CCcircleView::OnDraw(CDC* pDC){CCcircleDoc* pDoc = GetDocument();ASSERT_VALID(pDoc);// TODO: add draw code for native data hereCcricle r;r.DoModal();CCcircleView::Mbcircle(r.m_r);//画圆}4、//CcircleView.cpp//*******************八分法画圆*************************************/ void CCcircleView::CirclePoint(double x,double y){CClientDC dc(this);COLORREF rgb=RGB(0,0,255);dc.SetPixel((int)(300+x),(int)(300+y),rgb);dc.SetPixel((int)(300-x),(int)(300+y),rgb);dc.SetPixel((int)(300+x),(int)(300-y),rgb);dc.SetPixel((int)(300-x),(int)(300-y),rgb);dc.SetPixel((int)(300+y),(int)(300+x),rgb);dc.SetPixel((int)(300-y),(int)(300+x),rgb);dc.SetPixel((int)(300+y),(int)(300-x),rgb);dc.SetPixel((int)(300-y),(int)(300-x),rgb);}//**************************圆中点Bresenham函数*********************/ void CCcircleView::Mbcircle(double r){double x,y,d;COLORREF rgb=RGB(0,0,255);d=1.25-r;x=0;y=r;for(x=0;x<y;x++){CirclePoint(x,y); //调用八分法画圆子函数if(d<0)d+=2*x+3;else{d+=2*(x-y)+5;y--;}}}实验3：椭圆中点Bresenham算法1、//ellipse1.cpp// Cellipse dialogCellipse::Cellipse(CWnd* pParent /*=NULL*/) : CDialog(Cellipse::IDD, pParent){//{{AFX_DATA_INIT(Cellipse)m_a = 0;m_b = 0;//}}AFX_DATA_INIT}void Cellipse::DoDataExchange(CDataExchange* pDX) {CDialog::DoDataExchange(pDX);//{{AFX_DATA_MAP(Cellipse)DDX_Text(pDX, IDC_EDIT1, m_a);DDX_Text(pDX, IDC_EDIT2, m_b);//}}AFX_DATA_MAP}2、//EllipseView.hclass CEllipseView : public CView{......................public:CEllipseDoc* GetDocument();void EllipsePoint(double,double); //四分法画椭圆void Mbellipse(double a, double b); //椭圆中点Bresenham函数..................}3、//Ellipse.cpp//*****************四分法画椭圆********************************/void CEllipseView::EllipsePoint(double x,double y){CClientDC dc(this);COLORREF rgb=RGB(0,0,255);dc.SetPixel((int)(300+x),(int)(300+y),rgb);dc.SetPixel((int)(300-x),(int)(300+y),rgb);dc.SetPixel((int)(300+x),(int)(300-y),rgb);dc.SetPixel((int)(300-x),(int)(300-y),rgb);}//************************椭圆中点Bresenham函数*********************/ void CEllipseView::Mbellipse(double a, double b){double x,y,d1,d2;x=0;y=b;d1=b*b+a*a*(-b+0.25);EllipsePoint(x,y);while(b*b*(x+1)<a*a*(y-0.5))//椭圆AC弧段{if(d1<0)d1+=b*b*(2*x+3);else{d1+=b*b*(2*x+3)+a*a*(-2*y+2);y--;}x++;EllipsePoint(x,y);}d2=b*b*(x+0.5)*(x+0.5)+a*a*(y-1)*(y-1)-a*a*b*b;//椭圆CB弧段while(y>0){if(d2<0){d2+=b*b*(2*x+2)+a*a*(-2*y+3);x++;}elsed2+=a*a*(-2*y+3);y--;EllipsePoint(x,y);}}4、//EllipseView.cppvoid CEllipseView::OnDraw(CDC* pDC){CEllipseDoc* pDoc = GetDocument();ASSERT_VALID(pDoc);// TODO: add draw code for native data hereCellipse el;el.DoModal();//初始化CEllipseView::Mbellipse(el.m_a, el.m_b);//画椭圆}四、实结果验实验1：直线中点Bresenham算法实验2：圆中点Bresenham算法实验3：椭圆中点Bresenham算法实验二有效边表填充算法一、实验目的：1、设计有效边表结点和边表结点数据结构；2、设计有效边表填充算法；3、编程实现有效边表填充算法。

深圳大学实验报告课程名称：计算图形学实验名称：二维图形绘制学院：计算机与软件学院专业：计算机科学与技术报告人：学号：班级：同组人：无指导教师：周虹实验时间：2014/10/31实验报告提交时间：2014/11/3教务处制一．实验目的1、能正确使用OpenGL图元产生图画，并且学会使用多种生成图案的方式。

2、能正确设置图元属性，得到不同的绘制效果。

二．实验步骤1、用三角形模式画有颜色填充的太阳，圆心为（-0.5,0.7）2、直线模式，以-0.5,0.7为圆心画一些列直线作为太阳光3、用三角形画树，多边形画树干4、直线模式，以-0.5,0.7为圆心画一小花点缀树5、以三角形模式画一个小山坡，用天蓝色填充6、直线模式，以-0.5,0.7为圆心，以不同大小的直线画一系列小花点缀小山坡7、以不同大小的点形成双色围栏8、用不同的多边形模式画小树，用多边形模式画树干，并染上特别的颜色9、用虚线画零星的小草三．实验结果1、用三角形模式画有颜色填充的太阳，圆心为（-0.5,0.7）2、直线模式，以-0.5,0.7为圆心画一些列直线作为太阳光3、用三角形画树，多边形画树干4、直线模式，以-0.5,0.7为圆心画一小花点缀树5、以三角形模式画一个小山坡，用天蓝色填充6、直线模式，以-0.5,0.7为圆心，以不同大小的直线画一系列小花点缀小山坡7、以不同大小的点形成双色围栏8、用不同的多边形模式画小树，用多边形模式画树干，并染上特别的颜色9、用虚线画零星的小草四．实验心得通过这次实验，我比较深入地理解了二维图形的绘制过程和不同图元相关属性的设置，并学会运用不同的图元组合得到自己想要的画。

本次实验收获良多，主要体现在以下方面：作图时要善于运用函数。

例如在本次实验中涉及到画圆，可是opengl中并没有提供画圆的工具，这时函数就显得尤为重要了。

可是，有了函数还不够，得到函数后要根据自己要的属性选择适当的作图模式。

例如本次画太阳的过程中，一开始我选用GL_LINES的模式，当n趋向无穷大时得到一个圆，可是问题是这个圆是空心的，无法填充红色。

计算机图形学实验报告学号：********姓名：班级：计算机 2班指导老师：***2010.6.19实验一、Windows 图形程序设计基础1、实验目的1）学习理解Win32 应用程序设计的基本知识（SDK 编程）；2）掌握Win32 应用程序的基本结构（消息循环与消息处理等）； 3）学习使用VC++编写Win32 Application 的方法。

4）学习MFC 类库的概念与结构；5）学习使用VC++编写Win32 应用的方法（单文档、多文档、对话框）；6）学习使用MFC 的图形编程。

2、实验内容1）使用WindowsAPI 编写一个简单的Win32 程序，调用绘图API 函数绘制若干图形。

（可选任务）2 ）使用MFC AppWizard 建立一个SDI 程序，窗口内显示"Hello,Thisis my first SDI Application"。

（必选任务）3）利用MFC AppWizard(exe)建立一个SDI 程序，在文档视口内绘制基本图形（直线、圆、椭圆、矩形、多边形、曲线、圆弧、椭圆弧、填充、文字等），练习图形属性的编程（修改线型、线宽、颜色、填充样式、文字样式等）。

定义图形数据结构Point\Line\Circle 等保存一些简单图形数据（在文档类中），并在视图类OnDraw 中绘制。

3、实验过程1）使用MFC AppWizard(exe)建立一个SDI 程序,选择单文档；2）在View类的OnDraw（）函数中添加图形绘制代码，说出字符串“Hello,Thisis my first SDI Application”，另外实现各种颜色、各种边框的线、圆、方形、多边形以及圆弧的绘制；3）在类视图中添加图形数据point_pp,pp_circle的类，保存简单图形数据，通过在OnDraw（）函数中调用，实现线、圆的绘制。

4、实验结果正确地在指定位置显示了"Hello,This is my first SDI Application"字符串，成功绘制了圆，椭圆，方形，多边形以及曲线圆弧、椭圆弧，同时按指定属性改绘了圆、方形和直线。

计算机图形学实验报告
实验目的：通过本次实验，深入了解并掌握计算机图形学的基本原理和相关技术，培养对图形处理的理解和能力。

实验内容：
1. 图像的基本属性
- 图像的本质及表示方法
- 像素和分辨率的概念
- 灰度图像和彩色图像的区别
2. 图像的处理技术
- 图像的采集和处理
- 图像的变换和增强
- 图像的压缩和存储
3. 计算机图形学的应用
- 图像处理在生活中的应用
- 计算机辅助设计中的图形学应用
- 三维建模和渲染技术
实验步骤和结果：
1. 在计算机图形学实验平台上加载一张测试图像，分析其像素构成
和基本属性。

2. 运用图像处理技术，对测试图像进行模糊、锐化、色彩调整等操作，观察处理后的效果并记录。

3. 学习并掌握计算机图形学中常用的处理算法，如卷积、滤波等，
尝试应用到测试图像上并进行实验验证。

4. 探讨计算机图形学在数字媒体制作、虚拟现实、计算机辅助设计
等领域的应用案例，并总结其在实践中的重要性和价值。

结论：
通过本次实验，我对计算机图形学有了更深入的了解，掌握了图像
处理技术的基本原理和应用方法。

计算机图形学作为一门重要的学科，对多个领域有着广泛的应用前景，有助于提高数字媒体技术、虚拟现
实技术等领域的发展水平。

希望在未来的学习和工作中能进一步深化
对计算机图形学理论和实践的研究，不断提升自己在这一领域的专业
能力和创新意识。

图形学实验报告图形学实验报告概述：在本次图形学实验中，我们将探索和学习计算机图形学的基本概念和技术。

通过实验，我们深入了解了图形学的原理和应用，以及如何使用计算机生成和处理图像。

实验一：像素和颜色在这个实验中，我们学习了图像是由像素组成的，每个像素都有自己的颜色值。

我们使用了Python编程语言和PIL库来创建一个简单的图像，并设置了不同的像素颜色。

通过改变像素的颜色值，我们可以创建出各种各样的图像效果。

实验二：坐标系统和变换在这个实验中，我们学习了坐标系统和图形变换。

我们使用OpenGL库来创建一个简单的二维图形，并通过平移、旋转和缩放等变换操作来改变图形的位置和形状。

这些变换操作使我们能够在屏幕上创建出各种不同的图案和效果。

实验三：线段和多边形在这个实验中，我们学习了如何使用线段和多边形来绘制图形。

我们使用了Bresenham算法来绘制直线，并学习了如何使用多边形填充算法来填充图形。

通过这些技术，我们可以创建出更加复杂和精细的图像。

实验四：光照和阴影在这个实验中，我们学习了光照和阴影的原理和应用。

我们使用了光照模型来模拟光线的传播和反射，以及计算物体的明暗效果。

通过调整光照参数和材质属性，我们可以创建出逼真的光照和阴影效果。

实验五：纹理映射和渲染在这个实验中，我们学习了纹理映射和渲染的概念和技术。

我们使用了纹理映射来将图像贴到三维物体表面，以增加物体的细节和真实感。

通过渲染技术，我们可以模拟光线的折射和反射，以及创建出逼真的材质效果。

实验六：三维建模和动画在这个实验中，我们学习了三维建模和动画的基本原理和方法。

我们使用了三维建模工具来创建三维模型，并学习了如何使用关键帧动画来实现物体的运动和变形。

通过这些技术，我们可以创建出逼真的三维场景和动画效果。

总结：通过这次图形学实验，我们深入了解了计算机图形学的原理和应用。

我们学习了像素和颜色、坐标系统和变换、线段和多边形、光照和阴影、纹理映射和渲染，以及三维建模和动画等技术。

山东大学计算机科学与技术学院 计算机图形学课程实验报告
学号：2420430689 姓名： QQ
班级： 2014 级
实Байду номын сангаас题目：实现二维平面的基本变换
实验学时：4
实验日期： 2017 年 3 月 28 日
实验目的： 1. 掌握配置 OpenGL 环境的方法； 2. 熟悉 OpenGL 应用程序基本架构； 3. 学习 OpenGL 中的 gl、glu、glut 等库函数进行图形学算法编程和实现。
//填充右部 while (!judgeIfBoundary(x, y)) {
glBegin(GL_POINTS); glVertex2i(x, y); glEnd(); glFlush(); x = x + 1; } int xright = x - 1;
//填充左部 x = savex - 1; while (!judgeIfBoundary(x, y)) {
#include <cmath> #include <stack> #include <glut.h>
using namespace std;
struct mypoint {
GLint x; GLint y;
mypoint(GLint _x, GLint _y) :x(_x), y(_y) {}; mypoint() {}; };
x = x + 1; } } } } } 最后效果
结论分析与体会： 这次实验总的来讲比较繁琐，尤其是在计算校徽坐标的时候，当时是从学校官网 上找了一个比较正规的校徽，用 Windows 的画图工具打开，找出点的坐标然后用 数学方法变换的。
return true; else

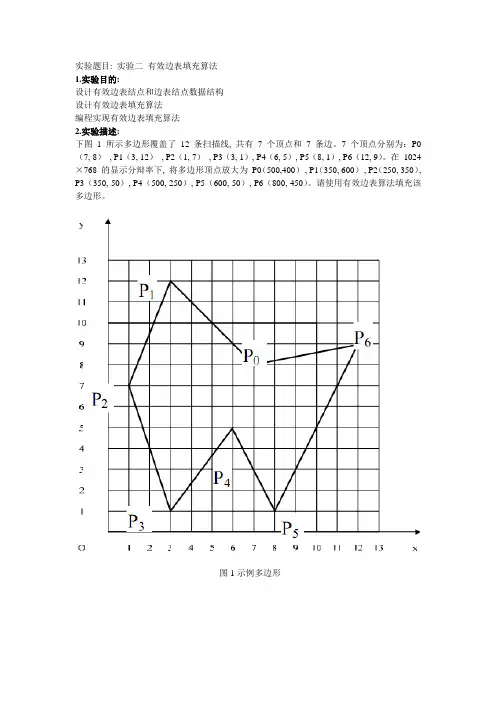
实验题目: 实验二有效边表填充算法1.实验目的:设计有效边表结点和边表结点数据结构设计有效边表填充算法编程实现有效边表填充算法2.实验描述:下图 1 所示多边形覆盖了12 条扫描线, 共有7 个顶点和7 条边。

7 个顶点分别为：P0（7, 8）, P1（3, 12）, P2（1, 7）, P3（3, 1）, P4（6, 5）, P5（8, 1）, P6（12, 9）。

在1024×768 的显示分辩率下, 将多边形顶点放大为P0（500,400）, P1（350, 600）, P2（250, 350）, P3（350, 50）, P4（500, 250）, P5（600, 50）, P6（800, 450）。

请使用有效边表算法填充该多边形。

图1示例多边形图2 屏幕显示多边形3.算法设计:（1）建立AET和BUCKET类；（2）初始化桶, 并在建立桶结点时为其表示的扫描线初始化为带头结点的链表；（3）对每个桶结点进行循环, 将桶内每个结点的边表合并为有效边表, 并进行有效边表循环；（4）按照扫描线从小到大的移动顺序, 计算当前扫描线与多边形各边的交点, 然后把这些交点按X值递增的顺序进行排序, 配对, 以确定填充区间；（5）用指定颜色点亮填充区间内的所有像素, 即完成填充工作。

4.源程序:1)//AET.hclass AET{public:AET();virtual ~AET();double x;int yMax;double k;//代替1/kAET *next;};//AET..cppAET::AET(){}AET::~AET(){}2) //Bucket.h#include "AET.h"class Bucket{public:Bucket();virtual ~Bucket();int ScanLine;AET *p;//桶上的边表指针Bucket *next;};// Bucket.cppBucket::Bucket(){}Bucket::~Bucket(){}3)//TestView.h#include "AET.h"//包含有效边表类#include "Bucket.h"//包含桶类#define Number 7//N为闭合多边形顶点数, 顶点存放在整型二维数组Point[N]中class CTestView : public CView{。

《计算机图形学》实验报告一、实验目的计算机图形学是一门研究如何利用计算机生成、处理和显示图形的学科。

通过本次实验，旨在深入理解计算机图形学的基本原理和算法，掌握图形的生成、变换、渲染等技术，并能够运用所学知识解决实际问题，提高对图形学的应用能力和编程实践能力。

二、实验环境本次实验使用的编程语言为 Python，使用的图形库为 Pygame。

开发环境为 PyCharm。

三、实验内容1、直线的生成算法DDA 算法（Digital Differential Analyzer）Bresenham 算法DDA 算法是通过计算直线的斜率来确定每个像素点的位置。

它的基本思想是根据直线的斜率和起始点的坐标，逐步计算出直线上的每个像素点的坐标。

Bresenham 算法则是一种基于误差的直线生成算法。

它通过比较误差值来决定下一个像素点的位置，从而减少了计算量，提高了效率。

在实验中，我们分别实现了这两种算法，并比较了它们的性能和效果。

2、圆的生成算法中点画圆算法中点画圆算法的核心思想是通过判断中点的位置来确定圆上的像素点。

通过不断迭代计算中点的位置，逐步生成整个圆。

在实现过程中，需要注意边界条件的处理和误差的计算。

3、图形的变换平移变换旋转变换缩放变换平移变换是将图形在平面上沿着指定的方向移动一定的距离。

旋转变换是围绕一个中心点将图形旋转一定的角度。

缩放变换则是改变图形的大小。

通过矩阵运算来实现这些变换，可以方便地对图形进行各种操作。

4、图形的填充种子填充算法扫描线填充算法种子填充算法是从指定的种子点开始，将相邻的具有相同颜色或属性的像素点填充为指定的颜色。

扫描线填充算法则是通过扫描图形的每一行，确定需要填充的区间，然后进行填充。

在实验中，我们对不同形状的图形进行了填充，并比较了两种算法的适用情况。

四、实验步骤1、直线生成算法的实现定义直线的起点和终点坐标。

根据所选的算法（DDA 或Bresenham）计算直线上的像素点坐标。

计算机图形学基础实验报告院系：计算机科学学院班级：2012级4班姓名：彭晓学号：21209010434实验二直线生成算法的实现1．实验目的：理解基本图形元素光栅化的基本原理，掌握一种基本图形元素光栅化算法，利用OpenGL 实现直线光栅化的DDA算法。

2．实验内容：（1）根据所给的直线光栅化的示范源程序，在计算机上编译运行，输出正确结果；（2）指出示范程序采用的算法，以此为基础将其改造为中点线算法或Bresenham算法，写入实验报告；（3）根据示范代码，将其改造为圆的光栅化算法，写入实验报告；（4）了解和使用OpenGL的生成直线的命令，来验证程序运行结果。

3．实验原理：示范代码原理参见教材直线光栅化一节中的DDA算法。

下面介绍下OpenGL画线的一些基础知识和glutReshapeFunc()函数。

（1）数学上的直线没有宽度，但OpenGL的直线则是有宽度的。

同时，OpenGL的直线必须是有限长度，而不是像数学概念那样是无限的。

可以认为，OpenGL的“直线”概念与数学上的“线段”接近，它可以由两个端点来确定。

这里的线由一系列顶点顺次连结而成，有闭合和不闭合两种。

前面的实验已经知道如何绘“点”，那么OpenGL是如何知道拿这些顶点来做什么呢？是一个一个的画出来，还是连成线？或者构成一个多边形？或是做其它事情呢？为了解决这一问题，OpenGL要求：指定顶点的命令必须包含在glBegin函数之后，glEnd函数之前（否则指定的顶点将被忽略），并由glBegin来指明如何使用这些点。

例如：glBegin(GL_POINTS);glVertex2f(0.0f, 0.0f);glVertex2f(0.5f, 0.0f);glEnd();则这两个点将分别被画出来。

如果将GL_POINTS替换成GL_LINES，则两个点将被认为是直线的两个端点，OpenGL将会画出一条直线。

还可以指定更多的顶点，然后画出更复杂的图形。

实验结果与结论
• 在本次实验中，我们成功地实现了复杂场景的渲染，得到了具有较高真实感和视觉效果的图像。通过对比 实验前后的效果，我们发现光线追踪和着色器的运用对于提高渲染质量和效率具有重要作用。同时，我们 也发现场景图的构建和渲染脚本的编写对于实现复杂场景的渲染至关重要。此次实验不仅提高了我们对计 算机图形学原理的理解和实践能力，也为我们后续深入研究渲染引擎的实现提供了宝贵经验。
2. 通过属性设置和变换操作，实现了对图形的定 制和调整，加深了对图形属性的理解。
4. 实验的不足之处：由于时间限制，实验只涉及 了基本图形的绘制和变换，未涉及更复杂的图形 处理算法和技术，如光照、纹理映射等。需要在 后续实验中进一步学习和探索。
02
实验二：实现动画效果
实验目的
掌握动画的基本原 理和实现方法
04
实验四：渲染复杂场景
实验目的
掌握渲染复杂场景的基本流程和方法 理解光线追踪和着色器在渲染过程中的作用
熟悉渲染引擎的实现原理和技巧 提高解决实际问题的能力
实验步骤
• 准备场景文件 • 使用3D建模软件（如Blender）创建或导入场景模型，导出为常用的3D格式（如.obj或.fbx）。 • 导入场景文件 • 在渲染引擎（如Unity或Unreal Engine）中导入准备好的场景文件。 • 构建场景图 • 根据场景的层次结构和光照需求，构建场景图（Scene Graph）。 • 设置光照和材质属性 • 为场景中的物体设置光照和材质属性（如漫反射、镜面反射、透明度等）。 • 编写渲染脚本 • 使用编程语言（如C或JavaScript）编写渲染脚本，控制场景中物体的渲染顺序和逻辑。 • 运行渲染程序 • 运行渲染程序，观察渲染结果。根据效果调整光照、材质和渲染逻辑。 • 导出渲染图像 • 将渲染结果导出为图像文件（如JPEG或PNG），进行后续分析和展示。

计算机图形学实验报告2计算机图形学实验报告实验⼆、三维⽹格模型光顺⼀、实验⽬的与基本要求：（1）掌握Obj⽂件的读⼊；（2）利⽤给定的数据结构类，建⽴读⼊⽹格模型数据结构；（3）利⽤OpenGL类库，对三维模型进⾏绘制；（4）利⽤OpenGL类库，增加采⽤⿏标交互⽅式对三维模型进⾏旋转、放缩、平移等操作；（5）实现Laplacian⽅法的三维模型光顺操作，并观察三维模型光顺过程；⼆、实验设备（环境）及要求1. 操作系统：Windows XP 或Windows 72. 编程环境：Microsoft Visual Studio 2010，OpenGL 库函数3. 界⾯框架：Win32，MFC，QT选择其中⼀种三、实验内容与步骤实验分为以下⼏个步骤：（1）掌握Obj⽂件的读⼊顶点和⾯的个数；（2）建⽴数组存储点的坐标及⾯上的点数；（3）存储顶点的邻接⾯数，并记录每个顶点周围的邻接点（4）计算每个⾯的法向利⽤OpenGL类库，增加采⽤⿏标交互⽅式对三维模型进⾏旋转、放缩、平移等操作；（5）利⽤⾯法向及顶点坐标进⾏绘制⼏何体（6）实现⿏标对物体旋转、平移、缩放的算法（7）实现Laplacian⽅法的三维模型光顺操作，并观察三维模型光顺过程；四、实现过程说明及成果展⽰：（1）掌握Obj⽂件的读⼊顶点和⾯的个数；由于obj⽂件的存储形式是v x1 x2 x3;…f v1 v2 v3;…这种形式，所以在记录点和⾯的数量时，只需按⾏读取，然后再判断⾸字母是v/f即可实现代码如下：（2）建⽴数组存储点的坐标及⾯上的点数；数组的⼤⼩由点数和⾯数决定，点数组和⾯数组均由0开始记录，故后⾯再⽤⾯对应点的时候，由于⾯上点是从1开始记录，故需要减1然后使⽤，代码如下：（3）存储顶点的邻接⾯数，并记录每个顶点周围的邻接点记录点邻接⾯的是新建⼀个数组，在读⾯的时候，将该⾯的序号存⼊对应点的数组中，然后再在每个⾯上取⼀点，记录到点的邻接点数组中，在每个⾯上取得的点为向外右⼿⽅向的下⼀个点，实现代码如下：（4）计算每个⾯的法向计算⾯的法向⽅式为⾯上右⼿⽅向上的两向量的叉乘得到，即所⽤代码为：（8）利⽤⾯法向及顶点坐标进⾏绘制⼏何体⽤法向绘制的⽅式是先⽤glNormal3fv(v)指出⾯的法向;再⽤glVertex3f传⼊⾯上点的坐标；由于我将glNormal3fv(v）中写在算法向所以我直接对此直接调⽤即可，代码如下：（9）实现⿏标对物体旋转、平移、缩放的算法平移：利⽤Transform函数和键盘事件来改变参数，w,s,a,d分别控制绘制的kitty猫的上下左右的移动：实现代码如下：旋转：利⽤gllookat();函数设定了观察⾓度，并⽤⿏标事件改变参数，⽤实现观察视⾓的变化实现物体的旋转，代码如下：缩放：运⽤glScalef⽅法和键盘事件改变参数，实现物体的放⼤和缩⼩，代码如下：（10）实现Laplacian⽅法的三维模型光顺操作，并观察三维模型光顺过程；Laplacian⽅法的原理是利⽤⽬标点与其所有邻接点平均后的点的差向量，对⽬标点的坐标进⾏变换的过程，具体⽅法是：①建⽴每个点的邻接顶点数组，存储每个点的邻接点②对每个顶点的邻接点进⾏求平均，即将邻接点的坐标求和后除以邻接点个数，从⽽得到邻接平均点③得到优化向量优化向量= 邻接平均点-⽬标点④设定优化度参数λ，得到优化后的新坐标新坐标= ⽬标点+ λ*优化向量在程序中，对于第num个顶点，我设定的变量为邻接平均点v0优化向量l新坐标数组vNewArr具体代码如下：五、结果展⽰及说明计算⾯法向后直接绘制（未光顺）：光顺进⾏⼀次后光顺多次后利⽤点绘制结果为旋转后缩放后平移后六、⼼得体会(1)计算⾯法向时法向量的⽅向没有运⽤右⼿⽅向，导致有的⾯法向向⾥，从⽽出现雪花(2)在运⽤Laplacian算法进⾏求邻接平均点时未初始化邻接平均点数组，导致平均点的累加从⽽出现越光顺越粗糙的现象(3)在obj⽂件中⾯对应顶点数和顶点数组的标号相差1.在运⽤的时候需减1，⾯从1开始记顶点，顶点数组从0开始记顶点七、实验代码#define GLUT_DISABLE_ATEXIT_HACK#include#include#include#include#include#include#include#includeusing namespace std;int v_num = 0; //记录点的数量int f_num = 0; //记录⾯的数量int vn_num = 0;//记录法向量的数量int vt_num = 0;GLfloat **vArr; //存放点的⼆维数组GLfloat **vNewArr;//存放点的⼆维数组int **fvArr; //存放⾯顶点的⼆维数组GLfloat **fnArr;//存放⾯法向量的⼆维数组int **ftArr;int **vfArr;//存放顶点临接的⾯数的数组int **nextVArr;//存放下⼀个临界顶点的数组GLfloat **vnArr;//存放点法向量的⼆维数组string s1, s2, s3, s4;GLfloat f2, f3, f4;int num1, num2, num3;typedef GLfloat point3[3];point3 x, y,l;//平⾯上的两个向量x,y和拉普拉斯向量lstatic GLfloat theta[] = { 0.0,0.0,0.0 };static GLint axis = 2;static GLdouble viewer[] = { 0.0, 0.0, 5.0 }; /* initial viewer location */ static GLdouble Tran[] = { 0.0,0.0,0.0 }; static GLdouble sca = 1.0;void getLineNum(string addrstr) //获取点和⾯的数量{ifstream infile(addrstr.c_str()); //打开指定⽂件if (!infile) {cout <<"open error!"<< endl;}string sline;//每⼀⾏int i = 0, j = 0;while (getline(infile, sline)) //从指定⽂件逐⾏读取{if (sline[0] == 'v'){v_num++;}if (sline[0] == 'f'){f_num++;}}}int readfile(string addrstr) //将⽂件内容读到数组中去{//getLineNum(addrstr);//new⼆维数组vArr = new GLfloat*[v_num];for (int i = 0; i < v_num; i++) {vArr[i] = new GLfloat[3];}vNewArr = new GLfloat*[v_num];for (int i = 0; i < v_num; i++) {vNewArr[i] = new GLfloat[3]; }vnArr = new GLfloat*[vn_num];for (int i = 0; i < vn_num; i++) {vnArr[i] = new GLfloat[3];}vfArr = new int*[v_num];for (int i = 0; i < v_num; i++) {vfArr[i] = new int[10];for (int j = 0; j < 10; j++) { vfArr[i][j] = -1;}}nextVArr = new int*[v_num];for (int i = 0; i < v_num; i++) {nextVArr[i] = new int[10];for (int j = 0; j < 10; j++) { nextVArr[i][j] = -1; }}fvArr = new int*[f_num];fnArr = new GLfloat*[f_num];ftArr = new int*[f_num];for (int i = 0; i < f_num; i++) {fvArr[i] = new int[3];fnArr[i] = new GLfloat[3];ftArr[i] = new int[10];}ifstream infile(addrstr.c_str()); if (!infile) { cout <<"open error!"<< endl;exit(1);}string sline;//每⼀⾏int ii = 0, jj = 0, kk = 0, mm = 0;while (getline(infile, sline)){if (sline[0] == 'v')//存储点{istringstream sin(sline);sin >> s1 >> f2 >> f3 >> f4;vArr[ii][0] = f2;vArr[ii][1] = f3;vArr[ii][2] = f4;ii++;}if (sline[0] == 'f') //存储⾯{istringstream in(sline);GLfloat a;in >> s1>>num1>>num2>>num3;//去掉f fvArr[kk][0] = num1;fvArr[kk][1] = num2;fvArr[kk][2] = num3;for (int i = 0; i < 10; i++) {if (vfArr[num1-1][i] == -1) {vfArr[num1-1][i] = kk;nextVArr[num1-1][i] = num2;break;}}for (int j = 0; j < 10; j++) {if (vfArr[num2-1][j] == -1) {vfArr[num2-1][j] = kk;nextVArr[num2-1][j] = num3;break;}}for (int i = 0; i < 10; i++) {if (vfArr[num3-1][i] == -1) {vfArr[num3-1][i] = kk;nextVArr[num3-1][i] = num1;break;}}kk++;}}return 0;}//计算⾯法向void nomal(point3p) {/*⽮量的归⼀化*///double sqrt();float d = 0.0;int i;for (i = 0; i < 3; i++)d += p[i] * p[i];d = sqrt(d);if (d > 0.0)for (i = 0; i < 3; i++)p[i] /= d;}void getFaceNormal(point3A, point3B, point3C) { x[0] = C[0] - A[0]; x[1] = C[1] - A[1];x[2] = C[2] - A[2];y[0] = A[0] - B[0];y[1] = A[1] - B[1];y[2] = A[2] - B[2];point3 v;v[0] = x[1] * y[2] - x[2] * y[1];v[1] = x[2] * y[0] - x[0] * y[2];v[2] = x[0] * y[1] - x[1] * y[0];nomal(v);glNormal3fv(v);}void Laplacian() {for (int num = 0; num < v_num; num++) {int m = 0;//求得点的邻接⾯数for (int i = 0; i < 10; i++) {if (nextVArr[num][i] != -1) {m++;}else {break;}}point3 v0;for (int i = 0; i < 3; i++) {v0[i] = 0;}for (int i = 0; i < m; i++) {v0[0] += vArr[nextVArr[num][i] - 1][0];v0[1] += vArr[nextVArr[num][i] - 1][1];v0[2] += vArr[nextVArr[num][i] - 1][2];}if (m != 0) {for (int i = 0; i < 3; i++)v0[i] /= m;}l[0] = v0[0] - vArr[num][0];l[1] = v0[1] - vArr[num][1];l[2] = v0[2] - vArr[num][2];vNewArr[num][0] = vArr[num][0] + l[0] * 0.3;vNewArr[num][1] = vArr[num][1] + l[1] * 0.3;vNewArr[num][2] = vArr[num][2] + l[2] * 0.3;}for (int i = 0; i < v_num; i++) {vArr[i][0] = vNewArr[i][0];vArr[i][1] = vNewArr[i][1];vArr[i][2] = vNewArr[i][2];}}void init(void){getLineNum("H:\\kitten_noisy.obj");readfile("H:\\kitten_noisy.obj");double viewer[] = { 0.0, 0.0, 8.0 }; /* initial viewer location */GLfloat mat_specular[] = { 1.0, 1.0, 1.0, 1.0 };GLfloat mat_shininess[] = { 50.0 };//材料的镜⾯指数，其值越⼤越精细GLfloat light_position[] = { 1.0, 1.0f, 1.0, 0.0 };GLfloat white_light[] = { 1.0, 1.0, 1.0, 1.0 };GLfloat lmodel_ambient[] = { 0.1, 0.1, 0.1, 1.0 };glClearColor(0.0, 0.0, 0.0, 0.0);glShadeModel(GL_SMOOTH);glMaterialfv(GL_FRONT, GL_SPECULAR, mat_specular);glMaterialfv(GL_FRONT, GL_SHININESS, mat_shininess);glLightfv(GL_LIGHT0, GL_POSITION, light_position);//光源位置glLightfv(GL_LIGHT0, GL_DIFFUSE, white_light);//漫反射光源glLightfv(GL_LIGHT0, GL_SPECULAR, white_light);//镜⾯反射光源glLightModelfv(GL_LIGHT_MODEL_AMBIENT, lmodel_ambient);//环境光源// glEnable(glMaterialf);glEnable(GL_LIGHTING);//启动光照glEnable(GL_LIGHT0);//启⽤0度光源glEnable(GL_DEPTH_TEST);//启动深度测试/*glShadeModel(GL_SMOOTH); // Enable Smooth ShadingglClearColor(0.0f, 0.0f, 0.0f, 0.5f); // ⿊⾊背景glClearDepth(1.0f);// 深度缓冲区设置glEnable(GL_DEPTH_TEST); // 允许深度测试glDepthFunc(GL_LEQUAL);// 定义深度测试类型glHint(GL_PERSPECTIVE_CORRECTION_HINT, GL_NICEST); // Really Nice Perspective Calculation */}。

#endif
/////////////////////////////////////////////////////////////////////////////
// CTransformView
IMPLEMENT_DYNCREATE(CTransformView, CView)
BEGIN_MESSAGE_MAP(CTransformView, CView)
}
/////////////////////////////////////////////////////////////////////////////
// CTransformView printing
BOOL CTransformView::OnPreparePrinting(CPrintInfo* pInfo)
//{{AFX_MSG_MAP(CTransformView)
ON_COMMAND(ID_MENU_TRANSFORM_TRANSLATE, OnMenuTransformTranslate)
ON_COMMAND(ID_MENU_TRANSFORM_SCALE, OnMenuTransformScale)
#include "TransformDoc.h"
#include "TransformView.h"
#include <math.h>
#ifdef _DEBUG
#define new DEBUG_NEW
#undef THIS_FILE
static char THIS_FILE[] = __FILE__;
{
// default preparation
return DoPreparePrinting(pInfo);

计算机科学与通信工程学院实验报告课程计算机图形学实验题目曲线拟合学生姓名学号专业班级指导教师日期成绩评定表曲线拟合1. 实验内容1. 绘制三次Bezier曲线（1）给定四个已知点P1—P4，以此作为控制顶点绘制一段三次Bezier曲线。

（2）给定四个已知点P1—P4，以此作为曲线上的点绘制一段三次Bezier曲线。

2. 绘制三次B样条曲线给定六个已知点P1—P6，以此作为控制顶点绘制一条三次B样条曲线。

2. 实验环境软硬件运行环境：Windows XP开发工具：visual studio 20083. 问题分析1. 绘制三次Bezier曲线Bezier曲线是用N+1个顶点（控制点）所构成的N根折线来定义一根N阶曲线。

本次实验中的三次Bezier曲线有4个顶点，设它们分别为P0，P1，P2，P3，那么对于曲线上各个点Pi（x,y）满足下列关系：P(t)=[(-P0+3P1-3P2+3P3)t3+(3P0-6P1+3P2)t2+(-3P0+3P2)t+(P0+4P1+P2)]/6X(t)=[(-X0+3X1-3X2+3X3)t3+(3X0-6X1+3X2)t2+(-3X0+3X2)t+(X0+4X1+X2)]/6Y(t)=[(-Y0+3Y1-3Y2+3Y3)t3+(3Y0-6Y1+3Y2)t2+(-3Y0+3Y2)t+(Y0+4Y1+Y2)]/6其中P0、P1、P2、P3为四个已知的点，坐标分别为(X0、Y0)、(X1、Y1)、(X1、Y2) 、(X3、Y3)。

所以只要确定控制点的坐标，该曲线可通过编程即可绘制出来。

2. 绘制三次B样条曲线三次B样条函数绘制曲线的光滑连接条件为：对于6个顶点，取P1、P2、P3、P4 4个顶点绘制在第一段三次样条曲线，再取P2、P3、P4、P5 这4个顶点绘制在第二段三次样条曲线，总计可绘制3段光滑连接的三次样条曲线。

4. 算法设计程序框架//DiamondView.hclass CDiamondView : public CView{ ……public://参数输入和提示对话框CDlgBezier dlgBezier;//Bezier曲线绘制中的参数输入对话框CDlgB dlgB;//B样条曲线绘制中的参数输入对话框//绘图函数，需要实现void DrawBezier1(POINT p[4]);//已知点作为控制点绘制Bezier曲线void DrawBezier2(POINT p[4]);//已知点作为曲线上的点绘制Bezier曲线void DrawBCurve(POINT p[6]);//绘制B样条曲线//DiamondView.cppvoid CDiamondView::OnMenuDiamond(){IsCutting = FALSE;if(dlgDiamond.DoModal()==IDOK)DrawDiamond(dlgDiamond.m_nVertex,dlgDiamond.m_nRadius,100);//调用绘制金刚石的函数} void CDiamondView::OnMenuBezier1(){IsCutting = FALSE;if(dlgBezier.DoModal() == IDOK)DrawBezier1(dlgBezier.m_nPoint);//调用已知点作为控制点绘制Bezier曲线的函数} //以已知的四个点为控制点绘制Bezier曲线//p:已知的四个控制点void CDiamondView::DrawBezier1(POINT p[4]){ }void CDiamondView::OnMenuBezier2(){IsCutting = FALSE;if(dlgBezier.DoModal() == IDOK)DrawBezier2(dlgBezier.m_nPoint);//调用已知点作为曲线上的点绘制Bezier曲线的函数}//以已知的四个点为Bezier曲线上的点来绘制Bezier曲线//p:已知的四个点void CDiamondView::DrawBezier2(POINT p[4]){ }void CDiamondView::OnMenuB(){IsCutting = FALSE;if(dlgB.DoModal() == IDOK)DrawBCurve(dlgB.m_nPoint);//调用绘制B样条曲线的函数} //以已知的六个点为控制点来绘制B样条曲线//p:已知的六个控制点void CDiamondView::DrawBCurve(POINT p[6]){ }5. 源代码//以已知的四个点为控制点绘制Bezier曲线//p:已知的四个控制点void CDiamondView::DrawBezier1(POINT p[4]){CDC *pDC = GetDC();CPen newPen,*oldPen;newPen.CreatePen(PS_SOLID,2,RGB(255,0,0));oldPen = pDC->SelectObject(&newPen);pDC->Polyline(p, 4);pDC->SelectObject(oldPen);newPen.DeleteObject();newPen.CreatePen(PS_SOLID,2,RGB(0,0,255));oldPen = pDC->SelectObject(&newPen);int x0=p[0].x;int y0=p[0].y;int x1=p[1].x;int y1=p[1].y;int x2=p[2].x;int y2=p[2].y;int x3=p[3].x;int y3=p[3].y;double x,y;int ax,ay,bx,by,cx,cy,dx,dy;int rate=1000;ax=-x0+3*x1-3*x2+x3;ay=-y0+3*y1-3*y2+y3;bx=3*x0-6*x1+3*x2;by=3*y0-6*y1+3*y2;cx=-3*x0+3*x1;cy=-3*y0+3*y1;dx=x0;dy=y0;pDC->MoveTo(x0,y0);for(double t=0;t<=1;t+=1.0/rate){x=ax*pow(t,3)+bx*pow(t,2)+cx*t+dx;y=ay*pow(t,3)+by*pow(t,2)+cy*t+dy;pDC->LineTo(Round(x),Round(y));Sleep(10);}pDC->SelectObject(oldPen);}//以已知的四个点为Bezier曲线上的点来绘制Bezier曲线//p:已知的四个点void CDiamondView::DrawBezier2(POINT p[4]){ InvalidateRgn(NULL);UpdateWindow();CDC *pDC = GetDC();CPen newPen,*oldPen;newPen.CreatePen(PS_DASH,1,RGB(0,0,0));oldPen=pDC->SelectObject(&newPen);CBrush newBrush,*oldBrush;newBrush.CreateSolidBrush(RGB(0,0,0));oldBrush=pDC->SelectObject(&newBrush);for(int i=0;i<=3;i++){pDC->Ellipse(p[i].x-3,p[i].y-3,p[i].x+3,p[i].y+3);} pDC->SelectObject(oldPen);pDC->SelectObject(oldBrush);Sleep(50);POINT q[4];q[0].x=p[0].x;q[0].y=p[0].y;q[1].x=(-5*p[0].x+18*p[1].x-9*p[2].x+2*p[3].x)/6;q[1].y=(-5*p[0].y+18*p[1].y-9*p[2].y+2*p[3].y)/6;q[2].x=(2*p[0].x-9*p[1].x+18*p[2].x-5*p[3].x)/6;q[2].y=(2*p[0].y-9*p[1].y+18*p[2].y-5*p[3].y)/6;q[3].x=p[3].x;q[3].y=p[3].y;DrawBezier1(q);}//以已知的六个点为控制点来绘制B样条曲线//p:已知的六个控制点void CDiamondView::DrawBCurve(POINT p[6]){InvalidateRgn(NULL);UpdateWindow();CDC *pDC = GetDC();CPen newPen,*oldPen;newPen.CreatePen(PS_SOLID,2,RGB(255,0,0)); oldPen = pDC->SelectObject(&newPen);int rate=1000;int ax,ay,bx,by,cx,cy,dx,dy;double x,y;pDC->Polyline(p, 6);pDC->SelectObject(oldPen);newPen.DeleteObject();newPen.CreatePen(PS_SOLID,3,RGB(0,0,255)); oldPen = pDC->SelectObject(&newPen);for(int i=0;i<3;i++){ax=-(p[i].x-3*p[i+1].x+3*p[i+2].x-p[i+3].x)/6;bx=(p[i].x-2*p[i+1].x+p[i+2].x)/2;cx=-(p[i].x-p[i+2].x)/2;dx=(p[i].x+4*p[i+1].x+p[i+2].x)/6;ay=-(p[i].y-3*p[i+1].y+3*p[i+2].y-p[i+3].y)/6;by=(p[i].y-2*p[i+1].y+p[i+2].y)/2;cy=-(p[i].y-p[i+2].y)/2;dy=(p[i].y+4*p[i+1].y+p[i+2].y)/6;for(double t=0;t<=1;t+=1.0/rate){x=ax*pow(t,3)+bx*pow(t,2)+cx*t+dx;y=ay*pow(t,3)+by*pow(t,2)+cy*t+dy;pDC->MoveTo(Round(x),Round(y));pDC->LineTo(Round(x),Round(y));Sleep(2); }}pDC->SelectObject(oldPen);}6. 程序运行结果图1 控制顶点一段三次Bezier曲线绘制图2 控制顶点一段三次Bezier曲线绘制图3 曲线上的点一段三次Bezier曲线的绘制—图4 控制顶点一条三次B样条曲线的绘制图5 控制顶点一条三次B样条曲线的绘制7. 总结通过这次实验，我对Bezier曲线有了一定的了解，同时也懂得了Bezier曲线和B样条曲线的参数表示法。

计算机图形学实验指导书信息科学技术学院二○一三年十一月计算机图形学实验报告实验名称直线、圆弧及曲线的生成算法评分实验日期2013 年11 月 6 日指导教师姓名专业班级11地信学号2011083027一、实验目的1、几种直线生成算法的比较，特别掌握用Bresenham直线生成算法。

2、掌握用像素点法直接生成其它曲线的方法。

二、实验要求1、用不同的生成算法在屏幕上绘制出直线的图形，对不同的算法可设置不同的线形或颜色表示区别。

2、用Bresenham生成算法在屏幕上绘制出圆弧的图形，用动画的方式表演图形的生成。

三、关键算法及实现原理1、有关直线生成算法有：DDA（数值微分）直线算法、逐点比较法、直线Bresenham 生成算法。

直线Bresenham生成算法思想如下（第一象限，且斜率k<1的情况图2-1 a 中的1a）：1)画点（x1，y1），dx=x2-x1，dy=y2-y1，计算误差初值P1=2dy-dx，i=1;2)求直线下一点位置x i+1=x i+1 如果P i>0，则y i+1=y i+1，否则y i+1=y i;3)画点（x i+1，y i+1）；4)求下一个误差P i+1点，如果P i>0，则P i+1=P i+2dy-2dx，否则P i+1=P i+2dy;5)i=i+1，如果i<dx+1则转步骤2，否则结束操作。

Bresenham生成算法的优点如下；1）不必计算直线的斜率，因此不做除法。

2）不用浮点数，只用整数。

3）只做整数加减运算和乘2运算，而乘2运算可以用移位操作实现。

Bresenham算法的速度很快，并适于用硬件实现。

对于图2-1 a中的2a，只需将x i+1=x i+1改为x i+1=x i-1。

对于图2-1 a中的1b，斜率k>1的情况，可交换变量x和y，y每次长1个单位。

对P i进行判断，x i+1=x i或x i+1=x i+1。

2、有关圆弧生成算法有：逐点比较法、DDA（数值微分）直线算法、圆的Bresenham生成算法。