实验三 戴维宁定理
- 格式:doc
- 大小:88.00 KB
- 文档页数:3

实验三:戴维宁定理随着化学科学的不断发展,我们对于分子的结构和性质的理解也逐渐深入。
在分子力学的研究过程中,分子的振动频率是一个十分重要的参数,它能够反映出分子内原子之间的相互作用和力常数。
因此,对于光谱学和声学等领域,振动谱的研究非常重要。
而振动光谱和振动声学实验中,戴维宁定理的应用便显得尤为重要,本文将对戴维宁定理的原理、研究对象以及实验操作等方面进行详细介绍。
一、戴维宁定理的原理戴维宁定理是关于固体振动的一个重要定理,它的主要内容是:对于其晶格由固定原子构成的一个固体而言,若波动的频率在一定范围内,则该固体上所有的小波都可以看作是谐振子,小波的总数可以表示为:N=3N-6其中N代表着整个固体晶格的总原子数,3代表三维空间,减去6则是由于整体平移和转动的自由度所造成的削减。
二、研究对象在振动光谱和振动声学实验中,我们研究的对象是分子或晶体的振动,即分子或晶体中各个原子相对于它们的平衡位置而进行的简谐振动。
具体来讲,我们需要对该分子或晶体进行高精度的振动谱测定,测定该物质在不同波长下的光谱或不同频率下的声谱变化。
同时,还需要测定该物质的核磁共振图谱,从而得到相关物理量的数值。
三、实验操作在振动光谱实验中,我们需要准备以下材料和仪器:1、激光和白光源2、与物质反应的物理性质3、分光计和探测器4、光栅光谱仪在实验过程中,首先需要分别将激光和白光照射到物质上,然后将分光计和探测器与物质进行连接,并进行信号输出和处理。
接下来,使用光栅光谱仪对测量到的信号进行分离和稳定,最终得到物质在不同波长下的光谱图谱。
1、声源2、振动传感器和信号放大器3、Oscilloscope。
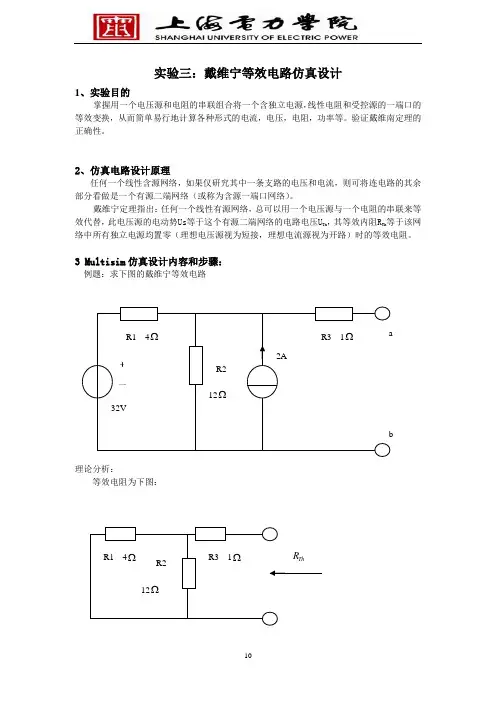
实验三:戴维宁等效电路仿真设计1、实验目的掌握用一个电压源和电阻的串联组合将一个含独立电源,线性电阻和受控源的一端口的等效变换,从而简单易行地计算各种形式的电流,电压,电阻,功率等。
验证戴维南定理的正确性。
2、仿真电路设计原理任何一个线性含源网络,如果仅研究其中一条支路的电压和电流,则可将连电路的其余部分看做是一个有源二端网络(或称为含源一端口网络)。
戴维宁定理指出:任何一个线性有源网络,总可以用一个电压源与一个电阻的串联来等效代替,此电压源的电动势Us等于这个有源二端网络的电路电压U Th,其等效内阻R Th等于该网络中所有独立电源均置零(理想电压源视为短接,理想电流源视为开路)时的等效电阻。
3 Multisim仿真设计内容和步骤:例题:求下图的戴维宁等效电路理论分析:等效电阻为下图:R Th =Ω=+⨯=+4116124112||4 等效电压如下图:我们设定两个回路电流i 1,i 2, 则根据回路法可得:0)(12432211=-++-II IA I 22-=A I 5.01=所以戴维宁等效电压为:V I I V Th 30)0.25.0(12)(1221=+=-=V所以戴维宁等效电路为:3、建立电路仿真图电路图:等效电压测试电路图:等效电阻测试电路图为:测试结果与计算值完全一致。
4、结果与误差分析戴维南等效电路无法一下子就求的,通过电路转换如测试等效电阻时,需将电源略去等,从而有效计算测量所需数值,通过计算等效电阻和等效电压,从而得到等效电路,由此证明了一个含独立电源、线性电阻和受控源的一端口,对外电路来说,可以用一个电压源和电阻的串联组合等效变换。
2、理论计算结果与仿真测量结果没有误差。
5.设计总结1、在本实验中我遇到的第一个问题是在连接好原件进行测量时无法测量,原因是未接地,经过接地后这个问题得以解决,它让我了解了在这个仿真系统中还是很多地方与实际连接中有很大的差异,接地原件就很好的表现了这一点。

【精品】电路实验3.戴维宁定理实验原理:戴维宁定理(Kirchhoff's Voltage Law, KVL):在任意封闭回路中,电动势的代数和等于电势降的代数和。
戴维宁定理是电路分析的基本原理之一。
该定理指出,在一条任意封闭回路中,电路中电源电势与电路中各元件的电势降之和必定相等。
具体而言,对于任意一条回路,我们可以从一个任意点开始绕回路走完它,如果绕路方向与电源电势方向相同,则经过电源时为正,经过电阻等元件时为负,如果绕路方向与电源电势方向相反,则经过电源时为负,经过电阻等元件时为正,最终经过回路的各个元件和电源时的电势降的代数和等于电源电势的代数和。
实验仪器:万用表、电路连接线、直流电源、电阻器、开关等。
实验过程:本实验选用基本的串联电路和并联电路搭建电路。
串联电路是把两个或更多的电阻器按顺序相连,电流通过电阻器1之后,到达电阻器2,再经过电源返回原点,组成一条回路。
并联电路是把两个或更多的电阻器按并联相连,电流从电源中依次进入各个电阻器,再重新汇入一个节点,也组成一条回路,如图所示。
图1 串并联电路1.串联电路:按照图1,将电阻R1和电阻R2串联连接,接入直流电源,测量电阻器两端的电压和电源的电压,记录数据。
实验结果:实验得到的数据如下表所示。
根据戴维宁定理,串联电路中电源电势与电阻器两端的电势降之和相等,即:U1 + U2 = E则有:U1 = IR1 = E * R1 / (R1 + R2)根据实验结果,我们可以使用戴维宁定理得到电路的电流和电压,进一步分析、设计和改造电路。
通过这次实验,我们成功地测量了串联电路和并联电路中电阻器两端的电势降和电源的电势,并使用戴维宁定理求解了电路的电流和电压。
我们得出了以下结论:1.在任意封闭回路中,电动势的代数和等于电势降的代数和。
2.串联电路中电源电势和电阻器两端的电势降之和相等,而并联电路中电源电势和电阻器两端的电势降之和也相等。
3.通过测量电路的电流和电压,可以设计和改造电路,实现我们想要的功能和效果。

戴维宁定理实验报告一、实验目的1、验证戴维宁定理的正确性,加深对该定理的理解。
2、掌握测量有源二端网络等效参数的一般方法。
3、学习使用电路实验仪器,如直流稳压电源、万用表等。
二、实验原理戴维宁定理指出:任何一个线性有源二端网络,对外电路来说,可以用一个电压源和一个电阻的串联组合来等效替代。
其中,电压源的电动势等于有源二端网络的开路电压$U_{OC}$,电阻等于有源二端网络除源(即理想电压源短路,理想电流源开路)后的等效电阻$R_{0}$。
三、实验设备1、直流稳压电源 1 台2、直流数字电压表 1 台3、直流数字电流表 1 台4、万用表 1 只5、电阻箱 1 个6、实验电路板 1 块7、连接导线若干四、实验内容与步骤1、测量有源二端网络的开路电压$U_{OC}$按图 1 所示连接电路,将负载电阻$R_{L}$开路,用直流数字电压表测量有源二端网络的开路电压$U_{OC}$,记录测量值。
!图 1 测量开路电压(此处应插入图 1)2、测量有源二端网络的短路电流$I_{SC}$将图 1 中的电路短路,用直流数字电流表测量有源二端网络的短路电流$I_{SC}$,记录测量值。
3、计算有源二端网络的等效内阻$R_{0}$根据公式$R_{0} =\frac{U_{OC}}{I_{SC}}$,计算有源二端网络的等效内阻$R_{0}$。
4、测量有源二端网络的外特性按图 2 所示连接电路,改变负载电阻$R_{L}$的值,测量不同负载电阻下的电流$I$ 和电压$U$ ,记录测量数据。
!图 2 测量外特性(此处应插入图 2)5、构建戴维宁等效电路根据测量得到的开路电压$U_{OC}$和等效内阻$R_{0}$,构建戴维宁等效电路,如图 3 所示。
!图 3 戴维宁等效电路(此处应插入图 3)6、测量戴维宁等效电路的外特性改变负载电阻$R_{L}$的值,测量戴维宁等效电路的电流$I'$和电压$U'$,记录测量数据。


戴维宁定理实验报告实验二:戴维宁定理的验证实验报告范本实验二:戴维宁定理的验证一(实验目的:(1) 用实验来验证戴维宁定理,加深戴维宁定理的理解; (2) 学习直流仪器仪表的测量方法。
二(实验原理:任何一个线性网络,如果只研究其中的一个支路的电压和电流,则可将电路的其余部分看作一个含源一端口网络,而任何一个线性含源一端口网络对外部电路的作用,可用一个等效电压源来代替,该电压源的电动势E,等于这个含源一端口网络的开路电压Uoc,其等效内阻Rs等于这个含源一端口网络中各电源均为零时(电压源短路,电流源断开)无源一端口网络的入端电阻R,这个结论就是戴维宁定理。
三(实验内容及步骤:(1) 按图(1)接线,改变负载电阻R,测量出UAB和IR的数值,特别注意要测量出R=?及R=0时的电压和电流,填写下表:AUocRABB(2) 测量无源一端口网络的入端电阻。
将电流源去掉(开路),电压源去掉(去除用导线短接),再将负载电阻开路,测量AB两端的电阻RAB,该电阻即为网络的入端电阻。
或通过计算公式:入端电阻RAB=UAB开路电压/IR短路电流。
(RAB=524欧)(3) 调节电阻箱的电阻,使其等于RAB,然后将稳压电源输出调到Uoc(步骤1的开路电压)与RAB串联,如图(2)。
重复测量UAB和IR,并与步骤1所测量的数值比较,验证戴维宁四(误差及结果分析:(1)根据所学理论知识,计算采用戴维宁定理计算在不同电阻R情况下UAB和IR。
(2)步骤1和步骤3测量的两组数据分析比较,分析产生误差的原因篇二:戴维宁定理实验报告 - 2《电路原理》实验报告实验时间:2012/4/26一、实验目的二、实验原理戴维宁定理指出:任何一个线性有源一端口网络,对于外电路而言,总可以用一个理想电压源和电阻的串联形式来代替,理想电压源的电压等于原一端口的开路电压Uoc,其电阻(又称等效内阻)等于网络中所有独立源置零时的入端等效电阻Req,见图2-1。


实验三 等效电源定理一、实验目的1. 验证等效电源定理。
2. 熟悉电路的开路和短路情况,掌握测量等效电压源的电动势、等效电流源的短路电流和等效内阻的方法。
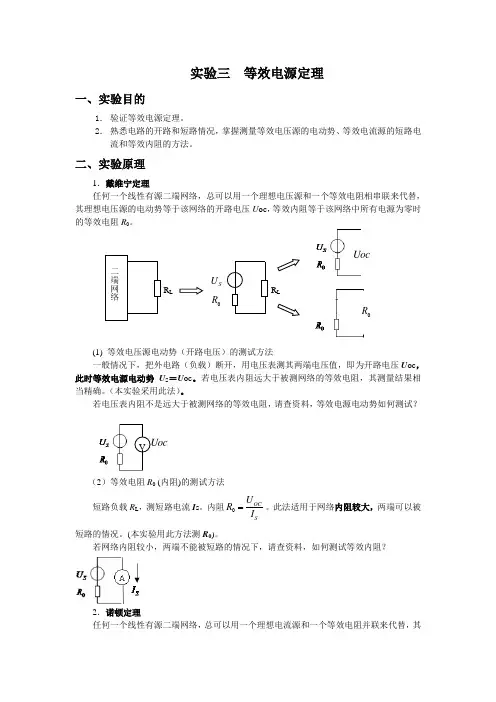
二、实验原理1.戴维宁定理任何一个线性有源二端网络,总可以用一个理想电压源和一个等效电阻相串联来代替,其理想电压源的电动势等于该网络的开路电压U oc ,等效内阻等于该网络中所有电源为零时的等效电阻R 0。
(1) 等效电压源电动势(开路电压)的测试方法一般情况下,把外电路(负载)断开,用电压表测其两端电压值,即为开路电压Uoc ,此时等效电源电动势U S =U oc 。
若电压表内阻远大于被测网络的等效电阻,其测量结果相当精确。
(本实验采用此法)。
若电压表内阻不是远大于被测网络的等效电阻,请查资料,等效电源电动势如何测试?(2)等效电阻R 0 (内阻)的测试方法短路负载R L ,测短路电流I s 。
内阻0OCSU R I。
此法适用于网络内阻较大,两端可以被短路的情况。
(本实验用此方法测R 0)。
若网络内阻较小,两端不能被短路的情况下,请查资料,如何测试等效内阻?2.诺顿定理任何一个线性有源二端网络,总可以用一个理想电流源和一个等效电阻并联来代替,其R L R LSU 0R Uoc0R V Uoc理想电流源的短路电流I S 等于该网络负载R L 的短路电流,等效内阻等于该网络中所有电源为零时的等效电阻R 0。
(1) 等效电流源短路电流的测试方法 一般情况下,测量负载短路电流即为I S (2)等效电阻R 0 (内阻)的测试方法 与戴维宁定理相同。
三、实验仪器和设备1.EEL -Ⅶ实验台 1台2.万用表 1块3.EEL -51组件、EEL -53组件四、实验内容及步骤1.测量有源二端网络的外部伏安特性本实验用EEL -53组件进行。
按下图接线,调节使电源电压 U S1 = 25V ,调节有源二端网络外接电阻R L 的数值,使其分别为表3中所示数值。
测量通过R L 的电流和R L 两端电压,将测量结果填入表1中。

戴维南定理的实验验证报告第一篇:戴维南定理的实验验证报告戴维南定理学号:姓名:成绩:一实验原理及思路一个含独立源,线性电阻和受控源的二端网络,其对外作用可以用一个电压源串联电阻的等效电源代替,其等效电压源的电压等于该二端网络的开路电压,其等效内阻是将该二端网络中所有的独立源都置为零后从从外端口看进去的等效电阻。
这一定理称为戴维南定理。
本实验采用如下所示的实验电路图a50%等效后的电路图如下b所示50%测它们等效前后的外特性,然后验证等效前后对电路的影响。
二实验内容及结果⒈计算等效电压和电阻计算等效电压:ΘR1R3=R11R33,∴电桥平衡。
Uoc=R1R1+R3=2.6087V。
计算等效电阻:R=⎛R2+11+R1R3⎝⎫⎪⎪⎪⎪⎭+⎛R22+11+R11R33⎝⎫⎪⎪⎪⎪⎭=250.355⒉用Multisim软件测量等效电压和等效电阻测量等效电阻是将V1短路,开关断开如下图所示Ro=250.335测量等效电压是将滑动变阻器短路如下图50%Uo=2.609V⒊用Multisim仿真验证戴维南定理仿真数据原电路数据8765电流/mA43210-1电压/V通过OriginPro 软件进行绘图,两条线基本一致。
电流/mA电压/V由上面的数据及图线得知等效前后不影响电路的外特性,即验证了戴维南定理。
三结论及分析本实验,验证了戴维南定理即等效前后的电路的外特性不改变。
进行板上实验时,存在一定的误差,而使电路线性图不是非常吻合。
可能是仪器的误差,数据不能调的太准确,也可能是内接和外接都有误差。
本实验最大的收获是学会用一些仿真软件,去准确的评估实际操作中的误差。
改进的地方是进行测量时取值不能范围太窄,要多次反复测量以防实验发生错误。
第二篇:实验三戴维南定理的验证实验三戴维南定理的验证一、实验目的1.验证戴维南定理。
2.加深对等效电路概念的理解。
3.掌握测量有源二端网络等效电路参数的方法。
二、实验原理与说明由戴维南定理可知:任何一个线性含源二端网络Ns,对外电路来说,可以用一个电压源和电阻的串联组合来等效,此电压源的电压等于该网络Ns的开路电压uoc,而电阻等于该网络中所有的独立电源置零后的输入电阻Req。

戴维宁定理的验证实验报告戴维宁定理的验证实验报告摘要:戴维宁定理是数学中的一个重要定理,它描述了一个函数在某个区间上的连续性与可导性之间的关系。
本实验旨在通过一系列实验验证戴维宁定理的有效性,并探讨其在实际问题中的应用。
引言:戴维宁定理是由数学家戴维宁在19世纪提出的,它被广泛应用于微积分和数学分析领域。
该定理指出,如果一个函数在某个区间上连续,并且在该区间上可导,则该函数在该区间上的可导性是连续性的充分必要条件。
本实验将通过一系列验证实验来检验戴维宁定理的有效性。
实验一:连续函数的可导性首先,我们选取一个连续函数f(x) = sin(x)作为实验对象。
通过计算f(x)在不同点的导数,我们可以观察到当x在区间[0, π]上连续变化时,f(x)的导数也在该区间上连续变化。
这验证了戴维宁定理中连续性与可导性之间的关系。
实验二:非连续函数的不可导性接下来,我们选取一个非连续函数g(x) = |x|作为实验对象。
通过计算g(x)在不同点的导数,我们可以观察到当x在区间[-1, 1]上连续变化时,g(x)的导数并不连续。
这进一步验证了戴维宁定理中连续性与可导性之间的关系。
实验三:应用于实际问题除了在数学领域中的应用,戴维宁定理也可以应用于实际问题的求解中。
我们选取一个实际问题来说明这一点。
假设我们有一个物体在空气中的下落过程,其速度随时间的变化可以表示为v(t) = 9.8t + C,其中t为时间,C为常数。
根据戴维宁定理,我们知道v(t)的可导性与其连续性相关。
通过对v(t)进行求导,我们可以得到物体的加速度a(t) = 9.8。
这意味着物体在空气中的下落过程是一个匀加速运动。
这个例子展示了戴维宁定理在实际问题中的应用。
结论:通过一系列验证实验和应用实例,我们验证了戴维宁定理的有效性。
该定理描述了一个函数在某个区间上的连续性与可导性之间的关系,为数学分析提供了重要的理论基础。
同时,戴维宁定理在实际问题的求解中也具有重要的应用价值。
戴维宁定理的验证实验报告一、实验目的1、深刻理解戴维宁定理的基本概念和原理。
2、掌握用实验方法测量有源二端网络的开路电压、等效电阻和短路电流。
3、学会使用直流电压表、电流表和电阻箱等仪器设备。
4、通过实验数据验证戴维宁定理的正确性。
二、实验原理戴维宁定理指出:任何一个线性有源二端网络,对外电路来说,可以用一个电压源和一个电阻的串联组合来等效替代。
其中,电压源的电压等于有源二端网络的开路电压$U_{OC}$,电阻等于有源二端网络除源后的等效电阻$R_{0}$。
1、开路电压$U_{OC}$的测量在有源二端网络输出端开路时,用电压表直接测量其输出端的电压,即为开路电压$U_{OC}$。
2、等效电阻$R_{0}$的测量(1)开路、短路法先测有源二端网络的开路电压$U_{OC}$,再测其短路电流$I_{SC}$,则等效电阻$R_{0} = U_{OC} / I_{SC}$。
但这种方法一般不适合于电流较大的情况,容易损坏电源。
(2)伏安法将有源二端网络中的所有独立源置零(电压源短路,电流源开路),然后在端口处施加一电压$U$,测量端口电流$I$,则等效电阻$R_{0} = U / I$ 。
(3)半电压法当负载电阻$R_{L}$等于有源二端网络的等效电阻$R_{0}$时,负载电阻两端的电压为开路电压的一半。
此时,可根据测量的负载电阻值确定$R_{0}$。
三、实验设备1、直流稳压电源(双路)2、直流电压表3、直流电流表4、电阻箱5、导线若干四、实验内容及步骤1、按图 1 连接实验电路,其中$R_{1} = 100\Omega$,$R_{2} = 200\Omega$,$U_{S} = 10V$ 。
!实验电路图 1(此处可插入实验电路图 1 的图片)2、测量有源二端网络的开路电压$U_{OC}$将负载电阻$R_{L}$开路,用直流电压表测量有源二端网络输出端的电压,即开路电压$U_{OC}$。
记录测量值。
3、测量有源二端网络的短路电流$I_{SC}$将有源二端网络输出端短路,用直流电流表测量短路电流$I_{SC}$。
戴维宁定理实验报告一、实验名称戴维宁定理验证二、实验目的1、验证戴维宁定理的正确性,加深对该定理的理解2、掌握测量有源二端网络等效的一般方法三、实验原理任何一个有源二端网络都可以用一个电动势为了E的理想电压源和内阻R串联的电源来等效代替.等效电源的电动势E就是有源二端网络的开路电压U bc,等效电源的内阻R等于有源二端网络中所有独立源均置零后所得到的无源网络的等效电阻.在有源二端网络输出端开路时吗, 用电压表直接输出端的开路电压U bc,然后再将其输出端短路,用电流表测其短路电流ISC, 那么等效内阻为了R)=Ubd sc.四、实验设备可调直流稳定电源(0—— 30V%可调直流恒流源(0—— 500mV、直流数字电压表(0—— 200V、直流数字毫安表(0一—200mV、万用表、可调电阻箱、电位器、戴维宁定理实验电路表五、实验内容1、按图接入稳定电源L S=12V和恒流源I s=10mV不接入RL,测出U bc和I sc,并计算出R,数据计入表1.2.1 ;二" (b)2、负载实验:按图接入RL,改变RL阻值,测量有源二端网络的外特性曲线,实验数据计入表 1.2.2 ;3、验证戴维宁定理:从电阻箱取得根据步骤1所得的有效电阻R0之值,然后令其与直流稳定电压电源相串联,计入表 1.2.3 .六、实验数据处理表 1.2.1表 1.2.2表 1.2.3由图可知,在误差允许的范围内, 表1.2.2和表1.2.3的数据根本吻合,由此可知,戴维宁定理成立.七、实验总结1、实验结论在误差允许的范围内,戴维宁定理成立.2、实验误差分析由于电路元件中肯定会存在无法消除的原理误差, 还有温度、压强等不可控的外界因素,等效变换后当然误差是难以防止的.。
戴维宁定理实验总结在数学领域中,戴维宁定理(Davenport's Theorem)是一个重要的定理,其可以用来描述逆序对的数量与循环置换的关系。
为了更好地理解和应用戴维宁定理,我们进行了一系列的实验,并在本文中对实验结果进行总结和分析。
实验一:了解戴维宁定理的原理为了更好地理解戴维宁定理,我们首先对其进行了深入的研究。
通过对相关文献的阅读和理论推导,我们深刻理解了戴维宁定理的原理及其数学背景。
同时,我们还使用数学软件编写了相关的模拟代码,通过对不同置换的实验验证,进一步巩固了对戴维宁定理的理解。
实验二:分析逆序对的数量与循环置换的关系在实验中,我们随机生成了一系列的置换,并统计了每个置换中逆序对的数量。
通过对数据的分析,我们发现逆序对的数量与循环置换之间存在着明显的关联。
当逆序对的数量较小时,循环置换的数量也较少;而当逆序对的数量增加时,循环置换的数量也随之增加。
这一结果进一步验证了戴维宁定理的准确性。
实验三:应用戴维宁定理解决实际问题除了在理论验证中的应用,戴维宁定理还可以用于解决一些实际问题。
在实验中,我们运用戴维宁定理对一组有序数据进行了分析,通过计算逆序对的数量,我们可以判断该组数据是否处于有序状态。
实验结果表明,逆序对的数量较少的数据更倾向于有序,而逆序对数量较多的数据则较可能处于无序状态。
这一应用为我们提供了一种可行的方法用于数据的判别和分析。
实验四:戴维宁定理在排序算法中的应用由于戴维宁定理与数据的有序性密切相关,我们进一步研究了其在排序算法中的应用。
通过对不同排序算法的比较和优化,在实验中发现,戴维宁定理可以用于评估排序算法的性能。
当排序算法的时间复杂度较高时,逆序对的数量也相应较多;而当排序算法的时间复杂度较低时,逆序对的数量也较少。
这为我们提供了一种新的角度来评估和优化排序算法的效率。
结论:通过一系列的实验和研究,我们对戴维宁定理有了更深入的理解,并探索了其在实际问题和排序算法中的应用。
实验三 戴维宁定理一、实验目的1、 验证戴维宁定理的正确性,加深对该定理的理解。
2、 测定线性有源一端口网络的外特性和戴维宁等效电路的外特性。
二、实验原理1、任何一个线性含源网络,如果仅研究其中一条支路的电压和电流,可将电路的其余部分看作是一个有源二端网络(或称为含源一端口网络)。
戴维宁定理指出:任何一个线性有源网络,对于外电路而言,总可以用一个理想电压源和电阻的串联形式来代替,理想电压源的电压等于原一端口的开路电压oc U ,其电阻(又称等效内阻)等于网络中所有独立源置零时的输入端等效电阻eq R ,见图3-1。
2、有源二端网络等效参数的测量方法 (1)开路电压、短路电流法在有源二端网络输出端开路时,用电压表直接测出其输出端的开路电压Uoc ,然后再将其输出端短路,用电流表测量其短路电流Isc ,则等效电阻为scoc eq I U R =这种方法适用于ab 端等效电阻eq R 较大,而短路电流不超过额定值的情形,否则有损坏电源的危险。
(2)两次电压测量法测量电路如图3-2,3-3所示,第一次测量ab 端的开路oc U ,第二次在ab 端接一已知电阻L R (负载电阻),测量此时a ,b 端的负载电压U ,则a ,b 端的等效电阻eq R 为:L oc eq R U U R ⎥⎦⎤⎢⎣⎡-1=图3-1图3-2 图3-3 这种方法在实际测量中常被采用。
(3)半电压法如图3-4所示,当负载电压为被测网络开路电压一半时,负载电阻(由电阻箱的读数确定)即为有源二端网络的等效电阻。
三、仪器设备1、戴维宁定理实验电路板2、电位器3、直流数字电压表、直流数字毫安表4、可调直流稳压电源 四、实验内容与步骤1、测定有源二端网络的开路电压oc U 和等效电阻R eq(1)按图3-5接线,经检查无误后,采用开路电压短路电流法测定有源二端网络的开路电压oc U ,电压表内阻应远大于二端网络的等效电阻R ’eq ,可直接测出短路电流,并将此短路电流sc I 数据记入表格3-1中。
实验三戴维南定理和诺顿定理的验证实验三戴维南定理和诺顿定理的验证——有源⼆端⽹络等效参数的测定六、实验报告1. 根据步骤2、3、4,分别绘出曲线,验证戴维南定理的正确性,并分析产⽣误差的原因。
答:曲线如下,U1为原电路参数,U2为等效电路参数。
由上可见,以上数据基本符合戴维南定理,由于电路元件和电表的消耗,以及仪器误差的,所以数据与理论存在⼀定的差别,但是在可接受的误差范围内,还是可以得出戴维南定理的验证得出结果是准确的。
2. 根据步骤1、5、6的⼏种⽅法测得的Uoc与R0与预习时电路计算的结果作⽐较,你能得出什么结论。
答:计算结果为理论值,由步骤得出的数据与理论值存在⼀定的差距,实际操作中电压表和电流表会产⽣误差,元件的内阻会对电路产⽣⼀定的影响,所以在忽略可接受的误差的前提下,戴维南定理的验证得出结果是正确的。
3. 归纳、总结实验结果。
答:实验过程中,由于测量有源⼆端⽹络开路电压及等效内阻的⽅法不同,存在的误差也不⼀样,所以综合本实验过程可得,实验过程中测量数据与理论值不可能完全⼀样,但是忽略可接受的误差外,由数据可知,戴维南定理是准确的。
4.⼼得体会通过这次做戴维南定理的课程设计报告,让我明⽩原来有些事并⾮我们以为的那么困难的。
很多时候都是我们为⾃⼰找理由。
最初听到⽼师给我们的课程设计报告的要求时,⼤多数同学都很吃惊,觉得⽼师的要求太难了。
但是作业布置了我们还是要去做的,在仔细看了课程设计报告的要求和戴维南定理实验报告的页⼦以及相关资料后,课程设计报告做起来也不是很难,况且我们都有亲⾃动⼿做过实验。
还记得在第⼀次上电路课时⽼师就告诉我们这门课很重要,是以后学习专业知识的基础。
两三个⽉过后,我也深有体会。
其实每次做实验都有助于我们巩固所学的知识,也能在⼀定程度上提升我们的学习兴趣,提⾼我们的动⼿能⼒。
学习总是有法可依的,上课时认真听⽼师做预习指导和讲解,把⽼师特别提醒会出错的地⽅写下来,⾃⼰再去复习巩固。
实验三 戴维宁定理
一、实验目的
1、 验证戴维宁定理的正确性,加深对该定理的理解。
2、 测定线性有源一端口网络的外特性和戴维宁等效电路的外特性。
二、实验原理
1、任何一个线性含源网络,如果仅研究其中一条支路的电压和电流,可将电路的其余部分看作是一个有源二端网络(或称为含源一端口网络)。
戴维宁定理指出:任何一个线性有源网络,对于外电路而言,总可以用一个理想电压源和电阻的串联形式来代替,理想电压源的电压等于原一端口的开路电压oc U ,其电阻(又称等效内阻)等于网络中所有独立源置零时的输入端等效电阻eq R ,见图3-1。
2、有源二端网络等效参数的测量方法 (1)开路电压、短路电流法
在有源二端网络输出端开路时,用电压表直接测出其输出端的开路电压Uoc ,然后再将
其输出端短路,用电流表测量其短路电流Isc ,则等效电阻为
sc
oc eq I U R =
这种方法适用于ab 端等效电阻eq R 较大,而短路电流不超过额定值的情形,否则有损坏电源的危险。
(2)两次电压测量法
测量电路如图3-2,3-3所示,第一次测量ab 端的开路oc U ,第二次在ab 端接一已知电阻L R (负载电阻),测量此时a ,b 端的负载电压U ,则a ,b 端的等效电阻eq R 为:
L oc eq R U U R ⎥⎦
⎤
⎢⎣⎡-1=
图3-1
图3-2 图3-3 这种方法在实际测量中常被采用。
(3)半电压法
如图3-4所示,当负载电压为被测网络开路电压一半时,负载电阻(由电阻箱的读数确
定)即为有源二端网络的等效电阻。
三、仪器设备
1、戴维宁定理实验电路板
2、电位器
3、直流数字电压表、直流数字毫安表
4、可调直流稳压电源 四、实验内容与步骤
1、测定有源二端网络的开路电压oc U 和等效电阻R eq
(1)按图3-5接线,经检查无误后,采用开路电压短路电流法测定有源二端网络的开路电压oc U ,电压表内阻应远大于二端网络的等效电阻R ’eq ,可直接测出短路电流,并将此短路电流sc I 数据记入表格3-1中。
图3-5
L
图3-4
oc /2
(2)利用二次电压测量法,接通负载电阻L R ,使L R =1K Ω,测出此时的负载端电压U ,并记入表格3-1中,求出相应的等效电阻R ’’eq 。
(3)取R ’eq 和R ’’eq 两次测量的等效电阻平均值作为eq R ,并记入表格3-1中。
表3-1
2、测定有源二端网络的外特性
改变负载电阻L R 之值,在不同负载的情况下,测量相应的负载端电压和流过负载的电流,共取五个点将数据记入自拟的表格3-2中。
表3-2
3、测定戴维宁等效电路的外特性。
如果用电压等于开路电压oc U 的理想电压源与等效电阻eq R 相串连的电路(称为戴维宁等效电路,参见图3-3)来代替原有原二端网络,则它的外特性()I f U =应与有源网络的外特性完全相同。
重复上述步骤测出负载电压和负载电流,并将数据记入自拟的表格3-3中。
表3-3
六、实验报告要求
1、判断戴维宁定理的正确性,并分析产生误差的原因。
2、在同一坐标纸上作出两种情况下的外特性曲线,并作适当分析。