3空气动力学基础-第3章 低速平面位流

空⽓动⼒学部分知识要点空⽓动⼒学及飞⾏原理课程空⽓动⼒学部分知识要点⼀、流体属性与静动⼒学基础1、流体与固体在⼒学特性上最本质的区别在于：⼆者承受剪应⼒和产⽣剪切变形能⼒上的不同。

2、静⽌流体在剪应⼒作⽤下（不论所加剪切应⼒τ多么⼩，只要不等于零）将产⽣持续不断的变形运动（流动），换句话说，静⽌流体不能承受剪切应⼒，将这种特性称为流体的易流性。

3、流体受压时其体积发⽣改变的性质称为流体的压缩性，⽽抵抗压缩变形的能⼒和特性称为弹性。

4、当马赫数⼩于0.3时，⽓体的压缩性影响可以忽略不计。

5、流层间阻碍流体相对错动（变形）趋势的能⼒称为流体的粘性，相对错动流层间的⼀对摩擦⼒即粘性剪切⼒。

6、流体的剪切变形是指流体质点之间出现相对运动（例如流体层间的相对运动）流体的粘性是指流体抵抗剪切变形或质点之间的相对运动的能⼒。

流体的粘性⼒是抵抗流体质点之间相对运动（例如流体层间的相对运动）的剪应⼒或摩擦⼒。

在静⽌状态下流体不能承受剪⼒；但是在运动状态下，流体可以承受剪⼒，剪切⼒⼤⼩与流体变形速度梯度有关，⽽且与流体种类有关7、按照作⽤⼒的性质和作⽤⽅式，可分为彻体⼒和表⾯⼒（⾯⼒）两类。

例如重⼒，惯性⼒和磁流体具有的电磁⼒等都属于彻体⼒，彻体⼒也称为体积⼒或质量⼒。

8、表⾯⼒：相邻流体或物体作⽤于所研究流体团块外表⾯，⼤⼩与流体团块表⾯积成正⽐的接触⼒。

由于按⾯积分布，故⽤接触应⼒表⽰，并可将其分解为法向应⼒和切向应⼒：9、理想和静⽌流体中的法向应⼒称为压强，其指向沿着表⾯的内法线⽅向，压强的量纲是[⼒]/[长度]210、标准⼤⽓规定在海平⾯上，⼤⽓温度为15℃或T0=288.15K ，压强p0 = 760 毫⽶汞柱= 101325⽜/⽶2，密度ρ0 =1.225千克/⽶311、从基准⾯到11 km 的⾼空称为对流层，在对流层内⼤⽓密度和温度随⾼度有明显变化，温度随⾼度增加⽽下降，⾼度每增加1km，温度下降6.5 K。

飞行原理空气动力学复习思考题第一章低速气流特性1．何谓连续介质为什么要作这样的假设连续介质——把空气看成是由空气微团组成的没有间隙的连续体。

作用——把空气压强（P）、密度（ρ）、温度（T）和速度(V)等状态参数看作是空间坐标及时间的连续函数，便于用数学工具研究流体力学问题。

2．何谓流场举例说明定常流动与非定常流动有什么区别。

流场——流体所占居的空间。

定常流动——流体状态参数不随时间变化；非定常流动——流体状态参数随时间变化；3．何谓流管、流谱、流线谱低速气流中，二维流谱有些什么特点流线谱——由许多流线及涡流组成的反映流体流动全貌的图形。

流线——某一瞬间，凡处于该曲线上的流体微团的速度方向都与该曲线相应点的切线相重合。

流管——通过流场中任一闭合曲线上各点作流线，由这些流线所围成的管子。

二维流谱——1.在低速气流中，流谱形状由两个因素决定：物体剖面形状，物体在气流中的位置关系。

2.流线的间距小，流管细，气流受阻的地方流管变粗。

3.涡流大小决定于剖面形状和物体在气流中的关系位置。

4．写出不可压缩流体和可压缩流体一维定常流动的连续方程，这两个方程有什么不同有什么联系连续方程是质量守恒定律应用于运动流体所得到的数学关系式。

在一维定常流动中，单位时间内通过同一流管任一截面的流体质量都相同。

方程表达式：m=ρVA不可压流中，ρ≈常数，方程可变为：VA=C（常数）气流速度与流管切面积成反比例。

可压流中，ρ≠常数，方程可变为：m=ρVA图1-7一翼剖面流谱适用于理想流体和粘性流体5． 说明气体伯努利方程的物理意义和使用条件。

方程表达式:常量=++gh V P ρρ221高度变化不大时，可略去重力影响，上式变为：常量==+0221p V p ρ 即:静压+动压=全压(P 0相当于V=0时的静压)方程物理意义:空气在低速一维定常流动中，同一流管的各个截面上，静压与动压之和（全压）都相等。

由此可知，在同一流管中，流速快的地方，压力（P ）小；流速慢的地方，压力（P ）大。

空气动力学基础（教学重点）绪论（1学时）第一章流体静力学（5学时）1、掌握连续介质假设的概念、意义和条件；2、了解掌握流体的基本物理属性，尤其是易流性、粘性、压缩性等属性的物理本质和数学表达；3、掌握流体力学中作用力的分类和表达、静止流体中压强的定义及其特性；4、初步掌握静止流体微团的力学分析方法，重点掌握流体平衡微分方程的表达及其物理意义；5、在流体平衡微分方程的应用方面，掌握重力场静止液体中的压强分布规律，重点掌握标准大气问题。

第二章流体运动学与动力学基础（12学时）1、了解两种描述流场的方法的区别与特点，重点掌握欧拉法下加速度的表达和意义2、掌握流体微团的几种变形和运动及其数学表达，掌握流体微团的运动分解与刚体运动的异同；3、了解系统分析方法与控制体分析方法的区别与联系，了解雷诺输运方程的表达及意义；4、空气动力学基本方程是本章重点，积分形式方程要掌握质量方程、动量方程和能量方程的表达和意义，并会用它们解决实际工程问题；微分形式方程要重点掌握连续方程、欧拉方程和能量方程的表达和意义；掌握微元控制体分析方法；掌握伯努利方程的表达、意义、条件和应用；5、重点需要掌握的概念：流线、流量、散度、旋度、位函数、流函数、环量与涡的表达、意义及其相互之间的关系；第3章低速平面位流（6学时）3．1 平面不可压位流的基本方程及其边界条件二维流动不可压无旋流动的基本方程是位函数满足的拉普拉斯方程不穿透条件（可滑移条件）拉普拉斯方程的叠加原理，速度也可叠加，压强不可叠加流函数也满足拉普拉斯方程3.2 几种简单的二维位流各基本解的速度、位函数、流函数直匀流源，汇偶极子，偶极子的形成，轴线，方向点涡点涡的环量3．3 一些简单的迭加举例直匀流加点源压强系数直匀流加偶极子达朗培尔疑题直匀流加偶极子加点涡儒可夫斯基升力定理了解二维对称物体绕流的数值解粘性流体动力学基础（4学时）流体粘性及其对流动的影响（流体的粘滞性，粘性流体运动特点）粘性流体的应力状态（理想流体与粘性流体作用面的受力特点，粘性流体的应力状态）广义牛顿内摩擦定理粘性流体动力学方程N-S方程粘性流体运动的基本性质（了解Re实验）边界层理论及其近似（6学时）边界层近似及其特征平面不可压缩流体层流边界层方程平板层流边界层相似解边界层动量积分方程（应用例子）边界层的分离现象第6章高速可压流(12)6.1 热力学基础知识（掌握）热力学的物系；平衡过程和可逆过程热力学一定律：内能和焓热力学第二定律，熵气体的状态方程完全气体等熵过程关系式6.2 音速和马赫数（重点）现象微弱扰动传播过程与传播速度——音速音速公式马赫数6.3 高速一维定常流（重点）一维定常绝热流的能量方程一维定常绝热流参数间的基本关系式总温T0,,总焓,临界点,速度系数使用驻点参考量的参数关系式使用临界参考量的参数关系式等熵管流的速度与截面积关系，拉瓦尔管喷管的设计压强比，M（λ）及流量的计算6.4 微弱扰动的传播区，马赫锥（重点）马赫角6.5 膨胀波（介绍）壁面外折dδ外折δ诸参数的变化趋势超音速流绕外钝角膨胀的计算6·6 激波正激波（重点）正激波的形成，计算弱激波可以看作等熵波斜激波（介绍）波前波后气流参数的关系激波图线及应用压强决定激波圆锥激波（介绍）收敛—扩张喷管在非设计状态下的工作（介绍）。

第三章- 飞行空气动力学飞行空气动力学介绍作用于飞机上的力的相互关系和由相关力产生的效应。

作用于飞机的力至少在某些方面，飞行中飞行员做的多好取决于计划和对动力使用的协调以及为改变推力，阻力，升力和重力的飞行控制能力。

飞行员必须控制的是这些力之间的平衡。

对这些力和控制他们的方法的理解越好，飞行员执行时的技能就更好。

下面定义和平直飞行(未加速的飞行)相关的力。

推力是由发动机或者螺旋桨产生的向前力量。

它和阻力相反。

作为一个通用规则，纵轴上的力是成对作用的。

然而在后面的解释中也不总是这样的情况。

阻力是向后的阻力，由机翼和机身以及其他突出的部分对气流的破坏而产生。

阻力和推力相反，和气流相对机身的方向并行。

重力由机身自己的负荷，乘客，燃油，以及货物或者行礼组成。

由于地球引力导致重量向下压飞机。

和升力相反，它垂直向下地作用于飞机的重心位置。

升力和向下的重力相反，它由作用于机翼的气流动力学效果产生。

它垂直向上的作用于机翼的升力中心。

在稳定的飞行中，这些相反作用的力的总和等于零。

在稳定直飞中没有不平衡的力(牛顿第三定律)。

无论水平飞行还是爬升或者下降这都是对的。

也不等于说四个力总是相等的。

这仅仅是说成对的反作用力大小相等，因此各自抵消对方的效果。

这点经常被忽视，而导致四个力之间的关系经常被错误的解释或阐明。

例如，考虑下一页的图3－1。

在上一幅图中的推力，阻力，升力和重力四个力矢量大小相等。

象下一幅图显示的通常解释说明(不保证推力和阻力就不等于重力和升力)推力等于阻力，升力等于重力。

必须理解这个基本正确的表述，否则可能误解。

一定要明白在直线的，水平的，非加速飞行状态中，相反作用的升力和重力是相等的，但是它们也大于相反作用的推力和阻力。

简而言之，非加速的飞行状态下是推力和阻力大小相等，而不是说推力和阻力的大小和升力重力相等，基本上重力比推力更大。

必须强调的是，这是在稳定飞行中的力平衡关系。

总结如下：向上力的总和等于向下力的总和向前力的总和等于向后力的总和对旧的“推力等于阻力，升力等于重力”公式的提炼考虑了这样的事实，在爬升中，推力的一部分方向向上，表现为升力，重力的一部分方向向后，表现为阻力。

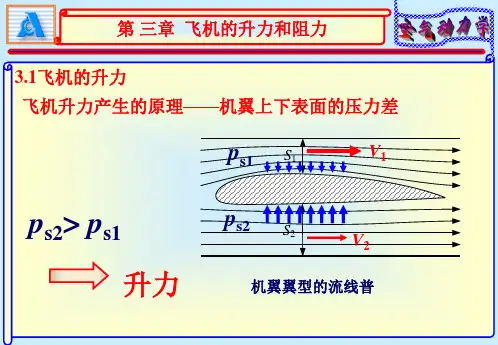
第三章理想不可压缩流体平面位流3-1 设有直匀流V ∞以正X 轴方向流过位于原点的点源，点源的强度为Q ，试求半无限体表面上最大垂直分速度max v 的位置及速度值，并证明，在该点处合速度的大小正好等于直匀流速度V ∞。

解：根据叠加原理，流函数为arctg 22Q Q y V y V y xψθππ∞∞=+=+（1） 利用流函数表达式（1），可以写出合速度场中的速度分量为222222Q x u V y x y Q y v x x y ψπψπ∞∂⎧==+⎪∂+⎪⎨∂⎪=-=⎪∂+⎩（2） 由（2）式可以确定流场中驻点A （即0A A u v ==的点）位置为20AAQ x V y π∞⎧=-⎪⎨⎪=⎩（3） 过驻点A 的流线，即为半无限体的表面，其方程为()sin 2Qy r V θπθπ∞==-（4） 半无限体表面上的垂直分速度为222sin sin 22-V Q y Q v x y r θθπππθ∞===+（5）由()222sin 2sin cos sin 0---V V V dv d d d θθθθθθπθπθπθ∞∞∞⎛⎫==+=⎪⎝⎭（6） 可得sin 0tg 2θθπθ=⎧⎪⎨=-⎪-⎩（7） 当0sin =θ时，θπ=，2sin 0-V v θπθ∞==当2-tg -=θπθ时，22sin 2sin sin2-tg V V v V θθθπθθ∞∞∞==-=-，即 1 1.9760315113.2183θ==，sin20.724611v V V θ∞∞=-= 2 4.3071538246.7817θ==，sin20.724611v V V θ∞∞=-=-所以，半无限体表面上最大的垂直分速度为max 0.724611v V ∞=（8）该点的位置为1.9760315113.2183θ==，()2Qy V πθπ∞=-（9） 在半无限体表面的水平速度分量为()22sin cos cos 22V Q x Q u V V V x y r θθθπππθ∞∞∞∞=+=+=++-（10） 在该点处的水平速度分量为()sin cos 0.689158V u V V θθπθ∞∞∞=+=-（11）则该点处的合速度为V V ∞==（12）3-2令(),G x y 是二维拉普拉斯方程的解，请证明(),G x y 可以代表二维无粘不可压缩流动的位函数或流函数。

空气动力学入门篇(1)空气动力学是十分重要的，这一点每个人似乎都知道。

特别是当我们越开越快的时候。

如果你不信在当今的遥控车比赛中，空气动力学扮演一个重要的角色，你可以试试不用车壳裸跑，就会发现巨大的差别。

但不幸的是，空气动力学所包含的物理学和数学知识是非常复杂的。

所以，在以下的文章，我们用一些现实生活中的事例和图片，为大家解释一下空气动力学的效果。

你是否留意过，多年以来，汽车变的越来越曲线化呢？有着柔和的表面和浑圆的边角。

反观几十年前的汽车，多数具有样子凶狠的鬼面罩、锋利的边角、外倾的车头和车尾、数个带碟子的天线，尾鳍，还有各式各样向外突出的东西。

以下方图片为证：这种进化的原因是因为所有有突出的形状或者锋利的边角的东西都会产生阻力，这种阻力会使车变慢。

一般来说，水滴形状是最好的，也就是说它产生最小的空气阻力。

近代的研究指出，企鹅形状的物体阻力甚至更小。

无论什么形状，其重点是：空气在形状平缓的物体的表面流动，是最有效率的。

平缓的表面，使空气在流动时不会破裂成很多小旋涡。

基本上，任何尖锐、突出形状的物体都会产生旋涡（旋涡就象我们冲厕所看到的水流那样）。

旋涡会带走能量，因为空气会自由流动，而不依附于车子的表面。

本来这些在空气摩擦中损失的能量是可以用于加速车子的。

我们可以把空气阻力分成两部分来研究：由空气对车的前方的压力，还有由车的后方的真空所产生的拉力。

这种分法比较直接，因为要使车子在空气中前进，首先车的前面要拨开空气；当车通过这些空气之后，空气会迅速填补“空”的地方。

车在空气中前进的时候，车首撞击一堆空气，并压缩其中的一部分。

其结果使车前方的空气压强增加。

大概我们每个人都会记得：“101物理定律”--压力=压强x面积。

因此，全车截面积乘以压强，就等于净阻力。

引擎动力要克服这种阻力，因此阻力可以减速你的车，或者消耗更多的能量。

所以，车的纵向截面积越大，产生的阻力就越大。

这就是为什么将车壳安装低几毫米（在规则之内），是明智之举。