惯性矩、抵抗矩、面积矩

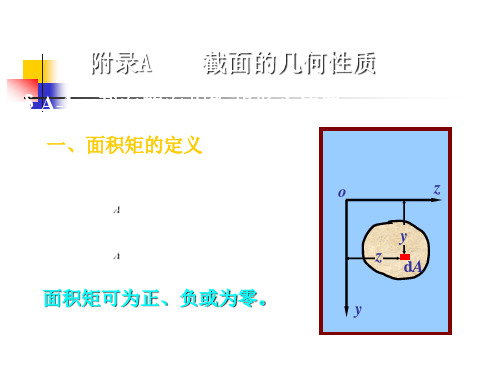
截面惯性矩和截面抵抗矩
梁的截面惯性矩和截面抗矩是有力学原理由力学原理计算得出，对于工程计算和设计十分重要。

截面惯性矩是指梁截面在任意方向和平面围绕其中心点，旋转一周所产生的力矩;而抗矩则
来源于求取梁截面在一起受力时所抵抗偏转作用的力矩。

简言之，截面惯性矩和抗矩表示了梁所能承受的偏转能力有多大。

梁的截面惯性矩计算时，需根据所使用的梁截面的几何形状不同，综合考虑其面积、外接图形的面积以及距离质心的距离大小等因素，综合计算所得结果是根据梁的几何形状所得的结果逐步的减小的。

抗矩的计算与计算惯性矩相同，也需要根据梁截面的形状来计算，不过抗矩采用的是恒压梁横向剖面质心与中心线距离来计算，这是因为梁蒙受的外力及其作用的方向改变时，偏转力也会改变，因此梁的抗矩会发生变化。

总的来说，梁的截面惯性矩和抗矩是非常重要的参数，在工程设计和分析中起着举足轻重的作用。

精确计算梁截面惯性矩及抗矩有助于更加准确地分析梁的偏转能力，从而降低设计梁容易出现破坏情况。

材料力学面积矩计算公式
材料力学中，面积矩是对于一个截面形状的横截面积乘以该截
面形状中各点到某一轴线（通常是截面的重心轴）的距离的乘积之和。

面积矩计算公式取决于截面形状的几何特征。

以下是一些常见
截面形状的面积矩计算公式：
1. 矩形截面：
对于矩形截面，其面积矩的计算公式为，Ix = (bh^3)/12，
Iy = (hb^3)/12，其中Ix和Iy分别代表截面对x和y轴的面积矩，b代表矩形截面的宽度，h代表矩形截面的高度。

2. 圆形截面：
对于圆形截面，其面积矩的计算公式为，Ix = Iy =
πr^4/4，其中r代表圆形截面的半径。

3. T形截面：
对于T形截面，其面积矩的计算公式需要分别计算上、下翼
缘对轴线的面积矩，并且考虑翼缘与腹板之间的距离。

4. 不规则形状：
对于不规则形状的截面，可以利用积分的方法来计算面积矩，将截面分割成小块，然后对每个小块的面积矩进行累加。

在工程实践中，计算截面的面积矩是非常重要的，因为它们在
计算截面的惯性矩、受弯构件的弯曲应力等方面起着关键作用。

因此，了解不同截面形状的面积矩计算公式对于工程设计和分析具有
重要意义。

惯性矩及惯性矩抵抗拒计算利用AutoCAD计算截面特性以计算一个50×50×5国标钢方管截面为例：1.在CAD中绘制截面2.将截面生成面域reg→选择截面→创建2个面域3.布尔运算su→选择截面外轮廓→选择截面内轮廓→创建完毕4.将UCS坐标移动至截面型心位置（见图1）massprop→选择创建的面域→记住质心的X和Y坐标→ucs→m→输入质心的X和Y坐标→移动完毕5.查询截面特性（见图2）massprop→选择面域这样就可以得到截面的面积、周长、边界框、质心、惯性矩、惯性积、旋转半径等相关参数6.计算截面的抵抗矩Wx1=惯性矩Ix÷边界框X的一个值Wx2=惯性矩Ix÷边界框X的另一个值Wy1=惯性矩Iy÷边界框Y的一个值Wy2=惯性矩Iy÷边界框Y的另一个值7.计算截面的面积矩（见图3）保留要计算面积矩的部分，按前述方法生成面域，查询面域特性S=该部分的面积×质心坐标Y值圆弧计算1.已知弦长拱高求半径弦长A2 拱高B2(弦长^2+4*拱高^2)/(8*拱高) =(A2*A2+4*B2*B2)/(8*B2)(弦长^2/4+拱高^2)/(2*拱高) =(A2*A2/4+B2*B2)/(2*B2)2.已知拱高半径求角度拱高B2 半径C2DEGREES(ACOS((半径-拱高)/半径))*2 =DEGREES(ACOS((C2-B2)/C2))*2 3.已知弦长半径求角度弦长A2 半径C2ASIN(A2/2/C2)*360/3.1416 =ASIN(A2/2/C2)*360/3.14164.已知半径角度求弧度半径C2 角度D22*3.1415926*半径*角度/360 =2*3.1415926*C2*D2/3605.已知弦长半径求弧度弦长A2 半径C22*3.1415926*半径*ASIN(弦长/2/半径)/3.1416 =2*3.1415926*C2*ASIN(A2/2/C2)/3.1416。

利用AutoCAD计算截面特性以计算一个50×50×5国标钢方管截面为例：1.在CAD中绘制截面2.将截面生成面域reg→选择截面→创建2个面域3.布尔运算su→选择截面外轮廓→选择截面内轮廓→创建完毕4.将UCS坐标移动至截面型心位置（见图1）massprop→选择创建的面域→记住质心的X和Y坐标→ucs→m→输入质心的X和Y坐标→移动完毕5.查询截面特性（见图2）massprop→选择面域这样就可以得到截面的面积、周长、边界框、质心、惯性矩、惯性积、旋转半径等相关参数6.计算截面的抵抗矩Wx1=惯性矩Ix÷边界框X的一个值Wx2=惯性矩Ix÷边界框X的另一个值Wy1=惯性矩Iy÷边界框Y的一个值Wy2=惯性矩Iy÷边界框Y的另一个值7.计算截面的面积矩（见图3）保留要计算面积矩的部分，按前述方法生成面域，查询面域特性S=该部分的面积×质心坐标Y值圆弧计算1.已知弦长拱高求半径弦长A2 拱高B2(弦长^2+4*拱高^2)/(8*拱高) =(A2*A2+4*B2*B2)/(8*B2)(弦长^2/4+拱高^2)/(2*拱高) =(A2*A2/4+B2*B2)/(2*B2)2.已知拱高半径求角度拱高B2 半径C2DEGREES(ACOS((半径-拱高)/半径))*2 =DEGREES(ACOS((C2-B2)/C2))*2 3.已知弦长半径求角度弦长A2 半径C2ASIN(A2/2/C2)*360/3.1416 =ASIN(A2/2/C2)*360/3.14164.已知半径角度求弧度半径C2 角度D22*3.1415926*半径*角度/360 =2*3.1415926*C2*D2/3605.已知弦长半径求弧度弦长A2 半径C22*3.1415926*半径*ASIN(弦长/2/半径)/3.1416=2*3.1415926*C2*ASIN(A2/2/C2)/3.1416。

惯性矩和面积
惯性矩是指对于某种物体来说，物体被外力旋转时所需要的转矩大小，或者说力作用点距物体质心的距离越大，物体质心旋转所需要的力也就越大。

用数学的表达可以表示为：惯性矩与物体的质量以及距离成正比，也就是说物体质量越大，惯性矩也就越大。

惯性矩的概念正是对平面物体的惯性的一个体现。

当给物体施加的外力恰好位于物体的质心上时，惯性矩为零，即物体不会沿物体质心的平行轴旋转。

如果外力作用点不在物体质心上，惯性矩就会大于零，物体就会沿物体质心的平行轴旋转。

圆面积是指在一个坐标系中，把圆心点定在坐标轴的原点，从原点出发，沿着圆的周内的某一点A，若点A的距离（称为半径）是r，穿过A点，到达圆的另一点B，那么，在这个坐标系中，这个圆面积就是SA=πr^2.惯性矩与面积之间存在着不可忽视的联系，它们发挥着重要的联系作用。

例如，如果惯性矩大，那么物体运动所需要的转矩就会增加，而如果物体面积大，则惯性矩也会增大，显然，这两者之间完全可以形成一种有效的联系，以实现物体的快速、高效的旋转运动。

因此，惯性矩和面积的关系可以概括为，惯性矩与物体质量和物体面积是正相关的，也就是说，物体质量越大，惯性矩与物体面积就越大，这也是物体快速、高效的旋转运动首先要满足的前提条件之一。

惯性矩是一个物理量，通常被用作述一个物体抵抗扭动，扭转的能力。

惯性矩的国际单位为千克乘以平方米(kg·m2)。

面积元素dA与其至y轴或z轴距离平方的乘积z^2dA或y^2dA，分别称为该面积元素对于y轴或z轴的惯性矩或截面二次轴矩。

Z轴的惯性矩：IX=∫Ay^2dAY轴的惯性矩：IY=∫Az^2dA截面对任意一对互相垂直轴的惯性矩之和，等于截面对该二轴交点的极惯性矩。

惯性矩计算公式：矩形：b*h^3/12三角形：b*h^3/36圆形：π*d^4/64环形：π*D^4*（1-α^4)/64;α=d/D^3表示3次静矩静矩（面积X面内轴一次）把微元面积与各微元至截面上指定轴线距离乘积的积分称为截面的对指定轴的静矩Sx＝ydA。

静矩就是面积矩，是构件的一个重要的截面特性，是截面或截面上某一部分的面积乘以此面积的型心到整个截面的型心轴之间的距离得来的，是用来计算应力的。

注意：惯性矩是乘以距离的二次方,静矩是乘以距离的一次方，惯性矩和面积矩（静矩）是有区别的。

截面惯性矩截面惯性矩（I=截面面积X截面轴向长度的二次方）截面惯性矩：the area moment of inertiacharacterized an object's ability to resist bending and is required to calculate displacement.截面各微元面积与各微元至截面某一指定轴线距离二次方乘积的积分Ix＝y^2dF.截面极惯性矩截面极惯性矩（Ip=面积X垂直轴二次）。

扭转惯性矩Ip: the torsional moment of inertia极惯性矩：the polar moment of inertia截面各微元面积与各微元至某一指定截面距离二次方乘积的积分Ip＝P↑2dF。

a quantity to predict an object's ability to resist torsion, to calculate the angular displacement of an object subjected to a torque.相互关系截面惯性矩和极惯性矩的关系截面对任意一对互相垂直轴的惯性矩之和，等于截面对该二轴交点的极惯性矩Ip＝Iy＋Iz。

史上最全的常用截面几何特性计算公式构件截面的几何性质，如静力矩、形心、轴向惯性矩、极惯性矩、惯性积和主惯性轴位置等，对构件的承载能力有影响，常用于分析构件的弯曲、扭转和剪切。

1.静态力矩:也称为面积力矩或静态表面力矩。

截面对轴线的静力矩等于每个微区的积分乘以整个截面上微区到轴线的距离。

静力矩可以是正的，也可以是负的。

它的维数是长度的三次方。

静力矩的力学意义是:如果有均布载荷作用在截面上，其值表示为单位面积的量，则该载荷在某一轴上的合成力矩等于分布载荷乘以该轴的静力矩。

2、形心：又称面积中心或面积重心，是截面上具有如下性质的点：截面对通过此点任一个轴的静矩等于零。

如果将截面看成一均质等厚板，则截面的形心就是板面的重心。

形心坐标xo、yo的计算公式为：3、惯性矩：反映截面抗弯特性的一个量，简称惯性矩。

截面对某个轴的轴惯性矩等于截面上各微面积乘微面积到轴的距离的平方在整个截面上的积分。

下图所示的面积为A的截面对x、y轴的轴惯性矩分别为：转动惯量总是正的，量纲是长度的四次方。

构件的抗弯能力与轴的惯性矩成正比。

一些典型截面的轴惯性矩可在专业手册中找到。

例如，平行四边形对中心线的惯性矩为4、极惯性矩：反映截面抗扭特性的一个量。

截面对某个点的极惯性矩等于截面上各微面积乘微面积到该点距离的平方在整个截面上的积分。

下图所示面积为A的截面对某点O的极惯性矩为：极惯性矩永远是正的，量纲是长度的四次方。

构件的抗扭能力与惯性矩成正比。

圆形截面相对于其中心的惯性矩为5、惯性积：截面对于两个正交坐标轴的惯性积等于截面上各个微面积乘微面积到两个坐标轴的距离在整个截面上的积分。

面积为A的截面对两个正交坐标轴x、y的惯性积为:惯性积的量纲是长度的四次方。

截面位于坐标系的一、三象限,Ixy为正，位于二、四象限则为负。

6.主惯性轴:使截面惯性积为零的一对正交坐标轴称为截面主惯性轴，简称主轴。

截面对主惯性轴的惯性矩称为主惯性矩。

若两条主惯性轴的交点为质心，则这两条轴称为质心主惯性轴(或称主质心惯性轴)。