离散数学(第五版)清华大学出版社第2章习题解答

习题参考解答习题1.11、（3）P：银行利率降低Q：股价没有上升P∧Q（5）P：他今天乘火车去了北京Q：他随旅行团去了九寨沟PQ（7）P：不识庐山真面目Q：身在此山中Q→P，或～P→～Q（9）P：一个整数能被6整除Q：一个整数能被3整除R：一个整数能被2整除T：一个整数的各位数字之和能被3整除P→Q∧R ，Q→T2、（1）T （2）F （3）F （4）T （5）F（6）T （7）F （8）悖论习题 1.31（3）)()()()()()(R P Q P R P Q P R Q P R Q P →∨→⇔∨⌝∨∨⌝⇔∨∨⌝⇔∨→（4）()()()(())()(()())(())()()()()P Q Q R R P P R Q R P P R R P Q R P P R P R Q R Q P ∧∨∧∨∧=∨∧∨∧=∨∨∧∧∨∧=∨∧∨∧∨∧∨=右2、不， 不， 能习题 1.41(3) (())~((~))(~)()~(~(~))(~~)(~)P R Q P P R Q P P R T P R P R Q Q P R Q P R Q →∧→=∨∧∨=∨∧=∨=∨∨∧=∨∨∧∨∨、主合取范式)()()()()()()()()()()()()()())(())(()()(())()())(()((Q P R P Q R P Q R R Q P R Q P R Q P Q P R Q P R P Q R P Q R R Q P R Q P R Q P R Q P Q Q P R P P Q R R R Q Q P P R Q R P P Q R P P Q R P ∧∧∨∧⌝∧∨⌝∧⌝∧∨∧⌝∧⌝∨⌝∧∧⌝∨⌝∧⌝∧⌝=∧∧∨⌝∧∧∨∧⌝∧∨⌝∧⌝∧∨∧⌝∧⌝∨∧⌝∧⌝∨⌝∧∧⌝∨⌝∧⌝∧⌝=∨⌝∧∧∨∨⌝∧⌝∧∨∨⌝∧∨⌝∧⌝=∧∨⌝∧∨⌝=∨⌝∧∨⌝=→∧→ ————主析取范式(2) ()()(~)(~)(~(~))(~(~))(~~)(~)(~~)P Q P R P Q P R P Q R R P R Q Q P Q R P Q R P R Q →∧→=∨∧∨=∨∨∧∧∨∨∧=∨∨∧∨∨∧∨∨ 2、()~()(~)(~)(~~)(~)(~~)P Q R P Q R P Q P R P Q R P Q R P R Q →∧=∨∧=∨∧∧=∨∨∧∨∨∧∨∨∴等价3、解：根据给定的条件有下述命题公式：（A →（C ∇D ））∧～（B ∧C ）∧～（C ∧D ）⇔（～A ∨（C ∧～D ）∨（～C ∧D ））∧（～B ∨～C ）∧（～C ∨～D ）⇔（（～A ∧～B ）∨（C ∧～D ∧～B ）∨（～C ∧D ∧～B ）∨（～A ∧～C ）∨（C ∧～D ∧～C ）∨（～C ∧D ∧～C ））∧（～C ∨～D ）⇔（（～A ∧～B ）∨（C ∧～D ∧～B ）∨（～C ∧D ∧～B ）∨（～A ∧～C ）∨（～C ∧D ∧～C ）） ∧（～C ∨～D ）⇔（～A ∧～B ∧～C ）∨（C ∧～D ∧～B ∧～C ）∨（～C ∧D ∧～B ∧～C ）∨ （～A ∧～C ∧～C ）∨（～C ∧D ∧～C ∧～C ）∨（～A ∧～B ∧～D ）∨（C ∧～D ∧～B ∧～D ）∨（～C ∧D ∧～B ∧～D ）∨（～A ∧～C ∧～D ）∨ （～C ∧D ∧～C ∧～D ）（由题意和矛盾律）⇔（～C ∧D ∧～B ）∨（～A ∧～C ）∨（～C ∧D ）∨（C ∧～D ∧～B ）⇔（～C ∧D ∧～B ∧A ）∨ （～C ∧D ∧～B ∧～A ）∨ （～A ∧～C ∧B ）∨ （～A ∧～C ∧～B ）∨ （～C ∧D ∧A ）∨ （～C ∧D ∧～A ）∨（C ∧～D ∧～B ∧A ）∨（C ∧～D ∧～B ∧～A ）⇔（～C ∧D ∧～B ∧A ）∨ （～A ∧～C ∧B ∧D ）∨ （～A ∧～C ∧B ∧～D ）∨（～A ∧～C ∧～B ∧D ）∨ （～A ∧～C ∧～B ∧～D ）∨（～C ∧D ∧A ∧B ）∨ （～C ∧D ∧A ∧～B ）∨ （～C ∧D ∧～A ∧B ）∨ （～C ∧D ∧～A ∧～B ）∨（C ∧～D ∧～B ∧A ）∨（C ∧～D ∧～B ∧～A ） ⇔（～C ∧D ∧～B ∧A ）∨ （～A ∧～C ∧B ∧D ）∨ （～C ∧D ∧A ∧～B ）∨ （～C ∧D ∧～A ∧B ） ∨（C ∧～D ∧～B ∧A ）⇔（～C ∧D ∧～B ∧A ）∨ （～A ∧～C ∧B ∧D ）∨（C ∧～D ∧～B ∧A ） 三种方案：A 和D 、 B 和D 、 A 和C习题 1.51、 （1）需证()(())P Q P P Q →→→∧为永真式()(())~(~)(~())~~(~)(()(~))~(~)(~)()P Q P P Q P Q P P Q P P P Q P Q TP Q P Q T P Q P P Q →→→∧=∨∨∨∧∨=∨∨∧∨=∨∨∨=∴→⇒→∧（3）需证S R P P →∧⌝∧为永真式SR P P T S F S R F S R P P ⇒∧⌝∧∴⇔→⇔→∧⇔→∧⌝∧3A B A B ⇒∴→ 、为永真式。

离散数学第五版课后答案【篇一：离散数学课后答案(四)】txt>4.1习题参考答案-------------------------------------------------------------------------------- 1、根据结合律的定义在自然数集n中任取 a,b,c 三数，察看 (a。

b)。

c=a。

(b。

c) 是否成立？可以发现只有 b、c 满足结合律。

晓津观点：b)满足结合律，分析如下： a) 若有a,b,c∈n，则(a*b)*c =(a-b)-c a*(b*c) =a-(b-c)在自然数集中，两式的值不恒等，因此本运算是不可结合的。

b)同上，(a*b)*c=max(max(a,b),c) 即得到a，b,c中最大的数。

a*(b*c)=max(a,max(b,c))仍是得到a,b,c中最大的数。

此运算是可结合的。

c)同上,(a*b)*c=(a+2b)+2c 而a*(b*c)=a+2(b+2c),很明显二者不恒等，因此本运算也不是可结合的。

d)运用同样的分析可知其不是可结合的。

-------------------------------------------------------------------------------- 2、d)是不封闭的。

--------------------------------------------------------------------------------其不满足交换律、满足结合律、不满足幂等律、无零元、无单位元晓津补充证明如下：(1)a*b=pa+qb+r 而b*a=pb+qa+r 当p,q取值不等时，二式不相等。

因此*运算不满足交换律。

(2)设a,b,c∈r则(a*b)*c=p(pa+qb+r)+qc+r=p^2a+pab+pr+qc+r 而a*(b*c)=pa+q(pb+qc+r)+r=pa+qpb+q^2c+qr+r 二式不恒等，因此*运算是不满足结合律的。

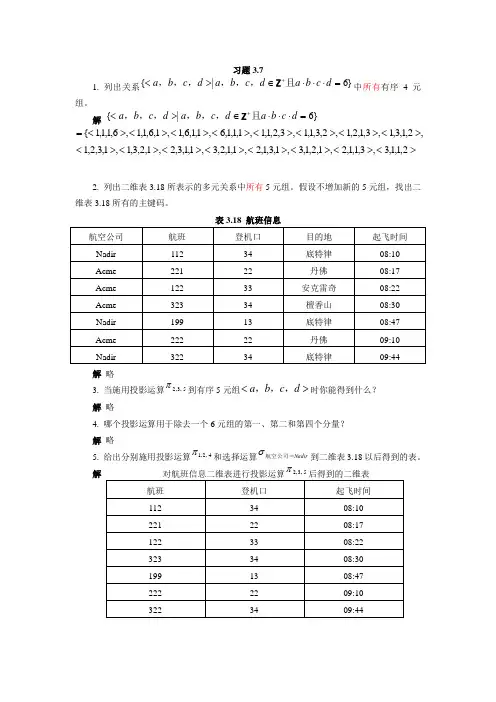
习题3.71. 列出关系}6|{=⋅⋅⋅∈><+d c b a d c b a d c b a 且，，，，，，Z 中所有有序4元组。

解 }6|{=⋅⋅⋅∈><+d c b a d c b a d c b a 且，，，，，，Z,2,1,3,1,3,1,2,1,2,3,1,1,3,2,1,1,1,1,1,6,1,1,6,1,1,6,1,1,6,1,1,1{><><><><><><><><=><><><><><><><><2,1,1,3,3,1,1,2,1,2,1,3,1,3,1,2,1,1,2,3,1,1,3,2,1,2,3,1,1,3,2,12. 列出二维表3.18所表示的多元关系中所有5元组。

假设不增加新的5元组，找出二维表3.18所有的主键码。

表3.18 航班信息航空公司 航班 登机口 目的地 起飞时间 Nadir 112 34 底特律 08:10 Acme 221 22 丹佛 08:17 Acme 122 33 安克雷奇 08:22 Acme 323 34 檀香山 08:30 Nadir 199 13 底特律 08:47 Acme 222 22 丹佛 09:10 Nadir 32234底特律09:44解 略3. 当施用投影运算5,3,2π到有序5元组><d c b a ，，，时你能得到什么？解 略4. 哪个投影运算用于除去一个6元组的第一、第二和第四个分量？ 解 略5. 给出分别施用投影运算4,2,1π和选择运算Nadir 航空公司＝σ到二维表3.18以后得到的表。

解对航班信息二维表进行投影运算5,3,2π后得到的二维表航班 登机口 起飞时间 112 34 08:10 221 22 08:17 122 33 08:22 323 34 08:30 199 13 08:47 222 22 09:10 3223409:44对航班信息二维表进行选择运算Nadir 航空公司＝ 后得到的二维表航空公司 航班 登机口 目的地 起飞时间 Nadir 112 34 底特律 08:10 Nadir 199 13 底特律 08:47 Nadir 32234底特律09:446. 把连接运算3J 用到5元组二维表和8元组二维表后所得二维表中有序多元组有多少个分量？解 略7. 构造把连接运算2J 用到二维表3.19和二维表3.20所得到的二维表。

离散数学（第五版）清华大学出版社第1章习题解答1．1除（3），（4），（5），（11）外全是命题，其中，（1），（2），（8），（9），（10），（14），（15）是简单命题，（6），（7），（12），（13）是复合命题。

分析首先应注意到，命题是陈述句，因而不是陈述句的句子都不是命题。

本题中，（3）为疑问句，（5）为感叹句，（11）为祈使句，它们都不是陈述句，所以它们都不是命题。

其次，4）这个句子是陈述句，但它表示的判断结果是不确定。

又因为（1），（2），（8），（9），（10），（14），（15）都是简单的陈述句，因而作为命题，它们都是简单命题。

（6）和（7）各为由联结词“当且仅当”联结起来的复合命题，（12）是由联结词“或”联结的复合命题，而（13）是由联结词“且”联结起来的复合命题。

这里的“且”为“合取”联结词。

在日常生活中，合取联结词有许多表述法，例如，“虽然……，但是……”、“不仅……，而且……”、“一面……，一面……”、“……和……”、“……与……”等。

但要注意，有时“和”或“与”联结的是主语，构成简单命题。

例如，（14）、（15）中的“与”与“和”是联结的主语，这两个命题均为简单命题，而不是复合命题，希望读者在遇到“和”或“与”出现的命题时，要根据命题所陈述的含义加以区分。

1．2（1）p:2是无理数，p为真命题。

（2）p:5能被2整除，p为假命题。

（6）p→q。

其中，p:2是素数，q：三角形有三条边。

由于p与q都是真命题，因而p→q为假命题。

（7）p→q，其中，p：雪是黑色的，q：太阳从东方升起。

由于p为假命可编辑范本题，q为真命题，因而p→q为假命题。

（8）p:2000年10月1日天气晴好，今日（1999年2月13日）我们还不知道p的真假，但p的真值是确定的（客观存在的），只是现在不知道而已。

（9）p：太阳系外的星球上的生物。

它的真值情况而定，是确定的。

1（10）p：小李在宿舍里. p的真值则具体情况而定，是确定的。

《离散数学》课后习题答案《离散数学》简介1、集合论部分：集合及其运算、二元关系与函数、自然数及自然数集、集合的基数2、图论部分：图的基本概念、欧拉图与哈密顿图、树、图的矩阵表示、平面图、图着色、支配集、覆盖集、独立集与匹配、带权图及其应用3、代数结构部分：代数系统的基本概念、半群与独异点、群、环与域、格与布尔代数4、组合数学部分：组合存在性定理、基本的计数公式、组合计数方法、组合计数定理5、数理逻辑部分：命题逻辑、一阶谓词演算、消解原理离散数学被分成三门课程进行教学，即集合论与图论、代数结构与组合数学、数理逻辑。

教学方式以课堂讲授为主，课后有书面作业、通过学校网络教学平台发布课件并进行师生交流。

《离散数学》学科内容随着信息时代的到来，工业革命时代以微积分为代表的连续数学占主流的地位已经发生了变化，离散数学的重要性逐渐被人们认识。

离散数学课程所传授的思想和方法，广泛地体现在计算机科学技术及相关专业的诸领域，从科学计算到信息处理，从理论计算机科学到计算机应用技术，从计算机软件到计算机硬件，从人工智能到认知系统，无不与离散数学密切相关。

由于数字电子计算机是一个离散结构，它只能处理离散的或离散化了的数量关系，因此，无论计算机科学本身，还是与计算机科学及其应用密切相关的现代科学研究领域，都面临着如何对离散结构建立相应的数学模型;又如何将已用连续数量关系建立起来的数学模型离散化，从而可由计算机加以处理。

离散数学是传统的逻辑学，集合论(包括函数)，数论基础，算法设计，组合分析，离散概率，关系理论，图论与树，抽象代数(包括代数系统，群、环、域等)，布尔代数，计算模型(语言与自动机)等汇集起来的一门综合学科。

离散数学的应用遍及现代科学技术的诸多领域。

离散数学也可以说是计算机科学的基础核心学科，在离散数学中的有一个著名的典型例子-四色定理又称四色猜想，这是世界近代三大数学难题之一，它是在1852年，由英国的一名绘图员弗南西斯格思里提出的，他在进行地图着色时，发现了一个现象，“每幅地图都可以仅用四种颜色着色，并且共同边界的国家都可以被着上不同的颜色”。

离散数学课后习题答案1. 第一章习题答案1.1 习题一答案1.1.1 习题一.1 答案根据题意，设集合A和B如下：Set A and BSet A and B在此情况下，我们可以得出以下结论：•A的幂集为{ {}, {a}, {b}, {a, b} }；•B的幂集为{ {}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} }；•A和B的笛卡尔积为{ (a, 1), (a, 2), (a, 3), (b, 1), (b, 2), (b, 3) }。

因此，习题一.1的答案为：•A的幂集为{ {}, {a}, {b}, {a, b} }；•B的幂集为{ {}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} }；•A和B的笛卡尔积为{ (a, 1), (a, 2), (a, 3), (b, 1), (b,2), (b, 3) }。

1.1.2 习题一.2 答案根据题意，集合A和B如下所示：Set A and BSet A and B根据集合的定义，习题一.2要求我们判断以下命题的真假性：a)$A \\cap B = \\{ 2, 3 \\}$b)$\\emptyset \\in B$c)$A \\times B = \\{ (a, 2), (b, 1), (b, 3) \\}$d)$B \\subseteq A$接下来，我们来逐个判断这些命题的真假性。

a)首先计算集合A和B的交集：$A \\cap B = \\{ x\\,|\\, x \\in A \\, \\text{且} \\, x \\in B \\} = \\{ 2, 3 \\}$。

因此，命题a)为真。

b)大家都知道，空集合是任意集合的子集，因此空集合一定属于任意集合的幂集。

根据题意，$\\emptyset \\in B$，因此命题b)为真。

c)计算集合A和B的笛卡尔积：$A \\times B = \\{ (x, y) \\,|\\, x \\in A \\, \\text{且} \\, y \\in B \\} = \\{ (a, 1), (a, 2), (a, 3), (b, 1), (b, 2), (b, 3) \\}$。

离散数学（第五版）清华大学出版社第2章习题解答2.1 本题没有给出个体域,因而使用全总个体域.(1) 令F(x):x是鸟G(x):x会飞翔.命题符号化为?x(F(x)→G(x)).(2)令F(x):x为人.G(x):x爱吃糖命题符号化为??x(F(x)→G(x))或者?x(F(x)∧?G(x))(3)令F(x):x为人.G(x):x爱看小说.命题符号化为?x(F(x)∧G(x)).(4) F(x):x为人.G(x):x爱看电视.命题符号化为??x(F(x)∧?G(x)).分析1°如果没指出要求什么样的个体域，就使用全总个休域，使用全总个体域时，往往要使用特性谓词。

（1）-（4）中的F(x)都是特性谓词。

2°初学者经常犯的错误是，将类似于（1）中的命题符号化为27?x(F(x)∧G(x))即用合取联结词取代蕴含联结词，这是万万不可的。

将（1）中命题叙述得更透彻些，是说“对于宇宙间的一切事物百言，如果它是鸟，则它会飞翔。

”因而符号化应该使用联结词→而不能使用∧。

若使用∧，使（1）中命题变成了“宇宙间的一切事物都是鸟并且都会飞翔。

”这显然改变了原命题的意义。

3°（2）与（4）中两种符号化公式是等值的，请读者正确的使用量词否定等值式，证明（2），（4）中两公式各为等值的。

2.2 (1)d (a),(b),(c)中均符号化为?xF(x)其中F(x):(x+1)2=x2+2x+1,此命题在(a),(b),(c)中均为真命题。

（2）在(a),(b),(c)中均符号化为?xG(x)其中G(x):x+2=0，此命题在（a）中为假命题，在(b)(c)中均为真命题。

（3）在(a),(b),(c)中均符号化为?xH(x)其中H(x):5x=1.此命题在(a),(b)中均为假命题，在(c)中为真命题。

分析1°命题的真值与个体域有关。

2°有的命题在不同个体域中，符号化的形式不同，考虑命题“人都呼吸”。

1-1，1-2（1） 解：a) 是命题，真值为T。

b) 不是命题。

c) 是命题，真值要根据具体情况确定。

d) 不是命题。

e) 是命题，真值为T。

f) 是命题，真值为T。

g) 是命题，真值为F。

h) 不是命题。

i) 不是命题。

（2） 解：原子命题：我爱北京天安门。

复合命题：如果不是练健美操，我就出外旅游拉。

（3） 解：a) (┓P ∧R)→Qb) Q→Rc) ┓Pd) P→┓Q（4） 解：a)设Q:我将去参加舞会。

R:我有时间。

P:天下雨。

Q (R∧┓P):我将去参加舞会当且仅当我有时间和天不下雨。

b)设R:我在看电视。

Q:我在吃苹果。

R∧Q:我在看电视边吃苹果。

c) 设Q:一个数是奇数。

R:一个数不能被2除。

（Q→R）∧(R→Q):一个数是奇数，则它不能被2整除并且一个数不能被2整除，则它是奇数。

(5) 解：a) 设P：王强身体很好。

Q：王强成绩很好。

P∧Qb) 设P：小李看书。

Q：小李听音乐。

P∧Qc) 设P：气候很好。

Q：气候很热。

P∨Qd) 设P： a和b是偶数。

Q：a+b是偶数。

P→Qe) 设P：四边形ABCD是平行四边形。

Q ：四边形ABCD的对边平行。

PQf) 设P：语法错误。

Q：程序错误。

R：停机。

（P∨ Q）→ R(6) 解：a) P:天气炎热。

Q:正在下雨。

P∧Qb) P:天气炎热。

R:湿度较低。

P∧Rc) R:天正在下雨。

S:湿度很高。

R∨Sd) A:刘英上山。

B:李进上山。

A∧Be) M:老王是革新者。

N:小李是革新者。

M∨Nf) L:你看电影。

M:我看电影。

┓L→┓Mg) P:我不看电视。

Q:我不外出。

R:我在睡觉。

P∧Q∧Rh) P:控制台打字机作输入设备。

Q:控制台打字机作输出设备。

P∧Q1-3（1）解：a) 不是合式公式，没有规定运算符次序（若规定运算符次序后亦可作为合式公式）b) 是合式公式c) 不是合式公式（括弧不配对）d) 不是合式公式（R和S之间缺少联结词）e) 是合式公式。

离散数学第五版课后习题答案离散数学是一门重要的数学学科，它研究的是离散对象和离散结构的性质和关系。

离散数学的应用广泛，涉及计算机科学、信息科学、通信工程、运筹学等领域。

而《离散数学》第五版是离散数学领域的经典教材，它详细介绍了离散数学的基本概念、方法和应用。

在学习离散数学的过程中，课后习题是非常重要的一部分。

通过解答习题，可以巩固理论知识，培养分析问题和解决问题的能力。

然而，由于离散数学的习题种类繁多，难度不一，很多学生在自学或课后复习时会遇到一些困难。

因此，提供《离散数学第五版》课后习题的答案可以帮助学生更好地学习和掌握相关知识。

首先，我们来看一下《离散数学第五版》课后习题的类型。

该教材的习题分为多个章节，每个章节都包含了基本概念、定理和算法的习题。

这些习题涵盖了集合论、逻辑、证明方法、图论、代数结构、计数原理等多个方面的内容。

习题的难度也有所不同，有一些是基础题，有一些是拓展题，还有一些是应用题。

通过解答这些习题，学生可以逐步提高自己的能力，掌握离散数学的核心概念和方法。

接下来，我们来讨论一下为什么提供《离散数学第五版》课后习题的答案是有意义的。

首先，课后习题的答案可以帮助学生检查自己的解答是否正确。

在学习过程中，学生可能会遇到一些难以理解或容易出错的问题，通过对比答案，可以及时发现和纠正错误，提高学习效果。

其次，答案还可以作为学生学习的参考，帮助他们理解问题的解题思路和方法。

有时候，学生可能会陷入思维定势，无法找到问题的突破口，而参考答案可以给他们一些启示和思路。

最后，答案还可以作为学生自学的辅助材料，帮助他们进行自主学习和巩固知识。

然而，提供《离散数学第五版》课后习题的答案也存在一些问题和挑战。

首先，习题的答案可能存在多种解法，因此提供一个标准答案并不容易。

不同的学生可能会有不同的思路和方法，他们的解答也可能会有所不同。

其次，习题的答案可能会涉及一些复杂的推理和证明过程，这些过程可能需要较长的篇幅来解释和讨论。

《离散数学1-5章》练习题答案第2，3章(数理逻辑)1.答：（2），（3），（4）2.答：（2），（3），（4），（5），（6）3.答：（1）是，T （2）是，F （3）不是（4）是，T （5）不是（6）不是4.答：（4）5.答：⌝P ，Q→P6.答：P(x)∨∃yR(y)7.答：⌝∀x(R(x)→Q(x))8、c、P→(P∧(Q→P))解：P→(P∧(Q→P))⇔⌝P∨(P∧(⌝Q∨P))⇔⌝P∨P⇔ 1 (主合取范式)⇔ m0∨ m1∨m2∨ m3 （主析取范式）d、P∨(⌝P→(Q∨(⌝Q→R)))解：P∨(⌝P→(Q∨(⌝Q→R)))⇔ P∨(P∨(Q∨(Q∨R)))⇔ P∨Q∨R⇔ M0 (主合取范式)⇔ m1∨ m2∨m3∨ m4∨ m5∨m6 ∨m7 (主析取范式) 9、b、P→(Q→R)，R→(Q→S) => P→(Q→S)证明：（1） P 附加前提（2） Q 附加前提（3） P→(Q→R) 前提（4） Q→R （1），（3）假言推理（5） R （2），（4）假言推理（6） R→(Q→S) 前提（7） Q→S （5），（6）假言推理（8） S （2），（7）假言推理d、P→⌝Q，Q∨⌝R，R∧⌝S⇒⌝P证明、(1) P 附加前提（2） P→⌝Q 前提（3）⌝Q （1），（2）假言推理（4） Q∨⌝R 前提(5) ⌝R （3），（4）析取三段论(6 ) R∧⌝S 前提（7） R （6）化简（8） R∧⌝R 矛盾（5），（7）合取所以该推理正确10.写出∀x(F(x)→G(x))→(∃xF(x) →∃xG(x))的前束范式。

解：原式⇔∀x(⌝F(x)∨G(x))→(⌝(∃x)F(x) ∨ (∃x)G(x))⇔⌝(∀x)(⌝F(x)∨G(x)) ∨(⌝(∃x)F(x) ∨ (∃x)G(x))⇔ (∃x)((F(x)∧⌝ G(x)) ∨G(x)) ∨ (∀x) ⌝F(x)⇔ (∃x)((F(x) ∨G(x)) ∨ (∀x) ⌝F(x)⇔ (∃x)((F(x) ∨G(x)) ∨ (∀y) ⌝F(y)⇔ (∃x) (∀y) (F(x) ∨G(x) ∨⌝F(y))（集合论部分）1、答：(4)2.答：323.答：（3）4. 答：（4）5.答：（2），（4）6、设Ａ，Ｂ，Ｃ是三个集合，证明：a、A⋂ (B－C)＝(A⋂B)－(A⋂C)证明：(A⋂B)－(A⋂C)= (A⋂B)⋂~（A⋂C）=(A⋂B) ⋂（~A⋃~C）=(A⋂B⋂~A)⋃(A⋂B⋂~C)= A⋂B⋂~C=A⋂（B⋂~C）=A⋂（B-C）b、(A－B)⋃(A－C)=A－(B⋂C)证明：(A-B)⋃(A-C)=(A⋂~B)⋃(A⋂⋂~C) =A⋂ (~B ⋃~C)=A⋂~（B⋂C）= A-(B⋂C)（二元关系部分）1、答：（1）R={<1,1>,<4,2>} (2) R1-={<1,1>,<2,4>}2.答：RοR ={〈1,1〉，〈1,3〉，〈2,2〉，〈2,4〉}R-1 =｛〈2,1〉，〈1,2〉，〈3,2〉，〈4,3〉｝3.答：R={<1,1>,<2,2>,<3,3>,<4,4>,<5,5>,<6,6>,<1,2>,<1,3>,<1,4>,<1,5>,<1,6>,<2,4>,<2,6>,<3,6>}4.答：R 的关系矩阵=⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡000000001000000001 R 1-的关系矩阵=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡0000000100000000015、解：（1）R={<2,1>,<3,1>,<2,3>};M R =⎪⎪⎪⎭⎫ ⎝⎛001101000;它是反自反的、反对称的、传递的；（2）R={<1,2>,<2,1>,<1,3>,<3,1>,<2,3>,<3,2>};M R =⎪⎪⎪⎭⎫⎝⎛011101110;它是反自反的、对称的；（3）R={<1,2>,<2,1>,<1,3>,<3,3>};M R =⎪⎪⎪⎭⎫⎝⎛100001110;它既不是自反的、也不是反自反的、也不是对称的、也不是反对称的、也不是传递的。

第1章习题1.1(2) 简单命题（3），（4），（5）不是命题(6) 复合命题1.5p∧，其中，p：2是偶数，q：2是素数。

（1）qp→，其中，p：天下大雨，q：他乘公共汽车上班（5）qq→，其中，p，q的含义同（5）（6）pq→，其中，p，q的含义同（5）（7）p1.7（1）对（1）采用两种方法判断它是重言式。

真值表法表1.2给出了（1）中公式的真值表，由于真值表的最后一列全为1，所以，（1）为重等值演算法→)p∨∨q(rp∨⇔（蕴含等值式）∨⌝qp∨(r)p∨⌝⇔)(（结合律）p∨∨rqp⇔1（排中律）∨rq∨⇔（零律）1由最后一步可知，（1）为重言式。

（3）用等值演算法判（3）为矛盾式(→⌝)p∧qq⌝⇔)(（蕴含等值式）⌝q∨qp∧⇔（德·摩根律）⌝∧p∧qq∧⇔（结合律）⌝(q)qp∧0∧⇔p （矛盾律）0⇔（零律）由最后一步可知，（3）为矛盾式。

（10）非重言式的可满足式 1.8（1）从左边开始演算)()(q p q p ⌝∧∨∧)(q q p ⌝∨∧⇔ （分配律）1∧⇔p （排中律） .p ⇔ （同一律）（2）从右边开始演算)(r q p ∧→)(r q p ∧∨⌝⇔ （蕴含等值式） )()(r p q p ∨⌝∧∨⌝⇔ （分配律） ).()(r p q p →∧→⇔ （蕴含等值式）1.9（1）))((p q p →∧⌝ ))((p q p ∨∧⌝⌝⇔ （蕴含等值式）p q p ⌝∧∧⇔（德·摩根律） q p p ∧⌝∧⇔)(（结合律、交换律）q ∧⇔0 （矛盾式）.0⇔（零律）由最后一步可知该公式为矛盾式。

（2）)())()((q p p q q p ↔↔→∧→)()(q p q p ↔↔↔⇔（等价等值式）由于较高层次等价号两边的公式相同，因而此公式无成假赋值，所以，它为重言式。

1.12 (1) 设(1)中公式为A.)())((r q p r q p A ∧∧→∧∨⇔ )())((r q p r q p A ∧∧∨∧∨⌝⇔)()(r q p r q p A ∧∧∨⌝∨⌝∧⌝⇔ )()()(r q p r p q p A ∧∧∨⌝∧⌝∨⌝∧⌝⇔)())(())((r q p r q q p r r q p A ∧∧∨⌝∧⌝∨∧⌝∨∨⌝∧⌝∧⌝⇔)()()()()(r q p r q p r q p r q p r q p A ∧∧∨⌝∧∧⌝∨⌝∧⌝∧⌝∨∧⌝∧⌝∨⌝∧⌝∧⌝⇔)()()()(r q p r q p r q p r q p A ∧∧∨⌝∧∧⌝∨∧⌝∧⌝∨⌝∧⌝∧⌝⇔7210m m m m A ∨∨∨⇔于是,公式A 的主析取范式为7210m m m m ∨∨∨易知,A 的主合取范式为6543M M M M ∨∨∨A 的成真赋值为000, 001, 010, 111A 的成假赋值为011,100,101,110(2)设(2)中公式为B)()(p q q p B ∨⌝→→⌝⇔ )()(p q q p ∨⌝→∨⌝⌝⇔ )()(p q q p ∨⌝→∨⇔ )()(p q q p ∨⌝∨∨⌝⇔ p q q p ∨⌝∨⌝∧⌝⇔)())(())(()(q q p q p p q p ⌝∨∧∨⌝∧⌝∨∨⌝∧⌝⇔)()()()()(q p q p q p q p q p ∧∨⌝∧∨⌝∧∨⌝∧⌝∨⌝∧⌝⇔ )()()(q p q p q p ∧∨⌝∧∨⌝∧⌝⇔320m m m ∨∨⇔所以,B 的主析取范式为320m m m ∨∨.B 的主合取范式为1M B 的成真赋值为00,10,11. B 的成假赋值为01. 1.14 设p:A 输入;设q:B 输入; 设r:C 输入;由题的条件,容易写出C B A F F F ,,的真值表,见表1.5所示.由真值表分别写出它们的主析范邓范式,而后,将它们都化成与之等值的}{↓中的公式即可.)()()()(r q p r q p r q p r q p F A ∧∧∨⌝∧∧∨∧⌝∧∨⌝∧⌝∧⇔)()()()(r r q p r r q p ∨⌝∧∧∨∨⌝∧⌝∧⇔)()(q p q p ∧∨⌝∧⇔ )(q q p ∨⌝∧⇔ p ⇔)()(r q p r q p F B ∧∧⌝∨⌝∧∧⌝⇔)()(r r q p ∨⌝∧∧⌝⇔ )(q p ∧⌝⇔ )(q p ∧⌝⌝⌝⇔ )(q p ⌝∨⌝⇔q p ⌝↓⇔)(q q p ↓↓⇔. )(r q p F C ∧⌝∧⌝⇔r q p ∧∨⌝⇔)(r q p ∧↓⇔)( ))((r q p ∧↓⌝⌝⇔ ))((r q p ⌝∨↓⌝⌝⇔ r q p ⌝↓↓⌝⇔)()())()((r r q p q p ↓↓↓↓↓⇔1．19 (1)证明 ①r q ∨⌝ 前提引入②r ⌝ 前提引入③q ⌝ ①②析取三段论 ④)(q p ⌝∧⌝ 前提引入 ⑤q p ∨⌝ ④置换⑥p ⌝ ③⑤析取三段论 (2)附加前提证明法：证明 ①r 附加前提引入 ②r p ⌝∨ 前提引入③p ①②析取三段论④)(s q p →→ 前提引入 ⑤s q → ③④假言推理 ⑥q 前提引入 ⑦s ⑤⑥假言推理 (5)归缪法：证明 ①q 结论的否定引入②s r ∨⌝ 前提引入 ③s ⌝ 前提引入④r ⌝ ②③析取三段论 ⑤r q p →∧)( 前提引入 ⑥)(q p ∧⌝ ④⑤拒取式 ⑦q p ⌝∨⌝ ⑥置换⑧p 前提引入⑨q ⌝ ⑦⑧析取三段论 ⑩q q ⌝∧ ①⑨合取 ⑪0 ⑩置换 1.20 设p ：他是理科生q ：他是文科生 r ：他学好数学 前提 r p q r p ⌝→⌝→,,结论q通过对前提和结论的观察，知道推理是正确的，下面用构造证明法给以证明。

祝清顺习题一(第1章集合)1.(1)A＝{0, 1, 2, 3};(2)A＝{(-2, 3), (-1, 0), (0, -1), (1, 0), (2, 3)};(3)A＝{-1, -2, -3};(4)A＝{1, 2, 3, 4, 5};(5) A＝{-6, 1}.2.(1) {x | x＝2k, k∈N+, k≤50};(2) {x | x＝6k, k∈Z};(3) {(x, y) | (x-x0)2+(y-y0)2＝r2};(4) {x | 15＜x＜40, x为素数}.3.(1)c＝a或c＝b;(2)a, b为任意值;(3)a＝c＝∅, b＝{∅};(4)b＝c＝d.4.当a=0时, 解得x=2/3满足题意; 当a≠0时, 由∆=9-8a≤0, 得a≥9/8.综上, 满足条件的a的范围是: {a | a≥9/8或a=0}.5.(1)∅, {a}, {{b}}, {c}, {a, {b}}, {a, c}, {{b}, c}, {a, {b}, c};(2)∅, {∅};(3)∅.6.(1) 2n;(2) 2n-1, n≥1, 当n＝0时不存在;(3) 没有. 因为集合只有n个元素, 其子集所含元素个数不可能比整个集合的元素个数多.7.(1) 成立; (2) 不成立; (3) 成立; (4) 成立.8.(1) 不正确, 例如A={a}, B={a, b}, C={{a}, {b}}, 从而A∈B且B∈C, 但A∈C.(2) 不正确, 例子同(1);(3) 不正确, 例如, A＝{1}, B＝{{1}, 2}, C＝{{1}, 3};(4) 不正确, 例如, A＝{1}, B＝{1, 2}, C＝{{1}, {1, 2}}.9.(1) 错误; (2) 正确; (3) 正确; (4) 错误; (5) 错误; (6) 错误; (7) 正确; (8) 正确; (9) 错误; (10) 错误.10.(1) {d }; (2) {a , c , e }; (3) {a , b , c , e }; (4) {b , d , e }. 11.各集合的文氏图如图所示(阴影部分).12.(a) B ∩(C -A );(b) (A -(B ∪C )∪(B ∩(C -A )); (c) C B A ∪(B ∩(C -A )). 13.A ∩B ＝{2, 3}; A ∪B ＝{1, 2, 3, 4, 5}; A -B ＝{1, 4}; B -A ＝{5}; A ⊕B ＝{1, 4, 5}. 14.(1) 不一定. 例如, A ={1, 2, 3}, B ={2, 3}, C ={1, 3}, 则A ∪B ＝A ∪C , 但是B ≠C . (2) 不一定; 例如, A ={1, 2, 3}, B ={2, 3}, C ={2, 3, 4}, 则A ∩B ＝A ∩C , 但是B ≠C . (3) 一定. 由条件有A ⊕(A ⊕B )＝A ⊕(A ⊕C ), 利用对称差的结合律, 有(A ⊕A )⊕B = (A ⊕A )⊕C ,因为A ⊕A = ∅, 有∅⊕B = ∅⊕C , 故有B =C .15.(1) 正确, 证明: 因为A ∩C ⊆ A ⊆ B , A ∩C ⊆ C ⊆ D , 故A ∩C ⊆ B ∩D . (2) 错误, 如A ＝C ＝{1}, B ＝{1, 2}, D ＝{1, 3}. 16.(1) {0, 1, 2, 3, 4, 5, 6, 7, 8}; (2) {1, 2}; (3) {4, 5}; (4) N . 17.由于A ∪B ＝B , 故有A ⊆B , 而B ＝{x | x ＞3}, 故a ≥3. 18.由题意可得 x =3是x 2＋cx ＋15＝0的根, 故有9+3c +15=0, 解之得c = -8, x 2＋cx ＋15＝0即x 2-8x ＋15＝0, 解之得 x =3或x =5, 故B ={3, 5}.由已知条件可得A ={3}, 故有9+3a+b =0, 且 a 2-4b =0. 解之得a = -6, b = 9. 综上可得 a ＝-6, b ＝9, c ＝-8. 19.(1) 因为集合B ＝{x | x 2-5x ＋6＝0}={2, 3}. 又A ∩B ＝A ∪B , 故集合A ＝{x | x 2-ax ＋(A ∩B )∪C B EA BA B E A C C B A -⊕)( B A C B E A C )()(B C B A -a2-19＝0} ={2, 3}, 由根与系数的关系, 有2+3=a, 即a=5.(2) 因为集合C＝{x | x2＋2x-8＝0}={2, -4}, 而∅⊊A∩B, A∩C=∅, 所以3∈A, 2∉A. 故9-3a+a2-19=0, 4-2a+a2-19≠0; 解之得, a = -2.20.因为A∩B＝{-3}, 所以-3∈B, 而x2+1>-3, 所以只可能x-3= -3或2x-1= -3.若x-3 = -3, 则x=0, 此时A={-3, 0, 1}, B={-3, -1, 1}, 故A∩B={-3, 1}, 不合题意.若2x-1= -3, 则x = -1, 此时A={-3, 1, 0}, B={-4, -3, 2}, 故A∩B={-3}, 满足题意.综上所述, x = -1, 且A∪B={-4, -3, 0, 1, 2}.21.由于B=(A∩B)∪(A∩B), 故B={1}∪{3}={1, 3}, B={2, 4}. 由此知A∩B＝{3}, 3∈A, 1∉A; 由A∩B＝{2}知, 2∈A, 4∉A, 从而2∉A, 4∈A, 故A={3, 4}.22.A- (B-C)＝)A=)B(CAB(C=)A=(A-B)∪(A∩C).B()(CA23.(1) ((A∪(B-C))∩A)∪(B- (B-A)) = ((A∪(B∩C))∩A)∪(B∩)B )(A= A∪(B∩(B∪A))= A∪(∅∪(B∩A))=A.(2) ((A∪B)∩B)-(A∪B) = ((A∪B)∩B)∩)A(B= ((A∪B)∩B)∩(A∩B)= (A∪B)∩B∩A∩B=∅(3) ((A∪B∪C)-( B∪C))∪A = ((A∪B∪C) ∩)(CB )∪A= ((A∪B∪C) ∪A) ∩(CB ∪A)= (A∪B∪C) ∩()B )∪A)(C= A∪((B∪C) ∩)(CB )= A∪∅=A.24.将不超过100的正整数排列如下：1 2 3 4 5 6 7 8 9 1011 12 13 14 15 16 17 18 19 2021 22 23 24 25 26 27 28 29 3031 32 33 34 35 36 37 38 39 4041 42 43 44 45 46 47 48 49 5051 52 53 54 55 56 57 58 59 6061 62 63 64 65 66 67 68 69 7071 72 73 74 75 76 77 78 79 8081 82 83 84 85 86 87 88 89 9091 92 93 94 95 96 97 98 99 100可以依次得到素数2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.25.由恒等式mq + np = (mn + pq) − (m− p)(n−q)及条件(m-p) | (mn+pq)可知, (m-p) | (mq+np).26.设n=2k+1, n2-1=(2k+1)2-1=4k(k+1). 因为k(k+1)是相邻两个自然数的乘积, 必然是2的倍数, 所以原式是8的倍数.27.101小于11的平方, 这样就可以只用2、3、5、7这四个质数来验证. 101无法被2、3、5、7整除, 所以101是质数.28.240=2⋅120=22⋅60=23⋅30=24⋅15=24⋅3⋅5.504=2⋅252=22⋅121=22⋅112.654=2⋅327=2⋅3⋅109=2⋅3⋅7⋅1751480 = 2⋅25740 = 22⋅12870 = 23⋅6435= 23⋅5⋅1287 = 23⋅5⋅3⋅429 = 23⋅5⋅32⋅143 = 23⋅32⋅5⋅11⋅13.29.(1) 因为258=21⨯12+6, 所以q=21, r=6.(2) 因为258=(-39)⨯( -15)+12, 所以q= -39, r=12.(3) 因为-367=(-16)⨯24+17, 所以q= -16, r=17.(4) 因为-334=26⨯(-13) +4, 所以q= 26, r=4.30.4475÷8=559⋅8+3559÷8=69⋅8+769÷8=8⋅8+58÷8=1⋅8+01÷8=0⋅8+1所以4475=(10573)8.31.(1) 运用辗转相除法可得934 = 4 ∙ 195 + 154195 = 1 ∙ 154 + 41 154 = 3 ∙ 41 + 31 41 = 1 ∙ 31 +10 31 = 3 ∙ 10 +1 10=10 ∙ 1 +0所以, gcd(934, 195) = 1. 代回去, 有gcd(540, 168) = 1 = 31 - 3 ∙ 10 = 31 - 3 ∙ (41 - 1∙31) = 4 ∙ 31 - 3 ∙ 41 = 4 ∙ (154 - 3 ∙ 41) - 3 ∙ 41 = 4 ∙ 154 - 15 ∙ 41= 4 ∙ 154 - 15 ∙ (195-1 ∙ 154) = 19 ∙ 154 - 15 ∙ 195 = 19 ∙ (934 - 4 ∙ 195) - 15 ∙ 195 = 19 ∙ 934 - 91 ∙ 195故gcd(540, 168) = 19 ∙ 934 - 91 ∙ 195, 其中m =19, n = - 91.(2) 方法同(1). 计算可得：gcd(369, 25) = 1, gcd(369, 25)= 4 ∙ 369 - 59 ∙ 25, 其中m =4, n = - 59. (3) 方法同(1). 计算可得：gcd(369, 25) = 33, gcd(369, 25)= 8 ∙ 165 - 1 ∙ 1287, 其中n =8, m = - 1. (4) 方法同(1). 计算可得：gcd(369, 25) = 2, gcd(369, 25)= 17 ∙ 42 - 2 ∙ 256, 其中n =8, m = - 1. 32.由定理1.3.8, 可得ab =lcm(a , b )⋅gcd(a , b )=24 ∙ 144. 由已知条件a +b =120, 根据根与系数的关系可构造一个一元二次方程x 2-120x +24 ∙ 144=0解之得, x 1=72, x 2=48. 由此可得a =72, b =48或a =48, b =72.33.(1) 运用辗转相除法可得10920 = 1 ∙ 8316 + 2604 8316 = 3 ∙ 2604 + 504 2604 = 5 ∙ 504 + 84 504 = 6 ∙ 84 +0所以, gcd(934, 195) = 84.(2) 对于(1)中各式回代过去, 有gcd(10920, 8316) = 84 = 2604 - 5 ∙ 504 = 2604 - 5 ∙ (8316 - 3 ∙ 2604)= 16 ∙ 2604 - 5 ∙ 8316= 16 ∙ (10920- 1 ∙ 8316) - 5 ∙ 8316 = 16 ∙ 10920- 21 ∙ 8316故gcd(10920, 8316) = - 21 ∙ 8316+16 ∙ 10920, 其中m = - 21, n =16.(3) 由最大公因子与最小公倍数的关系, 有84109208316),gcd(),(lcm ⨯==b a ab b a =1081080.34.记gcd(a , b )=d , 则有d | a 且d | b , 从而d | (ma+nb ), 即d | 1, 所以d =1. 35.由容斥原理, 得| A ∪B ∪C |＝| A |＋| B |＋| C |-| A ∩B |-| A ∩C |-| B ∩C |＋| A ∩B ∩C | | A ∩B ∩C |=| A ∪B ∪C |-(| A |＋| B |＋| C |-| A ∩B |-| A ∩C |-| B ∩C |)=11-(6+8+6-3-2-5) = 1.36.设A , B 分别表示在第一次和第二次考试中得5分的学生的集合, 那么有|S |=50, |A |=26, |B |=21, |)|B A =17. 由|)|B A = |S | – (|A | + |B |) + |A ∩B |, 得|A ∩B | =|)|B A – |S | + (|A | + |B |) = 17 – 50 + 26 + 21=14故有14人两次考试都得5分．37.令A ={修数学的学生}, B ={修物理的学生}, C={修化学的学生}, 则|A |=170, |B |=130, |C|=120, | A ∩B |=45, | A ∩C |=20, | B ∩C |=22, | A ∩B ∩C |=3, 故由容斥原理| A ∪B ∪C |＝| A |＋| B |＋| C |-| A ∩B |-| A ∩C |-| B ∩C |＋| A ∩B ∩C |=170+130+120-45-20-22+3=336.38.设A 3={被3整除的数}, A 5={被5整除的数}, 则|A 3|=166, |A 5|=100, |A 3∩A 5| = 33, 所以由容斥原理, 有| A 3∪A 5 |＝| A 3 |＋| A 5 |-| A 3∩A 5|=166+100-33=233. 39.(1) 取全集S = {1, 2,…, 1000}, 令A 1 = { i ︱i ∈S 且5整除i }, A 2 = { i ︱i ∈S 且6整除i }, A 3 ={ i ︱i ∈S 且8整除i }, 于是|A 1| =⎥⎦⎤⎢⎣⎡51000=200, |A 2| =⎥⎦⎤⎢⎣⎡61000=166, |A 3| =⎥⎦⎤⎢⎣⎡81000=125, |A 1∩A 2| =⎥⎦⎤⎢⎣⎡⨯651000=33,|A 1∩A 3| =⎥⎦⎤⎢⎣⎡⨯851000=25, |A 2∩A 3| =⎥⎦⎤⎢⎣⎡}8,6{lcm 1000=41, | A 1∩A 2∩A 3| =⎥⎦⎤⎢⎣⎡}8,6,5{lcm 1000=8, 则由容斥原理得| A 1∪A 2∪A 3 |＝|A 1|＋|A 2|＋|A 3|-|A 1∩A 2|-|A 1∩A 3|-|A 2∩A 3|＋|A 1∩A 2∩A 3 | = 200+166+125-33-25-41+8=400.(2) |1A ∩2A ∩3A |=|S |-| A 1∪A 2∪A 3 |=1000-400=600.即在1, 2, …, 1000中不能被5, 6和8中的任何一个数整除的数的个数为400个40.设U ={到游乐场去玩的儿童}, A ={骑旋转木马的儿童}, B ={坐滑行轨道的儿童}, C ={乘宇宙飞船的儿童}. 由题意得|U |=75, | A ∩B ∩C |=20, | A ∩B |+ |A ∩C |+ |B ∩C|-2| A ∩B ∩C |=55, 得| A∩B|+ A∩C|+ |B∩C|=55+2| A∩B∩C |=55+40=95,由700÷5=140知| A|+|B|+ |C|=140.| A∪B∪C |＝| A |＋| B |＋| C |-| A∩B |-| A∩C |-| B∩C |＋| A∩B∩C |=140-95+20=65.|A∩B∩C|=|U|-| A1∪A2∪A3|=75-65=10.因此有10名儿童没有玩过其中任何一种玩具.41.设U={被调查的大学生}, A={选修线性代数课程}, B={选修概率课程}, C={选修计算机科学课程}. 由题意得|U|=260, |A|=64, |B|=94, |C|=58, | A∩B|=26, |A∩C|=28, |B∩C|=22, | A∩B∩C |=14.利用容斥原理, 得(1) |A∩B∩C|=|U|-| A∪B∪C |=|U|-(| A |＋| B |＋| C |-| A∩B |-| A∩C |-| B∩C |＋| A∩B∩C|)=260-(64+94+58-26-28-22+14)=106.即三门课程都不选修的学生有106人.(2) |A∩B∩C|=|B|-| A∩B |-| B∩C |＋| A∩B∩C|)=94-26-22+14=60.即只选计算机科学课程的学生有60人.42.(1){∅, {a}, {{a}}, {a, {a}}}; (2){ ∅, {{1, {2, 3}}}};(3){∅, {∅}, {a}, {{b}}, {∅, a}, {∅, {b}}, {a, {b}}, {∅, a, {b}}}; (4){∅, {∅}};(5){∅, {∅}, {{∅}}, {∅, {∅}}}.43.A＝{m, n}.44.(1) C∈ρ(A)∩ρ(B) ⇔C∈P(A)∧C∈ρ(B)⇔C ⊆A∧C⊆B⇔C ⊆A∩B⇔C∈ρ(A∩B)所以, ρ(A)∩ρ(B)＝ρ(A∩B).(2) 由幂集的定义易知, B∈ρ(A) ⇔B⊆A. …..(*)必要性：对任意的C∈ρ(A), 则由(*)得C⊆A. 又A⊆B, 所以C ⊆ B. 再由(*)得B∈ρ(B). 所以, ρ(A) ⊆ρ(B).充分性：若ρ(A) ⊆ρ(B), 则由A∈ρ(A)得A∈ρ(B), 再由(*)得A⊆B.(3) 因为C∈ρ(A)∪ρ(B) ⇒C∈ρ(A) 或C∈ρ(B)⇒C ⊆A或C⊆B⇒C ⊆A∪B⇒C∈ρ(A∪B)所以, ρ(A)∪ρ(B) ⊆ρ(A∪B).例如, 设A={1}, B={2}, 则P(A)={∅, {1}}, ρ(B)={∅, {2}}, ρ(A)∪ρ(B)={∅, {1}, {2}}. 而A∪B={1, 2}, ρ (A∪B)={∅, {1}, {2}, {1, 2}}, 所以ρ(A)∪ρ(B) ≠ρ(A∪B).45.(1) A×B×C ={〈a, 1, α〉, 〈a, 1, β〉, 〈a, 2, α〉, 〈a, 2, β〉, 〈a, 4, α〉, 〈a, 4, β〉, 〈b, 1, α〉, 〈b, 1, β〉, 〈b, 2, α〉, 〈b, 2, β〉, 〈b, 4, α〉, 〈b, 4, β〉, 〈c, 1, α〉, 〈c, 1, β〉, 〈c, 2, α〉, 〈c, 2, β〉, 〈c, 4, α〉, 〈c, 4, β〉};(2) B×A ={〈1, a〉, 〈1, b〉, 〈1, c〉, 〈2, a〉, 〈2, b〉, 〈2, c〉, 〈4, a〉, 〈4, b〉, 〈4, c〉};(3)A×B2={〈a, 〈1, 1〉〉, 〈a, 〈1, 2〉〉, 〈a, 〈1, 4〉〉, 〈a, 〈2, 1〉〉, 〈a, 〈2, 2〉〉, 〈a, 〈2, 4〉〉, 〈a, 〈4, 1〉〉, 〈a, 〈4, 2〉〉, 〈a, 〈4, 4〉〉, 〈b, 〈1, 1〉〉, 〈b, 〈1, 2〉〉, 〈b, 〈1, 4〉〉, 〈b, 〈2, 1〉〉, 〈b, 〈2, 2〉〉, 〈b, 〈2, 4〉〉, 〈b, 〈4, 1〉〉, 〈b, 〈4, 2〉〉, 〈b, 〈4, 4〉〉, 〈c, 〈1, 1〉〉, 〈c, 〈1, 2〉〉, 〈c, 〈1, 4〉〉, 〈c, 〈2, 1〉〉, 〈c, 〈2, 2〉〉, 〈c, 〈2, 4〉〉, 〈c, 〈4, 1〉〉, 〈c, 〈4, 2〉〉, 〈c, 〈4, 4〉〉};(4)A×C={〈a, α〉, 〈b, α〉, 〈c, α〉, 〈a, β〉, 〈b, β〉, 〈c, β〉}×{〈a, α〉, 〈b, α〉, 〈c, α〉, 〈a, β〉, 〈b, β〉, 〈c, β〉}.(A×C)2={〈〈a, α〉, 〈a, α〉〉, 〈〈a, α〉, 〈b, α〉〉, 〈〈a, α〉, 〈c, α〉〉, 〈〈a, α〉, 〈a, β〉〉, 〈〈a, α〉, 〈b, β〉〉, 〈〈a, α〉, 〈c, β〉〉, 〈〈b, α〉, 〈a, α〉〉, 〈〈b, α〉, 〈b, α〉〉, 〈〈b, α〉, 〈c, α〉〉, 〈〈b, α〉, 〈a, β〉〉, 〈〈b, α〉, 〈b, β〉〉, 〈〈b, α〉, 〈c, β〉〉, 〈〈c, α〉, 〈a, α〉〉, 〈〈c, α〉, 〈b, α〉〉, 〈〈c, α〉, 〈c, α〉〉, 〈〈c, α〉, 〈a, β〉〉, 〈〈c, α〉, 〈b, β〉〉, 〈〈c, α〉, 〈c, β〉〉, 〈〈a, β〉, 〈a, α〉〉, 〈〈a, β〉, 〈b, α〉〉, 〈〈a, β〉, 〈c, α〉〉, 〈〈a, β〉, 〈a, β〉〉, 〈〈a, β〉, 〈b, β〉〉, 〈〈a, β〉, 〈c, β〉〉, 〈〈b, β〉, 〈a, α〉〉, 〈〈b, β〉, 〈b, α〉〉, 〈〈b, β〉, 〈c, α〉〉, 〈〈b, β〉, 〈a, β〉〉, 〈〈b, β〉, 〈b, β〉〉, 〈〈b, β〉, 〈c, β〉〉, 〈〈c, β〉, 〈a, α〉〉, 〈〈c, β〉, 〈b, α〉〉, 〈〈c, β〉, 〈c, α〉〉, 〈〈c, β〉, 〈a, β〉〉, 〈〈c, β〉, 〈b, β〉〉, 〈〈c, β〉, 〈c, β〉〉}46.(1) 对于任意a∈A, b∈B, 使得〈a, b〉∈A×B. 由于A ⊆C, B ⊆D, 故〈a, b〉∈ C×D, 即A×B ⊆C×D.(2) 对于任意a∈A, 因为〈a, a〉∈A×A, 而A×A＝B×B, 所以〈a, a〉∈B×B, 即a∈B, 从而有A⊆B. 反之, 类似地可以证明B ⊆ A, 因此A＝B.(3) 对于任意a∈A∪B, b∈A∩B, 使得〈a, b〉∈(A∪B)×(A∩B). 由于a∈A∪B, b∈A∩B, 而A∩B≠∅, 则有a∈A或a∈B, 从而〈a, b〉∈A×A或〈a, b〉∈B×B, 因此〈a, b〉∈(A×A)∪(B×B), 亦即(A∪B)×(A∩B) ⊆ (A×A)∪(B×B)成立.(4) 对于任意a∈ A∩B, b∈C∩D, 使得〈a, b〉∈(A∩B)×(C∩D). 由于a∈ A∩B, b∈C∩D,则有a∈A且a∈B, b∈C且b∈D, 从而〈a, b〉∈A×C且〈a, b〉∈B×D, 因此〈a, b〉∈(A×C)∩(B×D), 亦即(A∩B)×(C∩D)⊆ (A×C)∩(B×D)成立.类似地, 可以证明(A×C)∩(B×D)⊆(A∩B)×(C∩D)也成立. 故(A∩B)×(C∩D)＝(A×C)∩(B×D).习题 二 (第2章 关系)1.(1) R ={〈0, 0〉, 〈0, 2〉, 〈2, 0〉, 〈2, 2〉}; (2) R ={〈1, 1〉, 〈4, 2〉};(3) R ={〈5, 6〉, 〈5, 7〉, 〈5, 9〉, 〈4, 25〉, 〈4, 7〉, 〈4 9〉, 〈35, 6〉, 〈35, 9〉, 〈49, 6〉, 〈49, 25〉, 〈49, 9〉};(4) R ={〈2, 6〉, 〈4, 6〉, 〈5, 3〉, 〈5, 7〉, 〈11, 3〉, 〈11, 7〉}.2.dom(R )={a | a =2k , k ∈Z }, ran(R )={b | b =3k , k ∈Z }. 3.(1) 〈25, 5〉∈R ; (2) 〈1, 7〉∉R ; (3) 〈8, 2〉∈R ; (4) 〈3, 3〉∈R ; (5) 〈216, 6〉∈R . 4.(1) M R ＝⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0001100010000010, 关系图为: (2) M R ＝⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡0000011100111001110011100, 关系图为:(3) M R ＝⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡000000100000, 关系图为:(4) M R ＝⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡0000000100000000000001110000111100000000000000000, 关系图为: 5.R ＝{〈x , y 〉 | x ∈R , y ∈R 且0≤x ≤3, 0≤y ≤2}. 6.R ＝{〈b , a 〉, 〈b , d 〉, 〈b , e 〉, 〈c , c 〉, 〈c , a 〉, 〈c , e 〉, 〈d , f 〉, 〈d , c 〉, 〈f , e 〉}. 关系矩阵为:3∙14562 ∙0 ∙∙∙∙∙4 ∙ ∙ 1 23 ∙ ∙ ∙∙∙∙1 2 34 ∙0∙ ∙ ∙ ∙ 3 5 27 ∙ 6 8 1 ∙ ∙M R ＝⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡010000000000100100010101011001000000.7.(1) 对于任意x ∈dom(R ∪S ), 有x ∈dom(R ∪S ) ⇔ 存在y 使得〈x , y 〉∈ R ∪S ⇔存在y 使得〈x , y 〉∈R 或〈x , y 〉∈S⇔ 存在y 使得〈x , y 〉∈R 或存在y 使得〈x , y 〉∈S ⇔ x ∈ dom(R ) 或 x ∈ dom(S ) ⇔ x ∈dom(R )∪dom(S ).(2) 设b ∈ ran (R ∩S ), 则必存在a ∈A , 使得〈a , b 〉 ∈ R ∩S , 于是〈a , b 〉 ∈ R 且〈a , b 〉 ∈ S , 因此b ∈ran(R )且b ∈ran(S ), 由交集的定义, b ∈ran(R )∩ran(S ), 故ran(R ∩S ) ⊆ ran(R )∩ ran(S ).但是ran (R )∩ran (S )⊄ran (R ∩S ).设A ={1, 2, 3}, B ={2, 4, 5}, 且令R ={〈1, 2〉, 〈1, 4〉}, S ={〈3, 2〉, 〈1, 4〉, 〈3, 5〉}, 则R ∩S ={〈1, 4〉}. 于是ran(R )={2, 4}, ran(S )={2, 4, 5}, 因此ran(R )∩ran (S )={2, 4}, 而ran(R ∩S ) ={4}, 所以ran (R )∩ran (S )⊄ran (R ∩S ).8.(1) R ∪S ＝{〈1, 2〉, 〈1, 3〉, 〈2, 4〉, 〈3, 4〉, 〈4, 4〉, 〈4, 2〉, 〈4, 3〉}; R ∩S ＝{〈2, 4〉};R -S ＝{〈1, 2〉, 〈3, 4〉, 〈4, 4〉}, R -1＝{〈1, 2〉, 〈2, 4〉, 〈3, 4〉, 〈4, 4〉}.(2) dom(R )＝{1, 2, 3, 4}, ran R ＝{2, 4}, dom(R S )＝{2}, ran(R S )＝{4}. 9．R S ＝{〈1, 3〉 〈1, 2〉, 〈2, 4〉, 〈3, 3〉, 〈3, 2〉}, S R ＝{〈1, 1〉, 〈1, 3〉, 〈2, 4〉, 〈3, 4〉},R 2={〈1, 1〉, 〈1, 2〉, 〈1, 4〉, 〈3, 1〉, 〈3, 2〉, 〈3, 4〉}, R -1={〈1, 1〉, 〈2, 1〉, 〈4, 2〉, 〈1, 3〉, 〈3, 3〉}, S -1＝{〈3, 1〉, 〈2, 2〉, 〈2, 3〉, 〈4, 4〉}, R -1 S -1＝{〈1, 1〉, 〈4, 2〉, 〈4, 3〉, 〈3, 1〉}. 各关系图如下:R S S RR 2 R -1∙∙∙∙3 2 4 1 ∙∙∙∙1 3 4 2 1 23 ∙∙4∙∙∙∙∙∙3 1 2 4∙ ∙ ∙ ∙1 32 4 ∙ ∙ ∙ ∙1 32 4 ∙ ∙ ∙ ∙1 3 42 R -1 S -1 S -1 10．由已知条件, 可得关系R 1={〈0, 0〉, 〈0, 1〉, 〈1, 2〉, 〈2, 3〉, 〈2, 1〉}, R 2＝{〈2, 0〉, 〈2, 1〉}. 经计算得:R 1R 2＝{〈1, 0〉, 〈2, 1〉};R 2R 1＝{〈2, 0〉, 〈2, 1〉, 〈3, 2〉}; R 1R 2R 1＝{〈1, 0〉, 〈1, 1〉, 〈2, 3〉};21R ＝{〈0, 0〉, 〈0, 1〉, 〈0, 2〉, 〈1, 3〉, 〈1, 1〉, 〈2, 2〉}; 22R ＝∅.11.(1) R 1R 2＝{〈b , a 〉, 〈b , d 〉}, R 2R 1={〈d , a 〉}.(2) 写出相应R 1, R 2的关系矩阵为: ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=00000001011000001R M , ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=01001001000100002R M , 计算 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0000000101100000121R R R M ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0100100100010000⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0000000101100000=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0000000000000000= O . =21R M ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0000000101100000⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0000000101100000=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0000000001110000. =32R M ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0100100100010000⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0100100100010000⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0100100100010000=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0100100100000000 由此可得, R 1 R 2 R 1＝∅, 21R ＝{〈b , a 〉, 〈b , b 〉, 〈b , c 〉}, 32R ＝{〈c , a 〉, 〈c , d 〉, 〈d , c 〉}.(3) 由关系R 1, R 2可得其逆关系为: 1-1R ={〈b , b 〉, 〈c , b 〉, 〈a , c 〉}, 1-2R ={〈a , b 〉, 〈d , c 〉, 〈a , c 〉, 〈c , d 〉}, 由(1)得(R 1R 2)-1＝{〈a , b 〉, 〈d , b 〉}, 从而有关系矩阵:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=000000100010010011-R M , ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=010010000000011012-R M , ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=-0010000000000010121)(R R M . 12.(1) R ＝{〈1, 3〉, 〈2, 2〉, 〈3, 1〉, 〈4, 4〉}, 关系图:︒︒︒︒︒︒︒(2) 依次计算出R 的各次幂.⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=10000001001001001R M , ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=10000001001001002R M ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1000000100100100=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1000010000100001=E 4 (单位矩阵), =3R M ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1000010000100001⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1000000100100100=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1000000100100100=M R , =4R M E 4. 故有⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1000010000100001nR M , n ＝2k , k ∈N ; ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1000000100100100n R M , n ＝2k +1, k ∈N . 13.(1) 设〈x , y 〉∈ R 1 R 3, 则存在z ∈A , 使得〈x , z 〉∈ R 1且〈z , y 〉∈R 3, 由于R 1 ⊆ R 2, 所以〈x , z 〉∈ R 2, 由关系复合的定义, 有〈x , y 〉∈ R 2 R 3, 从而有R 1 R 3⊆ R 2 R 3.(2) 类似于(1)的方法证明. 14.写出相应R , S 的关系矩阵为: ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=0000000000010000001000010R M , ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=0000000010000011000000010S M , 计算M R ∩S ＝⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡0000000000000000000000010, M R ∪S ＝⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡000000010010011001000010, M R S ＝⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡0000000000000101000010000.15.由R , S 可得R -1＝{〈x , x 〉, 〈z , x 〉, 〈x , y 〉, 〈y , y 〉, 〈x , z 〉, 〈y , z 〉, 〈z , z 〉}, S -1＝{〈a , x 〉, 〈d , x 〉, 〈a , y 〉, 〈c , y 〉, 〈e , y 〉, 〈b , z 〉, 〈d , z 〉}, (R S )-1={〈a , x 〉, 〈a , y 〉, 〈a , z 〉, 〈b , x 〉, 〈b , z 〉, 〈c , y 〉, 〈c , z 〉, 〈d , x 〉, 〈d , y 〉, 〈d , z 〉, 〈e , y 〉, 〈e , z 〉}.写出相应的矩阵为:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=-1011101111R M , ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=-011010101000111S M , ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=-1101111101011111)(S R M ,o x y 11 o x y1 -1 o x y 11 -1 -1 而⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=⨯--1101111101011111011101110110101010001111R S M M 所以111)(---⨯=R S S R M M M .16.R 是自反的; S 是反自反的; T 既不是自反的也不是反自反的. 17.R 既是对称的也是反对称的; S 是对称的但不是反对称的; T 是反对称的但不是对称的; U 既不是对称的也不是反对称的.18.对于任意a ∈A , (a -a )/2=0, 所以〈a , a 〉∈R , 即R 是自反的.对于任意〈a , b 〉∈R , 则(a -b )/2是整数, 因为整数的相反数也是整数, 所以(b -a )/2是整数, 即〈b , a 〉∈R , 亦即R 是对称的.对于任意〈a , b 〉∈R , 〈b , c 〉∈R , 则(a -b )/2, (b -c )/2都是整数. 设(a -b )/2=m , (b -c )/2=k , 则a -b =2m , b -c =2k , 从而有a -c =2(m -k ), 即(a -c )/2=m -k , 故〈a , c 〉∈R , 因此R 是传递的.19.(1) 例如, 〈1, 2〉, 〈2,1〉∈R , 但〈1,1〉∉R , 故R 是不可传递的.(2) 例如, R 1={〈1,1〉, 〈1, 2〉, 〈2, 1〉, 〈2, 2〉, 〈3, 1〉, 〈3, 2〉, 〈4, 1〉, 〈4, 2〉, 〈4, 3〉}, 是包含R 且具有传递性的关系.(3) 因为R 1并非全域关系(否则, 当R 1是全域关系时, 就找不到了), 所以只要取R 2=A ×A 是A 上的全域关系就可满足R 2⊇R , R 2≠R , 并且全域关系R 2显然是一个传递关系.当然这样的R 2可以构造多个, 如, R 2={〈1,1〉, 〈1, 2〉, 〈2,1〉, 〈2, 2〉, 〈3, 1〉, 〈3, 2〉, 〈3, 3〉, 〈4, 1〉, 〈4, 2〉, 〈4, 3〉}也是满足R 2⊇R , R 2≠R 是一个传递关系.20.(1) 如图(a), 满足: 自反性, 对称性, 反对称性, 传递性. (2) 如图(b), 满足: 反对称性和传递性. (3) 如图(c), 满足: 传递性.(a) (b) (c )21.(1) 满足: 自反性、对称性与传递性, 不满足: 反自反性与反对称性. (2) 满足: 反自反性、反对称性与传递性, 不满足: 自反性、对称性.∙ ∙∙b c a (3) 不满足: 自反性、反自反性、对称性、反对称性、传递性.(4) 满足: 自反性、对称性、反对称性与传递性, 不满足: 反自反性. (5) 不满足: 自反性、反自反性、对称性、反对称性、传递性. 22.图2.26满足: 反对称性与传递性, 不满足: 自反性、反自反性与对称性. 图2.27满足: 反自反性、反对称性与传递性, 不满足: 自反性与对称性. 23.R 是反自反的, 既不是自反的, 对称的, 也不是反对称的, 也不具有传递性. R 的关系图如图所示.24.(1) 如, R ={〈1, 2〉, 〈2, 1〉, 〈4, 2〉, 〈2, 4〉}∪I A . (2) 如, R ={〈2, 1〉, 〈4, 2〉, 〈4, 1〉}∪I A . (3) 如, R ={〈4, 1〉, 〈1, 2〉}∪I A .(4) 如, R ={〈1, 1〉, 〈1, 2〉, 〈1, 3〉, 〈1, 4〉, 〈2, 2〉, 〈2, 3〉, 〈2, 4〉, 〈3, 3〉, 〈3, 4〉, 〈4, 4〉}. 25.(1) 对于R 的关系矩阵M R , 由于对角线上全为0, R 是反自反的, 但不是自反的; 由于矩阵是对称的, 所以R 是对称的, 而M R 关于对角线对称位置上的元素不同时为1, 故R 是反对称的.经过计算可得, ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=10101101101111012R M , 故R 2⊄R , 因此R 不具有传递性. (2) 对于R 的关系矩阵, 由于对角线上不全为1, R 不是自反的; 由于对角线上元素全部非0元, R 不是反自反的; 由于矩阵是对称的, 所有R 是对称的; 因为R -1∩R =R ⊄ I A , 所以R 不是反对称的.经过计算可得, =2R M ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1000010000110011=M R , 故R 2=R , 所以R 是传递的. 26.(1) 取最小集合A ＝{1, 2}, A 上关系R ＝{〈1, 1〉, 〈1, 2〉}, R 既不是自反的也不是反自反的.(2) 取最小集合A ＝{1, 2, 3}, A 上关系R ＝{〈1, 2〉, 〈2, 1〉, 〈2, 3〉}, R 既不是对称的也不是反对称的.(3) 空集合上的关系既是自反的, 又是反自反的; 既是对称的, 又是反对称的. 因此, 结果同(1), (2).(1) 设R 是自反的, 对任意的a ∈A , 〈a , a 〉∈R , 则〈a , a 〉∈R -1, 故R -1也是自反的.(2) 设R 是传递的. 对于任意〈a , b 〉∈R -1, 〈b , c 〉∈R -1. 所以〈c , b 〉∈R , 〈b , a 〉∈R ; 又因为R 是传递的, 所以〈c , a 〉∈R , 因此〈a , c 〉∈R -1, 故R -1也是传递的.(3) 设R 是反自反的, 对任意的a ∈A , 〈a, a 〉∉R , 则〈a, a 〉∉R -1, 故R -1也是自反的. (4) 对于任意的〈a, b 〉∈ R -1, 则〈b , a 〉∈R , 因为R 是对称的, 故〈a, b 〉∈R , 所以〈b , a 〉∈ R -1. 因此R -1是对称的.(5) 反证法证明. 设R -1不是反对称的, 则存在〈a , b 〉∈R -1, 〈b , a 〉∈R -1, a ≠b , 则〈a , b 〉∈ R , 〈b , a 〉∈R , 与R 是反对称的矛盾.28.(1) 因为R 和S 是自反的, 对任意的a ∈A , 〈a , a 〉∈R 并且〈a , a 〉∈S , 则〈a , a 〉∈R ∩S , 〈a , a 〉∈R ∪S , 故R ∩S 和R ∪S 也是自反的.(2) 对任意的a , b ∈A , a ≠b , 使得〈a , b 〉∈R ∩S . 因为〈a , b 〉∈R ∩S , 所以〈a , b 〉∈R 并且〈a , b 〉∈S ; 因为R 和S 是对称的, 所以〈b , a 〉∈R 并且〈b , a 〉∈S , 则〈b , a 〉∈R ∩S , 〈b , a 〉∈R ∪S , 故R ∪S 和R ∩S 也是对称的.(3) 任意的〈a, b 〉∈R ∩S , 〈b , c 〉∈R ∩S , 则〈a , b 〉∈ R , 〈a , b 〉∈S , 〈b , c 〉∈R , 〈b , c 〉∈S , 因为R 和S 是传递的, 因此〈a , c 〉∈R , 〈a , c 〉∈S , 所以〈a , c 〉∈ R ∩S , 即R ∩S 也是传递的.29.由关系R 可直接写出r (R )和s (R )r (R )＝{〈1, 1〉, 〈1, 2〉, 〈2, 2〉, 〈2, 3〉, 〈3, 1〉, 〈3, 3〉}. s (R )＝{〈1, 2〉, 〈2, 1〉, 〈2, 3〉, 〈3, 2〉, 〈3, 1〉, 〈1, 3〉}. 由关系R 写出关系矩阵M R , 并依次计算其幂为:M R =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡001100010, 2R M =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡010001100, 3R M =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡100010001, M t (R )=M R +2R M +3R M =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡111111111, 亦即t (R )为A 上的全域关系. 故t (R )＝{〈1, 1〉, 〈1, 2〉, 〈1, 3〉, 〈2, 1〉, 〈2, 2〉, 〈2, 3〉, 〈3, 1〉, 〈3, 2〉, 〈3, 3〉}. 30.由关系R 写出关系矩阵M R 并依次计算其幂为:M R =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1000010000111001, ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=10000100101110012R M =3R M =4R M . M t (R )=M R +2R M +3R M +4R M =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1000010010111001, 故 t (R )＝{〈1, 1〉, 〈1, 4〉, 〈2, 1〉, 〈2, 2〉, 〈2, 4〉, 〈3, 3〉, 〈4, 4〉}.由关系R 的关系矩阵M R , 经计算得M r (R )＝⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1101010111100101, M s (R )＝⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0111111111001101, ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=01010101010101012R M =3R M ＝4R M , M t (R )=M R +2R M =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0101010101010101. 32.(a) 自反闭包为: ; 对称闭包 ; 传递闭包 .(b) 自反闭包为: ; 对称闭包为: ; 传递闭包为: .(c) 自反闭包为: ; 对称闭包为: ; 传递闭包为: . 33.由关系R 的关系矩阵M R , 可直接写出r (R )和s (R )r (R ) =⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡1010001110001111011011001, s (R ) =⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡1011100111111111110011101.依次计算关系矩阵M R 的各次幂得2R M =⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡1011110111111111011111111, 3R M =⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡1111111111111111111111111=4R M =5R M ,因此有M t (R )=M R +2R M +3R M +4R M +5R M =⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡1111111111111111111111111, 亦即t (R )为A 上的全域关系.34.∙ ∙ ∙∙ ∙∙∙∙∙∙∙ ∙∙∙∙ ∙ ∙ ∙∙∙∙(1) r (R ), s (R ), t (R )的关系图如图所示.R 的自反闭包 R 的对称闭包 R 的传递闭包(2) r (R )={〈a , c 〉, 〈b , d 〉}∪I A ;s (R )={〈a , a 〉, 〈a , c 〉, 〈c , a 〉, 〈b , d 〉, 〈d , b 〉}; t (R )={〈a , a 〉, 〈b , d 〉, 〈a , c 〉}. 35.(1) 因为R 自反, 得r (R )=R , 即R ∪I A =R ,r (s (R ))=s (R )∪I A =(R ∪R -1)∪I A = (R ∪I A )∪R -1=r (R )∪R -1 =R ∪R -1 =s (R ),所以s (R )自反的.类似可以证明t (R )也是自反的. (2) 证明t (R )对称:(t (R ))-1=(R ∪R 2∪…∪R n ∪…)-1= R -1∪(R 2)-1 ∪…∪(R n )-1∪… = R -1∪(R -1)2 ∪…∪(R -1)n ∪…=R ∪R 2∪…∪R n ∪… (∵R 对称，∴R -1 =R ) =t (R )所以t (R )是对称的. 类似可以证明r (R )也是对称的.(3) 证明r (R )传递: 先用归纳法证明下面结论:(R ∪I A )i = I A ∪R ∪R 2∪…∪R i .(i) 当i =1时, R ∪I A = I A ∪R , 结论成立. (ii) 假设i ≤k 时结论成立, 即(R ∪I A )k = I A ∪R ∪R 2∪…∪R k .(iii) 当i =k +1时(R ∪I A )k +1=(R ∪I A )k (R ∪I A )= (I A ∪R ∪R 2∪…∪R k )(I A ∪R )= (I A ∪R ∪R 2∪…∪R k )∪(R ∪R 2∪…∪R k +1) = I A ∪R ∪R 2∪…∪R k ∪R k +1所以结论成立.t (r (R ))=t (R ∪I A )= (R ∪I A )∪(R ∪I A )2∪(R ∪I A )3∪…=(I A ∪R )∪(I A ∪R ∪R 2)∪(I A ∪R ∪R 2∪R 3)∪… = I A ∪R ∪R 2∪R 3∪…= I A ∪t(R ) = I A ∪R (R 传递t(R )=R ) =r (R )所以r (R )是传递的.∙∙ ∙∙a c b d ∙∙a cb ∙ ∙d ∙∙ ∙∙a c b d36.(1) 左边= r (R 1∪R 2)=R 1∪R 2 ⋃I A右边= r (R 1)∪r (R 2) =R 1∪I A ∪R 2∪I A =R 1∪R 2∪I A(1)式得证.(2) 左边=s (R 1∪R 2)=(R 1∪R 2)∪(R 1∪R 2)-1= R 1∪R 2∪R 1-1∪R 2-1= (R 1∪R 1-1)∪(R 2∪R 2-1)=s (R 1)∪s (R 2)(2)式得证.(3) 证明t (R 1∪R 2)⊇t (R 1)∪t (R 2).t (R 1∪R 2)=(R 1∪R 2)∪(R 1∪R 2)2∪┄∪(R 1∪R 2)n而 (R 1∪R 2)2= (R 1∪R 2)o(R 1∪R 2)=((R 1∪R 2)o R 1)∪((R 1∪R 2)o R 2)= R 12∪R 2o R 1∪R 1o R 2∪R 22 ⊇R 12∪R 22 ………(R 1∪R 2)n ⊇R 1n ∪R 2n . 于是有(R 1∪R 2)∪(R 1∪R 2)2 ∪…∪(R 1∪R 2)n ⊇R 1∪R 12∪…∪R 1n ∪R 2∪R 22∪R 22…∪R 2n 即t (R 1∪R 2) ⊇ t (R 1)∪t (R 2), (3)式得证．37.(1) 不满足自反性、反对称性, 所以不是偏序关系; (2) 是偏序关系;(3) 不是偏序关系. 因为若取a =2, 则22|/2, 所以〈2, 2〉∉R , 即R 不具有自反性.38.(a) R={〈5, 2〉, 〈5, 3〉, 〈5, 4〉, 〈5, 1〉, 〈2, 3〉, 〈2, 4〉, 〈1, 3〉, 〈1, 4〉, 〈3, 4〉} I A ; 关系矩阵为：M R =⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡11111010*******0111001101.(b) R={〈1, 2〉, 〈1, 3〉, 〈1, 4〉, 〈5, 2〉, 〈5, 3〉, 〈5, 4〉, 〈3, 4〉, 〈2, 4〉} I A ; 关系矩阵为: M R =⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡1111001000011000101001111.39. . 40. (a) ; (b) ; (c), 全序关系.∙∙∙∙∙12345∙∙∙∙1234∙∙∙∙1234∙∙∙∙123441. 哈斯图为：(1) ; (2) ; (3) ; (4) ,其中(2)、(3)是全序关系.42.因为R 1不满足自反性, 但满足反自反性和传递性, 因而R 1是拟序关系; 而R 2, R 3满足自反性, 反对称性和传递性, 故R 2, R 3是偏序关系.43.(1) 因为R 是S 上的偏序, 所以R 是自反的、反对称的、传递的. 因而对于任意x ∈S , 〈x , x 〉∈R , 又对于任意x ∈S ', 有〈x , x 〉∈ S '⨯S '. 所以对于任意x ∈S ', 有〈x , x 〉∈ R ', 所以R '是自反的.设〈x , y 〉∈ R ', 〈y , x 〉∈ R ', 则〈x , y 〉∈ R , 〈y , x 〉∈ R , 由R 是反对称的, 故x =y . 因而若R 是反对称的, 则R '也是反对称的.若R 在S 上是传递的, 则由〈a , b 〉∈ R ', 〈b , c 〉∈ R ', 有〈a , b 〉∈ R , 〈a , b 〉∈ S '⨯S ', 〈b , c 〉∈ R ', 〈b , c 〉∈ S '⨯S ', 故〈a , c 〉∈ R , 〈a , c 〉∈ S '⨯S ', 因此〈a , c 〉∈ R ', 即R '是传递的, 因此R 是也是传递的, 所以R '是偏序.(2) 因为R 是S 上的拟序, 所以R 是反自反的、传递的. 因而对于任意x ∈ S ', 〈x , x 〉∉R ,所以〈x , x 〉∉ R ', 因而R '也是反自反的. 由(1)的证明过程可以知道, R '是传递的, 因此R '是拟序.(3) 若R 是线序的, 则R 是偏序的, 且对于任意的a , b ∈S , 或者〈a , b 〉∈ R 或者〈b , a 〉∈ R .因而对于任意的x , y ∈ S ', 也有〈x , y 〉∈ R 或〈y , x 〉∈ R . 但〈x , y 〉∈ S '⨯S ', 〈y , x 〉∈ S '⨯S ', 所以, 或者〈x , y 〉∈ R '或者〈y , x 〉∈ R '. 因而S '上任一元素是可比较的, 又由(1)知R '也是偏序, 所以R '是S '上的线序.44.对于任意x ∈N , 则x 为自然数, 所以x ≥x , 所以〈x , x 〉∈ R ≥, 即为自反关系. 若〈x , y 〉∈ R ≥, 〈y , x 〉∈ R ≥, 则x ≥y 且y ≥x , 故x=y , 因此R ≥是反对称的. 若〈x , y 〉∈ R ≥, 〈y , z 〉∈ R ≥, 则x ≥y 且y ≥z , 故x ≥z , 因此R ≥是可传递的.综上所述, 关系R ≥是一种偏序关系. 又在N 上任意两个自然数都可以比较大小, 也就是在N 上关于关系R ≥都是可比较的, 因此R ≥是全序关系.45.由于包含关系R ⊆是一种偏序关系, 对于ρ的元素按照包含关系有：∅⊆{a }⊆{a , b }⊆{a , b , c }.由此可知ρ的元素按照包含关系存在一条链, 因此R ⊆是全序关系.46．在集合A ＝{x | x 是一个实数且-5≤x ≤20}中, 因为任意一个实数自身不会小于自身, 所以小于关系是反自反的; 又因为小于关系具有传递性; 所以小于关系是A 上的拟∙∙∙∙∙24816 32 ∙∙∙∙∙3612 36 72 ∙∙∙∙24 36 2 ∙ ∙ 36 12 ∙∙ 10 3 2 6 4 12∙ ∙ ∙ ∙ ∙130 ∙序关系.47.因为I A ⊆R , 所以R 具有自反性. R 的关系矩阵为:M R =⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡1000000011000000001000000011000000101000001111000011101000000001. 由关系矩阵可知, r ij +r ji ≤1, 故R 是反对称的; 可计算对应的关系矩阵为:⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=10000000110000000010000000110000001010000011110000111010000000012R M = M R 由以上矩阵可知R 是传递的. 所以, R 是偏序关系, 即〈A , R 〉是偏序集. 所对应的哈斯图如图所示:极大元：a , f , h ; 极小元：a , b , c , g.48.哈斯图为：(1) 上界12, 24, 36, 下界2; (2) 无上界, 下界2, 4, 6, 12. 49.(1) 哈斯图和关系图如图所示:∙ ∙ ∙∙ f c d b ∙ e ∙∙g h a∙∙∙ ∙ ∙ 24 2 4 8 ∙∙612 36 ∙(2) 没有最小元素 最大元素为a ; (3) 极小元为d , e , 极大元为a ;(4) 各子集的上界、下界, 最小上界、最大下界情况如下表:子集 上界 下界 最小上界最大下界{b , c , d } a , c d , c c d {c , d , e } a , c 不存在 c 不存在 {a , b , c }ab , dab50.最大元：9, 极大元：9, 上界：27, 18, 9, 最小上界：9, 最小元：3, 极小元：3, 下界：3, 最大下界：3.51.上界为f , 下界为a , b , 最大上界为f , 最小下界不存在. 52.B 的极大元为19, 极小元为2, 最大元为19, 最小元为2. 53.哈斯图如图所示. 对于集合B : 无最小元素, 最大元素, 下界和最大下界为1, 上界和最小上界不存在, 极大元不存在, 极小元为1.54.(1) 等价关系;(2) 不是等价关系; 因为〈2, 1〉, 〈1, 3〉∈R , 但〈2, 3〉∉R , 即传递性不成立. (3) 等价关系; (4) 等价关系; (5) 等价关系. 55.(1) 等价关系. 因为M R 主对角线上元素全为1, 所以R 是自反的; 又M R 是对称矩阵, 所以关系R 是对称的; 又⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1101100012R M=M R , 亦即R 2=R , 故R 具有传递性, 所以R ∙∙ ∙∙ a c b d e ∙ ∙ ∙ ∙ 5 13 6 ∙24∙∙ c ∙ ∙ ∙a eb d ∙是等价关系.(2) 不是等价关系. 因为M R不是对称矩阵, 所以关系R不具有对称性, 故R不是等价关系.56.(1) 不是A上等价关系. 因为A×A-R1不再满足自反性. 例如, A={a, b}, R1={〈a, a〉, 〈b, b〉}, 则A×A-R1={〈a, b〉, 〈b, a〉}, 显然A×A-R1不是A上等价关系.(2) 不是A上等价关系. 因为R1-R2不再满足自反性. 例如, A={a, b, c}, R1={〈a, b〉, 〈b, a〉, 〈b, c〉, 〈c, b〉, 〈a, c〉, 〈c, a〉, 〈a, a〉, 〈b, b〉, 〈c, c〉}, R2={〈b, c〉, 〈c, b〉, 〈a, a〉, 〈b, b〉, 〈c, c〉}, 则R1-R2={〈a, b〉, 〈b, a〉, 〈a, c〉, 〈c, a〉}, 显然R1-R2不是A上等价关系.(3) 21R是A上等价关系. (见67题证明)(4) r (R1-R2)不一定是A上等价关系. 例如, (2)中所设R1和R2是集合A上的等价关系, 但r (R1-R2)={〈a, b〉, 〈b, a〉, 〈a, c〉, 〈c, a〉, 〈a, a〉, 〈b, b〉, 〈c, c〉}不是A上等价关系.例如, A={a, b}, R1={〈a, b〉, 〈b, a〉, 〈a, a〉, 〈b, b〉}, R2={〈a, a〉, 〈b, b〉}, 则r (R1-R2)={〈a, b〉, 〈b, a〉, 〈a, a〉, 〈b, b〉}是A上等价关系.(5) 不是A上等价关系, 因为R1 R2不再满足对称性. 例如, A={a, b}, R1={〈a, b〉}, R2={〈b, a〉}, 则R1 R2={〈a, a〉}, 显然R1 R2不是A上等价关系.57.若任取〈x, y〉∈A, 因为|x-y|=|x-y|, 故〈x, y〉R〈x, y〉, 所以R是自反的;任取〈x, y〉,〈u, v〉∈A, 使得〈x, y〉R〈u, v〉, 则|x-y|=|u-v|, 故〈u, v〉 R〈x, y〉, 所以R是对称的;任取〈x, y〉, 〈u, v〉, 〈w, z〉∈A, 使得〈x, y〉R〈u, v〉, 〈u, v〉R〈w, z〉, 则有|x-y|=|u-v |, |u-v| = |w-z|, 从而有|x-y|= |w-z|, 即〈x, y〉R〈w, z〉, 所以R是传递的.综上, R是等价关系.A/R={{〈1, 1〉, 〈2, 2〉, 〈3, 3〉}, {〈1, 2〉, 〈2, 1〉, 〈2, 3〉, 〈3, 2〉, 〈3, 4〉}, {〈1, 3〉, 〈2, 4〉, 〈3, 1〉}, {〈1, 4〉}}.58.(1) 对于任意〈a, b〉∈A, 有a2+b2= a2+b2, 故〈a, b〉R〈a, b〉, 自反性成立.对于任意〈a, b〉∈A, 有a2+b2= a2+b2, 则有〈a, b〉R〈b, a〉, 对称性成立.若任意〈a, b〉, 〈c, d〉, 〈e, f〉∈A, 有〈a, b〉R〈c, d〉, 〈c, d〉R〈e, f〉, 即a2+b2= c2+d 2, c2+d 2= e2+f 2, 故a2+b2= e2+f 2, 则必有〈a, b〉R〈e, f〉, 传递性成立.综上R是A上等价关系.(2)A/R的等价类是以(0, 0)为中心的无穷多个同心圆, 包括半径为0的圆.59.(1) 由关系矩阵可知: 对角线元素全为1, 故R自反性成立; M R是对称矩阵, 故R是对称的; 又因为因为对于任意的a ij = 1, a jk = 1, 有a ik = 1, 故R传递性成立.综上R是等价关系.(2) 由等价关系可得其等价类为：[1]R= [2]R = [3]R =[5]R ={1, 2, 3, 5}, [4]R ={4}, 故A/R={{1, 2, 3, 5}, {4}}.(1)A上最大的等价关系是全域关系R=A×A={〈a, b〉 | a, b∈A}, 因此有n2个元素在A 上的最大的等价关系R中, 因为所有n2个二元组都在R=A×A中.(2) A上的最大的等价关系R的秩是1. 这是因为A中任何两个元素都有全域关系R= A×A, 因此R的等价块包含了A的所有元素, 即A的所有元素都在同一个等价块中. 所以商集只有一个等价块{A}, 它包含了A的所有元素.(3) A上的最小的等价关系是恒等关系I A={〈a, a〉 | a∈A }, 它中有n个元素, 即n个自反对.(4) A上的最小的等价关系的商集包含n个元素, 因为恒等关系的每一个元素都自成一个等价块, 每一等价块中也只有一个元素.61.等价关系R的等价类为[1]=[5]={1, 5}, [2]=[4]={2, 4}, [3]=[6]={3, 6}, 故R诱导的划分π={{1, 5}, {2, 4}, {3, 6}}.62.(1) 不是划分; 因为A≠{1, 3, 6}∪{2, 8, 10}∪{4, 5, 7}.(2) 不是划分; 因为{1, 5, 7}∩{3, 5, 6, 10}={5}≠∅.(3) 是划分, 它诱导的等价关系为：R={1, 2, 7}⨯{1, 2, 7}∪{3, 5, 10}⨯{3, 5, 10}∪{4, 6, 8}⨯{4, 6, 8}∪{9}⨯{9}={〈1, 1〉, 〈1, 2〉, 〈1, 7〉, 〈2, 1〉, 〈2, 2〉, 〈2, 7〉, 〈7, 1〉, 〈7, 2〉, 〈7, 7〉, 〈3, 3〉, 〈3, 5〉, 〈3, 10〉, 〈5, 3〉, 〈5, 5〉, 〈5, 10〉, 〈10, 3〉, 〈10, 5〉, 〈10, 10〉, 〈4, 4〉, 〈4, 6〉, 〈4, 8〉, 〈6, 4〉, 〈6, 6〉, 〈6, 8〉, 〈8, 4〉, 〈8, 6〉, 〈8, 8〉, 〈9, 9〉}.(4) 是划分, 它诱导的等价关系为：R={1, 2, 5}⨯{1, 2, 5}∪{3, 4}⨯{3, 4}∪{6, 7, 8}⨯{6, 7, 8}∪{9, 10}⨯{9, 10}={〈1, 1〉, 〈1, 2〉, 〈1, 5〉, 〈2, 1〉, 〈2, 2〉, 〈2, 5〉, 〈5, 1〉, 〈5, 2〉, 〈5, 5〉, 〈3, 3〉, 〈3, 4〉, 〈4, 3〉, 〈4, 4〉, 〈6, 6〉, 〈6, 7〉, 〈6, 8〉, 〈7, 6〉, 〈7, 7〉, 〈7, 8〉, 〈9, 9〉, 〈9, 10〉, 〈10, 9〉, 〈10, 10〉}.63.只要求出A上的全部划分, 即为等价关系.划分为一个块的情况: 1种, 即{a, b, c, d};划分为两个块的情况: 7种, 即{{a, b}, {c, d}}, {{a, c}, {b, d}}, {{a, d}, {b, c}}, {{a}, {b, c, d}}, {{b}, {a, c, d}}, {{c}, {a, b, d}}, {{d},{a, b, c}};划分为三个块的情况: 6种, 即{{a, b}, {c}, {d}}, {{a, c}, {b}, {d}}, {{a, d}, {b}, {c}}, {{a}, {b}, {c, d}}, {{a}, {c}, {b, d}}, {{a}, {d}, {b, c}};划分为四个块的情况: 1种, 即{{a}, {b}, {c}, {d}},因此, 共有15种不同的等价关系.。

第一章部分课后习题参考答案16 设p、q的真值为0；r、s的真值为1，求下列各命题公式的真值。

（1）p∨(q∧r)⇔0∨(0∧1) ⇔0（2）（p↔r）∧(﹁q∨s) ⇔（0↔1）∧(1∨1) ⇔0∧1⇔0.（3）（⌝p∧⌝q∧r）↔(p∧q∧﹁r) ⇔（1∧1∧1）↔ (0∧0∧0)⇔0(4)（⌝r∧s）→(p∧⌝q) ⇔（0∧1）→(1∧0) ⇔0→0⇔117．判断下面一段论述是否为真：“π是无理数。

并且，如果3是无理数，则2也是无理数。

另外6能被2整除，6才能被4整除。

”答：p: π是无理数 1q: 3是无理数0r: 2是无理数 1s:6能被2整除 1t: 6能被4整除0命题符号化为：p∧(q→r)∧(t→s)的真值为1，所以这一段的论述为真。

19．用真值表判断下列公式的类型：（4）(p→q) →(⌝q→⌝p)（5）(p∧r) ↔(⌝p∧⌝q)（6）((p→q) ∧(q→r)) →(p→r)答：（4）p q p→q ⌝q ⌝p ⌝q→⌝p (p→q)→(⌝q→⌝p)0 0 1 1 1 1 10 1 1 0 1 1 11 0 0 1 0 0 11 1 1 0 0 1 1所以公式类型为永真式（5）公式类型为可满足式（方法如上例）（6）公式类型为永真式（方法如上例）第二章部分课后习题参考答案3.用等值演算法判断下列公式的类型，对不是重言式的可满足式，再用真值表法求出成真赋值.(1) ⌝(p∧q→q)(2)(p→(p∨q))∨(p→r)(3)(p∨q)→(p∧r)答：(2)（p→(p∨q)）∨(p→r)⇔(⌝p∨(p∨q))∨(⌝p∨r)⇔⌝p∨p∨q∨r⇔1所以公式类型为永真式(3) P q r p ∨q p ∧r （p ∨q ）→(p ∧r)0 0 0 0 0 10 0 1 0 0 10 1 0 1 0 00 1 1 1 0 01 0 0 1 0 01 0 1 1 1 11 1 0 1 0 01 1 1 1 1 1所以公式类型为可满足式4.用等值演算法证明下面等值式：(2)(p →q)∧(p →r)⇔(p →(q ∧r))(4)(p ∧⌝q)∨(⌝p ∧q)⇔(p ∨q) ∧⌝(p ∧q)证明（2）(p →q)∧(p →r)⇔ (⌝p ∨q)∧(⌝p ∨r)⌝p ∨(q ∧r))p →(q ∧r)（4）(p ∧⌝q)∨(⌝p ∧q)⇔(p ∨(⌝p ∧q)) ∧(⌝q ∨(⌝p ∧q)(p ∨⌝p)∧(p ∨q)∧(⌝q ∨⌝p) ∧(⌝q ∨q)1∧(p ∨q)∧⌝(p ∧q)∧1(p ∨q)∧⌝(p ∧q)5.求下列公式的主析取范式与主合取范式，并求成真赋值(1)(⌝p →q)→(⌝q ∨p)(2)⌝(p →q)∧q ∧r(3)(p ∨(q ∧r))→(p ∨q ∨r)解：（1）主析取范式(⌝p →q)→(⌝q ∨p)⌝(p ∨q)∨(⌝q ∨p)(⌝p ∧⌝q)∨(⌝q ∨p)⇔ (⌝p ∧⌝q)∨(⌝q ∧p)∨(⌝q ∧⌝p)∨(p ∧q)∨(p ∧⌝q)(⌝p ∧⌝q)∨(p ∧⌝q)∨(p ∧q)⇔320m m m ∨∨⇔∑(0,2,3)主合取范式：(⌝p →q)→(⌝q ∨p)⌝(p ∨q)∨(⌝q ∨p)(⌝p∧⌝q)∨(⌝q∨p)⇔(⌝p∨(⌝q∨p))∧(⌝q∨(⌝q∨p))⇔1∧(p∨⌝q)⇔(p∨⌝q) ⇔ M1⇔∏(1)(2) 主合取范式为：⌝(p→q)∧q∧r⇔⌝(⌝p∨q)∧q∧r⇔(p∧⌝q)∧q∧r⇔0所以该式为矛盾式.主合取范式为∏(0,1,2,3,4,5,6,7)矛盾式的主析取范式为 0(3)主合取范式为：(p∨(q∧r))→(p∨q∨r)⌝(p∨(q∧r))→(p∨q∨r)(⌝p∧(⌝q∨⌝r))∨(p∨q∨r)(⌝p∨(p∨q∨r))∧((⌝q∨⌝r))∨(p∨q∨r))⇔1∧1⇔1所以该式为永真式.永真式的主合取范式为 1主析取范式为∑(0,1,2,3,4,5,6,7)第三章部分课后习题参考答案14.在自然推理系统P中构造下面推理的证明：(2)前提：p→q,⌝(q∧r),r结论：⌝p(4)前提：q→p,q↔s,s↔t,t∧r结论：p∧q证明：（2）①⌝(q∧r) 前提引入②⌝q∨⌝r ①置换③q→⌝r ②蕴含等值式④r 前提引入⑤⌝q ③④拒取式⑥p→q 前提引入⑦￢p（3）⑤⑥拒取式证明（4）：①t∧r 前提引入②t ①化简律③q↔s 前提引入④s↔t 前提引入⑤q↔t ③④等价三段论⑥（q→t）∧(t→q) ⑤置换⑦（q→t）⑥化简⑧q ②⑥假言推理⑨q→p 前提引入⑩p ⑧⑨假言推理(11)p∧q ⑧⑩合取15在自然推理系统P中用附加前提法证明下面各推理：(1)前提：p→(q→r),s→p,q结论：s→r证明①s 附加前提引入②s→p 前提引入③p ①②假言推理④p→(q→r) 前提引入⑤q→r ③④假言推理⑥q 前提引入⑦r ⑤⑥假言推理16在自然推理系统P中用归谬法证明下面各推理：(1)前提：p→⌝q,⌝r∨q,r∧⌝s结论：⌝p证明：①p 结论的否定引入②p→﹁q 前提引入③﹁q ①②假言推理④￢r ∨q 前提引入⑤￢r ④化简律⑥r ∧￢s 前提引入⑦r ⑥化简律⑧r ∧﹁r ⑤⑦ 合取由于最后一步r ∧﹁r 是矛盾式,所以推理正确.第四章部分课后习题参考答案3. 在一阶逻辑中将下面将下面命题符号化,并分别讨论个体域限制为(a),(b)条件时命题的真值:(1) 对于任意x,均有2=(x+)(x ).(2) 存在x,使得x+5=9.其中(a)个体域为自然数集合.(b)个体域为实数集合.解： F(x): 2=(x+)(x ). G(x): x+5=9.(1)在两个个体域中都解释为)(x xF ∀，在（a ）中为假命题，在(b)中为真命题。