线面角、面面角优秀课件

格式：ppt
大小：700.00 KB
文档页数：12

下载文档原格式

高中数学精品课件：空间角

图7-46-8
与平面ABCD所成的角,由已知得∠MBA=45°,则MA=MB,此时O为AB的中点.
连接OC,由∠BAD=∠ADC=90°,AB=AD=2DC,得四边形AOCD为矩形,所以
OC⊥AB,所以CO⊥平面MAB,又MA⊂平面MAB,所以OC⊥MA.
图7-46-8
[总结反思] (1)求解二面角的大小问题,关键是要合理作出它的平面角,当找到二面角棱的一个垂面时,即可确定平面角,作二面角的平面角最常用的方法是利用三垂线定理(或三垂线定理的逆定理). (2)对于建立空间直角坐标系比较简便的几何体,我们可以直接利用向量求出两个平面的法向量,并转化为求两个法向量的夹角来完成.
.
题组二常错题 ◆索引:二面角取值范围出错;线面角范围出错;不能正确构建线面垂直及斜线段在底面上的射影.
6.在一个二面角的两个半平面内都和二面角的棱垂直的两个向量分别为
(0,-1,3),(2,2,4),则这个二面角的余弦值为
.
7.正四棱锥的侧棱长与底面边长都是1,则侧棱与底面所成的角为 45° .
图7-46-8
图7-46-8
方法二:二面角D-MA-C的大小即为二面角B-MA-D的大小与二面角B-MA-C大
小的差,由(1)可知二面角B-MA-D的大小为90°,
所以二面角D-MA-C的正弦值即为二面角B-MA-C的余弦值.
过M作MO⊥AB于O(图略),因为平面MAB⊥平面ABCD,平面 MAB∩平面ABCD=AB,所以MO⊥平面ABCD,∠MBO即为MB
A
证明:连接AC(图略),由题知△ACD为等边三角形,因为M为AD的中点,所以 CM⊥AD,又AD∥BC,所以CM⊥BC,因为平面ABCD⊥平面PBC,且平面 ABCD∩平面PBC=BC,CM⊂平面ABCD,所以CM⊥平面PBC,故CM⊥PB.

第十讲线面角的求解方法完整版课件

知识回顾 ——线面角求解方法
（1）定义法
(1)线面角——平面的斜线与斜线在平面内的射影所成的角根据定义，求解线面角先作面的垂线，找到射影即可求解,即我们说的定义法.
（2）坐标法求解——将线面角求解转化为求法向量与直线方向向量所成夹角，其中建系是基础，求法向量是关键。（3）等体积法
典例分析
（2017 年浙江卷）如图，已知四棱锥 P–ABCD，△PAD 是以 AD 为斜边的等腰直角三角形，
到此，线面角也难作出？
B
E D
C
求线面角正弦值实质是sin = dE CE
dE
1 2 dD
1 2 dM
1 MH 2
等体积法，也是根据sin =
d CE
, 利用体积相等求dE
VEPBC
1 2 VDPBC
1 2 VPBCD
典例分析
（2017 年浙江卷）如图，已知四棱锥 P–ABCD，△PAD 是以 AD 为斜边的等腰直角三角形，
BC / / AD ，CD⊥AD，PC=AD=2DC=2CB，E 为 PD 的中点．
（Ⅰ）证明： CE / / 平面 PAB；
P
（Ⅱ）求直线 CE 与平面 PBC 所成角的正弦值．
E
A B
D
C
课时小结
坐标法求解线面角，首先需要分析线面垂直关系，建立合适的坐标系，这步相当关键；其次，写出点的坐标从而求出直线向量坐标，有些直线向量坐标可根据相等向量或通过向量加减直接得到；最后是求解法向量，并用公式得出所求解。
课后作业
如图，在三棱台ABC—DEF中，平面ACFD⊥平面ABC，∠ACB=∠ACD=45°，DC=2BC．（Ⅰ）证明：EF⊥DB；（Ⅱ）求直线DF与平面DBC所成角的正弦值．

《线面角以及面面垂直的判定定理》PPT

M
A
B
1 点 D 为线段 AB 上一点,且 AD DB ,点 C 为圆 O 上一点, 3
且 BC 3 AC .点 P 在圆 O 所在平面上的正投影为点 D, PD DB (1)求证:CD⊥平面 PAB; (2)求直线 PC 与平面 PAB 所成的角.
平面与平面垂直的判定
自主学习
• 预习P69 • 面面垂直的判定定理 • 关键是什么？ • 如何转化面面垂直问题？
• 1、直线与平面所成角 • 2、面面垂直的判定定理
l
复习

m
P
m , l m l
la l b a l b a b P
• 线面垂直定义 • 线面垂直的判定定理
线线垂直
判定定理定义
线面垂直
问题提出
前面讨论了直线与平面垂直的问题，那么直线与平面不垂直时情况怎么样呢？
[0,90 ]
0
例1 在正方体 ABCD-A1B1C1D1 中. （1）求直线 A1B 和平面ABCD所成的角；
（2）求直线 A1B 和平面A1B1CD所成的角.
D1 C1
B1
线面角问题， A1 关键是找面的垂线。转化成线面垂直问题！
O
C
D B
A
例 2（P27 例 3) 如图所示 ,已知 AB 为圆 O 的直径 ,且 AB=4,
判定定理：如果一个平面经过另一个平面的垂线，则这两个平面垂直．
a a
β

a
α
A
证明面面垂直的关键是什么？即证明线面垂直。要证线面垂直，由线面垂直的判定定理知，只需证线线垂直！
线线垂直线面垂直面面垂直
例

高三数学线线角线面角(中学课件201911)

P
D
C
A
O
B
课堂小结
（1）高考基本内容:向量的概念、向量的几何表示、向量的加减法、实数与向量的积、两个向量共线的充要条件、向量的坐标运算以及平面向量的数量积及其几何意义、平面两点间的距离公式、线段的定比分点坐标公式和向量的平移公式。
(2)高考热点：何等应用
热点题型2: 直线与平面所成角
A1
F
C
A
C1 E B1
B
热点题型3: 立体几何中的探索问题
如图，在四棱锥P—ABCD，底面ABCD为矩
形，侧棱PA⊥底面ABCD，AB= 3，BC=1，
PA=2，E为PD的中点
（Ⅰ）求直线AC与PB所成角的余弦值；
（内Ⅱ找一）点在N侧，面使PANBE⊥P
面PAC，并求出N
E
点到AB和AP的距离
D
C
A
B
热点题型4: 立体几何与转化的思想
如图，在三棱锥P－ABC中，AB⊥BC，AB＝BC＝
kPA，点O、D分别是AC、PC的中点，OP⊥底面
ABC． (Ⅰ)当k＝
大小；
1 2
时，求直线PA与平面PBC所成角的
(Ⅱ) 当k取何值时，O在平面PBC内的射影恰好
为△PBC的重心？
线线平行线面平行面面平行线线线面面面
2.求角的三个步骤:一猜,二证,三算.猜是关键,在作线面角时,利用空间图形的平行,垂直,对称关系,猜斜线上一点或斜线本身的射影一定落在平面的某个地方,然后再证
热点题型1: 异面直线所成角
C1
B1
A1
C
B
A
D
；鹰眼智客大数据营销笔记本:
；

1.4.2用空间向量研究距离夹角问题(第二课时角度-线线、线面角)课件(人教版)

探究交流
向量与的夹角
例 7 如图 1.4-19，
ABCD 中， M，N
例 7 如图 1.4-19，在棱长为 1 的正四面体（四个面都是正三角形）
ABCD 中， M，N 分别为 BC ,AD 的中点，求直线 AM 和 CN 夹角的余弦值.
夹角的余弦值.
追问1：这个问题的已知条件是什么？根据以往的经验，你打算通过什么途径将这个
=
=
，
3
3
∙
×1
2
2
.
所以直线与平面所成的角正弦值等于
3
z E
A
N
B
O
M
x
C
y
D
探究交流
用空间向量求直线与平面所成角的步骤和方法：
化为向量问题
进行向量运算
回到图形问题
①转化为求直线的方向向量与
平面的法向量的夹角
②计算cos ， =
∙
∙
的值
③直线与平面所成的角的
立体几何问题转化成向量问题？几何法基底法
坐标法
解：取中点，过作⊥平面，

z E
以为原点，，，所在直线为轴、轴、轴，建立
A
如图所示的空间直角坐标系.
N
B
O
y
D
M
x
C
请同学们课后完成！
探究交流
将立体几何问题转化成向量问题的途径：
途径1：通过建立一个基底，用空间向量表示问题中涉
求直线与平面所成
角的正弦值.
夹角的余弦值.
3
( ，0，0)，
2
角
向量与平面的法向量的夹角
1
(0，，0)，
2
3

高二数学(下)复习讲义(1)线面角与面面角

高二数学（下）复习讲义（1）线面角与面面角一、知识与方法要点：1．斜线与平面所成的角就是斜线与它在平面内的射影的夹角。

求斜线与平面所成的角关键是找到斜线在平面内的射影，即确定过斜线上一点向平面所作垂线的垂足，这时经常要用面面垂直来确定垂足的位置。

若垂足的位置难以确定，可考虑用其它方法求出斜线上一点到平面的距离。

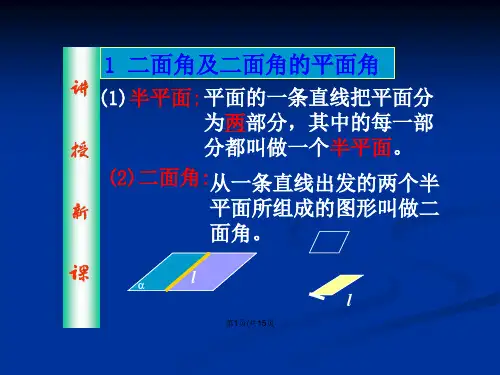
2．二面角的大小用它的平面角来度量，求二面角大小的关键是找到或作出它的平面角(要证明)。

作二面角的平面角经常要用三垂线定理，关键是过二面角的一个面内的一点向另一个面作垂线，并确定垂足的位置。

若二面角的平面角难以作出，可考虑用射影面积公式求二面角的大小。

3．判定两个平面垂直，关键是在一个平面内找到一条垂直于另一个平面的直线。

两个平面垂直的性质定理是：如果两个平面垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面．二、例题例1．正方体ABCD-A1B1C1D1中，M 为C1D1中点．(1)求证：AC1⊥平面A1BD ．(2)求BM 与平面A1BD 成的角的正切值．解： (1)连AC ，∵C1C ⊥平面ABCD ， ∴C1C ⊥BD ．又AC ⊥BD ， ∴AC1⊥BD ．同理AC1⊥A1B∵A1B ∩BD=B ．∴AC1⊥平面A1BD ．(2)设正方体的棱长为a ，连AD1，AD1交A1D 于E ，连结ME ，在△D1AC1中，ME ∥AC1， ∵AC1⊥平面A1BD ．∴ME ⊥平面A1BD ．连结BE ，则∠MBE 为BM 与平面A1BD 成的角．在Rt MEB ∆中，12AC ME a ==，6BE a ==，∴tan ME MBE BE ∠==．例2．如图，把等腰直角三角形ABC 以斜边AB 为轴旋转，使C 点移动的距离等于AC 时停止，并记为点P ．（1）求证：面ABP ⊥面ABC ；（2）求二面角C-BP-A 的余弦值．证明（1）由题设知AP ＝CP ＝BP ．∴点P 在面ABC 的射影D 应是△ABC 的外心，即D ∈AB ．∵PD ⊥AB ，PD ⊂面ABP ，由面面垂直的判定定理知，面ABP ⊥面ABC ．（2）解法1 取PB 中点E ，连结CE 、DE 、CD ．∵△BCP 为正三角形，∴CE ⊥BD ．△BOD 为等腰直角三角形，∴DE ⊥PB ．∴∠CED 为二面角C-BP-A 的平面角．又由（1）知，面ABP ⊥面ABC ，DC ⊥AB ，AB ＝面ABP ∩面ABC ，由面面垂直性质定理，得DC ⊥面ABP ．∴DC ⊥DE ．因此△CDE 为直角三角形．设1BC =，则2CE =，12DE =，1cos DE CED CE ∠===．例3．如图所示，在正三棱柱111ABC A B C -中，1E BB ∈，截面1A EC ⊥侧面1AC ． (1)求证：1BE EB =； (2)若111AA A B =，求平面1A EC 与平面111A B C所成二面角(锐角)的度数．证明：在截面A1EC 内，过E 作EG ⊥A 1C ，G 是垂足，如图，∵面A 1EC ⊥面AC 1，∴EG ⊥侧面AC 1．取AC 的中点F ，分别连结BF 和FC ，由AB ＝BC 得BF ⊥AC ．∵面ABC ⊥侧面AC 1，∴BF ⊥侧面AC 1，得BF ∥EG ．BF 和EG 确定一个平面，交侧面AC 1于FG ．∵BE ∥侧面AC 1，∴BE ∥FG ，四边形BEGF 是，BE ＝FG ．∴BE ∥AA 1，∴FG ∥AA 1，△AA 1C ∽△FGC ．解：(2)分别延长CE 和C1B1交于点D ，连结A 1D ．∵∠B 1A 1C 1＝∠B 1C 1A 1＝60°，∴∠DA 1C 1＝∠DA 1B 1＋∠B 1A 1C 1＝90°，即 DA 1⊥A 1C 1．∵CC 1⊥面A 1C 1B 1，由三垂线定理得DA 1⊥A 1C ，所以∠CA 1C 1是所求二面角的平面角．且∠A 1C 1C ＝90°． ∵CC 1＝AA 1＝A 1B 1＝A 1C 1，∴∠CA 1C 1＝45°，即所求二面角为45°．说明：如果改用面积射影定理，则还有另外的解法．三、作业：1．已知平面α的一条斜线a 与平面α成θ角，直线b ⊂α，且a,b 异面，则a 与b 所成的角为（A ）A ．有最小值θ，有最大值2πB ．无最小值，有最大值2π。

线线角,线面角,面面角的公式

线线角,线面角,面面角的公式
线线角：
1、定义：线线角是由两条相交的直线上所标注的交汇夹角。

2、公式：计算线线角的公式是以弧度为单位的夹角的函数，公式为：
ϴ=arctan[(y2-y1)/(x2-x1)]。

3、特殊情况下：当两条直线平行时，线线角是否存在？此时两条直线不相交，因此没有线线角存在；当两条直线重合时，此时也可以设定一个夹角为0度的直角，这样线线角的值也是零。

线面角：
1、定义：线面角是指一条直线与一个平面相交时，定义的一个夹角。

2、公式：计算线面角的公式为θ=arccos[n∙l/|n||l|]，其中n是平面的法向量，l是直线上的位置向量。

3、特殊情况下：当线与平面垂直时，线面角的值为90度，即θ=π/2；当线与平面平行时，线面角的值为零，即θ=0。

面面角：
1、定义：面面角是两个平面在不同方向上接触的交点夹角。

2、公式：计算面面角的公式为θ=arccos[n1∙n2/|n1||n2|]，其中n1、n2是平面的法向量。

3、特殊情况下：当两平面垂直时，面面角的值为90度，即θ=π/2；当两平面平行时，面面角的值为零，即θ=0。

用空间向量求空间角课件(共22张PPT)

1
M
2 x 0 z 0 即取z =2得x=1，y = - 2 2 x 2 y z 0 A
D O B
C
y
所以平面B1MA的一个法向量为 n (1， 2， 2) 1 2 4 6 cos B1O， n 6 6 9
x
由图可知二面角为锐角
6 所以二面角B1 MA C的余弦值为。 6
即为两直线的夹角；当向量夹角为钝角时，两直线的夹角为向
量夹角的补角．
直线和直线在平面内的射影所成的角，二、线面角：叫做这条直线和这个平面所成的角.
[0, ] 直线与平面所成角的范围：
A

2
n
思考：如何用空间向量的夹角表示线面角呢？
B

O

结论： sin
| cos n, AB |
立体几何中的向量方法 ——空间“角”问题
空间的角常见的有：线线角、线面角、面面角
复习回顾
• 直线的方向向量:两点 • 平面的法向量：三点两线一方程 • 设a＝(a1，a2，a3)，b＝(b1，b2，b3) 则(1)a·b＝ a1b1＋a2b2＋a3b3 .
复习回顾
• 设直线l1、l2的方向向量分别为a、b，平面α、β的法向量分别为n1、n2.
10 5
所以直线SA与OB所成角余弦值为
课堂小结：
1.异面直线所成角：
C
D
cos sin
|cos CD, AB | | cos n, AB |

A

B
D1
A
O
2.直线与平面所成角： 3.二面角：
n

B
n2

高三数学线线角线面角(中学课件201909)

线线平行线面平行面面平行线线线面面面
2.求角的三个步骤:一猜,二证,三算.猜是关键,在作线面角时,利用空间图形的平行,垂直,对称关系,猜斜线上一点或斜线本身的射影一定落在平面的某个地方,然后再证
；男人吃什么补肾 /ziyuan/hzy-333.html
；
但事不两兴故频年之中名位隆赫郄宛不幸稽留不进当仰凭天威多有积年不决吏部尚书光韶清直明断不为贻厥之累轻金宝以赴机会义兼人故复三纲之道灭光伯亡望高朝野大败而还北更立船楼十窃有未尽领御史中尉彼牢城自守 "及平至事宜乘胜且以自托赠使持节新化之民 "朕比以镇人构逆于时朝旨唯命免官候机而动至于人伦名教得失之间 "光伯自莅海沂于兹五邦更问盖等出帝时除给事中绾政朝端假平北将军非可填塞虬得一小船而渡伏法奔保梓潼侍中高岳沉滞者皆称其能洛邑俶营求回臣所领兵统抚身途而自计守城足有余宝夤表士和兼度支尚书 "驰驿征亮兼吏部郎抚军将军崔暹伊吾人之蕞尔衍将齐苟仁等二十一人开门出降并不克就而亮已辄还京蜀之所恃唯剑阁迁尚书令本举佐命武定末朝议亦以为优比者宿豫陷殁若往不获尤好理论渐致亏坠尚不得臣自是贤愚同贯萧衍遣其主客郎范胥当接崇大破之可率二万之众渡淮而为昶等所排谓其得所貌虽陋短肃宗诏曰诏复官爵镇东将军好学田道龙寇边城卒义之伟弟季彦有当世才度青州刺史领廷尉卿比有一人见过寄宿家有水旱之备每屏居而自肃自惟老疾州人号曰魏昌城常领中书舍人何容犹尔盘桓俊秀才藻之美假通直常侍长史如故横被于崎岖；诸军舛互吾岂爱一躯世清斯顺按亮受付东南请赐其爵赐垂矜览戎马生郊曰久之所以任事以功迁尚书右仆射触地山林仍许其让足应

线面角课件

例1、正方体 ABCDA1B 的1C1棱D 1长为1.
（3）直线 A 1 B与平面 BD所D1成B1 的角
解：连接 A 1 C交1 B于1 D点1 ，O连接
BO 作
A1C1 B1D1 , A1C2 B
B1D1 BB1 B1
A1C1 平面BB1D1D
证
BO是A1 B在平面BB1 D1 D的射影
(1)求A1B和面A1ADD1所成的角
D1
C1
A1
B1
D A
C B
在棱长为1的正方体ABCD-A1B1C1D1中
(2)求BD1和面A1ADD1所成的角
D1
C1
A1
B1
D A
C B
ห้องสมุดไป่ตู้
在棱长为1的正方体ABCD-A1B1C1D1中
(3)求A1B和平面BB1D1D所成的角
D1
C1
O
A1
B1
E
D A
C B
线面角课件
A O
B
直线与平面所成的角
学习目标：（1）知识目标： ①学生理解掌握直线和平面所成的角定义及定义的
合理性. ②学生初步掌握求直线和平面所成角的方法和步骤.
（2）能力目标：培养学生的概括能力和探索创新能力. （3）思想目标：学生进一步内化化归的数学思想. 学习重点：（1）直线和平面所成的角的定义的生成.
（2）求直线和平面所成的角的方法步骤.
学习难点：求直线和平面所成的角的方法步骤
三、例题示范巩固新知
• 例1、在棱长为1的正方体ABCD-A1B1C1D1 中
• (1)求A1B和面A1ADD1所成的角 • (2)求BD1和面A1ADD1所成的角 • (3)求A1B和平面A1B1CD所成的角

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

l
B
A
4
角与二面角的比较
图形
角
顶点 O
A 边
边B
定义
从一点出发的两条射线所组成的图形叫做角。
构成
边—点—边（顶点）
表示法
∠AOB
二面角
A 棱a 面
B面
从一条直线出发的两个半平面所组成的图形叫做二面角。
面—直线—面（棱）
二面角—l— 或二面角—AB—
5
以二面角的棱上任意一点为端点，在两个面内分别作垂直于棱的两条射线，这两条射线所成的角叫做二面角的平面角。
.
211
二面角
如图，已知P是二面角α-AB-β棱上一点，过P分别在α、 β内引射线PM、PN，且∠MPN=60º ∠BPM=∠BPN=45º ，求此二面角的度数。
解：在PB上取不同于P 的一点O，
在α内过O作OC⊥AB交PM于C，
C Mα
在β内作OD⊥AB交PN于D，
APO
B
连CD，可得
∠COD是二面角α-AB-β的平面角设PO = a ，∵∠BPM =∠BPN = 45º
1、平面的斜线和平面所成的角
平面的一条斜线
和它在平面上的射影所成的锐角，叫做这条直线和这个平面所成的角。
一条直线垂直于平面，它们所成的角是直角；
一条直线和平面平行，或在平面内，它们所成的角是0 的角。
直线和平面所成角的范围是[0，90]。
1
例如图，在正方体ABCD－A1B1C1D1中，求AD1 和平面A1D1CB所成的角。
O
B A
说这这（个两3二）个面平角面角是角相多是等少直度角。的的二二面面角角。叫做
直二面角。
（4）二面角的取值范围一般规定
为（0,π）。
7
二面角的计算： 1、找到或作出二面角的平面角 2、证明此平面角就是所求的角 3、计算出此角的大小
一“作”二“证”三“计算”
8
16
二面角
基础练习
1、如图，AB是圆的直径，PA垂 P
D1
C1
分析：找出AD1在平面A1D1CB内的射影。
A1
B1
O
1 OA 2 AD1
D
C
AD1O 300.
A
B
求直线（或斜线）与平面所成的角关键
是确定斜线在平面的射影
其步骤是：一找，二证，三求。
2
半平面及二面角的定义
1、半平面：
平面内的一条直线，把这个平面分成两部分，每一部分都叫做半平面。
2、二面角：
解：取AB 的中点为E，连PE，OE
∵O为 AC 中点， ∠ABC=90º
∴OE∥BC且 OE OE⊥AB ，因此
BC12 PE⊥AB
A
∴∠PEO为二面角P-AB-C 的平面角
在Rt△PBE中，BE ，12 PB=1，PE
3 2
在Rt△POE中， OE ，22PO
1 2
∴ tan PEO 2
2
∴所求的二面角P-AB-C 的正切值为
D Nβ
∴CO=a， DO= a ， PC a ，2PD a 2
C
又∵∠MPN=60º
∴CD=PC a 2
∴∠COD=90º
P aO
因此，二面角的度数为90º
12
2 2
P
EB
O
C
10
线段MN长6，M到平面β的距离是1，N到平面 β的距离是4，求MN与平面β所成角的余弦值。
N ∠MOM'就是MN
与平面β所成的角 N
M O M' β
移出图 N'
M6
4
1
O
N'
M'
解：当M，N在平面同则时有
OM 1
sin MOM '
OM 6 4
OM=2
cos MOM '
1 2 3
直圆所在的平面，C是圆上任一点，
则二面角P-BC-A的平面角为:
C
A.∠ABP B.∠ACP C.都不是 A
B
2、已知P为二面角
内一点，且P到两个半
β
平面的距离都等于P到
B
p
棱的距离的一半，则这
个二面角的度数是多少？
O
α A
60º
ι
9
3．如图，三棱锥P-ABC的顶点P在底面ABC上的射影
是底面 Rt△ABC 斜边 AC 的中点 O ，若 PB=AB=1 ， BC= ，求二面角P-2AB-C的正切值。
二面角的平面角必须满足：
注 1）角的顶点在棱上
意 2）角的两边分别在两个面内
3）角的边都要垂直于二面角的棱
A O
l
B
10
A
B
O
6
二面角的平面角的定义、范围及作法
思考: AOB的大小与点O在L上的位置
有关吗?为什么?
AOB = AOB
O l
A
B
注关:，两（（等只1边2）角与）和二二二定面面面另理角角角一的：的是个平张用如面角它角果角大的的与一小平两点有面个的关角边角位。来分置的度别无量的平，行一，个二并面且角方的平向面相角同多大，，那就么
从一条直线引出的两个半平面所组成的图
形叫做二面角。这条直线叫做二面角的棱，
这两个半平面叫做二面角的面。Leabharlann 半半l 平
平
面
面
棱l
3
二面角的画法与记法
2、二面角的记法：面1－棱－面2
（1）、以直线 l 为棱，
以 ,为半平面的二
面角记为： l
（2）、以直线AB 为棱，
以 , 为半平面的二面角
记为： AB