下载文档原格式
第⼆章-流体静⼒学⼀、学习导引1、流体静⽌的⼀般⽅程（1）流体静⽌微分⽅程x p f x ??=ρ1，y p f y ??=ρ1，zpf z ??=ρ1 （2）压强微分)(dz f dy f dx f dp z y x ++=ρ（3）等压⾯微分⽅程0=++dz f dy f dx f z y x2、液体的压强分布重⼒场中，液体的位置⽔头与压强⽔头之和等于常数，即C pz =+γ如果液⾯的压强为0p ，则液⾯下深度为h 处的压强为h p p γ+=03、固体壁⾯受到的静⽌液体的总压⼒物体受到的⼤⽓压的合⼒为0。
计算静⽌液体对物⾯的总压⼒时，只需考虑⼤⽓压强的作⽤。
（1）平⾯壁总压⼒：A h P c γ= 压⼒中⼼Ay J y y c cc D += 式中，坐标y 从液⾯起算；下标D 表⽰合⼒作⽤点；C 表⽰形⼼。
（2）曲⾯壁总压⼒：222z y x F F F F ++=分⼒：x xc x A h F γ=，y yc y A h F γ=，V F z γ=4、难点分析（1）连通器内不同液体的压强传递流体静⼒学基本⽅程式的两种表达形式为C pz =+γ和h p p γ+=0。
需要注意的是这两个公式只适⽤于同⼀液体，如果连通器⾥⾯由若⼲种液体，则要注意不同液体之间的压强传递关系。
（2）平⾯壁的压⼒中⼼压⼒中⼼的坐标可按式Ay J y y c cc D +=计算，⾯积惯性矩c J 可查表，计算⼀般较为复杂。
求压⼒中⼼的⽬的是求合⼒矩，如果⽤积分法，计算往往还简便些。
（3）复杂曲⾯的压⼒体压⼒体是这样⼀部分空间体积：即以受压曲⾯为底，过受压曲⾯的周界，向相对压强为零的⾯或其延伸⾯引铅垂投影线，并以这种投影线在相对压强为零的⾯或其延伸⾯上的投影⾯为顶所围成的空间体积。
压⼒体内不⼀定有液体。
正确绘制压⼒体，可以很⽅便地算出铅垂⽅向的总压⼒。
（4）旋转容器内液体的相对静⽌液体随容器作等⾓速度旋转时，压强分布及⾃由⾯的⽅程式为c z gr p +-=)2(22ωγc gr z +=2220ω恰当地选取坐标原点，可以使上述表达式简化。
第2章流体静力学第二章流体静力学流体静力学主要研究流体在静止状态下的平衡规律及其工程应用。
由于静止状态下流体之间及流体与物面之间的作用是通过静压力的形式来表现的。
所以，本章的中心问题是研究静止状态下静压力的分布规律，进而确定静止流体作用物面上的总压力，用以解决工程实际问题。
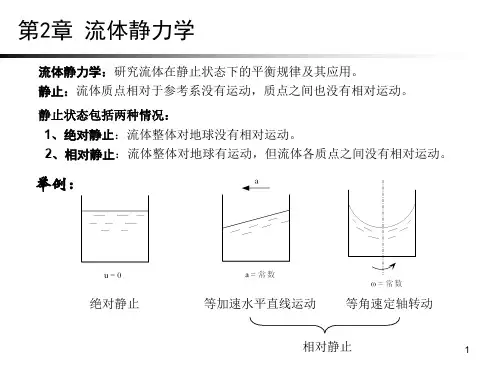
流体静力学中所说的静止是指流体质点间没有相对运动的状态。
所以，流体的静止包含以下两种情况：流体整体对地球没有相对运动的所谓绝对静止；流体整体对地球有相对运动，但流体质点之间没有相对运动的所谓相对静止。
流体静止时，流体质点之间没有相对运动，所以粘滞性在静止流体中显现不出来。
因此，本章所得到的流体平衡规律对理想流体和实际流体均适用。
§2－1 流体静压力及其特性一、静压力在静止流体中，不存在切应力。
因此，流体中的表面力就是沿受力面法线方向的正压力或法向力。
设在作用微元面积△A上的法向力为△P，则极限ΔP （2－1）ΔA?0ΔA就是流体单位面积上所受到的垂直于该表面的力，即物理学中的压强，称为流体静压力，简称压力，用p表示。
其单位为N/m2，称为帕斯卡，简称帕（Pa）。
作用在某一面积上的静压力的合力称为总压力，以P表示，其单位为牛顿（N）。
常用的压力单位有：帕(Pa)、巴(bar)、标准大气压(atm)、毫米汞柱(mmHg)、米水柱(mH2O)，其换算关系为：1bar=1×105 Pa；1atm=1.01325×105 Pa；1atm=760 mmHg；1atm=10.34 mH2O；1mmHg=133.28Pa；1mH2O=9800Pa。
由此可见静压力的单位非常的小，所以在工程实际中常用的单位是kPa(103Pa）或MPa(106Pa)。
p=lim二、静压力的两个重要特性特性之一：静压力沿着作用面的内法线方向，即垂直地指向作用面。
证明：一方面，流体静止时只有法向力，没有切向力，静压力只能沿法线方向；另一方面，流体不能承受拉力，只能承受压力。
所以，静压力唯一可能的方向就是内法线方向。
由这一特性可知，在流体与固体的接触面上静压力将垂直于接触面，见图2－1。
? ? 图2-1 静压力垂直于作用面特性二：静止流体中任何一点上各个方向的静压力大小相等，与作用方向无关。
证明：在静止流体中任取出如图2－2所示的，棱长为dx、dy、dz的微元正四面体oABC，取其内的静止流体为研究对象。
建立一个与其三个相互垂直的三个棱相重合的直角坐标系，以px、py、pz和pn依次表示作用在三个坐标面和△ABC上的静压力，用Px、Py、Pz和Pn依次表示作用在这四个面上的总压力。
由于dx、dy、dz的大小是任取的，所以z dz py dx o x A pz dy B y pn px △ABC的外法线方向n也是任意的。
流体处于静止状态时，作用在流体上的合外力在任一个方向的分量都应为零。
首先分析流体在x方向的受力，作用在流体上的质量力在x方向上的分量可表示为1Fx=Xρdxdydz。
6式中X表示作用在单位质量流体上的质量力在x方向上的分量。
同时，作用在流体上的表面力在x方向分量不为零的只有△oBC和△AB C上的总压力，即Px?和Pncos(n,x)=(pnSΔABC)cos(n,x)图2－2 静压力特性二1pxdydz。
2 =pn[SΔABCcos(n,x)] =pnSΔoBC1pndydz。
2注意，在这一公式的推导过程中利用乘法的结合律将力的投影转换成了面积的投影。
由于流体处于静止状态，其在x方向的合外力应为零，即=111pxdydz?pndydz?Xρdxdydz=0。
226令dx、dy、dz趋于零，即四面体缩小到原点o时，忽略高阶小量dxdydz则可得px=pn。
同理，分析y和z方向上的受力及静止条件可得py=pn； pz=pn，即px=py=pz=pn=p （2－2）由于方向n代表任意方向，所以上式表明：静止流体中任意一点上的流体静压力，无论来自何方均相等，或者说与作用方向无关。
p代表一点处的流体静压力，永远为正值。
因此，在连续介质中研究一点的静压力p时不必考虑其作用方向，只需计算或测量出其在空间的分布函数p=p(x, y, z)即可。
§2－2 流体平衡方程一、流体平衡微分方程式的建立（标题位置提到这里）通过分析静止流体中流体微团的受力，可以建立起平衡微分方程式，然后通过积分便可得到各种不同情况下流体静压力的分布规律。
因此，首先要建立起流体平衡微分方程式。
现在讨论在平衡状态下作用在流体上的力应满足的关系，建立平衡条件下的流体平衡微分方程式。
（删除这段话中红字部分的内容）在静止流体中任取出棱长各为dx、dy、dz的微元正六面体，如图2－3所示，并建立图示的直角坐标系。
首先，我们分析作用在这个微元六面体内流体上的力在x方向上的分量。
微元体以外的流体作用于其上的表面力均与作用面相垂直。
因此，只有与x方向相垂直的前后两个面上的总压力在x轴上的分量不为零。
设六面体中心点A处的静压力为p(x，y，z)，则作用在A1和A2点的压力可以表示为z p1 A1・ A・・A2 dy p2 x 图2－3 六面体受力分析 dx dz ?pdx?pdx；p2=p?。
?x2?x2所以作用在A1和A2点所在面上的总压力分别为p1=p?1?p1?p(p?dx)dydz、(p?dx)dydz。
2?x2?xo y 微元体内流体所受质量力在x方向的分力为Xρdxdydz，由于流体处于平衡状态，则1?p1?p(p?dx)dydz?(p+dx)dydz+Xρdxdydz=0。
2?x2?x用ρdxdydz除上式，简化后得?1?p=0?ρ?x??1?p=0?。
（2－3）同理，在y、z方向，可得Y? ρ?y??1?pZ?=0?ρ?z?X?这就是1755年由欧拉建立的流体平衡微分方程式，又称为欧拉平衡方程式。
根据这个方程可以解决流体静力学中许多基本问题，它在流体静力学中具有重要地位，既适用于绝对静止状态也适用于相对静止状态。
同时，推导中也没有考虑整个空间密度ρ是否变化及如何变化，所以它不但适用于不可压缩流体，而且也适用于可压缩流体。
该方程的物理意义：当流体处于平衡状态时，作用在单位质量流体上的质量力与压力的合力相平衡。
将式（2－3）中的三个方程分别乘以i、j、k再相加可得流体平衡微分方程式的矢量形式，即f=二、等压面1?p。
（2－4）ρ在充满平衡流体的空间里，静压力相等的各点所组成的面称为等压面。
因为在等压面上p为常数，即dp=0。
液体的自由液面便是一个特殊的等压面。
（删除红字部分的内容）将（2－3）的三个方程分别乘以dx、dy、dz再相加，整理后可得dp=ρ(Xdx+Ydy+Zdz)。
（2－5）由于等压面上的静压力处处相等，所以等压面方程为Xdx?Ydy?Zdz=0 （2－6）等压面最重要的一个性质是：等压面与质量力垂直。
现证明如下：设dl = dxi + dyj + dzk是等压面上的任意微元矢量，作用在单位质量流体上的质量力为f = Xi + Yj + Zk。
将dl与f做数量积，则有dlgf=Xdx?Ydy?Zdz=dp=0 由矢量分析可知dl与f互相垂直。
由于质量力与等压面内任意的微元矢量互相垂直，所以等压面与质量力相互垂直。
由此可知，根据质量力的方向可以确定等压面的形状，也可以根据等压面的形状确定质量力的方向。
例如对只受重力作用的静止的流体，因为重力的方向总是铅直向下的，所以其等压面必定是水平面。
读者不妨试着分析液体在匀加速水平直线运动容器中和绕中心轴等角速度旋转的容器内的等压面的形状。
三、静力学基本方程式图2－4所示为一敞口容器，其中盛有静止的均质液体, 其密度为ρ=c。
液体所受的质量力只有重力，在图示的坐标系中，单位质量流体所受到的质量力可表示为X=Y=0；Z=?g，?1・ z0 o z1 2・ z p0 代入（2－5），可得dp=?ρgdzz2 y 或dp+ρgdz=0。
x 对均质流体，密度ρ为常数，则有d(p+ρgz)=0，图2－4 重力作用下流体的平衡所以有p+ρgz=c。
（2－7）式中c为积分常数。
两端同除以ρg则有 z+p=c。
（2－8a）ρg对如图2－4所示的静止流体中的任意两点，上式可写成z1?p1p=z2?2。
（2－8b）ρgρg式（2－8）称为静力学基本方程式。
其适用条件是：重力作用下静止的均质流体。
对于分装在互不相同的两个容器内的流体或装在同一容器中的不同密度的两种流体之间，流体静力学基本方程式不成立。
四、静力学基本方程式的意义1.几何意义在一个容器侧壁上打一个小孔，接上与大气相通的玻璃管，这样就形成一根测压管。
如果容器中装的是静止流体，液面为大气压，则测压管内液面与容器内液面是齐平的，如图 2－5所示。
pa p1?p1ρgp0> pa ・1 ・1 ?p2ρg ρgp2ρg z1 2・ z2 z2・ z2 0 图2－5 敞口容器中的水头0 0 图2－6密闭容器中的水头从中可以看出，则测压管到基准面高度由z和p/ρg组成，z表示该点位置到基准面的高度，p/ρg表示该点压力折算的液柱高度。
在流体力学中，约定俗成地将高度称为“水头”，z称为位置水头，p/ρg称为压力水头，而z＋p/ρg称为测压管水头。
因此，静力学基本方程的几何意义是：静止流体中测压管水头为常数。
如果容器内液面压力p0大于或小于大气压pa，则测压管液面会高于或低于容器液面，但不同点的测压管水头仍是常数，如图2－6所示。
2.物理意义质量为m的流体处在z高度时，所具有的位置势能为mgz，那么单位重力流体所具有的位置势能为mgz=z。
mg因此，流体力学中也将z称为比位能。
力学中能够相加的两项应该具有相同的物理意义，所以p/ρg也应是单位重量流体所具有的某种能量。
压力同重力一样，也具有潜在的做功能力。
如果流体中某点的压力为p，在该处接测压管后，在压力作用下液面会上升高度p/ρg，压力势能变为位置势能。
因此，p/ρg代表单位重力流体所具有的压力势能，简称比压能。
（删除红字部分的内容）对于单位重力的流体来说，比位能与比压能之和叫做静止流体的比势能或总比能。
因此，流体静力学基本方程的物理意义是：静止流体中总比能为常数。
感谢您的阅读，祝您生活愉快。
