双代号网络图

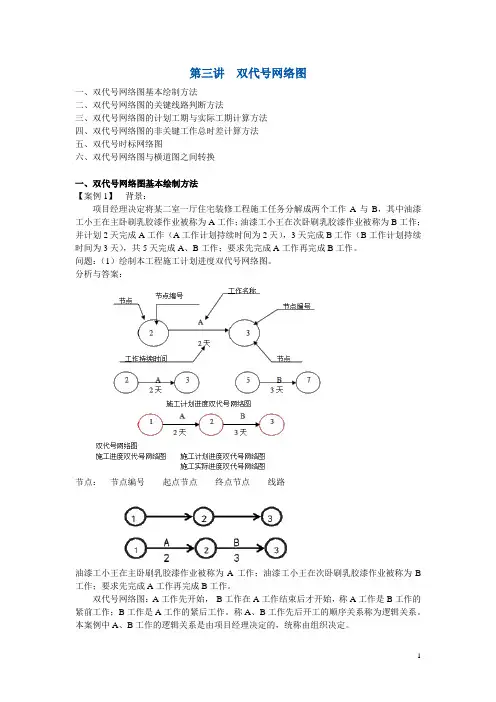
第三讲双代号网络图一、双代号网络图基本绘制方法二、双代号网络图的关键线路判断方法三、双代号网络图的计划工期与实际工期计算方法四、双代号网络图的非关键工作总时差计算方法五、双代号时标网络图六、双代号网络图与横道图之间转换一、双代号网络图基本绘制方法【案例1】背景：项目经理决定将某二室一厅住宅装修工程施工任务分解成两个工作A与B，其中油漆工小王在主卧刷乳胶漆作业被称为A工作；油漆工小王在次卧刷乳胶漆作业被称为B工作；并计划2天完成A工作（A工作计划持续时间为2天），3天完成B工作（B工作计划持续时间为3天），共5天完成A、B工作；要求先完成A工作再完成B工作。

问题：（1）绘制本工程施工计划进度双代号网络图。

分析与答案：节点：节点编号起点节点终点节点线路油漆工小王在主卧刷乳胶漆作业被称为A工作；油漆工小王在次卧刷乳胶漆作业被称为B 工作；要求先完成A工作再完成B工作。

双代号网络图：A工作先开始，B工作在A工作结束后才开始，称A工作是B工作的紧前工作；B工作是A工作的紧后工作。

称A、B工作先后开工的顺序关系称为逻辑关系。

本案例中A、B工作的逻辑关系是由项目经理决定的，统称由组织决定。

如需要表达A工作是B、C工作的紧前工作；B、C工作是A工作的紧后工作，则：如需要表达A、B工作是C工作的紧前工作；C工作是A 、B工作的紧后工作。

则：【案例2】背景项目经理决定将某二室一厅住宅装修工程施工任务分解成两个工作A与B，木工小李在主卧钉地龙骨施工作业被称为A工作；木工小李在主卧铺木地板施工作业被称为B工作，要求5天完成A、B工作，其中A工作计划持续时间是2天，B工作计划持续时间是3天。

问题:（1）绘制本工程施工计划进度双代号网络图。

分析与答案：A工作是B工作的紧前工作；B工作是A工作的紧后工作。

A、B工作先后开工的顺序关系称为逻辑关系。

本案例中A、B工作的逻辑关系是由工艺决定的。

根据案例1、案例2可以得出结论：A、B工作的逻辑关系，或者是由组织决定的；或者是由工艺决定的。

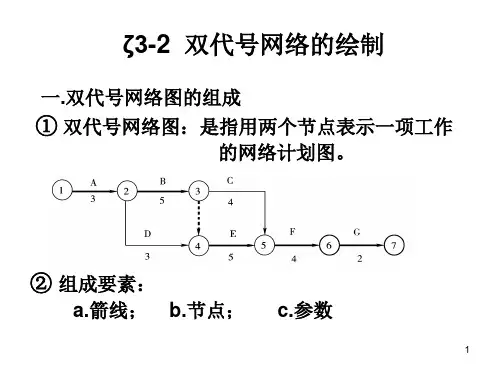
双代号网络图总结
概念：
1、ESi-j最早开始时间：所有紧前工作都完成后，本工作能开始的最早时间
2、EFi-j最早完成时间：所有紧前工作都完成前提下，本工作能完成的最早时间
3、LSi-j最迟开始时间：不影响整个任务的前提下，工作必须开始的最迟时间
4、LFi-j最迟完成时间：不影响整个工作前提下，完成工作的最迟时间
5、TFi-j总时差：不影响总工期的前提下，本工作可利用的机动时间（工期索赔看此条是否成立）
6、FFi-j自由时差：不影响今后工作最早开始时间的前提下，本工作可以利用的机动时间
7、D工作持续时间
计算规则：
1、ES计算：自起点至终点计算，第一项工作ES为0，中间工作为紧前工作EF的最大值
2、EF计算：EF=ES+D
3、LS计算：自终点至起点计算，以终点为结点的工作LS=LF-D
4、LF计算：自终点至起点计算，先算LF=TP=LS+D
5、TF计算：=LS-ES=LF-EF
6、FF计算：自终点向起点计算，以终点为结点的工作=TP-EF，其他LF=紧后工作LS的最小值。

双代号网络图计算
i--工作开始
j--工作结束
ES--最早开始时间：取i之前的各个工作EF的最大值
EF--最早结束时间：ES+D
（持续时间）
LS--最晚开始时间：LF-D
LF--最晚结束时间：取j之后的各个工作LS的最小值
TF--总时差:ES-LS
-EF
FF--自由时差:ES
(后一项工作)
总时差最小的工作为关键工作，全部由关键工作组成的线路为关键线路，关键线路是总的持续时间最长的线路。

涉及到进度控制问题，即需要调整工期时，赶工费低的工作优先压缩工作时间。

以下内容将有助于理解：
怎样理解虚箭头：
当两项工作（图(a)中A和B）的代号相同时，
使用虚工作加以区分。

由此来理解逻辑关系:
规律是：
正推求ES、EF，取紧前工作中的最大值；反推求LS、LF，取紧后工作中的最小值。

双代号网络图绘制方法双代号网络图（bipartite graph），也被称为二分图或二部图，是一种特殊的网络图。

它的节点可以分为两个不相交的集合，两个集合内的节点之间没有连接，而两个集合之间的节点之间有连接。

在双代号网络图中，用边表示两个集合之间的连接关系。

绘制双代号网络图的方法可以分为以下几个步骤：1. 确定要绘制的双代号网络图的节点。

首先，确定两个集合的节点数量，假设集合A的节点数量为m，集合B的节点数量为n。

将集合A的节点标记为A1、A2、...、Am，将集合B的节点标记为B1、B2、...、Bn。

2. 确定节点之间的连接关系。

根据实际情况，确定哪些集合A中的节点与集合B中的节点之间存在连接关系。

将连接关系用边表示，可以用直线或曲线表示，一般用直线表示。

连接关系可以是一个集合A中的节点与一个集合B中的节点之间的连接，也可以是一个集合A中的节点与多个集合B中的节点之间的连接，同样也可以是一个集合B中的节点与多个集合A中的节点之间的连接。

3. 绘制节点和连接关系。

将节点按照规定的数量和标记绘制在纸上或绘图软件中。

节点可以用圆形或方形表示，并在节点上标记节点的标签。

在节点之间用直线表示连接关系，将边绘制在相应的节点之间。

可以使用不同的颜色或线型表示不同的连接关系，以区分不同的边。

4. 调整布局和位置。

根据需要，调整节点和连接关系的位置和布局。

可以通过拖动节点和边的位置来实现。

调整布局和位置的目标是使得网络图更加清晰和易读，边的交叉尽量减少。

5. 添加辅助元素。

根据需要，可以添加辅助元素来增强网络图的表达能力和可读性。

辅助元素可以包括节点的颜色、大小、标签的显示方式等。

可以添加文本标签来说明节点或边的含义。

还可以添加图例和标题来说明图的含义和目的。

绘制双代号网络图的关键是确定节点和连接关系，以及调整布局和位置。

对于较大的网络图，可能需要使用专业的绘图软件来绘制，以便更好地管理和调整元素。

在绘制过程中，要注意边的交叉尽量减少，节点和边的位置要符合逻辑和布局美观的要求。

双代号网络图绘制例题详解双代号网络图是一种用于描述和分析复杂系统的工具，它可以帮助我们理清系统中各个因素之间的关系和影响，从而更好地进行规划和决策。

在本文中，我们将通过一个例题详细解释如何绘制双代号网络图，并对其进行分析和解释。

例题描述：某公司计划开展一个新产品的研发项目，该项目需要进行市场调研、技术开发、生产试验和市场推广等工作。

为了更好地组织和管理这个项目，公司决定使用双代号网络图来描述和分析项目的关键活动和其之间的关系。

现在，请你根据以下信息绘制该项目的双代号网络图，并分析关键路径和关键活动。

1. 市场调研需要2个月时间，完成后可以开始技术开发；2. 技术开发需要3个月时间，完成后可以进行生产试验；3. 生产试验需要1个月时间，完成后可以进行市场推广；4. 市场推广需要2个月时间，完成后项目结束。

解题步骤：1. 确定活动和活动之间的关系。

首先，我们需要确定该项目的关键活动和它们之间的先后关系。

根据题目描述，我们可以得出以下关键活动和其之间的关系：市场调研→技术开发。

技术开发→生产试验。

生产试验→市场推广。

市场推广→项目结束。

2. 绘制双代号网络图。

根据上述关键活动和其之间的关系，我们可以绘制出该项目的双代号网络图。

在双代号网络图中，活动用圆圈表示，活动之间的关系用箭头表示。

具体绘制过程如下：首先，在纸上绘制一个大圆圈，代表整个项目；然后，在大圆圈内部依次绘制代表各个活动的小圆圈，并用箭头连接它们，表示活动之间的关系；最后，在箭头上标注活动所需的时间。

3. 分析关键路径和关键活动。

在绘制完双代号网络图后，我们可以通过分析图中的路径和活动来确定项目的关键路径和关键活动。

关键路径是指项目中最长的路径，它决定了项目的最短完成时间；而关键活动是指在关键路径上的活动，它们的延误会直接影响整个项目的完成时间。

在该例题中，我们可以通过双代号网络图来确定关键路径和关键活动：首先，我们可以计算出各个路径的长度，从而确定最长的路径，即为关键路径；然后，我们可以找出关键路径上的活动，即为关键活动。