2018年普通高等学校招生全国统一考试数学试题理(全国卷2,无答案)

2018年普通高等学校招生全国统一考试理科综合能力测试（Ⅱ）二、选择题：本题共8小题，每小题6分，共48分。

在每小题给出的四个选项中，第14~18题只有一项符合题目要求，第19~21题有多项符合题目要求。

全部选对的得6分，选对但不全的得3分，有选错的得0分。

学科&网14．如图，某同学用绳子拉动木箱，使它从静止开始沿粗糙水平路面运动至具有某一速度，木箱获得的动能一定A ．小于拉力所做的功B ．等于拉力所做的功C ．等于克服摩擦力所做的功D ．大于克服摩擦力所做的功15．高空坠物极易对行人造成伤害。

若一个50 g 的鸡蛋从一居民楼的25层坠下，与地面的撞击时间约为2 ms ，则该鸡蛋对地面产生的冲击力约为 A ．10 NB ．102 NC ．103 ND ．104 N16．2018年2月，我国500 m 口径射电望远镜（天眼）发现毫秒脉冲星“J0318+0253”，其自转周期T =5.19 ms ，假设星体为质量均匀分布的球体，已知万有引力常量为11226.6710N m /kg -⨯⋅。

以周期T 稳定自转的星体的密度最小值约为 A ．93510kg /m ⨯ B ．123510kg /m ⨯C ．153510kg /m ⨯D ．183510kg /m ⨯17．用波长为300 nm 的光照射锌板，电子逸出锌板表面的最大初动能为1.28⨯10-19 J 。

已知普朗克常量为6.63⨯10-34J·s ，真空中的光速为3.00⨯108 m·s -1，能使锌产生光电效应的单色光的最低频率约为A ．1⨯1014 HzB ．8⨯1014 HzC ．2⨯1015 HzD ．8⨯1015 Hz18．如图，在同一平面内有两根平行长导轨，导轨间存在依次相邻的矩形匀强磁场区域，区域宽度均为l ,磁感应强度大小相等、方向交替向上向下。

一边长为32l 的正方形金属线框在导轨上向左匀速运动，线框中感应电流i 随时间t 变化的正确图线可能是19．甲、乙两汽车同一条平直公路上同向运动，其速度—时间图像分别如图中甲、乙两条曲线所示。

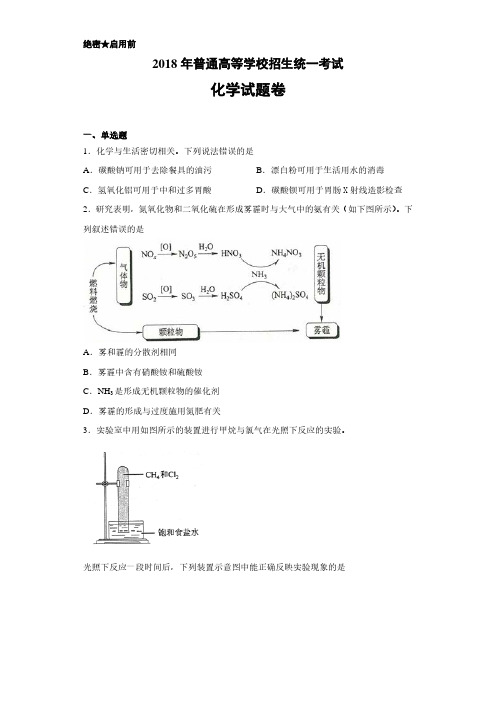
2018年普通高等学校招生全国统一考试（浙江卷）数学（理科）一．选择题：本大题共10小题，每小题5分，共50分. 在每小题给出的四个选项中，只有一项是符合题目要求的.（1）设全集{}2|≥∈=x N x U ，集合{}5|2≥∈=x N x A ，则=A C U （ ）A. ∅B. }2{C. }5{D. }5,2{（2）已知i 是虚数单位，R b a ∈,,则“1==b a ”是“i bi a 2)(2=+”的（ ）A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件（3）某几何体的三视图（单位：cm ）如图所示，则此几何体的表面积是A. 902cmB. 1292cmC. 1322cmD. 1382cm4.为了得到函数x x y 3cos 3sin +=的图像，可以将函数x y 3sin 2=的图像（ ）A.向右平移4π个单位B.向左平移4π个单位 C.向右平移12π个单位 D.向左平移12π个单位 5.在46)1()1(y x ++的展开式中，记n m y x 项的系数为),(n m f ，则=+++)3,0(2,1()1,2()0,3(f f f f ）（ ）A.45B.60C.120D. 2106.已知函数则且,3)3()2()1(0,)(23≤-=-=-≤+++=f f f c bx ax x x f （ ）A.3≤cB.63≤<cC.96≤<cD. 9>c7.在同一直角坐标系中，函数x x g x x x f a a log )(),0()(=≥=的图像可能是（ ）。

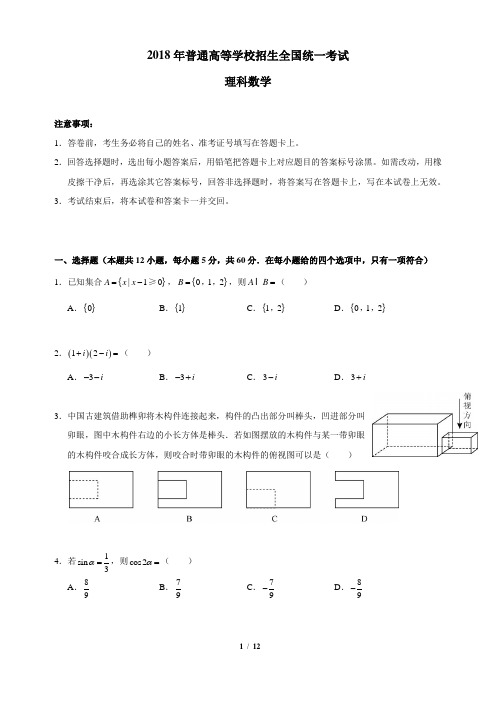
2018年普通高等学校招生全国统一考试理科数学注意事项：1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号，回答非选择题时，将答案写在答题卡上，写在本试卷上无效。

3．考试结束后，将本试卷和答案卡一并交回。

一、选择题（本题共12小题，每小题5分，共60分．在每小题给的四个选项中，只有一项符合）1．已知集合{}|10A x x =-≥，{}012B =，，，则A B =（ ）A ．{}0B ．{}1C ．{}12，D ．{}012，，2．()()12i i +-=（ ） A ．3i --B ．3i -+C ．3i -D ．3i +3．中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫棒头，凹进部分叫卯眼，图中木构件右边的小长方体是棒头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是（ ）4．若1sin 3α=，则cos 2α=（ ）A ．89B ．79C ．79-D ．89-5．522x x ⎛⎫+ ⎪⎝⎭的展开式中4x 的系数为（ ）A ．10B ．20C ．40D ．806．直线20x y ++=分别与x 轴，y 轴交于A ，B 两点，点P 在圆()2222x y -+=上，则ABP ∆面积的取值范围是（ ）A ．[]26，B ．[]48，C ．D ．⎡⎣7．函数422y x x =-++的图像大致为（ ）8．某群体中的每位成品使用移动支付的概率都为p ，各成员的支付方式相互独立，设X 为该群体的10位成员中使用移动支付的人数， 2.4DX =，()()46P X P X =<=，则p =（ ） A ．0.7B ．0.6C ．0.4D ．0.39．ABC △的内角A B C ，，的对边分别为a ，b ，c ，若ABC ∆的面积为2224a b c +-，则C =（ ）A ．2πB ．3πC ．4πD ．6π10．设A B C D ，，，是同一个半径为4的球的球面上四点，ABC ∆为等边三角形且其面积为三棱锥D ABC -体积的最大值为（ ）A ．B ．C ．D ．11．设12F F ，是双曲线22221x y C a b-=：（00a b >>，）的左，右焦点，O 是坐标原点．过2F 作C 的一条渐近线的垂线，垂足为P ．若1PF OP ，则C 的离心率为（ ）AB ．2CD12．设0.2log 0.3a =，2log 0.3b =，则（ ）A ．0a b ab +<<B ．0ab a b <+<C ．0a b ab +<<D ．0ab a b <<+二、填空题（本题共4小题，每小题5分，共20分）13．已知向量()=1,2a ，()=2,2-b ，()=1,λc ．若()2∥c a +b ，则λ=________．14．曲线()1x y ax e =+在点()01，处的切线的斜率为2-，则a =________．15．函数()cos 36f x x π⎛⎫=+ ⎪⎝⎭在[]0π，的零点个数为________．16．已知点()11M -，和抛物线24C y x =：，过C 的焦点且斜率为k 的直线与C 交于A ，B 两点．若90AMB =︒∠，则k =________．三、解答题（共70分，解答应写出文字说明、证明过程或演算步骤，第17~31题为必考题，每个试题考生都必须作答，第22、23题为选考题，考生根据要求作答．） （一）必考题：共60分。

绝密★启用前2018年普通高等学校招生全国统一考试理科数学本试卷共23题，共150分，共5页，考试结束后，将本试卷和答题卡一并交回。

注意事项：1.答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码准确粘贴在条形码区域内。

2.选择题必须使用2B 铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。

3.请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试卷上答题无效。

4.作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

5.保持卡面清洁，不要折叠、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题（本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1.1212ii+=- 43. 55A i -- 43. 55B i -+ 34. 55C i -- 34. 55D i -+2.已知集合(){}22,3,,A x y x y x Z y Z =+≤∈∈,则A 中元素的个数为. 9A. 8B . 5C . 4D3.函数2()x xe ef x x--=的图象大致为4.已知向量,a b 满足1,1a a b =⋅=-,则()2a a b ⋅-=. 4A . 3B . 2C . 0D5.双曲线()222210,0x y a b a b-=>>的离心率为3,则其渐近线方程为. 2A y x =± . 3B y x =± 2. 2C y x =± 3. 2D y x =±6.在ABC ∆中,5cos ,1,5,25C BC AC ===则AB = . 42A . 30B . 29C. 25D 7.为计算11111123499100S =-+-++-,设计了右侧的程序框图,则在空白框中应填入. 1A i i =+ . 2B i i =+ . 3C i i =+ . 4D i i =+8.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果,哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30=7+23. 在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是1.12A 1. 14B 1. 15C 1. 18D 9.在长方体1111ABCD A B C D -中,11,3,AB BC AA ===则异面直线1AD 与1DB 所成角的余弦值为1. 5A5. 6B 5. 5C 2.2D 10.若()cos sin f x x x =-在[],a a -是减函数,则a 的最大值是.4A π.2B π3.4C π .D π-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------姓名________________ 准考证号_____________11.已知()f x 是定义域为(),-∞+∞的奇函数,满足(1)(1)f x f x -=+.若(1)2f =,则(1)(2)(3)(50)f f f f ++++=. 50A -. 0B . 2C . 50D12.已知12,F F 是椭圆2222:1(0)x y C a b a b+=>>的左、右焦点,A 是C 的左顶点,点P 在过A且斜率为6的直线上,12PF F ∆为等腰三角形,12120F F P ∠=,则C 的离心率为2. 3A 1. 2B 1. 3C 1. 4D二、填空题（本题共4小题，每小题5分，共20分）13.曲线2ln(1)y x =+在点()0,0处的切线方程为_____________.14.若,x y 满足约束条件250,230,50,x y x y x +-≥⎧⎪-+≥⎨⎪-≤⎩则z x y =+的最大值为________.15.已知sin cos 1,cos sin 0αβαβ+=+=,则()sin αβ+=__________.16.已知圆锥的顶点为S ,母线SA 、SB 所成角的余弦值为78,SA 与圆锥底面所成角为45.若SAB ∆的面积为则该圆锥的侧面积为__________.三、解答题（共70分。

2018年普通高等学校招生全国统一考试(新课标Ⅰ卷)一、选择题1．设，则（）A．0 B．C．D．2．已知集合，则（）A．B．C．D．3．某地区经过一年的新农村建设，农村的经济收入增加了一倍．实现翻番．为更好地了解该地区农村的经济收入变化情况，统计了该地区新农村建设前后农村的经济收入构成比例．得到如下饼图：则下面结论中不正确的是（）A．新农村建设后，种植收入减少B．新农村建设后，其他收入增加了一倍以上C．新农村建设后，养殖收入增加了一倍D．新农村建设后，养殖收入与第三产业收入的总和超过了经济收入的一半4．记为等差数列的前项和．若，，则（）A．B．C．D．125．设函数．若为奇函数，则曲线在点处的切线方程为（）A．B．C．D．6．在中，为边上的中线，为的中点，则（）A．B．C．D．7．某圆柱的高为2，底面周长为16，其三视图如右图所示，圆柱表面上的点在正视图上的对应点为，圆柱表面上的点在左视图上的对应点为，则在此圆柱侧面上，从到的路径中，最短路径的长度为（）A．B．C．D．28．设抛物线的焦点为，过点且斜率为的直线与交于，两点，则（）A．5 B．6 C．7 D．89．已知函数，，若存在2个零点，则的取值范围是（）A．B．C．D．10．下图来自古希腊数学家希波克拉底所研究的几何图形，此图由三个半圆构成，三个半圆的直径分别为直角三角形的斜边，直角边，，的三边所围成的区域记为Ⅰ，黑色部分记为Ⅱ，其余部分记为Ⅲ，在整个图形中随机取一点，此点取自Ⅰ，Ⅱ，Ⅲ的概率分别记为，，，则（）A．B．C．D．11．已知双曲线，为坐标原点，为的右焦点，过的直线与的两条渐近线的交点分别为，．若为直角三角形，则（）A．B．3 C．D．412．已知正方体的棱长为1，每条棱所在直线与平面所成的角都相等，则截此正方体所得截面面积的最大值为（）A．B．C．D．二、填空题（本题共4小题，每小题5分，共20分）13．若满足约束条件，则的最大值为________．14．记为数列的前项和．若，则________．15．从2位女生，4位男生中选3人参加科技比赛，且至少有1位女生入选，则不同的选法共有________种．（用数字填写答案）16．已知函数，则的最小值是________．三、解答题（共70分。

2018年成人高等学校招生全国统一考试专升本高等数学（二）本试卷分第Ⅰ卷（选择题）和第卷（非选择题）两部分，满分150分，考试时间120分.第Ⅰ卷(选择题，共40分)一、选择题(1~10小题，每小题4分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的)1. lim x→0xcosx =( )A. eB.2C. 1D. 02. 若y =1+cosx ,则dy = ( )A. (1+ sinx)dxB. (1−sinx)dxC. sinxdxD.−sinxdx3. 若函数f(x)=5x ，则f′(x)= ( )A. 5x−1B. x5x−1C. 5x ln5D.5x4. 曲线y =x 3+2x 在点(1,3)处的法线方程是 ( )A. 5x +y −8=0B. 5x −y −2=0C. x +5y −16=0D. x −5y +14=05. ∫12−xdx =( )A. ln |2−x|+CB. −ln |2−x|+CC.−1(2−x)2+C D. 1(2−x )2+C6. ∫f′(2x)dx = ( )A. 12f(2x)+CB. f(2x)+CC. 2f(2x)+CD. 12f(x)+C7. 若f(x)为连续的奇函数，则∫f(x)1−1dx = ( )A. 0B. 2C. 2f(−1)D. 2f(1)8. 若二元函数z =x 2y +3x +2y ，则ðz ðx=( )A. 2xy +3+2yB. xy +3+2yC. 2xy +3D. xy +39. 设区域D ={(x ，y)|0≤y ≤x 2,0≤x ≤1}，则D 绕x 轴旋转一周所得旋转体的体积为 ( )A. π5B. π3C. π2D. π10. 设A ，B 为两个随机事件，且相互独立，P(A)=0.6，P(B)=0.4，则P(A −B )=( )A. 0.24B. 0.36C. 0.4D. 0.6第Ⅱ卷(非选择题，共110分)二、填空题(11~20小题，每小题4分，共40分)11. 曲线y =x 3−6x 2+3x +4的拐点为 . 12. lim x→0(1−3x )1x = .13.若函数f(x)=x −arctanx ，则f′(x)= . 14. 若y =e 2x 则dy = . 15. 设f(x)=x 2x ,则f′(x)= . 16. ∫(2x +3)dx = . 17. ∫(x 5+x 2)1−1dx = . 18. ∫sin x 2π0dx = . 19. ∫e−x +∞0dx = .20. 若二元函数：z =x 2y 2，则ð2z ðxðy= .三、解答题(21~28题，共70分。

理科数学a 2b 2 1 a2 x 2 x准确粘贴在条 __ 卷__ _ __ __ __ 5.保持卡面清洁，不要折叠、不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

考 上--------------------本题共 12 小题，每小题 5 分，共 60 分．在每小题给出的四个选项中，只7.为计算 S 1 1__ 答A. 4B.3C.3 4 D. 3 4__ 5 5 i55i 5 5 i 5 5 i __ __ __ -------------------- ee x 2的图象大致为A.1-------------绝密 ★ 启用前2018 年普通高等学校招生全国统一考试在--------------------本试卷共 23 题，共 150 分，共 5 页，考试结束后，将本试卷和答题卡一并交回。

4.已知向量 a,b 满足 a 1,a b 1 ,则 a 2a bA. 4B. 3C. 2D. 0x 2 y 25.双曲线 0,b 0 的离心率为 3 ,则其渐近线方程为注意事项：1.答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码A. y 2xB. y 3xC.y 2D.y 3此--------------------形码区域内。

6.在 ABC 中, cos C 2 55 ,BC1,AC 5,则 AB =__3.请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效； 号 证 准__1 2i__名 A.9 B. 8 C. 5 D. 4姓 题2.选择题必须使用 2B 铅笔填涂；非选择题必须使用 0.5 毫米黑色字迹的签字笔书写， 字体工整、笔迹清楚。

--------------------在草稿纸、试卷上答题无效。

4.作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。

有一项是符合题目要求的．）__ 1. 1 2i-------------------- 3 42.已知集合 A x,y x 2 y 2 3,x Z ,y Z ,则 A 中元素的个数为x x3.函数 f(x)5B.4D.A .42B. 30 C . 29 D . 251 1 1 1234 99 100 ,设计了右侧的程序框图,则在空白框中应填入 A. i i 1B. i i 2C.i i 3D.i i 48.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果 ,哥德巴赫猜想是“每个大于 2 的偶数可以表示为两个素数的和”,如 30=7+23 . 在不超过 30 的素数中,随机选取两个不同的数,其和等于 30 的概率是1 1 112 B. 14 C. 15 D.18无--------------------9.在长方体 ABCD A B C D 中, AB BC 1,AA1 1 1 1成角的余弦值为1 3,则异面直线 AD 1 与 DB 1 所A. 15 6 C.5 5 D. 2210.若 f(x) cosx sinx 在 a,a 是减函数,则 a 的最大值是效----------------A.4 B.2 C.3理科数学试题 A 第 1 页（共 24 页）理科数学试题 A 第 2 页（共 24 页）6的直线上,PF F为等腰三角形,3B.8,SA与圆锥底面所成角为45.n 的通项公式；11.已知f(x)是定义域为,的奇函数,满足f(1x)f(1x).若f(1)2,则f(1)f(2)f(3)f(50)A.50B.0C.2D.50下图是某地区2000年至2016年环境基础设施投资额y(单位：亿元)的折线图.12.已知F,F是椭圆C:12x2y2a2b21(a b0)的左、右焦点,A是C的左顶点,点P在过A且斜率为312F F P120,则C的离心率为12A.212C.113D.4二、填空题（本题共4小题，每小题5分，共20分）13.曲线y2ln(x1)在点0,0处的切线方程为_____________.x2y50,14.若x,y满足约束条件x2y30,则z x y的最大值为________.x50,15.已知sin cos1,cos sin0,则sin__________.16.已知圆锥的顶点为S,母线SA、SB所成角的余弦值为7若SAB的面积为515,则该圆锥的侧面积为__________.三、解答题（共70分。