非线性整数规划的蚁群算法

蚁群算法的
蚁群算法是近几十年来智能计算领域中新兴的最重要的优化技
术之一，它被认为是能够模拟蚂蚁群体寻找最优解的算法，已经被广泛应用于工程中，包括机器的设计、航运系统的优化，和物流系统的规划等等代表众多应用。

蚁群算法是模拟蚂蚁群体搜索食物的行为，从而求解一个待求解的问题的优化技术，早在1995年的时候就已经被提出，在大规模问题下有很好的搜索性能。

蚁群算法通过模拟蚁群通过特定路径来搜索资源来求解优化问题，模拟理论上这是一个有效的优化算法，可以帮助系统找到最优解并获得最大回报。

蚁群算法的工作原理是通过模拟蚁群通过特定路径来搜索资源，每只蚂蚁经过一条路径时，就会根据路径的特性来选择继续前进的方向，而其他的蚂蚁也会根据当前的状态来决定自己前进的路径，从而形成一种合作的局部路径，一旦有蚂蚁发现有较好的路径就会被其他蚂蚁模仿，最终有效地把所有蚂蚁引导到最优解。

蚁群算法具有几个显著的优点，首先它所耗费的计算资源要比其他算法少得多，其次它的实施简单，能够快速的数据搜索，并且运行简单，容易理解，最后，它可以自我改进，也就是说，它能够实时地进行调整，以适应变化的环境。

虽然蚁群算法有许多优点，但它也有一些限制，首先，蚁群算法对全局最优解的搜索能力有限，其次，它容易陷入局部最优点，最后，它也存在一定的调参不利，对于参数的调整可能会导致算法效率的降
低。

总结而言，蚁群算法是一种有效的优化技术，使用它可以快速有效的搜索解决问题，在几乎所有的行业中都能取得较好的效果。

然而，它也需要注意参数的调整，以及全局最优解的搜索能力，才能发挥出最大的效力。

蚁群算法概述一、蚁群算法蚁群算法(ant colony optimization, ACO)，又称蚂蚁算法，是一种用来寻找最优解决方案的机率型技术。

它由Marco Dorigo于1992年在他的博士论文中引入，其灵感来源于蚂蚁在寻找食物过程中发现路径的行为。

蚂蚁在路径上前进时会根据前边走过的蚂蚁所留下的分泌物选择其要走的路径。

其选择一条路径的概率与该路径上分泌物的强度成正比。

因此，由大量蚂蚁组成的群体的集体行为实际上构成一种学习信息的正反馈现象：某一条路径走过的蚂蚁越多，后面的蚂蚁选择该路径的可能性就越大。

蚂蚁的个体间通过这种信息的交流寻求通向食物的最短路径。

蚁群算法就是根据这一特点，通过模仿蚂蚁的行为，从而实现寻优。

这种算法有别于传统编程模式，其优势在于，避免了冗长的编程和筹划，程序本身是基于一定规则的随机运行来寻找最佳配置。

也就是说，当程序最开始找到目标的时候，路径几乎不可能是最优的，甚至可能是包含了无数错误的选择而极度冗长的。

但是，程序可以通过蚂蚁寻找食物的时候的信息素原理，不断地去修正原来的路线，使整个路线越来越短，也就是说，程序执行的时间越长，所获得的路径就越可能接近最优路径。

这看起来很类似与我们所见的由无数例子进行归纳概括形成最佳路径的过程。

实际上好似是程序的一个自我学习的过程。

3、人工蚂蚁和真实蚂蚁的异同ACO是一种基于群体的、用于求解复杂优化问题的通用搜索技术。

与真实蚂蚁通过外激素的留存/跟随行为进行间接通讯相似，ACO中一群简单的人工蚂蚁（主体）通过信息素（一种分布式的数字信息，与真实蚂蚁释放的外激素相对应）进行间接通讯，并利用该信息和与问题相关的启发式信息逐步构造问题的解。

人工蚂蚁具有双重特性：一方面，他们是真实蚂蚁的抽象，具有真实蚂蚁的特性，另一方面，他们还有一些在真实蚂蚁中找不到的特性，这些新的特性，使人工蚂蚁在解决实际优化问题时，具有更好地搜索较好解的能力。

人工蚂蚁与真实蚂蚁的相同点为：1．都是一群相互协作的个体。

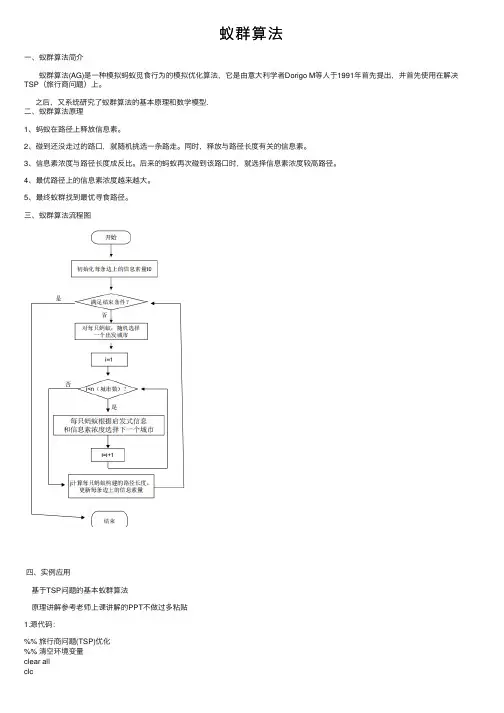
蚁群算法⼀、蚁群算法简介 蚁群算法(AG)是⼀种模拟蚂蚁觅⾷⾏为的模拟优化算法，它是由意⼤利学者Dorigo M等⼈于1991年⾸先提出，并⾸先使⽤在解决TSP（旅⾏商问题）上。

之后，⼜系统研究了蚁群算法的基本原理和数学模型.⼆、蚁群算法原理1、蚂蚁在路径上释放信息素。

2、碰到还没⾛过的路⼝，就随机挑选⼀条路⾛。

同时，释放与路径长度有关的信息素。

3、信息素浓度与路径长度成反⽐。

后来的蚂蚁再次碰到该路⼝时，就选择信息素浓度较⾼路径。

4、最优路径上的信息素浓度越来越⼤。

5、最终蚁群找到最优寻⾷路径。

三、蚁群算法流程图四、实例应⽤基于TSP问题的基本蚁群算法原理讲解参考⽼师上课讲解的PPT不做过多粘贴1.源代码：%% 旅⾏商问题(TSP)优化%% 清空环境变量clear allclc%% 导⼊数据citys = ceil(rand(50,2)*50000)%load newcitys.mat%% 计算城市间相互距离fprintf('Computing Distance Matrix... \n');n = size(citys,1);D = zeros(n,n);for i = 1:nfor j = 1:nif i ~= jD(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2));elseD(i,j) = 1e-4;endendend%% 初始化参数fprintf('Initializing Parameters... \n');m = 50; % 蚂蚁数量alpha = 1; % 信息素重要程度因⼦beta = 5; % 启发函数重要程度因⼦rho = 0.05; % 信息素挥发因⼦Q = 1; % 常系数Eta = 1./D; % 启发函数Tau = ones(n,n); % 信息素矩阵Table = zeros(m,n); % 路径记录表iter = 1; % 迭代次数初值iter_max = 150; % 最⼤迭代次数Route_best = zeros(iter_max,n); % 各代最佳路径Length_best = zeros(iter_max,1); % 各代最佳路径的长度Length_ave = zeros(iter_max,1); % 各代路径的平均长度%% 迭代寻找最佳路径figure;while iter <= iter_maxfprintf('迭代第%d次\n',iter);% 随机产⽣各个蚂蚁的起点城市start = zeros(m,1);for i = 1:mtemp = randperm(n);start(i) = temp(1);endTable(:,1) = start;% 构建解空间citys_index = 1:n;% 逐个蚂蚁路径选择for i = 1:m% 逐个城市路径选择for j = 2:ntabu = Table(i,1:(j - 1)); % 已访问的城市集合(禁忌表)allow_index = ~ismember(citys_index,tabu);allow = citys_index(allow_index); % 待访问的城市集合P = allow;% 计算城市间转移概率for k = 1:length(allow)P(k) = Tau(tabu(end),allow(k))^alpha * Eta(tabu(end),allow(k))^beta; endP = P/sum(P);% 轮盘赌法选择下⼀个访问城市Pc = cumsum(P);target_index = find(Pc >= rand);target = allow(target_index(1));Table(i,j) = target;endend% 计算各个蚂蚁的路径距离Length = zeros(m,1);for i = 1:mRoute = Table(i,:);for j = 1:(n - 1)Length(i) = Length(i) + D(Route(j),Route(j + 1));endLength(i) = Length(i) + D(Route(n),Route(1));end% 计算最短路径距离及平均距离if iter == 1[min_Length,min_index] = min(Length);Length_best(iter) = min_Length;Length_ave(iter) = mean(Length);Route_best(iter,:) = Table(min_index,:);else[min_Length,min_index] = min(Length);Length_best(iter) = min(Length_best(iter - 1),min_Length);Length_ave(iter) = mean(Length);if Length_best(iter) == min_LengthRoute_best(iter,:) = Table(min_index,:);elseRoute_best(iter,:) = Route_best((iter-1),:);endend% 更新信息素Delta_Tau = zeros(n,n);% 逐个蚂蚁计算for i = 1:m% 逐个城市计算for j = 1:(n - 1)Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i); endDelta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i); endTau = (1-rho) * Tau + Delta_Tau;% 迭代次数加1，清空路径记录表% figure;%最佳路径的迭代变化过程[Shortest_Length,index] = min(Length_best(1:iter));Shortest_Route = Route_best(index,:);plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...[citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');pause(0.3);iter = iter + 1;Table = zeros(m,n);% endend%% 结果显⽰[Shortest_Length,index] = min(Length_best);Shortest_Route = Route_best(index,:);disp(['最短距离:' num2str(Shortest_Length)]);disp(['最短路径:' num2str([Shortest_Route Shortest_Route(1)])]);%% 绘图figure(1)plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...[citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');grid onfor i = 1:size(citys,1)text(citys(i,1),citys(i,2),[' ' num2str(i)]);endtext(citys(Shortest_Route(1),1),citys(Shortest_Route(1),2),' 起点');text(citys(Shortest_Route(end),1),citys(Shortest_Route(end),2),' 终点');xlabel('城市位置横坐标')ylabel('城市位置纵坐标')title(['蚁群算法优化路径(最短距离:' num2str(Shortest_Length) ')'])figure(2)plot(1:iter_max,Length_best,'b',1:iter_max,Length_ave,'r:')legend('最短距离','平均距离')xlabel('迭代次数')ylabel('距离')title('各代最短距离与平均距离对⽐')运⾏结果：利⽤函数citys = ceil(rand(50,2)*50000) 随机产⽣五⼗个城市坐标2.研究信息素重要程度因⼦alpha, 启发函数重要程度因⼦beta,信息素挥发因⼦rho对结果的影响为了保证变量唯⼀我重新设置五⼗个城市信息进⾏实验在原来设值运⾏结果：实验结果可知当迭代到120次趋于稳定2.1 alpha值对实验结果影响（1）当alpha=4时运⾏结果实验结果可知当迭代到48次左右趋于稳定（2）当alpha=8时运⾏结果：有图可知迭代40次左右趋于稳定，搜索性较⼩（3）当alpha= 0.5运⾏结果：有图可知迭代到140次左右趋于稳定（4）当alpha=0.2时运⾏结果：结果趋于110次左右稳定所以如果信息素因⼦值设置过⼤，则容易使随机搜索性减弱；其值过⼩容易过早陷⼊局部最优2.2 beta值对实验影响（1）当 beta=8时运⾏结果结果迭代75次左右趋于稳定（2）当 beta=1时运⾏结果：结果迭代130次左右趋于稳定所以beta如果值设置过⼤，虽然收敛速度加快，但是易陷⼊局部最优；其值过⼩，蚁群易陷⼊纯粹的随机搜索，很难找到最优解2.3 rho值对实验结果影响(1)当rho=3时运⾏结果：结果迭代75次左右趋于稳定（2）当rho=0.05运⾏结果：结果迭代125次左右趋于稳定所以如果rho取值过⼤时，容易影响随机性和全局最优性；反之，收敛速度降低总结：蚁群算法对于参数的敏感程度较⾼，参数设置的好，算法的结果也就好，参数设置的不好则运⾏结果也就不好，所以通常得到的只是局部最优解。

蚁群算法求函数最大值的程序蚁群算法是一种模拟蚂蚁觅食行为的启发式算法，常用于求解函数最大值问题。

本文将详细介绍蚁群算法的原理和实现步骤，以及一个示例程序。

1.蚁群算法原理蚁群算法基于蚁群觅食行为中的信息素交流和随机跳跃，通过多个智能体（模拟蚂蚁）在解空间中的和信息传递，逐步寻找到函数的最大值。

具体而言，蚁群算法包含以下关键要素：-蚂蚁：代表着算法解空间的个体，通过在解空间中的移动来探索新的解。

-信息素：用于模拟蚂蚁之间的信息传递和集体合作，蚂蚁在移动过程中会根据信息素浓度进行选择。

-目标函数：蚁群算法通过目标函数来评估到的解的优劣，从而引导蚂蚁进行。

-路径选择规则：蚂蚁在移动过程中根据一定的规则选择下一步的移动路径。

信息素浓度、目标函数值等因素都可以作为路径选择规则的参考。

-信息素更新规则：当蚂蚁选择了条路径后，会根据该路径的质量（目标函数值等）来更新路径上的信息素浓度。

2.蚁群算法步骤蚁群算法的一般步骤如下：1.初始化蚂蚁群和信息素矩阵。

2.对每只蚂蚁，计算其适应度并选择下一步的移动方向。

3.更新每只蚂蚁的位置，并根据移动结果更新信息素矩阵。

4.检查是否满足停止条件，如果满足则输出最优解，否则返回步骤23.蚁群算法示例程序下面是一个求解函数f(x)=x^2在[-10,10]范围内的最大值的蚁群算法示例程序。

```pythonimport randomimport math#目标函数def target_function(x):return x ** 2#初始化蚂蚁群ant_count = 100ants = [random.uniform(-10, 10) for _ in range(ant_count)] #初始化信息素矩阵pheromones = [1 for _ in range(ant_count)]#蚁群算法参数max_iter = 100 # 最大迭代次数alpha = 1 # 信息素重要程度因子beta = 1 # 启发因子rho = 0.1 # 信息素挥发因子Q=1#信息素强度best_solution = None#迭代优化过程for iter in range(max_iter):#计算每只蚂蚁的适应度并选择下一步移动方向for i in range(ant_count):ant = ants[i]fitness = target_function(ant)#选择下一步移动方向if random.random( < pheromones[i]:ant += random.uniform(-1, 1) # 信息素浓度高的蚂蚁随机选择一个方向else:ant += random.uniform(-0.1, 0.1) # 信息素浓度低的蚂蚁随机选择一个方向ants[i] = ant#更新最优解if best_solution is None or target_function(ant) >target_function(best_solution):best_solution = ant#更新信息素矩阵for i in range(ant_count):#蚂蚁越接近最优解，释放的信息素越多pheromones[i] = (1 - rho) * pheromones[i] + Q *(target_function(ants[i]) / target_function(best_solution)) #输出最优解print("最大值点坐标为：", best_solution)print("最大值为：", target_function(best_solution))```4.程序解释该示例程序使用Python编写，实现了蚁群算法来求解函数f(x)=x^2在[-10, 10]范围内的最大值。

蚁群算法蚁群算法⽬录1 蚁群算法基本思想 (1)1.1蚁群算法简介 (1)1.2蚁群⾏为分析 (1)1.3蚁群算法解决优化问题的基本思想 (2)1.4蚁群算法的特点 (2)2 蚁群算法解决TSP问题 (3)2.1关于TSP (3)2.2蚁群算法解决TSP问题基本原理 (3)2.3蚁群算法解决TSP问题基本步骤 (5)3 案例 (6)3.1问题描述 (6)3.2解题思路及步骤 (6)3.3MATLB程序实现 (7)3.1.1 清空环境 (7)3.2.2 导⼊数据 (7)3.3.3 计算城市间相互距离 (7)3.3.4 初始化参数 (7)3.3.5 迭代寻找最佳路径 (7)3.3.6 结果显⽰ (7)3.3.7 绘图 (7)1 蚁群算法基本思想1.1 蚁群算法简介蚁群算法（ant colony algrothrim，ACA）是由意⼤利学者多⾥⼽（Dorigo M）、马聂佐（Maniezzo V ）等⼈于20世纪90初从⽣物进化的机制中受到启发，通过模拟⾃然界蚂蚁搜索路径的⾏为，提出来的⼀种新型的模拟进化算法。

该算法⽤蚁群在搜索⾷物源的过程中所体现出来的寻优能⼒来解决⼀些系统优化中的困难问题，其算法的基本思想是模仿蚂蚁依赖信息素，通过蚂蚁间正反馈的⽅法来引导每个蚂蚁的⾏动。

蚁群算法能够被⽤于解决⼤多数优化问题或者能够转化为优化求解的问题，现在其应⽤领域已扩展到多⽬标优化、数据分类、数据聚类、模式识别、电信QoS管理、⽣物系统建模、流程规划、信号处理、机器⼈控制、决策⽀持以及仿真和系统辩识等⽅⾯。

蚁群算法是群智能理论研究领域的⼀种主要算法。

1.2 蚁群⾏为分析Bm=20t=0 m=10m=10t=11.3 蚁群算法解决优化问题的基本思想⽤蚂蚁的⾏⾛路径表⽰待优化问题的可⾏解，整个蚂蚁群体的所有路径构成待优化问题的解空间。

路径较短的蚂蚁释放的信息量较多，随着时间的推进，较短路径上积累的信息浓度逐渐增⾼，选择该路径的蚂蚁个数愈来愈多。

蚁群算法公式蚁群算法(AntColonyAlgorithm)是一种基于自然生态的数学优化模型，是一个迭代的搜索算法，用来解决动态规划问题。

这种算法是在蚂蚁群体行为的理论的基础上发展出来的，通过模拟蚂蚁如何寻找最佳的路径来寻找最优解。

它是一种用于解决复杂优化问题的自然计算算法，它可以分析解决复杂系统中大量变量和限制条件所建立的非线性优化问题。

蚁群算法是一种基于概率的搜索算法，它采用“相互学习”的方式，通过种群间的信息共享，形成一个多维度的相互关联的搜索空间。

由于蚁群算法可以获得更多关于搜索空间的信息，它比传统的优化算法更有效地搜索最优解。

蚁群算法是一种非治疗性的优化算法，它可以用来解决多种复杂的优化问题，如全局优化、组合优化、最佳化框架优化以及机器学习等。

蚁群算法是基于规则的智能算法，它包括四个主要部分：蚁群、时间、规则和变量。

在运行蚁群算法的过程中，先生成一组初始解，再根据算法的规则（也可称为搜索引擎）进行蚁群迭代，每次迭代会更新解的模型和搜索空间的参数，直到达到最优解。

蚁群算法的核心公式如下：第一步：更新ij：ρij = (1-ρ)*ij +*Δρij其中，ρji表示节点i到j转移的概率ρ为一个参数，表示蚂蚁搜索行为的一致性Δρji为一个参数，表示节点i到j路径的通过数量第二步：更新ρij：Δρij = q/Lij + (1-q)*Δρij其中，Lij表示节点i到j路径的长度q为一个参数，表示蚂蚁搜索行为的一致性Δρji为一个参数，表示节点i到j路径的通过数量第三步：更新tij：tij = (1-ρ)*tij +*Δtij其中，tji表示节点i到j转移的概率ρ为一个参数，表示蚂蚁搜索行为的一致性Δtij为一个参数，表示节点i到j路径的通过次数以上就是蚁群算法的核心公式，它结合了蚂蚁的行为，通过迭代的方式，找到最佳的路径，路径的长度由节点之间转移的概率决定，路径的变化则由节点之间通过的次数来决定。

蚁群算法简介蚁群算法是一种优化技术，受到自然界中蚂蚁寻找食物的行为的启发。

这种算法模拟了蚂蚁的信息共享和移动模式，用于解决复杂的组合优化问题，如旅行商问题（TSP）、车辆路径问题（VRP）等。

一、蚁群算法的基本原理在自然界中，蚂蚁寻找食物的行为非常有趣。

它们会在路径上留下信息素，后续的蚂蚁会根据信息素的强度选择路径，倾向于选择信息素浓度高的路径。

这样，一段时间后，大多数蚂蚁都会选择最短或最佳的路径。

这就是蚁群算法的基本原理。

二、蚁群算法的主要步骤1.初始化：首先，为每条边分配一个初始的信息素浓度。

通常，所有边的初始信息素浓度都是相等的。

2.路径选择：在每一步，每个蚂蚁都会根据当前位置和周围信息素浓度选择下一步的移动方向。

选择概率与信息素浓度成正比，与距离成反比。

这意味着蚂蚁更倾向于选择信息素浓度高且距离短的路径。

3.释放信息素：当蚂蚁完成一次完整的路径后，它会在其经过的边上留下信息素。

信息素的浓度与解决问题的质量成正比，即如果蚂蚁找到了一条更好的路径，那么这条路径上的信息素浓度会增加。

4.更新：经过一段时间后，信息素会随时间的推移而挥发，这使得那些不再被认为是最优的路径上的信息素浓度逐渐减少。

同时，每条边上的信息素浓度也会随着时间的推移而均匀增加，这使得那些从未被探索过的路径也有被选择的可能性。

5.终止条件：算法会在找到满足条件的最优解或达到预设的最大迭代次数后终止。

三、蚁群算法的优势和局限性蚁群算法的优势在于其对于组合优化问题的良好性能和其自然启发式的搜索过程。

这种算法能够有效地找到全局最优解，并且在搜索过程中能够避免陷入局部最优解。

此外，蚁群算法具有较强的鲁棒性，对于问题的规模和复杂性具有较强的适应性。

然而，蚁群算法也存在一些局限性。

首先，算法的性能高度依赖于参数的设置，如信息素的挥发速度、蚂蚁的数量、迭代次数等。

其次，对于一些复杂的问题，可能需要很长的计算时间才能找到最优解。

此外，蚁群算法可能无法处理大规模的问题，因为这可能导致计算时间和空间的复杂性增加。

蚁群算法概念
蚁群算法是一种模拟昆虫行为的启发式算法，最初由Dorigo等人在1992年提出。

它模拟了蚂蚁在寻找食物、建立路径以及与其他蚂蚁进行通信等活动中的行为规律，以解决优化问题。

蚁群算法基于分布式计算思想，将问题抽象为蚂蚁在问题空间中的移动和信息交流过程。

每只蚂蚁沿着路径进行移动，并在路上留下信息素。

蚂蚁在选择下一步移动方向时会受到信息素浓度和路径长度的影响。

当蚂蚁找到更优解后，会在回程过程中增加相应路径上的信息素浓度，从而吸引其他蚂蚁走相同的路径。

蚁群算法的核心是信息素的概念。

信息素是一种虚拟的物质，由蚂蚁在路径上释放，并随着时间的变化而挥发。

信息素的浓度代表路径的可行性和优越性，蚂蚁倾向于选择浓度较高的路径。

信息素也会随着时间的推移而逐渐衰减，使得算法具有自我适应的能力。

蚁群算法的主要优点是适用于解决具有大规模、复杂性和非线性特征的实际问题。

它能够在较短的时间内搜索到近似最优解，并且具有良好的鲁棒性和适应性。

蚁群算法还具有较强的并行性，可以通过增加蚂蚁数量来提高算法的搜索性能。

然而，蚁群算法也存在一些不足之处。

由于信息素的作用，算法容易陷入局部最优解，导致搜索效果不佳。

算法的参数选择和调整也对算法性能有重要影响，需要进行合理的设置和优化。

蚁群算法是一种以蚂蚁行为为模型的优化算法，通过模拟蚂蚁的移动和信息交流，不断搜索问题空间，以找到近似最优解。

它在解决复杂、大规模问题方面具有一定的优势，但也需要针对具体问题进行适当的参数调整和优化。

1. 蚁群算法简介蚁群算法（Ant Clony Optimization，ACO）是一种群智能算法，它是由一群无智能或有轻微智能的个体（Agent）通过相互协作而表现出智能行为，从而为求解复杂问题提供了一个新的可能性。

蚁群算法最早是由意大利学者Colorni A., Dorigo M. 等于1991年提出。

经过20多年的发展，蚁群算法在理论以及应用研究上已经得到巨大的进步。

蚁群算法是一种仿生学算法，是由自然界中蚂蚁觅食的行为而启发的。

在自然界中，蚂蚁觅食过程中，蚁群总能够按照寻找到一条从蚁巢和食物源的最优路径。

图（1）显示了这样一个觅食的过程。

图（1）蚂蚁觅食在图1（a）中，有一群蚂蚁，假如A是蚁巢，E是食物源（反之亦然）。

这群蚂蚁将沿着蚁巢和食物源之间的直线路径行驶。

假如在A和E之间突然出现了一个障碍物（图1（b）），那么，在B点（或D点）的蚂蚁将要做出决策，到底是向左行驶还是向右行驶？由于一开始路上没有前面蚂蚁留下的信息素（pheromone），蚂蚁朝着两个方向行进的概率是相等的。

但是当有蚂蚁走过时，它将会在它行进的路上释放出信息素，并且这种信息素会议一定的速率散发掉。

信息素是蚂蚁之间交流的工具之一。

它后面的蚂蚁通过路上信息素的浓度，做出决策，往左还是往右。

很明显，沿着短边的的路径上信息素将会越来越浓（图1（c）），从而吸引了越来越多的蚂蚁沿着这条路径行驶。

2. TSP问题描述蚁群算法最早用来求解TSP问题，并且表现出了很大的优越性，因为它分布式特性，鲁棒性强并且容易与其它算法结合，但是同时也存在这收敛速度慢，容易陷入局部最优（local optimal）等缺点。

TSP问题（Travel Salesperson Problem，即旅行商问题或者称为中国邮递员问题），是一种，是一种NP-hard问题，此类问题用一般的算法是很大得到最优解的，所以一般需要借助一些启发式算法求解，例如遗传算法（GA），蚁群算法（ACO），微粒群算法（PSO）等等。

蚁群算法Ant Colony Algorithms真实世界的蚂蚁行为真实世界的蚂蚁行为即使两条路径一样长，蚂蚁也会强化对其中一条的选择（收敛性）蚁群算法（Ant Algorithms）蚂蚁几乎是没有视力的，它们是如何找到食物和家之间的路径的？在觅食过程中,蚂蚁在它所经过的路径上留下浓度与食物源质量成比例的信息素(pheromone) ,并能够感知信息素的存在及其浓度,以此指导自己的运动方向,倾向于朝着信息素浓度高的方向移动.蚁群算法（Ant Algorithms）于是,蚁群的集体行为便表现出一种信息正反馈现象:某一路径上走过的蚂蚁越多,则后来者选择该路径的概率就越大,因此质量好、距离近的食物源会吸引越来越多的蚂蚁,信息素浓度的增长速度会更快. 蚂蚁个体之间就是通过这种信息的交流达到寻找食物和蚁穴之间最短路径的目的蚁群算法（d=1d=1A蚁群算法（Ant Algorithms）我们感兴趣的是对解空间的探索，而非简单的数路径； 应允许蚂蚁们以概率的方式选择路径以及确定最佳路径，概率与信息素的浓度成比例。

不希望蚂蚁们简单地根据最高浓度来选择路径，如果这样的话，搜索会迅速地陷入局部最优。

一个蚂蚁选择一个确定路径的概率，不仅取决于信息素地浓度，同时也取决于该蚂蚁所看到的信息。

信息素的痕迹不能无限增加，因此，需要引入“挥发”机制。

蚁群算法（Ant Algorithms）由此获得灵感而设计出的算法称蚁群算法ant algorithms(或蚁群系统ant systems)蚁群算法（系统）是一种基于群体策略的搜索方法。

有一群蚂蚁，每个蚂蚁找到一个解，然后通过某种方式(信息素)与其它蚂蚁通信。

以加速群体向最优解的收敛。

利用条件概率p ij描述前一状态i与后一状态j之间的转移概率。

属于bivariate model。

蚁群算法（Ant Algorithms）蚁群算法可以用于解决许多组合优化问题,只要能做到用一个图表来阐述将要解决的问题,能定义一种正反馈过程(如TSP 问题中的残留信息) ,问题结构本身能提供解题用的启发式信息(如TSP 问题中城市间的距离) ,约束机制的建立(如TSP 问题中已访问城市的列表) 。

数学建模中大规模优化问题的求解在数学建模领域中，大规模优化问题的求解一直是一个令人困扰的难题。

随着科学技术的进步和数学建模的广泛应用，大规模优化问题的求解变得越来越重要。

本文将探讨大规模优化问题的求解方法，并介绍几种常用的技术。

1. 线性规划（Linear Programming）线性规划是一种经典的大规模优化问题求解方法。

它的目标是将一个线性目标函数最大化或最小化，同时满足一组线性等式或不等式约束条件。

线性规划的求解算法有很多种，其中最著名的是单纯形法（Simplex Method）。

单纯形法通过沿着目标函数增长的方向移动，不断改善解的质量，直到找到最优解。

虽然单纯形法在实践中表现良好，但对于某些特殊的问题，它的效率可能会很低。

2. 非线性规划（Nonlinear Programming）与线性规划不同，非线性规划处理的是目标函数和约束条件中包含非线性项的优化问题。

非线性规划的求解方法有很多种，其中最常用的是梯度法（Gradient Method）。

梯度法通过计算目标函数在当前解处的梯度，沿着梯度下降的方向更新解，直到找到最优解。

然而，非线性规划的求解通常较为困难，因为梯度法可能陷入局部最优解，而无法找到全局最优解。

3. 整数规划（Integer Programming）整数规划是一类特殊的优化问题，它要求变量的取值必须为整数。

与线性规划相比，整数规划更为复杂和困难。

整数规划的求解方法有很多种，其中最常用的是分支定界法（Branch and Bound）。

分支定界法将整数规划问题转化为一系列线性规划问题，并通过剪枝策略来降低问题规模，最终找到最优解。

然而，由于整数规划涉及到离散取值，它的求解通常是一个非常耗时的过程。

4. 蚁群算法（Ant Colony Optimization）蚁群算法是一种基于模拟蚂蚁寻找食物的行为而发展起来的优化算法。

蚁群算法的基本思想是通过模拟蚂蚁在问题空间中的搜索行为，找到最优解。

毕业论文蚁群算法蚁群算法（Ant Colony Optimization，ACO）是一种模拟蚂蚁寻找食物的行为而发展而来的一种计算智能算法。

该方法利用蚂蚁在寻找食物过程中留下的信息素来指导其他蚂蚁选择路径，从而达到最优路径的目的。

本文将介绍蚁群算法的基本原理、应用领域以及算法的优缺点。

一、算法原理1.1信息素在蚁群算法中，信息素是指蚂蚁在寻找食物时分泌的一种化学物质，它会留在路径上，用于指导其他蚂蚁选择路径。

当一条路径上的信息素浓度足够高时，其他蚂蚁会更倾向于选择这条路径。

1.2蚁群算法过程（1）初始化：随机放置一些蚂蚁并随机设置它们的起点和终点。

（2）蚂蚁选择路径：每个蚂蚁根据当前位置的信息素浓度，选择下一步要走的路径。

选择路径的规则可以根据具体问题来设计。

（3）信息素更新：当蚂蚁完成任务后，会在其经过的路径上留下一定量的信息素。

信息素的更新可以通过公式：$ T_{ij}=(1-ρ) ·T_{ij}+∑\\frac{\\Delta T_{ij}^{k}}{L_{k}} $ 来完成，其中 $ T_{ij} $ 表示在第 $i$ 个节点到第 $j$ 个节点之间路径的信息素，$ L_{k} $ 表示第 $k$ 只蚂蚁走过的路径长度，$ \\Delta T_{ij}^{k} $ 表示第 $k$ 只蚂蚁在第 $i$ 个节点到第$j$ 个节点之间路径上留下的信息素。

（4）重复执行步骤（2）和（3），直到满足算法终止条件。

二、应用领域由于蚁群算法具有寻优能力和适应性强等优点，因此在多个应用领域得到了广泛的应用：2.1路线规划将蚁群算法应用到路线规划中，可以帮助人们更快捷、更准确地规划出最优路径。

例如，在地图搜索、货车路径规划、船只导航等领域都有广泛的应用。

2.2优化问题蚁群算法能够在多种优化问题中得到应用，例如在图像处理、模式识别、网络优化中，通过不断地调节参数，可以找出最佳的结果。

2.3组合优化问题在组合优化问题中，由于问题的规模较大，常规优化算法很容易陷入局部最优解中无法跳出。

蚁群算法毕业论文蚁群算法毕业论文引言在当今信息时代，人工智能和智能算法的发展日新月异。

蚁群算法作为一种模拟生物群体行为的优化算法，已经在多个领域取得了优秀的成果。

本篇论文将探讨蚁群算法的原理、应用以及未来的发展方向。

一、蚁群算法的原理蚁群算法是一种基于蚂蚁觅食行为的启发式算法。

蚂蚁在觅食过程中通过信息素的沉积和蒸发来实现信息的传递和集成，从而找到最优的路径。

蚁群算法利用这种信息素机制，通过模拟蚂蚁的觅食行为来求解优化问题。

蚁群算法的基本原理包括两个方面：正向反馈和负向反馈。

正向反馈是指蚂蚁在觅食过程中，发现食物后释放信息素，吸引其他蚂蚁前往。

负向反馈是指蚂蚁在觅食过程中，经过的路径上的信息素会逐渐蒸发，从而减少后续蚂蚁选择该路径的概率。

二、蚁群算法的应用蚁群算法在多个领域都有广泛的应用。

其中最为著名的应用之一是在旅行商问题（TSP）中的应用。

旅行商问题是指在给定的一组城市中，找到一条最短路径，使得旅行商能够经过每个城市且只经过一次，最后回到起点城市。

蚁群算法通过模拟蚂蚁的觅食行为，成功地解决了这个NP难问题。

除了旅行商问题，蚁群算法还被广泛应用于图像处理、机器学习、网络优化等领域。

在图像处理中，蚁群算法可以用于图像分割、图像匹配等任务。

在机器学习中，蚁群算法可以用于优化神经网络的权重和偏置。

在网络优化中，蚁群算法可以用于优化网络拓扑结构，提高网络的性能。

三、蚁群算法的发展方向尽管蚁群算法已经取得了一定的成果，但仍然存在一些问题和挑战。

首先，蚁群算法在处理大规模问题时，容易陷入局部最优解。

其次，蚁群算法对参数的选择比较敏感，需要经验调整。

此外，蚁群算法在处理动态环境下的问题时，效果不尽如人意。

为了解决这些问题，研究者们提出了一些改进的蚁群算法。

例如，基于混沌理论的蚁群算法、蚁群算法与遗传算法的融合等。

这些改进算法在一定程度上提高了蚁群算法的性能和鲁棒性。

此外，蚁群算法还可以与其他智能算法相结合，形成混合算法。

蚁群算法概念
蚁群算法（Ant Colony Algorithm，ACA）是一种模拟蚁群觅食行为的启发式优化算法，被广泛应用于求解组合优化问题。

其基本思想是通过多个“蚂蚁”在问题的解空间中搜索最优解，并通过互相交流信息来引导搜索过程。

蚂蚁在搜索过程中通过携带的信息素标记路径，信息素浓度表示路径的好坏程度。

路径上的信息素浓度增加与蚂蚁对路径的评价正相关，蚂蚁根据信息素浓度的大小选择下一步的移动方向。

同时，信息素会随着时间的推移逐渐挥发，从而模拟蚁群搜索过程中信息的传递与更新。

蚁群算法的主要步骤包括初始化信息素、蚂蚁的移动、更新信息素以及重复执行这些步骤。

通过多次迭代，蚁群算法能够逐步搜索到问题的最优解。

蚁群算法具有全局优化能力和强鲁棒性，在解决复杂优化问题和组合优化问题方面具有较高的效果和应用价值。

它在路线规划、物流配送、旅行商问题等领域都有广泛的应用。

蚁群算法这算是填3年前的⼀个坑吧，已经懒癌晚期了，想必也还是要挣扎下，那今天先从蚁群算法这个坑说起，如果你是要寻找怎么优化蚁群算法，可以直接跳过本⽂，如果你还不了解什么是蚁群算法，或许本⽂能够提起你的兴趣。

如果你同样对遗传算法和粒⼦群算法感兴趣，请查看3年前我对于这两个算法见解的⽂章。

简单蚁群算法模拟实验：这个模拟实验⽐较简单，并没有对信息素、路径选择等做优化，主要是⽅便⼤家查看简单的蚂蚁系统能够带来⼀个什么样的效果,详细说明见后⽂。

什么是蚁群算法按百度百科的话来说，蚁群算法(ant colony optimization, ACO)，⼜称蚂蚁算法，是⼀种⽤来在图中寻找优化路径的机率型算法。

它由Marco Dorigo于1992年在他的博⼠论⽂中提出，其灵感来源于蚂蚁在寻找⾷物过程中发现路径的⾏为。

蚁群算法是⼀种模拟进化算法，初步的研究表明该算法具有许多优良的性质，并且现在已⽤于我们⽣活的⽅⽅⾯⾯。

基本原理蚂蚁在运动过程中，会留下⼀种称为信息素的东西，并且会随着移动的距离，播散的信息素越来越少，所以往往在家或者⾷物的周围，信息素的浓度是最强的，⽽蚂蚁⾃⾝会根据信息素去选择⽅向，当然信息素越浓，被选择的概率也就越⼤，并且信息素本⾝具有⼀定的挥发作⽤。

蚂蚁的运动过程可以简单归纳如下：1. 当周围没有信息素指引时，蚂蚁的运动具有⼀定的惯性，并有⼀定的概率选择其他⽅向2. 当周围有信息素的指引时，按照信息素的浓度强度概率性的选择运动⽅向3. 找⾷物时，蚂蚁留下家相关的A信息素，找家时，蚂蚁留下⾷物相关的B信息素，并随着移动距离的增加，洒播的信息素越来越少4. 随着时间推移，信息素会⾃⾏挥发⼀个简单的例⼦，如果现在有两条通往⾷物的路径，⼀条较长路径A,⼀条较短路径B,虽然刚开始A,B路径上都有蚂蚁，⼜因为B⽐A短，蚂蚁通过B花费的时间较短，随着时间的推移和信息素的挥发，逐渐的B上的信息素浓度会强于A，这时候因为B的浓度⽐A强，越来越多多蚂蚁会选择B，⽽这时候B上的浓度只会越来越强。