二元函数的图形

MATL AB绘制二元函数的图形【实验目的】1.了解二元函数图形的绘制。

2.了解空间曲面等高线的绘制。

3.了解多元函数插值的方法。

4.学习、掌握MATLAB软件有关的命令。

【实验内容】画出函数22yz+=的图形，并画出其等高线。

x【实验准备】1.曲线绘图的MATLAB命令MATLAB中主要用mesh,surf命令绘制二元函数图形。

主要命令mesh（x，y，z）画网格曲面，这里x，y，z是数据矩阵，分别表示数据点的横坐标，纵坐标和函数值，该命令将数据点在空间中描出，并连成网格。

surf（x，y，z）画完整曲面，这里x，y，z是数据矩阵，分别表示数据点的横坐标，纵坐标和函数值，该命令将数据点所表示曲面画出。

【实验重点】1. 二元函数图形的描点法2. 曲面交线的计算3. 地形图的生成【实验难点】1. 二元函数图形的描点法2. 曲面交线的计算【实验方法与步骤】练习1画出函数22y=的图形，其中]3,3xz+⨯-yx。

∈,[]3,3[(-)用MATLAB作图的程序代码为>>clear;>>x=-3:0.1:3; %x的范围为[-3，3]>>y=-3:0.1:3; %y的范围为[-3，3]>>[X,Y]=meshgrid(x,y); %将向量x,y指定的区域转化为矩阵X,Y >>Z=sqrt(X.^2+Y.^2); %产生函数值Z>>mesh(X,Y,Z)运行结果为图5.3如果画等高线，用contour，contour3命令。

contour画二维等高线。

contour3画三维等高线。

画图5.3所示的三维等高线的MA TLAB 代码为>>clear;>>x=-3:0.1:3;>>y=-3:0.1:3;>>[X,Y]=meshgrid(x,y);>>Z=sqrt(X.^2+Y.^2);>>contour3(X,Y,Z,10); %画10条等高线>>xlabel('X-axis'),ylabel('Y-axis'),zlabel('Z-axis'); %三个坐标轴的标记>>title('Contour3 of Surface') %标题>>grid on %画网格线运行结果为图5.4如果画图5.4所示的二维等高线，相应的MATLAB代码为>>clear;x=-3:0.1:3;y=-3:0.1:3;>>[X,Y]=meshgrid(x,y);Z=sqrt(X.^2+Y.^2);>>contour (X,Y,Z,10);>>xlabel('X-axis'),ylabel('Y-axis');>>title('Contour3 of Surface')>>grid on运行结果为如果要画z=1的等高线，相应的MATLAB代码为>>clear;x=-3:0.1:3;y=-3:0.1:3;>>[X,Y]=meshgrid(x,y);Z=sqrt(X.^2+Y.^2);>>contour(X,Y,Z,[1 1])运行结果为练习2 二次曲面的方程如下222222x y z d a b c++= 讨论参数a ,b ,c 对其形状的影响。

第二节 多元函数的基本概念内容分布图示★ 领域 ★ 平面区域的概念★ 多元函数的概念 ★ 例1 ★ 例2★ 二元函数的图形★ 二元函数的极限 ★ 例3 ★ 例4★ 例5 ★ 例6 ★ 例7★ 例8 ★ 例9★ 二元函数的连续性 ★ 例 10★ 二元初等函数 ★ 例 11-12★ 闭区域上连续函数的性质★ 内容小结 ★ 课堂练习★ 习题6-2 ★ 返回内容提要：一、平面区域的概念：内点、外点、边界点、开集、连通集、区域、闭区域二、多元函数的概念定义1 设D 是平面上的一个非空点集，如果对于D 内的任一点),(y x ，按照某种法则f ，都有唯一确定的实数z 与之对应，则称f 是D 上的二元函数，它在),(y x 处的函数值记为),(y x f ，即),(y x f z =，其中x ，y 称为自变量， z 称为因变量. 点集D 称为该函数的定义域，数集}),(),,(|{D y x y x f z z ∈=称为该函数的值域.类似地，可定义三元及三元以上函数. 当2≥n 时, n 元函数统称为多元函数.二元函数的几何意义三、二元函数的极限定义2 设函数),(y x f z =在点),(000y x P 的某一去心邻域内有定义，如果当点),(y x P 无限趋于点),(000y x P 时，函数),(y x f 无限趋于一个常数A ，则称A 为函数),(y x f z =当),(y x ),(00y x →时的极限. 记为A y x f y y x x =→→),(lim 00.或 A y x f →),( （),(),(00y x y x →）也记作A P f P P =→)(lim 0或 A P f →)( )(0P P → 二元函数的极限与一元函数的极限具有相同的性质和运算法则，在此不再详述. 为了区别于一元函数的极限，我们称二元函数的极限为二重极限.四、二元函数的连续性定义3 设二元函数),(y x f z =在点),(00y x 的某一邻域内有定义，如果),(),(lim 0000y x f y x f y y x x =→→,则称),(y x f z =在点),(00y x 处连续. 如果函数),(y x f z =在点),(00y x 处不连续，则称函数),(y x f z =在),(00y x 处间断.与一元函数类似，二元连续函数经过四则运算和复合运算后仍为二元连续函数. 由x 和y 的基本初等函数经过有限次的四则运算和复合所构成的可用一个式子表示的二元函数称为二元初等函数. 一切二元初等函数在其定义区域内是连续的. 这里定义区域是指包含在定义域内的区域或闭区域. 利用这个结论，当要求某个二元初等函数在其定义区域内一点的极限时，只要算出函数在该点的函数值即可.特别地，在有界闭区域D 上连续的二元函数也有类似于一元连续函数在闭区间上所满足的定理. 下面我们不加证明地列出这些定理.定理1（最大值和最小值定理） 在有界闭区域D 上的二元连续函数, 在D 上至少取得它的最大值和最小值各一次.定理2（有界性定理）在有界闭区域D 上的二元连续函数在D 上一定有界.定理3（介值定理）在有界闭区域D 上的二元连续函数, 若在D 上取得两个不同的函数值, 则它在D 上取得介于这两值之间的任何值至少一次.例题选讲：多元函数的概念例1（讲义例1）求二元函数222)3arcsin(),(y x y x y x f ---=的定义域.例2（讲义例2）已知函数,),(2222y x y x y x y x f +-=-+ 求),(y x f . 二元函数的极限例3（讲义例3）求极限 2222001sin )(lim yx y x y x ++→→. 例4 求极限.)sin(lim 22200y x y x y x +→→例5（讲义例4）求极限 22limy x y x y x ++∞→∞→. 例6 求极限 .2lim 42430y x x xy y x ++→→ 例7 求 .)(lim 220xy y x y x +→→例8（讲义例5）证明2200lim yx xy y x +→→不存在. 例9 证明26300lim y x y x y x +→→不存在. 二元函数的连续性例10（讲义例6）讨论二元函数⎪⎩⎪⎨⎧=≠++=)0,0(),(,0)0,0(),(,),(2233y x y x y x y x y x f 在)0,0(处的连续性.例11 求.1)ln(lim 210⎥⎥⎦⎤⎢⎢⎣⎡-+-→→x y x y y x 例12 求.lim 10yx y e x y x ++→→课堂练习1.设,,22y x x y y x f -=⎪⎭⎫ ⎝⎛- 求).,(y x f 2. 若点),(y x 沿着无数多条平面曲线趋向于点),(00y x 时, 函数),(y x f 都趋向于A , 能否断定?),(lim ),(),(00A y x f y x y x =→3.讨论函数⎪⎩⎪⎨⎧=+≠++=0,00,),(2222422y x y x y x xy y x f 的连续性.。

二元函数的定义与几何意义以前所学的函数都是一元函数，但是在实际问题中，所涉及的函数的自变量的个数往往不只是一个，有的是两个，甚至更多。

例如，一个圆锥体的体积，它有两个独立的变量r 、h 。

某种商品的市场需求量Q 不仅与市场价格p 有关，而且与消费者平均收入以及需要这种商品的人数N 有关,同时，还与这种商品的其他代用品的价格等因素有关；从而决定该商品需求量的自变量不只一个而是多个可见在许多实际问题中往往需要研究因变量与几个自变量之间的关系，为此，就需要进一步讨论自变量为两个，或者更多情形下的多元函数。

本节以二个独立的变量为基础，首先给出二元函数的概念。

213V r h π=函数的微分法从一元函数发展到二元函数本质上要出现一些新东西，但从二元函数到二元以上函数则可以类推，因此这里基本上只讨论二元函数。

本章内容为多元函数微分学。

多元微积分的概念、理论、方法是一元微积分中相应概念、理论、方法的推广和发展，它们既有相似之处（概念及处理问题的思想方法）又有许多本质的不同，要善于进行比较，既要认识到它们的共同点和相互联系，更要注意它们的区别，研究新情况和新问题，深刻理解，融会贯通。

本节以二个独立的变量为基础，首先给出二元函数的概念。

1.二元函数若对于变量x ,y 在其可能取值的某一范围D 内的每一组值(x ,y )，依照某一对应法则f ，变量z 都有确定的值与之相对应，则称变量z 为变量x ,y 的二元函数，记为z= f (x ,y )，其中x ,y 称为自变量，D 称为二元函数的定义域．定义8.1.1数集{|(,),(,)}z z f x y x y D =∈称为该函数的值域.类似地，可以定义三元函数以及三元以上的函数.二元以及二元以上的函数统称为多元函数.约定用算式表达的二元函数z= f (x ,y )的定义域，是使该算式有意义的自变量的全体所确定的平面点集.具体在求二元函数的定义域时与一元函数相仿．例如：求二元函数定义域为{}22(,)1x y x y +≤圆域图形为中心在原点的上半球面.221z x y=--xzy1o一组概念：1.区域：全部xOy 坐标平面或由曲线所围成的部分平面常用字母D 表示2.边界：围成区域的曲线称为该区域的边界3.开区域：不包括边界的区域4.闭区域：连同边界在内的区域二元函数的定义域通常是由一条或几条曲线所围成的平面区域，围成区域的曲线叫做该区域边界.注5.有界区域与无界区域：如果一个区域可以被包含在一个以原点为圆心，适当长为半径的圆内，否则为无解区域6.内点：开区域内的点7.边界点：边界上的点8.区域的表示：与用区间表示不定式一样，区域也可以用不等式或不等式组表示22{(,)14},x y x y <+<例如开区域:其图形为：其图形为：xy o22{(,)14},x y x y ≤+≤又如闭区域:xy o{(,)0}x y x y+≥闭区域：其图形为：其图形为：O xyx y+=x y+>{(,)0}x y x y+>开区域：O x yx y+=0x y +≥例1求函数1ln()z x y x=+的定义域．解：ln()x y +由于分式的分母不能为零，开偶次方根时根号下的表达式不小于零，因此应有x >0，而中真数必须大于零，即x +y >0，因此所给函数的定义域为00x x y >⎧⎨+>⎩0=+y x xyD图1图1所示阴影区域D.解：函数的定义域为⎩⎨⎧>-+≥--01092222y x y x 即⎩⎨⎧>+≤+192222y x y x 综上有22{(,)|19}D x y x y =<+≤表示圆的外侧（不包括圆周）和122=+y x 圆的内侧（包括圆周）内的所有点. 如图2所示阴影区域D.922=+y x 11D x y 33图.21192222-++--=y x y x z 例2求函数的定义域．二元函数的几何意义一元函数一般表示平面上的一条曲线；对于二元函数，在空间直角坐标系中一般表示曲面∑如图，定义域就是曲面在面上的投影区域D xy∑x y z o 2222x y z a a ++=例如，表示的曲面为球心在原点，半径为的球面（见右图）222z a x y =--而表示的为上半球面222z a x y =---表示的是下半球面。

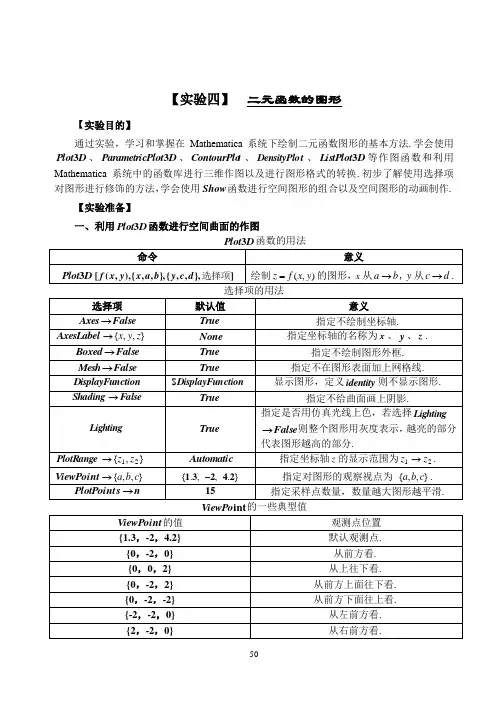
【实验四】 二元函数的图形【实验目的】通过实验，学习和掌握在Mathematica 系统下绘制二元函数图形的基本方法.学会使用D Plot 3、D Plot Parametric 3、t ContourPlo 、t DensityPlo 、D ListPlot 3等作图函数和利用Mathematica 系统中的函数库进行三维作图以及进行图形格式的转换.初步了解使用选择项对图形进行修饰的方法，学会使用Show 函数进行空间图形的组合以及空间图形的动画制作.【实验准备】一、利用D Plot 3函数进行空间曲面的作图例1 作出22),(y xe y xf --=的图形，并利用选择项对所作图形进行修饰.解 In[1]:= Plot3D Exp x ^2y^2,x,2,2,y,2,2Out[1]:= ?SurfaceGraphics ? 去掉刻度In[2]:= Plot3D Exp x ^2y^2,x,2,2,y,2,2,TicksFalseOut[2]:= ?SurfaceGraphics ?去掉图形上的网格线Plot3D Exp x^2y^2,x,2,2,y,2,2,Mesh False不画出图形上的阴影In[4]:=Plot3D Exp x^2y^2,x,2,2,y,2,2,Shading FalseOut[4]:=? SurfaceGraphics?不用仿真光线上色In[4]:=Plot3D Exp x^2y^2,x,2,2,y,2,2,Lighting FalseOut[4]:=? SurfaceGraphics?去掉外框In[5]:=Plot3D Exp x^2y^2,x,2,2,y,2,2,Boxed False分别以x、y 、z定义坐标轴的名称In[6]:=Plot3D Exp x^2y^2,x,2,2,y,2,2,Boxed False,AxesLabel x,y,zOut[6]:=? SurfaceGraphics?定义以每个方向以36个点绘图，观测点为从前方看.In[7]:=Plot3D Exp x^2y^2,x,2,2,y,2,2,PlotPoints36,ViewPoint0,2,0,Boxed FalseOut[7]:=? SurfaceGraphics?将绘图的范围限制在2≤z0≤In[8]:=Plot3D Exp x^2y^2,x,2,2,y,2,2,PlotRange0,2Out[8]:= ?SurfaceGraphics ? 二、利用D Plot Parametric 3函数进行空间曲面（曲线）的参数作图如果函数是),(y x f z =的形式，则可以利用D Plot 3命令绘制这个函数的曲面.但有些空间曲面（曲线）无法表示成),(y x f z =的形式，例如球面、螺旋线等.对于这种空间曲面（曲线），有时可以利用一组参数方程来表示.关于这类用参数方程表示的曲面（曲线），我们用D Plot Parametric 3函数进行作图，其格式如下：由上表可以看出，如果参数方程有两个变量，所作图形为空间曲面.如果参数方程只有一个变量，所作图形为空间曲线.选择项与D Plot 3作图选择项类似，只是所取样点的默认值有所不同，曲面参数作图的默认值为→s int PlotPo },{1515，而曲线参数作图的默认值为75→s int PlotPo ，必要时可加大此值以求得更平滑的曲面或曲线.例2 作出由参数方程⎪⎩⎪⎨⎧===v cos z v sin u sin y v sin u cos x ，πππ≤≤≤≤v u 5.0,20所确定的曲面图形.解 In[1]:=ParametricPlot3D @8C os @u DSin @v D ,Sin @u D Sin @v D ,Cos @v D <,8u ,0,2Pi <,8v ,0.5 Pi,Pi <D例3 作出由参数方程⎪⎩⎪⎨⎧===t .z t cos y tsin x 10，π≤≤80t 所确定的圆柱螺旋线的图形.解 In[1]:= ParametricPlot3DSin t ,Cos t ,0.1t ,t,0,8三、使用Show 函数拼合多张曲面使用函数可以将已作好的一些图形组合在一起，其格式如下：例4 作出由参数方程⎪⎪⎪⎩⎪⎪⎪⎨⎧===2cos 2sin sin 2cos sin v z u v y u v x ，π≤≤π≤≤v u 0,20所确定的曲面，并与例2中所作的曲面进行拼合.解 In[1]:= f1ParametricPlot3DSin v Cos u 2,Sin v Sin u2,Cos v 2,u,0,2,v,0,,DisplayFunctionIdentityOut[1]:= ?Graphics3D ? In[2]:= f2ParametricPlot3D Cos u Sin v ,Sin u Sin v ,Cos v ,u,0,2,v,0.5,,DisplayFunction IdentityOut[2]:= ?Graphics3D ? In[3]:= Show f1,f2,DisplayFunction$DisplayFunctionOut[3]:= ?Graphics3D ? 注：利用Show 命令可以作出两个曲面的交线以及曲面的切平面.方法是：分别作出两个空间曲面或一个曲面与其切平面，然后用Show 命令再现这组已作好的空间图形.四、绘制空间曲面的等高线图等高线图（t ContourPlo ）是将三维空间中高度相等的点连接起来.等高线图在弹性力学（力的分布），热传学（温度的分布）以及空间曲面求最值问题中有着广泛的应用.下面介绍作图格式：例 5 作出函数22122)2(),(y xe y x y xf --+=在22(≤≤-x ，)22≤≤-y 范围内所表示的空间曲面及等高线图，并对等高线图进行适当的修饰.解 In[1]:= f x_,y_:x^22y^21x 2y 2; (为作图方便先定义函数)In[2]:= Plot3D f x,y ,x,2,2,y,2,2Out[2]:= ?Graphics3D ? 作出等高线图In[3]:= ContourPlot f x,y ,x,2,2,y,2,2Out[3]:=? ContourGraphics?图形中较亮的部分为空间曲面中较高的位置，较暗的部分为空间曲面中较低的位置. 加大sPlotPo的值可以使等高线图形更加平滑，如下图：intIn[4]:=ContourPlot f x,y,x,2,2,y,2,2,PlotPoints400Out[4]:=? ContourGraphics?改变Contours 的值可以指定等高线的数目，如下图：In[5]:= ContourPlot f x,y ,x,2,2,y,2,2,Contours20Out[5]:= ?ContourGraphics ?五、绘制空间曲面的密度图密度图)(t DensityPlo 和等高线图有些类似，只是密度图用了一个上了色的方格数组，配合颜色的深浅代表函数值的大小.其作图格式如下：选择项例6 作出函数22122)2(),(y x e y x y x f --+=在22(≤≤-x ，)22≤≤-y 范围内的密度图，并注意选择项的效果.解 In[1]:= f x_,y_:x^22y^21x 2y 2;In[2]:= DensityPlot f x,y ,x,2,2,y,2,2,MeshFalse,PlotPoints50Out[2]:= ?DensityGraphics ?六、图形格式的转换如果图形是以D Plot 3、t ContourPlo 和)(t DensityPlo 等命令绘制的，则可以在这三者之间做图形转换.例如可以把一个空间曲面图形转换成等高线图，或把一个密度图转换为空间曲面图形.其转换图形格式的命令如下：例7 作出由函数y x y x f cos sin ),(=确定的空间曲面，并将其转换为等高线图和密度图.解 In[1]:= Plot3D @S in @x DCos @y D ,8x ,0,2 Pi <,8y ,0,2 Pi <DOut[1]:= ?SurfaceGraphics ?In[2]:= Show @C ontourGraphics @%DOut[2]:= ?ContourGraphics ?In[3]:= Show @DensityGraphics @%DOut[3]:= ?DensityGraphics ? 七、利用函数库绘制三维图形1. 利用`D t ContourPlo `Graphics 3绘图函数库绘制空间曲面对于用方程表示的曲面，如：椭球面、椭圆抛物面和双曲抛物面等不能用D Plot 3函数进行作图，而要用Mathematica 系统函数库中提供的D t ContourPlo 3命令进行作图. 在使用D t ContourPlo 3函数之前，首先要加载`D t ContourPlo `Graphics 3绘图函数库，其格式如下：注：1.选择项与D Plot 3函数作图的选择项相同.2.s int PlotPo 的默认值为}5,3{较为粗糙，可加大s int PlotPo 的值使图形更加平滑. 例8 绘制由方程12222=+--z y x 所确定的在)22,22,33(≤≤-≤≤-≤≤-z y x 区域内的双叶双曲面，并进行适当的修饰.解 In[1]:= <<Graphics`ContourPlot3D` In[2]:= ContourPlot3Dx 22y 2z 21,x,3,3,y,2,2,z,2,2,PlotPoints6,8,Boxed FalseOut[2]:= ?Graphics3D ? 2.由曲线生成的旋转曲面首先加载`volution Re SurfaceOf `Graphics <<函数库，然后使用volution Re SurfaceOf 命令进行作图，其格式如下：例9 作出正弦曲线x sin z =，]2,0[π∈x 绕z 轴旋转一周形成的曲面解 In[1]:= <<Graphics`SurfaceOfRevolution`In[2]:= SurfaceOfRevolution@S in @x D ,8x ,0,2 Pi <,AxesLabel ?8x ,y,z <DOut[2]:= ?Graphics3D ?*例10 作出曲线2x z =绕起点在原点的向量}1,1,1{旋转的曲面 解 In[1]:=<<Graphics`SurfaceOfRevolution`In[2]:= SurfaceOfRevolution@x ^2,8x ,0,1<, RevolutionAxis ?81,1,1<,AxesLabel ?8x ,y,z<D3.空间曲面在坐标面上的投影绘制空间曲面在各个坐标面上的投影需要使用投影函数Shadow .在利用Shadow 绘制空间曲面的投影之前，需要加载Graphics`Graphics3D`函数库. 例11 按照下列要求作出椭圆抛物面12222=++z y x 在坐标面上的投影.(1)三个坐标平面上的投影；(2)一个坐标面上的投影.解 In[1]:= <<Graphics`ContourPlot3D` In[2]:= A 8<(1)In[3]:= <<Graphics`Graphics3D` In[4]:= Shadow @u D(2)In[5]:=*例12 绘制由参数方程⎪⎩⎪⎨⎧--===)sin 2(3sin cos 22t r z t r y t r x 与⎪⎩⎪⎨⎧+===)sin 1(sin cos 22t r z t r y tr x )10(≤≤r ，)20π≤≤t 所确定的两个曲面围成的立体图形，并将它投影到坐标面上.解 In[1]:= <<Graphics`Graphics3D`In[2]:= u1ParametricPlot3Dr Cos t ,r Sin t ,3r22Sin t ^2, r,0,1,t,0,2Pi ,DisplayFunction Identity Out[2]:= Graphics3DIn[3]:=u2ParametricPlot3Dr Cos t,r Sin t,r21Sin t^2,r,0,1,t,0,2Pi,DisplayFunction Identity Out[3]:=Graphics3DIn[4]:=u Show u1,u2,DisplayFunction$DisplayFunctionIn[5]:=八、空间图形的动画制作制作空间图形的动画可以用有关循环结构的命令(如：For 、Table 、Do 等)，将作图函数作出的图形按照时间顺序生成动画，下面举例说明例13 制作在区域1010≤≤-x ，1010≤≤-y 内，由函数22221)sin(10),(yx y x y x f +++=所确定的曲面变化的动画过程.解 In[1]:= For i1,i30,i,Plot3D10Sinx ^2y^21x^2y ^2,x,10,10i 30,y,10,10i 30,PlotPoints50,Boxed False执行程序后得到一组图形，鼠标左键双击工作区右端包含全部图形的兰色线框，保留最上面的图形（如上图）而关闭其它图形，然后用鼠标左键双击该图即可播放动画.注：In[1]中的“30/i ”的含义是每隔单位长度的30i作出一张图形，根据i 的不同取值得到多幅图形，读者可以根据不同情况自行设置.【实验任务】一、作出下列函数所确定的空间曲面，并根据下列要求修饰图形：(1)去掉网格；(2)使图形平滑；(3)指定坐标轴的名称为“x 、y 、z ”；(4)去掉图形外框.1.228sin 41),(y x y x f +=，11≤≤-x ，11≤≤-y ； 2.y xy y x y x f +-+=6),(22，30≤≤x ,30≤≤y ；3.)sin(),(y x y x f +=，ππ≤≤-x ， ππ≤≤-y ；4.22),(y x y x f +=，ππ22≤≤-x ，ππ22≤≤-y .二、作出由参数方程⎪⎪⎩⎪⎪⎨⎧===t z t y t x 51cos sin 所确定的空间曲线的图形.三、根据给出的参数方程作出下列曲面的图形.1. 椭圆抛物面⎪⎩⎪⎨⎧===24cos 2sin 3u z v u y vu x ，π≤≤≤≤-20,11v u ；2.双曲抛物面⎪⎪⎩⎪⎪⎨⎧-===322v u z v y u x ，22,11≤≤-≤≤-v u ；3.圆锥面⎪⎩⎪⎨⎧===u z v u y vu x cos sin ，π≤≤≤≤-20,11v u .四、作出由方程z y x 422=+确定的空间曲面，并去掉网格、外框，使图形更加平滑. 五、已知球面由方程14222=++z y x 确定，球面的切平面由方程01432=-++z y x 确定，在同一坐标系下作出球面及其切平面的图形.六、作出由曲线x z cos =，]2,0[π∈x 绕z 轴旋转一周形成的曲面. 七、作出由直线x z =绕x 轴旋转一周形成的一个锥面，并标注三个坐标轴.*八、作出曲面：⎪⎩⎪⎨⎧==+=u z v y v x sin 1cos )20,31(π≤≤≤≤v u ；与曲面：⎪⎩⎪⎨⎧===u z v u y vu x sin sin cos sin)20,0(ππ≤≤≤≤v u ；围成的立体图形，并将其投影到xOy 面上.九、制作由函数22sin y x y +=在)20,20(π≤≤π≤≤y x 区域内的动画.。

第一节 二元函数的概念一、 二元函数的概念 1、二元函数——已知变量x 、变量y 及变量z ，当变量x ，y 相互独立的在某范围D 内任取一组确定的值时，若变量z 按照一定的规律f ，总有唯一确定的值与之对应，则称变量z 为变量x ，y 的二元函数，记作)(y x f z ，=。

其中变量x ，y 称为自变量，取值范围D 称为二元函数定义域；二元函数z 也称为因变量，二元函数z 的取值范围G 称为二元函数值域；“f”称为对应关系或函数关系。

2、表达式——①二元显函数)(y x f z ，=；②二元隐函数0)(F =z y x ，，。

3、定义域——D={)(P |)(y x y x ，，}：xy 平面上点的集合，简称平面点集。

平面区域：整个xy 平面或xy 平面上由几条曲线围成的一部分称为平面区域，围成平面区域的曲线称为区域边界； 开区域：不包含边界的区域称为开区域； 闭区域：包含全部边界的区域称为闭区域；半开区域：包含部分边界的区域称为半开半闭区域； 有界区域：不延伸到无穷远处的区域称为有界区域； 无界区域：延伸到无穷远处的区域称为无界区域。

4、函数值——对于二元函数)(y x f z ，=，当自变量x ，y在定义域内取一组数值)(00y x ，时，对应的二元函数值记作)(|0000y x f z y y x x ，===。

5、极值——已知二元函数)(y x f z ，=在点)(00y x ，处及其附近有定义，对于点)(00y x ，处附近很小范围内任意点)(y x ，≠)(00y x ，，若总有)()(00y x f y x f ，，>，则称)(00y x f ，为)(y x f ，的极大值，点)(00y x ，为)(y x f ，的极大值点；反之，若总有)()(00y x f y x f ，，<，则称)(00y x f ，为)(y x f ，的极小值，点)(00y x ，为)(y x f ，的极小值点。