工程力学第13章答案

13工程力学-正式网上考试试题及答案一、单项选择题(共 5 题、共 15 分)1.图A中的链杆和图B中的链杆分别为（）。

答案：CA、两个约束和一个约束B、两个约束和两个约束C、一个约束和一个约束D、一个约束和两个约束2.图示体系为（）。

答案：C—不确定A、有多余约束几何不变体系B、无多余约束几何不变体系C、瞬变体系D、常变体系3.能提供三个反力的支座是（）。

答案：DA、定向支座B、固定铰支座C、固定端支座D、可动铰支座4.图示体系为（）。

答案：C—不确定A、常变体系B、无多余约束几何不变体系C、瞬变体系D、有多余约束几何不变体系5.连接两个杆端的刚结点相当于多少个约束？（）答案：DA、四个B、一个C、两个D、三个二、判断题(共 5 题、共 15 分)1.几何不变体系的基本组成规则可用于分析所有体系的几何组成性质。

答案：错误正确错误2.剪应力和剪应变都是不均分布的，基于截面进行剪切分析时，通常会简化其为均匀分布。

答案：正确正确错误3.刚体或刚片也可以写作钢体或钢片，是指用钢材制成的物体。

答案：错误正确错误4.几何常变体系中，各部件的自由度数之和必然大于全部约束数。

答案：错误正确错误5.广义坐标法是通过坐标变换进行动力自由度简化分析的方法。

答案：正确正确错误三、填空题(共 6 题、共 24 分)—答案在最后1.图示结构中，内力为零的杆段为____________。

请将答案写在附件中上传！2.图示四个体系的多余约束数目，从左至右分别为____、____、____、____。

请将答案写在附件中上传！3.荷载应简化成集中荷载还是分布荷载的决定因素是该荷载的__________与构件尺寸之比。

请将答案写在附件中上传！4.图示刚架中，杆CD的轴力F NCD=_____kN。

请将答案写在附件中上传！5.利用影响线求多个固定位置的集中力所引起的量值时，应用了______原理。

请将答案写在附件中上传！6.当仅有荷载作用于基本部分上时，多跨静定梁的______部分不产生内力。

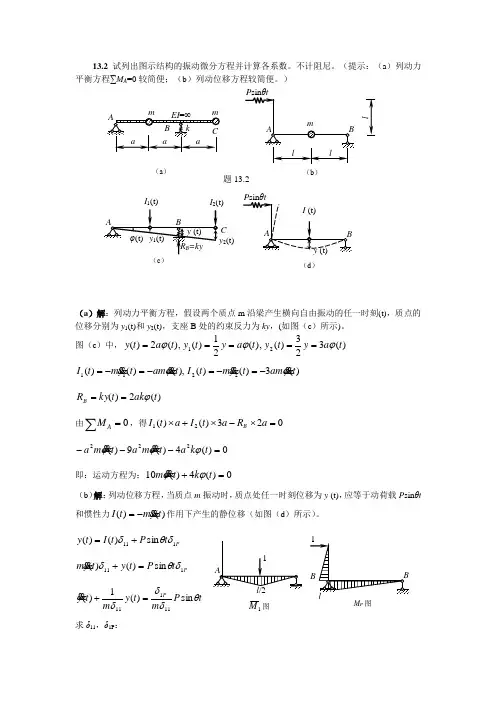
13.2 试列出图示结构的振动微分方程并计算各系数。

不计阻尼。

（提示：（a ）列动力平衡方程∑M A =0较简便；（b ）列动位移方程较简便。

）（a ）解：列动力平衡方程，假设两个质点m 沿梁产生横向自由振动的任一时刻(t)，质点的位移分别为y 1(t)和y 2(t)，支座B 处的约束反力为ky ，(如图（c ）所示)。

图（c ）中，)(323)(),(21)(),(2)(21t a y t y t a y t y t a t y ϕϕϕ=====)(3)()(),()()(2211t am t y m t I t am t y m t I ϕϕ -=-=-=-= )(2)(t ak t ky R B ϕ==由0=∑AM，得023)()(21=⨯-⨯+⨯a R a t I a t I B0)(4)(9)(222=---t k a t m a t m a ϕϕϕ即：运动方程为：0)(4)(10=+t k t m ϕϕ（b ）解：列动位移方程，当质点m 振动时，质点处任一时刻位移为y (t)，应等于动荷载P sin θt和惯性力)()(t ym t I -=作用下产生的静位移（如图（d ）所示）。

P t P t I t y 111sin )()(δθδ+= P t P t y t y m 111sin )()(δθδ=+ t P m t y m t yP θδδδsin )(1)(11111=+求δ11，δ1P ：（a ）题C y 2(t)I 2(t)I 1(t)（d ）M P 图EIll l l EI6)2232221(1311=⨯⨯⨯⨯⨯=δ，EIll l l EIP 4)22221(131=⨯⨯⨯=δ13.3 试求图示各结构的自振频率，略去杆件自重及阻尼影响。

（a ）解：首先绘出质点m 处作用单位力时的弯矩图（图（e ）），其柔度系数为：EIll l l l l l EI3114)2322221232221(1=⨯⨯⨯⨯+⨯⨯⨯⨯=δ（a ）（c ）（d ）题13.3（e ）（g ）l /4l （h ）l /2自振频率为：31141mlEI m ==δω（b ）解：首先绘出质点m 处作用单位力时的弯矩图（图（f ）），其柔度系数为： EIEI312824324421111=⨯⨯⨯⨯⨯⨯=δ自振频率为：mEI m 25632111==δω（c ）解：首先绘出质点m 处作用单位力时的弯矩图（图（g ）），其柔度系数为：EIll l l l l l EI485)24324221232221(1311=⨯⨯⨯⨯⨯+⨯⨯⨯⨯=δ自振频率为：3115481mlEI m ==δω（d ）解：首先绘出质点m 处作用单位力时的弯矩图（图（h ）），其柔度系数为： 111111δδδ''+'= EIll l l EI 6)22231(1311=⨯⨯⨯⨯='δ，k 2111=''δ kEIl216311+=δ自振频率为：)62(121311EI kl m EIk m +==δω。

工程力学练习册学校学院专业学号教师姓名第一章静力学基础 1第一章静力学基础1-1 画出下列各图中物体A，构件AB，BC或ABC的受力图，未标重力的物体的重量不计，所有接触处均为光滑接触.（a）（b）（c)2 第一章静力学基础（d）（e）（f)（g）第一章静力学基础 3 1—2 试画出图示各题中AC杆(带销钉）和BC杆的受力图（a）（b）（c)（a)4 第一章静力学基础1—3 画出图中指定物体的受力图。

所有摩擦均不计,各物自重除图中已画出的外均不计.（a)第一章静力学基础 5 （b）（c）（d）6 第一章静力学基础（e）第一章静力学基础7 （f)（g）8 第二章 平面力系第二章 平面力系2-1 电动机重P=5000N ，放在水平梁AC 的中央,如图所示。

梁的A 端以铰链固定，另一端以撑杆BC 支持，撑杆与水平梁的夹角为30 0.如忽略撑杆与梁的重量，求绞支座A 、B 处的约束反力。

题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ，用绳子挂在支架的滑轮B 上，绳子的另一端接在绞车D 上,如图第二章 平面力系 9所示。

转动绞车，物体便能升起。

设滑轮的大小及轴承的摩擦略去不计，杆重不计，A 、B 、C 三处均为铰链连接。

当物体处于平衡状态时，求拉杆AB 和支杆BC 所受的力。

题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F AB BC 732.2732.3=-=2-3 如图所示，输电线ACB 架在两电线杆之间，形成一下垂线,下垂距离CD =f =1m ，两电线杆间距离AB =40m.电线ACB 段重P=400N ，可近视认为沿AB 直线均匀分布，求电线的中点和两端的拉力.题2—3图以AC 段电线为研究对象,三力汇交NF N F F F FF F F C A GA yC A x 200020110/1tan sin ,0,cos ,0=======∑∑解得：ααα2-4 图示为一拔桩装置。

工程力学第二版答案工程力学是工程学的基础学科之一，通过研究物体的力学行为来解决工程问题。

本文档是对工程力学第二版教材的习题答案的整理和总结。

希望能对学习该科目的学生以及工程领域从业者提供帮助。

第一章矢量代数与力学基本原理习题1-11.如何判断两个向量相等？2.什么是矢量的加法和减法？3.如何计算矢量的模和方向？答案：1.两个矢量相等的条件是它们的模和方向完全相同。

2.矢量的加法就是将两个矢量的对应分量相加，矢量的减法是将两个矢量的对应分量相减。

3.矢量的模可以通过计算矢量的分量的平方和的平方根来得到，矢量的方向可以通过计算矢量的分量的比值和反三角函数得到。

习题1-21.什么是力的平衡？2.如何判断一个物体在平衡状态下的受力情况？3.什么是支撑反力？答案：1.力的平衡指的是物体所受的合力为零的情况，物体处于静止或匀速直线运动的状态。

2.在平衡状态下，物体所受的合力为零，因此可以通过将所有作用力相互抵消来判断物体的受力情况。

3.支撑反力是指物体在受到外界作用力时，支持物体的支点对物体施加的反作用力。

第二章刚体力学基础习题2-11.什么是刚体？2.刚体有几个自由度？3.刚体在平面上的运动有哪些约束条件？答案：1.刚体指的是物体在力作用下，保持形状和大小不变的物体。

2.刚体有6个自由度，包括3个平移自由度和3个旋转自由度。

3.刚体在平面上的运动有3个约束条件，包括沿x轴平移、沿y轴平移和绕z轴旋转三个约束。

习题2-21.什么是力矩？2.如何计算力矩？3.力矩的方向规定是怎样的？答案：1.力矩是衡量力对物体旋转影响的物理量，也可以理解为力的偏转能力。

2.力矩可以通过力与力臂的乘积来计算，其中力臂是力对旋转轴的垂直距离。

3.力矩的方向遵循右手定则，即当右手握住力臂并使之指向力的方向时，拇指所指的方向即为力矩的方向。

结论本文档对工程力学第二版教材中的一些重要概念和习题进行了解答。

通过学习这些答案，读者可以更好地理解工程力学的基本原理和刚体力学基础，进一步提升解决工程问题的能力。

C1mABD441ADCP i=11B1(a)(b)习题13-2图13-2解：（1）建立支座移动的实状态（a ），和虚设单位力状态（b ）。

(2)由∑-=∆C R iiC 公式求三种情况时的D 点的水平位移：1）当只有支座A 发生向左10mm 的位移时)(1001.0)01.01(←-=-=⨯-=-=∆=∆∑mm m m C R i iC H D (负号表示D 点的水平位移与所设的向右的单位力方向相反，向左。

)2）当只有支座A 只发生向下10mm 的位移时)(5.20025.0)01.041(←-=-=⨯-=-=∆=∆∑mm m m C R i iCH D 3）当只有支座B 只发生向下10mm 的位移时)(5.20025.0)01.041(→==⨯--=-=∆=∆∑mm m m C R i iCH D （正号表示D 点的水平位移与所设的向右的单位力方向相同，向右。

）CBqAaM=qa 2aqa 223qax x2a2a1A1B2aM i=1A11aB22xx aP i=1a 1) a 2) a 3)习题13-5a)图13-5a 解：(1) 荷载作用的实状态如图13-5 a 1)。

其弯矩方程如a 1）式)]2,0[212a a x qx qa M P ∈=21-x(2) 选虚拟状态如图13-5 a 2)、a 3)。

其弯矩方程分别如a 2）、a 3）式)]2,0[2121a a x aM ∈-=x)]2,[21)(21],0[2132a a a x a x a x x a x M ⎪⎪⎩⎪⎪⎨⎧∈+-=--∈=x(3)由求位移公式知：1）积分实状态a 1) 和虚拟状态a 2)的弯矩表达式求B ϕ。

EIqa dx qx qa x a EI ds EI M M a P B 3)2)(21(132021-=-==∑⎰∑⎰21-x ϕ()2）积分实状态a 1) 和虚拟状态a 3)的弯矩表达式求VC ∆。

∑⎰=∆ds EIM M PV C 2)(24)2)(21()2)(21(1422022202↑-=⎥⎦⎤⎢⎣⎡+-+=+=⎰⎰⎰⎰EIqa dx qx qa a x dx qx qa x EI dx EIM M dx EI M M a a a a a PaP 21-x 21-x 右左C B 5m10mA xxP i=1xxCB A xxB ACP i=1CAB xxM i=1a 1) a 2) a 3) a 4)13-6a)13-6a) 解：(1) 荷载作用的实状态如图a 1)。

第13章点的运动学与刚体的基本运动13.1 点的运动学本节要点：ϕ=（ω为常例13.1 杆AB绕A点转动时，带动套在半径为R的固定大圆环上的小护环M运动，已知tω数）。

求小环M的运动方程、速度和加速度。

解2（用自然坐标法）例13.2 在曲柄摇杆机构中，曲柄OA 与水平线夹角的变化规律为24t πϕ=，设cm O O OA 101==，cm B O 241=，求B 点的运动方程和s t 1=时B 点的速度和加速度。

24B θθ==2ϕθ==例13.3一点作平面曲线运动，其速度在x 轴上的投影始终为一常数C 。

试证明在此情形下，点的加速度的大小为ρC v a 3=。

其中v 为点的速度的大小，ρ为轨迹的曲率半径。

13.2 刚体的基本运动本节要点：例13.4 荡木用两条等长的钢索平行吊起，如图所示，钢索长为l ，长度单位为m ，当荡木摆动时，钢索的摆动规律为t 6sin2ππϕ=，其中t 以s 计，试求当0=t 和1=t 时荡木中点M 的速度，加速度。

例13.5 已知：重物A 的（常数）初瞬时速度m/s 5.10=v 2m/s 1=A a 方向如图示。

m 30 .r =,m 5.0=R 求：①滑轮3s 内的转数；②重物B 在3s 内的行程；③重物B 在ｔ＝3s 时的速度；④滑轮边上C 点在初瞬时的加速度； ⑤滑轮边上C 点在ｔ＝3s 时的加速度。

2当t =3s 时，=τa a C =+=∴405.40122C a ⑤滑轮边上C 点在ｔ＝齿轮传动简介外啮合直齿轮 内啮合直齿轮齿轮齿条啮合轮系的传动比已知轮系中各齿轮的齿数Z 1、Z 2、Z 2’、Z 3、Z 3’、Z 4、Z 5，求i 15 。

例13.6 减速箱由四个齿轮构成如图所示。

齿轮2和齿轮3安装在同一轴上，与轴II 一起转动。

各齿轮的齿数分别为361=z ，1122=z ，z 3=32，z 4=128。

如主动轴Ⅰ的转速14501rn =，试求从动轴III1515n n i =的转速4n ？1 2 I II III3 42013年6月5日31n 1ⅣⅠⅡⅢ例减速箱由四个齿轮构成，如图所示。