3-3-2 两点间的距离公式

初中数学几何公式定理超全汇总140条01线1、同角或等角的余角相等2、过一点有且只有一条直线和已知直线垂直3、过两点有且只有一条直线4、两点之间线段最短5、同角或等角的补角相等6、直线外一点与直线上各点连接的所有线段中，垂线段最短7、平行公理经过直线外一点，有且只有一条直线与这条直线平行8、如果两条直线都和第三条直线平行，这两条直线也互相平行9、定理线段垂直平分线上的点和这条线段两个端点的距离相等10、逆定理和一条线段两个端点距离相等的点，在这条线段的垂直平分线上11、线段的垂直平分线可看作和线段两端点距离相等的所有点的集合12、定理1 关于某条直线对称的两个图形是全等形13、定理 2 如果两个图形关于某直线对称，那么对称轴是对应点连线的垂直平分线14、定理3 两个图形关于某直线对称，如果它们的对应线段或延长线相交，那么交点在对称轴上15、逆定理如果两个图形的对应点连线被同一条直线垂直平分，那么这两个图形关于这条直线对称02角16、同位角相等，两直线平行17、内错角相等，两直线平行18、同旁内角互补，两直线平行19、两直线平行，同位角相等20、两直线平行，内错角相等21、两直线平行，同旁内角互补22、定理1 在角的平分线上的点到这个角的两边的距离相等23、定理2 到一个角的两边的距离相同的点，在这个角的平分线上24、角的平分线是到角的两边距离相等的所有点的集合03三角形25、定理三角形两边的和大于第三边26、推论三角形两边的差小于第三边27、三角形内角和定理三角形三个内角的和等于180°28、推论1 直角三角形的两个锐角互余29、推论2 三角形的一个外角等于和它不相邻的两个内角的和30、推论3 三角形的一个外角大于任何一个和它不相邻的内角31、勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方，即a+b=c32、勾股定理的逆定理如果三角形的三边长a、b、c有关系a+b=c，那么这个三角形是直角三角形04等腰、直角三角形33、等腰三角形的性质定理等腰三角形的两个底角相等34、推论1 等腰三角形顶角的平分线平分底边并且垂直于底边35、等腰三角形的顶角平分线、底边上的中线和高互相重合36、推论3 等边三角形的各角都相等，并且每一个角都等于60°37、等腰三角形的判定定理如果一个三角形有两个角相等，那么这两个角所对的边也相等(等角对等边)38、推论1 三个角都相等的三角形是等边三角形39、推论 2 有一个角等于60°的等腰三角形是等边三角形40、在直角三角形中，如果一个锐角等于30°那么它所对的直角边等于斜边的一半41、直角三角形斜边上的中线等于斜边上的一半05相似、全等三角形42、定理平行于三角形一边的直线和其他两边(或两边的延长线)相交，所构成的三角形与原三角形相似43、相似三角形判定定理1 两角对应相等，两三角形相似(ASA)44、直角三角形被斜边上的高分成的两个直角三角形和原三角形相似45、判定定理2 两边对应成比例且夹角相等，两三角形相似(SAS)46、判定定理3 三边对应成比例，两三角形相似(SSS)47、定理如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似48、性质定理1 相似三角形对应高的比，对应中线的比与对应角平分线的比都等于相似比49、性质定理2 相似三角形周长的比等于相似比50、性质定理3 相似三角形面积的比等于相似比的平方51、边角边公理有两边和它们的夹角对应相等的两个三角形全等52、角边角公理有两角和它们的夹边对应相等的两个三角形全等53、推论有两角和其中一角的对边对应相等的两个三角形全等54、边边边公理有三边对应相等的两个三角形全等55、斜边、直角边公理有斜边和一条直角边对应相等的两个直角三角形全等56、全等三角形的对应边、对应角相等06四边形57、定理四边形的内角和等于360°58、四边形的外角和等于360°59、多边形内角和定理n边形的内角的和等于(n-2)×180°60、推论任意多边的外角和等于360°61、平行四边形性质定理1 平行四边形的对角相等62、平行四边形性质定理2 平行四边形的对边相等63、推论夹在两条平行线间的平行线段相等64、平行四边形性质定理3 平行四边形的对角线互相平分65、平行四边形判定定理1 两组对角分别相等的四边形是平行四边形66、平行四边形判定定理2 两组对边分别相等的四边形是平行四边形67、平行四边形判定定理3 对角线互相平分的四边形是平行四边形68、平行四边形判定定理4 一组对边平行相等的四边形是平行四边形初中几何公式定理：矩形69、矩形性质定理1 矩形的四个角都是直角70、矩形性质定理2 矩形的对角线相等71、矩形判定定理1 有三个角是直角的四边形是矩形72、矩形判定定理2 对角线相等的平行四边形是矩形初中几何公式：菱形73、菱形性质定理1 菱形的四条边都相等74、菱形性质定理2 菱形的对角线互相垂直，并且每一条对角线平分一组对角75、菱形面积=对角线乘积的一半，即S=(a×b)÷276、菱形判定定理1 四边都相等的四边形是菱形77、菱形判定定理2 对角线互相垂直的平行四边形是菱形07正方形78、正方形性质定理1 正方形的四个角都是直角，四条边都相等79、正方形性质定理2正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角80、定理1 关于中心对称的两个图形是全等的81、定理2 关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分82、逆定理如果两个图形的对应点连线都经过某一点，并且被这一点平分，那么这两个图形关于这一点对称08等腰梯形83、等腰梯形性质定理等腰梯形在同一底上的两个角相等84、等腰梯形的两条对角线相等85、等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形86、对角线相等的梯形是等腰梯形09等分87、平行线等分线段定理如果一组平行线在一条直线上截得的线段相等，那么在其他直线上截得的线段也相等88、推论1 经过梯形一腰的中点与底平行的直线，必平分另一腰89、推论2 经过三角形一边的中点与另一边平行的直线，必平分第三边90、三角形中位线定理三角形的中位线平行于第三边，并且等于它的一半91、梯形中位线定理梯形的中位线平行于两底，并且等于两底和的一半L=(a+b)÷2 S=L×h92 、(1)比例的基本性质如果a:b=c:d,那么ad=bc 如果ad=bc,那么a:b=c:d93、(2)合比性质如果a/b=c/d,那么(a±b)/b=(c±d)/d94、(3)等比性质如果a/b=c/d=…=m/n(b+d+…+n≠0)，那么，(a+c+…+m)/(b+d+…+n)=a/b95、平行线分线段成比例定理三条平行线截两条直线，所得的对应线段成比例96、推论平行于三角形一边的直线截其他两边(或两边的延长线)，所得的对应线段成比例97、定理如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例，那么这条直线平行于三角形的第三边98、平行于三角形的一边，并且和其他两边相交的直线，所截得的三角形的三边与原三角形三边对应成比例99、任意锐角的正弦值等于它的余角的余弦值，任意锐角的余弦值等于它的余角的正弦值100、任意锐角的正切值等于它的余角的余切值，任意锐角的余切值等于它的余角的正切值10圆101、圆是定点的距离等于定长的点的集合102、圆的内部可以看作是圆心的距离小于半径的点的集合103、圆的外部可以看作是圆心的距离大于半径的点的集合104、同圆或等圆的半径相等105、到定点的距离等于定长的点的轨迹，是以定点为圆心，定长为半径的圆106、和已知线段两个端点的距离相等的点的轨迹，是着条线段的垂直平分线107、到已知角的两边距离相等的点的轨迹，是这个角的平分线108、到两条平行线距离相等的点的轨迹，是和这两条平行线平行且距离相等的一条直线109、定理不在同一直线上的三个点确定一条直线110、垂径定理垂直于弦的直径平分这条弦并且平分弦所对的两条弧111、推论 1 ①平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧②弦的垂直平分线经过圆心，并且平分弦所对的两条弧③平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧112、推论2 圆的两条平行弦所夹的弧相等113、圆是以圆心为对称中心的中心对称图形114、定理在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦的弦心距相等115、推论在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两弦的弦心距中有一组量相等那么它们所对应的其余各组量都相等116、定理一条弧所对的圆周角等于它所对的圆心角的一半117、推论1 同弧或等弧所对的圆周角相等;同圆或等圆中，相等的圆周角所对的弧也相等118、推论2 半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径119、推论3 如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形120、定理圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角121、①直线L和⊙O相交d﹤r ②直线L和⊙O相切d=r ③直线L和⊙O相离d﹥r122、切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线123、切线的性质定理圆的切线垂直于经过切点的半径124、推论1 经过圆心且垂直于切线的直线必经过切点125、推论2 经过切点且垂直于切线的直线必经过圆心126、切线长定理从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角127、圆的外切四边形的两组对边的和相等128、弦切角定理弦切角等于它所夹的弧对的圆周角129、推论如果两个弦切角所夹的弧相等，那么这两个弦切角也相等130、相交弦定理圆内的两条相交弦，被交点分成的两条线段长的积相等131、推论如果弦与直径垂直相交，那么弦的一半是它分直径所成的两条线段的比例中项132、切割线定理从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项133、推论从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等134、如果两个圆相切，那么切点一定在连心线上135、①两圆外离d﹥R+r ②两圆外切d=R+r③两圆相交R-r﹤d﹤R+r(R﹥r)④两圆内切d=R-r(R﹥r) ⑤两圆内含d﹤R-r(R﹥r)136定理相交两圆的连心线垂直平分两圆的公共弦137、定理把圆分成n(n≥3):⑴依次连结各分点所得的多边形是这个圆的内接正n边形⑵经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形138、定理任何正多边形都有一个外接圆和一个内切圆，这两个圆是同心圆139、正n边形的每个内角都等于(n-2)×180°/n140、定理正n边形的半径和边心距把正n边形分成2n个全等的直角三角形141、正n边形的面积Sn=pnrn/2 p表示正n边形的周长142、正三角形面积√3a/4 a表示边长143、如果在一个顶点周围有k个正n边形的角，由于这些角的和应为360°，因此k×(n-2)180°/n=360°化为(n-2)(k-2)=4144、弧长计算公式：L=nπR/180145、扇形面积公式：S扇形=nπR/360=LR/2146、内公切线长= d-(R-r) 外公切线长= d-(R+r）。

向量的概念一、高考要求：理解有向线段及向量的有关概念,掌握求向量和与差的三角形法则和平行四边形法则,掌握向量加法的交换律和结合律.二、知识要点：1. 有向线段:具有方向的线段叫做有向线段,在有向线段的终点处画上箭头表示它的方向.以A 为始点,B 为终点的有向线段记作AB ,注意:始点一定要写在前面,已知AB ,线段AB 的长度叫做有向线段AB 的长(或模),AB 的长度记作AB ||.有向线段包含三个要素:始点、方向和长度.2. 向量:具有大小和方向的量叫做向量,只有大小和方向的向量叫做自由向量.在本章中说到向量,如不特别说明,指的都是自由向量.一个向量可用有向线段来表示,有向线段的长度表示向量的大小,有向线段的方向表示向量的方向.用有向线段AB 表示向量时,我们就说向量AB .另外,在印刷时常用黑体小写字母a 、b 、c 、…等表示向量;手写时可写作带箭头的小写字母a 、b 、c 、…等.与向量有关的概念有:(1) 相等向量:同向且等长的有向线段表示同一向量或相等的向量.向量a 和b 同向且等长,即a 和b 相等,记作a =b .(2) 零向量:长度等于零的向量叫做零向量,记作0.零向量的方向不确定.(3) 位置向量:任给一定点O 和向量a ,过点O 作有向线段OA a =,则点A 相对于点O 的位置被向量a 所唯一确定,这时向量a 又常叫做点A 相对于点O 的位置向量.(4) 相反向量:与向量a 等长且方向相反的向量叫做向量a 的相反向量,记作a -.显然,()0a a +-=.(5) 单位向量:长度等于1的向量,叫做单位向量,记作e .与向量a 同方向的单位向量通常记作0a ,容易看出:0a a a =│ │. (6) 共线向量(平行向量):如果表示一些向量的有向线段所在的直线互相平行或重合,即这些向量的方向相同或相反,则称这些向量为共线向量(或平行向量).向量a 平行于向量b ,记作a ∥b .零向量与任一个向量共线(平行).三、典型例题：例:在四边形ABCD 中,如果AB DC =且AB BC =│ │ │ │ ,那么四边形ABCD 是哪种四边形? 四、归纳小结：1. 用位置向量可确定一点相对于另一点的位置,这是用向量研究几何的依据.2. 共线向量(平行向量)可能有下列情况: (1)有一个为零向量;(2)两个都为零向量;(3)方向相同,模相等(即相等向量);(4)方向相同,模不等;(5)方向相反,模相等;(6)方向相反,模不等.五、基础知识训练：（一）选择题：1. 下列命题中: (1)向量只含有大小和方向两个要素. (2)只有大小和方向而无特定的位置的向量叫自由向量. (3)同向且等长的有向线段表示同一向量或相等的向量. (4)点A 相对于点B 的位置向量是BA . 正确的个数是( )A.1个B.2个C.3个D.4个2. 设O 是正△ABC 的中心,则向量,,AO OB OC 是( )A.有相同起点的向量B.平行向量C.模相等的向量D.相等向量3. a b =的充要条件是( )A.a b =│ │ │ │ B.a b =│ │ │ │ 且a b ∥ []l C.a b ∥ D.a b =│ │ │ │ 且a 与b 同向 4. AA BB ''=是四边形ABB A ''是平行四边形的( )A.充分条件B.必要条件C.充要条件D.既非充分又非必要条件5. 依据下列条件,能判断四边形ABCD 是菱形的是( )A.AD BC =B.AD BC ∥且AB CD ∥C.AB DC =且AB AD =│ │ │ │ D.AB DC =且AD BC = 6. 下列关于零向量的说法中,错误的是( )A.零向量没有方向B.零向量的长度为0C.零向量与任一向量平行D.零向量的方向任意7. 设与已知向量a 等长且方向相反的向量为b ,则它们的和向量a b +等于( )A.0B.0C.2aD.2b（二）填空题：8. 下列说法中: (1)AB 与BA 的长度相等 (2)长度不等且方向相反的两个向量不一定共线 (3)两个有共同起点且相等的向量,终点必相同(4)长度相等的两个向量必共线。

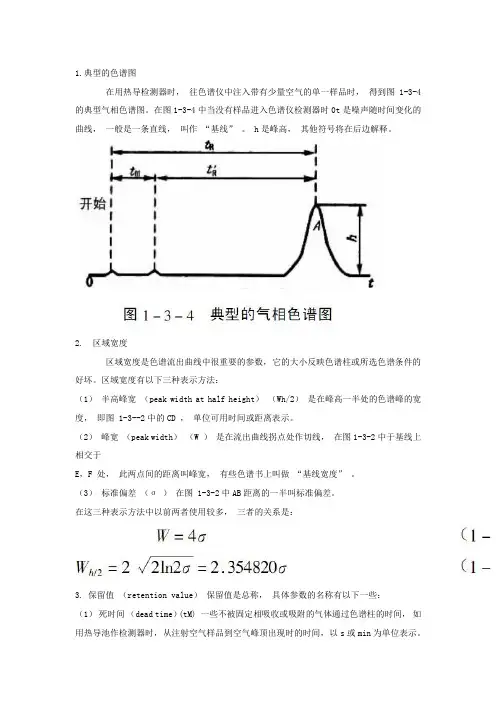
1.典型的色谱图在用热导检测器时，往色谱仪中注入带有少量空气的单一样品时，得到图1-3-4的典型气相色谱图。

在图1-3-4中当没有样品进入色谱仪检测器时0t是噪声随时间变化的曲线，一般是一条直线，叫作“基线” 。

h是峰高，其他符号将在后边解释。

2. 区域宽度区域宽度是色谱流出曲线中很重要的参数，它的大小反映色谱柱或所选色谱条件的好坏。

区域宽度有以下三种表示方法：（1）半高峰宽（peak width at half height）（Wh/2）是在峰高一半处的色谱峰的宽度，即图 1-3--2中的CD ，单位可用时间或距离表示。

（2）峰宽（peak width）（W ）是在流出曲线拐点处作切线，在图1-3-2中于基线上相交于E，F 处，此两点间的距离叫峰宽，有些色谱书上叫做“基线宽度” 。

（3）标准偏差（σ ）在图 1-3-2中AB距离的一半叫标准偏差。

在这三种表示方法中以前两者使用较多，三者的关系是：3. 保留值（retention value）保留值是总称，具体参数的名称有以下一些：（1）死时间（dead time）(tM) 一些不被固定相吸收或吸附的气体通过色谱柱的时间，如用热导池作检测器时，从注射空气样品到空气峰顶出现时的时间，以s或min为单位表示。

（2）死体积（dead volume）（Vm）指色谱柱中不被固定相占据的空间及进样系统管道和检测系统的总体积，等于死时间乘以载气的流速。

（3）死区域（dead zone）（ Vg）指色谱柱中不被固定相占据的空间。

（4）保留时间（retention time）（ tR）从注射样品到色谱峰顶出现时的时间，以s或min为单位表示。

（5）调整保留时间（adjusted retention time）保留时间减去死时间即为调整保留时间（tR-tM）。

（6）保留体积（retention volume）（ Vr）从注射样品到色谱峰顶出现时，通过色谱系统载气的体积，一般可用保留时间乘载气流速求得，以mL为单位表示。

学而思奥数模块之行程问题1、基本行程问题：基本概念：行程问题是研究物体运动的，它研究的是物体速度、时间、行程三者之间的关系。

基本公式：路程＝速度×时间；路程÷时间＝速度；路程÷速度＝时间关键问题：确定行程过程中的位置2、简单的相遇、追及问题：相遇问题：速度和×相遇时间＝相遇路程追击问题：追击时间＝路程差÷速度差简单的相遇与追及问题各自解题时的入手点及需要注意的地方1.相遇问题：与速度和、路程和有关⑴是否同时出发⑵是否有返回条件⑶是否和中点有关：判断相遇点位置⑷是否是多次返回：按倍数关系走。

⑸一般条件下，入手点从"和"入手，但当条件与"差"有关时，就从差入手，再分析出时间，由此再得所需结果2.追及问题：与速度差、路程差有关⑴速度差与路程差的本质含义⑵是否同时出发，是否同地出发。

⑶方向是否有改变⑷环形时：慢者落快者整一圈(1) 甲、乙两列火车同时从相距700千米的两地相向而行，甲列车每小时行85千米，乙列车每小时行90千米，几小时两列火车相遇？(2) 两列火车从两个车站同时相向出发，甲车每小时行48千米，乙车每小时行78千米，经过2.5小时两车相遇。

两个车站之间的铁路长多少千米？(3) 甲、乙两列火车同时从相距988千米的两地相向而行，经过5.2小时两车相遇。

甲列车每小时行93千米，乙列车每小时行多少千米？（1）师徒两人合作加工520个零件，师傅每小时加工30个，徒弟每小时加工20个，几小时以后还有70个零件没有加工？（2）甲、乙两队合挖一条水渠，甲队从东往西挖，每天挖75米；乙队从西往东挖，每天比甲队少挖5米，两队合作8天挖好，这条水渠一共长多少米？(3) 甲、乙两艘轮船从相距654千米的两地相对开出而行，8小时两船还相距22千米。

已知乙船每小时行42千米，甲船每小时行多少千米？（4）一辆汽车和一辆自行车从相距172.5千米的甲、乙两地同时出发，相向而行，3小时后两车相遇。

四年级数学上、下册计算公式大全，学习收藏一份四年级数学上册数学公式1、两点之间的所有连线中，线段最短。

2、两点之间线段的长度，叫做两点间的距离。

3、由一点引出的两条射线，所组成的圆形叫角。

4、小于90度的角叫锐角，大于90度而小于180度的角叫钝角。

5、角的两边在一条直线上，这样的角叫做平角。

6、一个、十、百、千、万、十万、百万、千万、亿、十亿、百亿都是计数单位。

7、把计数单位按一定的顺序排列起来，他们所占的位置叫做数位。

8、两条直线相交可以组成四个角。

9、两条直线相交只(多品小学教育张老师分享)有一个交点。

10、两条直线相交成直角时，这两条直线叫做互相垂直，其中一条直线叫做另一条直线的垂线。

11、从直线外一点到这条直线所画的垂直线段的长度，叫做这点到直线的垂直距离。

12、在同一个平面内，不想交的两条直线叫做平行线，也可以说两条直线互相平行。

13、所有垂直线段的长度都相等。

14、像1、2、3、4、5、6......这样一个一个的数，都是自然数。

15、一颗也看不见，用0表示，0也是自然数。

16、5的倍数，个位上不是5，就是0。

16、一个数它各数位上的数之和是3的倍数，那这个数一定是3的倍数。

18、只有1和它本身两个因数的数叫做质数，（也叫做素数）。

除了1和它本身外，还有其它因数的数叫做合数。

19、1既不是质数，也不是合数。

20、2、3、5、7、都是质数。

21、1是每个数的因数，而且是最小的一个。

22、一个数最大的因数就是它自己。

23、任何一个合数都可以写成几个质因数相乘的形式。

24、把一个数写成几个质数相乘的形式，叫做分解质因数。

25、个位和十位上的数的和也是3的倍数。

26、一组数据出现最多的那个数叫做这组数据的众数。

27、2的倍数，个位上是0、2、4、6、828、4、6、8、9、10都是合数。

29、乘数也叫做因数。

四年级数学下册公式大全一、四则运算各部分间的关系：1、和=加数+加数加数＝和-另一个加数2、差=被减数－减数减数＝被减数－差被减数＝差+减数3、积=乘数×乘数乘数=积÷另一个乘数4、商=被除数÷除数除数＝被除数÷商被除数＝商×除数5、被除数＝商×除数+余数除数＝（被除数-余数）÷商商=（被除数-余数）÷除数余数=被除数-商×除数二、与简便运算有关的知识：(重要的算式:25×4=100125×8=1000)1、加法交换律：两个数相加，交换加数的位置，和不变。

高中物理（选修3-2）公式1、磁通量：θsin BS Φ=，θ是磁场方向与导体面的夹角。

2、磁通量的变化量：12ΦΦΦ-=∆,取绝对值计算。

3、磁通量的变化率(感应电动势)：t ΦE ∆∆=4、)()(磁场不变，面积变面积不变，磁场变tS nB t B nS t n E ∆∆=∆∆=∆∆Φ=(n 指匝数)，适宜求平均感应电动势5、θsin BLv E =，θ是磁场与运动方向的夹角，适宜求瞬时感应电动势6、直导体绕一端转动切割磁感线：ω221BL E =7、感应电量：RΦn t t R Φn t R E t I q ∆=∆⋅∆∆=∆⋅=∆= 6、自感电动势：t I L E ∆∆=，L 为线圈的自感系数 7、交变电流的电动势峰值：ωnBS E m =8、正余弦交变电流的瞬时电动势：t E e t E e m m ωωcos sin ==或9、周期与频率：fT 12==ωπ10、理想变压器的变压、变流规律和功率关系⑴变压规律：2121n n u u =； ⑵变流规律：1221n n I I =； ⑶功率：出入P P =11、变压器有二个副线圈的情况⑴变压规律：tn u n u n u ∆∆===φ332211； ⑵变流规律：332211n I n I n I +=；⑶功率：出入P P =12、理想变压器各种物理量的决定关系。

⑴输入电压决定输出电压；⑵输出电流决定输入电流；⑶输出功率决定输入功率13、远距离输电各物理量关系 ⑴发电机的输出功率为：2211I U I U P ==； ⑵输电线路上的电压损失为：322U U R I U -==损 ⑶输电线上功率损失为：R I P 22=损 ⑷用户得到的功率为：损用P P P -=。

多次相遇问题（解析版）一、多次相遇与全程的关系1. 两地相向出发：第1次相遇，共走1个全程；第2次相遇，共走3个全程；第3次相遇，共走5个全程；…………， ………………；第N 次相遇，共走2N-1个全程；注意：除了第1次，剩下的次与次之间都是2个全程。

即甲第1次如果走了N 米，以后每次都走2N 米。

2. 同地同向出发：第1次相遇，共走2个全程；第2次相遇，共走4个全程；第3次相遇，共走6个全程；…………， ………………；第N 次相遇，共走2N 个全程；3、多人多次相遇追及的解题关键多次相遇追及的解题关键 几个全程多人相遇追及的解题关键 路程差【例 1】 小明和小红两人在长100米的直线跑道上来回跑步，做体能训练，小明的速度为6米/秒，小红的速度为4米/秒．他们同时从跑道两端出发，连续跑了12分钟．在这段时间内，他们迎面相遇了多少次？【解析】 第一次相遇时，两人共跑完了一个全程，所用时间为：1006410÷+=（）(秒)．此后，两人每相遇一次，就要合跑2倍的跑道长，也就是每20秒相遇一次，除去第一次的10秒，两人共跑了126010710⨯-=(秒)．求出710秒内两人相遇的次数再加上第一次相遇，就是相遇的总次数．列式计算为：1006410÷+=（）(秒)，1260101023510⨯-÷⨯=（）（），共相遇35136+=(次)。

注：解决问题的关键是弄清他们首次相遇以及以后每次相遇两人合跑的路程长．【例 2】 A 、B 两地间有条公路，甲从A 地出发，步行到B 地，乙骑摩托车从B 地出发，不停地往返于A 、B 两地之间，他们同时出发，80分钟后两人第一次相遇，100分钟后乙第一次追上甲，问：当甲到达B 地时，乙追上甲几次？【解析】第一次追上第一次相遇乙甲F E B由上图容易看出：在第一次相遇与第一次追上之间，乙在1008020-=(分钟)内所走的路程恰等于线段FA 的长度再加上线段AE 的长度，即等于甲在(80100+)分钟内所走的路程，因此，乙的速度是甲的9倍(18020=÷)，则BF 的长为AF 的9倍，所以，甲从A 到B ，共需走80(19)800⨯+=(分钟)乙第一次追上甲时，所用的时间为100分钟，且与甲的路程差为一个AB 全程．从第一次追上甲时开始，乙每次追上甲的路程差就是两个AB 全程，因此，追及时间也变为200分钟(1002=⨯)，知识精讲所以，在甲从A到B的800分钟内，乙共有4次追上甲，即在第100分钟，300分钟，500分钟和700分钟．【例 3】（难度等级3）甲、乙两人分别从A、B两地同时出发相向而行，乙的速度是甲的23，二人相遇后继续行进，甲到B地、乙到A地后立即返回．已知两人第二次相遇的地点距第三次相遇的地点是100千米，那么，A、B两地相距千米．【解析】由于甲、乙的速度比是2:3，所以在相同的时间内，两人所走的路程之比也是2:3．第一次相遇时，两人共走了一个AB的长，所以可以把AB的长看作5份，甲、乙分别走了2份和3份；第二次相遇时，甲、乙共走了三个AB，乙走了236⨯=份；第三次相遇时，甲、乙共走了五个AB，乙走了2510⨯=份．乙第二次和第三次相距10－6=4（份）所以一份距离为：100÷4=25（千米），那么A、B两地距离为：5×25＝125（千米）【巩固】（难度等级※※※）小王、小李二人往返于甲、乙两地，小王从甲地、小李从乙地同时出发，相向而行，两人第一次在距甲地3千米处相遇，第二次在距甲地6千米处相遇(追上也算作相遇)，则甲、乙两地的距离为千米．【解析】由于两人同时出发相向而行，所以第一次相遇一定是迎面相遇；由于本题中追上也算相遇，所以两人第二次相遇可能为迎面相遇，也可能为同向追及．①如果第二次相遇为迎面相遇，如下图所示，两人第一次在A处相遇，第二次在B处相遇．由于第一次相遇时两人合走1个全程，小王走了3千米；从第一次相遇到第二次相遇，两人合走2个全程，所以这期间小王走了326⨯=千米，由于A、B之间的距离也是3千米，所以B与乙地的距离为(63)2 1.5-÷=千米，甲、乙两地的距离为6 1.57.5+=千米；李王乙甲甲王李乙②如果第二次相遇为同向追及，如上图，两人第一次在A处相遇，相遇后小王继续向前走，小李走到甲地后返回，在B处追上小王．在这个过程中，小王走了633-=千米，小李走了639+=千米，两人的速度比为3:91:3=．所以第一次相遇时小李也走了9千米，甲、乙两地的距离为9312+=千米．所以甲、乙两地的距离为7.5千米或12千米．【巩固】（难度级别3）A，B两地相距540千米。

高一下册数学教案全册高一下册数学教案电子版(三篇)高一下册数学教案全册高一下册数学教案电子版篇一1、结合实际问题情景，理解分层抽样的必要性和重要性；2、学会用分层抽样的方法从总体中抽取样本；3、并对简单随机抽样、系统抽样及分层抽样方法进行比较，揭示其相互关系。

教学重点：通过实例理解分层抽样的方法。

教学难点：分层抽样的步骤。

教学过程：一、问题情境1、复习简单随机抽样、系统抽样的概念、特征以及适用范围。

2、实例：某校高一、高二和高三年级分别有学生名，为了了解全校学生的视力情况，从中抽取容量为的样本，怎样抽取较为合理？二、学生活动能否用简单随机抽样或系统抽样进行抽样，为什么？指出由于不同年级的学生视力状况有一定的差异，用简单随机抽样或系统抽样进行抽样不能准确反映客观实际，在抽样时不仅要使每个个体被抽到的机会相等，还要注意总体中个体的层次性。

由于样本的容量与总体的个体数的比为100∶2500=1∶25，所以在各年级抽取的个体数依次是。

即40，32，28。

三、建构数学1、分层抽样：当已知总体由差异明显的几部分组成时，为了使样本更客观地反映总体的情况，常将总体按不同的特点分成层次比较分明的几部分，然后按各部分在总体中所占的比进行抽样，这种抽样叫做分层抽样，其中所分成的各部分叫“层”。

说明：①分层抽样时，由于各部分抽取的个体数与这一部分个体数的比等于样本容量与总体的个体数的比，每一个个体被抽到的可能性都是相等的；②由于分层抽样充分利用了我们所掌握的信息，使样本具有较好的代表性，而且在各层抽样时可以根据具体情况采取不同的抽样方法，所以分层抽样在实践中有着非常广泛的应用。

高一下册数学教案全册高一下册数学教案电子版篇二教学目标：1、知识与技能目标：理解并掌握圆的标准方程，会根据不同条件求圆的标准方程，能从圆的标准方程熟练地写出它的圆心坐标与半径。

2、过程与方法目标：通过对圆的标准方程的推导及应用，渗透数形结合、待定系数法等数学思想方法，提高学生的观察、比较、分析、概括等思维能力。

物理公式（必修1）1.速度：v=△x△t单位：m/s△x:位移△t:发生这个位移所用时间2.平均速度：⎺v=△x△t单位：m/s△x:路程△t:发生这个路程所用总时间⎺v:平均速度3.加速度：a=△v△t=v-v0t单位:m/s2或m·s-2△v:速度变化量△t:发生这一变化所用时间 v:末速度v0：初速度 t:运动时间4.匀变速直线运动公式V=v0+at 单位：m/sV：末速度 v0:初速度 a:加速度 t：运动时间X=v0t+12at2单位：mX：位移 v0:初速度 t：运动时间 a:加速度V2-v02=2ax 单位：m/sV：末速度 v0:初速度 a:加速度 X:位移⎺V=v0+v2单位:m/s⎺v:平均速度v0:初速度 V：末速度5.自由落体运动公式V=gt单位：m/sV:自由落体速度 g:10m/s2 t:自由落体时间h=12gt2单位：mh:自由落体高度 g:10m/s2 t:自由落体时间v2=2gh单位：m/sV:自由落体速度 g:10m/s2 h:自由落体高度6.重力：G=mg 单位：NG:重力 m:质量 g:10m/s27.滑动摩擦力:F=μF N 单位:NF:滑动摩擦力μ：摩擦因数（只与接触面材质有关）F N:正压力8.胡克定律：F=kx单位：NF:弹力 k:劲度系数(弹簧自身性质) x:弹簧伸长量9.牛顿第二定律：F=ma单位：NF：力 m:质量 a:加速度10.牛顿第三定律：F=-F,单位:NF:作用力–F:反作用力11.超重：F=m(g+a)单位：NF:力 m:质量 g:10m/s2 a:加速度12.失重：F=m(g-a)单位：NF:力 m:质量 g:10m/s2 a:加速度物理公式（必修2）1.平抛运动公式v x=v0单位：m/sv x：水平速度 v0:初速度v y=gt 单位:m/sv y:竖直速度 g:10m/s2 t:时间x=v0t单位：mx:水平位移 v0:初速度 t:时间y=12gt2单位：my:竖直位移 g:10m/s2 t：时间2.圆周运动公式V=△s△t单位：m/sV:线速度△s:通过的弧长△t:时间ω=△θ△t单位：rad/sω:角速度△θ：扫过的角度△t:时间V=ωr单位：m/sV：线速度ω：角速度 r:半径V=2∏rT单位：m/sV:线速度 r:半径 T:周期ω=2∏T单位：rad/sω:角速度 T:周期F=m v2r=mrω2=mr(2∏T)2=ma n 单位：NF:向心力 m:质量 v:线速度 r:半径ω：角速度 T:周期a n:向心加速度3．万有引力定律：F=G m1m2r2单位：NF:万有引力 G:6.67×10-11N·m2/kg2 m1,m2:两物体的质量r:半径4.天体运动：G Mmr2=mv2r=mrω2=m4∏2T2r=ma n单位：NG:6.67×10-11N·m2/kg2 M:中心天体质量 m:环绕天体质量 r:半径 v:环绕角速度ω：环绕线速度 T:周期a n：向心加速度5.黄金带换式：G Mmr2=mg（m在M表面）G:6.67×10-11N·m2/kg2 M:中心天体质量 m:环绕天体质量r:半径 g:10m/s26.功W=Flcosθ单位：JW:功 F:力 l:在力的方向上移动的距离θ:力和运动方向的夹角7.功率：P=Wt=Fvcosα单位：wP:功率 W：功 t:做工时间 F：力 v：速度α：夹角8.重力势能：E p=mgh单位：JE P:重力势能 m:质量 g:10m/s2 h:高度9.重力做功：W G=mgh1-mgh2=E p1-E p2单位：JW G: 重力做功 m:质量 g:10m/s2 h1,h2:高度E p1,E p2:初末位置重力势能10.动能：E k=12mv2单位:JE k:动能 m:质量 v：速度11.动能定理：W=12mv22-12mv12单位：JW：功 m:质量 v1v2:初末速度12.机械能守恒定律：E k1+E p1=E k2+E p2E k1:初状态势能 E p1：初状态动能 E k2：末状态势能E p2：末状态动能物理公式（选修3-1）1.库仑定律：F=kq1q2r2单位：NF:库仑力 k:9.0×109N·m2/C2 q1q2:两个点电荷的电荷量r：两个点电荷之间的距离2.电场强度：E=Fq=kQr2=Ud单位：N/C或V/mE:电场强度 F:电荷受到的电场力 q:电荷所带电荷量k:9.0×109N·m2/C2 Q:场源电荷的电荷量r:到场源电荷的距离 U:电势d:两点沿电场强度方向距离3.电势：φ=E pq单位：Vφ:电势 E p:某一点电势能 q:电荷量4.电势差：U AB=φA-φB=W ABq=Ed单位：VU AB:电势差φA,φB:A,B点电势W AB:在AB两点间移动点电荷时静电力做的功q:点电荷电荷量 E:电场强度 d:两点沿电场方向的距离5.电容:C=QU=εr S4∏kd单位：FC:电容 Q:电容器所带电荷量 U:两极板间电势差εr:介电常数 S:两极板间正对面积 k:9.0×109N·m2/C2 d:极板距离6.带电粒子在电场中的偏转y=qUl22mv02d ,tanθ=qUlmv02dy：偏移量 tanθ:偏转角的正切值。

高中物理公式汇编一、力学公式1、胡克定律： F = Kx (x为伸长量或压缩量,K为倔强系数，只与弹簧的原长、粗细和材料有关)2、重力：G = mg (g随高度、纬度、地质结构而变化)3、求F!、F2两个共点力的合力的公式：F= F,2F222F,F2COS^合力的方向与F i成二角：F2 sin 0tg ：■=F, + F2 cos日注意：(1)力的合成和分解都均遵从平行四边行法则。

(2) 两个力的合力范围：F i—F2 < F_ F i +F2(3) 合力大小可以大于分力、也可以小于分力、也可以等于分力。

4、两个平衡条件：(1)共点力作用下物体的平衡条件：静止或匀速直线运动的物体，所受合外力为零。

' F=0 或' F x=0 x F y=0推论：［1］非平行的三个力作用于物体而平衡，则这三个力一定共点。

［2］几个共点力作用于物体而平衡，其中任意几个力的合力与剩余几个力(一个力)的合力一定等值反向(2 )有固定转动轴物体的平衡条件：力矩代数和为零.力矩：M=FL (L为力臂，是转动轴到力的作用线的垂直距离)5、摩擦力的公式：(1 )滑动摩擦力：f=収说明：a、N为接触面间的弹力，可以大于G;也可以等于G;也可以小于Gb、」为滑动摩擦系数，只与接触面材料和粗糙程度有关，与接触面积大小、接触面相对运动快慢以及正压力N无关.(2 )静摩擦力：由物体的平衡条件或牛顿第二定律求解，与正压力无关•大小范围：0辽f静冬f m (f m为最大静摩擦力，与正压力有关)说明：a、摩擦力可以与运动方向相同，也可以与运动方向相反，还可以与运动方向成一定夹角。

b、摩擦力可以作正功，也可以作负功，还可以不作功。

c、摩擦力的方向与物体间相对运动的方向或相对运动趋势的方向相反。

d、静止的物体可以受滑动摩擦力的作用，运动的物体可以受静摩擦力的作用。

6、浮力: F= : Vg (注意单位)7、万有引力：(1).适用条件m1m2F=G丁r(2) . G为万有引力恒量(3) .在天体上的应用：(M —天体质量R 一天体半径g 一天体表面重力a 、万有引力=向心力匀速：V t/2 =V s/2 ；匀加速或匀减速直线运动： V t/2 <V s/2(4)初速为零的匀加速直线运动 ，在1s 、2s 、3s ……ns 内的位移之比为12： 22：32..... n 2; 在第1s 内、第2s 内、第3s 内 ....... 第ns 内的位移之比为1: 3: 5 .......(2n-1);在第1米内、第2米内、第3米内 ........ 第n 米内的时间之比为1: (、• 2-1):■- 3 〜》2) .... ( . n i ：；n ^1)(5) 初速无论是否为零，匀变速直线运动的质点，在连续相邻的相等的时间间隔内的位移之差为加速度) Mm 2(R h)V 2 (R h)2(R h)b 、在地球表面附近，重力 =万有引力 Mmmg = G 亍R 2c 、第一宇宙速度V 2mg = m ——RM g = G 2R 2v= .. gR = GM / Rq 1q 2 &库仑力：F=K±2" r9、 电场力：F=qE (适用条件)(F 与电场强度的方向可以相同，也可以相反)10、磁场力：(1)洛仑兹力：磁场对运动电荷的作用力。

专题十三 模型专题（5） 传送带模型【重点模型解读】传送带模型是高中既典型又基础的物理模型，且容易结合生活实际来考察生活实际问题，传送带模型的考查分为两方面，一方面是动力学问题考察(包括划痕)，另一方面是能量转化问题考查。

一、模型认识 项目 图示滑块可能的运动情况滑块受（摩擦）力分析 情景1①可能一直加速受力f=μmg②可能先加速后匀速先受力f=μmg ，后f=0情景2①v 0>v 时,可能一直减速,也可能先减速再匀速 受力f=μmg 先受力f=μmg ，后f=0②v 0<v 时,可能一直加速,也可能先加速再匀速 受力f=μmg 先受力f=μmg ，后f= 情景3①传送带较短时,滑块一直减速达到左端受力f=μmg②传送带较长时,滑块还要被传送带传回右端。

其中,若v 0>v,返回时速度为v;若v 0<v,返回时速度为v 0 受力f=μmg （方向一直向右）减速和反向加速时受力f=μmg （方向一直向右），匀速运动f=0 情景4①可能一直加速受摩擦力f =μmg cos θ ②可能先加速后匀速先受摩擦力f=μmgcosθ，后f=mgsinθ（静） 情景5①可能一直以同一加速度a 加速 受摩擦力f=μmgcosθ ②可能先加速后匀速 先受摩擦力f=μmgcosθ，后f=mgsinθ（静） ③可能先以a 1加速后以a 2加速先受摩擦力f=μmgcosθ，后受反向的摩擦力f=μmgcosθ二、传送带模型问题的关键(1)对物体所受的摩擦力进行正确的分析判断。

(2)物体的速度与传送带速度相等的时刻就是物体所受摩擦力发生突变的时刻。

三、解答传送带问题应注意的事项(1)比较物块和传送带的初速度情况，分析物块所受摩擦力的大小和方向，其主要目的是得到物块的加速度。

(2)关注速度相等这个特殊时刻，水平传送带中两者一块匀速运动，而倾斜传送带需判断μ与tan θ的关系才能决定物块以后的运动。

（3）要注意摩擦力做功情况的分析，摩擦生热的能量损失计算时要注意相对位移的分析。

七年级数学上册数轴上的动点问题专题复习动点问题处理策略1、数轴上两点间的距离，即为这两点所对应的坐标差的绝对值，也即用右边的数减去左边的数的差。

即数轴上两点间的距离=右边点表示的数－左边点表示的数。

2、如何表示运动过程中的数：点在数轴上运动时，由于数轴向右的方向为正方向，因此向右运动的速度看作正速度，而向左运动的速度看作负速度。

这样在起点的基础上加上点的运动路程就可以直接得到运动后点的坐标。

即一个点表示的数为a ，向左运动b 个单位后表示的数为a －b ；向右运动b 个单位后所表示的数为a+b 。

（简单说成左减右加）3、分类讨论的思想：数轴是数形结合的产物，分析数轴上点的运动要结合图形进行分析，注意多种情况种的分类讨论4、绝对值策略：对于两个动点P,Q ，若点P,Q 的左右位置关系不明确或有多种情况，可用p,q 两数差的绝对值表示P,Q 两点距离，从而避免分复杂分类讨论5、中点公式：若数轴上点A,B 表示的数分别为a,b ，M 为线段AB 中点，则M 点表示类型一、数轴上两点距离的应用例1、已知数轴上A,B 两点表示的数分别为-2和5，点P 为数轴上一点 （1）若点P 到A,B 两点的距离相等，求P 点表示的数（2）若PA=2PB,求P 点表示的数（3）若点P到点A和点B的距离之和为13，求点P所表示的数。

练、已知数轴上A、B两点对应数分别为-2和4，P为数轴上一动点，对应数为x．（1）若P为线段AB的三等分点，则x的值为_________（2）若线段PA=3PB,则P点表示的数为__________（3）若点P到A点、B点距离之和为10，则P点表示的数为_________类型二、绝对值的处理策略例2、已知数轴上A,B两点表示的数分别为-8和20，点P,Q分别从A,B两点同时出发，P点运动速度为每秒3个单位，Q点运动速度为每秒1个单位，设运动时间为t秒（1）点P向右运动，Q点向左运动，当t为何值时，P,Q两点之间距离为8？（2）若P点和Q点都向右运动，多少秒后，P,Q两点之间距离为8？（3）在（2）的条件下，另一动点M同时从O点出发，以每秒2个单位的速度向右运动，多少秒后，点M到点P和点Q的距离相等？练、已知在数轴上有A，B两点，点A表示的数为-8，点B表示的数为4．动点P从数轴上点A出发，以每秒2个单位长度的速度运动，同时动点Q从点B出发，以每秒1个单位长度的速度，设运动时间为t秒。

高中物理选修3-1、3-2的认识和做法08.7.27潍坊一中物理组孙景杰把握教材是教师永远的基本功。

怎样把握教材，要靠教师的物理素养。

高中物理选修3系列侧重让学生较全面地学习物理学的基本内容，进一步了解物理学的思想和方法，较为深入地认识物理学在技术中的应用以及对经济、社会的影响。

其中物理选修3-1、3-2（电磁学）是理科生的必考内容，继承了必修1、2的要求，即循序渐进、改变学习方式、贯穿探究精神、增强实践意识、重视科学思想与科学方法、渗透情感态度价值观的教育等几个方面。

一、学习高中物理课标教学目标与要求（一）三维目标着眼点在于学生的发展而不局限于知识的传承。

对教师的高要求（从教书到育人的转化）。

1、知识与技能（掌握知识）需要学生学习概念、定律、模型以及实验技能。

此外，学生还应该了解物理学与自然、社会、科学技术的相互关系。

2．过程与方法（培养能力）需要学生经历科学探究的过程，动手实践，学习科学方法，体会科学思想，形成自主学习的能力。

教师要充分认识学生的学习体验对学习的重要意义。

3．情感态度与价值观（形成价值取向）需要培养学生学习物理的兴趣和激情，感受自然规律的和谐与奇妙，领悟其中的意义，养成科学精神和科学态度。

4、实施课程三维目标的基本原则：①融合原则。

物理教学的三维目标是以知识与技能的学习为载体来实现的，教师在实施时不要将三维目标割裂开来，要力求三维目标的融合。

②渐进原则。

知识与技能、过程与方法、情感态度与价值观这三维目标都是有层次的，教师在实施时不能一蹴而就，要循序渐进。

③差异原则。

虽然任何知识的教学都具有实现三维目标的价值，但对不同的学习内容，三维目标的要求并不是均等的，要根据具体的教学内容区别对待，有所侧重。

近几年高考注重考查能力，坚持考察概念、规律的理解和应用，实验的设计、探究和思考能力。

（二）理解《标准》中教学要求中的行为动词二、人教版选修3-1、3-2模块的教学认识和做法（一）几点认识：1.教师应重点研究人教版教科书，参考鲁科版等多种教科书。

湖南省永州市中考数学2024-2025学年试卷班级：________________ 学号：________________ 姓名：______________一、单选题（每题3分）1.下列计算正确的是（）A.a2⋅a3=a6B.a6÷a2=a3C.3a−2a=1D.(a3)2=a6答案： D2.下列调查中，适合采用全面调查（普查）的是（）A. 了解某市中小学生的视力情况B. 了解一批灯泡的使用寿命C. 了解某班学生的身高情况D. 了解全国中学生的节水意识答案： C3.下列二次根式中，最简二次根式是（）A.√8B.√12C.√30D.√12答案： C4.下列关于x的一元二次方程中，有两个不相等的实数根的方程是（）A.x2+2x+1=0B.x2+√2x+1=0C.x2−2x+2=0D.x2−2x−3=0答案： D5.已知扇形的圆心角为120∘，半径为3，则该扇形的弧长为（）A.π2B.πC.2πD.3π答案： B二、多选题（每题4分）1.下列说法中，正确的是（）A. 射线AB与射线BA是同一条射线B. 连接两点的线段叫做两点间的距离C. 两点之间，线段最短D. 经过两点有一条直线，并且只有一条直线答案：CD2. 下列各组数中，以它们为边长的线段能构成三角形的是（ ）A. 1cm ，2cm ，3cmB. 8cm ，6cm ，4cmC. 12cm ，5cm ，6cmD. 2cm ，3cm ，5cm答案：B3. 下列关于单项式的说法中，正确的是（ ）A. 单项式−2πxy 23的系数是−23B. 单项式a 的次数是0C. 单项式−23a 2b 7的系数是−87D.π不是单项式答案：C4. 下列各式中，能用平方差公式分解因式的是（ ）A.a 2+b 2B.a 2−2ab +b 2C.−a 2+b 2D.a 2+2ab −b 2答案：C5. 下列计算正确的是（ ）A.5a −2b =3B.7a +a =7a 2C.7a2−a2=6D.3x2+2x2=5x2答案：D注意：由于题目要求每题多选、少选、错选均不得分，且给出的答案选项是按照题目描述来选择的，但在实际情况下，有些题目可能只有一个正确答案（如第2、4题），但为了符合题目要求，这里仍然列出了多选题的格式。

二次函数知识点总结在数学中，二次函数的最高阶必须是二次的。

在数学中，二次函数主要研究学生对公式的应用，是数学知识的重点。

二次函数知识点总结有哪些？一起来看看二次函数知识点总结，欢迎查阅！数学二次函数知识点归纳计算方法1.样本平均数：⑴ ;⑵若，，…， ,则(a―常数，，，…，接近较整的常数a);⑶加权平均数：;⑷平均数是刻划数据的集中趋势(集中位置)的特征数。

通常用样本平均数去估计总体平均数，样本容量越大，估计越准确。

2.样本方差：⑴ ;⑵若, ,…, ,则(a―接近、、…、的平均数的较“整”的常数);若、、…、较“小”较“整”，则;⑶样本方差是刻划数据的离散程度(波动大小)的特征数，当样本容量较大时，样本方差非常接近总体方差，通常用样本方差去估计总体方差。

3.样本标准差：三、应用举例(略)初三数学知识点：第四章直线形重点相交线与平行线、三角形、四边形的有关概念、判定、性质。

☆ 内容提要☆一、直线、相交线、平行线1.线段、射线、直线三者的区别与联系从“图形”、“表示法”、“界限”、“端点个数”、“基本性质”等方面加以分析。

2.线段的中点及表示3.直线、线段的基本性质(用“线段的基本性质”论证“三角形两边之和大于第三边”)4.两点间的距离(三个距离：点-点;点-线;线-线)5.角(平角、周角、直角、锐角、钝角)6.互为余角、互为补角及表示方法7.角的平分线及其表示8.垂线及基本性质(利用它证明“直角三角形中斜边大于直角边”)9.对顶角及性质10.平行线及判定与性质(互逆)(二者的区别与联系)11.常用定理：①同平行于一条直线的两条直线平行(传递性);②同垂直于一条直线的两条直线平行。

12.定义、命题、命题的组成13.公理、定理14.逆命题二、三角形分类：⑴按边分;⑵按角分1.定义(包括内、外角)2.三角形的边角关系：⑴角与角：①内角和及推论;②外角和;③n 边形内角和;④n边形外角和。

⑵边与边：三角形两边之和大于第三边，两边之差小于第三边。