框架梁内力调整例题

第8章 一榀框架计算8.7框架内力计算框架结构承受的荷载主要有恒载、活载、风荷载、地震作用。

其中恒载、活载为竖向荷载,风荷载和地震为水平作用。

手算多层多跨框架结构的内力和侧移时，采用近似方法。

求竖向荷载作用下的内力采用分层法，求水平荷载作用下的内力采用反弯点法、D 值法。

在计算各项荷载作用下的效应时,一般按标准值进行计算，然后进行荷载效应组合。

8.7.2框架内力计算1。

恒载作用下的框架内力 (1）计算简图将图8-12（a ）中梁上梯形荷载折算为均布荷载。

其中a=1。

8m ，l=6.9m ，=1800/69000.26a α==,顶层梯形荷载折算为均布荷载值:232312+=120.26+0.2621.31=18.8kN m q αα-⨯-⨯⨯（）（），顶层总均布荷载为18.8+4.74=23.54kN m 。

其他层计算方法同顶层，计算值为21.63kN m 。

中间跨只作用有均布荷载,不需折算。

由于该框架为对称结构,取框架的一半进行简化计算,计算简图见8-19。

（2）弯矩分配系数节点A 1:101044 1.18 4.72A A A A S i ==⨯=111144 1.33 5.32A B A B S i ==⨯=12120.940.94 1.61 5.796A A A A S i =⨯=⨯⨯=()0.622 1.3330.84415.836AS =++=∑1010 4.720.29815.836A A A A AS S μ===∑图8-19 恒载作用下计算简图（括号内数值为梁柱相对线刚度）1111 5.320.33615.836A B A B AS S μ===∑1212 5.7960.36615.836A A A A AS S μ===∑ 节点B 1:11112 1.12 2.24B D B D S i ==⨯=18.076BS =∑1111 5.320.29418.076B A B A BS S μ===∑1010 4.720.32118.076B B B B BS S μ===∑ 1212 5.7960.32118.076B B B B BS S μ===∑1111 2.240.12418.076B D B D BS S μ===∑节点A 2:()210.94 1.610.4170.94 1.610.776 1.33A A μ⨯⨯==⨯⨯++230.940.7760.20113.91A A μ⨯⨯==224 1.330.38213.91A B μ⨯==节点B 2:224 1.330.3294 1.330.94 1.61+0.940.7762 1.12B A μ⨯==⨯+⨯⨯⨯⨯+⨯210.94 1.610.35916.15B B μ⨯⨯==212 1.120.13916.15B C μ⨯==230.940.7760.17316.15B B μ⨯⨯==节点A 3 、A 4、A 5与A 2相同B 3、B 4、B 5与B 2相同。

结构内力计算分析案例以下是一个关于结构内力计算分析的案例，以帮助读者更好地理解该过程。

案例：栋多层住宅楼的楼板结构受力分析和计算。

1.结构描述：该楼为一栋钢筋混凝土框架结构的多层住宅楼，楼高5层，每层高度为3米。

楼板采用承重梁和板的形式，梁间距为6米，梁宽为0.3米。

2.受力分析：根据力学原理，梁和板在受力作用下会产生内力。

梁的受力情况分为竖向和横向两个方向：-竖向受力：竖向受力主要包括自重、活载和楼层间的等分荷载。

自重一般按照材料密度计算，活载是指居住者的活动荷载，楼层间的等分荷载指的是各个楼层产生的附加荷载。

-横向受力：横向受力主要包括风荷载和地震荷载。

这些荷载会通过墙体和梁传递到结构内部。

3.内力计算：根据受力分析结果，可以进行结构内力的计算。

具体计算方法有两种：静力分析和弹性力学方法。

-静力分析：这是一种通过平衡受力和力矩的方法进行计算的方法。

根据平衡条件，可以得到各个构件的内力。

-弹性力学方法：这是一种通过应力和应变的关系进行计算的方法。

根据材料力学性质和结构的几何形状，可以计算出各个构件的内力。

4.结果分析和验证：计算得到的结构内力结果需要进行分析和验证。

主要包括两个方面：构件强度和位移。

-构件强度：计算得到的内力和构件的截面尺寸一起，可以判断构件是否满足强度要求。

如果内力超过了构件材料的承载力，需要进行加固。

-位移：根据结构内力和材料的弹性模量，可以计算出结构的位移。

结构的位移应该满足设计的要求，如果超过了预定的限值，需要进行刚度调整。

总结：结构内力计算分析是工程的关键环节，其目的是保证结构的安全性和可靠性。

通过对不同构件的受力分析和力学计算，可以得到结构的内力结果，并进行分析和验证。

这样可以确保结构的设计和施工符合规范，并达到预期的使用寿命和性能要求。

结构力学课程大作业——多层多跨框架结构内力及位移计算班级学号姓名华中科技大学土木工程与力学学院年月日结构力学课程大作业——多层多跨框架结构内力与位移计算一、任务1、计算多层多跨框架结构在荷载作用下的弯矩和结点位移。

2、计算方法要求：（1）用迭代法、D 值法、反弯点法及求解器计算框架结构在水平荷载作用下的弯矩，并用迭代法的结果计算其结点位移。

（2）用迭代法、分层法、二次力矩分配法及求解器计算框架结构在竖向荷载作用下的弯矩，并用迭代法的结果计算其结点位移。

3、分析近似法产生误差的原因。

二、计算简图及基本数据本组计算的结构其计算简图如图1所示，基本数据如下。

混凝土弹性模量：723.010/h E kN m =⨯构件尺寸：柱：底 层：23040b h cm ⨯=⨯其它层：23030b h cm ⨯=⨯ 梁：边 梁：22560b h cm ⨯=⨯中间梁：22530b h cm ⨯=⨯ 水平荷载：'15P F kN ＝，30P F kN ＝（见图2）竖向均布恒载：17/q kN m 顶＝ 21/q kN m 其它＝（见图8） 图1各构件的线刚度：EIi L =，其中312b h I ⨯=边 梁：33410.250.6 4.51012I m -⨯==⨯F 7311 3.010 4.510225006EI i kN m L -⨯⨯⨯===⋅ 中间梁： 34420.250.3 5.6251012I m -⨯==⨯ 7422 3.010 5.6251067502.5EI i kN m L -⨯⨯⨯===⋅ 底层柱： 33440.30.4 1.61012I m -⨯==⨯ 7344 3.010 1.61096005EI i kN m L -⨯⨯⨯===⋅ 其它层柱：34430.30.3 6.751012I m -⨯==⨯ 7433 3.010 6.75106136.43.3EI i kN m L -⨯⨯⨯===⋅ 三、水平荷载作用下的计算 （一）用迭代法计算1、计算各杆的转角分配系数ikμ' 转角分配系数计算公式：()2ikikiki i i μ'=-∑结点“1”：12225000.3932(6136.422500)μ'=-=-⨯+156136.40.1072(6136.422500)μ'=-=-⨯+结点“2”：21225000.3182(67506136.422500)μ'=-=-⨯++图2232(67506136.422500)⨯++266136.40.0872(67506136.422500)μ'=-=-⨯++由于该结构是对称结构，因此结点“3”的分配系数应该等于结点“2”的，结点“4”的分配系数应该与结点“1”的相等，所以本题只需计算1、2、5、6、9、10、13、14、17、18结点的分配系数。

框架结构的内力与位移计算4．1 概述框架结构是目前多、高层建筑中常采用的结构形式之一。

框架在结构力学中称为刚架，结构力学中已经比较详细地介绍了超静定刚架(框架)内力和位移的计算方法，比较常用的手算方法有全框架力矩分配法、无剪力分配法和迭代法等，均为精确算法。

但在实用中大多已被更精确、更省人力的计算机分析方法(矩阵位移法)所代替。

不过，其中有些手算近似计算方法由于其计算简单、易于掌握，又能反映刚架受力和变形的基本特点，目前在实际工程中应用还很多，特别是在初步设计时的估算，手算的近似方法仍为设计人员所常用。

多、高层建筑结构在进行内力与位移计算中，为使计算简化，必须作出一些假定，以下将讨论一些结构计算中的基本假定：(1)弹性工作状态假定：结构在荷载作用下的整体工作按弹性工作状态考虑，内力和位移按弹性方法计算。

但对于框架梁及连梁等构件，可考虑局部塑性变形，内力重分布。

(2)平面结构假定：任何结构都是一个空间结构，实际风荷载及地震作用方向是随意的、不定的。

为简化计算，对规则的框架、框架—剪力墙、剪力墙结构体系及框筒结构，可将结构沿两个正交主轴方向划分为若干平面抗侧力结构—若干榀框架、若干片墙，以承受该框架、墙平面方向的水平力(风荷载及水平地震作用)，框架、墙不承受垂直于其平面方向的水平力。

(3)刚性楼面假定：各平面|考试大|抗侧力结构之间通过楼板相互联系并协同工作。

一般情况下，可认为楼板在自身平面内刚度无限大，而楼板平面外刚度很小，可以不考虑。

为保证楼面在平面内刚度，在设计中应采取相应的构造措施。

但当楼面有大开孔、楼面上有较长的外伸段、底层大空间剪力墙结构的转换层楼面以及楼面的整体性较差时，宜对采用刚性楼面假定的计算结果进行调整或在计算中考虑楼面的平面内刚度。

在上述假定下，内力分析时要解决两个问题：一个是按各片抗侧力结构的相对刚度大小，分配水平荷载至各片抗侧力结构；另一个是计算每片抗侧力结构在所分到的水平荷载作用下的内力及位移。

7内力组合及内力调整内力组合各种荷载情况下的框架内力求得后，根据最不利又是可能的原则进行内力组合。

当考虑结构塑性内力重分布的有利影响时，应在内力组合之前对竖向荷载作用下的内力进行增幅。

分别考虑恒荷载和活荷载由可变荷载效应控制的组合和由永久荷载效应控制的组合，并比较两种组合的内力，取最不利者。

由于构件控制截面的内力值应取自支座边缘处，为此，进行组合前，应先计算各控制截面处的（支座边缘处的）内力值。

1）、在恒载和活载作用下，跨间M max可以近似取跨中的M代替，在重力荷载代表值和水平地震作用下，跨内最大弯矩M max采用解析法计算：先确定跨内最大弯矩M max的位置，再计算该位置处的M max。

当传到梁上的荷载为均布线荷载或可近似等效为均布线荷载时，按公式7-1计算。

计算方式见图7-1、7-2括号内数值，字母C D仅代表公式推导，不代表本设计实际节点标号字母。

M max gql2 M左。

M右且满足M max 丄（7-1）8 2 16式中：q ------ 作用在梁上的恒荷载或活荷载的均布线荷载标准值；M左、M右一一恒载和活载作用下梁左、右端弯矩标准值；l ――梁的计算跨度。

2）、在重力荷载代表值和地震作用组合时，左震时取梁的隔离体受力图，见图7-1 所示，调幅前后剪力值变化，见图7-2。

图7-1框架梁内力组合图图7-2调幅前后剪力值变化图中：M GC、M GD――重力荷载作用下梁端的弯矩;M EC、M CD——水平地震作用下梁端的弯矩R C、R D――竖向荷载与地震荷载共同作用下梁端支座反力、ql 1左端梁支座反力：R C= M GD M GC M EC M ED；2 l由啦0，可求得跨间M max的位置为：X! R c/q ；dx将X i代入任一截面x处的弯矩表达式，可得跨间最大弯矩为：弯矩最大点位置距左端的距离为X i，X1 = R E /q ；0 X1 1 ；最大组合弯矩值： 2；当X1 0或X1 1时，表示最大弯矩发生在支座处，取X1=0或X1 = l，最大弯矩组合设计值的计算式为： 2；右震作用时，上式中的M GE、M EF应该反号。

7 内力组合及内力调整7.1内力组合各种荷载情况下的框架内力求得后，根据最不利又是可能的原则进行内力组合。

当考虑结构塑性内力重分布的有利影响时，应在内力组合之前对竖向荷载作用下的内力进行增幅。

分别考虑恒荷载和活荷载由可变荷载效应控制的组合和由永久荷载效应控制的组合，并比较两种组合的内力，取最不利者。

由于构件控制截面的内力值应取自支座边缘处，为此，进行组合前，应先计算各控制截面处的（支座边缘处的）内力值。

1）、在恒载和活载作用下，跨间max M 可以近似取跨中的M 代替，在重力荷载代表值和水平地震作用下，跨内最大弯矩max M 采用解析法计算：先确定跨内最大弯矩max M 的位置，再计算该位置处的max M 。

当传到梁上的荷载为均布线荷载或可近似等效为均布线荷载时，按公式7-1计算。

计算方式见图7-1、7-2括号内数值，字母C 、D 仅代表公式推导，不代表本设计实际节点标号字母。

2max182M M M ql +≈-右左 且满足2max 116M ql = （7-1） 式中：q ——作用在梁上的恒荷载或活荷载的均布线荷载标准值；M 左、M 右——恒载和活载作用下梁左、右端弯矩标准值；l ——梁的计算跨度。

2）、在重力荷载代表值和地震作用组合时，左震时取梁的隔离体受力图，见图7-1所示, 调幅前后剪力值变化,见图7-2。

图7-1 框架梁内力组合图图7-2 调幅前后剪力值变化图中：GC M 、GD M ——重力荷载作用下梁端的弯矩； EC M 、CD M ——水平地震作用下梁端的弯矩C R 、D R ——竖向荷载与地震荷载共同作用下梁端支座反力。

左端梁支座反力：()C 1=2GD GC EC ED ql R M M M M l--++；由0M ddx=，可求得跨间max M 的位置为:1C /X R q = ； 将1X 代入任一截面x 处的弯矩表达式,可得跨间最大弯矩为： 弯矩最大点位置距左端的距离为1X ，1=/E X R q ；()101X ≤≤； 最大组合弯矩值：2max 1/2GE EF M qX M M =-+；当10X <或11X >时，表示最大弯矩发生在支座处，取1=0X 或1=X l ，最大弯矩组合设计值的计算式为：2max C 11/2GE EF M R X qX M M =--+； 右震作用时，上式中的GE M 、EF M 应该反号。

梁端简支框架合理计算内力方法第10卷2期19g1年I2月包头钢铁学院Jourma[ofBaotouInsti~uteofIronandsteelTechnologyV0l_10No.2Decemherlg91刘继明(建筑工程系)!摘要对于粱端简支框架计算内力的方法,一般是按规则框架用D值法计算本文对梁端简支框架采用台理的简图推导出修正刚度D和反弯点高度比的计算公式.关-词坚支,坚,津姥皂-～?—一一.,卜,,Ⅵ,'l'I.\.1框架粱一端为简支时,修正后的柱侧移刚度值的推导框架受力作用变形,AB柱到达新位置AB,水平方向位移差△.柱的弦转角忙,柱的上,下端产生转角e,假定:(1)柱AB以及与柱AB相邻的非铰支端各杆端(即A,B,c,D,G,H)的转角皆为0.(2)与柱AB上下相邻的两个柱的弦转角皆为,并与柱AB的弦转角相等(3)与柱AB相邻的两个柱的线刚度皆为i,并与柱AB的线刚度i相等.根据杆件的转角位移方程',我们可得:两端固定的杆端弯矩方程:MAB一2i(2e+一3qJ一)M=2i(2%+0…3q:.).^B一一+nH锄一)D:lIF日"一.『】iE^GiC1.}HK—计算简图位移图对于A端刚接,B端铰接的杆端弯矩程:72●●■●●M^B:3i(0A—A日)M^B=OQl^B=兰(日B—e^)对于一般层的框架柱AB:由节点A和节点B的平衡条件:4i0+2i06i~+4i0+2i0-6i~+4i~0+2i'0+3is0=04坩+2坩一6+4i.+2i0—6i~+4120+20+3i,0=0 {12i0-12+6i0+3i30—012i0-12+6i20+3h0=0两式相加,化简得:24i.一24+6(b+i.)0十3(i十iz)O=O.一—8i+2—(h+iO+一(i~+iO一蠡——西!令同全部刚接刚架比较一,趸变小即得:.?0e丑.一等(=K黑?:??△令一则Qe—12i△.柱AB的侧移刚度D,~B--即.(i)(2)(1)(2)(3)(4)反弯点法的侧移刚度为d一12i.可知,是考虑梁,柱线刚度比值对柱侧移刚度的影响系数底层柱JK的D值:把JK情况作为研究对象:M一3isOMH==4i60+2is0K一4i0—6设令(40-6△/h)i(i5+2i6)?3O(扯§△/m,豁一———一-73?则得a一,.一志一志会Q一一:一=6i志?[一是]:?则令.一一?:{0.3～0.5),a:{一0.¨～一0.5cq:{0.3～0.84)若令a为一常数,且等于f一百11,则有{0.35～0.79)对影响不大.化简为框架梁端部为简支时.与端部为固定相比较,得知不论是一般层和底层其前者在梁桂线刚度比较比值影响系数较小,柱的修正刚度D值也小.即产生单位倒移需要的剪力小-分配的剪力也小.2框架梁一端为简支时,反弯点高度比2.1基本方程与推导在水平荷载作用下,可假定框架梁的反弯点在中间且无竖向位移多层多跨框架一端为铰支的可简化成如下计算简图,左右梁是以一端固定,一端铰支的情况而将其线刚度比叠加起来的.这样它的计算简图与规则框架计算简图相类似,只是i的含义不同.对于这种结构,我们采用力法求解,其基本方程为:6l1Ml+6l2M2+…6M+△lD一06M1+6n2M2+…M+△=0kMI+62M2+…kmMm+△m,:0从单位弯矩图中可看出,除6n…-,,6+和△外其余系数均为零. 第1"1个方程转化为:6n…IMJ+6…M+6n.+1M叶l+△p一0其中t~n,a一+击+.16n…一一瓦一一击Ao0一一1+瓦1)(.h忐(Qh)n']74(1)(a)(b)(c)(d)●●,●●(Qh)一第n层中柱的剪力Q和柱高之积.以上公式适应于二层至m—l层.对于顶层,n—mM1L一0删l=0得:…jM-F6…M-F△一0(2)对于底层:n一1iL.一..,6llc一0得:lMJ-F6J2M2-F△【一0(3)解以上力法方程.得柱底弯矩M,从而可按下式计算用2?2规则框架的反弯点高度比T1对于规则框架承受倒三角形分布水平力作1]l|々一+I』一一—_'^j+—≯一r'r—'=.¨十咖J一—厂——广『IjL号—r1～^^一^——扫一—由上述可知:每层可以组成一个包含三个未知弯矩的方程式,一共有IF1个方程,可以求解m个未知弯矩.为了求解方便,我们可以假设这些方程是一个微分方程的差分表达式,其步距为层高h.我们设想,这些差分方程还原为楼层弯矩M的微分方程,我们假定这个微分方程包含特解和M,即对n层:M一丽-FM一丽-F0Jr-i-c2r.nM是某特征方程的根r的幂函数,然后求出r值,则可求得通解M..令特解祈:丽一A-FBn-FCn然后将丽代入楼层弯矩M的表达式,由系数比较法可以决定A,B,C的数值.由此可得.特解矾:厩=[一百2--3kn等]Q|I㈣为求出一般解.可先写出第i层弯矩的齐次式,M一(2-F6k)M--FM=0(6)为了满足这一式,令M一D?r,其中D为任意常数,得:l一(2+6k)r+r0解得:卜=(1-F3k)而从而可写出层弯矩的解Mj一菥,+cI+c2rm(7)c为常数,由边界条件确定,将(7)代入第一层,第1FI层弯矩表达式,再代入第n层弯矩表达式可得关于C,C的两个方程.求出C,C后,各层弯矩均可得出.标准反弯点高度比rh由下式可求得:n=将M…Q代入,可得各层的标准反弯点高度比n75一f0.5+2n+l2K(c1r+C2r…)m一总层数,K—KiL梁柱刚度比值;r一(1+3k)一.厂订=可(8)式表明,反弯点高度比和框架层数m,梁柱刚度比K及所在层数n有关从框架梁一端为简支时,令梁柱线刚度比一+(一般层)霞一(底层)与规则框架梁柱线刚度比来比较,一生+(一般层)霞一_i~+i6(底层)(8)前者很明显的是较小.对于总层数rn相同,所在层相同El,前者的反弯点应比后者较低一点,依据推导出的公式,来制定出六层框架各层的反弯点高度比Tb,列于下表框架承受倒三角形分布水平力作用反弯高度比值0.20.30.40.50.60.70.80.91.02.03.0?060.040.10.150.20.250.250.30.30.30.350.0.●.?0_50?...?..?.._.5.?.5._._._.?.?0.30.350.350.d0.0.40.0.0.40.450.450.450.0.0.0.0.d0.0.0.40.450.450.450.450.60.50.50.50.50.450.450.450.450.450.450.450.90.750.70.650.60.60.60.60.60.50.50.53三种方法计算内力的比较3.1由梁端简支框架推导的公式.以Tb值求出底层,二层横向框架中,边柱的反弯点高度,及MT,Mt值底层,中柱:Y?h一0.59×5.1—3.01mM一37.63,M一26.12,边柱:Yh051×5.1—2.6mMT—l7.17,ML—l6.5二层,中柱:Y㈣h041×3.2—1.32mMF一13.86,M一19.8576?I654321●边柱;Yh0d3×3.2:1.38mMT一9.95,M=l3.16.3.2利用反弯点法求底层,二层的内力值反弯点法;按柱线刚度配柱各层间剪力.规定反弯点位嚣在一般层柱吉高处,底层在柱高的号处底层:EQ~19.1'按分配蔓『柱:K^一7.×l0～KB一3.26×】0QA一一I3.26Q=∑Q=×19.18dy_h一h2=号×5.1—3.4m'.…一''一一工"^一MD3.4×l3.26=45.08,MD=34×5.84=19.86 二层:K一6.dl×l0"K自=3.7l×l0∑O=17.79tQ::一437×l76,l+.1…'6317×l7.dl×.'.79一l1.27t79=6.52ty?h一击h一击×3.2一16mM一1.6×1I.27=18.03M一1.6×6.52=10.433.3比较全刚接方法一端铰接方法反弯点法中柱边柱中柱边柱中柱边柱反弯点高度yh底层柱剪力底层柱MM反弯点高yh二层柱剪力M二层柱M3.29d1.12 22.62 3.O6 6.62O.2 l3.46 3.O1 12.5 37.63 26,l2 2.6 6.6l7.17 16.5 3.4l3.26 45.O8 22.54 3,4 5.8d l9.86 9.96 】.47 l0.56 l5.52 l8.27 1.54 7.23 11.311.32lO.56l3.8619.851.387.239.9513.J61.6l1.2718.O318.O31.66.521O.43j0.d377l4结论4?1从以上表中可以看出,全刚接方法和一端铰接框架法反弯点较接近,而对于底层,全刚结方法与反弯点方法较接近.而较合理的方法,从理论上来讲应该是一端铰接框架的方法.-4?2对于一端铰接,一端刚接的刚架,重新推导其反弯点,高度比公式是较台理,也是必要的4?3从以上三种方法的不同反弯点高度比的比较来看,本文指出的反弯点高度比的公式是有一定精度的,可供计算同类型框架作参考.参考文献l同济大学.多层与高层房屋结构设计,上海:上海科学技术出版社,19822中国建筑科学研究院建筑结构研究所主编.高层建筑结构设计,北京:北京科学出版社,1982THEREASONABLEMETH0DOFOALCIII.A TING THEINTERNALFORCESOFTHEFRAMEW【TH THEBEAMSCONNECTEDTOITBYHlNGSLiuj'蚰ing剜删Thegeneralmethod,whichisusedtocalculatetheinternalforcesoftheframe.nwhichtheberin gareconnectedtonbyhings'istheD—valuemethodaccedingtotheuniqueframs. Inthispaperthefor—mulasofthemodifiedstiffnessDandtheroversepointsr~tioaboutthiskindOrframearededuc edbyusingthereasonableabOrcviateddrawing.Keyw帅曲:~ucture,frame,support,hInstiffness.Bend,moment,internalforce78?●。

高层建筑结构辅导资料十六主题：第六章钢筋混凝土框架结构设计（第4—5节）学习时间：2014年7月14日--7月20日内容：这周我们将学习第六章中的第4—5节，这部分主要介绍钢筋混凝土框架结构框架内力调整及框架梁的设计，下面整理出的框架供同学们学习，希望能够帮助大家更好的学习这部分知识。

一、学习要求1、掌握框架内力调整方法；2、掌握框架梁的抗弯和抗剪承载力计算与构造要求。

二、主要内容（一）框架内力调整进行框架结构抗震设计时，允许在梁端出现塑性铰。

为了便于浇捣混凝土，也往往希望节点处梁的负钢筋放得少些。

对于装配式或装配整体式框架，节点并非绝对刚性，梁端实际弯矩将小于其弹性计算值。

因此，在进行框架结构设计时，一般均对梁端弯矩进行调幅，即人为地减小梁端负弯矩，减小节点附近梁顶面的配筋量。

设某框架梁AB 在竖向荷载作用下，计算出梁端的最大负弯矩分别为AO M 、BO M ，梁跨中最大正弯矩为CO M ，则调幅后梁端弯矩如下式中：β——弯矩调幅系数。

对于现浇框架，可取0.80.9β=；对于装配整体式框架，由于接头焊接不牢或由于节点混凝土灌筑不密实等原因，节点容易产生变形而达不到绝对刚性，框架梁端的实际弯矩比弹性计算值要小，因此，弯矩调幅系数允许取得低一些，一般取0.70.8β=。

梁端弯矩调幅后，在相应荷载作用下的跨中弯矩必将增加，这时应校核梁的静力平衡条件，如下图1所示。

支座弯矩调幅后梁端弯矩A M 、B M 的平均值与跨中调整后的正弯矩C M 之和不应小于按简支梁计算的跨中弯矩值0M 。

图1 支座弯矩调幅必须指出，我国有关规范规定：弯矩调幅只对竖向荷载作用下的内力进行，即水平荷载作用下产生的弯矩不参加调幅，因此，弯矩调幅应在内力组合之前进行。

同时还规定，梁截面设计时所采用的跨中正弯矩不应小于按简支梁计算的跨中弯矩的一半。

（二）框架梁的设计1、框架设计抗震等级我国《建筑抗震设计规范》(GB50011-2010)采用二阶段设计方法。

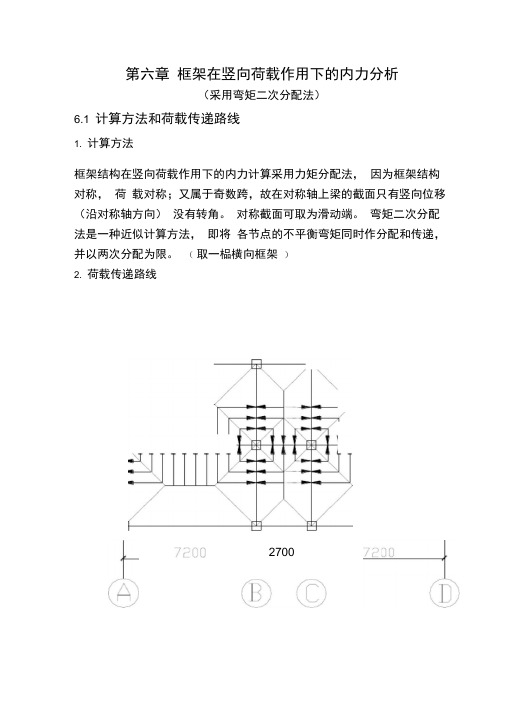
第六章框架在竖向荷载作用下的内力分析（采用弯矩二次分配法）6.1 计算方法和荷载传递路线1. 计算方法框架结构在竖向荷载作用下的内力计算采用力矩分配法，因为框架结构对称，荷载对称；又属于奇数跨，故在对称轴上梁的截面只有竖向位移（沿对称轴方向）没有转角。

对称截面可取为滑动端。

弯矩二次分配法是一种近似计算方法，即将各节点的不平衡弯矩同时作分配和传递，并以两次分配为限。

（取一榀横向框架）2. 荷载传递路线2700对于边跨板，为7.2 m×4.5m,由于7.2/4.5<3.0 所以按双向板计算对于中跨板，为 4.5m×2. 7m,由于 4.5/2.7 〈3.0 所以按双向板计算6.2 竖向荷载计算5.2.1 A-B(C-D) 轴间框架梁板传至梁上的三角形或梯形荷载等效为均布荷载。

1. 屋面板传载恒载： 5.0 ×4.5/2 ×(1-2 ×0.312+0.313) ×2=18.85kN/m活载：0.5 ×4.5/2 ×(1-2 ×0.312+0.313) ×2=1.89kN/m2. 楼面板传荷载恒载： 3.99 ×4.5/2 ×(1-2 × 0.31 2+0.31 3) ×2=15.08kN/m活载： 2.0 ×4.5/2 ×(1-2 ×0.312+0.313) ×2=7.56kN/m3. 梁自重： 5.46 kN/mA-B(C-D) 轴间框架梁均布荷载为：屋面梁：恒载=梁自重+板传荷载=5.46 kN/m+18.85 kN/m=24.31 kN/m 活载=板传荷载=1.89 kN/m楼面梁：恒载=梁自重+板传荷载=5.46 kN/m+15.08 kN/m=20.54 kN/m 活载=板传荷载=7.56 kN/m5.2.2 B-C 轴间框架梁1. 屋面板传载恒载： 5.0 ×2.4/2 ×5/8 ×2=8.44kN/m活载：0.5 ×2.7/2 ×5/8 ×2=0.84kN/m2. 楼面板传荷载恒载： 3.99 ×2.7/2 ×5/8 ×2=6.73kN/m活载： 2.0 ×2.7/2 ×5/8 ×2=4.22kN/m3. 梁自重： 3.9kN/mB-C 轴间框架梁均布荷载为：屋面梁：恒载=梁自重+板传荷载=3.9 kN/m+8.44kN/m=12.34kN/m 活载=板传荷载=0.84kN/m楼面梁：恒载=梁自重+板传荷载=3.9 kN/m+6.73kN/m=10.63kN/m 活载=板传荷载=4.22kN/m6.3 框架计算简图g=24.31KN/m g=12.34KN/m g=24.31KN/m(q=1.89KN/m)2700框架计算简图6.4. 梁固端弯矩梁端弯矩以绕杆端顺时针为正，反之为负。

竖向荷载作用下框架结构的内力计算6.1计算单元的选择确定取③轴线横向框架进行计算，如下图所示：图6.1框架计算简图计算单元宽度为6.4 m，由于房间内布置有次梁，故直接传给该框架的楼面荷载如图中的水平阴影所示。

计算单元范围内的其余楼面荷载则通过次梁和纵向框架梁以集中力的形式传给横向框架，作用于各节点上。

由于纵向框架梁的中心线与柱的中心线不重合，所以在框架节点上还作用有集中力矩。

6.2荷载计算6.2.1恒载作用下柱的内力计算：恒荷载作用下各层框架梁上的荷载分布如下图所示：2图6.2恒荷载作用下各层框架梁上的荷载分布图（1）、对于顶层屋面，q1、q1＇代表横梁自重，为均布荷载形式。

q1=0.3×0.75×25=5.625kN/mq1＇=0.3×0.75×25=5.625kN/mq2为屋面板传给横梁的梯形荷载。

q2=5.29×3.2=16.928kN/mP1、P2分别由边纵梁、中纵梁直接传给柱的恒载，它包括主梁自重、次梁自重、楼板重等重力荷载，计算如下：P1=6.4*0.3*0.75*25+8.5/2*0.25*0.6*25+5.29*3.2*1.6+(5.3+8.5)*1.6*5.29/4=108.223KN P2=6.4*0.3*0.75*25+6.4/2*0.25*0.6*25+5.29*3.2*1.6 +(3.2+6.4)*1.6*5.29/4=95.398KN P3=6.4*0.3*0.75*25+(8.5+6.4)*0.5*0.25*0.6*25+5.29*3.2*1.6*2++(3.2+6.4)*1.6*5.29/4= 190.64KN集中力矩M1=P1e1=108.223×（0.6 -0.3）/2=16.23kN·mM2=P2e2=147.23×（0.6 -0.3）/2=14.31kN·m（2）、对于3层，包括梁自重和其上横墙自重，为均布荷载，其它荷载的计算方法同第顶层。

结构在各种荷载作用下的内力经内力组合后，还要根据规范对其进行调整。

调整主要体现在抗震等级为一、二级的结构构件，规范还有特殊规定需要调整的构件。

内力调整主要遵循“强柱弱梁、强剪弱弯、强节点”的思想，以保证结构安全。

TBSA、TAT或SATW A的做法，是将构件在不同位置、不同情况下所具有的差别数值化，如TAT，它将这种差别叫“设计内力调整系数”。

TA T或SATW A软件采用的设计内力调整系数如下：1、一级抗震：框架柱Ucm＝1.331 Ucv＝1.464 Ucn＝1.0底层框架柱Ucm＝1.997 Ucv＝2.196 Ucn＝1.0底层加强区剪力墙Uwm＝1.000 Uwv＝1.331 Uwm＝1.0连梁、框架梁无Ubv＝1.271 无2、二级抗震：框架柱Ucm＝1.100 Ucv＝1.210 Ucn＝1.0底层框架柱Ucm＝1.250 Ucv＝1.375 Ucn＝1.0底层加强区剪力墙Uwm＝1.000 Uwv＝1.100 Uwm＝1.0连梁、框架梁无Ubv＝1.050 无3、三级抗震及四级抗震：其调整系数均为1.0以上调整系数的符号说明：Ucm－柱端弯矩调整系数Ucv－柱端剪力调整系数Ucn－柱端轴力调整系数Uwm－墙端弯矩调整系数Uwv－墙端剪力调整系数Uwn－墙端轴力调整系数Ubv－梁端剪力调整系数4、框支柱：设计剪力不小于基底剪力的2％（Vc≥2%Q0）；地震力产生的轴力放大1.2；设计弯矩放大1.5，即Ucm＝1.5（不分抗震等级）。

5、角柱混凝土角柱：Ucm＝1.3；Ucv＝1.3钢角柱、钢管角柱和劲性角柱：仅将地震力产生的内力放大1.3倍。

（一、二级框架底层柱下端截面的弯矩设计值，系数改为1.5,高规5.2.8条，上述一级和二级调整系数表内已有体现）一级抗震设计内力调整系数的来历是：柱端弯矩放大系数UcmUcm＝1.1x1.1x1.1＝1.331由高规第5.2.6条：一级框架梁柱节点处，柱端弯矩应符号下列要求：∑Mc ≥1.1∑MbuE （5.2.6-1）〖强柱弱梁原则〗而MbuE＝fyk·As·(hb0-as')/γRE （规范5.2.26条）Ucm中的三个1.1就是：（5.2.6-1）中的第一个1.1；MbuE公式中fyk≈1.1fy提供的第二个1.1；MbuE公式中的As提供第三个1.1，因规范要求的截面抗震设计是验算设计，软件认为实际配筋大约为计算配筋的1.1倍。