全等三角形思维导图

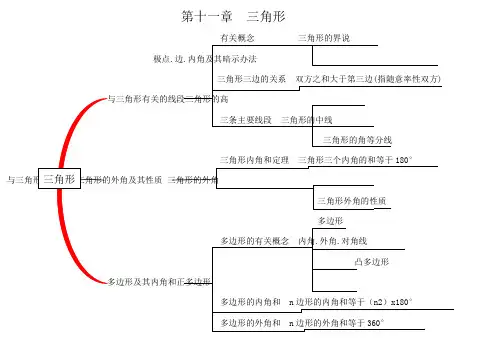
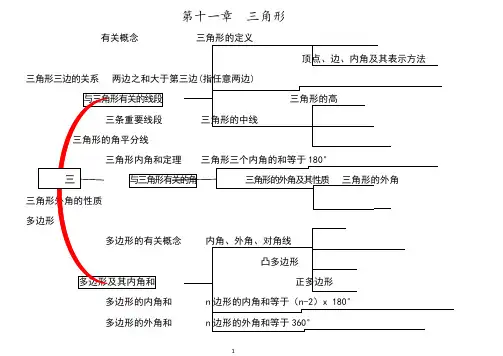
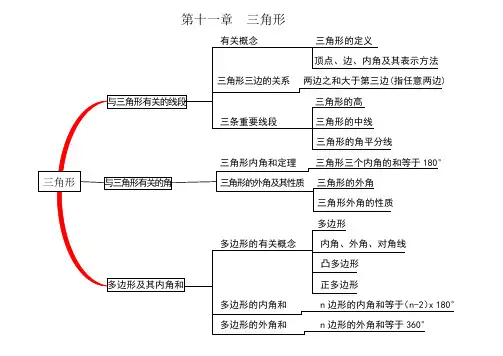
第十一章三角形
有关概念三角形的界说
极点.边.内角及其暗示办法
三角形三边的关系双方之和大于第三边(指随意率性双方)与三角形有关的线段三角形的高
三条主要线段三角形的中线
三角形的角等分线
三角形内角和定理三角形三个内角的和等于180°
三角形的外角
三角形外角的性质
多边形
多边形的有关概念内角.外角.对角线
凸多边形
多边形及其内角和正多边形
多边形的内角和 n边形的内角和等于（n2）x180°
多边形的外角和 n边形的外角和等于360°
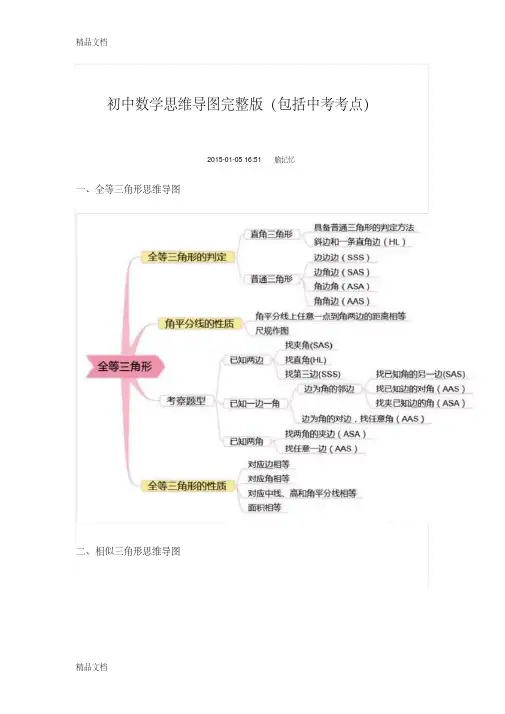
第十二章全等三角形
全等三角形的对应边相等
全等三角形的性质全等三角形的对应角相等
角边角ASA 三角形全等的剖断角角边AAS
SSS,SAS,ASA,AAS
直角三角形HL只实用于直角三角形
第十五章分式
第十六章二次根式第十七章勾股定理第十八章平行四边形第十九章一次函数第二十章数据的剖析。

初中数学《全等三角形》单元教学设计以及思维导图全等三角形”是八年级数学教材第十一章的重要内容，旨在让学生掌握全等三角形的概念和性质，以及五种判定全等的方法和角平分线的性质和判定方法，进而解决实际问题。

本单元共分三个专题，通过小组讨论和交流，引导学生进行探索、猜想、证明的过程，发展学生的推理意识和能力，课堂效果良好。

研究重点是全等三角形的性质和判定的综合运用，难点在于让学生理解证明的基本过程和用综合法证明的格式，并能灵活运用。

研究目标包括知识与技能、过程与方法、情感态度与价值观三个方面，旨在培养学生的空间观念、几何直觉、合作交流意识、大胆猜想和解决问题的能力。

本文介绍了数学中的两个重要概念：全等三角形和角平分线。

全等三角形的概念包括对应顶点、对应边和对应角等，掌握全等三角形的判定方法和证明格式是必要的。

角平分线的性质包括将一个角平分成两个相等的角，掌握角平分线的判定方法也是必要的。

在研究全等三角形时，需要掌握全等三角形的概念和性质，以及准确地辨认全等三角形中的对应元素。

通过观察、操作、想象、交流等教学活动，让学生经历理解全等三角形性质的过程。

同时，运用多媒体演示图形的位置变化，让学生从中了解、体会图形的变换思想，逐步培养学生动态研究几何图形的意识。

在研究角平分线时，需要掌握角平分线的性质和判定方法。

角平分线将一个角平分成两个相等的角，可以通过作图来判定角平分线。

在教学中可以使用多媒体课件、几何画板课件、作图工具和纸笔等教学资源，让学生通过动手操作、分组讨论、归纳结论等方式来探究全等三角形和角平分线的概念和性质。

总之，掌握全等三角形和角平分线的概念、性质和判定方法对于研究数学和几何学都是必要的。

在教学中，可以通过多种方式来引导学生探究和理解这些概念和性质，培养学生动态研究几何图形的意识，激发学生热爱科学、勇于探索的精神。

提出问题：两个全等的三角形，能否任意摆放并重合？如何放置才能重合？活动二：探究全等三角形的性质1、提出问题：观察图中两个三角形的对应边和对应角有什么关系？2、让学生观察图形、动手操作、分组讨论得出结论。

知识梳理——圆
页脚内容
7
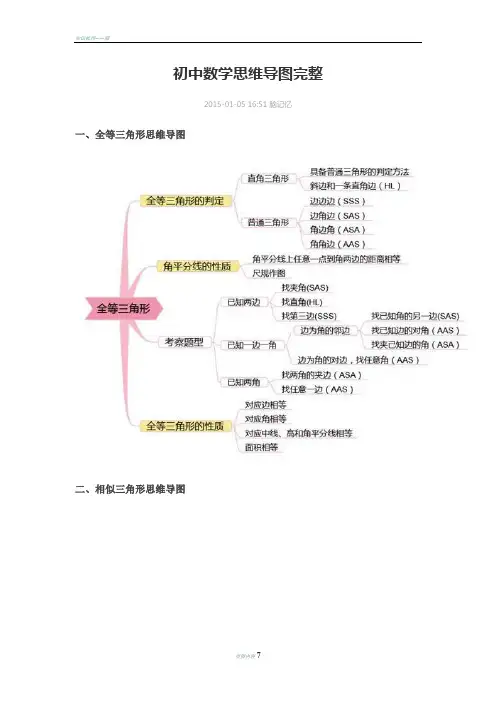
初中数学思维导图完整

2015-01-05 16:51 脑记忆
一、全等三角形思维导图

二、相似三角形思维导图
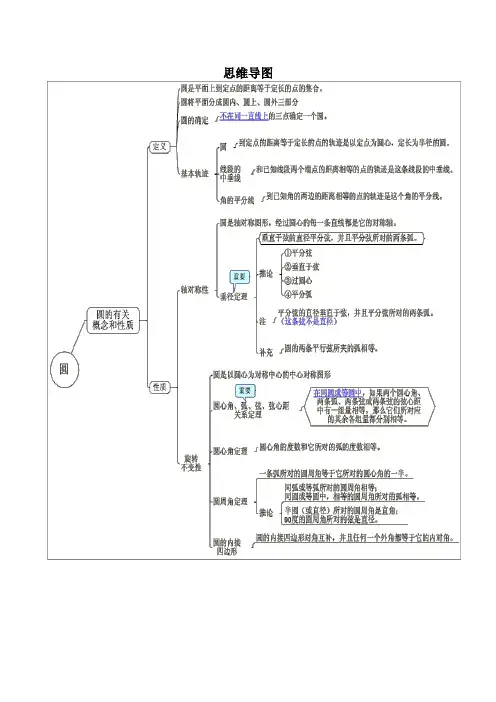
知识梳理——圆

页脚内容
7
三、几何初步和三角形思维导图
知识梳理——圆

页脚内容
7
四、投影与视图思维导图
知识梳理——圆

页脚内容
7
五、圆思维导图
知识梳理——圆

页脚内容
7
六、实数思维导图
知识梳理——圆

页脚内容
7
七、代数式思维导图
知识梳理——圆

页脚内容
7

八年级上册浙教版第三单元不等式,思维导图
1.基本定义：
⑴全等形：能够完全重合的两个图形叫做全等形.
⑵全系列等三角形：能全然重合的两个三角形叫作全系列等三角形.
⑶对应顶点：全等三角形中互相重合的顶点叫做对应顶点.
⑷对应边：全系列等三角形中互相重合的边叫作对应边.
⑸对应角：全等三角形中互相重合的角叫做对应角.
2.基本性质：
⑴三角形的稳定性：三角形三边的长度确定了，这个三角形的形状、大小就全确定，这个性质叫做三角形的稳定性.
⑵全系列等三角形的性质：全系列等三角形的对应边成正比，对应角成正比.
3.全等三角形的判定定理：
⑴边边边()：三边对应成正比的两个三角形全系列等.
⑵边角边()：两边和它们的夹角对应相等的两个三角形全等.
⑶角边角()：两角和它们的夹边对应成正比的两个三角形全系列等.
⑷角角边()：两角和其中一个角的对边对应相等的两个三角形全等.
⑸斜边、直角边()：斜边和一条直角边对应成正比的两个直角三角形全系列等.
4.角平分线：
⑴画法：
⑵性质定理：角平分线上的点到角的两边的距离相等.
⑶性质定理的逆定理：角的内部至角的两边距离成正比的点在角的平分线上.
5.证明的基本方法：
⑴明晰命题中的未知和澄清.(包含暗含条件，例如公共边、公共角、对顶
角、角平分线、中线、高、等腰三角形等所隐含的边角关系)
⑵根据题意，图画出来图形，用数字符号则表示未知和澄清.
⑶经过分析，找出由已知推出求证的途径，写出证明过程.。

第十一章三角形
第十二章全等三角形
全等三角形的对应边相等
第十三章轴对称
第十四章整式的乘法与因式分解
第十五章分式
第十六章 二次根式
二次根式
定义：式子(a ≥0)叫做二次根式
(a ≥0)是一个非负数
(a ≥0)
运算二次根式的乘法二次根式的除法
二次根式的混合运算二次根式的加减
二次根式加减是，可以先将二次根式化成最简二次根式，再合并同类二次根式
满足下列两个特点的二次根式，叫最简二次根式.
（1）被开方数不含分母，分母
中不含二次根式；
（2）被开方数中不含开得尽方
的因数或因式.
最简二次根式
性质
(a ≥0,b ≥0)(a ≥0,b ＞0)
(a ≥0,b ＞0)
第十七章勾股定理第十八章平行四边形
第十九章一次函数
第二十章数据的分析。

初二数学第一章思维导图一、全等形1、定义：能够完全重合的两个图形叫做全等图形，简称全等形。

2、一个图形经过翻折、平移和旋转等变换后所得到的图形一定与原图形全等。

反之，两个全等的图形经过上述变换后一定能够互相重合。

二、全等多边形1、定义：能够完全重合的多边形叫做全等多边形。

互相重合的点叫做对应顶点，互相重合的边叫做对应边，互相重合的角叫做对应角。

2、性质：(1)全等多边形的对应边相等，对应角相等。

(2)全等多边形的面积相等。

三、全等三角形1、全等符号：≌。

如图，不是为：△ABC≌△ABC。

读作：三角形ABC全等于三角形ABC。

2、全等三角形的判定定理：(1)有两边和它们的夹角对应相等的两三角形全等。

(即SAS，边角边)(2)有两角和它们的夹边对应相等的两三角形全等。

(即ASA，角边角)(3)有两角和其中一角的对边对应相等的两三角形全等。

(即AAS，角角边)(4)有三边对应相等的两三角形全等。

(即SSS，边边边)(5)有斜边和一条直角边对应相等的两直角三角形全等。

(即HL，斜边直角边)3、全等三角形的性质：(1)全等三角形的对应边相等、对应角相等(2)全等三角形的周长相等、面积相等(3)全等三角形对应边上的中线、高，对应角的平分线都相等。

4、全等三角形的作用：(1)用于直接证明线段相等，角相等。

(2)用于证明直线的平行关系、垂直关系等。

(3)用于测量人不能的到达的路程的长短等。

(4)用于间接证明特殊的图形。

(如证明等腰三角形、等边三角形、平行四边形、矩形、菱形、正方形和梯形等)。

(5)用于解决有关等积等问题。

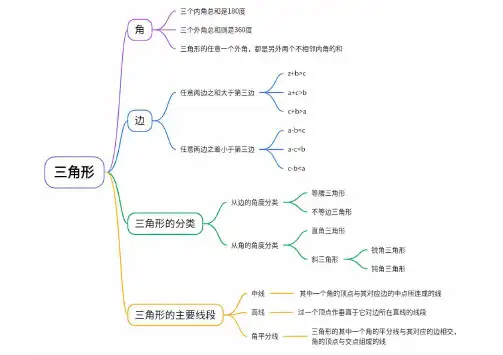
三角形的主要特点1.三角形的任意两边的和一定大于第三边，由此亦可证明三角形的两边的差一定小于第三边。

2.三角形内角和等于180度。

3.等腰三角形的顶角平分线，底边的中线，底边的高重合，即三线合一。

4.直角三角形的两条直角边的平方和等于斜边的平方--勾股定理。

直角三角形斜边的中线等于斜边的一半。

5.三角形的外角(三角形内角的一边与其另一边的延长线所组成的角)等于与其不相邻的两个内角之和。

第十一章三角形
第十二章全等三角形
全等三角形的对应边相等
第十三章轴对称
第十四章整式的乘法与因式分解
第十五章分式
第十六章 二次根式
二次根式
定义：式子(a ≥0)叫做二次根式
(a ≥0)是一个非负数
(a ≥0)
运算二次根式的乘法二次根式的除法
二次根式的混合运算二次根式的加减
二次根式加减是，可以先将二次根式化成最简二次根式，再合并同类二次根式
满足下列两个特点的二次根式，叫最简二次根式.
（1）被开方数不含分母，分母
中不含二次根式；
（2）被开方数中不含开得尽方
的因数或因式.
最简二次根式
性质
(a ≥0,b ≥0)(a ≥0,b ＞0)
(a ≥0,b ＞0)
第十七章勾股定理第十八章平行四边形
第十九章一次函数
第二十章数据的分析。