三角形思维导图

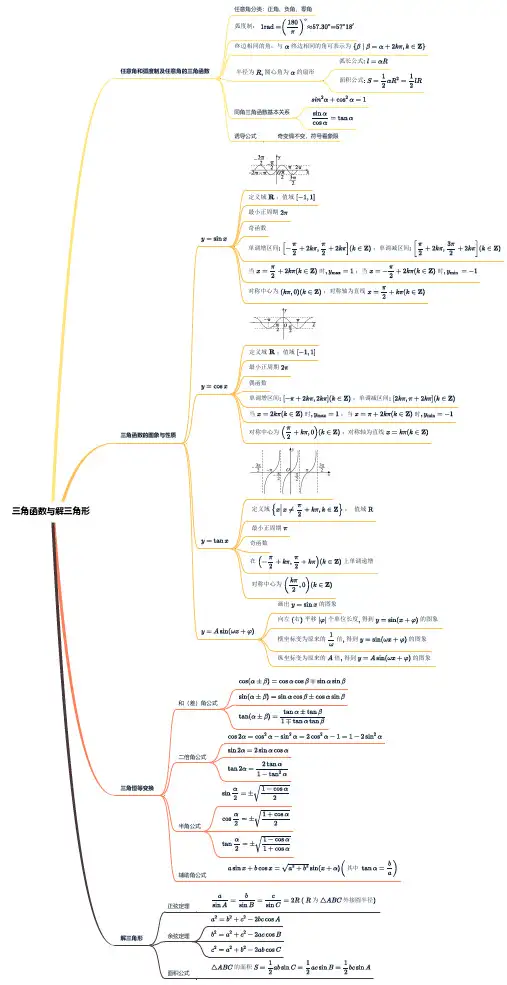
三角函数与解三角形任意角和弧度制及任意角的三角函数
三角函数的图象与性质
三角恒等变换
解三角形
任意角分类：正角、负角、零角
终边相同的角：与终边相同的角可表示为
半径为圆心角为的扇形
弧度制：
弧长公式
面积公式
同角三角函数基本关系
诱导公式奇变偶不变，符号看象限
定义域；值域
最小正周期
奇函数
单调增区间；单调减区间
当时；当时
对称中心为；对称轴为直线
定义域；值域
最小正周期
单调增区间；单调减区间
当时；当时
对称中心为；对称轴为直线
定义域；值域
最小正周期
在上单调递增
对称中心为
偶函数
奇函数
和（差）角公式
二倍角公式
半角公式
辅助角公式
其中
正弦定理
余弦定理
面积公式
画出的图象
向左右平移个单位长度得到的图象
横坐标变为原来的倍得到的图象
纵坐标变为原来的倍得到的图象
为外接圆半径
的面积。

你现在的努力要对得起别人对你的好！
Math 实验室-1-人教版八年级数学上册章节思维导图
共5章
人教版八年级数学上册教材目录
第11章三角形的思维导图
11.1与三角形有关的线段
11.2与三角形有关的角
11.3多边形及其内角和
第12章全等三角形的思维导图
12.1全等三角形
12.2三角形全等的判定
12.3角的平分线的性质
第13章轴对称的思维导图
13.1轴对称
13.2画轴对称图形
13.3等腰三角形
13.4课题学习最短路径问题
第14章整式的乘法与因式分解的思维导图
14.1整式的乘法
14.2乘法公式
14.3因式分解
第15章分式的思维导图
15.1分式
15.2分式的运算
15.3
分式方程。

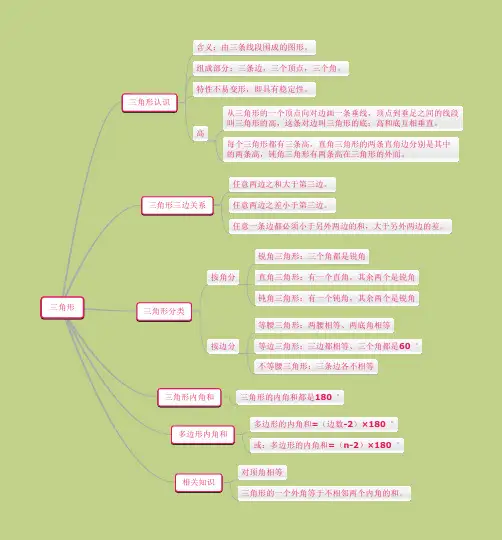
三角形三角形认识
含义：由三条线段围成的图形。

组成部分：三条边，三个顶点，三个角。

特性不易变形，即具有稳定性。

高
从三角形的一个顶点向对边画一条垂线，顶点到垂足之间的线段
叫三角形的高，这条对边叫三角形的底；高和底互相垂直。

每个三角形都有三条高，直角三角形的两条直角边分别是其中
的两条高，钝角三角形有两条高在三角形的外面。

三角形三边关系
任意两边之和大于第三边。

任意两边之差小于第三边。

任意一条边都必须小于另外两边的和，大于另外两边的差。

三角形分类
按角分
锐角三角形：三个角都是锐角
直角三角形：有一个直角，其余两个是锐角
钝角三角形：有一个钝角，其余两个是锐角
按边分
等腰三角形：两腰相等、两底角相等
等边三角形：三边都相等、三个角都是60︒
不等腰三角形：三条边各不相等
三角形内角和三角形的内角和都是180︒
多边形内角和
多边形的内角和=（边数­2）×180︒
或：多边形的内角和=（n­2）×180︒
相关知识
对顶角相等
三角形的一个外角等于不相邻两个内角的和。

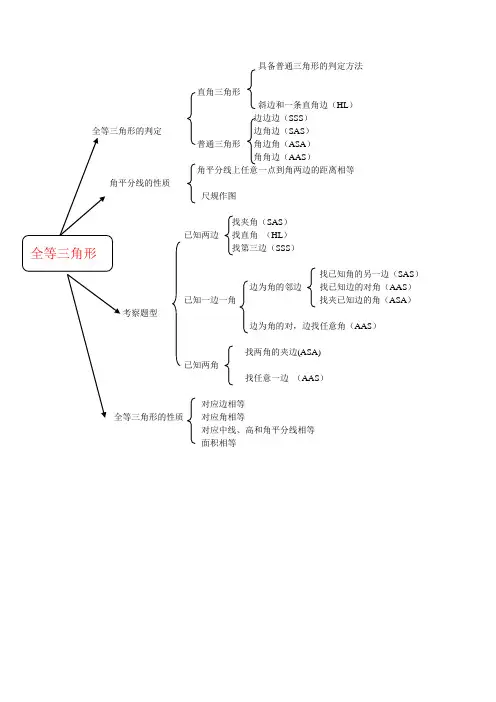
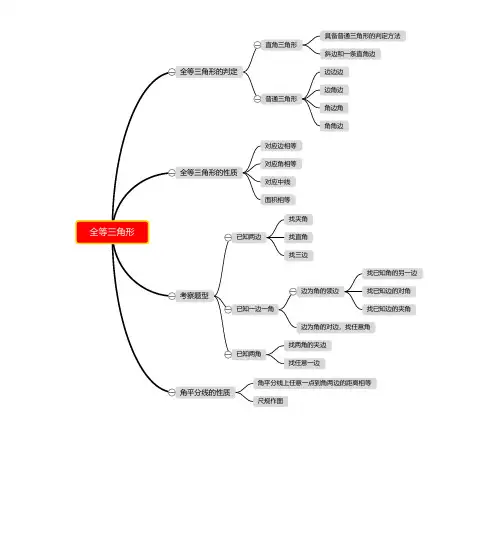
具备普通三角形的判定方法
直角三角形
斜边和一条直角边（HL）
边边边（SSS）
边角边（SAS）
普通三角形角边角（ASA）
角角边（AAS）
角平分线上任意一点到角两边的距离相等
尺规作图
找夹角（SAS）
已知两边找直角（HL）
找第三边（SSS）
找已知角的另一边（SAS）
边为角的邻边找已知边的对角（AAS）已知一边一角找夹已知边的角（ASA）考察题型
边为角的对，边找任意角（AAS）
找两角的夹边(ASA)
已知两角
找任意一边（AAS）
对应边相等
全等三角形的性质对应角相等
对应中线、高和角平分线相等
面积相等。

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。

如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。

㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。

(2 列出开发利用方案编制所依据的主要基础性资料的名称。

如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。

对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。

二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。

2、国内近、远期的需求量及主要销向预测。

㈡产品价格分析
1、国内矿产品价格现状。

2、矿产品价格稳定性及变化趋势。

三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。

2、矿区矿产资源概况。

3、该设计与矿区总体开发的关系。

㈡该设计项目的资源概况
1、矿床地质及构造特征。

2、矿床开采技术条件及水文地质条件。

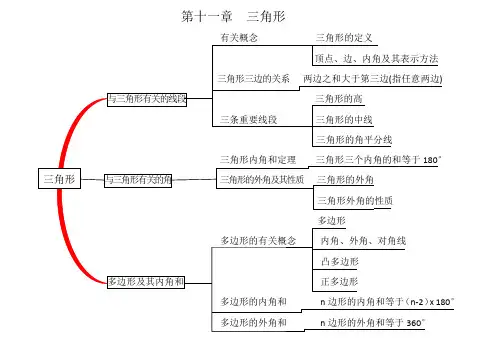
第十一章三角形
第十二章全等三角形
全等三角形的对应边相等
第十三章轴对称
第十四章整式的乘法与因式分解
第十五章分式
第十六章 二次根式
二次根式
定义：式子(a ≥0)叫做二次根式
(a ≥0)是一个非负数
(a ≥0)
运算二次根式的乘法二次根式的除法
二次根式的混合运算二次根式的加减
二次根式加减是，可以先将二次根式化成最简二次根式，再合并同类二次根式
满足下列两个特点的二次根式，叫最简二次根式.
（1）被开方数不含分母，分母
中不含二次根式；
（2）被开方数中不含开得尽方
的因数或因式.
最简二次根式
性质
(a ≥0,b ≥0)(a ≥0,b ＞0)
(a ≥0,b ＞0)
第十七章勾股定理
第十八章平行四边形
第十九章一次函数
第二十章数据的分析。

全等三角形思维导图1. 什么是全等三角形？全等三角形是指具有相同大小和形状的两个三角形。

两个三角形完全一致，每个角度和每条边的长度都相等，可以重合在一起。

2. 全等三角形的性质•相等的角度：两个全等三角形的对应角度相等。

例如，两个全等三角形的对应的三个内角都是60°。

•相等的边长：两个全等三角形的对应边的长度相等。

对应边分别是对边、邻边和斜边。

•相等的面积：两个全等三角形的面积相等。

3. 判断全等三角形的条件要判断两个三角形是否全等，可以使用以下条件：•SSS准则（边-边-边）：两个三角形的三条边分别相等。

•SAS准则（边-角-边）：两个三角形的两边和夹角分别相等。

•ASA准则（角-边-角）：两个三角形的两角和夹边分别相等。

•AAS准则（角-角-边）：两个三角形的两角和夹边分别相等。

如果两个三角形满足以上任意一个准则，则可以判定它们是全等三角形。

4. 全等三角形的应用全等三角形在几何学中有广泛的应用，主要包括：4.1 证明定理在几何证明中，全等三角形的性质常常用来推导和证明一些定理。

通过证明两个三角形全等，可以推导出它们的性质相等，从而得到更深入的结论。

4.2 解决几何问题全等三角形的性质可以帮助我们解决一些几何问题。

例如，当我们知道一个三角形全等于另一个三角形时，我们可以利用这个性质来求解其它未知边或角的数值。

这在建筑、工程和导航等领域非常有用。

4.3 设计和制作全等三角形的性质在设计和制作中也有应用。

通过构造全等三角形的模型，我们可以精确地复制和制作一些复杂形状的物体，如建筑、雕塑、模型等。

5. 总结全等三角形是具有相同大小和形状的三角形。

它们有相等的角度、边长和面积。

我们可以根据SSS、SAS、ASA和AAS准则来判断两个三角形是否全等，这些准则在几何证明和解决问题中有广泛的应用。

同时，在设计和制作中，全等三角形的性质也为我们提供了便利。

希望本文对你了解全等三角形有所帮助！。