关于行列式的计算方法8页word文档
- 格式:doc
- 大小:477.50 KB
- 文档页数:8

行列式的几种计算方法行列式是线性代数中非常重要的概念,它可以帮助我们理解矩阵的性质和求解线性方程组。
行列式的计算方法有多种,下面将详细介绍几种常用的计算方法。
一、按定义式计算行列式:按照定义式计算行列式是最基本的一种方法。
对于一个n阶矩阵A,其行列式记作det(A),可以按照以下公式进行计算:det(A) = Σ(−1)^σ(π_1,π_2,…,π_n)a_{1π_1}a_{2π_2}⋯a_{nπ_n}σ(π_1,π_2,…,π_n)是排列(π_1,π_2,…,π_n)的符号,a_{iπ_i}表示矩阵A的第i行第π_i列的元素,Σ表示对所有可能的排列进行求和。
按照定义式计算行列式需要对所有可能的排列进行求和,计算量较大,对于较大阶的矩阵来说并不实用。
我们通常会采用其他方法来计算行列式。
计算行列式时,我们可以利用其性质来简化计算过程。
行列式有一些基本的性质,如行列式中某一行(列)所有元素都乘以一个数k,行列式的值也要乘以k;行列式中某一行(列)元素乘以某个数加到另一行(列)上去后,行列式的值不变等。
利用这些性质,我们可以通过变换行列式中的元素或行列式本身,从而简化计算过程。
对于一个3阶矩阵A,我们可以利用做行列变换将其变换为上三角矩阵,这样计算其行列式就会变得非常简单。
具体地,我们可以通过交换行或列,将矩阵A变换为上三角矩阵,然后利用上三角矩阵的行列式的性质求解行列式的值。
三、按矩阵的余子式和代数余子式计算行列式:对于一个n阶矩阵A,其(i,j)位置的余子式M_{ij}定义为将A的第i行第j列划去后,剩下的元素按原来的次序组成的(n-1)阶行列式。
即M_{ij} = (-1)^{i+j} \cdot \det(A_{ij})其中A_{ij}是将矩阵A的第i行第j列元素划掉后得到的(n-1)阶子式矩阵。
矩阵的代数余子式A_{ij}定义为A_{ij} = (-1)^{i+j} \cdot M_{ij}。

行列式的计算方法及应用行列式是线性代数中一个重要的概念,它是一个正方形矩阵的特殊的函数,用于描述线性方程组的解的唯一性、可解性以及一些几何性质。
本文将介绍行列式的计算方法及其应用。
一、行列式的计算方法1.二阶行列式的计算方法对于一个二阶的矩阵A=[[a,b],[c,d]],其行列式的计算方法为:det(A) = ad - bc。
2.三阶行列式的计算方法对于一个三阶的矩阵A=[[a,b,c],[d,e,f],[g,h,i]],其行列式的计算方法为:det(A) = aei + bfg + cdh - ceg - afh - bdi。
3.一般的行列式计算方法对于一个n阶的矩阵A,其行列式的计算方法可以通过展开定理进行计算。
展开定理的思想是通过将行列式展开为更小规模的行列式的和来计算。
假设A为n阶矩阵,其元素为a[i][j],行列式记为det(A),则行列式的计算方法为:det(A) = a[1][1] * A[1][1] + (-1)^(1+2) * a[1][2] * A[1][2] + ... + (-1)^(1+n) * a[1][n] * A[1][n]其中,A[1][k]为将矩阵A的第1行和第k列删去后的(n-1)阶矩阵,det(A)为其中的行列式。
二、行列式的应用1.线性方程组的解的唯一性和可解性判断对于一个线性方程组Ax=b,其中A为系数矩阵,x为未知数向量,b 为常数向量。
若A的行列式不为0,则方程组有唯一解;若A的行列式为0,则方程组可能有无穷多个解或无解。
2.矩阵的可逆性判断一个矩阵A为可逆矩阵的充分必要条件是其行列式不为0。
可逆矩阵在数值计算和理论推导中有着重要的应用,例如求解线性方程组的解、求逆矩阵以及解线性变换等。
3.几何性质的判断行列式可以用来判断空间中向量的线性相关性和共面性。
对于一个n 维空间中的n个向量,若这些向量的行列式为0,则说明这些向量线性相关,存在一些向量可以由其他向量线性表示;若行列式不为0,则说明这些向量线性无关,对应n维空间中的一个n维平行体。

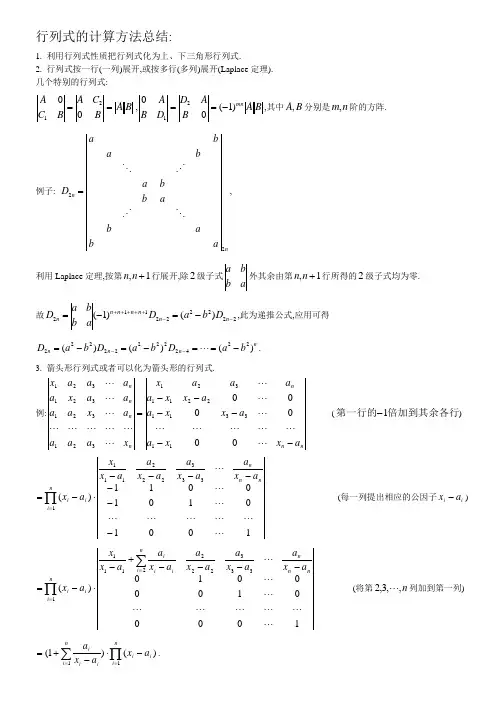
行列式的计算方法总结:1. 利用行列式性质把行列式化为上、下三角形行列式.2. 行列式按一行(一列)展开,或按多行(多列)展开(Laplace 定理). 几个特别的行列式:B A BC A BC A ==0021,B A BA D DB Amn )1(0021-==,其中B A ,分别是n m ,阶的方阵. 例子: nn abab ab b a b abaD 22=,利用Laplace 定理,按第1,+n n 行展开,除2级子式ab ba 外其余由第1,+n n 行所得的2级子式均为零. 故222222112)()1(--+++++-=-=n n n n n n n D b a D ab b a D ,此为递推公式,应用可得n n n n b a D b a D b a D )()()(224222222222-==-=-=-- .3. 箭头形行列式或者可以化为箭头形的行列式.例:nn n n n n n a x x a a x x a a x x a a a a x x a a a a x a a a a x a a a a x ------=0001133112211321321321321321 -----(倍加到其余各行第一行的1-) 100101010011)(3332221111-------⋅-=∏=nn n n i i i a x a a x a a x a a x x a x --------(每一列提出相应的公因子i i a x -) 1001000010)(33322221111nn n ni ii i n i i i a x a a x a a x a a x a a x x a x ----+-⋅-=∑∏== --------(将第n ,,3,2 列加到第一列)其它的例子:特点是除了主对角线,其余位置上的元素各行或各列都相同.n x a aa a a x a a a a a x a a a aa x a ++++ 321,nn n n a x a a a a a x a a a a a x a a a a a x ++++ 321321321321. 4. 逐行逐列相减法.行列式特点是每相邻两行(列)之间有许多元素相同.用逐行(列)相减可以化出零. 5. 升阶法(或加边法, 添加一行一列,利于计算,但同时保持行列式不变).例子:nn n n nnn n nn n n nn b a b a b a a b a b a b a a b a b a b a a b b b b a b a b a b a b a b a b a b a b a ++++-++++-++++----=++++++++++++10101010000011112122212212111121212221212111∑∑∑∑∑∑======+--+=---+--+=------=ni in i i i ni in ni i n i i i ni in n b b a na b b b b b a na a a ab b b 1112111121211110100000101111111010100111011101∑∑∑∑∑∑∑=≠======-+++=-++=nj nji i j i j ni i ni i ni i i ni i ni i a a b b a b a n b a 1111111)(1)1)(1(.例子:nnx a aaaa x a a a a a x a a a a a x a a a a a x a aaaa x a a a a a x a aa a a x a ++++=++++0001321321).1(00000000000010100010001000111213211321∑∑==+=+=----=ni in nni inx a x x x x x x x a a a a x a x x x x a a a a6. 利用范德蒙德行列式.计算行列式: n nn n nn nn n n nnx x x x x x x x x x x x x x x x D321223222122322213211111----=解: 令: nnnn nn n nn n n n nn n n ny x x x y x x x y x x x y x x x y x x x D211112112222212222212111111--------=,这是一个1+n 级范德蒙德行列式. 一方面,由范德蒙德行列式得)())(()(2111n ni j j ix y x y x y x xD ---⋅-=∏≤<≤ .可看做是关于y 的一个n 次多项式.另一方面,将1D 按最后一列展开,可得一个关于y 的多项式01111p y p y p y p D n n n n ++++=-- ,其中1-n y 的系数1-n p 与所求行列式D 的关系为1--=n p D .由)())(()(2111n ni j j ix y x y x y x xD ---⋅-=∏≤<≤ 来计算1-n y的系数1-n p 得:∑∏=≤<≤-⋅--=ni i ni j j in x x xp 111)(,故有∑∏=≤<≤-⋅-=-=ni i ni j j in x x xp D 111)(其它的例子:=+-+++-++-++------n n n n n n n n n n n n n n n n n n nn n n nb b a b a b a a b b a b a b a a b b a b a b a a 111121211111212222222122111121211111……每一行提公因子n i a ,nn n n n n n n n n n n n n nn n n a b a b a b a b a ba b a b a b a b a b a ba b a a a )()()()(1)()()()(1)()()()(1111112111122122222221111121111121++-++++++--+=).(1121∏≤<≤+-=n i j j j ii nn n n a b a b a a a7.利用数学归纳法证明行列式.(对行列式的级数归纳)证明当βα≠时,,1000001000100011βαβαβααββαβααββααββα--=+++++=++n n n D证明时,将n D 按第一行(或第一列)展开得21)(---+=n n n D D D αββα,利用归纳假设可得. 8. 利用递推公式.例子: 计算行列式,10000010001000βααββαβααββααββα+++++=n D 解: 按第一行展开得: 21)(---+=n n n D D D αββα,将此式化为:(1) )(211----=-n n n n D D D D αβα或 (2) )(211----=-n n n n D D D D βαβ 利用递推公式(1)得:n n n n n n n n D D D D D D D D βαβαβαβα=-==-=-=-------)()()(122322211 ,即n n n D D βα+=-1. (3)利用递推公式(2)得:n n n n n n n n D D D D D D D D αβαβαβαβ=-==-=-=-------)()()(122322211 ,即n n n D D αβ+=-1. (4)由(3)(4) 解得: ,,)1(,11⎪⎩⎪⎨⎧=+≠--=++βααβαβαβαn n n n n D其它的例子nn acb a ac b a c b a D00000000000=,按第一行展开可得21---=n n n bcD aD D ,此时令,,bc a ==+αββα则21)(---+=n n n D D D αββα,变形为211)(----=-n n n n D D D D αβα,此为递推公式.利用刚才的例子可求得结果. 这里,,bc a ==+αββα即βα,是方程02=+-bc ax x 的两个根.9. 分拆法.将行列式的其中一行或者一列拆成两个数的和,将行列式分解成两个容易求的行列式的和.例子:accccb ac c c bb ac c bbbac b b b b c a c accccb ac c c bb ac c bbbacb b b b a D n-+==210000V V acccb ac c b b a c b b b a b b b b c a accccb ac c c b b a c c b b b a c b b b b c +=-+=1V : 除第一行外,其余各行加上第一行的1-倍,所得行列式按第一列展开,2V 按第一列展开.11)(0000000--=----------=n b a c ba b c b c bc ba b c b c b b b a b c ba b b b b c V12)(--=n D c a V , 故11)()(---+-=n n n D c a b a c D ,由c b ,的对称性质,亦可得11)()(---+-=n n n D b a c a b D ,这两个式子中削去1-n D ,可得结论,bc c a b b a c D nn n ----=)()(.注: (1) 同一个行列式,可有多种计算方法.要利用行列式自身元素的特点,选择合适的计算方法. (2) 以上的各种方法并不是互相独立的,计算一个行列式时,有时需要综合运用以上方法,。

行列式的几种计算方法7篇第1篇示例:行列式是线性代数中的一个重要概念,它是一个方阵中的一个数值,可以帮助我们判断矩阵的性质,计算行列式的值是线性代数中的基础技能之一。
下面我们将介绍几种行列式的计算方法以及其应用。
一、直接展开法计算行列式最基本的方法就是直接展开法。
以3阶行列式为例,一个3阶方阵的行列式可以表示为:\[\begin{vmatrix}a &b &c \\d &e &f \\g & h & i\end{vmatrix}\]通过公式展开,可以得到:\[\begin{aligned}\begin{vmatrix}a &b &c \\d &e &f \\g & h & i\end{vmatrix} & = aei + bfg + cdh - ceg - bdi - afh \\& = a(ei - fh) - b(di - fg) + c(dh - eg)\end{aligned}\]这样就可以直接计算出行列式的值。
但是这种方法比较繁琐,不适用于高阶行列式的计算。
二、拉普拉斯展开法\[\begin{vmatrix}a_{11} & a_{12} & \cdots & a_{1n} \\a_{21} & a_{22} & \cdots & a_{2n} \\\vdots & \vdots & & \vdots \\a_{n1} & a_{n2} & \cdots & a_{nn} \\\end{vmatrix}\]以第一行为例,可以按照以下公式展开:\[ \text{det}(A) = a_{11}C_{11} + a_{12}C_{12} + \cdots +a_{1n}C_{1n} \]C_{ij}表示元素a_{ij}的代数余子式,通过递归计算代数余子式,最终可以得到行列式的值。

资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载行列式的计算方法-计算行列式的格式地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容行列式的计算方法摘要:线性代数主要内容就是求解多元线性方程组,行列式产生于解线性方程组, 行列式的计算是一个重要的问题。
本文依据行列式的繁杂程度,以及行列式中字母和数字的特征,给出了计算行列式的几种常用方法:利用行列式的定义直接计算、化为三角形法、降阶法、镶边法、递推法,并总结了几种较为简便的特殊方法:矩阵法、分离线性因子法、借用“第三者”法、利用范德蒙德行列式法、利用拉普拉斯定理法,而且对这些方法进行了详细的分析,并辅以例题。
关键词:行列式矩阵降阶The Methods of Determinant CalculationAbstract:Solving multiple linear equations is the main content of the linear algebra, determinants produced in solving linear equations, determinant calculation is an important issue.This article is based on the complexity degree of the determinant, and the characteristics of letters and numbers of the determinant ,and then gives several commonly used methods to calculate the determinant: direct calculation using the definition of determinant, into the triangle, reduction method, edging method , recursion, and summarizes several relatively simple and specific methods: matrix, linear separation factor method, to borrow "the third party" method, using Vandermonde determinant method, using Laplace theorem,also analyze these methods in detail,and supported by examples.Keywords: determinant matrix reduction.1.引言线性代数主要内容就是求解多元线性方程组,行列式产生于解线性方程组,然而它除了用于研究线性方程组、矩阵、特征多项式等代数问题外,还在各种工程领域有着广泛的应用,是一种不可缺少的运算工具,所以说行列式的计算是一个重要的问题。

行列式计算方法行列式的计算是线性代数中的重要内容,有以下几种常用的方法:1. 代数余子式法:给定一个n阶矩阵A,取A的第i行第j列元素a_ij为基准,计算它的代数余子式A_ij的值。
代数余子式的定义是,在A中划去第i行和第j列后,剩余元素构成的(n-1)阶子矩阵的行列式。
然后,根据代数余子式的符号规律,求得A_ij*(-1)^(i+j),再将所有的代数余子式乘以对应位置的元素,再求和即可得到行列式的值。
2. 拉普拉斯展开法:选择A的任意一行或一列,例如第i行,根据拉普拉斯展开定理,将行列式的计算转化为n个(n-1)阶行列式的计算,然后依次递归地计算(n-1)阶行列式,最后累加得到行列式的值。
3. 对角线法则:对于一个n×n的矩阵A,按照对角线上的元素(从左上角到右下角)出现的顺序,将对应的元素乘积相加,再减去按照对角线下方的元素(从左上角到右下角)出现的顺序,将对应的元素乘积相加。
这个过程可以用一个式子来表示:det(A) = a_11 * a_22 * ... * a_nn - a_21 * a_32 * ... * a_n1。
4. 公式法:对于一个3阶矩阵A,可以利用公式来计算行列式的值。
行列式的计算可以表示为:det(A) = a_11 * a_22 * a_33+ a_12 * a_23 * a_31 + a_13 * a_21 * a_32 - a_31 * a_22 * a_13 - a_32 * a_23 * a_11 - a_33 * a_21 * a_12。
对于4阶及以上的矩阵,复杂度较高,通常情况下不会直接使用公式法计算,而是选择其他方法。
以上是几种常用的求行列式的方法,不同的方法适用于不同的情况,在实际计算中可以根据需要选择合适的方法来求解。

行列式的多种计算方法行列式是线性代数中一个重要的概念,常用于表示线性方程组的性质和解的情况。
本文将介绍行列式的多种计算方法,包括定义法、按行展开法、秩法、特殊行列式计算法以及Laplace展开法。
一、定义法行列式的定义法是最基本也是最直观的计算方法。
对于二阶行列式,定义为:abcd行列式的值等于对角线上元素的乘积减去反对角线上元素的乘积,即ad-bc。
对于高阶行列式,可以通过对行列式进行展开,将矩阵分解成若干个二阶行列式,然后递归地计算这些二阶行列式的值,最终得到整个行列式的值。
二、按行展开法按行展开法是一种递归计算行列式的方法。
对于n阶行列式,可以通过展开第一行或第一列得到:a11a12 (1)a21a22 (2)............an1 an2 ... ann按照第一行展开:det(A) = a11 * det(A11) - a12 * det(A12) + a13 * det(A13) - ... + (-1)^(1+n) * a1n * det(A1n)其中Aij是删除第i行第j列后剩下的(n-1)阶行列式。
通过递归计算子行列式的方法,可以得到整个行列式的值。
三、秩法秩法是一种基于线性方程组的计算方法。
对于n个未知数的线性方程组,可以写成矩阵形式AX=B,其中A是一个n×n的矩阵,X和B都是n 维向量。
如果A的行列式非零,方程组有唯一解;如果A的行列式为零,则方程组无解或者有无穷多解。
所以,通过计算矩阵A的行列式,可以判断线性方程组的解的情况。
具体计算方法是将A进行行变换,化为上三角矩阵,然后将对角线上的元素相乘即得行列式的值。
四、特殊行列式计算法对于一些特殊的行列式,可以使用简便的计算方法。
例如,对于单位矩阵I,其行列式的值为1、对于对角矩阵D,其行列式的值等于对角线上元素的乘积。
对于三角形上下边对称的矩阵,其行列式的值为对角线元素与次对角线元素的乘积之差。
五、Laplace展开法Laplace展开法是一种递归计算行列式的方法。

行列式的几种计算方法行列式是线性代数中的一个重要概念,它在矩阵和向量运算中起着关键作用。
行列式的计算方法有多种,接下来将介绍几种常用的计算方法。
1. 代数余子式法代数余子式法是最基本的行列式计算方法之一。
对于一个n阶行列式A,我们可以通过以下公式进行计算:Det(A) = a11A11 + a12A12 + ... + a1nA1na11是矩阵A的元素,A11是a11的代数余子式。
代数余子式的计算方法是对矩阵A的每个元素求其代数余子式,然后再按照公式相加,得到最终的行列式值。
代数余子式法的优点是直观易懂,适用于任意阶数的行列式。
但是当阶数比较大时,计算量较大,需要进行大量的矩阵代数运算,因此效率较低。
2. 初等变换法初等变换法是另一种常用的行列式计算方法。
该方法通过对矩阵进行一系列的初等变换,将矩阵化简为上三角矩阵或对角矩阵,然后再通过对角线元素的乘积得到行列式的值。
初等变换包括三种操作:互换两行(列)、某一行(列)乘以一个非零数、某一行(列)加上另一行(列)的若干倍。
通过这三种操作,我们可以将矩阵变换为三角形式,从而更容易计算行列式的值。
初等变换法的优点是可以有效地简化矩阵,使得行列式的计算更加简单。
但是这种方法对于高阶矩阵来说,计算量仍然较大,且需要一定的技巧和经验。
3. 克拉默法则克拉默法则是一种利用矩阵的逆矩阵来计算行列式的方法。
对于一个n阶行列式A,其公式如下:Det(A) = (A^-1) * Adj(A)A^-1表示矩阵A的逆矩阵,Adj(A)表示矩阵A的伴随矩阵。
利用克拉默法则进行行列式的计算,首先需要求出矩阵A的逆矩阵,然后再求出伴随矩阵,最后通过矩阵相乘得到行列式的值。
克拉黫法则的优点是适用于任意阶数的行列式,且对于n阶行列式的计算只需要进行一次逆矩阵的运算和一次矩阵相乘,计算量较小。
4. 三角阵法三角阵法是通过将矩阵化成上三角形式或下三角形式,来简化行列式的计算。
对于一个n阶行列式A,我们可以通过初等变换将矩阵A化为上(下)三角矩阵T:然后再通过上(下)三角矩阵T的对角线元素的乘积得到行列式的值。

专题五行列式的计算方法1.递推法例1求行列式的值:(1)的构造是:主对角线元全为;主对角线上方第一条次对角线的元全为,下方第一条次对角线的元全为1,其余元全为0;即为三对角线型。
又右下角的(n)表示行列式为n阶。
解把类似于,但为k阶的三对角线型行列式记为。
把(1)的行列式按第一列展开,有两项,一项是另一项是上面的行列式再按第一行展开,得乘一个n– 2阶行列式,这个n– 2阶行列式和原行列式的构造相同,于是有递推关系:(2)移项,提取公因子β:类似地:(递推计算)直接计算若;否则,除以后移项:再一次用递推计算:∴,当β≠α(3)当β=α,从从而。
由(3)式,若。
注递推式(2)通常称为常系数齐次二阶线性差分方程.注1仿照例1的讨论,三对角线型的n阶行列式(3)和三对角线型行列式(4)有相同的递推关系式(5)(6)注意两个序列和的起始值相同,递推关系式(5)和(6)的构造也相同,故必有由(4)式,的每一行都能提出一个因子a,故等于乘一个n阶行列式,这一个行列式就是例1的。
前面算出,故例2 计算n阶范德蒙行列式行列式解:即n阶范德蒙行列式等于这n个数的所有可能的差的乘积2.拆元法例3:计算行列式解①×(x + a)②×(x – a)3.加边法例4计算行列式分析:这个行列式的特点是除对角线外,各列元素分别相同.根据这一特点,可采用加边法.解4.数学归结法例5计算行列式解:猜测:证明(1)n = 1, 2, 3时,命题成立。
假设n≤k– 1时命题成立,考察n=k的情形:故命题对一切自然数n成立。
5.消去法求三对角线型行列式的值例6求n阶三对角线型行列式的值:(1)的构造是:主对角线元全为2,主对角线上方第一条次对角线与下方第一条次对角线的元全为1,其余的元全为0。
解用消去法,把中主对角线下方第一条次对角线的元1全部消成0:首先从第二行减去第一行的倍,于是第二行变为其次从第三行减去第二行(指新的第二行,以下同)的倍,则第三行变为再从第四行减去第三行的倍,则第四行变为类似地做下去,直到第n行减去第n– 1行的倍,则第n行变为最后所得的行列式为(2)上面的行列式是三角型行列式,它的主对角线元顺次为93)又主对角线下方的元全为0。

例文一:行列式的计算方法介绍7种常用方法1 三角化方法:通过行列初等变换将行列式化为三角型行列式. 例1 计算n+1阶行列式xa a a a a x a a a a x D nnn32121211=+2 把某一行(列)尽可能化为零 例2 计算:yy x x D -+-+=222222222222222243 递归法(数学归纳法):设法找出D n 和低级行列式间的关系,然后进行递归.例4 证明:βαβαβαβααββααββα--=++++=++1110000010001000n n n D例5 证明范德蒙行列式(n ≥2)∏≤<≤-----==nj i jin nn n n n nn x x x x x x x x x x x x x x V 111312112232221321)(11114 加边法:对行列式D n 添上一适当行和列,构成行列式D n+1,且D n+1=D n 例6 证明:)11(11111111111111111111121321∑=+=++++=ni in nn a a a a a a a a D5 拆分法:将行列式表为行列式的和的方法.即如果行列式的某行(或列)元素均为两项和,则可拆分为两个行列式之和 例7 设abcd=1,求证:011111111111122222222=++++ddd d c c c c b b b b a a a a6 利用行列式的乘积:为求一个行列式D 的值,有时可再乘上一个适当的行列式∆;或把D 拆分为两个行列式的积. 例8(1)1)cos()cos()cos()cos(1)cos()cos()cos()cos(1)cos()cos()cos()cos(1121332312322113121n n n n n n D αααααααααααααααααααααααα------------=(2)设S k =λ1k +λ2k +⋯+λn k (k =1,2…),求证:∏≤<≤-+-+--=nj i j in n n n n nn s s s s s s s s s s s s s s s n 1222111432321121)(λλ7 利用拉普拉斯定理求行列式的值.拉普拉斯定理是行列式按某一行(或列)展开定理的推广.定义(1) 在n 阶行列式D 中,任取k 行k 列(1≤k ≤n),位于这k 行k 列交叉处的k 2个元素按原来的相对位置组成的k 阶行列式S ,称为D 的一个k 阶子式.如:D=3751485210744621则D 的一个2阶子式为:S=8261在一个n 阶行列式中,任取k 行,由此产生的k 阶子式有C kn 个.(2) 设S 为D 的一个k 阶子式,划去S 所在的k 行k 列,余下的元素按原来的相对位置组成的n-k 阶行列式M 称为S 的余子式.又设S 的各行位于D 中的第i 1,i 2…i k 行,S 的各列位于D 中的第j 1,j 2…j k 列,称A=(-1)(i1+i2+…+ik)+(j1+j2+…+jk)M.如:3751485210744621则D 的一个2阶子式为:S=8261M=3517为S 的2阶子式 M=(-1)(1+3)+(1+3)3517为S 的代数余子式.拉普拉斯定理:若在行列式D 中任取k 行 (1≤k ≤n-1),则由这k 行所对应的所有k 阶子式与它们的代数余子式的乘积等于D. 例9 计算2112100012100012100012=D 例10 块三角行列式的计算 设:⎪⎪⎭⎫ ⎝⎛=⨯⨯n n m m C B A *0或 ⎪⎪⎭⎫⎝⎛=⨯⨯n n m m C B A 0* 则:detA=(detB)(detC).特别地:若A=diag(A 1,A 2,…,A t ),则DetA=(detA 1)(detA 2)…(detA t ).例11 设分块矩阵⎪⎪⎭⎫⎝⎛=D C B A 0,其中0为零阵,B 和D 可逆,求A -1.例12 计算nn b b b a a a D 101000102121=例13 设:⎪⎪⎭⎫⎝⎛=C B A , BC T =0. 证明:|AA T|=|BB T||CC T |.例文2:行列式的多种计算方法行列式是线性代数的一个重要组成部分,行列式的计算方法多种多样,常见的几种行列式的方法有:定义法、三角化法、降阶法、升阶法、递推法、归纳法、利用范德蒙德行列式法、变换元素法、拆项法、分解乘积法等,可根据行列式选择相应的计算方法,从而减轻计算量.1定义法:n 阶行列式等于所有取自不同列的n 个元素的乘积的代数和.例1:nn n n n D ⨯-=000100002000010解:在n !项中只有一项1n ),n 3,2(,11342312-=+-a a a a a a nn n n π且不为零 !n )1(n 1n 21)1()1(D 1n 1n 1123121n n ⋅-=⋅-⋅-=-=∴--+-- nn n n a a a a2 三角化法:通过变换将行列式变换成三角行列式,再利用形式求出行列式的值. 2.1特殊行列式n21nn n 21nn n 21nn n 210*00000000*0000000)1(λλλλλλλλλλλλ===⨯⨯⨯下三角行列式上三角行列式对角行列式n212)1(nn n 21nn n 21nn n n 21)1(000000000000000)2(λλλλλλλλλλλλλ-⨯⨯⨯-===n n 次下三角行列式次上三角行列式次对角行列式2.2 箭形行列式例2 nn n n D ⨯=001030100211111解:)11(!0000300002011111221,3,21∑∑==⨯=-=-=-nj nn nj C jC nj njn n j D j2.3 可化为箭形的行列式∏∑∏∑=∏===+===⨯--+=---+⨯------=------==≠=n 1i i i n1k 222n1k i iC C n,2j n 333222111n1i i i n 1133112211321r -r n 2,i n 321321321321)x ()1(10101)(x101-0101-0011-)(x x 00x 0x 0x 00x x x D :,,2,1,j11i a a x a a x a a x a a x a a a x a a x a a x a a x x a a a a a a a a a a ni a x x a a a a x a a a a x a a a a x D k k kkk n kk knn n n i i nn nn n n n解3 降阶法 降阶法是利用行列式按其行(列)展开的性质,将高阶行列 式转化为低阶行列式进行计算)!1()1(21)1(00000000000)1(00000000000000000000004111+-=-++-+=-++=n b a ba b b b b ab a a b a a a b b a b a b a D n n n n n按第一列展开例4 升阶法 将原行列式增加一行一列,而保持原行列式值不变或与原行列式有某种巧妙的关系,且便于后面的计算)()1(00000001c c c c 010010011r r r r ,r r 00011n nax 112ax 11nn 1n 1312==-⋅-+=---+++---------=≠=-⨯---⨯n n nn ax a n n D a x a x ax naa x a x a x a a aa x a x a x a a a xa a a x aa a x aa a D a x xaa a a x a a a a x a a a a x D 时当时当5 递推法:利用行列式的性质,找出所求行列式与其相应的n-1,n ,2-阶行列式之间的递推关系,再根据次递推关系式求出所给行列式的值:,)()(:,)()(0000000)(000000000611111得由此递推下去得递推公式由此例----⨯-⨯⨯⨯⨯-+-=-+-=---+-=+-=+-+++==n n n n n nn n n n nn nn nn n a x a D a x D a x a D a x a aa x a a x a a x D a x a a a a a x a a a a x a a a a x a x a a a x a a a x a a a x a a x a a a x aa a x a a a x x a a a a x a a a a x a a a a x D])1([)()()1()()(])())[((1111122a n x a x a x a n D a x a x a a x a D a x a x D n n n n n n n -+-=--+-=-+-+--=------6数学归纳法:先利用不完全归纳法寻找行列式之间的规律,得出一般性结论,再用数学归纳法证明其正确性,从而得出所给行列式的值)1(1n .)1)(11()11(1111)11(101111111111117111211121212121211112121∑∑∑-=--==+=-≥+=+⋅=++=+=+=≠+++=n i in n ni in n i in nn a a a a a D n a a a a D a a a a a D a a a D a a a a a a D的情形猜测正确,即设对假确的下面证明这一猜测是正于是可猜测解其中例1121121212111110000000011111111111111111111---+=+=+++++=n n n n n nn D a a a a D a a a a a a a a D于是又归纳假设得:)11()11(12111121121∑∑=-=--+=++=ni in n i i n n n n a a a a a a a a a a a a D故对一切自然数n 猜得正确,即1),11(121≥+=∑=n a a a a D ni in n7 利用范德蒙行列式的结果计算:是将原行列式利用性质化成范德蒙行列式,再利用范德蒙行列式的结果计算出原行列式 例8nnn n nn nn n n n n x x x x x x x x x x x x D32122322213211111----=n 阶范德蒙行列式为∏≤<≤-----=nj i i jn nn n n nna aa a a a a a a a a a a a 111312112232221321)(1111解 构造n+1阶范德蒙行列式=)(x f 1,11,11,221,21,1)1()1(123211213231222112132111111+++-+--+++⨯+----------+++=n n n n n n n n n n n n n n n n nnn n nn n n nn n n n n n n A x A x A x xA A x x xx x x x x x xx xx xx xx x x x∏≤<≤-⋅---=ni j j in x xx x x x x x 121)()())((1,1,++-==n n n n n A M D 由f(x)的表达式知,1-n x 的系数为∏∏≤<≤≤<≤+-+++=∴-+++-=ni j j in n ni j j in n n x xx x x D x xx x x A 1211211,)()()()(8 拆项法:当行列式中的元素有两数相加时将原行列式拆成n 个简单的行列式加以计算例9 设nnn na a a a D1111=nnn n n nn n n n x a x a x a x a x a x a D ++++++=221122221211212111解n nn n n nn n n n x a x a a x a x a a x a x a a D ++++++=221222221121211nnn n nn n n x a x a x x a x a x x a x a x +++++++2212222112121∑=+++++++=ni i nnn n n nn n n A x x a x a a x a x a a x a x a a 111221222221121211∑∑∑∑====+=+++==ni ij nj j ni i ni in n A x D A x A x D 1111119 变换元素法:变换所给行列式中元素的形式,再利用已知行列式的结果,最终得到所求行列式的结果 例10211121112a a aa a a D n ------=解令a x -=1,由(拆项法例题结果)知∑∑==-++++=-++-+-+-+-++-+-+-+-++=ni nj ijn A a aa a a a aaa a a a a a a a D 11)1(10010001111010101110101011因为)]1()1[()1(0)1(11n a n a D j i j i a A n n n ij -+++=∴≠= ⎝⎛-=-- 10 分解乘积法:根据所给行列式的特点利用行列式的乘法公式,把所给行列式分解成两个易求解的行列式之积,通过对这两个行列式的计算,从而得到所给行列式之值 例11nn nn n n n nn b a b a b a b a b a b a D ⨯++++++=212221212111解213))((0000001111001001001001122111321321==≥⎪⎩⎪⎨⎧--+=⋅=n n n b b a a b a b b b b a a a a D nn n例题。
行列式的计算方法-计算行列式的格式行列式的计算方法计算行列式的格式行列式是线性代数中的一个重要概念,在数学、物理、工程等领域都有广泛的应用。
计算行列式是解决线性方程组、求矩阵的逆等问题的基础。
要准确计算行列式,掌握正确的格式和方法至关重要。
首先,我们来了解一下什么是行列式。
行列式是一个数值,它是由一个方阵的元素按照一定的规则计算得到的。
对于一个\(n\)阶方阵\(A =(a_{ij})\),其行列式记为\(\vert A \vert\)。
常见的计算行列式的方法有以下几种:一、二阶和三阶行列式的直接计算二阶行列式\(\begin{vmatrix}a_{11} & a_{12} \\ a_{21} &a_{22}\end{vmatrix}\)的计算方法为:\(a_{11}a_{22}a_{12}a_{21}\)三阶行列式\(\begin{vmatrix}a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{vmatrix}\)的计算方法为:\\begin{align}&a_{11}a_{22}a_{33} + a_{12}a_{23}a_{31} +a_{13}a_{21}a_{32} a_{13}a_{22}a_{31} a_{12}a_{21}a_{33}a_{11}a_{23}a_{32}\\\end{align}\在计算二阶和三阶行列式时,要严格按照上述公式的格式进行计算,注意符号的正负。
二、按行(列)展开法对于\(n\)阶行列式,我们可以将其按某一行(列)展开来进行计算。
设\(A\)为\(n\)阶方阵,\(a_{ij}\)为其元素,\(A_{ij}\)为\(a_{ij}\)的代数余子式,则行列式\(\vert A \vert\)等于\(a_{i1}A_{i1} + a_{i2}A_{i2} +\cdots + a_{in}A_{in}\)(按第\(i\)行展开)或\(a_{1j}A_{1j} + a_{2j}A_{2j} +\cdots +a_{nj}A_{nj}\)(按第\(j\)列展开)。
关于行列式的计算方法行列式是线性代数中非常重要的一个概念,它在矩阵和线性方程组的求解中都有广泛的应用。
本文将介绍关于行列式的定义、计算方法及其性质,以及一些常用的行列式计算技巧。
一、行列式的定义行列式是一个方阵(只有行数和列数相等的矩阵才有行列式)所具有的一个确定的数值。
对于一个n阶的方阵,其行列式记作det(A),其中A 表示矩阵。
行列式的计算方法主要有三种:代数余子式法、按行(列)展开法和逆序数法。
二、代数余子式法对于一个n阶方阵A,它的第i行第j列元素的代数余子式表示为Mij,定义为:将A的第i行和第j列元素划去,然后找出剩余元素所形成的n-1阶方阵的行列式。
即:Mij = det(Aij)其中Aij表示由第i行和第j列元素删去后所得到的(n-1)阶方阵。
根据代数余子式的定义,行列式的计算可以通过以下公式进行求解:det(A) = a11M11 - a12M12 + a13M13 - ... + (-1)^(i+j)aijMij + ...其中a11,a12,a13,...是第一行元素,M11,M12,M13,...是它们对应的代数余子式。
三、按行(列)展开法按行(列)展开法是行列式计算中最常用的一种方法。
对于一个n阶方阵A,选择其中任意一行或者一列,然后按照一定规律展开计算。
以按第一行展开为例,按照以下规律进行展开:det(A) = a11C11 + a12C12 + a13C13 + ... + a1nC1n其中Cij表示第一行第j列元素aij的余子式,定义为:将A的第一行和第j列元素划去,然后找出剩余元素所形成的(n-1)阶方阵的行列式。
将Cij的计算公式中的行列式再按行(列)展开,可以得到更小阶的余子式,直到降阶为2阶方阵时,余子式的计算直接是两个元素之差。
四、逆序数法逆序数法是行列式计算中的另一种方法。
对于一个n阶方阵A,按照以下步骤进行计算:1.首先,将方阵A展开至最小的单位(1阶方阵)。
计算行列式常用的7种方法行列式是线性代数中的重要概念,用于描述线性方程组的性质和解的情况。
在计算行列式时,有多种方法可供选择,下面将介绍行列式的常用计算方法。
1.代数余子式展开法代数余子式展开法是计算行列式的最常用方法之一、对于n阶行列式,可以选择其中的任意一行或一列展开。
选择一行展开时,可以使用代数余子式,即将每一元素乘以其代数余子式后再求和。
例如,对于3阶行列式\(\begin{bmatrix}a & b & c\\ d & e & f\\ g & h &i\end{bmatrix}\)选择第一行展开,计算行列式的值为\(aA_{11} - bA_{12} +cA_{13}\),其中\(A_{ij}\)表示第i行第j列元素的代数余子式。
类似地,可以选择列展开,使用代数余子式计算行列式的值。
2.初等变换法初等变换法是计算行列式的另一种常用方法。
通过一系列的行变换或列变换,将行列式转化为三角形矩阵或对角矩阵。
对于三角形矩阵,行列式的值即为对角线上元素的乘积;对于对角矩阵,行列式的值即为对角线上元素的乘积。
初等变换包括行交换、行缩放和行加减,可以有效地简化行列式的计算过程。
3.拉普拉斯展开法拉普拉斯展开法是计算行列式的一种常用方法,适用于任意阶的行列式。
选择其中的一行或一列展开,将行列式拆解为一系列子行列式的乘积。
每个子行列式的阶数比原行列式小1,可以继续进行递归的计算。
拉普拉斯展开法可以使用代数余子式进行计算,也可以利用构造矩阵的方式计算。
4.三对角矩阵法三对角矩阵法适用于计算特殊形式的行列式,即矩阵中除了对角线和相邻对角线上的元素外,其他元素都为0的情况。
计算三对角矩阵的行列式可以通过逐步化简为二阶或一阶行列式进行计算。
这种方法可以加速计算过程,特别适用于较大阶数的行列式。
5.特殊行列式法对于特殊形式的行列式,例如范德蒙行列式、希尔伯特行列式等,可以利用其特殊性质进行计算。
行列式计算方法首先,我们来介绍行列式的定义。
行列式是一个数学对象,它是一个关于矩阵的函数,可以用来判断矩阵是否可逆、求解方程组的解等。
对于一个n阶矩阵A,其行列式记作|A|或det(A),定义为一个数,它是由矩阵A的元素所确定的。
行列式的计算方法可以分为多种,包括拉普拉斯展开法、三角形法、性质法等。
下面我们将逐一介绍这些方法。
首先是拉普拉斯展开法。
对于一个n阶矩阵A,其行列式的计算可以通过对任意一行(或一列)的元素进行展开来实现。
具体来说,我们可以选择其中一行(或一列)的元素,以该行(或列)的元素为基础,按照"+ +"的规律,将矩阵A中除去该行(或列)的元素构成的n-1阶矩阵的行列式与该行(或列)的元素相乘,然后将所有这些乘积相加,即可得到矩阵A的行列式的值。
这种方法在计算过程中需要多次进行n-1阶矩阵的行列式计算,比较繁琐,但在理论上是可行的。
其次是三角形法。
对于一个n阶矩阵A,我们可以通过初等变换将其化为上(下)三角矩阵,然后利用上(下)三角矩阵的行列式的性质来计算整个矩阵A的行列式的值。
这种方法的优点在于可以通过初等变换将矩阵化简为三角形矩阵,从而简化计算过程,但在实际操作中需要注意初等变换的过程,以及上(下)三角矩阵的行列式的计算。
最后是性质法。
行列式有一系列重要的性质,例如行列式与其转置矩阵的关系、两行(列)互换行列式变号等。
利用这些性质,我们可以将矩阵A化简为对角矩阵,然后直接计算对角矩阵的行列式,从而得到整个矩阵A的行列式的值。
这种方法在实际操作中比较灵活,可以根据具体矩阵的性质进行化简,但需要熟练掌握行列式的性质。
总的来说,行列式的计算方法有多种,每种方法都有其适用的场景和特点。
在实际应用中,我们可以根据具体的矩阵和计算要求选择合适的方法进行计算,以便更高效地求得行列式的值。
希望本文介绍的行列式计算方法能够对读者有所帮助,让大家更好地理解和运用行列式的相关知识。
「行列式的计算方法」1.定义法:行列式的定义是通过递归来定义的。
对于一个1×1的矩阵A=[a],其行列式为det(A)=,a。
对于一个n×n的矩阵A=[aij],其中i代表行数,j代表列数,行列式可以通过以下方式递归计算:det(A)=Σ(-1)^(i+j)×aij×det(Aij)其中,Aij是将A中第i行和第j列删除后得到的(n-1)×(n-1)的子矩阵。
2.展开法:根据定义法,展开法也是一种递归的计算方法。
展开法是通过在行或列上选择一个元素展开计算行列式。
通常选择展开的元素是行列式中非零元素最多的行或列。
假设我们选择第i行展开,那么行列式可以表示为:det(A)=Σ(-1)^(i+j)×aij×det(Aij)其中,Aij是将A中第i行和第j列删除后得到的(n-1)×(n-1)的子矩阵。
通过递归计算Aij的行列式,最后可以得到det(A)的值。
3.克拉默法则:克拉默法则是行列式计算的一种特殊方法,适用于求解n元线性方程组。
对于一个n×n的方阵A=[aij],其行列式为det(A),方程组为Ax=b。
克拉默法则根据公式xk=det(Bk)/det(A),其中Bk是将A的第k列替换为b后的矩阵,det(Bk)是Bk的行列式,det(A)是A的行列式。
通过计算det(Bk)和det(A),可以求解方程组的解向量x。
4.LUP分解法:LUP分解法是行列式计算的一种常用方法,也适用于求解线性方程组。
LUP分解法通过将矩阵A分解为三个矩阵的乘积A=LU,其中L是一个下三角矩阵,U是一个上三角矩阵,P是一个置换矩阵。
LUP分解可以通过高斯消元法和选主元的方式得到。
通过进行LUP分解后,原方程组Ax=b可以表示为LUx=Pb,令Ux=y,则Ly=Pb。
通过先解y的方程组,再解x的方程组,可以求解出方程组的解向量x。
5.次序化方法:次序化方法是通过行列式的性质来计算行列式。
行列式的计算方法综述
目录
1.定义法(线性代数释疑解难参考)
2.化三角形法(线性代数释疑解难参考)
3.逐行(列)相减法(线性代数释疑解难参考)
4.升降法(加边法)(线性代数释疑解难参考)
5.利用范德蒙德行列式(线性代数释疑解难参考)
6.递推法(线性代数释疑解难参考)
7.数学归纳法(线性代数释疑解难参考)
8.拆项法(课外辅导书上参考)
9.换元方法(课外辅导书上参考)
10.拆因法(课外辅导书上参考)
线性代数主要内容就是求解多元线性方程组,行列式的计算其中起重要作用。
下面由我介绍几种常见的计算行列式的方法:
1.定义法
由定义看出,n级行列式有!n个项。
n较大时,!n是一个很大的数字。
直接用定义来计算行列式是几乎不可能的事。
但在n级行列式中的等于零的项的个数较多时,它展开式中的不等于零的项就会少一些,这时利用行列式的定义来计算行列式较方便。
例1.算上三角行列式
解:展开式的一般项为
同样,可以计算下三角行列式的值。
2.化三角形法
画三角形法是先利用行列式的性质将原行列式作某种保值变形,化为上
第 1 页
(下)三角形行列式,再利用上(下)三角形行列式的特点(主对角线上元素的乘积)求出值。
例2.计算
解:各行加到第一行中
把第二列到第n 列都分别加上第一列的()1-倍,有
3.逐行(列)相减法
有这样一类行列式,每相邻两行(列)之间有许多元素相同,且这些相同元素都集中在某个角上。
因此可以逐行(列)相减的方法化出许多零元素来。
例3.计算n 级行列式
解:从第二行起,每一行的()1-倍都加上上一行,有
上式还不是特殊三角形,但每相邻两行之间有许多相同元素()10或,且最后一行有()1n -元素都是x 。
因此可再用两列逐列相减的方法:第()1n -列起,每一列的()1-倍加到后一列上
4.升降法(加边法)
升降法是在原行列式中再添加一列一行,是原来的n 阶成为()1n +阶,且往往让()1n +阶行列式的值与原n 阶行列式的值相等。
一般说,阶数高的比阶数低的计算更复杂些。
但是如果合理的选择所添加的行,列元素,是新的行列式更便于“消零”的话,则升降后有利于计算行列式的值。
例4.计算n 级行列式
第 2 页
解: 1212121
2
10
10
10
1n n n
n D αααααααααααα+=++L L L
M M
M
M L
121110010101
000
n
ααα-=--L
L L M M M M L
121
110100
100100001
n
i n
n i ααααα+=
=+∑∑L
L L M M M M L
5.利用范德蒙德行列式
例5. 计算n 级行列式
解:这个行列式与范德蒙行列式很相似,可以利用行列式的性质将它化为范德蒙行列式。
n D 的第n 行依次与1n -行,2n -行,K ,2行,1行对换,再将所得到的行
列式的第n 行,依次与1n -行,2n -行,L ,2行对换。
如此继续下去,直到最后将第n 行与1n -行对换,这样经过()()()1
122112
n n n n -+-+++=-L L 次对换后,得到
这是一个范德蒙行列式。
于是有
范德蒙行列式是一个重要的行列式,它可以作为公式应用。
6.递推法
这种方法是计算n 阶行列式较有用的一种方法。
首先利用行列式性质把给
第 3 页
定的n 阶行列式n D 用同样形式的低阶行列式表示出来,这种表示式称为递推关系式。
然后从递推关系式出发求出n D 的一般表示式。
例6. 计算n 级行列式
解:本题第一列只有两个非零元素,且11a 的余子式恰为1n D -。
因此我们有可能找出递推关系式。
按第一列展开得
故
这就是本题行列式的一个递推关系式,往n 减少方向递推有 故有
7.数学归纳法
计算和证明一些行列式时用数学归纳法来计算和证明比较方便,所以我们就用数学归纳法。
数学归纳法一般是在已知行列式的结果或猜出其结果作严格论证时用的方法。
例7.试证n 阶行列式 证明:用归纳法步骤 1.验证:当2n =时, 左()212122
11
x x a x a x a x a a a x
-=
=++=+++ 右212
x a x a =++∴左边=右边
注意:当本题行列式为2阶时,应取右下角的2阶与12,a a 有关的行列式,而不能取左上角的。
第 4 页
2设当1n -阶时,结论成立。
则将n D 用第一列展开,有()
1
11000100100000
1
n n n n x D xD a x x +---=+--L L L M M M M L =右
8.拆项法
由行列式拆项性质知,将已知行列式拆成若干个行列式之和,计算其值,再得原行列式值。
此法称为拆行(列)法。
例8. 0000000000n a a a a a a b
a a
b a a D b
b a b b a b b b
b b b
a a
--==--L L L L L L M M M M M M M M L L 对于上面的第一行列式,将第n 列乘()b -加到其余各列上,对第二个行列式按第n 列展开,最后可得:
这样我们得一个递推公式:()
1
1n n n D a b aD --=-+
如果将第一列对b 按类此方法拆项,又可得到另一递推公式:
()
1
1n n n D b a bD --=--
取立上述两递推公式()()1
11
1
n n
n n n n D a b aD D b a bD ----⎧=--⎪⎨=--⎪⎩
第 5 页
当a b ≠时,()
11
1
1n n n n a b D ab
a b
----=-- 当a b =时,()
()1
11n n n D n a -=--
9.换元方法
这种方法利用行列式的这样一条性质:
设11121111212122221222112
12,n n n
n n n nn n n nn x x x x x x
D D x x x
αααααααααααααααααα++++++=
=
+++L L L
L
L
L
L L
L L L L
L
L
则1,1
n
ij i j D D x A ==+∑
例9.计算n 阶行列式n x
x D x
ααα
α
αα
=
L
L L
L
L L L
解: ()()()000000n x x D x αα
ααααα
α
α
ααα
-++++-++=
++-+L L L L L L
L
()1
000000
n x x n x x ααααα
---=+--L L L L L L L
10.拆因法
如果行列式D 中有一些元素是x 的多项式,那么可以将行列式D 当作一个多
第 6 页
项式()f x ,然后对行列式施行某些变换,求出()f x 的互素的一次因式,使得()f x 与这些因式的乘积()g x 只相差一个常数因子c ,根据多项式相等的定义,比较()f x 与()g x 的某一项的系数,求出c 的值,便可求得()D cg x =
例10.计算1
231
131
211231
n n x n D x n x +=++L
L L L L L L L L 解:已知行列式n D 是x 的()1n -次多项式,利用行列式的性质我们把
()1n -次多项式分解成n D 的一次因式的乘积。
当1x =时,n D 的第一列和第二
列的对应元素成比例,所以0n D =。
显然1x -是n D 的一个因式。
当2x =时,n D 的第一列和第三列的对应元素成比例,所以0n D =。
显然2x -是n D 的一个因式。
同法得出()3,4,,1x x x n ----L L 是n D 的因式。
因为x i -和 x j -(),,1,2,,1i j i j n ≠=-L L 为互素,所以
()()()121n
x x x n D --⎡--⎤⎣⎦L
,但n
D 的展开式中的最高项1n x -的系数是1,因此
总结
以上我们介绍了计算行列式的10种方法。
在具体计算时,要根据行列式构造上的特点,利用行列式的性质,选用适当的方法来计算。
这就需要我们熟悉个类型行列式的构造上的特点及善于不断的归纳总结。
学无止境。
明天,将是我终身学习另一天的开始。
在此谨向帮助过我的所有老师和同学表示诚挚的感谢!
此致
敬礼
潘滨
2013年12月28日希望以上资料对你有所帮助,附励志名言3条::
1、世事忙忙如水流,休将名利挂心头。
粗茶淡饭随缘过,富贵荣华莫强求。
2、“我欲”是贫穷的标志。
事能常足,心常惬,人到无求品自高。
3、人生至恶是善谈人过;人生至愚恶闻己过。
第7页。