华师大版-数学-九年级上册-导学案-直角三角形的性质

直角三角形的性质课题直角三角形的性质课时1课时上课时间教学目标1.知识与技能(1)梳理并掌握直角三角形的性质.(2)通过对直角三角形的性质的探索，进一步明确直角三角形的边角关系. 2.过程与方法经历对直角三角形的性质的探索过程，进一步培养学生的收集、描述、分析数据的技能.3.情感、态度与价值观培养学生对知识的整理和梳理的习惯.教学重难点重点:直角三角形的性质的论证. 难点:直角三角形的性质的应用.教学活动设计二次设计课堂导入直角三角形有哪些性质？性质1:直角三角形的两个锐角互余;性质2:直角三角形两直角边的平方和等于斜边的平方(勾股定理).探索新知合作探究自学指导自学教材P102~103的内容.合作探究探究性质3:直角三角形斜边上的中线等于斜边的一半.已知:在Rt△ABC中，∠ACB=90°，CD是斜边AB 上的中线.求证:CD=AB.证明:延长CD至点E，使DE=CD，连结AE，BE.∵CD是斜边AB上的中线，∴AD=DB.又∵DE=CD，∴四边形ACBE是平行四边形.又∵∠ACB=90°，∴四边形ACBE是矩形，∴CE=AB，∴CD=CE=AB.续表探索新知合作探究教师指导1.易错点:一定要注意性质的前提是在直角三角形中.2.归纳小结:(1)直角三角形的两个锐角互余;(2)直角三角形两直角边的平方和等于斜边的平方(勾股定理).(3)直角三角形斜边上的中线等于斜边的一半.3.方法规律:解决直角三角形的问题，通常还需要添加辅助线.当堂训练1.在△ABC中，∠ACB=90°，CE是AB边上的中线，那么与CE相等的线段有______，与∠A相等的角有_______ .若∠A=35°，那么∠ECB= _______.2.在直角三角形中，斜边及其中线之和为6，那么该三角形的斜边长为_______.3.如图，在△ABC中，AD⊥BC，E，F分别是AB，AC的中点，且DE=DF.求证:AB=AC.板书设计直角三角形的性质1.性质:(1)直角三角形的两个锐角互余;(2)直角三角形两直角边的平方和等于斜边的平方(勾股定理);(3)直角三角形斜边上的中线等于斜边的一半.2.例题.教学反思。

华师大版数学九年级上册24.4《直角三角形的性质》教学设计一. 教材分析《直角三角形的性质》是华师大版数学九年级上册第24章《三角形的性质》的最后一节内容，也是整个初中数学中关于三角形性质的重要部分。

本节内容主要介绍直角三角形的性质，包括直角三角形的边角关系、勾股定理及其应用。

通过本节的学习，学生能进一步理解直角三角形的特征，掌握直角三角形的相关性质，提高解题能力。

二. 学情分析九年级的学生已经学习了锐角三角形和钝角三角形的性质，对三角形的性质有一定的了解。

但是，对于直角三角形的性质，特别是勾股定理的理解和应用，部分学生可能还存在困难。

因此，在教学过程中，需要关注学生的学习差异，针对性地进行教学。

三. 教学目标1.理解直角三角形的性质，掌握直角三角形的边角关系。

2.掌握勾股定理，并能运用勾股定理解决实际问题。

3.培养学生的空间想象能力，提高解题能力。

4.激发学生学习数学的兴趣，培养学生的合作意识和探究精神。

四. 教学重难点1.教学重点：直角三角形的性质，勾股定理的推导和应用。

2.教学难点：勾股定理的理解和应用，解决实际问题。

五. 教学方法1.采用问题驱动的教学方法，引导学生主动探究直角三角形的性质。

2.运用多媒体辅助教学，直观展示直角三角形的性质，提高学生的空间想象能力。

3.采用合作学习的方式，让学生在讨论中解决问题，培养学生的合作意识。

4.通过举例讲解，引导学生学会运用勾股定理解决实际问题。

六. 教学准备1.准备相关的教学课件和教学素材。

2.准备练习题和拓展题，以便进行课堂练习和课后巩固。

3.准备黑板和粉笔，以便进行板书。

七. 教学过程1.导入（5分钟）利用多媒体展示一些生活中的直角三角形，如教室的黑板、楼梯的台阶等，引导学生关注直角三角形的存在。

提问：这些直角三角形有什么特殊的性质吗？2.呈现（10分钟）通过PPT展示直角三角形的性质，包括直角三角形的边角关系、勾股定理。

在展示过程中，引导学生思考这些性质是如何得出的。

教学设计
小结：直角三角形斜边上的中线等于斜边的一半
三、合作交流、尝试练习
利用直角三角形的上述性质，可以解决某些与直角三角形有关的问题 例：在Rt △ABC 中，∠ACB=90°，∠A=30°，求证：BC=2
1AB
小结：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半。

四、联系实际、应用拓展
教材104页练习1、2、3；
五、归纳小结
谈谈本节课你的收获，与同学进行分享。

六、布置作业
教材104-105页1、2、3题
板书设计
24.2直角三角形的性质
直角三角形的性质
（1）直角三角形的两个锐角互余。

（2）直角三角形两条直角边的平方和等于斜边的平方。

（勾股定理）
（3）直角三角形斜边上的中线等于斜边的一半。

几何语言：在Rt △ABC 中,∠ACB=90°，CD 是斜边AB 上的中线，
（1）∠A+∠B = 90°
（2）AC 2+ BC 2=AB 2
（3）CD=2
1AB。

华师大版数学九年级上册《解直角三角形》教学设计3一. 教材分析华师大版数学九年级上册《解直角三角形》是学生在初中阶段最后一节关于三角形的课程，学生在之前的学习中已经掌握了锐角三角形和钝角三角形的性质以及三角形的分类。

本节课主要让学生了解直角三角形的性质，学会用勾股定理计算直角三角形的边长，并用三角函数表示直角三角形的边角关系。

教材通过丰富的情境图和实例，激发学生的学习兴趣，引导学生探究直角三角形的性质，培养学生的动手操作能力和数学思维能力。

二. 学情分析九年级的学生已经具备了一定的几何知识，对三角形有了一定的了解。

但是部分学生对三角形性质的掌握不够扎实，对勾股定理的理解和应用还不够熟练。

此外，学生在学习过程中往往存在对理论知识掌握较好，但实际操作能力较弱的问题。

因此，在教学过程中，需要注重引导学生运用已有的知识解决实际问题，提高学生的动手操作能力和解决问题的能力。

三. 教学目标1.知识与技能：让学生掌握直角三角形的性质，学会用勾股定理计算直角三角形的边长，会用三角函数表示直角三角形的边角关系。

2.过程与方法：通过观察、操作、探究等活动，培养学生合作交流、归纳总结的能力，提高学生解决实际问题的能力。

3.情感态度与价值观：让学生在解决实际问题的过程中，体验数学学习的乐趣，增强学生对数学学科的学习兴趣。

四. 教学重难点1.重点：让学生掌握直角三角形的性质，会用勾股定理计算直角三角形的边长。

2.难点：让学生会用三角函数表示直角三角形的边角关系。

五. 教学方法1.情境教学法：通过情境图和实例，激发学生的学习兴趣，引导学生探究直角三角形的性质。

2.启发式教学法：在教学过程中，教师提问引导学生思考，激发学生的求知欲，培养学生独立思考的能力。

3.合作学习法：学生进行小组讨论，培养学生的团队协作能力和归纳总结能力。

4.实践操作法：让学生动手操作，解决实际问题，提高学生的动手能力和解决问题的能力。

六. 教学准备1.教学课件：制作华师大版数学九年级上册《解直角三角形》的教学课件。

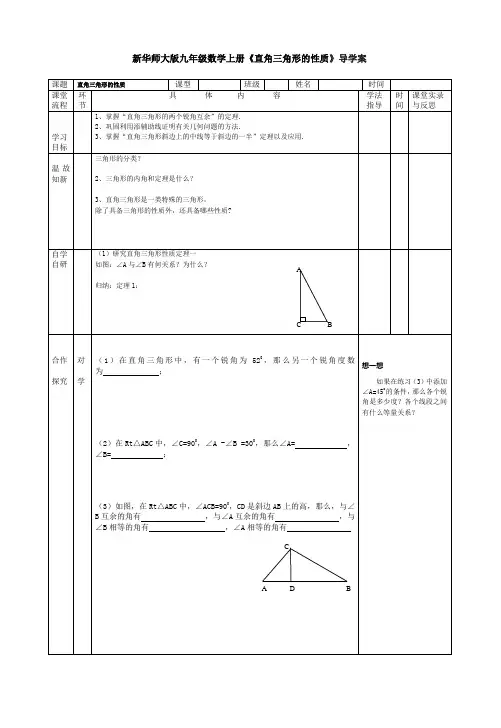
直角三角形的性质一、学习目标1.回顾勾股定理，知道直角三角形两角互余。

2.探索直角三角形斜边上的中线等于斜边的一半以及30°角所对的直角边等于斜边的一半二、学习重点直角三角形斜边上的中线等于斜边的一半。

三自主预习旧知回顾（1）勾股定理相关内容？（2）直角三角形锐角关系？四、合作探究性质1.任意画一个直角三角形AB C，并画出斜边上的中线CD。

（1）(量一量)自己动一动手，量一量CD与AB的长度并比较它们有什么关系？和你的同桌对比一下结论一致吗？（2）（证一证）你能证明这一性质吗？性质2.（1）(量一量). 自己动一动手用刻度尺测量含30°角的直角三角形的斜边和短直角边，比较它们之间的数量关系，你有什么发现？（2）（拼一拼）.小组合作初中-数学-打印版将两个含有30°的三角板如图摆放在一起，你能借助这个图形找到Rt△ABC的直角边BC(30°角所对的)与斜边AB之间的数量关系吗？（3）（证一证）你能证明这一性质吗？归纳：直角三角形斜边上的中线等于_________________________________________.几何语言：在RT△ABC中，∠C=90，∠A＝30°∴BC= 21AB(或AB = 2BC)五、巩固反馈1．在直角三角形ABC中，∠ACB=90度，CD是AB边上中线，若CD=5cm，则AB=_____三角形ABC的面积=____________2顶角为30度的等腰三角形，若腰长为2，则腰上的高__________，三角形面积是________ 3．在直角三角形中，斜边及其中线之和为6，那么该三角形的斜边长为________．4．等腰三角形顶角为120°，底边上的高为3，则腰长为_________5．屋架设计图，点D是斜梁AB的中点，立柱BC.DE垂直于横梁AC，AB＝8m，∠A＝30°则BC= __________，DE=______________.6．如图，在△ABC中，∠B=∠C，D.E分别是BC.AC的中点，AB=6，求DE的长。

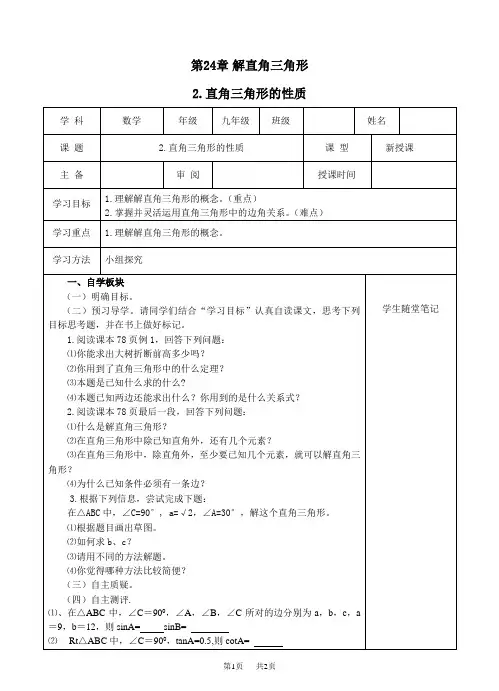
第24章解直角三角形24．2直角三角形的性质课题24.2直角三角形的性质授课人教学目标知识技能1.会利用直角三角形斜边上中线等于斜边的一半进行线段的计算和证明.2.能应用30°角所对的直角边等于斜边的一半进行计算和证明.3.知道把非30°角的问题转化为30°角所对的直角边和斜边的关系进行计算．数学思考直角三角形除了有两锐角互余和勾股定理这两个性质外，还有斜边上的中线等于斜边的一半和30°角所对的直角边等于斜边的一半的性质．问题解决通过直角三角形斜边上的中线和斜边的关系及边之间的关系的计算，进一步深入地理解和应用直角三角形的性质．情感态度通过角与边的关系的探究，拓展学生的思维，培养学生的转化意识和探究能力．教学重点“直角三角形斜边上的中线等于斜边的一半”和“在直角三角形中，30°角所对的直角边等于斜边的一半”的应用．教学难点直角三角形的性质的推导.授课类型新授课课时教具多媒体教学活动教学步骤师生活动设计意图回顾1什么是直角三角形？2. 直角三角形的两锐角有啥关系？3. 直角三角形的三边有啥关系？学生回忆并回答，为本课的学习提1 / 112 / 113 / 114 / 115 / 116 /11图24－2－102） 如图，△ABC 中，BC ＝18，若BD ⊥AC 于点D ，CE ⊥AB 于 点E ，F ，G 分别为BC ，DE 的中点．若ED ＝10，则FG 的长为多少？活动二：实践【探究1】1. 量一量：拿出你手中的三角板，量一量30度 的角所对的直角边的长度，在量一量斜边的长，你有何发现？通过回答探究1，回顾7 / 118 / 119 / 1110 / 1111 / 11。

华师⼤版-数学-九年级上册-24.2直⾓三⾓形的性质教学设计证明命题：（教师引导，学⽣讨论，共同完成证明过程）应⽤定理：已知：如图，在△ABC 中，∠B=∠C ，AD 是∠BAC 的平分线，E 、F 分别AB 、AC 的中点。

求证：DE=DF分析：可证两条线段分别是两直⾓三⾓形的斜边上的中线，再证两斜边相等即可证得。

（上⼀题我们是两个直⾓三⾓形的⼀条较长直⾓边重合，现在我们将图形变化使斜边重合，我们可以得到哪些结论？）（三）例题讲解例1：已知，Rt △ABC 中，∠ACB=90°，AB=8cm ，D 为AB 中点，DE ⊥AC 于E ，∠A=30°，求BC ，CD 和DE 的长分析：由30°的锐⾓所对的直⾓边为斜边的⼀半，BC 可求，由直⾓三⾓形斜边中线的性质可求CD.在Rt △ADE 中，有∠A=30°，则DE 可求. 解：在Rt △ABC 中∵∠ACB=90 ∠A=30°∴AB BC 21= ∵AB=8 ∴BC=4∵D 为AB 中点，CD 为中线∴421==AB CD ∵DE ⊥AC ，∴∠AED=90° 在Rt △ADE 中，AD DE 21=， AB AD 21= ∴241==AB DE 例2：已知：△ABC 中，AB=AC=BC （△ABC 为等边三⾓形）D 为BC 边上的中点，DE ⊥AC 于E.求证：AC CE 41=. 分析：CE 在Rt △DEC 中，可知是CD 的⼀半，⼜D 为中点，故CD 为BC 上的⼀半，因此可证.证明：∵DE⊥AC于E，∴∠DEC=90°(垂直定义)∵△ABC为等边三⾓形，∴AC=BC ∠C=60°∵在Rt△EDC中，∠C=60°，∴∠EDC=90°-60°=30°∴CD=∵D为BC中点，∴BCDC21=∴ACDC21=∴ACCE41=.（四）练习变式：1、已知：在△ABC中，BD、CE分别是边AC、AB上的⾼，F是BC的中点。

24.2直角三角形的性质一、知识回顾如图，在△ABC中，∠C=90°（1）若∠A=40°,则∠B=（2）若AB=10,BC=6,则AC=设计意图：通过题组引导，培养学生将直角三角形的性质不断提取再现与归纳，引导学生学会总结，学会数学地思维.二、新知导学1.若CD是中线,若AC=8,BC=6,则 CD=2.若∠A=30°,BC=6,则AB=三、例题讲解四、当堂检测1 如图，在△ABC中，∠ACB=90°,CD⊥AB于D，∠A=30°,BC=4，那么∠1=， BD= ，AD=2、已知△ABC中, ∠A=900, ∠B=4 ∠C,则∠B=3、满足下列条件的△ABC，不是直角三角形的是（）A、b2 = c2 - a2B、∠C=∠A - ∠BC、∠A︰∠B︰∠ C=3︰4︰5D、a︰b︰c=3︰4︰54、现有两根木棒长为4cm和3cm，若要钉成一个直角三角形木架，则所需的木棒长为多少_________cm.5、如图，在Rt△ABC中， AB=10，BC=8CD是斜边AB上的高线，则CD= 。

CE是斜边AB上的中线，则CE= 。

6、今年“莫拉克”台风严重影响了我们宝岛台湾，一棵树在离开地面6米A处折断倒下，与地面成30°，那么树折断之前是______米？(A) 12 (B) 18 (C) 20 (D)24；设计意图：复习直角三角形有关角的特有性质：进行巩固并回忆。

设计意图：通过题组引导，培养学生将直角三角形的性质不断提取再现与归纳，引导学生学会总结，学会数学地思维.四、综合应用如图，折叠长方形ABCD的一边AD，使点D落在BC边上的一点F处。

已知AB=8,BC=10,求 EC 的长并求出最小路程。

五、小结设计意图：学生讲知识点、收获、一点遗憾，并强调数学思想方法.七、作业教师个人研修总结在新课改的形式下，如何激发教师的教研热情，提升教师的教研能力和学校整体的教研实效，是摆在每一个学校面前的一项重要的“校本工程”。

华师大版数学九年级上册《解直角三角形》教学设计一. 教材分析华师大版数学九年级上册《解直角三角形》是学生在学习了平面几何、立体几何的基础上，进一步研究三角形的性质和解法。

本节课的内容包括直角三角形的定义、性质，锐角三角函数的定义和计算，以及解直角三角形的方法。

教材通过丰富的例题和练习题，帮助学生掌握解直角三角形的基本技能，提高解决实际问题的能力。

二. 学情分析学生在学习本节课之前，已经掌握了平面几何和立体几何的基本知识，具备了一定的逻辑思维和空间想象能力。

但解直角三角形这一部分内容较为抽象，需要学生能够将实际问题与数学知识相结合，进行合理的转化和推导。

因此，在教学过程中，需要关注学生的学习困惑，引导他们积极参与，提高他们的学习兴趣和自信心。

三. 教学目标1.理解直角三角形的定义和性质，掌握锐角三角函数的定义和计算方法。

2.学会解直角三角形的方法，能够运用所学知识解决实际问题。

3.培养学生的空间想象能力，提高他们的逻辑思维和解决问题的能力。

四. 教学重难点1.直角三角形的定义和性质。

2.锐角三角函数的定义和计算。

3.解直角三角形的方法及应用。

五. 教学方法1.采用问题驱动的教学方法，引导学生主动探究，发现规律。

2.利用多媒体课件和实物模型，直观展示直角三角形的性质和解法，增强学生的空间想象力。

3.采用合作学习的方式，让学生在讨论和交流中，共同解决问题，提高他们的团队协作能力。

六. 教学准备1.多媒体课件和教学软件。

2.直角三角形模型和实物。

3.练习题和测试题。

七. 教学过程1.导入（5分钟）利用多媒体课件展示一些生活中的直角三角形实例，如建筑物的楼梯、自行车的三角架等，引导学生关注直角三角形在实际生活中的应用。

提问：这些实例中的三角形有什么共同的特点？引出直角三角形的定义和性质。

2.呈现（10分钟）讲解直角三角形的定义和性质，引导学生通过观察和思考，发现直角三角形的特殊性和重要性。

同时，介绍锐角三角函数的定义和计算方法，让学生了解解直角三角形的工具。

华师大版数学九年级上册《解直角三角形》教学设计5一. 教材分析华师大版数学九年级上册《解直角三角形》是学生在学习了平面几何、相似三角形等知识后的进一步拓展。

本节课的主要内容是让学生掌握解直角三角形的方法，理解直角三角形的性质，能够运用勾股定理和锐角三角函数解决实际问题。

教材通过丰富的例题和练习题，帮助学生巩固知识，提高解题能力。

二. 学情分析九年级的学生已经具备了一定的几何知识基础，对相似三角形、勾股定理等概念有一定的了解。

但学生在解直角三角形时，仍存在对概念理解不深刻、解题方法不灵活、解决实际问题能力不强等问题。

因此，在教学过程中，需要关注学生的知识基础，引导学生理解和掌握解直角三角形的方法，提高解决实际问题的能力。

三. 教学目标1.知识与技能目标：使学生掌握解直角三角形的方法，理解直角三角形的性质，能够运用勾股定理和锐角三角函数解决实际问题。

2.过程与方法目标：通过观察、操作、探究等活动，培养学生独立思考、合作交流的能力。

3.情感态度与价值观目标：激发学生学习数学的兴趣，培养学生的数学素养，使学生感受到数学在生活中的应用。

四. 教学重难点1.教学重点：使学生掌握解直角三角形的方法，能够运用勾股定理和锐角三角函数解决实际问题。

2.教学难点：对直角三角形性质的理解和应用，以及解决实际问题的能力。

五. 教学方法采用问题驱动法、合作学习法、案例教学法等，引导学生通过自主学习、合作交流，主动探究解直角三角形的方法，提高解决实际问题的能力。

六. 教学准备1.教师准备：熟练掌握解直角三角形的相关知识，准备好教学课件、例题、练习题等教学资源。

2.学生准备：预习相关知识，了解直角三角形的概念和性质。

七. 教学过程1.导入（5分钟）教师通过提问方式引导学生回顾直角三角形的概念和性质，为新课的学习做好铺垫。

2.呈现（10分钟）教师通过多媒体课件展示直角三角形的图像，引导学生观察和描述直角三角形的特征。

然后，介绍勾股定理和锐角三角函数的概念，引导学生理解解直角三角形的原理。

华师大版数学九年级上册24.4《直角三角形的性质》说课稿一. 教材分析华师大版数学九年级上册第24.4节《直角三角形的性质》是学生在学习了锐角三角形、钝角三角形的基础上，进一步探讨直角三角形的性质。

本节课的内容包括直角三角形的定义、直角三角形的边角关系、直角三角形的内切圆等。

通过本节课的学习，学生能够深入理解直角三角形的性质，提高解决问题的能力。

二. 学情分析九年级的学生已经掌握了锐角三角形和钝角三角形的基本知识，对于三角形的性质有一定的了解。

但是，对于直角三角形的特殊性质，学生可能还比较陌生。

因此，在教学过程中，我将会以引导为主，让学生通过观察、思考、讨论，自主地发现和总结直角三角形的性质。

三. 说教学目标1.知识与技能目标：让学生掌握直角三角形的定义和性质，能够运用这些性质解决实际问题。

2.过程与方法目标：通过观察、思考、讨论等过程，培养学生的逻辑思维能力和团队协作能力。

3.情感态度与价值观目标：激发学生对数学的兴趣，培养学生的自主学习能力。

四. 说教学重难点1.教学重点：直角三角形的定义和性质。

2.教学难点：直角三角形性质的推导和应用。

五. 说教学方法与手段在本节课的教学中，我将采用问题驱动的教学方法，引导学生通过观察、思考、讨论等方式自主地发现和总结直角三角形的性质。

同时，我会运用多媒体教学手段，如PPT、几何画板等，为学生提供丰富的教学资源，帮助学生更好地理解和掌握知识。

六. 说教学过程1.导入：通过复习锐角三角形和钝角三角形的性质，引出直角三角形的性质，激发学生的学习兴趣。

2.新课导入：介绍直角三角形的定义，引导学生观察和思考直角三角形的特殊性质。

3.性质探究：引导学生通过观察、思考、讨论等方式，自主地发现和总结直角三角形的性质。

4.性质证明：运用几何画板等教学手段，引导学生证明直角三角形的性质。

5.性质应用：通过实例，引导学生运用直角三角形的性质解决实际问题。

6.课堂小结：总结本节课的主要内容和知识点，帮助学生巩固所学。