201X春八年级数学下册20数据的分析20.1数据的集中趋势20.1.2中位数和众数第1课时学案 新
- 格式:doc
- 大小:153.50 KB
- 文档页数:4

陕西省安康市石泉县池河镇八年级数学下册第20章数据的分析20.1 数据的集中趋势20.1.1 平均数(1)教案(新版)新人教版
编辑整理:
尊敬的读者朋友们:
这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(陕西省安康市石泉县池河镇八年级数学下册第20章数据的分析20.1 数据的集中趋势20.1.1 平均数(1)教案(新版)新人教版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为陕西省安康市石泉县池河镇八年级数学下册第20章数据的分析20.1 数据的集中趋势20.1.1 平均数(1)教案(新版)新人教版的全部内容。
平均数。

其次十章数据的分析20.1 数据的集中趋势20.1.1 平均数第1课时加权平均数学问点加权平均数和算术平均数1.7名学生的体重(单位: kg)分别是40,42,43,45,47,47,58,则这组数据的平均数是( )A.44 B.45 C.46 D.472.2024·聊城为了满意顾客的需求,某商场将5 kg奶糖,3 kg酥心糖和2 kg水果糖混合成什锦糖出售.已知奶糖的售价为每千克40元,酥心糖为每千克20元,水果糖为每千克15元,混合后什锦糖的售价应为每千克( )A.25元 B.28.5元C.29元 D.34.5元3.[2024·上海] 某校调査了20名男生某一周参与篮球运动的次数,调査结果如下表所示,那么这20名男生该周参与篮球运动次数的平均数是( )次数 2 3 4 5人数 2 2 10 6A.3 B.3.5 C.4 D.4.54.某中学实行校内歌手大赛,7位评委给选手小明的评分如下表:评委 1 2 3 4 5 6 7得分(分) 9.8 9.5 9.7 9.8 9.4 9.5 9.4 若竞赛的计分方法如下:去掉一个最高分,去掉一个最低分,其余分数的平均值作为该选手的最终得分,则小明的最终得分为( )A.9.56分B.9.57分C.9.58分D.9.59分5.某校规定学生的数学学期综合成果是由平常、期中和期末三项成果按3∶3∶4的比例计算所得.若某同学本学期数学的平常、期中和期末成果分别是90分、90分和85分,则他本学期数学学期综合成果是________分.6.某次射击训练中,一小组的成果(单位:环)如下表所示,已知该小组的平均成果为8环,那么成果为9环的人数是环数7 8 9人数 3 47.一次考试中,甲组12人的平均分数为70分,乙组8人的平均分数为80分,那么这两组20人的平均分数为________.8.某班有学生52人,期末数学考试平均成果是72分,有两名同学下学期要转学,已知他俩的成果分别为70分和80分,求他俩转学后该班的数学平均分.9.某公司聘请一名工作人员,对甲、乙两名应聘者进行笔试与面试,他们的成果(百分制)如下表所示.若公司分别给予面试成果和笔试成果6和4的权,计算甲、乙两人各自的平均成果.从他们的成果看,谁将被录用?应聘者面试笔试甲87 90乙91 8210写作实力一般话水平计算机水平小亮90分75分51分小丽60分84分72分将写作实力、一般话水平、计算机水平这三项的总分由原先按3∶5∶2计算,变成按5∶3∶2计算,则总分改变状况是( )A.小丽成果增加的多B.小亮成果增加的多C.两人成果均不改变D.改变状况无法确定11.如图20-1-1是依据今年某校九年级学生体育考试跳绳的成果绘制成的统计图.假如该校九年级共有200名学生参与了这项跳绳考试,依据该统计图给出的信息,可得这些同学跳绳考试的平均成果为________个.图20-1-112.某公司需聘请一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核,甲、乙、丙各项得分(单位:分)如下表:笔试面试体能甲83 79 90乙85 80 75丙80 90 73(1)(2)该公司规定:笔试、面试、体能得分分别不得低于80分、80分、70分,并按60%,30%,10%的比例计入总分,依据规定,请你说明谁将被录用.13.某班为了从甲、乙两位同学中选出班长,进行了一次演讲答辩与民主测评,A,B,C,D,E五位老师作为评委,对“演讲答辩”状况进行评价,全班50位同学参与了民主测评,结果如下表所示:A B C D E甲90 92 94 95 88乙89 86 87 94 91“好”票数“较好”票数“一般”票数甲40 7 3乙42 4 4测评分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分;综合得分=演讲答辩分×(1-a)+民主测评分×a(0.5≤a≤0.8).(1)当a=0.6时,甲的综合得分是多少?(2)当a在什么范围内时,甲的综合得分高?当a在什么范围内时,乙的综合得分高?。




20.1.1 平均数(1)【教学目标】1.知识与技能(1)理解数据的权和加权平均数的概念;(2)掌握加权平均数的计算方法。
2.过程与方法初步经历数据的收集与处理过程,发展学生初步的统计意识和数据处理能力。
3.情感态度和价值观通过解决身边的实际问题,让学生初步认识数学与人类生活的密切联系及对人类历史发展的作用。
【教学重点】会求一组数据的算术平均数和加权平均数。
【教学难点】理解加权平均数的概念。
【教学方法】自学与小组合作学习相结合的方法。
【课前准备】教学课件。
【课时安排】1课时【教学过程】一、情景导入【过渡】在小学的时候,我们就接触过平均数这个概念。
而我们日常生活中,也经常能遇到这类问题,比如我们在每次考试结束后要进行横向对比,看本班级在年级中的所排名次如何,自己在本班中排名第几,这就需要知道各科分数这些数据,并要对数据进行处理之后才能得出结论,现在,我们就来回忆一下平均数。
1、如何求一组数据的平均数?2、七位裁判给某体操运动员打的分数分别为:7.8,8.1,9.5,7.4,8.4,6.4,8.3.如果去掉一个最高分,去掉一个最低分,那么,这位运动员平均得分是多少?(学生回答)【过渡】刚刚的问题呢,都是比较简单的问题,今天我们就来学习一下更进一步的关于平均数的问题。
二、新课教学 1.平均数【过渡】通过之前的学习,我们知道了平均数可以反映一组数据的平均水平,那么,在实际问题中,我们有该如何理解平均数的统计意义呢?课本问题1.【过渡】对于问题(1),我们之前学习过,平均数表示一组数据的“平均水平”。
因此我们对这两个应聘者的成绩求取平均值,即能得到两者的综合成绩。
(学生计算回答)【过渡】通过比较,我们发现,显然甲的成绩比乙高,所以从成绩看,应该录取甲。
但是在生活中,我们会发现,有些时候会侧重其中一点考虑,这个时候又该如何选择呢?我们看一个第二个小问题。
【过渡】对(2)理解发现,(2)中更侧重于读写,因此,在求平均数时,我们不能像上一个那样,而应该将不同项目的比例考虑进去。

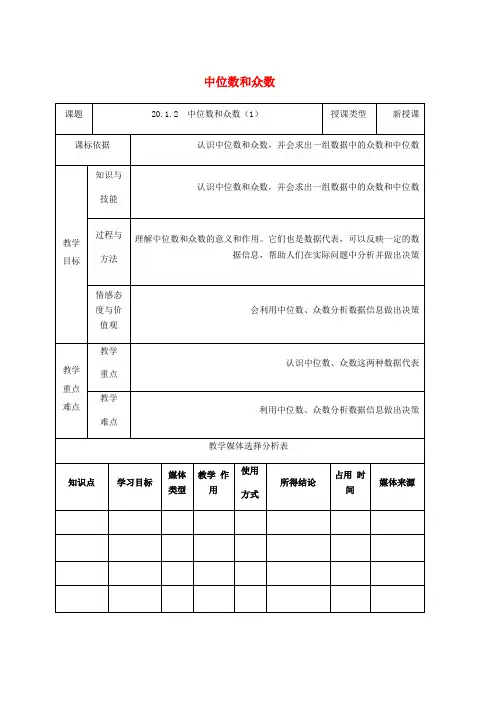
20.1.2 中位数和众数(1)【教学目标】1.知识与技能(1)知道什么是中位数,能够准确确定出一组数据的中位数,并能说出其代表意义;(2)知道什么是众数,准确确定出一组数据的众数,并能提出其代表的意义。
2.过程与方法通过对实际问题情境的探究,形成中位数和众数的概念,感知其代表数据的意义。
3.情感态度和价值观以积极情感态度投入到探究问题的过程中去,学会从不同的角度看问题和处理问题。
【教学重点】理解中位数和众数所代表数据的意义。
【教学难点】能否准确描述出具体问题,中位数和众数的意义。
【教学方法】自学与小组合作学习相结合的方法。
【课前准备】教学课件。
【课时安排】1课时【教学过程】一、复习导入【过渡】在上节课的学习中,我们学习了平均数的计算及其所能代表的实际意义,现在,我们来看一下这个简单的问题,看谁能回答的又快又准。
用两种方法计算下列数据的平均数:30,33,57,57,40,33,30.(学生回答)【过渡】大家回答的都很正确,这是我们上节课学习的加权平均数,它代表了一组数据的平均水平,但是,它是否在任何情况下都适合代表一组数据呢?我们今天就来探讨一下。
二、新课教学1.中位数【过渡】在日常生活中,我们经常会听到一些关于平均的话语,比如说我们的课本中的这个问题,某公司员工月收入的资料,大家能计算出它的平均数吗?(学生回答)【过渡】从平均数看,这个公司员工的平均收入在6276元,但是结合表中的数据,我们发现,只有3名员工的工资是在这个平均值之上的,那这个平均值代表这个公司全体员工月收入水平,你认为合适吗?(学生回答)【过渡】那么我们如何才能更合理的反映员工月收入平均水平?(学生讨论回答)根据实际情况,我们使用这样一个数值:一半人月工资高于该数值,另一半人月工资低于该数值,才能合适的表示平均水平。
如何才能得到这样的数值呢?【过渡】在这里,我们引入这样一个概念:中位数。
将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则称处于中间位置的数为这组数据的中位数。
20.1中位数和众数(第1课时
)
学习目标
1.理解中位数和众数的统计意义;
2.会计算中位数、众数,能选择适当的统计量表示数据的集中趋势;
3.通过具体例子感受统计在生活和生产中的作用,养成用数据说话的习惯和实事求是的科学态度.
学习过程
一、合作探究
该公司员工的月薪如下:
员工经理
副经
理
职员
A
职员
B
职员
C
职员
D
职员
E
职员
F
杂工
G
月薪(元)12
000
8 0003 2002 6002 4002 2002 2002 2001 200
问题1:请大家仔细观察表格中的数据,计算该公司的月平均工资是多少?
问题2:平均月工资能否客观地反映员工的实际收入?
问题3:再仔细观察表中的数据,你们认为用哪个数据反映一般职员的实际收入比较合适?
二、探索新知
1.中位数的定义:
将一组数据按照(或)的顺序排列,如果数据的个数是奇数,则称处于的数为这组数据的中位数;如果数据的个数是偶数,则称中间为这组数据的中位数.
2.众数的定义:
一组数据中出现称为这组数据的众数.
三、跟踪练习
1.下面两组数据的中位数分别是多少?
(1)5,6,2,3,2
(2)5,6,2,4,3,5
2.说出下列各组数据的众数:
(1)2,5,3,5,1,5,4
(2)2,2,3,4,3
(3)5,2,6,7,6,3,3,4,3,7,6
(4)1,2,3,5,7
四、变化演练
1.(xx·重庆A)在某校九年级二班组织的跳绳比赛中,第一小组五位同学跳绳的个数分别为198,230,220,216,209,则这五个数据的中位数为()
A.220
B.218
C.216
D.209
2.某校为纪念世界反法西斯战争胜利70周年,举行了主题为“让历史照亮未来”的演讲比赛,其中八年级的5位参赛选手的比赛成绩(单位:分)分别为:8.6,9.5,9.7,8.8,9,则这5个数据中的中位数是()
A.9.7
B.9.5
C.9
D.8.8
3.在xx年重庆市初中毕业生体能测试中,某校初三有7名同学的体能测试成绩(单位:分)如下:50,48,47,50,48,49,48.这组数据的众数是.
4.某届青年歌手大奖赛上,七位评委为甲选手打出的分数分别
是:96.5,97.1,97.5,98.1,98.1,98.3,98.5.则这组数据的众数是.
五、达标检测
1.今年4月,其中8名选手某项得分如下表:
得分8
8
5
8
7
9
人
数
1322
则这8名选手得分的众数、中位数分别是()
A.85,85
B.87,85
C.85,86
D.85,87
2.为了了解开展“孝敬父母,从家务事做起”活动的实施情况,某校抽取八年级某班50名学生,调查他们一周做家务所用时间,得到一组数据,并绘制成下表,请根据下表完成各题:
每周做家
务
的时间(小时)01234
合
计
人数262
0 550
(1)填写图中未完成的部分.
(2)该班学生每周做家务的平均时间是,这组数据的中位数是,众数是.
(3)请你根据(2)的结果,用一句话谈谈自己的感受.
3.已知一组数据x,-5,4,-3,2,-5,根据下列条件确定x的值;
(1)中位数为-1;
(2)平均数是3;
(3)x是唯一的众数.
4.下面的条形图描述了某车间工人日加工零件数的情况:
请找出这些工人日加工零件数的中位数,说明这个中位数的意义.
参考答案
一、合作探究
问题1:解:
=4 000.
问题2:解:不能,因为只有两人超过4 000.
问题3:解:2 400为中位数,2 200为众数,这两个数能较好地反映公司员工收入的一般水平.
二、探索新知
1.从小到大从大到小中间两数的平均数
2.次数最多的数
三、跟踪练习
1.(1)3(2)4.5
2.解:(1)5(2)2和3(3)3和6(4)3
四、变化演练
1.C
2.C
3.48
4.98.1
五、达标检测
1.C
2.解:(1)50-(2+6+20+5)=17,
故答案为17.
(2)该班学生每周做家务的平均时间是:(0×2+1×6+2×17+3×20+4×5)=×120=2.4;
将这组数据从大到小的顺序排列后中位数是:(2+3)÷2=2.5
众数是一组数据中出现次数最多的数据,所以众数为3;
故答案为2.4;2.5;3.
(3)学生做家务所用时间普遍偏少,应加强爱劳动,讲卫生等方面的教育.
3.解:(1)因为这组数据的中位数是-1,所以把这组数据按照从小到大的顺序排列应
为:-5,-5,-3,x,2,4,
=-1,∴x=1.
(2)根据题意得=3,解得x=25.
(3)∵-5已经出现了2次,其他数值只出现了一次,且x是唯一的众数,
∴x=-5.
4.解:中位数是大小处于中间位置的数,共有36个数,中间位置的是第18个与第19个数的平均数,这两个数都是6,因而中位数是6,这个中位数意义为:日加工零件数多于或少于6的各有一半.
感谢您的支持,我们会努力把内容做得更好!。