行程问题中的图示解法
- 格式:pdf
- 大小:257.98 KB
- 文档页数:3

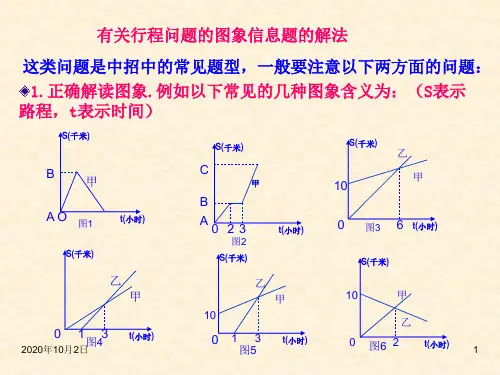
行程问题中的图示解法一、S-T图竖轴表示路程,一般为出发后的每一时刻离出发的距离,出发时此距离为0。
横轴表示时间,一般从出发开始计时,出发点处时间为0。
图形中的每个点均表示在某一时刻时的位置。
如下图,小明从家出发去上学,家和学校的距离为2千米。
规定竖轴为离家的距离,横轴为出发的时间。
其中A点表示出发5分钟后小明在离家1千米的位置,B点表示出发10分钟后小明在离家2千米的位置,即到达学校。
可以看到B点之后,随着时间的改变小明的位置并未发生改变,即这个阶段小明均在学校里,距离家都是2千米。
在S-T图中,每个点的路程数值和时间数值的比值即为速度。
图中OB为一条直线,由三角形相似的知识我们可以知道,此直线上的任意一点的路程与时间的比值都相等,即由O到B这个阶段速度是不变的。
我们可以用OB上任意一点的数据求出速度,如看A点,路程为1千米,时间为5分钟,速度为1÷5=0.2千米/分钟。
二、柳卡图法国数学家柳卡·施斗姆生于瑞士,因数学上的成就,于1836年当选为法国科学院院士。
在十九世纪的一次国际数学会议期间,有一天,正当来自世界各国的许多著名数学家晨宴快要结束的时候,法国数学家柳卡向在场的数学家提出困扰他很久、自认“最困难”的题目:“某轮船公司每天中午都有一艘轮船从哈佛开往纽约,并且每天的同一时刻也有一艘轮船从纽约开往哈佛。
轮船在途中所花的时间来去都是七昼夜,而且都是匀速航行在同一条航线上。
问今天中午从哈佛开出的轮船,在开往纽约的航行过程中,将会遇到几艘同一公司的轮船从对面开来?”(此即著名的“柳卡趣题”)【分析】法一:推理从哈佛开出的轮船遇到的纽约开来的轮船有两类,一类是该船出发前已从纽约发出且尚未到达哈佛的轮船,即该船出发前7天内纽约发出的轮船,除出发时纽约刚到达伦敦的一艘船外途中共遇到6艘。
另一类是该船出发后从纽约发出的轮船,即该船出发后7天内纽约发出的轮船,除到达伦敦时刚发出的船外途中共遇到7艘。

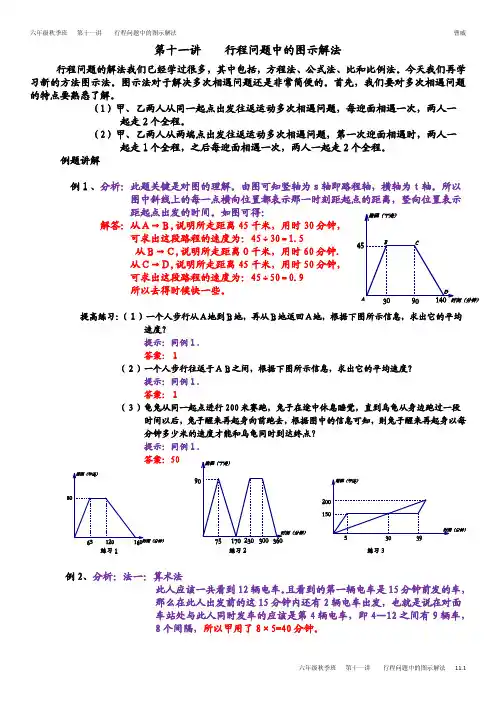
行 程 问 题行程问题为小学和初中数学学习的重要应用问题,在行程问题中,除特别指出外,都假定速度是常数,即匀速运动,匀速运动的基本公式十分简单: 路程=时间⨯速度但是由于路程的多样化,时间前后的差别,以及速度的变化,使得行程问题变得复杂而丰富多彩。
行程问题虽然是实际问题的初级近似,但地,由于它的各色各样的变化,使得中小学的数学知识中的许多知识点能有趣而生动地融汇其中,而成为学生能力培养的有力工具。
在各届华杯赛中,行程问题是各类问题出现频率最高的问题之一。
求解行程问题一般分如下步骤:1。
审题 2。
画示意图 3。
找关键要素 4。
列关系式 5。
分析 6。
给出答案。
下面将通过具体的问题来解释这六个步骤。
行程问题中的方程方法列方程求解行程问题是最通常的方法,也是最为有效的方法。
多数行程问题可以用列方程解方程的方法来求解。
列方程就是上述步骤中第四步中建立一个或几个含有未知数的条件等式,而第五步中的分析就是解方程。
例1.甲、乙二人从相距60千米的两地同时相向而行,6小时后相遇。
如果二人的速度每小时个增加1千米,那么相遇地点距前一次相遇地点1千米。
问:甲、乙二人速度个多少?解。
设甲的速度为每小时v 千米。
因为,两人6小时相遇,所以,二人的速度和为10千米。
乙的速度为每小时10-v 千米。
二人的速度个增加1千米,速度和为12千米,因此,需要小时)(51260=相遇。
第一次甲的行程为6v ,第二次甲的行程为5(v +1),相差1千米: .6 ,1)1(56==+-v v v答。
二人的速度分别为每小时6千米和每小时4千米。
例2. 快、中、慢三辆车同时从同一地出发, 沿一公路追赶前面一个骑自行车的人,这三辆车分别用6分钟、10分钟、12分钟追上骑自行车的人。
现知快车每小时走24千米,中车每小时走20千米。
那么慢车每小时走多少千米?解。
设自行车速度为每小时v 千米,慢车每小时a 千米,三车出发时自行车在他们前面L 千米。

行程问题中的图示解法一、S-T图竖轴表示路程,一般为出发后的每一时刻离出发的距离,出发时此距离为0。
横轴表示时间,一般从出发开始计时,出发点处时间为0。
图形中的每个点均表示在某一时刻时的位置。
如下图,小明从家出发去上学,家和学校的距离为2千米。
规定竖轴为离家的距离,横轴为出发的时间。
其中A点表示出发5分钟后小明在离家1千米的位置,B点表示出发10分钟后小明在离家2千米的位置,即到达学校。
可以看到B点之后,随着时间的改变小明的位置并未发生改变,即这个阶段小明均在学校里,距离家都是2千米。
在S-T图中,每个点的路程数值和时间数值的比值即为速度。
图中OB为一条直线,由三角形相似的知识我们可以知道,此直线上的任意一点的路程与时间的比值都相等,即由O到B这个阶段速度是不变的。
我们可以用OB上任意一点的数据求出速度,如看A点,路程为1千米,时间为5分钟,速度为1÷5=0.2千米/分钟。
二、柳卡图法国数学家柳卡·施斗姆生于瑞士,因数学上的成就,于1836年当选为法国科学院院士。
在十九世纪的一次国际数学会议期间,有一天,正当来自世界各国的许多著名数学家晨宴快要结束的时候,法国数学家柳卡向在场的数学家提出困扰他很久、自认“最困难”的题目:“某轮船公司每天中午都有一艘轮船从哈佛开往纽约,并且每天的同一时刻也有一艘轮船从纽约开往哈佛。
轮船在途中所花的时间来去都是七昼夜,而且都是匀速航行在同一条航线上。
问今天中午从哈佛开出的轮船,在开往纽约的航行过程中,将会遇到几艘同一公司的轮船从对面开来?”(此即著名的“柳卡趣题”)【分析】法一:推理从哈佛开出的轮船遇到的纽约开来的轮船有两类,一类是该船出发前已从纽约发出且尚未到达哈佛的轮船,即该船出发前7天内纽约发出的轮船,除出发时纽约刚到达伦敦的一艘船外途中共遇到6艘。
另一类是该船出发后从纽约发出的轮船,即该船出发后7天内纽约发出的轮船,除到达伦敦时刚发出的船外途中共遇到7艘。

行程问题画图分析的方法与技巧————向量构图法列方程解应用题可简单概括为“审、析、列、算、查”五个步骤。
即“审题、分析、列式、计算、检查”。
其中找等量关系式就是解题的关键,然而较复杂的行程应用题的等量关系式就是很难一下子找出来的,这就需要我们在“审题”的基础上认真分析,通过不断地把未知量用含未知数的代数式表示出来,即不断地扩大已知,使等量关系“水到渠成”。
在解行程应用题时,采取画图分析的方法不仅能有利的协调学生左、右脑(科学用脑),锻炼学生分析问题的能力,而且能激发学生的学习兴趣,培养学生的创新能力。
此外,通过对物体运动、联系、发展、变化的分析与再现,也为学生不断形成辩证唯物主义世界观打下良好的基础。
⒈图的构成:行程问题都与物体的位移有着直接的关系,而速度就是既有大小,又有方向的量,所以图的主要构成就是向量。
此外,一幅完整的图还应包括图标、数据、文字、注解等,其中构成向量的有向线段有虚实、粗细及不同颜色的变化。
⒉绘图原则:在画图过程中应坚持的原则有:⑴要坚持认真审题。
审题就是解答应用题的第一步,能否顺利、准确的分析,审清题目的已知条件与问题就是基础。
⑵在认真审题基础上,“边读边画,兼顾协调”的原则。
即:在审清题目的已知条件与问题后,边读边画,并兼顾题中数据的比例关系、前后联系及隐含条件等,展开联想,合理安排。
⑶画图力求简洁与清晰明了,防止混淆不清。
在画图时要坚持画彩色图并利用有向线段的粗细与虚实等合理区分,防止混淆不清。
⑷根据题目的特点,灵活创新。
⒊绘图技巧⑴“速度、路程(数值型)”分别标在对应向量的“上、下”。
一般情况下,含未知数的代数式所表示的路程标在它们中间。
⑵用同种颜色表达同一事物及变化。
⑶用“粗细”搭配来区分物体的“同时性”与否。
同时运动的物体,用较粗的有向线段来表示。
⑷用虚、实来区分物体的“假设运动”与“真实运动”等。
1.5·V 甲 千米 1·V甲千米 2、5 V 甲千米/时30千米说明:通过运用相同较粗的有向线段表示同时性,不仅表达出了题目中的隐含条件(同时的路程),而且有利于我们联想出“相同时间内,路程比=速度比”,为解答此题提供依据。




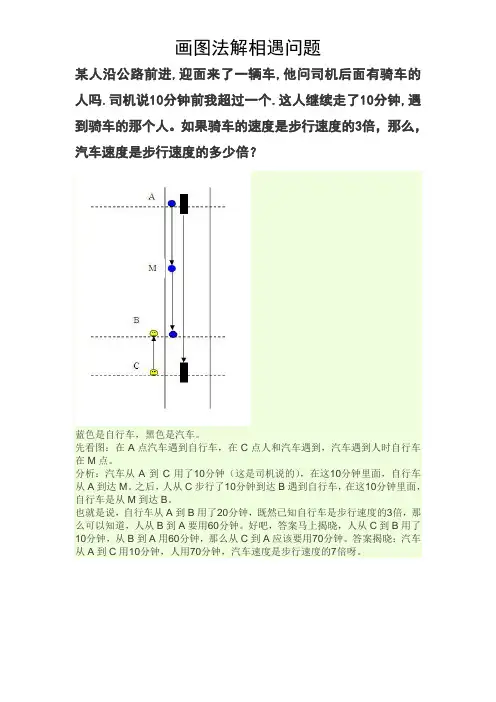
画图法解相遇问题
某人沿公路前进,迎面来了一辆车,他问司机后面有骑车的人吗.司机说10分钟前我超过一个.这人继续走了10分钟,遇到骑车的那个人。
如果骑车的速度是步行速度的3倍,那么,汽车速度是步行速度的多少倍?
蓝色是自行车,黑色是汽车。
先看图:在A点汽车遇到自行车,在C点人和汽车遇到,汽车遇到人时自行车在M点。
分析:汽车从A到C用了10分钟(这是司机说的),在这10分钟里面,自行车从A到达M。
之后,人从C步行了10分钟到达B遇到自行车,在这10分钟里面,自行车是从M到达B。
也就是说,自行车从A到B用了20分钟,既然已知自行车是步行速度的3倍,那么可以知道,人从B到A要用60分钟。
好吧,答案马上揭晓,人从C到B用了10分钟,从B到A用60分钟,那么从C到A应该要用70分钟。
答案揭晓:汽车从A到C用10分钟,人用70分钟,汽车速度是步行速度的7倍呀。
公考图示法解行程问题技巧实例随着2011年各个省份的招考公告的发布,省公务员考试的紧张备考已经进入冲刺时刻。
在公务员行测考试中,运用图形展示应用在数量关系和思维过程成为近年来行测考试的重要方法。
图示法具有直观、便捷、高效的特点,在此,就图示割补法、转换法和逆向法作介绍,希望能够帮助你顺利通过考试。
例1、A、B 两站之间有一条铁路,甲、乙两列火车分别停在 A 站和 B 站,甲火车4分钟走的路程等于乙火车5分钟走的路程。
乙火车上午8 时整从B 站开往A站,开出一段时问后,甲火车从 A 站出发开往 B 站,上午 9时整两列火车相遇。
相遇地点离A、。
B两站的距离比是15:16.那么。
甲火车在( ) 从 A 站出发开往 B 站。
(2007年国家公务员考试真题)A.8时12 分B.8时15 分C. 8 时 24 分D.8 时 30 分解析:本题属于比例行程问题,由“甲火车4分钟走的路程等于乙火车5分钟走的路程”这句话可得:路程不变,时间和速度成反比,则,v甲:v乙=5:4。
可作下图:“开出一段时问后,甲火车从 A 站出发开往 B 站,上午 9时整两列火车相遇”表明甲乙两人不是同时出发,则假设甲乙是同时出发,可通过“补”的方法完善图形:即假设甲从M、乙从B于上午8点同时出发出发,则可得出MC=20份,AM=5份。
再由AM:AC=1:3,根据速度不变,路程和时间成正比,得甲走完MA和AC的路程所用时间之比为1:3,即甲到达A点的时刻为:8时15 分。
答案选B。
例2、甲车从A 地,乙车从B地以不同的速度匀速相向开出。
两车相遇后分别掉头,并以对方的速率进行。
甲车返回A地后又一次掉头以同样的速率沿公路向B地开动。
最后甲、乙两车同时到达B地。
如果最开始时甲车的速度为 x ,则最开始时乙车的速率为( )。
(2006年国家公务员考试真题)A.4xB.2xC. 0.5xD.无法判断解析:该题的难点有二:其一甲乙相遇后各自回头,而没有继续向前走;其二是甲乙相遇后速度改变,并以对方的速度行驶。
⾏程问题的画图⽅法与技巧⾏程问题画图分析的⽅法与技巧————向量构图法列⽅程解应⽤题可简单概括为“审、析、列、算、查”五个步骤。
即“审题、分析、列式、计算、检查”。
其中找等量关系式是解题的关键,然⽽较复杂的⾏程应⽤题的等量关系式是很难⼀下⼦找出来的,这就需要我们在“审题”的基础上认真分析,通过不断地把未知量⽤含未知数的代数式表⽰出来,即不断地扩⼤已知,使等量关系“⽔到渠成”。
在解⾏程应⽤题时,采取画图分析的⽅法不仅能有利的协调学⽣左、右脑(科学⽤脑),锻炼学⽣分析问题的能⼒,⽽且能激发学⽣的学习兴趣,培养学⽣的创新能⼒。
此外,通过对物体运动、联系、发展、变化的分析与再现,也为学⽣不断形成辩证唯物主义世界观打下良好的基础。
⒈图的构成:⾏程问题都与物体的位移有着直接的关系,⽽速度是既有⼤⼩,⼜有⽅向的量,所以图的主要构成是向量。
此外,⼀幅完整的图还应包括图标、数据、⽂字、注解等,其中构成向量的有向线段有虚实、粗细及不同颜⾊的变化。
⒉绘图原则:{在画图过程中应坚持的原则有:⑴要坚持认真审题。
审题是解答应⽤题的第⼀步,能否顺利、准确的分析,审清题⽬的已知条件和问题是基础。
⑵在认真审题基础上,“边读边画,兼顾协调”的原则。
即:在审清题⽬的已知条件和问题后,边读边画,并兼顾题中数据的⽐例关系、前后联系及隐含条件等,展开联想,合理安排。
⑶画图⼒求简洁和清晰明了,防⽌混淆不清。
在画图时要坚持画彩⾊图并利⽤有向线段的粗细和虚实等合理区分,防⽌混淆不清。
⑷根据题⽬的特点,灵活创新。
⒊绘图技巧#⑴“速度、路程(数值型)”分别标在对应向量的“上、下”。
⼀般情况下,含未知数的代数式所表⽰的路程标在它们中间。
⑵⽤同种颜⾊表达同⼀事物及变化。
⑶⽤“粗细”搭配来区分物体的“同时性”与否。
同时运动的物体,⽤较粗的有向线段来表⽰。
⑷⽤虚、实来区分物体的“假设运动”与“真实运动”等。
4.实例分析:⑴巧⽤粗细及虚实的分析举例:例1:有AB两城相距30千⽶,甲骑⾃⾏车从A往B,出发1⼩时30分钟后,—⼄骑摩托车也从A到B,已知⼄的速度是甲的倍,且⼄⽐甲早到1⼩时,求甲的速度。
第四讲 行程问题—火车过桥与错车超车问题【例题1】★一列列车长150米,每秒钟行19米。
问全车通过420米的大桥,需要多少时间?【分析与解】如图,列车过桥所行距离为:车长+桥长。
(420+150)÷19=30(秒)答:列车通过这座大桥需要30秒钟.【例题2】★一列车通过530米的隧道要40秒钟,以同样的速度通过380米的大桥要用30秒钟。
求这列车的速度及车长.【分析与解】列车过隧道比过桥多行(530-380)米,多用(40-30)秒。
列车的速度是:(530-380)÷(40-30)=15(米/秒)列车的长度是:15×40-530=70(米)答:列车每秒行15米,列车长70米.【例题3】★★火车通过长为102米的铁桥用了24秒,如果火车的速度加快1倍,它通过长为222米的隧道只用了18秒。
求火车原来的速度和它的长度。
【考点分析】如果火车仍用原速,那么通过隧道要用36秒。
【分析与解】列车原来的速度是(222-102)÷(18×2-24)=10(米/秒)火车长为10×24—102=138(米)答:列车原来每秒行10米,车长为138米.【例题4】★★一个车队以4米/秒的速度缓缓通过一座长200米的大桥,共用115秒钟.已知每辆车长5火车过桥是一种特殊的行程问题。
需要注意从车头至桥起,到车尾离桥止,火车所行距离等于桥长加上车长。
列车过桥问题的基本数量关系为:车速×过桥时间=车长+桥长。
火车过桥问题:(1)解题思路:先车速归一,再用公式“桥长之差÷时间之差=归一后的车速”,即=V t S ⨯差差,(2)画示意图,分析求解。
列车所行路程为车头到车头或车尾到车尾的距离,而不是车头到车尾的距离。
(3)与追及问题的区另:追及问题所用公式=V t S ⨯差差,要求时间归一。
关于S=Vt 公式的拓展初步探讨(1)S=vt =(2) S =v t = (3) S =v t = (4) S =vt = S vt ⨯⨯=⇒⨯⨯和和差差差差行程问题:路程速度时间相遇问题:路程和速度和时间(时间归一,能求路程和)追及问题:路程差速度差时间(时间归一,能求路程差)火车过桥:路程差车速度时间差(速⎧⎪⎪⎨⎪⎪⎩度归一,求出车速) 火车过桥好题精讲 火车过桥问题米,两车间隔10米,问这个车队共有多少辆车?【分析与解】4×115-200=260(米)……队伍长(260-5)÷(10+5)+1=18(辆)答:这个车队共用18辆车.【附加题】★★★(《小学生数学报》第八届竞赛试题)一列火车通过长320米的隧道,用了52秒。
第十一讲行程问题中的图示解法补充练习
1、龟、兔从同一起点进行200米赛跑,兔子在途中
睡觉休息,直到乌龟从身边跑过一段时间后,兔子
醒来再起身向前跑去。
根据图中的信息可知,则兔
子醒来再起身以每分钟______米的速度才能在和乌
龟同时到达终点。
2、甲、乙两人在相距180米的直路两端同时出发来回散步,甲每秒走2米,乙每秒走2.5米,每人都走了6.5分钟。
那么这段时间内他们共相遇了(迎面或同向)多少次?
3、甲、乙二人同时从A地出发同向而行去往B地,甲的速度是每小时30千米,乙的速度是每小时20千米,二人相遇后继续行进,甲、乙到达B地后立即返回A地。
已知两个人第四次相遇的地点距离第三次相遇的地点20千米,那么,A、B两地相距多少千米?
4、甲、乙两车的速度分别为52千米/时和40千米/时,他们同时从A地出发去B地,在A、B两地间往返而行,从开始走到第三次相遇,共用了6小时。
A、B 两地相距多少千米?
5、小张与小王分别从甲、乙两村同时出发,在两村之间往返行走(到达另一村后就马上返回),他们在离甲村3.5千米处第一次相遇,在离乙村2千米处第二次相遇。
问他们两人第六次相遇的地点离乙村多远(相遇指迎面相遇)?
答案:
1、解析:
兔子开始的速度150÷5=30米/分钟。
乌龟的速度150÷30=5米/分钟。
乌龟到达终点的时间200÷5=40分钟
兔子醒来后需要以(200-150)÷(40-39)=50米/分钟的速度才能和乌龟同时到达终点。
2、解析:甲行全程用180÷2=90秒,乙行全程用180÷2.5=72秒。
画出柳卡图:
由图得,一共相遇5次。
3、解析:
4、解析:同向出发,第一次相遇时,两车走的路程和是2个AB之长;而到第三次相遇,两车走的路程和是2×3=6个AB之长,是(52+40)×6=552(千米),所以,A、B两地相距552÷6=92(千米)。
5、解析:二次相遇时两人已共同走了甲、乙两村距离的3倍,因此张走了3.5×3=10.5(千米)。
第二次相遇处离乙村2千米,因此,甲、乙两村的距离是10.5-2=8.5(千米)。
第六次相遇时,两人已共同走了两村距离2×6-1=11倍的行程,其中张走了3.5×11=38.5(千米),38.5÷8.5=4…4.5,就知道第六次相遇处,离乙村8.5-4.5=4千米。