第3章 连接-2
- 格式:ppt
- 大小:3.19 MB
- 文档页数:79


3.2 函数的基本性质 3.2.1 函数的单调性与最值教材要点要点一 函数最大(小)值设D 是函数f (x )的定义域,I 是D 的一个非空的子集.(1)如果有a ∈D ,使得不等式f (x )≤f (a )对一切x ∈D 成立,就说f (x )在x =a 处取到最大值M =f (a ),称M 为f (x )的最大值,a 为f (x )的最大值点;(2)如果有a ∈D ,使得不等式f (x )≥f (a )对一切x ∈D 成立,就说f (x )在x =a 处取到最小值M =f (a ),称M 为f(x )的最小值,a 为f (x )的最小值点.状元随笔 最大(小)值必须是一个函数值,是值域中的一个元素,如函数y =-x 2(x ∈R )的最大值是0,有f (0)=0.要点二 增函数与减函数的定义状元随笔 定义中的x 1,x 2有以下3个特征(1)任意性,即“任意取x 1,x 2”中“任意”二字绝不能去掉,证明时不能以特殊代替一般;(2)有大小,通常规定x 1<x 2; (3)属于同一个单调区间. 要点三 单调性与单调区间如果函数y =f (x )在区间I 上是增函数或减函数,那么就说函数y =f (x )在这一区间上具有(严格的)________,区间I 叫作y =f (x )的________.状元随笔 一个函数出现两个或者两个以上的单调区间时,不能用“∪”连接,而应该用“和”连接.如函数y =1x 在(-∞,0)和(0,+∞)上单调递减,却不能表述为:函数y =1x 在(-∞,0)∪(0,+∞)上单调递减.基础自测1.思考辨析(正确的画“√”,错误的画“×”) (1)函数f (x )≤1恒成立,则f (x )的最大值是1.( )(2)函数y =f (x )在[1,+∞)上是增函数,则函数的单调递增区间是[1,+∞).( ) (3)函数y =1x 的单调递减区间是(-∞,0)∪(0,+∞).( )(4)如果函数y =f (x )在区间[a ,b ]上单调递减,在区间[b ,c ]上单调递增,则函数y =f (x )在区间[a ,c ]上在x =b 处有最小值f (b ).( )2.函数y =-2x 2+3x 的单调递减区间是( ) A .[0,+∞) B .(-∞,0) C .(−∞,34]D .[34,+∞)3.(多选)如果函数f (x )在[a ,b ]上是增函数,对于任意x 1,x 2∈[a ,b ](x 1≠x 2),则下列结论中正确的是( )A .f (x 1)−f (x 2)x 1−x 2>0B .(x 1-x 2)[f (x 1)-f (x 2)]>0C .f (a )≤f (x 1)<f (x 2)≤f (b )D .f (x 1)>f (x 2)4.函数f (x )在[-2,2]上的图象如图所示,则此函数的最小值、最大值分别是________.题型1 利用图象求函数的单调区间例1 已知函数f(x)=x2-4|x|+3,x∈R.(1)将函数写成分段函数的形式;(2)画出函数的图象;(3)根据图象写出它的单调区间.方法归纳(1)求函数单调区间时,若所给函数是常见的一次函数、二次函数、反比例函数等,可根据其单调性写出函数的单调区间,若函数不是上述函数且函数图象容易作出,可作出其图象,根据图象写出其单调区间.(2)一个函数出现两个或两个以上的单调区间时,不能用“∪”连接两个单调区间,而要用“和”或“,”连接.跟踪训练1 (1)已知函数y=f(x)的图象如图所示,则该函数的减区间为( )A.(-3,1)∪(1,4)B.(-5,3)∪(−1,1)C.(-3,-1),(1,4)D.(-5,-3),(-1,1)(2)函数y=-x2+2|x|+3的单调递增区间是__________,递减区间是__________________.题型2 函数的单调性判断与证明例2 用定义证明函数f(x)=x+k(k>0)在(0,+∞)上的单调性.x方法归纳利用定义证明函数单调性的步骤注:作差变形是解题关键.跟踪训练2 已知函数f (x )=xx 2+4,判断并用定义证明f (x )在(0,+∞)上的单调性.题型3 函数单调性的应用 角度1 比较大小例3 已知函数y =f (x )在[0,+∞)上是减函数,则( ) A .f (34)>f (a 2-a +1) B .f (34)<f (a 2-a +1)C .f (34)≥f (a 2-a +1) D .f (34)≤f (a 2-a +1)状元随笔 利用单调性比较函数值或自变量的大小时,要注意将对应的自变量转化到同一个单调区间上.角度2 解不等式例4 f (x )是定义在(-2,2)上的减函数,若f (m -1)>f (2m -1),则实数m 的取值范围是( )A .m >0B .0<m <32 C .-1<m <3D .-12<m <32状元随笔 利用单调性解不等式,就是根据单调性去掉函数的对应法则,构造不等式(不等式组)求解,注意函数的定义域,所有自变量都必须在函数的定义域内.角度3 利用函数的单调性求参数的取值范围例5 若f(x)=-x2+4mx与g(x)=2m在区间[2,4]上都是减函数,则m的取值范围x+1是( )A.(-∞,0)∪(0,1] B.(−1,0)∪(0,1]C.(0,+∞) D.(0,1]方法归纳“函数的单调区间为I”与“函数在区间I上单调”的区别单调区间是一个整体概念,说函数的单调递减区间是I,指的是函数递减的最大范围为区间I,而函数在某一区间上单调,则指此区间是相应单调区间的子区间.所以我们在解决函数的单调性问题时,一定要仔细读题,明确条件含义.角度4 求函数的最值例6 已知函数f(x)=2(x∈[2,6]),求函数的最大值和最小值.x−1方法归纳1.利用单调性求函数的最大(小)值的一般步骤(1)判断函数的单调性.(2)利用单调性求出最大(小)值.2.函数的最大(小)值与单调性的关系(1)若函数f(x)在区间[a,b]上是增(减)函数,则f(x)在区间[a,b]上的最小(大)值是f(a),最大(小)值是f(b).(2)若函数f(x)在区间[a,b]上是增(减)函数,在区间[b,c]上是减(增)函数,则f(x)在区间[a,c]上的最大(小)值是f(b),最小(大)值是f(a)与f(c)中较小(大)的一个.跟踪训练3 (1)已知函数f (x )=x 2+bx +c 图象的对称轴为直线x =2,则下列关系式正确的是( )A .f (-1)<f (1)<f (2)B .f (1)<f (2)<f (-1)C .f (2)<f (1)<f (-1)D .f (1)<f (-1)<f (2)(2)函数y =f (x )在R 上为增函数,且f (2m )>f (-m +9),则实数m 的取值范围是( ) A .(-∞,-3) B .(0,+∞)C .(3,+∞)D .(-∞,-3)∪(3,+∞)(3)已知函数f (x )=|2x -a |的单调递增区间是[3,+∞),则a 的值为________. (4)已知函数f (x )=32x−1,求函数f (x )在[1,5]上的最值.易错辨析 忽视函数的定义例7 已知函数f (x )={−x 2−ax −5(x ≤1),ax(x >1),是R 上的增函数,则a 的取值范围是( )A .-3≤a <0B .a ≤-2C .a <0D .-3≤a ≤-2解析:函数f (x )={−x 2−ax −5(x ≤1),ax (x >1),是R 上的增函数,则f (x )=-x 2-ax -5(x ≤1)单调递增,故它的对称轴-a 2≥1,即a ≤-2,此时f (x )=ax (x >1)也单调递增,所以a <0,要保证在R 上是增函数.还需在x =1处满足-12-a ×1-5≤a1,即a ≥-3.综上所述,-3≤a ≤-2.答案:D 易错警示课堂十分钟1.(多选)如图所示的是定义在区间[-5,5]上的函数y =f (x )的图象,则下列关于函数f (x )的说法正确的是( )A .函数在区间[-5,-3]上单调递增B .函数在区间[1,4]上单调递增C .函数在区间[-3,1]∪[4,5]上单调递减D .函数在区间[-5,5]上没有单调性 2.函数y =1x−1的单调减区间是( )A .(-∞,1),(1,+∞)B .(-∞,1)∪(1,+∞) C{x ∈R |x ≠1}D .R3.函数y =2x+1在[2,3]上的最小值为( ) A .1B .13 C .23D .124.设关于x 的函数y =(k -2)x +1是R 上的增函数,则实数k 的取值范围是________. 5.已知f (x )是定义在[-1,1]上的增函数,且f (x -2)<f (1-x ),求x 的取值范围.3.2 函数的基本性质3.2.1 函数的单调性与最值新知初探·课前预习要点二f(x1)<f(x2) f(x1)>f(x2) 增函数减函数要点三单调性单调区间[基础自测]1.答案:(1)×(2)×(3)×(4)√,+∞).2.解析:借助图象得y=-2x2+3x的单调减区间是[34答案:D3.解析:由函数单调性的定义可知,若函数y=f(x)在给定的区间上是增函数,则x1-x2与f(x1)-f(x2)同号,由此可知,选项A,B正确;对于C,D,因为x1,x2的大小关系无法判断,则f(x1)与f(x2)的大小关系也无法判断,故C、D不正确.故选AB.答案:AB4.解析:由图象知点(1,2)是最高点,点(-2,-1)是最低点,∴y max=2,y min=-1.答案:-1,2题型探究·课堂解透例1 解析:(1)f (x )=x 2-4|x |+3={x 2−4x +3,x ≥0,x 2+4x +3,x <0.(2)如图.(3)由图象可知单调递增区间为[-2,0),[2,+∞),单调递减区间为(-∞,-2),[0,2).跟踪训练1 解析:(1)在某个区间上,若函数y =f (x )的图象是上升的,则该区间为增区间,若是下降的,则该区间为减区间,故该函数的减区间为(-3,-1),(1,4).(2)y =-x 2+2|x |+3={−x 2+2x +3,x ≥0,−x 2−2x +3,x <0.画出函数图象如图,由图可知函数y =-x 2+2|x |+3的单调递增区间是:(-∞,-1],(0,1].递减区间是:[-1,0],[1,+∞).答案:(1)C (2)(-∞,-1],(0,1] [-1,0],[1,+∞) 例2 证明:设x 1,x 2∈(0,+∞),且x 1<x 2,则f (x 1)-f (x 2)=(x 1+k x 1)−(x 2+k x 2)=(x 1-x 2)+(k x 1−k x 2)=(x 1-x 2)+k ·x 2−x1x 1x2=(x 1-x 2)-k ·x 1−x 2x 1x 2=(x 1-x 2)·x 1x 2−k x 1x 2,因为0<x 1<x 2,所以x 1-x 2<0,x 1x 2>0.当x 1,x 2∈(0,√k ]时,x 1x 2-k <0⇒f (x 1)-f (x 2)>0,此时函数f (x )为减函数; 当x 1,x 2∈(√k ,+∞)时,x 1x 2-k >0⇒f (x 1)-f (x 2)<0,此时函数f (x )为增函数. 综上,函数f (x )=x +kx (k >0)在区间(0,√k ]上为减函数,在区间(√k ,+∞)上为增函数.跟踪训练2 解析:f (x )在(0,2)上单调递增,在(2,+∞)上单调递减. 证明如下:∀x 1,x 2∈(0,+∞),且x 1<x 2,有f (x 1)-f (x 2)=x 1x +124-x2x +224=x 1(x +224)-x2(x +124)(x +124)(x +224)=(x 2−x 1)(x 1x 2−4)(x +124)(x +224),因为0<x 1<x 2,所以x 2−x 1>0,(x +124)(x 22+4)>0.当x >2时,x 1x 2−4>0,(x 2−x 1)(x 1x 2−4)(x +124)(x +224)>0,f (x 1)-f (x 2)>0,即f (x 1)>f (x 2),此时f (x )单调递减. 当0<x <2时,x 1x 2−4<0,(x 2−x 1)(x 1x 2−4)(x +124)(x +224)<0,f (x 1)-f (x 2)<0,即f (x 1)<f (x 2),此时f (x )单调递增.所以,f (x )在(0,2)上单调递增,在(2,+∞)上单调递减.例3 解析:∵a 2-a +1=(a −12)2+34≥34.又∵函数y =f (x )在[0,+∞)是减函数,∴f (a 2-a +1)≤f (34).故选C.答案:C例4 解析:由题意知{−2<m −1<2,−2<2m −1<2,m −1<2m −1,解得0<m <32.故选B.答案:B例5 解析:函数f (x )=-x 2+4mx 的图象开口向下,且以直线x =2m 为对称轴,若在区间[2,4]上是减函数,则2m ≤2,解得m ≤1,g (x )=2m x+1的图象由y =2m x 的图象向左平移一个单位长度得到的,若在区间[2,4]上是减函数,则2m >0,解得m >0.综上可得m 的取值范围是(0,1].故选D.答案:D例6 解析:∀x 1,x 2∈[2,6],且x 1<x 2,则f (x 1)-f (x 2)=2x 1−1−2x 2−1=2[(x 2−1)−(x 1−1)](x 1−1)(x 2−1)=2(x 2−x 1)(x 1−1)(x 2−1). 由2≤x 1<x 2≤6,得x 2-x 1>0,(x 1-1)(x 2-1)>0,于是f (x 1)-f (x 2)>0,即f (x 1)>f (x 2).所以,函数f (x )=2x−1在区间[2,6]上单调递减.因此,函数f (x )=2x−1在区间[2,6]的两个端点处分别取得最大值与最小值.在x =2时取得最大值,最大值是2;在x =6时取得最小值,最小值是0.4.跟踪训练3 解析:(1)因为该二次函数的图象开口向上,对称轴为直线x =2,所以f (x )在(-∞,2]上单调递减,因为2>1>-1,所以f (2)<f (1)<f (-1).故选C.(2)因为函数y =f (x )在R 上为增函数,且f (2m )>f (-m +9),所以2m >-m +9,即m >3.故选C.(3)f (x )=|2x -a |={2x −a ,x ≥a 2−2x +a ,x <a 2, 所以f (x )=|2x -a |的单调递减区间是(−∞,a 2),单调递增区间是[a 2,+∞), 若函数f (x )=|2x -a |的单调递增区间是[3,+∞),则a 2=3,解得a =6.(4)先证明函数f (x )=32x−1的单调性,设x 1,x 2是区间(12,+∞)上的任意两个实数,且x 2>x 1>12, f (x 1)-f (x 2)=32x1−1−32x 2−1=6(x 2−x 1)(2x 1−1)(2x 2−1). 由于x 2>x 1>12,所以x 2-x 1>0,且(2x 1-1)·(2x 2-1)>0,所以f (x 1)-f (x 2)>0,即f (x 1)>f (x 2),所以函数f (x )=32x−1在区间(12,+∞)上是单调递减的,所以函数f (x )在[1,5]上是单调递减的,因此,函数f (x )=32x−1在区间[1,5]的两个端点上分别取得最大值与最小值,即最大值为f (1)=3,最小值为f (5)=13.答案:(1)C (2)C (3)6 (4)见解析 [课堂十分钟]1.解析:若一个函数出现两个或两个以上的单调性相同的区间,不一定能用“∪”连接.故选ABD.答案:ABD2.解析:单调区间不能写成单调集合,也不能超出定义域,故C ,D 不对,B 表达不当.故选A.答案:A3.解析:∵函数y =2x+1在[2,3]上单调递减,∴当x =3时,y =2x+1有最小值12. 故选D.答案:D4.解析:f (x )为R 上的增函数,则k -2>0,k >2.答案:(2,+∞)5.解析:∵f (x )是定义在[-1,1]上的增函数,且f (x -2)<f (1-x ),∴{−1≤x −2≤1,−1≤1−x ≤1,x −2<1−x ,解得1≤x <32, 所以x 的取值范围为1≤x <32.。

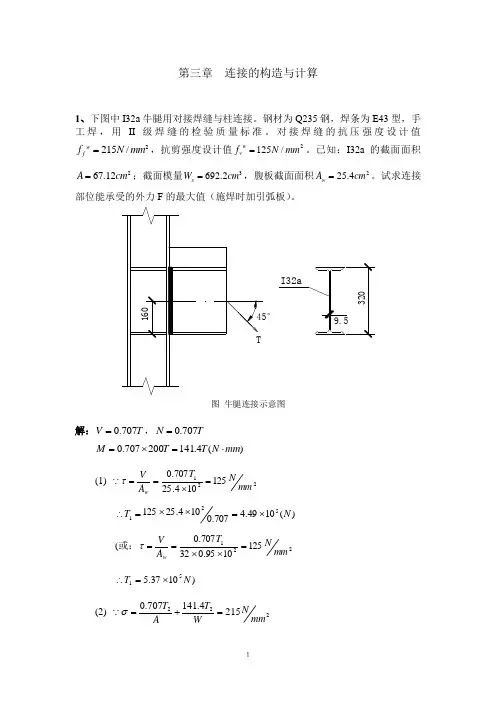
第三章 连接的构造与计算1、下图中I32a 牛腿用对接焊缝与柱连接。
钢材为Q235钢,焊条为E43型,手工焊,用II 级焊缝的检验质量标准。
对接焊缝的抗压强度设计值2215/w f f N mm =,抗剪强度设计值2125/w v f N mm =。
已知:I32a 的截面面积267.12A cm =;截面模量3692.2x W cm =,腹板截面面积225.4w A cm =。
试求连接部位能承受的外力F 的最大值(施焊时加引弧板)。
°图 牛腿连接示意图解:T V 707.0=,T N 707.0=)(4.141200707.0mm N T T M ⋅=⨯=(1) 221125104.25707.0mm N T A V w =⨯==τ )(1049.4707.0104.25125521N T ⨯=⨯⨯=∴(或:2211251095.032707.0mm N T A Vw =⨯⨯==τ )1037.551N T ⨯=∴(2) 2222154.141707.0mm N WT A T =+=σ2232215)102.6924.1411012.67707.0(mm N T =⨯+⨯∴ )(1094.652N T ⨯=∴(3) 折算应力(在顶部中点亦可)()2151.11.1000555.0000278.03000276.03)000233.0104.30707.0( 000278.0104.25707.0000276.01605.26160102.6924.1411012.67707.03322212133213321333231⨯=≤=⨯+=+=⨯==⨯==-⨯⨯+⨯=w f f T T T T T T T T T τσττσ或得:)(1.4263KN T ≤ (KN T f T 3wf 33.484 1.10.000488≤≤或)由T 1、T 2、T 3中取最小值,得T =426.1(KN )m KN M Nmm ⋅=⨯⨯=4104105 N V 5104⨯=f ff f h h W M 6.4283.93331046=⨯==σ22.1=f β, f ff f h h A V 6.14282801045=⨯==τ 2002.1471)6.1428()22.16.428()(2222≤=+=+ff f f f f h h h τβσ mm h f 4.7≥,取mm h f 8=.3、如图所示的牛腿用角焊缝与柱连接。


第3章第2节[基础达标]题组一目的基因的筛选与获取1.在基因工程的基本操作程序中,目的基因的获取途径不包括()A.从基因文库中获取目的基因B.利用PCR技术扩增目的基因C.人工合成目的基因D.利用DNA分子杂交技术,获取目的基因【答案】D【解析】可以从基因文库中获取目的基因,A不符合题意;获取目的基因的方法之一是PCR技术,B不符合题意;可以通过人工合成的方法获取目的基因,C不符合题意;DNA 分子杂交技术不能用于获取目的基因,D符合题意。
2.(2023·广东广州阶段练习)PCR是一种体外迅速扩增DNA片段的技术。
PCR过程一般经历下述30多次循环:95 ℃下使模板DNA变性、解链→55 ℃下复性(引物与DNA模板链结合)→72 ℃下引物链延伸(形成新的DNA链)。
下列有关PCR过程的叙述中不正确的是() A.变性过程中破坏的是DNA分子内碱基对之间的氢键B.复性过程中引物与DNA模板链的结合是依靠碱基互补配对原则完成C.延伸过程中需要DNA聚合酶、A TP、四种核糖核苷酸D.PCR与细胞内DNA复制相比所需酶的最适温度较高【答案】C【解析】变性是DNA分子解旋,该过程中破坏的是DNA分子内碱基对之间的氢键,A 正确;复性过程中引物与DNA模板链的结合是依靠碱基互补配对原则完成的,B正确;延伸是合成DNA的子链,所以该过程中需要DNA聚合酶、A TP、四种脱氧核糖核苷酸,C错误;PCR与细胞内DNA复制相比所需酶的最适温度较高,因为PCR过程需要高温变性,即使在复性时的温度也比较高,D正确。
题组二基因表达载体的构建3.下列对基因表达载体构建的叙述,不正确的是()A.需要限制酶和DNA连接酶等特殊工具B.基因表达载体中有的含有启动子和密码子C.标记基因不一定是抗生素抗性基因D.基因表达载体的构建是基因工程的核心【答案】B【解析】基因表达载体是目的基因与载体的结合,在此过程中通常用同一种限制酶切割目的基因与载体,用DNA连接酶将相同的末端连接起来,A正确;基因表达载体含有启动子、终止子、标记基因和目的基因,密码子位于mRNA上,B错误;抗生素抗性基因可作为标记基因,但标记基因不都是抗生素抗性基因,C正确;基因表达载体的构建是基因工程的核心,在细胞外进行,使目的基因在受体细胞中稳定存在并且可以遗传给下一代并表达和发挥作用,D正确。


第三章习题解答3.1 简述数据链路层的功能。
答:数据链路层是在物理层提供的比特流传送服务的基础上,通过一系列的控制和管理,构成透明的、相对无差错的数据链路,向网络层提供可靠、有效的数据帧传送的服务。
其主要功能包括:链路管理,帧定界,流量控制,差错控制,数据和控制信息的识别,透明传输,寻址。
3.2 试解释以下名词:数据电路,数据链路,主站,从站,复合站。
答:数据电路是一条点到点的,由传输信道及其两端的DCE构成的物理电路段,中间没有交换节点。
数据电路又称为物理链路,或简称为链路。
数据链路是在数据电路的基础上增加传输控制的功能构成的。
一般来说,通信的收发双方只有建立了一条数据链路,通信才能够有效地进行。
在链路中,所连接的节点称为“站”。
发送命令或信息的站称为“主站”,在通信过程中一般起控制作用;接收数据或命令并做出响应的站称为“从站”,在通信过程中处于受控地位。
同时具有主站和从站功能的,能够发出命令和响应信息的站称为复合站。
3.3 数据链路层流量控制的作用和主要功能是什么?答:流量控制简称“流控”,是协调链路两端的发送站、接收站之间的数据流量,以保证双方的数据发送和接收达到平衡的一种技术。
在计算机网络中,由于接收方往往需要对接收的信息进行识别和处理,需要较多的时间,通常发送方的发送速率要大于接收方的接收能力。
当接收方的接收处理能力小于发送方的发送能力时,必须限制发送方的发送速率,否则会造成数据的丢失。
流量控制就是一种反馈机制,接收方随时向发送方报告自己的接收情况,限制发送方的发送速率。
保证接收方能够正常、有序地接收数据。
3.4 在停止-等待协议中,确认帧是否需要序号?为什么?答:在停止-等待协议中,由于每次只确认一个已经发送的帧,确认帧可以不需要序号。
但在一些特殊情况下会出现问题。
如果发送方在超时重发一个帧后又收到了迟到的确认,就不能确定该应答是对哪一个帧的确认,并可能导致随后的传送过程重新差错。
3.5 解释为什么要从停止-等待协议发展到连续ARQ协议。
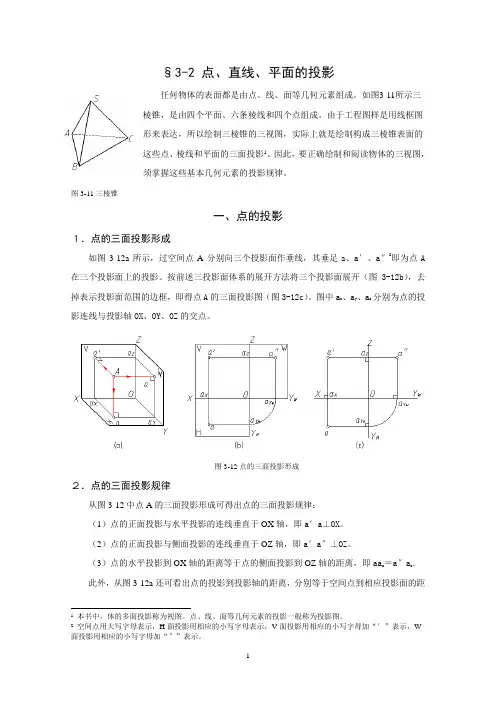
§3-2 点、直线、平面的投影任何物体的表面都是由点、线、面等几何元素组成。
如图3-11所示三棱锥,是由四个平面、六条棱线和四个点组成。
由于工程图样是用线框图形来表达,所以绘制三棱锥的三视图,实际上就是绘制构成三棱锥表面的这些点、棱线和平面的三面投影1。
因此,要正确绘制和阅读物体的三视图,须掌握这些基本几何元素的投影规律。
图3-11三棱锥一、点的投影1.点的三面投影形成如图3-12a所示,过空间点A分别向三个投影面作垂线,其垂足a、a′、a″2即为点A 在三个投影面上的投影。
按前述三投影面体系的展开方法将三个投影面展开(图3-12b),去掉表示投影面范围的边框,即得点A的三面投影图(图3-12c)。
图中a x、a y、a z分别为点的投影连线与投影轴OX、OY、OZ的交点。
图3-12点的三面投影形成2.点的三面投影规律从图3-12中点A的三面投影形成可得出点的三面投影规律:(1)点的正面投影与水平投影的连线垂直于OX轴,即a′a⊥OX。
(2)点的正面投影与侧面投影的连线垂直于OZ轴,即a′a″⊥OZ。
(3)点的水平投影到OX轴的距离等于点的侧面投影到OZ轴的距离,即aa x=a″a z.此外,从图3-12a还可看出点的投影到投影轴的距离,分别等于空间点到相应投影面的距1本书中,体的多面投影称为视图。
点、线、面等几何元素的投影一般称为投影图。
2空间点用大写字母表示,H面投影用相应的小写字母表示,V面投影用相应的小写字母加“′”表示,W 面投影用相应的小写字母加“″”表示。
离。
如:a′a z=aa YH反映点A到W面的距离;a′a x=a″a Yw反映点A到H面的距离; aa x=a″a z反映点A到V面的距离.根据上述点的三面投影规律,在点的三面投影中,只要知道其中任意两个面的投影,就可求作出该点的第三面投影。
〔例3-2〕已知点B的V面投影b′与H面投影b,求作W面投影b″(图3-13a)。
第2节DNA的结构课标内容要求核心素养对接概述DNA分子是由四种脱氧核苷酸构成的,通常由两条碱基互补配对的反向平行长链形成双螺旋结构,碱基的排列顺序编码遗传信息。
1.生命观念:说明DNA双螺旋结构模型的特点。
2.科学思维:思考在DNA分子中碱基的比例和数量之间的规律,总结有关碱基计算的方法和规律。
3.科学探究:动手制作模型,培养观察能力、空间想象能力、分析和理解能力。
一、DNA双螺旋结构模型的构建1.构建者:沃森和克里克。
2.构建过程3.新模型的特点及意义(1)特点:A—T碱基对与G-C碱基对具有相同的形状和直径,这样组成的DNA分子具有恒定的直径。
(2)意义①能解释A、T、G、C的数量关系.②能解释DNA的复制.③模型与X射线衍射照片完全相符。
二、DNA的结构1.平面结构基本组成元素↓组成物质↓基本组成单位↓DNA C、H、O、N、P[①]碱基,[②]脱氧核糖,[③]磷酸[④]脱氧核苷酸,共4种两条链反向平行2.空间结构(1)名称:双螺旋结构。
(2)特点:整体结构由两条链按反向平行方式盘旋成双螺旋结构结构特点外侧(基本骨架)由脱氧核糖和磷酸交替连接内侧碱基之间通过氢键连接;遵循碱基互补配对原则,即T(胸腺嘧啶)一定与[⑥]腺嘌呤配对,C(胞嘧啶)一定与[⑦]鸟嘌呤配对判断对错(正确的打“√”,错误的打“×”)1.沃森和克里克在构建DNA双螺旋结构模型过程中,碱基配对方式经历了相同碱基配对到嘌呤与嘧啶配对的过程。
( ) 2.组成DNA分子的基本单位是4种脱氧核苷酸,其中所含的碱基是A、U、G、C。
() 3.在DNA分子中一定存在如下关系:C=T,A=G。
()4.双链DNA分子中的每个磷酸都与2个五碳糖连接. ()[答案]1.√2.×提示:U(尿嘧啶)只在RNA中含有,DNA中含有的是T(胸腺嘧啶)。
3.×提示:在DNA分子双链上,A和T配对,C与G配对,一定存在的关系:A=T,G=C。
⾼中⽣物_第3章第2节DNA分⼦的结构教学设计学情分析教材分析课后反思教学设计⼀、创设情境,导⼊新课以学⽣熟悉的公益活动“宝贝回家”视频为情境,设问:公益者以什么⽅式帮助离散的孩⼦和⽗母确定亲缘关系的?---DNA。
抛出问题:DNA究竟应该具有怎样的结构才能担当起遗传的重任呢?引⼊本节课的学习多媒体展⽰:本节课的内容及学习⽬标展⽰中关村DNA的双螺旋结构模型,介绍此模型是谁建⽴的以及意义,并因此获得诺贝尔奖。
引导学⽣进⼊DNA双螺旋结构模型的构建历程的学习⼆、DNA双螺旋模型的构建历程依据沃森和克⾥克的研究历程分层次学习(⼀)沃森和克⾥克开始研究DNA的结构以前:科学界已经认识到DNA时由4种脱氧核苷酸连接成的长链。
引导学⽣结合必修⼀学过的有关DNA的化学组成,回顾DNA的基本单位的相关知识。
【过渡】沃森和和克⾥克根据科学界对DNA的已有认识,利⽤⾦属材料模拟DNA的组成部分进⽽组装起来,从⽽把DNA的抽象的结构形象的直观的表达出来,这种⽣物学研究⽅法属于⽅法模型构建⼀:利⽤组件构建4种脱氧核苷酸【过渡】这4种脱氧核苷酸是如何连接形成脱氧核苷酸长链的?类⽐蛋⽩质中氨基酸的脱⽔缩合过程模型构建⼆:利⽤已构建的4种脱氧核苷酸连接成脱氧核苷酸长链【探究活动】DNA双螺旋结构模型的构建历程阅读课本P47-48,⼩组合作讨论以下问题1、当时是什么深深触动了沃森和克⾥克开始对DNA结构进⾏研究?并由此得到什么结论?2、沃森和克⾥克借鉴科学家们的发现,先后建⽴了什么样的DNA模型?1、不同⼩组构建的不同DNA分⼦中:哪些结构是稳定不变的?(供选:DNA的空间结构、碱基互补配对的⽅式、基本⾻架、脱氧核苷酸数量、碱基对的排列顺序)这与DNA分⼦可作为遗传物质的哪个特性相适应?2、不同⼩组构建的不同DNA分⼦中:哪些结构是可变的?(供选:DNA的空间结构、碱基互补配对的⽅式、基本⾻架、脱氧核苷酸数量、碱基对的排列顺序)这体现了DNA分⼦具有什么特性?3、DNA作为遗传物质,是通过什么储存⼤量的遗传信息?4、对于⼀个特定对的DNA分⼦来说,碱基排列顺序是⼀定的,这⼜体现了DNA的什么特性?亲⼦鉴定是利⽤了DNA分⼦的哪个特性?【知识⽹络构建】DNA分⼦的结构与功能【规律总结】DNA分⼦结构的“⼀⼆三四五”【课堂⼩结】【作业布置】学情分析1、【知识⽅⾯】本节是⾼中⽣物⼈教版必修⼆《遗传与变异》模块中第3章第2节《DNA 分⼦的结构》。
第三章连接课后习题参考答案第三章连接课后习题参考答案焊接连接参考答案一、概念题3.1 从功能上分类,连接有哪几种基本类型?3.2 焊缝有两种基本类型—对接坡口焊缝和贴角焊缝,二者在施工、受力、适用范围上各有哪些特点?3.3 对接接头连接需使用对接焊缝,角接接头连接需采用角焊缝,这么说对吗?3.4 h和lw相同时,吊车梁上的焊缝采用正f面角焊缝比采用侧面角焊缝承载力高?3.5 为何对角焊缝焊脚尺寸有最大和最小取值的限制?对侧面角焊缝的长度有何要求?为什么?【答】(1)最小焊脚尺寸:角焊缝的焊脚尺寸不能过小,否则焊接时产生的热量较小,致使施焊时冷却速度过快,导致母材开裂。
《规范》规定:h f≥1.5t,式中:t2——较厚焊件厚度,单2位为mm。
计算时,焊脚尺寸取整数。
自动焊熔深较大,所取最小焊脚尺寸可减小1mm;T形连接的单面角焊缝,应增加1mm;当焊件厚度小于或等于4mm时,则取与焊件厚度相同。
(2)最大焊脚尺寸:为了避免焊缝区的主体金属“过热”,减小焊件的焊接残余应力和残余变形,角焊缝的焊脚尺寸应满足12.1t h f式中: t 1——较薄焊件的厚度,单位为mm 。
(3)侧面角焊缝的最大计算长度侧面角焊缝在弹性阶段沿长度方向受力不均匀,两端大而中间小,可能首先在焊缝的两端破坏,故规定侧面角焊缝的计算长度l w ≤60h f 。
若内力沿侧面角焊缝全长分布,例如焊接梁翼缘与腹板的连接焊缝,可不受上述限制。
3.6 简述焊接残余应力产生的实质,其最大分布特点是什么? 3.7 画出焊接H 形截面和焊接箱形截面的焊接残余应力分布图。
3.8 贴角焊缝中,何为端焊缝?何为侧焊缝?二者破坏截面上的应力性质有何区别?3.9 规范规定:侧焊缝的计算长度不得大于焊脚尺寸的某个倍数,原因何在?规范同时有焊缝最小尺寸的规定,原因何在? 3.10 规范禁止3条相互垂直的焊缝相交,为什么。
3.11 举3~5例说明焊接设计中减小应力集中的构造措施。
第三章 连通度、匹配⎧⎪⎨⎪⎩顶点连通度和边连通度门格尔定理匹配、霍尔定理 本章的特点:(1)理论深;(2)本科基本用不上(计算机体系结构上用到一点),只有研究生才能用上;(3)只介绍这个领域最基本的概念和一些有用的结果。
一个图是否是连通的,这是图的一个重要性质。
内容:本章首先引入图的顶点连通度和边连通度,由此可以比较两个图中哪个“更加连通”;接着讨论了它们的一些简单性质;然后讨论偶图的匹配问题。
第一节 顶点连通度和边连通度χγχλδ⎧⎪⎪⎨⎪⎪⎩动机和目的顶点连通度(G)、边连通度(G)(G)、(G)、(G)关系n-顶点连通、n-边连通1.1 动机和目的一个图是否是连通的,是图的一个重要性质。
于是,我们就想来刻画两个图“连通程度”的大小,但是刻画两个图“连通程度”的大小方法很多,我们只介绍两个常用的方法:顶点连通度和边连通度例:树的每个度大于1的顶点都是割点。
一个具有割点的连通图,当去掉这个割点时,就产生了一个不连通图。
对于一个没有割点的连通图,必须去掉多于一个顶点才有可能得到一个不连通图。
于是,具有割点的连通图较之没有割点的连通图的“连通程度”要低。
类似地,树的每条边的都是桥。
有桥的连通图,当去掉桥时,就产生了一个不连通图。
对于无桥的连通图,要想去掉一些边得到不连通图,至少要去掉两条才有可能得到不连通图。
从去掉边来获得不连通图的角度看,有桥的连通图较之无桥的连通图的“连通程度”要低。
特别是,一个非平凡树是一个有最少边连通图。
图的顶点和边,在不同应用中有不同意义。
在通讯网络中,通讯站是顶点,通讯线路是边。
它们的失灵势必危机系统的通讯。
所以,网络图的“连通程度”越高,通讯网络越可靠。
这种直观的想法,启发我们建立以下的严格概念:1.2 顶点连通度(连通度)定义1 设G=(V ,E)是一个无向图,要想从G 中得到一个不连通图或平凡图所需要从G中去掉的最少顶点数称为G 的顶点连通度,简称连通度。
记为)(G χχ=。