《数字信号处理》课程几个容易混淆的问题
- 格式:doc
- 大小:124.00 KB
- 文档页数:6

西南大学培训与继续教育学院课程代码:1077学年学季:20202窗体顶端判断题1、应用DFT分析无限长信号的频谱时,必然会产生误差。
A.√B.×2、离散周期信号的DFS中,频域的周期N对应数字频率为2π。
A.√B.×3、实数序列的DFT为共轭对称的序列。
A.√B.×4、一个域的周期性,对应另一域的离散性。
A.√B.×5、信号的最高频率为3π/5,则最大程度减小数据量的I/D值为3/5。
A.√B.×6、单位圆上的零点,对应幅频特性的零值。
A.√B.×7、LP表示的滤波器类型是低通滤波器。
A.√B.×8、通带最平坦的滤波器是巴特沃思滤波器。
A.√B.×9、陷波器必然有零点位于单位圆上。
A.√B.×10、圆周卷积和线卷积相等的条件是圆周卷积的点数不小于线性卷积的长度。
A.√B.×11、按照最大误差最小准则设计的滤波器,具有等波纹的特点。
A.√B.×12、单位脉冲序列的DTFT结果为1。
A.√B.×13、x(n)与h(n)的卷积的Z变换为X(Z)H(Z)。
A.√B.×14、所谓全通系统,就是其频率响应的幅度在任意需要考虑的频率点处均为常数。
A.√B.×15、FIR滤波器由于无原点外的极点,故相比IIR阶次更高。
A.√B.×16、对连续信号作频谱分析,设信号的采样频率为10KHz,频域的分辨能力为不大于10Hz,则对应DFS点数为1000点。
A.√B.×17、靠近单位圆上的极点,对应幅频特性的极大值。
A.√B.×18、线性相位可分为第一类与第二类线性相位两种情况。
A.√B.×19、为满足线性相位要求,窗函数本身也应满足相应的对称性。
A.√B.×20、冲激响应不变法由于存在混叠,不能设计高通、带通滤波器。
A.√B.×21、FIR滤波器的结构往往是非递归型的。
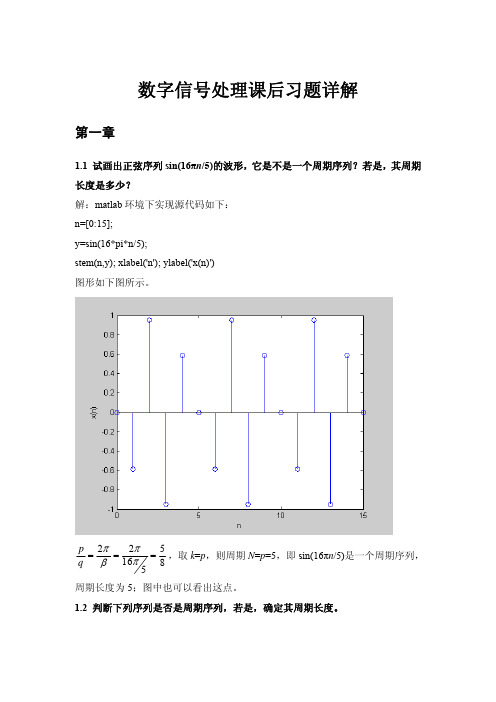
数字信号处理课后习题详解第一章1.1 试画出正弦序列sin(16πn /5)的波形,它是不是一个周期序列?若是,其周期长度是多少?解:matlab 环境下实现源代码如下: n=[0:15]; y=sin(16*pi*n/5);stem(n,y); xlabel('n'); ylabel('x(n)') 图形如下图所示。
2251685p q πππβ===,取k =p ,则周期N =p =5,即sin(16πn /5)是一个周期序列,周期长度为5;图中也可以看出这点。
1.2 判断下列序列是否是周期序列,若是,确定其周期长度。
(1) 3()cos(74x n n ππ=−解:2214337p q πππβ===∵ p ,q 是互为质数的整数,取k =q 则周期N =p =14∴周期长度为14 (2) 7cos()4sin()(nnn x ππ−=解:1284N ππ== 22147N ππ==∵N 1,N 2最小公倍数为56 ∴其周期长度为561.3 试画出如下序列的波形(1) x(n)=3δ(n+3)+2δ(n+1)-4δ(n-1)+2δ(n-2) (2)x(n)= 0.5n R 5(n)解:(1)(2)1.4 今对三个正弦信号)2cos()(1t t x a π=、)6cos()(2t t x a π−=、)10cos()(3t t x a π=进行理想采样,采样频率为π8=Ωs ,求这三个采样输出序列,比较其结果。
画出x a 1(t )、x a 2(t )、x a 3(t )的波形及采样点位置并解释频谱混叠现象。
解:matlab 环境下实现源代码如下:t=-1:0.01:1; x1=cos(2*pi*t); x2=-cos(6*pi*t); x3=cos(10*pi*t); t2=-1:0.25:1; y1=cos(2*pi* t2);y2=-cos(6*pi* t2);y3=cos(10*pi* t2);subplot(311)plot(t,x1);xlabel('t');ylabel('Xa1(t)') holdstem(t2, y1)subplot(312)plot(t,x2);xlabel('t');ylabel('Xa2(t)') holdstem(t2, y2)subplot(313)holdstem(t2, y3)plot(t,x3);xlabel('t');ylabel('Xa3(t)') 三个信号波形已知πω8=,则4182,42===πππωs T 。


数字信号处理简答题一.数字信号处理与模拟信号处理比较1模拟通信的优点是直观且容易实现,但存在两个主要缺点:保密性差;抗干扰能力弱。
2数字通信(1)数字化传输与交换的优点:加强了通信的保密性;提高了抗干扰能力;可构建综合数字通信网(2)数字化通信的缺点:占用频带较宽;技术要求复杂;进行模数转换时会带来量化误差二.利用DFT计算模拟信号可能出现的问题1.频率响应的混叠失真及参数的选择时域抽样:频域抽样:2频谱泄漏,对时域截短,使频谱变窄拖尾,称为泄漏。
改善方法:增加x(n)长度;缓慢截短。
3栅栏效应DFT只计算离散点的频谱而不是连续函数改善方法增加频域抽样点数N(时域补零)使谱线更密4频率分辨率提高频率分辨率的方法:增加信号实际记录长度补零不能提高频率分辨率可克服栅栏效应三按时间抽选与按频率抽选的异同相同之处1DIF与DIT均为原位元算2运算量相同3是两种等价的FFT算法不同1DIF输入是自然顺序输出是倒位序DIT相反2两者根本区别在于蝶形结构不同:DIF的复数乘法出现在减法之后,DIT的复数乘法出现在减法之前四改善DFT的运算效率的基本途径利用DFT运算的系数的固有对称性和周期性,改善DFT的运算效率1分解法:将长序列DFT利用对称性和周期性,分解为短序列DFT2合并法:合并DFT运算中得某些项五.IIR和FIR数字滤波器的特点IIR数字滤波器的特点:1系统的单位抽样乡音h(n)为无限长2系统函数H(z)在有限z平面上有极点存在3存在输出到输入的反馈,递归型结构FIR数字滤波器的特点1系统的单位抽样响应h(n)有限长2系统函数H(z)在IzI>0处收敛,有限Z平面只有零点,全部极点在Z=0处3无输出到输入的反馈,一般为非递归型结构六.冲激响应不变法和双线性不变法优缺点比较1冲激响应不变法优点a. h(n)完全模仿模拟滤波器的单位抽样响应h(t)的时域逼近良好b.保持线性关系:线性相位模拟滤波器转变为线性相位数字滤波器缺点a.频率响应混叠,只适用于带限的低通带通滤波器2 双线性变换法优点a.避免了频率响应的混叠现象缺点a.线性相位模拟滤波器转变为非线性相位滤波器b.要求模拟滤波器的频率响应为分段常数型,不然会产生畸变七几种窗函数的优缺点1矩形窗矩形窗属于时间变量的零次幂窗。


1 系统因果稳定性系统因果稳定性的判断方法有三种。
第一种是定义法,即因果系统是指某时刻的输出只取决于此时刻和此时刻以前时刻的输入,稳定系统是指有界输入产生有界输出。
第二种方法是线性时不变系统的充分必要条件,因果性是指n<0时,冲激响应函数h(n)=0。
稳定性是|()|n h n P ∞=-∞=<∞∑。
第三种方法是线性时不变系统的收敛域法,即系统函数H(z)必须在从单位圆到无穷的整个z 域内收敛。
注意第一种判断法是通式,可适用于任何系统,而第二、三种方法仅适用于线性时不变系统。
例题1:判断系统()()[()]x n y n T x n e==的因果稳定性。
解法一:定义法。
y(n)只与x(n)有关,∴是因果系统。
又|()|,()AAx n A y n e e-<<<∴ 则系统稳定。
解法二:充分必要条件法。
()()()0()10|()|||...1111...n n n n h n n h n h n e ee eδδ∞∞=-∞=-∞=<==≠∴==++++++→∞∴∑∑当时,是非因果系统。
又是非稳定系统。
为什么用两种方法得出相反的结论呢? 分析一下, 第一种判断法是通式,可适用于任何系统,而第二、三种方法仅适用于线性时不变系统。
那么此系统是否为线性时不变系统呢?由于1212()()12()()1212()()()()()()n n n n ax bx T n n ax bx T n T n aT n bT n ax bx e e e ax bx x x +⎡⎤=⎣⎦=⎡⎤⎡⎤=⎣⎦⎣⎦⎡⎤⎡⎤≠+⎣⎦⎣⎦+所以此系统为非线性系统,不能用第二种方法判断。
因此,解法一的答案正确。
此题告诉我们,应用定理时要注意定理的应用范围。
2 翻褶移位函数的实现及其z 变换大多数教科书中分别介绍了移位和翻褶这两种运算。
若某序列为x(n),则x(n+m) 表示x(n)逐项依次左移(m>0)位。
数字信号处理的常见问题及解决方法总结数字信号处理在科学、工程领域中的应用越来越广泛。
在实际应用过程中,我们常常会遇到一些问题。
本文总结了一些常见的问题及其解决方法,以帮助读者更好地理解和应用数字信号处理技术。
问题一:信号滤波数字信号往往包含噪声和干扰,需要进行滤波处理以提取有效信息。
常见的信号滤波问题包括滞后滤波器、移动平均滤波器、低通滤波器等。
解决这些问题的方法通常包括设计合适的滤波器参数、选择适当的滤波器类型,并进行滤波器性能评估。
问题二:信号采样率选择在数字信号处理中,采样率的选择对信号重构和频谱分析等方面具有重要影响。
选择过低的采样率会导致信号失真,选择过高的采样率会浪费存储和计算资源。
解决这个问题的方法包括根据信号的带宽和特性选择合适的采样率,并根据需要进行抽取或插值处理。
问题三:频谱分析频谱分析是数字信号处理中的重要步骤,用于研究信号的频域特性。
常见的频谱分析问题包括功率谱密度估计、傅里叶变换等。
解决这些问题的方法包括选择合适的频谱分析方法(如快速傅里叶变换)、处理频谱分辨率问题,并进行频谱分析结果的解释和应用。
问题四:数字滤波器设计数字滤波器的设计是数字信号处理领域的关键问题之一。
常见的数字滤波器设计问题包括低通滤波器设计、高通滤波器设计、带通滤波器设计等。
解决这些问题需要根据滤波器的要求和性能指标,选择适当的设计方法(如窗函数法、频率抽样法),并进行滤波器参数调整和性能评估。
问题五:数字信号压缩数字信号压缩是在保证信号质量的前提下,减少信号数据量的一种技术。
常见的数字信号压缩问题包括有损压缩和无损压缩。
解决这些问题的方法通常包括选择适当的压缩算法(如哈夫曼编码、小波变换压缩),根据压缩效率和信号质量要求进行参数调整。
以上是数字信号处理中常见问题的一些总结及解决方法。
希望能够帮助读者更好地应用数字信号处理技术,解决实际应用中的问题。
数字信号处理参考答案《解答题及分析题》一、解释下列名词:(1)DSP: 数字信号处理或者数字信号处理芯片;(2)MIPS: 每秒执行百万条指令 ;(3)MOPS: 每秒执行百万条操作 ;(4)FFT: 快速傅里叶变换 ;(5)MAC 时间: 完成一次乘法和一次加法的时间 ;(6)指令周期:执行一条指令所需要的时间,单位通常为(ns );(7)BOPS:每秒执行十亿次操作;(8)MFLOPS :每秒执行百万次浮点操作;(9)TMS320C54X :TI 公司的54系列定点DSP 芯片;(10)ADSP21XX:AD :公司的21系列定点DSP 芯片;二、已知)()()]([n x n g n x T =判断系统是否为:① 因果系统;② 稳定系统;③ 线性系统;④ 移不变系统解:(1)求解系统的单位取样响应)(n h令)()(n n x δ=,则系统的单位取样响应)()()(n n g n h δ=① 当0<n 时,0)(=n h ,系统为因果系统;②0)(=∑+∞-∞=n n h ,是稳定系统; ③ 设)()()(),()()(2211n g n x n y n g n x n y ==由于)()()()([)(2121n by n ay n bx n ax T n y +=+=,④ 由于)()]([),()()(k n y k n X T k n g k n x k n y -≠---=-而, 因此,系统为移变系统。
其余几个题的判断方法与这个相同,略。
三、画方框图说明DSP 系统的设计步骤。
设计步骤:(1)根据实际问题的要求写出任务书确定设计目标;(2)算法研究并确定系统的性能指标;(3)选择DSP 芯片和外围芯片;(4)完成系统的硬件设计和软件设计;(5)完成系统的硬件仿真和软件调试;(6)系统集成和测试。
四、以TMS320C5402为例,说明一个典型的DSP 实时数字信号处理系统通常有哪些部分组成?画出系统组成的方框图。
数字信号处理(简答题)1、在A/D 变换之前和D/A 变换之后都要让信号通过一个低通滤波器,它们分别起什么作用?答:在A/D 变化之前让信号通过一个低通滤波器,是为了限制信号的最高频率,使其满足当采样频率一定时,采样频率应大于等于信号最高频率2倍的条件。
此滤波器亦称位“抗折叠”滤波器。
在D/A 变换之后都要让信号通过一个低通滤波器,是为了滤除高频延拓谱,以便把抽样保持的阶梯形输出波平滑化,故友称之为“平滑”滤波器。
2.何谓最小相位系统?最小相位系统的系统函数)(min Z H 有何特点?解:一个有理系统函数,如果它的零点和极点都位于单位圆内,则有最小相位。
一个稳定的因果线性移不变系统,其系统函数可表示成有理方程式∑∑=-=--==N k kk Mr rr Z a Zb Z Q Z P Z H 101)()()(,它的所有极点都应在单位圆内,即1 k α。
但零点可以位于Z 平面的任何地方。
有些应用中,需要约束一个系统,使它的逆系统)(1)(Z H Z G =也是稳定因果的。
这就需要)(Z H 的零点也位于单位圆内,即1 r β。
一个稳定因果的滤波器,如果它的逆系统也是稳定因果的,则称这个系统是最小相位。
3.何谓全通系统?全通系统的系统函数)(Z H ap 有何特点?解:一个稳定的因果全通系统,其系统函数)(Z H ap 对应的傅里叶变换幅值1)(=jw e H ,该单位幅值的约束条件要求一个有理系统函数方程式的零极点必须呈共轭倒数对出现,即∏∑∑=-*-=-=---=-==Nk k kN k kk Mr rr ap Z Z Z a Zb Z Q Z P Z H 1111011)()()(αα。
因而,如果在k Z α=处有一个极点,则在其共轭倒数点*=kZ α1处必须有一个零点。
4.在离散傅里叶变换中引起混迭效应的原因是什么?怎样才能减小这种效应? 解:因为为采样时没有满足采样定理减小这种效应的方法:采样时满足采样定理,采样前进行滤波,滤去高于折叠频率2s f 的频率成分。
1 系统因果稳定性系统因果稳定性的判断方法有三种。
第一种是定义法,即因果系统是指某时刻的输出只取决于此时刻和此时刻以前时刻的输入,稳定系统是指有界输入产生有界输出。
第二种方法是线性时不变系统的充分必要条件,因果性是指n<0时,冲激响应函数h(n)=0。
稳定性是|()|n h n P ∞=-∞=<∞∑。
第三种方法是线性时不变系统的收敛域法,即系统函数H(z)必须在从单位圆到无穷的整个z 域内收敛。
注意第一种判断法是通式,可适用于任何系统,而第二、三种方法仅适用于线性时不变系统。
例题1:判断系统()()[()]x n y n T x n e==的因果稳定性。
解法一:定义法。
y(n)只与x(n)有关,∴是因果系统。
又|()|,()AAx n A y n e e-<<<∴ 则系统稳定。
解法二:充分必要条件法。
()()()0()10|()|||...1111...n n n n h n n h n h n e ee eδδ∞∞=-∞=-∞=<==≠∴==++++++→∞∴∑∑当时,是非因果系统。
又是非稳定系统。
为什么用两种方法得出相反的结论呢? 分析一下, 第一种判断法是通式,可适用于任何系统,而第二、三种方法仅适用于线性时不变系统。
那么此系统是否为线性时不变系统呢?由于1212()()12()()1212()()()()()()n n n n ax bx T n n ax bx T n T n aT n bT n ax bx e e e ax bx x x +⎡⎤=⎣⎦=⎡⎤⎡⎤=⎣⎦⎣⎦⎡⎤⎡⎤≠+⎣⎦⎣⎦+所以此系统为非线性系统,不能用第二种方法判断。
因此,解法一的答案正确。
此题告诉我们,应用定理时要注意定理的应用范围。
2 翻褶移位函数的实现及其z 变换大多数教科书中分别介绍了移位和翻褶这两种运算。
若某序列为x(n),则x(n+m) 表示x(n)逐项依次左移(m>0)位。
x(-n)表示以n=0的纵轴为对称轴将x(n)加以翻褶。
那翻褶移位合并起来,如x(-n+m)怎样实现,书中没有给出,很多学生理解有误,表现在求其z 变换上出错。
下面举例说明x(-n+m)的含义。
例题2:设x(n)=[1 2 3],求x(-n+1)及其z 变换。
解法一:思路:序列先移位后翻褶。
用Matlab 画图表示。
-220123-220123-220123图1. 解法一序列波形图x(n+1)表示将x(n)左移一位,x(-n+1)表示将x(n+1)翻褶。
相应的z 变换:1()()()()1()()()()mmx n X z x n m X z x n x n m X z X z z z--↔+↔--↔-+↔m=1即为答案。
解法二:思路:序列先翻褶后移位。
用Matlab 画图表示。
-220123-22-220123图2. 解法二序列波形图x(-n)表示将x(n) 翻褶,x(-(n-1)) 表示将x(-n)右移一位,而不是左移。
相应的z 变换:1()()1()()(())()()mx n X z x n x n m x n m X X z z z --↔--↔-+=--↔两种解法答案一样。
通过这个例题,可注意到x(-n)的移位与x(n)的移位方向相反。
3 卷积与相关卷积和相关有类似的数学公式,即 线性卷积:()()()m z n x m y n m ∞=-∞=-∑ 线性相关:*()()()xym n x m m n y r∞=-∞=-∑容易混淆。
但它们的物理概念完全不同,应用不同。
卷积反映了线性时不变系统输入和输出的关系,而相关只是反映两个信号的相似程度,和系统本身的特性无关。
例如,语音信号是由激励源与声道传输函数卷积得到,对于浊音部分可通过求自相关函数得到它的基音周期。
掌握了概念的物理意义,就不会混淆了。
但在数学计算上他们确实有类似的地方,相关可以用卷积形式表示, 如*()()()xy m n x m m n y r ∞=-∞=-∑=x(n)*y *(-n)4 四种傅里叶变换的关系四种傅里叶变换:连续时间非周期信号的傅里叶变换(CTFT ) 连续时间周期信号的傅里叶级数(CFS) 离散时间非周期信号的傅里叶变换(DTFT) 离散时间周期信号的傅里叶级数(DFS) 之后,离散傅里叶变换(DFT )是不是第五种傅里叶变换形式呢?不是。
前四种傅里叶变换揭示出傅里叶变换的真正含义——时域信号和它的频谱的对应关系,一个域的连续或离散,对应变换域的非周期或周期,并且这四种傅里叶变换形式真正表示信号的频谱,而DFT 实际上来自DFS ,只不过仅在时域和频域各取一个周期而已,对应在时域和频域都是离散、有限长序列,它不是一种新的傅里叶变换形式,是为了计算和处理方便引入的。
在讨论其性质时, 无论在时域还是频域都要时刻注意所隐含的周期性,即参于计算的序列是周期序列的一个周期,因而DFT 中的移位为循环移位。
这些傅里叶变换的形式和性质可以对照着记忆。
5傅里叶变换的对称性一个序列x(n)可以分解为实部x R (n)和虚部x I (n),也可分解为共轭对称部分x e (n)和反共轭对称部分x o (n)。
相应的x(n)的频域值()j X eω也可分解为实部()j R eX ω和虚部()j I eX ω,也可分解为共轭对称部分()j e e X ω和反共轭对称部分()j o e X ω。
由于习惯上将小写字母对应于时域信号,相应的大写字母就是它的频域形式,所以学生就容易想当然的认为x R (n)和()j R eX ω构成一对傅里叶变换对,x e (n)和()j e e X ω构成一对傅里叶变换对。
这是错误的,正确的对应关系为:()()()()()()()()()()ReoIj j j o Ix n n n n n j j X e R jx xx x jXe e e X e e X X ωωωωω=+=+=+=+简单证明一个()()j R e n x eX ω↔关系,如下: ()()**1[()][[()()]]21[]()2e j j j R DTFT n DTFT x n n X x x e e e X X ωωω=+-=+=相应的离散傅里叶DFT 变换也有类似的结论,可以联合起来一起记忆,但要注意到正是由于有限长序列被看成周期序列的一个周期,或者说是进行了周期性延拓,所以有了圆周共轭对称的定义。
由此可见,不能按照思维定式,想当然的推理,要理解公式含义,正确推导。
6 高密度谱和高分辨率谱高密度谱和高分辨率谱也是两个不同的概念。
高密度谱是通过补零操作得到更光滑的谱线,减少栅栏效应。
高分辨率谱是通过增加信号的记录长度得到,频率分辨力与信号的实际长度成反比,信号越长,其分辨力越高。
下面举例说明这两种谱的区别。
例题3: 设x(n) = cos(0.48πn)+cos(0.52πn); 099n ≤≤,分别用Matlab 语言编程画出下列函数的波形及幅度谱: (1) x(n)的前10点;(2) x(n)的前10点,后面补上90个零值; (3) x(n)的前100点。
解:Matlab 语言编程程序省略,这里直接给出图形,见图3所示。
x(n), 0 <= n <= 9n00.51Magnitude spectrum frequency in pi unitsx(n), 0 <= n <= 9 + 90 zeros n 00.510246810High density spectrum frequency in pi unitsx(n), 0 <= n <= 99n00.510204060High resolution spectrum frequency in pi units(a) (b) (c)图3. 序列的波形图及幅度谱图3(a )为x(n)前10点的波形及幅度谱,(b )为x(n)的前10点,后面补上90个零值的函数波形及幅度谱,(c )为x(n)前100点的波形及幅度谱。
比较图3(a )和(b ),发现两者有用的信息量相同,但用不同的点数N 做DFT ,N 值越大,谱线更光滑,使原来漏掉的某些频谱分量被检测出来,改善了栅栏效应,但是频谱包络线不变,因此并不能提高频谱分辨率。
分析函数x(n)知,它应有两个频率成分,分别为0.48πrad/s 和0.52πrad/s ,而图3(b )虽然使谱线更光滑,但只给出一个峰值,没有检测出x(n)的两个频率成分。
图3(c )增加了采样点数,则可在幅度谱上清晰的分辨出两个谱峰。
因此图3(b )对应的是高密度谱,图3(c )对应的是高分辨率谱。
由此可见,补零操作可以使谱的外观得到平滑,减小了栅栏效应,信号的频谱看得更清楚,但不能提高频度分辨率。
提高分辨率是通过增加信号的记录长度得到的。
7 重叠相加法和重叠保留法对于很长序列和短序列进行卷积,可采用重叠相加法和重叠保留法进行快速实现。
课本上只是通过公式图形来讲解,十分抽象。
许多同学对这两种方法产生混淆,不理解,不会应用,特别是重叠保留法。
下面就先给出基本原理,再用实例讲解分析。
设h(n)的点数为M ,信号x(n)为很长的序列。
重叠相加法是将长序列x(n)分解为很多段,每段x i (n)长度为L ,L 和M 数量级相同。
将每段x i (n)和h(n)补零到N 点(N>=L+M-1),用圆周卷积得到每段线性卷积的值,相邻两段输出序列的重叠M-1值相加得到正确值。
重叠保留法也是将长序列x(n)分解为很多段x i (n),但是每相邻段重叠M-1值取值(对第一段采取前面补M-1个零值),使得每段长度为N 点,做N 点的x i (n)和h(n)圆周卷积,将每段输出结果前M-1值去掉,剩下的值连结起来就是正确值。
下面就举例说明它们的用法。
例题4:已知 x(n)=(n+1), 05n ≤≤, h(n)={1,0,1},分别用重叠相加法和重叠保留法求解x(n)*h(n)。
解:通过直接卷积可知x(n)*h(n)值为 {1 2 2 2 2 2 -5 -6}。
解法一:重叠相加法已知M=3,令L=4, 将x(n)分段,得: x1(n)={1 2 3 4 }; x2(n)={5 6 0 0 };将每段做N=8的圆周卷积。
x1(n) ⑧ h(n) ={1 2 2 2 -3 -4 0 0 } x2(n) ⑧ h(n) ={5 6 -5 -6 0 0 0 0} 则:y1=x1(n)* h(n)= {1 2 2 2 -3 -4}y2=x1(n)* h(n)= {5 6 -5 -6}将y1尾部和y2头部值重叠 M-1=2点相加,得到y(n)={ 1 2 2 2 2 2 -5 -6}。