高中数学函数解析式求法

高中函数解析式的七种求法函数解析式的七种求法一、待定系数法：在已知函数解析式的构造时，可用待定系数法。

例1设是一次函数，且，求解：设，则二、配凑法：已知复合函数的表达式，求的解析式，的表达式容易配成的运算形式时，常用配凑法。

但要注意所求函数的定义域不是原复合函数的定义域，而是的值域。

例2已知，求的解析式解：，三、换元法：已知复合函数的表达式时，还可以用换元法求的解析式。

与配凑法一样，要注意所换元的定义域的变化。

例3已知，求解：令，则，四、代入法：求已知函数关于某点或者某条直线的对称函数时，一般用代入法。

例4已知：函数的图象关于点对称，求的解析式解：设为上任一点，且为关于点的对称点则，解得：，点在上把代入得：整理得五、构造方程组法：若已知的函数关系较为抽象简约，则可以对变量进行置换，设法构造方程组，通过解方程组求得函数解析式。

例5设求解①显然将换成，得：②解①②联立的方程组，得：例6 设为偶函数，为奇函数，又试求的解析式解为偶函数，为奇函数，又①，用替换得：即②解①②联立的方程组，得，六、赋值法：当题中所给变量较多，且含有“任意”等条件时，往往可以对具有“任意性”的变量进行赋值，使问题具体化、简单化，从而求得解析式。

例7已知：，对于任意实数x、y，等式恒成立，求解对于任意实数x、y，等式恒成立，不妨令，则有再令得函数解析式为：七、递推法：若题中所给条件含有某种递进关系，则可以递推得出系列关系式，然后通过迭加、迭乘或者迭代等运算求得函数解析式。

例8设是定义在上的函数，满足，对任意的自然数都有，求解，不妨令，得：，又①分别令①式中的得：将上述各式相加得：，。

求函数解析式的六种常用方法一、换元法已知复合函数f [g （x ）]的解析式，求原函数f （x ）的解析式.令g （x ）= t ，求f （t ）的解析式，再把t 换为x 即可.例1 已知f （xx 1+）= x x x 1122++，求f （x ）的解析式. 解： 设x x 1+= t ，则 x= 11-t （t ≠1）， ∴f （t ）= 111)11(1)11(22-+-+-t t t = 1+2)1(-t +（t －1）= t 2－t+1 故 f （x ）=x 2－x+1 （x ≠1）.评注: 实施换元后,应注意新变量的取值范围,即为函数的定义域.二、配凑法例2 已知f （x +1）= x+2x ，求f （x ）的解析式.解： f （x +1）= 2)(x +2x +1－1=2)1(+x －1，∴ f （x +1）= 2)1(+x －1 （x +1≥1），将x +1视为自变量x ，则有f （x ）= x 2－1 （x ≥1）.评注: 使用配凑法时，一定要注意函数的定义域的变化，否则容易出错.三、待定系数法例3 已知二次函数f （x ）满足f （0）=0，f （x+1）= f （x ）+2x+8，求f （x ）的解析式.解：设二次函数f （x ）= ax 2+bx+c ，则 f （0）= c= 0 ①f （x+1）= a 2)1(+x +b （x+1）= ax 2+（2a+b ）x+a+b ② 由f （x+1）= f （x ）+2x+8 与①、② 得⎩⎨⎧=++=+822b a b b a 解得 ⎩⎨⎧==.7,1b a 故f （x ）= x 2+7x. 评注: 已知函数类型，常用待定系数法求函数解析式.x ≥0， x ＜0. 四、消去法例4 设函数f （x ）满足f （x ）+2 f （x1）= x （x ≠0），求f （x ）函数解析式. 分析：欲求f （x ），必须消去已知中的f （x 1），若用x1去代替已知中x ，便可得到另一个方程，联立方程组求解即可. 解：∵ f （x ）+2 f （x1）= x （x ≠0） ① 由x 1代入得 2f （x ）+f （x 1）=x1（x ≠0） ② 解 ①② 构成的方程组，得 f （x ）=x 32－3x （x ≠0）. 五、特殊值法例5 设是定义在R 上的函数，且满足f （0）=1，并且对任意的实数x ，y ， 有f （x －y ）= f （x ）－ y （2x －y+1），求f （x ）函数解析式.分析：要f （0）=1，x ，y 是任意的实数及f （x －y ）= f （x ）－ y （2x －y+1），得到f （x ）函数解析式，只有令x = y.解： 令x = y ，由f （x －y ）= f （x ）－ y （2x －y+1） 得f （0）= f （x ）－ x （2x －x+1），整理得 f （x ）= x 2+x+1.六、对称性法即根据所给函数图象的对称性及函数在某一区间上的解析式，求另一区间上的解析式.例6 已知是定义在R 上的奇函数，当x ≥0时，f （x ）=2x －x 2，求f （x ）函数解析式.解：∵y=f （x ）是定义在R 上的奇函数， ∴y=f （x ）的图象关于原点对称. 当x ≥0时，f （x ）=2x －x 2的顶点（1，1），它关于原点对称点（－1，—1），因此当x<0时，y=2)1(+x －1= x 2 +2x.故 f （x ）=⎩⎨⎧+-xx x x 2222 评注: 对于一些函数图象对称性问题,如果能结合图形来解,就会使问题简单化.。

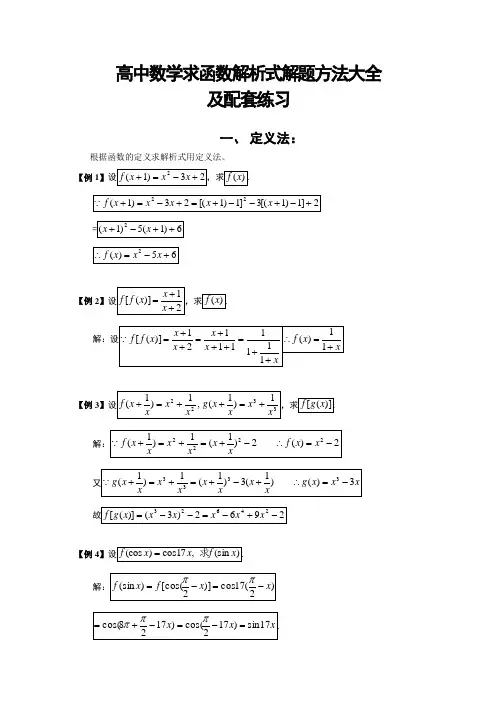
高中数学求函数解析式解题方法大全及配套练习一、定义法：根据函数的定义求解析式用定义法。

【例1】【例2】【例3】【例4】二、待定系数法：（主要用于二次函数）已知函数解析式的类型，可设其解析式的形式，根据已知条件建立关于待定系数的方程，从而求出函数解析式。

它适用于已知所求函数类型（如一次函数，二次函数，正、反例函数等）及函数的某些特征求其解析式的题目。

其方法：已知所求函数类型，可预先设出所求函数的解析式，再根据题意列出方程组求出系数。

【例1】【解析】【例2】已知二次函数f（x）满足f（0）=0，f（x+1）= f（x）+2x+8，求f（x）的解析式.解：设二次函数f（x）= ax2+bx+c，则f（0）= c= 0 ①f（x+1）（x+1）= ax2+（2a+b）x+a+b②由f（x+1）= f（x）+2x+8 与①、②得解得故f（x）= x2+7x.【例3】三、换元（或代换）法：道所求函数的类型，且函数的变量易于用另一个变量表示的问题。

使用换元法时要注意新元定义域的变化，最后结果要注明所求函数的定义域。

如：已知复合函数f [g（x）]的解析式，求原函数f（x）的解析式，把g（x）看成一个整体t，进行换元，从而求出f（x）的方法。

实施换元后,应注意新变量的取值围,即为函数的定义域.【例1】【解析】【例2】【例3】【例4】（1）在（1（2）1（3）【例5】（1（2）由【例6】四、代入法：求已知函数关于某点或者某条直线的对称函数时，一般用代入法．【例1】解则解得，上，(五)配凑法【例1】：2x当然，上例也可直接使用换元法即由此可知，求函数解析式时，可以用配凑法来解决的，有些也可直接用换元法来求解。

【例2】：分析：此题直接用换元法比较繁锁，而且不易求出来，但用配凑法比较方便。

实质上，配凑法也缊含换元的思想，只是不是首先换元，而是先把函数表达式配凑成用此复合函数的函数来表示出来，在通过整体换元。

和换元法一样，最后结果要注明定义域。

函数是高中数学的重要内容之一，贯彻于中学数学的各个部分，是中学数学主线，要掌握函数先要知道解析式，本文对根据已知条件求函数的解析式的方法进行了分析。

一、待定系数法已知函数类型，假定函数的解析式，由题设条件列方程，求待定系数值。

例1：求一个实数的一次函数f（x），使得f{f}=8x+7。

解：设f（x）=ax+b（a，b∈r）f{f［f（x）］}=a［a（ax+b）+b］=ax+ab+ab+b=8x+7∴a=8ab+ab+b=7，∴a=2b=1，∴f（x）=2x+1。

二、换元法已知f［g（x）］是关于x的函数，即f［g（x）］=f（x）。

求f（x）的解析式，通常令g（x）=t，x=φ（t），代入f［g（x）］=f（x）中，求得f （t）的解析式，再用x替换t便得f（x）的解析式。

例2：（1）已知f（x-2）=3x-5，求f（x）；（2）已知f（1-cosx）=sinx，求f（x）。

解：（1）令t=x-2，则x=t+2，t∈r由已知有f（t）=3（t+2）-5=3t+1，故f（x）=3x+1。

（2）t=1-cosx，则cosx=1-t，f（t）=1-cosx=1-（1-t）=-t+2t，故f（x）=-x+2x（0≤x≤2）。

三、消去法在题设条件中，已含有所需函数的隐式，充分利用已知条件消去其余部分。

例3：设f（x）满足f（x）-2f（）=x，求f（x）的解析式。

解：∵f（x）-2f（）=x，（x≠0）①∴将x换成，原方程为f（）-2f（x）= ②联立①②消去f（），得f（x）=--。

四、特殊值法将适当变量取特殊值，使问题具体化、简单化，从而找出规律，求出解析式。

例4：已知f（0）=1，f（a-b）=f（a）-b（2a-b+1），求f（x）。

解：令a=0，则f（-b）=f（0）-b（-b+1）=1+b-b。

再令-b=x，即得f（x）=1+x（x+1）=x+x+1。

五、分段函数的解析式对分段函数应分别求出各区间内的函数关系，再组合在一起。

高中数学例题：函数解析式的求法例. 求函数的解析式(1)已知()f x 是二次函数，且(0)2,(1)()1f f x f x x =+-=-，求()f x ；(2)若f(2x-1)=x 2，求f(x)；（3）已知3()2()3f x f x x +-=+，求()f x .【答案】（1）213()222f x x x =-+；（2）21()()2x f x +=；（3）3()5f x x =+． 【解析】求函数的表达式可由两种途径.(1)设2()(0)f x ax bx c a =++≠，由(0)2,f =得2c =由(1)()1f x f x x +-=-，得恒等式2ax+a+b=x-1,得13,22a b ==-，故所求函数的解析式为213()222f x x x =-+. (2) ∵f(2x-1)=x 2，∴令t=2x-1，则12t x += 2211()(),()()22t x f t f x ++∴=∴= （3）因为3()2()3f x f x x +-=+，①x 用x -代替得3()2()3f x f x x -+=-+，②由①②消去()f x -，得3()5f x x =+. 【总结升华】（1）解析式类型已知的，如本例（1），一般用待定系数法，对于二次函数问题要注意对一般式2y ax bx c =++，顶点式2()y a x h k =-+和两点式12()()y a x x x x =--的选择.（2）已知[()]f g x 求()f x 的问题，方法一是用配凑法；方法二是用换元法，如本例（2）.（3）函数方程问题，需建立关于()f x 的方程组，如本例（3），若函数方程中同时出现()f x 、1()f x ，则一般x 用1x代之，构造另一个方程.举一反三：【变式1】 已知f(x+1)=x 2+4x+2，求f(x)．【答案】f(x)=x 2+2x-1．【解析】(1)(法1)f(x+1)=x 2+4x+2=(x+1)2+2(x+1)-1 ∴f(x)=x 2+2x-1；(法2)令x+1=t ，∴x=t-1，∴f(t)=(t-1)2+4(t-1)+2=t 2+2t-1 ∴f(x)=x 2+2x-1；(法3)设f(x)=ax 2+bx+c 则f(x+1)=a(x+1)2+b(x+1)+c∴a(x+1)2+b(x+1)+c=x 2+4x+21x 2x )x (f 1c 2b 1a 2c b a 4b a 21a 2-+=∴⎪⎩⎪⎨⎧-===⇒⎪⎩⎪⎨⎧=++=+=∴；【总结升华】求函数解析式常用方法：(1)换元法；(2)配凑法；(3)定义法；(4)待定系数法等.注意：用换元法解求对应法则问题时，要关注新变元的范围.。

高中数学:函数解析式的十一种方法一、定义法 二、待定系数法 三、换元(或代换）法 四、配凑法 五、函数方程组法七、利用给定的特性求解析式.六、特殊值法 八、累加法 九、归纳法 十、递推法 十一、微积分法一、定义法:【例1】设23)1(2+-=+x x x f ,求)(x f .2]1)1[(3]1)1[(23)1(22+-+--+=+-=+x x x x x f =6)1(5)1(2++-+x x65)(2+-=∴x x x f【例２】设21)]([++=x x x f f ，求)(x f ． 【解析】设xx x x x x f f ++=+++=++=111111121)]([xx f +=∴11)(【例３】设33221)1(,1)1(x x x x g x x x x f +=++=+，求)]([x g f .【解析】2)(2)1(1)1(2222-=∴-+=+=+x x f x x x x x x f又x x x g x x x x xx x x g 3)()1(3)1(1)1(3333-=∴+-+=+=+ 故2962)3()]([24623-+-=--=x x x x x x g f【例4】设)(sin ,17cos )(cos x f x x f 求=.【解析】)2(17cos )]2[cos()(sin x x f x f -=-=ππx x x 17sin )172cos()1728cos(=-=-+=πππ．二、待定系数法：在已知函数解析式的构造时，可用待定系数法。

【例１】 设)(x f 是一次函数，且34)]([+=x x f f ,求)(x f 【解析】设b ax x f +=)( )0(≠a ,则bab x a b b ax a b x af x f f ++=++=+=2)()()]([∴⎩⎨⎧=+=342b ab a ∴⎩⎨⎧⎩⎨⎧=-===3212b a b a 或 32)(12)(+-=+=∴x x f x x f 或 【例2】已知1392)2(2+-=-x x x f ,求)(x f ．【解析】显然,)(x f 是一个一元二次函数。

高一数学求函数的定义域与值域的常用方法一. 求函数的定义域与值域的常用方法求函数的解析式，求函数的定义域，求函数的值域，求函数的最值二. 求函数的解析式3、求函数解析式的一般方法有：（1）直接法：根据题给条件，合理设置变量，寻找或构造变量之间的等量关系，列出等式，解出y。

（2）待定系数法：若明确了函数的类型，可以设出其一般形式，然后代值求出参数的值；（3）换元法：若给出了复合函数f［g（x）］的表达式，求f（x）的表达式时可以令t＝g（x），以换元法解之；（4）构造方程组法：若给出f（x）和f（－x），或f（x）和f（1/x）的一个方程，则可以x代换－x（或1/x），构造出另一个方程，解此方程组，消去f（－x）（或f（1/x））即可求出f（x）的表达式；（5）根据实际问题求函数解析式：设定或选取自变量与因变量后，寻找或构造它们之间的等量关系，列出等式，解出y的表达式；要注意，此时函数的定义域除了由解析式限定外，还受其实际意义限定。

（二）求函数定义域1、函数定义域是函数自变量的取值的集合，一般要求用集合或区间来表示；2、常见题型是由解析式求定义域，此时要认清自变量，其次要考查自变量所在位置，位置决定了自变量的范围，最后将求定义域问题化归为解不等式组的问题；3、如前所述，实际问题中的函数定义域除了受解析式限制外，还受实际意义限制，如时间变量一般取非负数，等等；4、对复合函数y＝f［g（x）］的定义域的求解，应先由y＝f（u）求出u的范围，即g（x）的范围，再从中解出x的范围I1；再由g（x）求出y＝g（x）的定义域I2，I1和I2的交集即为复合函数的定义域；5、分段函数的定义域是各个区间的并集；6、含有参数的函数的定义域的求解需要对参数进行分类讨论，若参数在不同的范围内定义域不一样，则在叙述结论时分别说明；7、求定义域时有时需要对自变量进行分类讨论，但在叙述结论时需要对分类后求得的各个集合求并集，作为该函数的定义域；一：求函数解析式1、换元法：题目给出了与所求函数有关的复合函数表达式，可将内函数用一个变量代换。

求函数解析式的几种方法及题型【最新版3篇】篇1 目录一、引言二、求函数解析式的常用方法1.待定系数法2.交点式3.顶点式4.换元法5.归纳法三、求函数解析式的题型及应用1.已知三个点求解析式2.已知顶点求解析式3.已知交点求解析式4.抽象复杂函数问题四、结论篇1正文一、引言求函数解析式是高中数学中的常见问题，也是高考的常规题型之一。

解决这类问题需要掌握一定的方法和技巧。

本文将介绍几种常用的求函数解析式的方法及题型，帮助同学们更好地理解和应用这些方法。

二、求函数解析式的常用方法1.待定系数法待定系数法是一种求未知数的方法。

将一个多项式表示成另一种含有待定系数的新的形式，这样就得到一个恒等式。

然后根据恒等式的性质得出系数应满足的方程或方程组，其后通过解方程或方程组便可求出待定的系数，或找出某些系数所满足的关系式。

2.交点式交点式适用于已知抛物线与 x 轴的两个交点的情况。

通过已知的交点，我们可以得到两个方程，解这两个方程可以求得抛物线的解析式。

3.顶点式顶点式适用于已知抛物线的顶点的情况。

通过已知的顶点，我们可以得到一个方程，这个方程包含了抛物线的顶点坐标和抛物线的解析式中的待定系数。

解这个方程可以求得抛物线的解析式。

4.换元法换元法是一种通用的求函数解析式的方法，适用于各种复杂的函数问题。

通过换元，我们可以将复杂的函数问题转化为简单的函数问题，从而求得函数的解析式。

5.归纳法归纳法适用于具有一定规律的函数问题。

通过观察函数的规律，我们可以猜测函数的解析式，然后通过数学归纳法证明我们的猜测是正确的。

三、求函数解析式的题型及应用1.已知三个点求解析式已知函数上的三个点，我们可以通过待定系数法求解函数的解析式。

设定函数的形式为 y=ax^2+bx+c，然后将三个点的坐标代入方程，得到三个方程组成的线性方程组，解这个方程组可以求得函数的解析式。

2.已知顶点求解析式已知抛物线的顶点，我们可以通过顶点式求解抛物线的解析式。

高中数学：求函数解析式的10种常见方法一、配凑法：给定$f(x+1)=x-3x+2$，求$f(x)$。

练1：设函数$f(x)=2x+3$，$g(x+2)=f(x)$，求$g(x)$。

练2：设$f(f(x))=x^2+2$，求$f(x)$。

练3：设$f(x+2)+f(x)=x^3+x$，求$f(x)$。

二、待定系数法：例1：如果反比例函数的图像经过点$(1,-2)$，那么这个反比例函数的解析式为$\frac{-2}{x-1}$，求$f(x)$。

练1：在反比例函数$y=\frac{k}{x}$的图像上有一点P，它的横坐标$m$与纵坐标$n$是方程$t^2-4t-2=0$的两个根，求$k$。

练2：已知二次函数$f(x)$满足$f(x+1)=f(x)+2x+8$，求$f(x)$的解析式。

练3：已知$f(x-2)=2x-9x+13$，求$f(x)$。

三、换元（或代换）法：例1：已知函数$f(\frac{1-x}{1+x})=\frac{1+x}{1-x}$，求：（1）$f(2)$的值；（2）$f(x)$的表达式。

练1：已知$f(x+1)=x+2x$，求$f(x)$及$f(x^2)$；练2：已知$f(x)=\frac{1}{2}x+\frac{1}{x}$，求$f(x+1)$．四、消去法：例1：设函数$f(x)$满足$f(x)+2f(\frac{1}{x})=x$，求$f(x)$．练1：已知$f(x)-2f(-x)=3x+2$，求$f(x)$．练2：已知定义在R上的函数$f(x)$满足$f(-x)+2f(x)=x+1$，求$f(x)$．练3：已知$f(x)+3f(-x)=2x+1$，求$f(x)$.练4：设函数$f(x)$满足$af(x)+bf(\frac{1}{x})=cx$（其中$a,b,c$均不为$0$，且$a\neq\pm b$），求$f(x)$．五、反函数法：例1：已知$f(a^2-x^2)=x$，求$f(x)$。

高中数学-求函数解析式的六种常用方法求函数解析式是高中数学中的重要内容之一，常用的方法有六种。

下面分别介绍这六种方法。

一、换元法如果已知复合函数$f[g(x)]$的解析式，要求原函数$f(x)$的解析式，可以令$g(x)=t$，求$f(t)$的解析式，再把$t$换为$x$即可。

例如，已知$f(x)=\frac{x^2+11x+1}{x(x+1)}$，要求$f(x)$的解析式。

设$g(x)=\frac{1}{x}$，则$x=\frac{1}{g(x)}$，代入$f(x)$得$f(g(x))=\frac{g(x)^2+11g(x)+1}{g(x)+1}$，再令$t=g(x)$，则$f(t)=\frac{t^2+11t+1}{t+1}$，最后把$t$换为$x$，得到$f(x)=\frac{x^2+11x+1}{x(x+1)}$。

二、配凑法如果已知$f(x+1)=x+2x^2$，要求$f(x)$的解析式，可以使用配凑法。

首先，把$x+1$视为自变量$x$，则有$f(x)=x^2-1$，但要注意函数的定义域的变化，即$x+1\geq 1$，即$x\geq 0$。

三、待定系数法如果已知函数类型，可以使用待定系数法求函数的解析式。

例如，已知二次函数$f(x)$满足$f(0)=0$，$f(x+1)=f(x)+2x+8$，要求$f(x)$的解析式。

设$f(x)=ax^2+bx+c$，代入已知条件得到$c=0$，$a+b=8$，$2a+b=0$，解得$a=1$，$b=7$，$c=0$，所以$f(x)=x^2+7x$。

四、消去法如果已知$f(x)+2f(\frac{1}{x})=\frac{x}{x-1}$，要求$f(x)$的解析式，可以使用消去法。

把已知中的$f(\frac{1}{x})$用$f(x)$表示出来，得到$2f(x)+f(\frac{1}{x})=\frac{x}{x-1}$，再把$x$换成$\frac{1}{x}$，得到$2f(\frac{1}{x})+f(x)=\frac{1}{x-1}$，解得$f(x)=-\frac{x}{3(x-1)}$。

高中数学：函数解析式的十一种方法一、定义法六、特殊值法二、待定系数法八、累加法三、换元（或代换）法九、归纳法四、配凑法十、递推法五、函数方程组法十一、微积分法七、利用给定的特性求解析式.一、定义法：2 x【例1】设f (x 1) x 3 2，求f ( x) .2 x x 2 x 2 xf ( x 1) x 3 2 [( 1)1] 3[( 1) 1] 2 = (x 1) 5( 1) 6f (x) 2 xx 56【例2】设x 1f [ f ( x)] ，求f (x) .x 2【解析】设 f [ f ( x)] xx12x 11f(x)1x 1 1 111x1x【例3】设1 2 1 1 13f (x ) x , g(x ) x ，求f [ g( x)] .2 3x x x x1 1 12 f x x2 2【解析】) 2 ( ) 2f (x) x (x2x x x1 1 1 13 3 3又g x x xg( x) x (x ) 3(x ) ( ) 33x x x x3 x x x x2 6 4 2故f [ g( x)] (x 3 ) 2 6 9 2【例4】设f (cos x) cos17 x, 求f (sin x) .【解析】)f (sin x) f [cos( x)] cos17 ( x2 2cos(8 17 x) cos( 17 x) sin17x.2 2二、待定系数法：在已知函数解析式的构造时，可用待定系数法。

【例1】设f (x) 是一次函数，且 f [ f ( x)] 4x3，求 f (x)【解析】设f (x) ax b (a 0)，则f [ f ( x)] af (x) b a( ax b) b a 2 x ab ba ab 2 4b 3ab2 a或1 b23f (x) 2x 1或 f (x) 2x 32 x【例2】已知f (x 2) 2x 9 13，求f (x) .2 bx c a 【解析】显然， f (x) 是一个一元二次函数。

函 数 解 析 式 的 八 种 求 法一．待定系数法：（已知函数类型如：一次、二次函数、反比例函数等）若已知)(x f 的结构时，可设出含参数的表达式，再根据已知条件，列方程或方程组，从而求出待定的参数，求得)(x f 的表达式。

【例1】已知函数f(x)是一次函数，且满足关系式3f(x+1)-2f(x -1)=2x +17，求f(x )的解析式。

分析：所求的函数类型已定，是一次函数。

设f(x)=ax+b(a≠0)则f(x+1)=?，f(x-1)=?解：设f(x)=ax+b(a≠0)，由条件得：3[a(x+1)+b]-2[a(x-1)+b]=ax+5a+b=2x+17，∴f(x)=2x+7 【例2】求一个一次函数f(x)，使得f{f[f(x)]}=8x+7分析：所求的函数类型已定，是一次函数。

设f(x)=ax+b(a≠0)则f{f[f(x)]}=f{f[ax+b]}=f[a(ax+b)+b]=? 解：设f(x)=ax+b （a≠0)，依题意有a[a(ax+b)+b]+b=8x+7 ∴x a 3+b(2a +a+1)=8x+7，∴f(x)=2x+1例 设)(x f 是一次函数，且34)]([+=x x f f ，求)(x f 解：设bax x f +=)( )0(≠a ，则bab x a b b ax a b x af x f f ++=++=+=2)()()]([∴⎩⎨⎧=+=342b ab a ∴⎩⎨⎧⎩⎨⎧=-===3212b a b a 或 32)(12)(+-=+=∴x x f x x f 或 例、已知二次函数)(x f y =满足),2()2(--=-x f x f 且图象在y 轴上的截距为1，被x 轴截得的线段长为22，求函数)(x f y =的解析式。

分析：二次函数的解析式有三种形式： ① 一般式：)0()(2≠++=a c bx ax x f② 顶点式：()为函数的顶点点其中k h a kh x a x f ,,0)()(2≠++=③ 双根式：的两根是方程与其中0)(,0))(()(2121=≠--=x f x x a x x x x a x f解法1：设)0()(2≠++=a cbx ax x f ，则由y 轴上的截距为1知：1)0(=f ，即c=1 ① ∴ 1)(2++=bx ax x f由)2()2(--=-x f x f 知：1)2()2(1)2()2(22+--+--=+-+-x b x a x b x a 整理得：0)4(=-x b a , 即： 04=-b a ②由被x 轴截得的线段长为22知，22||21=-x x ， 即84)()(21221221=-+=-x x x x x x . 得:814)(2=--aab .整理得： 2284a a b =- ③ 由②③得： 2,21==b a , ∴ 1221)(2++=x x x f .解法2：由)2()2(--=-x f x f 知：二次函数对称轴为2-=x ，所以设)0()2()(2≠++=a kx a x f ；以下从略。

求解函数解析式基本方法（附例题）一、求解函数解析式 1、换元法汇总，切记定义域综上所述：新元代换旧元可化作：则取值范围换元，立刻确定新元的则令变形由解：由题意可知：的解析式求已知11,1)(f t 1f(t)①1t 1,cos t 1sin cos ①cos 1)(cos )(f ,sin )(cos f 222222≤≤--=-=≤≤-==+-==x x x x x x x x f x x x 练习一：）的解析式（答案见文末求已知)(,2)1(2x f x x x f -=+2、凑配法汇总，切记定义域求解定义域又运用完全平方公式解：的解析式求已知2,2)(21,02)1()1()(,0,1)1(2222≥-=∴≥+∴>-+=+>+=+x x x f xx x xx x x f x f x x x x x f练习二：解析式求已知)(,45)2(2x f x x x f ++=+换元法和凑配法在实际运用过程中，以计算简单、准确为原则，根据题目恰当选择。

3、待定系数法5)1(5)(505)10()0(0,05)1()(5,15,1)()()(5,1)(2222+--=-==+-=∴+-===+-=x x f a a f x a x f h k hk x a x f x f x f 综上所述，解得：）点，代入计算图像过（图像过原点又故值根据物理意义，直接赋）可得，由顶点为（数顶点式根据题意，选择二次函解：由题意可设：的解析式），且经过原点，求（是二次函数，其顶点为已知练习三：的解析式（求且是二次函数，已知),3)0(,12)()1()(x f f x x f x f x f =+=-+4、构造方程组法：），（联立方程组，求解：）式联立方程组，解得）、（将（合适替换元得：替换用注意定义域，选取），（，且解：的解析式（求满足）上的函数，定义在（∞+∈--==-∴∞+∈=-=-∞+0,323)(21)2(1)(2)1(,10)1()1(2)(),)1(2)()(0x xx x f x x f x f x xx x xf x f x f x xf x f x f 练习四：的解析式求满足）上的函数定义在（)(,1)1(2)()(,0x f x xf x f x f -⋅=+∞求解函数解析式，一般出填空题，或者大题的第一小问。

求函数解析式的几种常用方法一、配凑法：例1：设23)1(2+-=+x x x f ，求)(x f .练1：设函数()23,(2)()f x x g x f x =++=，求()g x 。

练2：设21)]([++=x x x f f ，求)(x f .练3：设33221)1(,1)1(xx x x g x x x x f +=++=+，求)]([x g f .二、待定系数法：例1：如果反比例函数的图象经过点(1,2)-，那么这个反比例函数的解析式为 。

练1：在反比例函数k y x=的图象上有一点P ，它的横坐标m 与纵坐标n 是方程2420t t --=的两个根，求反比例解析式。

练2：已知二次函数()x f 满足()00=f ，()()821++=+x x f x f ，求()x f 的解析式。

练3：已知1392)2(2+-=-x x x f ，求)(x f .三、换元（或代换）法： 例1：已知函数1()1x f x x-=+. 求：（1）(2)f 的值； （2）()f x 的表达式练1：已知1)f x =+()f x 及2()f x ；练2：已知22111(),x x f x x x++=+求()f x ．四、消去法：例1：设函数()f x 满足()x x f x f =⎪⎭⎫ ⎝⎛+12，()0≠x ，求()f x ．练1：已知1()2()32f x f x x-=+，求()f x ．练2：已知定义在R 上的函数()f x 满足()()12+=+-x x f x f ，()0≠x ，求()f x ．练3：已知()3()21f x f x x +-=+，求()f x .练4：设函数()f x 满足1()()af x bf cx x+=（其中,,a b c 均不为0，且a b ≠±），求()f x ．五、反函数法：例1：已知2)(21+=-x af x ，求)(x f .练1：已知函数1ln +=x y ,()0>x ,求它的反函数六：函数性质法例1：已知()f x 是定义在R 上的奇函数，当0x >时，2()31f x x x =+-，求()f x 的解析式．练1：已知()f x 是定义在R 上的奇函数，当0<x 时，()13-=x x f ，求()f x 的解析式．例1：设)(x f 是定义在N 上的函数，满足1)1(=f ，对于任意正整数y x ,，均xy y x f y f x f -+=+)()()(，求)(x f .练1：设定义在R 上的函数)(x f ，且满足()10=f ，并且对于任意实数y x ,均有()()()12+--=-y x y x f y x f ，求)(x f .练2：设定义在R 上的函数)(x f ，对于任意实数y x ,均有()()()()1232++-+=-y x x y f x f y x f ，求)(x f .练3：已知偶函数()f x 的定义域是R ，当0x ≤时2()31f x x x =--，求()f x 的解析式.例1：已知a f N x x f x f =*∈+=+)1()(),(212)1(且，求)(x f .综合运用 例1：（1）已知3311()f x x x x+=+，求()f x ； （2）已知2(1)lg f x x+=，求()f x ； （3）已知()f x 是一次函数，且满足3(1)2(1)217f x f x x +--=+，求()f x ；（4）已知()f x 满足12()()3f x f x x+=，求()f x 。

高中数学函数解析式解法教案教学目标：1. 学生能够理解函数的概念和解析式的定义；2. 学生能够根据题意，找出函数的解析式，并进行简化；3. 学生能够运用解析式解法，解决实际问题。

教学重点：1. 函数的概念和解析式的定义；2. 解析式的求法和简化；3. 解析式解法在实际问题中的应用。

教学准备：1. 教师准备黑板、彩色粉笔、教学PPT等教学工具；2. 学生准备笔记本、铅笔等学习工具。

教学过程：一、导入（5分钟）教师向学生提问：什么是函数？函数的解析式是什么？引导学生了解函数的概念和解析式的定义。

二、讲解与示范（15分钟）1. 解析式求法：通过例题，讲解如何根据函数的题意，找出解析式的求法。

2. 解析式简化：通过例题，讲解如何对解析式进行简化。

三、练习与讨论（20分钟）1. 学生进行练习：学生完成相关练习题，学生可以相互讨论求解过程。

2. 教师辅导：教师对学生的求解过程进行点评和指导。

四、应用与拓展（15分钟）1. 实际问题解析：教师给出相关实际问题，学生根据解析式解法进行求解。

2. 拓展练习：学生对所学知识进行拓展，进行更加复杂的问题求解。

五、总结与反思（5分钟）教师总结本节课的重点内容，学生进行知识点的吸收和反思。

教学延伸：1. 学生可通过课后练习，加深对函数解析式的理解和应用；2. 学生可以自主探索更多实际问题的解析式解法。

教学反思：本节课通过讲解和示范，引导学生掌握了函数解析式的求法和简化方法，在实际问题中进行运用。

希望通过这节课的学习，学生能够更深入地理解解析式解法的重要性和实用性。