高考培优课程秋季数学讲义：三角函数-图像与性质【讲师版】

【讲义课题】： 三角函数图像和性质 【考点及考试要求】1．正弦函数、余弦函数、正切函数的图像 2．三角函数的单调区间：x y sin =的递增区间是⎥⎦⎤⎢⎣⎡+-2222ππππk k ，)(Z k ∈， 递减区间是⎥⎦⎤⎢⎣⎡++23222ππππk k ，)(Z k ∈； x y cos =的递增区间是[]πππk k 22，-)(Z k ∈， 递减区间是[]πππ+k k 22，)(Z k ∈， x y tan =的递增区间是⎪⎭⎫ ⎝⎛+-22ππππk k ，)(Z k ∈，3．函数B x A y ++=)sin(ϕω），（其中00>>ωA最大值是B A +，最小值是A B -，周期是ωπ2=T ，频率是πω2=f ，相位是ϕω+x ，初相是ϕ；其图象的对称轴是直线)(2Z k k x ∈+=+ππϕω，凡是该图象与直线B y =的交点都是该图象的对称中心。

4．由y ＝sin x 的图象变换出y ＝sin(ωx ＋ϕ)的图象一般有两个途径，只有区别开这两个途径，才能灵活进行图象变换。

利用图象的变换作图象时，提倡先平移后伸缩，但先伸缩后平移也经常出现无论哪种变形，请切记每一个变换总是对字母x 而言，即图象变换要看“变量”起多大变化，而不是“角变化”多少。

途径一：先平移变换再周期变换(伸缩变换)先将y ＝sin x 的图象向左(ϕ＞0)或向右(ϕ＜0＝平移｜ϕ｜个单位，再将图象上各点的横坐标变为原来的ω1倍(ω＞0)，便得y ＝sin(ωx ＋ϕ)的图象。

途径二：先周期变换(伸缩变换)再平移变换。

先将y ＝sin x 的图象上各点的横坐标变为原来的ω1倍(ω＞0)，再沿x 轴向左(ϕ＞0)或向右(ϕ＜0＝平移ωϕ||个单位，便得y ＝sin(ωx ＋ϕ)的图象。

5．由y ＝A sin(ωx ＋ϕ)的图象求其函数式：给出图象确定解析式y =A sin （ωx +ϕ）的题型，有时从寻找“五点”中的第一零点（－ωϕ，0）作为突破口，要从图象的升降情况找准．．第一个零点的位置。

三角函数图像和性质专题讲义1．正弦函数、余弦函数、正切函数的图象与性质π2．用“五点法”作图，就是令ωx＋φ取下列5个特殊值：0, π2, π,3π2, 2π，通过列表，计算五点的坐标，描点得到图象.3．三角函数图象变换4[常用结论]（1）对称与周期的关系正弦曲线、余弦曲线相邻的两个对称中心、相邻的两条对称轴之间的距离是半个周期，相邻的对称中心与对称轴之间的距离是四分之一个周期；正切曲线相邻两个对称中心之间的距离是半个周期． （2）与三角函数的奇偶性相关的结论若y ＝A sin(ωx ＋φ)为偶函数，则有φ＝k π＋π2(k ∈Z )；若为奇函数，则有φ＝k π(k ∈Z )．若y ＝A cos(ωx ＋φ)为偶函数，则有φ＝k π(k ∈Z )；若为奇函数，则有φ＝k π＋π2(k ∈Z )．若y ＝A tan(ωx ＋φ)为奇函数，则有φ＝k π(k ∈Z )． 题型一 三角函数的5大性质例1 已知函数f (x )＝2cos x ·sin ⎪⎭⎫⎝⎛+3πx －3sin 2x ＋sin x cos x ＋1. (1)求函数f (x )的最小正周期；(2)当x ∈⎪⎭⎫⎝⎛20π，时，求函数f (x )的最大值及最小值；(3)写出函数f (x )的单调递增区间． (4)写出函数f (x )的对称轴和对称中心.(5)函数f (x )向右平移t 个单位为偶函数，求t 的最小正值。

[玩转跟踪]1．函数2()cos 3f x x π⎛⎫=+⎪⎝⎭的最小正周期为（ ）A ．4π B ．2πC ．2π D ．π2．已知函数()()()2sin 20f x x ϕϕπ=+<<，若将函数()f x 的图象向右平移6π个单位长度后，所得图象关于y 轴对称，则下列结论中正确的是( ) A ．56πϕ= B ．,012π⎛⎫⎪⎝⎭是()f x 图象的一个对称中心 C ．()2fϕ=-D ．6x π=-是()f x 图象的一条对称轴3.已知函数21()2cos 22f x x x =-+. (1)求2()3f π的值及f (x )的对称轴； (2)将()f x 的图象向左平移6π个单位得到函数()g x 的图象，求()g x 的单调递增区间. 题型二 三角函数模型中“ω”范围的求法探究 例2 已知函数 f (x )＝sin ⎪⎭⎫⎝⎛+6πωx (ω>0)在区间]32,4[ππ-上单调递增，则ω的取值范围为( ) A.]830(， B.]210(， C.]8321[， D.]2,83[ 例3 已知函数f (x )＝cos ⎪⎭⎫⎝⎛+3πωx (ω>0)的一条对称轴x ＝π3，一个对称中心为点⎪⎭⎫⎝⎛0,12π，则ω有( ) A ．最小值2 B ．最大值2 C ．最小值1D ．最大值1例4 已知函数f (x )＝2sin ωx 在区间]4,3[ππ-上的最小值为－2，则ω的取值范围是________．[玩转跟踪]1．若函数f (x )＝23sin ωx cos ωx ＋2sin 2ωx ＋cos 2ωx 在区间]23,32[ππ-上单调递增，则正数ω的最大值为( )A.18 B ．16 C.14 D.13 2.已知函数f (x )＝A sin(ωx ＋φ)(A >0，ω>0)，若f (x )在区间]2,0[π上是单调函数，且f (－π)＝f (0)＝－f )2(π，则ω的值为( )A.23 B ．23或2 C.13 D ．1或13 3.设函数f (x )＝cos ⎪⎭⎫⎝⎛-6πωx (ω>0)．若f (x )≤f )4(π对任意的实数x 都成立，则 ω的最小值为________． 题型三 三角函数的图像和图像变换 例5设函数，其中．已知．（Ⅰ）求；（Ⅱ）将函数的图象上各点的横坐标伸长为原来的2倍（纵坐标不变），再将得到的图象向左平移个单位，得到函数的图象，求在上的最小值． [玩转跟踪]1．将函数y ＝3sin ⎪⎭⎫⎝⎛+32πx 的图象向右平移π2个单位长度，所得图象对应的函数( ) A ．在区间]127,12[ππ上单调递减 B ．在区间]127,12[ππ上单调递增C ．在区间]3,6[ππ-上单调递减 D ．在区间]3,6[ππ-上单调递增 2.已知曲线C 1：y =cos x ，C 2：y =sin (2x +2π3)，则下面结论正确的是 A ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2B ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 2 C ．把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2D ．把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 2()sin()sin()62f x x x ππωω=-+-03ω<<()06f π=ω()y f x =4π()y g x =()g x 3[,]44ππ-3将函数()3cos 213f x x π⎛⎫=+- ⎪⎝⎭的图象向左平移3π个单位长度，再向上平移1个单位长度，得到函数()g x 的图象，则下列关于函数()g x 的说法正确的是（ ） A ．最大值为3，图象关于直线12x π=对称 B ．图象关于y 轴对称C ．最小正周期为πD ．图象关于点,04π⎛⎫⎪⎝⎭对称 题型四 由图象求y ＝A sin(ωx ＋φ)的解析式例6 (1)若函数y ＝A sin(ωx ＋φ)的部分图象如图所示，则y ＝ .(2)已知函数f (x )＝sin(ωx ＋φ) )2,0(πϕω<>的部分图象如图所示，则y ＝f ⎪⎭⎫ ⎝⎛+6πx 取得最小值时x 的集合为 ．[玩转跟踪]1．函数f (x )＝2sin(ωx ＋φ))2,0(πϕω<>的部分图象如图所示，则ω，φ的值分别是( ) A ．2，－π3 B ．2，－π6 C ．4，－π6D ．4，π32已知函数f (x )＝A sin(ωx ＋φ)＋B )2,0,0(πϕω<>>A 的部分图象如图所示，将函数f (x )的图象向左平移m (m >0)个单位长度后，得到函数g (x )的图象关于点)23,3(π对称，则m 的值可能为( )A.π6B.π2C.7π6D.7π12题型五 三角函数大题 例7 已知函数f (x )＝23sin ⎪⎭⎫ ⎝⎛+42πx ·co ⎪⎭⎫⎝⎛+42πx －sin(x ＋π)． (1)求f (x )的最小正周期；(2)若将f (x )的图象向右平移π6个单位长度，得到函数g (x )的图象，求函数g (x )在区间[0，π]上的最大值和最小值． [玩转跟踪]1．已知函数4()cos f x x =-42sin cos sin x x x - （1）求()f x 的单调递增区间； （2）求()f x 在0,2π⎡⎤⎢⎥⎣⎦上的最小值及取最小值时的x 的集合. 2．设函数f (x )＝32－3sin 2ωx －sin ωx cos ωx (ω＞0)，且y ＝f (x )图象的一个对称中心到最近的对称轴的距离为π4. (1)求ω的值；(2)求f (x )在区间[π，3π2]上的最大值和最小值．[玩转练习]1．函数y ＝2cos ⎪⎭⎫⎝⎛+62πx 的部分图象大致是( )2．已知函数f (x )＝4sin(ωx ＋φ)(ω＞0)．在同一周期内，当x ＝π6时取最大值，当x ＝－π3时取最小值，则φ的值可能为( )A.π12B.π3C.13π6D.7π6 3．将曲线y ＝sin(2x ＋φ))2(πϕ<向右平移π6个单位长度后得到曲线y ＝f (x )，若函数f (x )的图象关于y 轴对称，则φ＝( )A.π3 B ．π6 C ．－π3 D ．－π6 4．已知曲线C 1：y ＝cos x ，C 2：y ＝sin ⎪⎭⎫⎝⎛-322πx ，则下列结论正确的是( ) A ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移7π12个单位长度，得到曲线C 2B ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2C ．把C 1上各点的横坐标缩短到原来的12，纵坐标不变，再把得到的曲线向右平移7π12个单位长度，得到曲线C 2D ．把C 1上各点的横坐标缩短到原来的12，纵坐标不变，再把得到的曲线向左平移π6个单位长度，得到曲线C 25.(多选)已知函数f (x )＝A sin ωx (A >0，ω>0)与g (x )＝A2cos ωx 的部分图象如图所示，则( )A ．A ＝1B ．A ＝2C ．ω＝π3D ．ω＝3π6．(多选)函数f (x )＝2sin ⎪⎭⎫⎝⎛-32πx 的图象为C ，如下结论正确的是( ) A ．f (x )的最小正周期为π B ．对任意的x ∈R ，都有f ⎪⎭⎫⎝⎛+6πx ＋f ⎪⎭⎫⎝⎛+-6πx ＝0 C ．f (x )在)125,12(ππ-上是减函数D ．由y ＝2sin 2x 的图象向右平移π3个单位长度可以得到图象C7．将函数y ＝sin x 的图象上所有的点向右平移π10个单位长度，再把所得各点的横坐标伸长到原来的2倍(纵坐标不变)，所得图象的函数解析式是____________．8．函数f (x )＝tan ωx (ω>0)的图象的相邻两支截直线y ＝2所得线段长为π2，则f )6(π的值是________．9．将函数y ＝cos x 的图象向左平移φ(0≤φ<2π)个单位长度后，得到函数y ＝sin ⎪⎭⎫⎝⎛-6πx 的图象，则φ＝____. 10．(一题两空)已知函数f (x )＝2sin(ωx ＋φ))2,0(πϕω<>一部分图象如图所示，则ω＝________，函数f (x )的单调递增区间为________．11．已知函数f (x )＝A sin(ωx ＋φ))2,0,0(πϕω<>>A 的图象过点P )0,12(π，图象上与点P 最近的一个最高点是Q )5,3(π.(1)求函数f (x )的解析式； (2)求函数f (x )的单调递增区间． 12．设函数f (x )＝sin ⎪⎭⎫⎝⎛-6πωx ＋sin ⎪⎭⎫ ⎝⎛-2πωx ，其中0<ω<3，且f )6(π＝0. (1)求ω；(2)将函数y ＝f (x )的图象上各点的横坐标伸长为原来的2倍(纵坐标不变)，再将得到的图象向左平移π4个单位，得到函数y ＝g (x )的图象，求g (x )在]43,4[ππ-上的最小值．。

三角函数的图象与性质教学目标：1、掌握正、余弦函数的定义域和值域；2、进一步理解三角函数的周期性和奇偶性的概念，会求它们的周期，会判断它们的奇偶性；3、能正确求出正、余弦函数的单调区间教学重点：正、余弦函数的性质教学难点：正、余弦函数的单调性知识要点：1、定义域：函数sin y x =及cos y x =的定义域都是(),-∞+∞，即实数集R2、值域：函数sin y x =，x R ∈及cos y x =，x R ∈的值域都是[]1,1-理解：（1）在单位圆中，正弦线、余弦线的长都是等于或小于半径的长1的，所以sin 1x ≤，cos 1x ≤，即1sin 1x -≤≤，1cos 1-≤≤。

（2）函数sin y x =在2,()2x k k Z ππ=+∈时，y 取最大值1，当22x k ππ=-，()k Z ∈时，y 取最小值-1；函数cos y x =在2x k π=，()k Z ∈时，y 取最大值1，当2x k ππ=+，()k Z ∈时，y 取最小值-1。

正弦函数s i n y x =，x R ∈和余弦函数cos y x =，x R ∈是周期函数，2k π(0)k Z k ∈≠且都是它们的周期，最小正周期是2π。

4、奇偶性正弦函数sin y x =，x R ∈是奇函数，余弦函数cos y x =，x R ∈是偶函数。

理解：（1）由诱导公式()sin sin x x -=-，cos()cos x x -=可知以上结论成立；（2）反映在图象上，正弦曲线关于原点O 对称，余弦曲线关于y 轴对称。

5、单调性（1）由正弦曲线可以看出：当x 由2π-增大到2π时，曲线逐渐上升，sin x 由-1增大到1；当x 由2π增大到32π时，曲线逐渐下降，sin x 由1减至-1，由正弦函数的周期性知道：①正弦函数sin y x =在每一个闭区间2,222k k ππππ⎡⎤-++⎢⎥⎣⎦()k Z ∈上，都从-1增大到1，是增函数； ②在每一个闭区间32,222k k ππππ⎡⎤++⎢⎥⎣⎦()k Z ∈上，都从1减小到-1，是减函数。

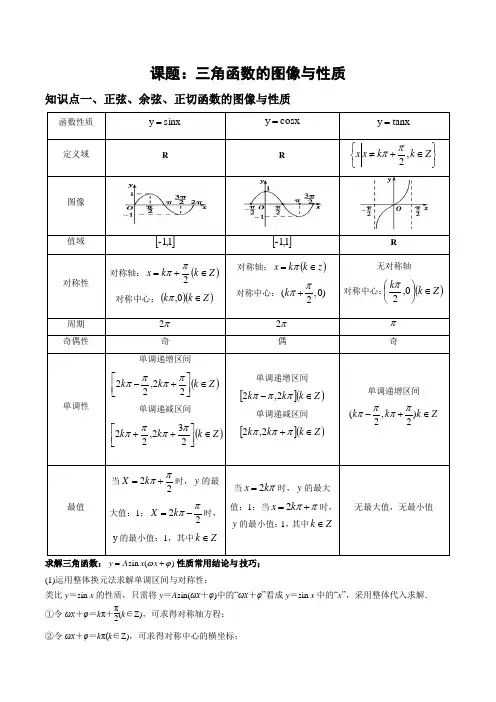
课题：三角函数的图像与性质知识点一、正弦、余弦、正切函数的图像与性质函数性质sinx y =cosx y =tanx y =定义域RR⎭⎬⎫⎩⎨⎧∈+≠Z k k x x ,2ππ图像值域[]1,1-[]1,1-R 对称性对称轴：()Z k k x ∈+=2ππ对称中心：()()Z k k ∈0,π对称轴：()z k k x ∈=π 对称中心：(,0)2k ππ+无对称轴对称中心：()Z k k ∈⎪⎭⎫⎝⎛0,2π 周期 π2π2π奇偶性奇 偶奇单调性单调递增区间()Z k k k ∈⎥⎦⎤⎢⎣⎡+-22,22ππππ 单调递减区间()Z k k k ∈⎥⎦⎤⎢⎣⎡++232,22ππππ单调递增区间[]()Z k k k ∈-πππ2,2单调递减区间[]()Z k k k ∈+πππ2,2单调递增区间Z k k k ∈+-)2,2(ππππ最值当22ππ+=k X 时，y 的最大值：1；22ππ-=k X 时，y 的最小值：1，其中Z k ∈当πk x 2=时，y 的最大值：1；当ππ+=k x 2时，y 的最小值：1，其中Z k ∈无最大值，无最小值求解三角函数：sin ()y A x x ωϕ=+性质常用结论与技巧； (1)运用整体换元法求解单调区间与对称性：类比y ＝sin x 的性质，只需将y ＝A sin(ωx ＋φ)中的“ωx ＋φ”看成y ＝sin x 中的“x ”，采用整体代入求解．①令ωx ＋φ＝k π＋π2(k ∈Z)，可求得对称轴方程；②令ωx ＋φ＝k π(k ∈Z)，可求得对称中心的横坐标；(2)周期性：函数y ＝A sin(ωx ＋φ)(或y ＝A cos(ωx ＋φ))的最小正周期T ＝2π|ω|，注意y ＝Atan (ωx ＋φ)的周期T ＝π|ω|.(3)最值(或值域)：求最值(或值域)时，一般要确定u ＝ωx ＋φ的范围，然后结合函数y ＝sin u 或y ＝cos u 的性质可得函数的最值(值域)．【典型例题】【例1】函数cos()3y x π=-的单调增区间是（ ）A ．42,2()33k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦ B ．22,2()33k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦C ．32,2()88k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦ D ．52,2()66k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦【例2】函数[]1sin ,2,223y x x πππ⎛⎫=+∈-⎪⎝⎭的单调递增区间是（ ）A ．52,3ππ⎡⎤--⎢⎥⎣⎦ B ．52,,233ππππ⎡⎤⎡⎤--⎢⎥⎢⎥⎣⎦⎣⎦和 C ．5,33ππ⎡⎤-⎢⎥⎣⎦ D ．,23ππ⎡⎤⎢⎥⎣⎦ 【例3】函数)62cos()(π+=x x f 的一条对称轴为（ ）A ．6πB ．125πC ．32πD ．32π-【例4】函数2()cos cos f x x x x =+（[0,]x π∈）的单调递减区间为（ ）A ．[0,]3πB ．2[,]63ππC ．5[,]36ππD ．5[,]6ππ 【例5】函数()sin 24f x x π⎛⎫=- ⎪⎝⎭在区间0,2π⎡⎤⎢⎥⎣⎦上的最小值是（ ）A. 1-B.C.D. 0 【例6】已知函数2()sin 2+sin 22cos 1.33=+-+-∈f x x x x x R ππ（）（），（Ⅰ）求函数)(x f 的最小正周期； （Ⅱ）求函数)(x f 在区间[,]44ππ-上的最大值和最小值.【举一反三】1．余弦函数cos()4y x π=+在下列哪个区间为减函数（ ）A ．3,44ππ⎡⎤-⎢⎥⎣⎦B ．[],0π-C ．3,44ππ⎡⎤-⎢⎥⎣⎦ D ．,22ππ⎡⎤-⎢⎥⎣⎦2．函数的最小正周期为（ ）A. B. C. D.3．下列函数中，周期为π，且在⎥⎦⎤⎢⎣⎡2,4ππ上为减函数的是（ ）A.)2sin(π+=x y B.)2cos(π+=x y C.)22cos(π+=x y D.)22sin(π+=x y4．已知函数2()3cos sin f x x x x =-，则()f x 的最小正周期为 ；单调减区间为 ．5．若函数()()13cos ,36f x x x x ππ=+-≤≤，则()f x 的最大值为（ ）A.1B.2 3 31 6．已知函数()sin sin()6f x x x π=+.（1）求()f x 的最小正周期；（2）当[0,]2x π∈时，求()f x 的取值范围.【课堂巩固】1．已知函数))(32cos(3)(R x x x f ∈-=π，下列结论错误的是（ ）A ．函数)(x f 的最小正周期为πB ．函数)(x f 图象关于点)0,125(π对称 C. 函数)(x f 在区间]2,0[π上是减函数 D ．函数)(x f 的图象关于直线6π=x 对称2．设函数()sin()3)f x x x ωϕωϕ=++（0ω>，||2πϕ<）的最小正周期为π，且()()f x f x -=，则（ ）A ．()f x 在(0,)2π单调递减 B ．()f x 在3(,)44ππ单调递减 C ．()f x 在(0,)2π单调递增 D ．()f x 在3(,)44ππ单调递增 3．函数3sin 6y x π⎛⎫=+⎪⎝⎭的单调递增区间为_________.4．函数x x y 2cos 32sin -=的图象的一条对称轴方程为（ ） A ．12π=x B ．12π-=x C. 6π=x D ．6π-=x5．函数的最小正周期是__________ .6．函数2sin 2y x ππ⎛⎫=+⎪⎝⎭的最小正周期是 ． 7．已知函数3()2sin cos()32f x x x π=++. （Ⅰ）求函数()f x 的单调递减区间；（Ⅱ）求函数()f x 在区间[0,]2π上的最大值及最小值.【课后练习】正确率：________1．当函数（）取得最大值时，（ ）A. B. C. D.2．设函数()()()sin 30,2f x x x πωϕωϕωϕ⎛⎫=++>< ⎪⎝⎭的最小正周期为π，且()()f x f x -=，则（ ） A ．()f x 在0,2π⎛⎫ ⎪⎝⎭单调递减 B ．()f x 在3,44ππ⎛⎫⎪⎝⎭单调递减 C ．()f x 在0,2π⎛⎫ ⎪⎝⎭单调递增 D ．()f x 在3,44ππ⎛⎫⎪⎝⎭单调递增 3．已知函数()()()2sin 20f x x θθπ=-+<<，14f π⎛⎫=-⎪⎝⎭则()f x 的一个单调递减区间是（ ） A ．5,1212ππ⎛⎫-⎪⎝⎭ B ．7,1212ππ⎛⎫ ⎪⎝⎭ C ．,63ππ⎛⎫- ⎪⎝⎭ D ．5,1212ππ⎛⎫- ⎪⎝⎭4．函数()sin cos()6f x x x π=--的值域为（ ）A ．33⎡⎢⎣⎦B ．3,3⎡-⎣C ．[]2,2-D ．[]1,1-5．函数)2sin()(ϕ-=x A x f 的图象关于点)0,34(π成中心对称，则ϕ最小的ϕ的值为（ ） A ．3π B ．6πC ．3π-D ．6π- 6．已知角ϕ的终边经过点(3,4)P -，函数()sin()(0)f x x ωϕω=+>图像的相邻两条对称轴之间的距离等于2π，则()4f π=（ ） A ．35- B ．35C ．45-D ．457．设函数()sin(2)cos(2)44f x x x ππ=+++，则（ ）A 、()y f x =在(0,)2π单调递增，其图象关于直线4x π=对称B 、()y f x =在(0,)2π单调递增，其图象关于直线2x π=对称C 、()y f x =在(0,)2π单调递减，其图象关于直线4x π=对称D 、()y f x =在(0,)2π单调递减，其图象关于直线2x π=对称8．函数sin 22y x x =的图象的一条对称轴方程为（ ） A. π12x =B.π12x =-C.π6x =D.π6x =-9．已知函数2()cos cos f x x x x =+，x R ∈．（1）求4()3f π；（2）求函数()f x 的最小正周期与单调减区间．。

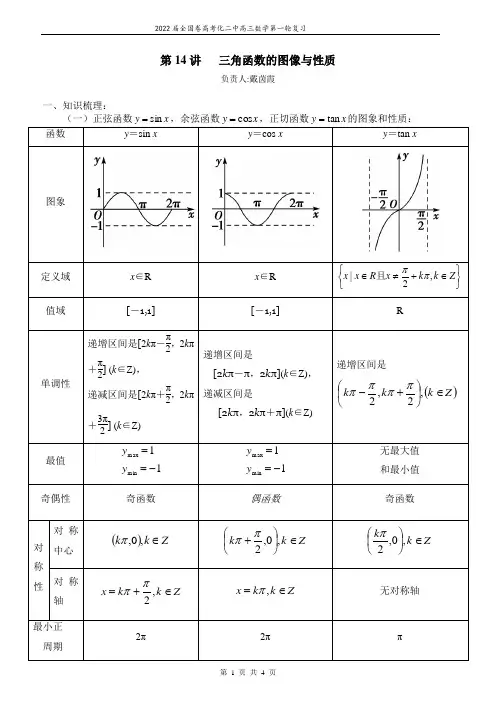
第14讲 三角函数的图像与性质负责人:戴茵霞一、知识梳理：（一）正弦函数x y sin =，余弦函数x y cos =，正切函数x y tan =的图象和性质： 函数 y ＝sin x y ＝cos x y ＝tan x图象定义域 x ∈R x ∈R ⎭⎬⎫⎩⎨⎧∈+≠∈Z k k x R x x ,2|ππ且 值域[－1,1][－1,1]R单调性递增区间是[2k π－π2，2k π＋π2] (k ∈Z)， 递减区间是[2k π＋π2，2k π＋3π2] (k ∈Z)递增区间是[2k π－π，2k π](k ∈Z)，递减区间是[2k π，2k π＋π](k ∈Z)递增区间是()Z k k k ∈⎪⎭⎫ ⎝⎛+-,2,2ππππ最值11min max -==y y11min max -==y y无最大值 和最小值 奇偶性 奇函数偶函数奇函数对称性对称中心 ()Z k k ∈,0,πZ k k ∈⎪⎭⎫⎝⎛+,0,2ππ Z k k ∈⎪⎭⎫⎝⎛,0,2π 对称轴 Z k k x ∈+=,2ππZ k k x ∈=,π无对称轴最小正 周期2π 2π π（二）)sin(ϕω+=x A y 图象的性质： 1、简谱运动的有关概念对于简谱运动)sin(ϕω+=x A y )),0[,0,0(+∞∈>>x A ω，振幅是A ，最小正周期是||2ωπ=T ,频率是T1，相位是ϕω+x ，初相是ϕ； 2、三角函数图象的变换⑴平移变换：()ϕ+=→=x y x y sin sin ⑵伸缩变换：x y x y ωsin sin =→= ⑶上下平移：()()b x f y x f y +=→= ⑷综合应用)sin()sin(sin )2()sin()sin()1(sin ϕωϕωωϕωϕ+=→+=→=+=→+=→=x A y x y xy x y x y x y3、)sin(ϕω+=x A y 图象的性质：讨论)sin(ϕω+=x A y 图象的性质，通常用换元法，设ϕω+=x t ，再结合x y sin =的性质求之. 4、由y ＝A sin(ωx ＋ϕ)的图象求其函数解析式：与“五点”作图法对应； 5、对于函数b x A y ++=)sin(ϕω)0,0(>>ωA ，有)(21min max y y A -=，)(21min max y y b +=. 二、例题分析：题型一：三角函数的定义域1.若10,lg(sin )2x y x π<<=-+则函数 ） A.[ππ32,3) B.)65,6(ππ C.)65,3[ππ D.),65(ππ题型二：三角函数的值域 2.求下列函数的值域：① 【2017课标II ，理14】函数()23sin 4f x x x =-（0,2x π⎡⎤∈⎢⎥⎣⎦）的最大值是 。

三角函数的图像和性质1、知识点分布：1.三角函数的图像与性质2.三角函数的图像变换3.反三角函数4.三角函数的值域求法2、考纲考点分析：1.复习四个三角函数的性质及图像；2.拓展三角函数的应用；3.复习四个反三角函数的性质及图像4.复习三角方程的通解；3、细节易错关注：1. 三角函数的化简、单调性与最值2. 三角函数的应用3. 反三角函数的主值区间例1：三角函数的性质与图像1、若函数()2cos 417f x x π⎛⎫=+- ⎪⎝⎭与函数()()5tan 12g x ax =-+的最小正周期相同，则实数a =__________；【答案】2±2、求下列函数的值域： （1）sin 22sin x y x +=-，0,2x π⎡⎤∈⎢⎥⎣⎦；（2）sin 22cos x y x +=-；【答案】（1）[]1,3；（2）⎣⎦3、已知函数()2sin f x x ω=在区间,34ππ⎡⎤-⎢⎥⎣⎦上的最小值是2-，则实数ω的取值范围为（ ） A ．(]3,2,2⎡⎫-∞-+∞⎪⎢⎣⎭ B ．(],2-∞- C ．9,2⎛⎤-∞- ⎥⎝⎦ D ．[)9,6,2⎛⎤-∞-+∞ ⎥⎝⎦【答案】A4、已知函数()sin 03y x πωω⎛⎫=+> ⎪⎝⎭的最小正周期为π，若将该函数的图像向左平移()0m m >个单位后，所得图像关于原点对称，则m 的最小值为__________；【答案】3π5、函数()()sin 0,0,2f x A x A πωϕωϕ⎛⎫=+>><⎪⎝⎭的部分图像如右图所示，则()f x =__________；【答案】2sin 4x π6、设函数()23sin 2cos 2f x x x ωω=+，其中02ω<<； （1）若()f x 的最小正周期为π，求()f x 的单调增区间；（2）若函数()f x 的图像的一条对称轴为3x π=，求ω的值；【答案】（1）22cos 12sin 23)(x x x f ωω++=.2162sin +⎪⎭⎫ ⎝⎛+=πωx.1,22,0,=∴=∴>=ωπωπωπT 令,,226222Z k k x k ∈+≤+≤+-πππππ得，,,63z k k x k ∈+≤≤+-ππππ所以，)(x f 的单调增区间为：.,6,3Z k k k ∈⎥⎦⎤⎢⎣⎡++-ππππ（2） 2162sin )(+⎪⎭⎫ ⎝⎛+=πωx x f 的一条对称轴方程为.3π.,2632z k k ∈+=+⋅∴ππππω.2123+=∴k ω又20<<ω，∴.131<<-k .21,0=∴=∴ωk7、设函数()22cos 2sin 24f x x x π⎛⎫=++ ⎪⎝⎭； （1）求函数()f x 的最小正周期； （2）设函数()g x 对任意x R ∈，有()2g x g x π⎛⎫+= ⎪⎝⎭，且当0,2x π⎡⎤∈⎢⎥⎣⎦时，()()12g x f x =-，求函数()g x 在[],0π-上的解析式；【答案】22111()cos(2)sin cos 2sin 2(1cos 2)24222f x x x x x x π=++=-+-11sin 222x =-，（1）函数()f x 的最小正周期22T ππ== （2）当[0,]2x π∈时，11()()sin 222g x f x x =-=当[,0]2x π∈-时，()[0,]22x ππ+∈ 11()()sin 2()sin 22222g x g x x x ππ=+=+=-当[,)2x ππ∈--时，()[0,)2x ππ+∈ 11()()sin 2()sin 222g x g x x x ππ=+=+=得函数()g x 在[,0]π-上的解析式为1sin 2(0)22()1sin 2()22x x g x x x πππ⎧--≤≤⎪⎪=⎨⎪-≤<⎪⎩。

高考数学专题讲座 第6讲三角函数的图象与性质一、考纲要求1．理解任意角的概念、弧度的意义，能正确地进行弧度与角度的换算．2．掌握任意角的正弦、余弦、正切的定义，了解余切、正割、余割的定义，掌握同角三角函数的基本关系式，掌握正弦、余弦的诱导公式，理解周期函数与最小正周期的意义．3．了解正弦函数、余弦函数、正切函数的图象和性质，会用“五点法”画正弦函数、余弦函数和函数)sin(ϕω+=x A y )的简图，理解A 、ω、ϕ的物理意义． 二、基础过关1．函数||sin x x y +=，],[ππ-∈x 的大致图象是（ ）．A B C D2．（2002北京）已知)(x f 是定义在)3,3(-上的奇函数，当30<<x 时，)(x f 的图象如图所示，那么不等式0cos )(<x x f 的解集是（ ）．A ． )3,2()1,0(2,3(ππ --B ． )3,2()1,0()1,2(ππ --C ． )3,1()1,0()1,3( --D ．)3,1()1,0(2,3( π--3．定义在R 上的函数)(x f 既是偶函数又是周期函数，若)(x f 的最小正周期是π，且当]2,0[π∈x 时，x x f sin )(=，则)35(πf 的值为（ ）． A ．21-B ．21 C ．23-D ．23 4．给定性质: ①最小正周期为π；②图象关于直线x=3π对称，则下列四个函数中，同时具有性质①、②的是（ ）． A ．y = sin(2x +6π) B ．y = sin(2x+6π) C ．y = sin|x| D ．y = sin(2x －6π) 5．下列四个结论中正确的个数有 ( )．①y = sin|x|的图象关于原点对称；②y = sin(|x|+2)的图象是把y = sin|x|的图象向左平移2个单位而得；③y = sin(x+2)的图象是把y = sinx 的图象向左平移2个单位而得；④y = sin(|x|+2)的图象是由y = sin(x+2)( x ≥0)的图象及y = －sin(x-2) ( x<0)的图象组成的． A ．1个 B ．2个 C ．3个 D ．4个6．把函数y = cos(x+3π)的图象向左平移m 个单位(m>0), 所得图象关于y 轴对称, 则m 的最小值是 ． 7．函数y = 2sin(4π+2x )cos(4π+2x )+asinx (x ∈R)的图象关于x=8π对称, 则g(x)= asin(a+1)x 的最小正周期是 ． 三、典型例题例1 已知函数f(x)=tan(3πsinx)． （1）求f(x)的定义域和值域；（2）在（－π，π）中，求f(x)的单调区间； （3）判定方程f(x)=tan 32π在区间（－π，π）上解的个数．例2 已知函数()b a x x a x a x f++--=2cos sin 322cos 的定义域为⎥⎦⎤⎢⎣⎡20π，，值域为 [ －5，1]，求常数a 、b 的值．例3 已知函数3cos 33cos3sin )(2x x x x f +=． （1）将)(x f 写成)sin(φω+x A 的形式，并求其图象对称中心的横坐标；（2）函数的图象可由)(sin R x x y ∈=的图象经过怎样的变换得到？（3）如果△ABC 的三边a 、b 、c 满足b 2=ac ，且边b 所对的角为x ，试求x 的范围及此时函数f(x)的值域．例4 设二次函数),()(2R c b c bx x x f ∈++=，已知不论βα,为何实数恒有)(sin αf ≥0，)cos 2(β+f ≤0．（1）求证：1-=+c b ； （2）求证：c ≥3；（3）若函数)(sin αf 的最大值为8，求b ，c 的值．四、 热身演练1．在)2,0(π内，使x x cos sin >成立的x 取值范围为（ ）．A ．)45,()2,4(ππππ B ．),4(ππ C ．)45,4(ππ D ．)23,45(),4(ππππ2．已知sin α>sin β，那么下列命题成立的是（ ）．A ．若α、β是第一象限角，则cos α>cos βB ．若α、β是第二象限，则tan α>tan βC ．若α、β是第三象限角，则cos α>cos βD ．若α、β是第四象限角，则tan α>tan β 3．下列命题中正确的是（ ）．A ．x y tan =是增函数B ．x y sin =在第一象限是增函数C ．x y arccos 2-=π是奇函数D ．x y sin =的反函数是x y arcsin =4．要得到函数⎪⎭⎫ ⎝⎛-=42cos 3πx y 的图象，可以将函数x y 2sin 3=的图象( )．A ．沿x 轴向左平移8π单位 B ．沿x 轴向右平移8π单位 C ．沿x 轴向左平移4π单位 D ．沿x 轴向右平移4π单位5．若2sin 2α+sin 2β－2sin α=0则cos 2α+cos 2β的取值范围是（ ）．A ．[1,5]B ．[1,2]C ．[1,49] D ．[－1,2]6．在ABC 中，已知A 、B 、C 成等差数列，求 2tan 2tan 32tan 2tanCA C A ⋅++的值 为 ．7．设直角三角形ABC 的内切圆半径与外接圆半径分别为r 的R ，则Rr的最大值为 ．8．设函数)sin()(ϕω+=x x f ，（0>ω，22πϕπ<<-）给出下列四个论断：（1）它的周期为π； （2）它的图象关于直线x =12π对称；（3）它的图象关于点（3π,0）对称； （4）在区间(－6π,0)上是增函数．以其中两个论断为条件，另两个论断为结论，写出你认为正确的一个命题： ． 9．（1）已知sin(4π+α)·sin(4π－α)=61, α∈(2π,π)，求sin4α；（2）已知 cos(x+4π)=53,45π<x<47π，求xxx tan 1sin 22sin 2-+的值．10．如下图，某地一天从6时到14时的温度变化曲线近似满足函数y=A sin(ωx+φ)+b．（1）求这段时间的最大温差；（2）写出这段曲线的函数解析式．11．已知函数f(x)是定义域为一切实数且图象关于x=3对称的奇函数，f(1)=1且 523sin cos =-x x ． 求证：（1）函数)(x f 是周期函数；（2）求])4cos(2sin 15[π+x xf 的值．12．已知⊙O 的半径为2，在它的内接三角形ABC 中，有()()B b a C A sin sin sin 2222-=-成立，求△ABC面积S 的最大值．三角函数的图象与性质一、考纲要求1．理解任意角的概念、弧度的意义，能正确地进行弧度与角度的换算．2．掌握任意角的正弦、余弦、正切的定义，了解余切、正割、余割的定义，掌握同角三角函数的基本关系式，掌握正弦、余弦的诱导公式，理解周期函数与最小正周期的意义．3．了解正弦函数、余弦函数、正切函数的图象和性质，会用“五点法”画正弦函数、余弦函数和函数)sin(ϕω+=x A y )的简图，理解A 、ω、ϕ的物理意义． 二、基础过关1．函数||sin x x y +=，],[ππ-∈x 的大致图象是（ C ）．A B C D2．（2002北京）已知)(x f 是定义在)3,3(-上的奇函数，当30<<x 时，)(x f 的图象如图所示，那么不等式0cos )(<x x f 的解集是（ B ）．A ． )3,2()1,0(2,3(ππ --B ． )3,2()1,0()1,2(ππ --C ． )3,1()1,0()1,3( --D ．)3,1()1,0(2,3( π--3．定义在R 上的函数)(x f 既是偶函数又是周期函数，若)(x f 的最小正周期是π，且当]2,0[π∈x 时，x x f sin )(=，则)35(πf 的值为（ D ）． A ．21-B ．21 C ．23-D ．23 4．给定性质: ①最小正周期为π；②图象关于直线x=3π对称，则下列四个函数中，同时具有性质①、②的是（ D ）． A ．y = sin(2x +6π) B ．y = sin(2x+6π) C ．y = sin|x| D ．y = sin(2x －6π) 5．下列四个结论中正确的个数有（ B ）．①y = sin|x|的图象关于原点对称；②y = sin(|x|+2)的图象是把y = sin|x|的图象向左平移2个单位而得；③y = sin(x+2)的图象是把y = sinx 的图象向左平移2个单位而得；④y = sin(|x|+2)的图象是由y = sin(x+2)( x ≥0)的图象及y = －sin(x-2) ( x<0)的图象组成的． A ．1个 B ．2个 C ．3个 D ．4个6．把函数y = cos(x+3π)的图象向左平移m 个单位(m>0), 所得图象关于y 轴对称, 则m 的 最小值是 ．32π 7．函数y = 2sin(4π+2x )cos(4π+2x )+asinx (x ∈R)的图象关于x=8π对称, 则g(x)= asin(a+1)x 的最小正周期是 ．π2三、典型例题： 例1 已知函数f(x)=tan(3πsinx)． （1）求f(x)的定义域和值域；（2）在（－π，π）中，求f(x)的单调区间； （3）判定方程f(x)=tan32π在区间（－π，π）上解的个数． 解：（1）∵－1≤sinx ≤1 ∴ －3π≤3πsinx ≤3π．又函数y=tanx 在x=k π+2π(k ∈Z)处无定义， 且（－2π，2π）[－3π,3π]（－π, π），∴令3πsinx=±2π，则sinx=±23解之得：x=k π±3π(k ∈Z)∴f(x)的定义域是A={x|x ∈R ，且x ≠k π±3π，k ∈Z}∵tanx 在（－2π，2π）内的值域为（－∞，+∞），而当x ∈A 时，函数y=13πsinx 的值域B 满足（－2π，2π） B∴f(x)的值域是（－∞，+∞）．（2）由f(x)的定义域知，f(x)在[0，π]中的x=3π和x=32π处无定义．设t=3πsinx ，则当x ∈[0, 3π)∪（3π，32π）∪（32π，π）时，t ∈[0, 2π)∪(2π,3π]，且以t 为自变量的函数y=tant 在区间（0，2π），（2π，3π]上分别单调递增． 又∵当x ∈[0，3π]时，函数t=3πsinx 单调递增，且t ∈[0, 2π)，当x ∈（3π，2π]时，函数t=3πsinx 单调递增，且t ∈（2π,3π] 当x ∈[2π，32π)时，函数t=3πsinx 单调递减，且t ∈（2π, 3π]当x ∈（32π，π）时，函数t=3πsinx 单调递减，且t ∈（0，2π） ∴f(x)=tan(13πsinx)在区间[0，3π),（3π,2π]上分别是单调递增函数；在),32(),32,2[ππππ上是单调递减函数．又f(x)是奇函数，所以区间（－3π，0]，[－2π，－3π)也是f(x)的单调递增区间]2,32(),32,[ππππ----是f(x)的递减区间． 故在区间（－π，π）中,f(x)的单调递增区间为：[－2π，－3π)，（－3π，3π），（3π，2π]单调递减区间为),32(),32,32(),32,[ππππππ---． （3）由f(x)=tan 32π得：tan(3πsinx)=tan(32π)⇔3πsinx=k π+32π （k ∈Z ）⇔sinx=k 3+36(k ∈Z)① 又∵－1≤sinx ≤1，∴323323-≤≤--k ∴k=0或k= －1当k=0时，从①得方程sinx=36当k=1时，从①得方程sinx= －3+36 显然方程sinx=36,sinx= －3+36，在（－π, π）上各有2个解，故f(x)=tan 32π在区间（－π，π）上共有4个解．例2 已知函数()b a x x a x a x f++--=2cos sin 322cos 的定义域为⎥⎦⎤⎢⎣⎡20π，，值域为 [ －5，1]，求常数a 、b 的值． 解：∵ ()b a x a x a x f++--=22sin 32cos ，b a x a ++⎪⎭⎫ ⎝⎛--=232cos 2π ．∵ 20π≤≤x ，∴ 32323πππ≤-≤-x ，∴ 1 32cos 21≤⎪⎭⎫ ⎝⎛-≤-πx ．当a > 0时，b ≤ f ( x ) ≤ 3a + b ，∴ ⎩⎨⎧-==+.513b b a ， 解得 ⎩⎨⎧-==.52b a ，当a < 0时，3a + b ≤ f ( x ) ≤ b ．∴ ⎩⎨⎧=-=+.153b b a ， 解得 ⎩⎨⎧=-=.12b a ，故a 、b 的值为 ⎩⎨⎧-==52b a 或 ⎩⎨⎧=-=12b a例3 已知函数3cos 33cos3sin )(2x x xx f +=． （1）将)(x f 写成)sin(φω+x A 的形式，并求其图象对称中心的横坐标；（2）函数的图象可由)(sin R x x y ∈=的图象经过怎样的变换得到？（3）如果△ABC 的三边a 、b 、c 满足b 2=ac ，且边b 所对的角为x ，试求x 的范围及此时函数f(x)的值域． 解：（1）23)332sin(2332cos 2332sin 21)32cos 1(2332sin 21)(++=++=++=πx x x x x x f由)332sin(π+x =0即z k k x z k k x ∈-=∈=+πππ213)(332得即对称中心的横坐标为z k k ∈-，π213 （2）将函数x y sin =的图象依次进行如下变换：① 把函数x y sin =的图象向左平移3π，得到函数)3sin(π+=x y 的图象； ② 把得到的图象上各点横坐标伸长到原来的23倍（纵坐标不变），得到函数)632sin(π+=x y 的图象；③把得到的图象向上平移23个单位长度，得到函数)632sin(π+=x y +23的图象；（3）由已知b 2=a c，，，，，，231)332sin(31)332sin(3sin |295||23|953323301cos 21212222cos 22222+≤+<∴≤+<∴->-≤+<≤<<≤∴=-≥-+=-+=πππππππππππx x x x x ac ac ac ac ac c a ac b c a x 即)(x f 的值域为]231,3(+.综上所述，]3,0(π∈x ， )(x f 值域为]231,3(+ .例4 设二次函数),()(2R c b c bx x x f ∈++=，已知不论βα,为何实数恒有)(sin αf ≥0，)cos 2(β+f ≤0．（1）求证：1-=+c b ； （2）求证：c ≥3；（3）若函数)(sin αf 的最大值为8，求b ，c 的值．解： (1) ]1,1[sin -∈α ， ]3,1[cos 2∈β+， 0)(sin f ≥α 又 ， 0)cos 2(f ≤β+ 恒成立.0)1(f ≥∴ ， 0)1(f ≤， 即 0)1(f = 恒成立. ∴01=++c b ， 即 1c b -=+.（2）0)3(f ≤ ， 0c b 39≤++∴， ∴0)1(39≤+--+c c ， ∴3≥c .（3）由题意可知： 上为减函数，在]11[)x (f -，∴c b f +-=-=1)1(8 ①， 1c b -=+ ② ，由 ① ，② 可得 b = 4- ,c = 3 .四、热身演练：1．在)2,0(π内，使x x cos sin >成立的x 取值范围为（ C ）．A ．)45,()2,4(ππππ B ．),4(ππ C ．)45,4(ππ D ．)23,45(),4(ππππ2．已知sin α>sin β，那么下列命题成立的是（ D ）．A ．若α、β是第一象限角，则cos α>cos βB ．若α、β是第二象限，则tan α>tan βC ．若α、β是第三象限角，则cos α>cos βD ．若α、β是第四象限角，则tan α>tan β 3．下列命题中正确的是（ C ）．A ．x y tan =是增函数B ．x y sin =在第一象限是增函数C ．x y arccos 2-=π是奇函数D ．x y sin =的反函数是x y arcsin =4．要得到函数⎪⎭⎫ ⎝⎛-=42cos 3πx y 的图象，可以将函数x y 2sin 3=的图象（ A ）．A ．沿x 轴向左平移8π单位 B ．沿x 轴向右平移8π单位 C ．沿x 轴向左平移4π单位 D ．沿x 轴向右平移4π单位5．若2sin 2α+sin 2β－2sin α=0则cos 2α+cos 2β的取值范围是（ A ）．A ．[1,5]B ．[1,2]C ．[1,49] D ．[－1,2]6．在ABC 中，已知A 、B 、C 成等差数列，求 2tan 2tan 32tan 2tanCA C A ⋅++的值 为 ．37．设直角三角形ABC 的内切圆半径与外接圆半径分别为r 的R ，则Rr的最大值为 ．12-8．设函数)sin()(ϕω+=x x f ，（0>ω，22πϕπ<<-）给出下列四个论断：（1）它的周期为π； （2）它的图象关于直线x =12π对称； （3）它的图象关于点（3π,0）对称； （4）在区间(－6π,0)上是增函数．以其中两个论断为条件，另两个论断为结论，写出你认为正确的一个命题： ． （1）（2）→（3）（4）或（1）（3）→（2）（4）9．（1）已知sin(4π+α)·sin(4π－α)=61, α∈(2π,π)，求sin4α；（2）已知 cos(x+4π)=53,45π<x<47π，求xxx tan 1sin 22sin 2-+的值．解 （1）∵α+4π+4π－α=2π∴sin(4π－α)=cos(4π+α)∴sin(4π+α)·sin(4π－α)=sin(4π+α)·cos(4π+α)=21sin(2π+2α)= 21cos2α= 61又∵π<2α<2π,cos2α=31，∴sin2α= －322， ∴sin4α=2sin2α·cos2α= －924．（2）原式=xx x x x sin cos )sin (cos cos sin 2-+α=)4cos(2)4sin(22sin ππ++⋅x x x =－cos(2x+2π)tan(x+4π)=[1－2cos 2(x+4π)]tan(x+4π)而cos(x+4π)=53,tan(x+4π)= －34，代入得：原式= －7528．10．如下图，某地一天从6时到14时的温度变化曲线近似满足函数y =A sin(ωx +φ)+b ．（1）求这段时间的最大温差； （2）写出这段曲线的函数解析式．解：（1）由图示，这段时间的最大温差是30－10=20(℃)；（2）图中从6时到14时的图象是函数y =A sin(ωx +φ)+b 的半个周期的图象． ∴ωπ221⋅=14－6，解得ω=8π，由图示A =21(30－10)=10，b =21(30+10)=20， 这时y =10sin(8πx +φ)+20，将x =6,y =10代入上式可取φ=43π．综上所求的解析式为y =10sin(8πx +43π)+20,x ∈［6,14］．11．已知函数f(x)是定义域为一切实数且图象关于x=3对称的奇函数，f(1)=1且 523sin cos =-x x ． 求证：（1）函数)(x f 是周期函数；（2）求])4cos(2sin 15[π+x x f 的值．解：∵函数f(x)的图象关于x=3对称，∴f(－x)=f(6+x)，∵函数f(x)又是奇函数，∴f(6+x)=f(－x)=—f(x)，f(x+12)=－f(x+6)=f(x)，∴函数f(x)的周期为1， ∴函数f(x)是周期函数．cosx －sinx=2cos(x+4π)=523，∴cos(x+4π)=53,)4cos(2sin 15π+x x =)4cos()22cos(15ππ++-x x =－)4cos()1)4(cos 2(152ππ+-+x x =7,f[)4cos(2sin 15π+x x ]=f(7)=f(6+1)=f(－1)=－f(1)=－1．12．已知⊙O 的半径为2，在它的内接三角形ABC 中，有()()B b a C A sin sin sin 2222-=-成立，求△ABC面积S 的最大值．解：∵()()B b a C A sin sin sin 2222-=-，又2R=22，由正弦定理得：22[22)2()2(Rc R a -]=（a －b ）R b2，∴a 2+b 2－c 2=ab,∴cosC=21∴∠C=3π．S=21absinC=B A B R A R sin sin 32sin 2sin 243=⋅⋅=－3[cos(A+B)－cos(A-B)]．∵A+B=32π，∴s=23+3cos(A －B), 故当cos(A －B)=1时,即A=B=3π时,△ABC 面积S 的最大值为233．。

sin y x =，x R ∈ππ- 2π- cos y x =，x R ∈2π32π2π-32π-1.3.2 三角函数的图像与性质1．利用单位圆中正弦线作正弦函数图象作法：（几何作法） （1）在直角坐标系的x 轴上任取一点O 1，以O 1为圆心作单位圆，从⊙O 1与x 轴的交点A 起，把⊙O 1分成12等份，过⊙O 1上各点作x 轴的垂线，可得对应于0,,,,,2632ππππ等角的正弦线； （2）把x 轴上0~2π这一段分成12等份，把角x 的正弦线向右平行移动，使正弦线的起点与x 轴上的点x 重合；（3）用光滑曲线把这些正弦线的终点连结起来，就得到正弦函数sin y x =，[0,2]x π∈的图象。

因为终边相同的角的函数值相同，所以，函数sin y x =，[2,2(1)]x k k ππ∈+（k Z ∈）且0k ≠的图象与函数sin y x =，[0,2]x π∈的图象的形状完全相同，只是位置不同，于是只要将函数sin y x =，[0,2]x π∈的图象向左、右平移，就可得到函数sin y x =，x R ∈的图象。

2．余弦函数的图象由于cos cos()sin[()]sin()22y x x x x ππ==-=--=+，所以余弦函数cos y x =，x R ∈与函数sin()2y x π=+,x R ∈是同一个函数；这样，余弦函数的图象可由：正弦曲线向左平移2π个单位得到，即：3．五点法作图（1）sin y x =，[0,2]x π∈；自变量 x2π π32π 2π函数值y1－1（2）sin 1y x =+，[0,2]x π∈． 自变量x0 2π π 32π 2πsin x11-函数值y12114．正弦、余弦函数的定义域、值域 函 数 sin y x =cos y x = 函 数 sin y x = cos y x =定义域x R ∈x R ∈值 域[1,1]-[1,1]-5．正切函数tan y x =的定义域是什么？ ⎭⎬⎫⎩⎨⎧∈+≠z k k x x ,2|ππyx O 32π12π 2π向左平移2π个单位 32π2ππ 2π6．正切函数是不是周期函数？()tan tan ,,2x x x R x k k z πππ⎛⎫+=∈≠+∈ ⎪⎝⎭且， ∴π是tan ,,2y x x R x k k z ππ⎛⎫=∈≠+∈ ⎪⎝⎭且的一个周期。