第六章 模糊关系方程
- 格式:ppt
- 大小:444.00 KB
- 文档页数:26



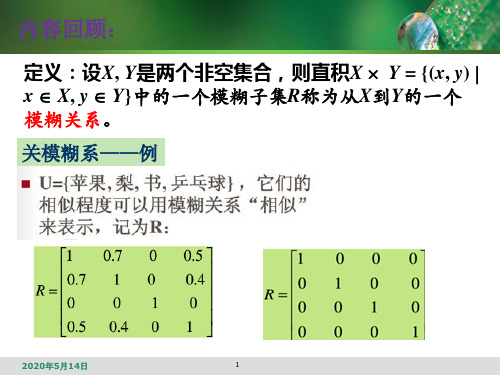

模糊关系方程的求解
模糊关系方程在现代数学领域占据了诸多重要位置。
换句话说,模糊关系方程是一种特殊的参数形式,这种参数形式可以用来处理领域涉及的系统的模糊关系,它可以表示特定的复杂性矩阵。
模糊关系方程又称为Foetisch模糊关系方程,它是现代数学中重要的一种概念,可以用来解决模糊、复杂范畴系统关系模糊关系的描述问题。
模糊关系方程按其形式表示,可以分为两部分,即等式及其参数。
等式的形式通常为将未知值一侧,等式的右侧表示模糊关系的关联函数,即通常被称为模糊子空间的值。
参数部分用来表示系统的决策,用来解释系统的非线性关系。
模糊关系方程具有许多值得研究的特点,所引起的模糊关系经常不是清晰可用的。
因此,求解模糊关系方程变得相当困难。
一般情况下,采用解析求解、数值求解和感知求解等方法可以解决Foetisch模糊关系方程的求解问题。
解析求解是以Foetisch模糊关系方程的解析形式求解的相关方法,实施解析求解可以明确求解的基本原理和求解所需要计算的细节;数值求解是用许多数值技术总结问题,把Foetisch模糊关系方程拆分成多个子问题,再分别解决每个子问题;而感知求解是以模糊关系中提出的模糊子空间等非常量参数解决问题,采用多项式构建模型,使结果获得更高的精度。
总的来说,模糊关系方程的求解是一个非常重要的问题,它可以帮助学术界解决模糊关系研究和讨论一些重要的应用实例,也可以为现实世界的复杂系统关系提供更有效的模型。

fuzzy关系方程的几种特殊解1模糊关系方程模糊关系方程是一种描述模糊概念引导人们去推导数学表达式和进行计算的主要工具,它可以将讨论话题的实际经验转换为形式化的、定量的表示,从而让研究者轻松地观察分析相关现象。
模糊关系方程可以分为承载系统、模糊集的关系方程和模糊支配函数的关系方程三种类型,其中有一些特殊解。
2承载系统的特殊解承载系统的特殊解是模糊关系方程的最基本情形,它们包括模糊集表达式、模糊系统表达式和模糊决策表达式。
模糊集表达式(FSM)通过一系列概念性变量表达系统的特征,并利用条件判定的方式快速推导出系统的有关参数;模糊系统表达式(FSM)通过一系列先验变量和约束条件,准确地刻画出系统内部的复杂特征;模糊决策表达式(FM)则通过一系列概念性变量,设定出适当的模糊规则,辅以数学抽象技术,以期得出有效的决策计划。
3模糊集关系方程的特殊解模糊集关系方程是模糊关系方程实施过程中很重要的一个要素,它将文字描述的思想转换成流程性问题,然后再将其转换为数学运算,从而实现有效的概念实现。
常见的模糊集关系方程的特殊解有:逻辑推理关系,其表达形式为“逻辑推理”,用于描述客观存在的原则;绝缘图法,用于加强模糊集的描述能力;联调图法,用于调整模糊集的边界;交互式调整,用于实施模糊集的调整,以及一些其他表示模糊集的精确或者近似计算方法等等。
4模糊支配函数的特殊解模糊支配函数使用有限参数概念去抽象表达模糊概念,可以有效地解决实际问题中存在的复杂性及不确定性问题,它是模糊关系方程的重要组成部分。
常见的模糊支配函数的特殊解可以分为常见的模糊控制函数和灰色关联函数两类,常见的模糊控制函数包括:线性函数,主要用于模拟判断规则中包含表达式;幂函数,因其函数参数灵活性,而得到广泛应用;指数函数,主要用于模拟表达式中包含趋势;并行形式模糊函数,有利于表达多角度的主观概念;灰色关联函数,它的优势在于能够表达出领域中出现的线性以及非线性复杂度等特性。
关于模糊关系与模糊子群的注记模糊关系和模糊子群是模糊数学中的两个重要概念,它们在各个领域中都有着广泛的应用。
本文将对这两个概念进行详细讨论,并介绍其相关的性质和应用。
一、模糊关系模糊关系是指一种不确定性的关系,它通常用来描述两个或多个对象之间的某种程度的关联性。
在模糊关系中,每个对象都被赋予了一个模糊度,表示其与其他对象的关系的不确定程度。
例如,在描述人与人之间的关系时,我们可以使用模糊关系来表示两个人之间的亲密程度、朋友关系等。
在模糊关系中,我们通常使用模糊矩阵来表示。
模糊矩阵是一个n×n的矩阵,其中每个元素都是一个[0,1]之间的实数,表示两个对象之间的模糊关系的强度。
如果两个对象之间的模糊关系越强,那么它们之间的模糊矩阵元素就越接近于1;反之,如果它们之间的关系越弱,那么元素就越接近于0。
模糊关系的应用非常广泛,例如在社交网络分析、人际关系建立、图像处理等领域都有着重要的应用。
在社交网络分析中,我们可以使用模糊关系来描述人与人之间的社交关系,从而分析社交网络的结构和特征。
在图像处理中,我们可以使用模糊关系来进行图像分割和图像识别等工作。
二、模糊子群模糊子群是指在一个群中的一个子集,它具有一定的模糊性质。
在模糊子群中,每个元素都被赋予了一个模糊度,表示它与子群中的其他元素的关系的不确定程度。
例如,在描述一个人群中的子群时,我们可以使用模糊子群来表示某些人之间的某种程度的关联性。
在模糊子群中,我们通常使用模糊子群矩阵来表示。
模糊子群矩阵是一个n×n的矩阵,其中每个元素都是一个[0,1]之间的实数,表示子群中两个元素之间的模糊关系的强度。
如果两个元素之间的模糊关系越强,那么它们之间的模糊子群矩阵元素就越接近于1;反之,如果它们之间的关系越弱,那么元素就越接近于0。
模糊子群的应用也非常广泛,例如在人际关系建立、图像处理、数据挖掘等领域都有着重要的应用。
在人际关系建立中,我们可以使用模糊子群来描述某些人之间的某种程度的关联性,从而为社交网络分析提供基础。
模糊关系方程的求解方法(ⅰ)模糊关系方程(Fuzzy Relation Equation,FRE)是模糊数学中的一种重要工具,用于描述两个或多个模糊集之间的关系。
在实际应用中,模糊关系方程可以用来分析和处理各种信息不确定性问题,具有很高的实用性和广泛的应用前景。
一、模糊关系方程的定义模糊关系方程是一种表示模糊关系的数学工具,它定义了一个模糊集关系,用于描述两个或多个模糊集之间的关系。
它的一般形式为:R = R(x, y)其中,x、y是两个变量,R(x, y)是它们之间的模糊关系,通常用一个模糊规则来定义,如下所示:IF x is A and y is B, THEN R(x, y) is C其中,A、B、C分别是三个模糊集,表示变量x、y和它们的关系R(x, y)。
这个规则是根据当前问题场景和需求来确定的,可以人工经验或使用专家系统等技术来定义。
二、模糊关系方程的求解方法模糊关系方程的求解方法有很多,本文介绍以下三种常用方法:1.等价变换法等价变换法是一种利用变换函数将原问题转化为等价的新问题去求解的方法。
该方法的基本思想是将原问题中的变量通过变换函数映射到新的变量上,然后求解等价的新问题,最后再将结果通过逆变换函数还原回原问题中的变量上。
这种方法适用于模糊化程度较低的问题,计算量较小,但容易出现误差。
2.迭代逼近法迭代逼近法是一种通过迭代计算来逐步逼近模糊关系方程解的方法。
该方法的基本思想是先给出一个初始的解或解集,然后通过迭代计算的方式逐步不断地优化解的准确度和稳定性,直到满足一定的收敛条件为止。
这种方法适用于任意模糊度的问题,计算效率较高,但容易受到初始解的影响。
3.逻辑推理法逻辑推理法是一种利用模糊逻辑运算规则和模糊推理机制来推导求解模糊关系方程的方法。
该方法的基本思想是先将模糊关系方程转化为一组模糊规则或模糊逻辑表达式,然后通过运用模糊逻辑运算规则和模糊推理机制来推导求解出问题的答案。