成都市2014年一诊成绩文理科一分段统计表
- 格式:pdf
- 大小:78.72 KB
- 文档页数:2

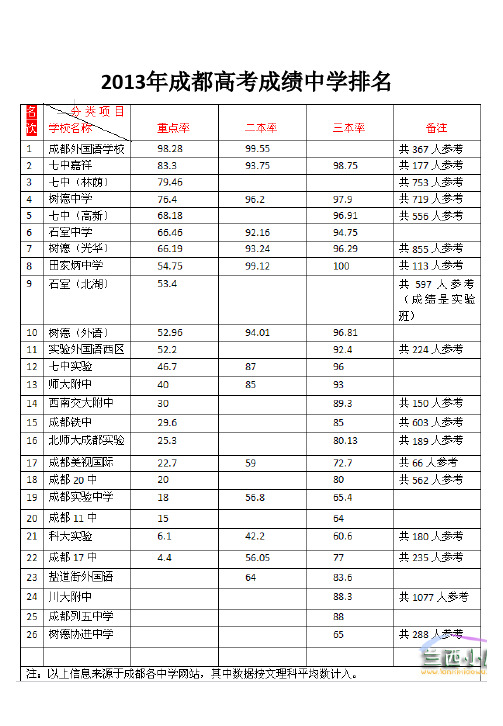
2014年成都五城区及高新区中考成绩分段统计表2014年成都中考结束,2014年成都中考查分入口和2014年成都中考分数线公布,2014年成都中考每个中考分数段的人数也公布,请看2014年成都中考每个中考分数段的人数。
2014年成都中考重点线571分,普高分数线542分成都四七九师大川大附中历年中考录取分数线汇总(供2014届考生初升高报考参考使用)石室中学文庙校区2008年:统招线630、调招线631.(重点线为585,录取线高出重点线45-46分)。
2009年:统招线639,、调招线646.(重点线为580,录取线高出重点线59-66分)。
2010年:统招线627、调招线625(实验班640).(重点线为560,录取线高出重点线65-80分)。
2011年:统招线606、调招线620.(重点线555,录取线高出重点线51-65分)。
2012年:统招线637、实验班655.(重点线588,录取线高出重点线52-67分)。
石室中学北湖校区2010年:统招线560、调招线610.(重点线560,录取线高出重点线0-50分)。
2011年:统招线580、调招线594.(重点线555,录取线高出重点线25-39分)。
2012年:统招线621、调招线635.(重点线588,录取线高出重点线33-47分)。
2013年:统招线613、调招线621.(重点线573,录取线高出重点线40-48分)。
七中林荫校区2008年:统招线649、调招线650.(重点线585,录取线高出重点线64-65分)。
2009年:统招线665、调招线663.(重点线580,录取线高出重点线83-85分)。
2010年:统招线631、调招线620.(重点线560,录取线高出重点线60-61分)。
2011年:统招线634、调招线631.(重点线555,录取线高出重点线76-79分)。
2012年:统招线655、调招线655.(重点线588,录取线高出重点线67分)。

成都市2014届高中毕业班第一次诊断性检测理科综合 物理局部理科综合共300分,考试用时150分钟。
1.物理试卷分为第I 卷〔选择题〕和第2卷〔非选择题〕两局部,第I 卷1至3页,第2卷4至5页,共110分。
2.答卷前,考生务必将自己的姓名、考籍号填写在答题卡上;并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试完毕后,只将答题卡交回。
第I 卷须知事项:1.每题选出答案后,用2B 铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共7题,每题6分,共42分。
每一小题给出的四个选项中,有的只有一个选项正确,有的有多个选项正确,全部选对的得6分,选对但不全的得3分,有选错的得0分。
1.如下表述正确的答案是A. 焦耳发现了电流通过导体时产生热效应的规律B .库仑发现了点电荷间的相互作用规律,并通过油滴实验测定了元电荷的电荷量 C. 电荷在电场中会受到电场力作用,电流在磁场中也一定会受到磁场力的作用D .由公式2QE k r =可知,E 与Q 成正比;由公式2v F m r =可知,F 与r 成反比 【答案】A【解析】A 、焦耳发现了电流通过导体时产生热效应的规律,故A 正确;B 、密立根过油滴实验测定了元电荷的电荷量,故B 错误;C 、电荷在电场中会受到电场力作用,电流平行于在磁场方向如此不受到磁场力的作用,故C 错误;D 、公式2QE k r =是点电荷的场强决定式,故E 与Q 成正比;向心力公式2v F m r =中,当r 变化时,v 也变化,故F 不与r 成反比,故D 错误。
应当选A 。
【考点】电场强度;物理学史 2.如下说法正确的答案是【答案】DA 、大力扣篮时,人的肢体动作不能忽略,即不能忽略人的大小和形状,物体不能看作质点,故A 错误;B 、“313k m“指的是列车行驶的距离,指的是火车的路程,不是位移,故B 错误;C 、跳水运动员在空中时只受重力,故处于失重状态,故C 错误;D 、只有同步卫星才是相对于地面静止,而周期为24h 的卫星并不一定都是同步卫星,故D 正确。

本试卷分选择题和非选择题两部分。
第I 卷(选择题)1至2页,第Ⅱ卷(非选择题)2至4页,共4页,满分150分,考试时间120分钟。
注意事项:1.答题前,务必将自己的姓名、考籍号填写在答题卡规定的位置上。
2.答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其它答案标号。
3.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上。
4.所有题目必须在答题卡上作答,在试题卷上答题无效。
5.考试结束后,只将答题卡交回。
第I 卷(选择题,共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,有且只有一项是符合题目要求的.1.已知集合{}{}2,3,|0A B x x =-=≥,则A B = (A){一2) (B){3) (C)(-2,3} (D)∅ 2.若复数z 满足(12)5z i -=(i 为虚数单位),则复数z 为 (A) 12i + (B)2-i (C)12i - (D)2+i i 3.在等比数列{}n a 中,若181564a a a =,则8a = (A)16 (B)8 (C) (D)4 4.计算125log 4-所得的结果为(A)52(B) 2 (D)1 4.在等差数列{口。
)中.a8 =15,则al+a7+a9+a15一 (A)15 (B)30 (C)45 (D) 605.已知m ,n 是两条不同的直线,α为平面,则下列命题正确的是 (A) //,////m n m n αα若则 (B),,m n m n αα⊥⊥⊥若则 (C),//,m n m n αα⊥⊥若则(D)若m 与α相交,n 与α相交,则m,n 一定不相交6.如图,在平面直角坐标系xOy 中,角,αβ的顶点与坐标原点重 合,始边与x 轴的非负半轴重合,它们的终边分别与单位圆相交于A ,B 两点.若点A,B 的坐标分别为34,55⎛⎫ ⎪⎝⎭和43,55⎛⎫-⎪⎝⎭,则c o s ()αβ+的值为 (A) 2425-(B)725- (C)0 (D)24257.已知,22a ππ⎡⎤∈-⎢⎥⎣⎦,则的概率为 (A)13 (B)12 (C)23 (D)348.一个长方体被一个平面截去一部分后所剩几何体的三视图如图所示(单位:cm),则该几何体的体积为(A)1202cm (B) 1002cm (C) 802cm (D)602cm9.某种特色水果每年的上市时间从4月1号开始仅能持续5个月的时间.上市初期价格呈现上涨态势,中期价格开始下跌,后期价格在原有价格基础之上继续下跌.若用函数[]2()47(0,5,)f x x x x x N =-++∈∈进行价格模拟.(注:x=0表示4月1号,x=1表示5月1号,…,以此类推.)过多年的统计发现:当函数()213()1f x xg x x --=+取得最大值时,拓展外销市场的效果最为明显,请你预测明年拓展外销市场的时间为(A)5月1日 (B) 6月1日 (C)7月1日 (D) 8月1日10.已知函数ln , 14()12ln , 14x x f x x x ≤≤⎧⎪⎨-≤<⎪⎩,若函数()()F x f x kx =-在区间1,44⎡⎤⎢⎥⎣⎦上恰有一个零点,则k 的取值范围为(A){}1,16ln 20e ⎛⎤ ⎥⎝⎦ (B){}1,0e ⎡⎫+∞⎪⎢⎣⎭(C){}ln 2,16ln 202⎡⎫⎪⎢⎣⎭ (D){}ln 2,16ln 202⎛⎤⎥⎝⎦第Ⅱ卷(非选择题,共100分)二、填空题:本大题共5小题,每小题5分,共25分.11.若2()(1)1f x x a x =+-+是定义在R 上的偶函数,则实数a=________.12.某公司生产A .B .C 三种型号的轿车,产量分别是600辆,1200辆和1800辆,为检验产品质量.现从这三种型号的轿车中,用分层抽样的方法抽取n 辆作为样本进行检验,若B 型号轿车抽取了2辆,,则样本容量n=_________.13.已知向量a,b 夹角为60,2,1a b ==,则b a -=_________.14.设12,x x 是函数322()2f x x ax a x =-+的两个极值点,若122x x <<,则实数a 的取值范围是________.15.已知()2|2||1|1f x x =--+和2()2()g x x x m m R =-+∈是定义在R 上的两个函数,则下列命题正确的是(A)函数()f x 的图象关于直线x=0对称;(B)关于x 的方程()0f x k -=恰有四个不相等实数根的充要条件是(1,1)k ∈- (C)当m=l 时,对[][]12121,0,1,0,()()x x f x g x ∀∈-∃∈-<成立 (D)若[][]12121,1,1,1,()()x x f x g x ∃∈-∃∈-<成立,则(1,)m ∈-+∞ 其中正确的例题有______________(写出所有正确例题的序号)。
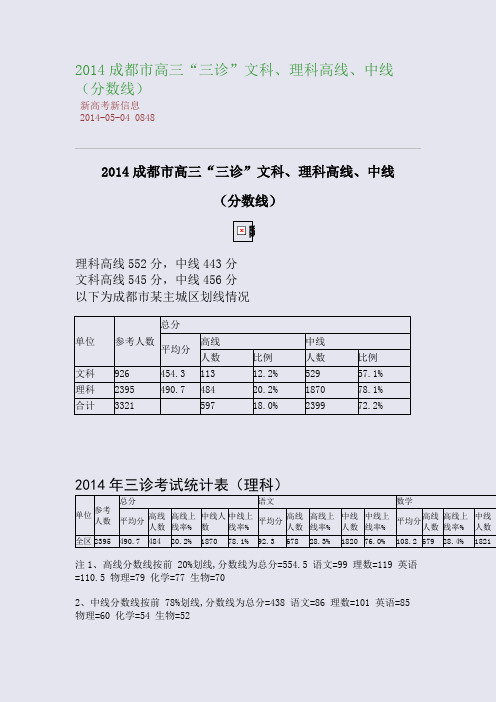
2014成都市高三“三诊”文科、理科高线、中线(分数线)新高考新信息2014-05-04 08482014成都市高三“三诊”文科、理科高线、中线(分数线)理科高线552分,中线443分文科高线545分,中线456分以下为成都市某主城区划线情况单位参考人数总分平均分高线中线人数比例人数比例文科926 454.3 113 12.2% 529 57.1% 理科2395 490.7 484 20.2% 1870 78.1% 合计3321 597 18.0% 2399 72.2%2014年三诊考试统计表(理科)单位参考人数总分语文数学平均分高线人数高线上线率%中线人数中线上线率%平均分高线人数高线上线率%中线人数中线上线率%平均分高线人数高线上线率%中线人数全区2395490.748420.2%187078.1%92.367828.3%182076.0%108.267928.4%1821注1、高线分数线按前 20%划线,分数线为总分=554.5 语文=99 理数=119 英语=110.5 物理=79 化学=77 生物=702、中线分数线按前 78%划线,分数线为总分=438 语文=86 理数=101 英语=85物理=60 化学=54 生物=522014年高三三诊考试统计表(文科)单位参考人数总分语文数学平均分高线人数高线上线率%中线人数中线上线率%平均分高线人数高线上线率%中线人数中线上线率%平均分高线人数高线上线率%中线人数全区926454.311312.2%52957.1%92.321122.8%53758.0%93.418119.5%535注1、高线分数线按前 12%划线,分数线为总分=541.5 语文=102 文数=116 英语=111.5 地理=71 历史=71 政治=702、中线分数线按前 57%划线,分数线为总分=454.5 语文=92 文数=95 英语=91.5 地理=56 历史=61 政治=59。
成都市高中2014届一诊语文阅卷分析报告成都市高中2014届一诊语文阅卷分析报告金牛区高中语文组2014.1.10一、第四大题文言翻译、简答及断句部分成都二十中欧拥军1.得分情况本部分赋分17分,考生总体得分较低。
2.命题要求评价:本题以人物传记为对象,选料传统,难易适中。
文字解读总体障碍不大,且文中所涉事迹学生较为熟悉。
加之传主以孝心为是,约有与课文《陈情表》相通之意。
由此可见,命题注重了求稳原则和以教材为基的原则。
3.典型失分错误例举:(1)翻译:一旦未作翻译茕译为茕茕孑立或不译。
怙译为凭借。
清朝未作翻译。
遗译为遗留苟因不知何意,翻译时干脆省掉但译为但是(2)简答:照抄原文:事母孜孜。
概括重复:如前面已道出不注重个人的利益而后又说淡泊名利等。
答题不规范,未分点作答。
(3)断句少数人未认真审题,断句出现9处以上。
主要问题在第五处,大多数人都断在野人者后,而未联系下文考虑几希和及其的安排。
此外,第八处错误也相对较多,部分学生断在了沛然后。
4.错误原因简析:翻译失误的主因:一是教材文言实词积累不够牢固,或知识迁移的能力较弱;二是语境意识不强,结合上文的推断能力有待提高;(一旦不能结合上文翻译成一下子)三是语言的换能力不强,对文言文理解中化单为双(不能将朽钝翻译为腐朽鲁钝之身)化含蓄为直白(不能将尘默翻译为玷污)特殊用法清障法等技巧掌握不熟。
简答题失误的主因:文章理解不到位,概括提炼意识不强,语言的换能力不强,啰嗦重复缺乏规范的答题意识。
断句题失误的主因:语意理解不清;结构意识不强;缺乏语境意识,未能瞻前顾后。
5.模块教学建议:针对上述情况,建议在一诊后的复习中注意以下几点:1.强化学生对文言实词的积累、重点特殊句式的理解以及活用等特殊用法的判断等;2.强调知识的迁移,尤其注重教材知识和成语文言现象的迁移(如孜孜可从孜孜不倦中迁移);3.强化学生在翻译时字字落实的意识,清楚并尝试用多种方式清除障碍;四是加大对学生概括意识和语言换能力培养的力度,力争达到简洁、准确的目的。
市2014级高中毕业班第一次诊断性检测数学〔文科〕本试卷分选择题和非选择题两局部。
第I卷〔选择题〕1至2页,第二卷〔非选择题〕2至4页,共4页,总分值150分,考试时间120分钟。
第I卷〔选择题,共60分〕一、选择题:本大题共12小题,每题5分,共60分.在每题给出的四个选项中,只有一项为哪一项符合题目要求的.(1)设集合U=R,A={x|(x+l) (x -2)<0},那么(A)〔一∞,-1) (2,+∞) (B)[-l,2](C)(一∞,-1] [2,+∞) (D)〔一1,2〕(2)命题“假设a>b,那么a+c>b+c〞的逆命题是(A)假设a>b,那么a+c≤b+c (B)假设a+c≤b+c,那么a≤b(C)假设a+c>b+c,那么a>b (D)假设a≤b,那么a+c≤b+c(3)双曲线22154x y-=的离心率为(A)4 (B)35(C)5(D)32(4)α为锐角,且sinα=詈,那么cos〔π+α〕=(A)一35 (B)35 (C) —45 (D)45(5)执行如下图的程序框图,如果输出的结果为0,那么输入的x为(A)19 (B) -1或1 (C) –l (D)l(6)x与y之间的一组数据:假设y关于x的线性回归方程为=2.lx-1.25,那么m的值为(A)l (B)0. 85 (C)0.7 (D)0.5(7)定义在R上的奇函数f(x)满足f(x+3〕=f(x),且当x∈[0,32〕时,f(x)= 一x3.那么f〔112〕=(A) - 18 (B)18 (C) -1258 (D)1258 (8)如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,那么该四棱锥的所有棱中,最长的棱的长度为(A)41 (B)34 (C)5 (D) 32(9)将函数f(x)=sin2x+3cos2x 图象上所有点向右平移6π个单位长度,得到函数g (x)的图象,那么g(x)图象的一个对称中心是(A)〔3π,0〕 (B)(4π,0) (C)〔一12π,0〕 (D)〔2π,0〕(10)在直三棱柱ABC-A 1B l C 1中,平面α与棱AB ,AC ,A 1C 1,A 1B 1分别交于点E ,F ,G , H ,且直线AA 1∥平面α.有以下三个命题:①四边形EFGH 是平行四边形;②平面α∥平面BCC 1B 1;③平面α上平面BCFE .其中正确的命题有(A)①② (B)②③ (C)①③ (D)①②③(11)A,B 是圆O:x 2+y 2=4上的两个动点,假设M 是线段AB 的中点,那么的值为 (A)3 (B) 23(C)2 (D) -3(12)曲线C 1:y 2 =tx (y>0,t>0)在点M(4t ,2)处的切线与曲线C 2:y=e x+l +1也相切,那么t 的值为(A) 4e 2(B) 4e (C) 4x e (D) 4e第二卷〔非选择题,共90分〕二、填空题:本大题共4小题,每题5分,共20分.(13)复数z=21ii +〔i 为虚数单位〕的虚部为.(14)我国南北朝时代的数学家祖暅提出体积的计算原理〔祖暅原理〕:“幂势既同,那么积不容异〞.“势〞即是高,“幂〞是面积.意思是:如果两等高的几何体在同高处截得两几何体的截面积恒等,那么这两个几何体的体积相等,类比祖暅原理,如下图,在平面直角坐标系中,图1是一个形状不规那么的封闭图形,图2是一个矩形,且当实数t 取[0,4]上的任意值时,直线y=t 被图1和图2所截得的线段长始终相等,那么图1的面积为.(15)假设实数x ,y 满足约束条件,那么3x-y 的最大值为(16)△ABC 中,AC=2,BC=6,△ABC 的面积为32,假设线段BA 的延长线上存在点D ,使∠BDC =4,那么CD =.三、解答题:本大题共6小题,共70分.解容许写出文字说明、证明过程或演算步骤.(17)〔本小题总分值12分〕某省2016年高中数学学业水平测试的原始成绩采用百分制,发布成绩使用等级制.各等级划分标准为:85分与以上,记为A 等;分数在[70,85),记为B 等;分数在[60,70〕,记为C 等;60分以下,记为D 等.同时认定A ,B ,C 为合格,D 为不合格.甲,乙两所学校学生的原始成绩均分布在[50,100],为了比拟两校学生的成绩,分别抽取50名学生的原始成绩作为样本进展统计.按照[50,60〕,[60,70〕,[70,80〕,[80,90〕,[90,100]的分组作出甲校的样本频率分布直方图如图1所示,乙校的样本中等级为C ,D 的所有数据的茎叶图如图2所示.(I)求图中x 的值,并根据样本数据比拟甲乙两校的合格率;(Ⅱ)在乙校的样本中,从成绩等级为C ,D 的学生中随机抽取两名学生进展调研,求抽出的两名学生中至少有一名学生成绩等级为D 的概率.(18)〔本小题总分值12分〕在等比数列{a n }中,a 4=8a 1,且a 1,a 2 +1,a 3成等差数列.(I)求数列{a n }的通项公式;(Ⅱ)求数列{|a n -4|}的前n 项和S n .(19)〔本小题总分值12分〕如图l ,在正方形ABCD 中,点E ,F 分别是AB ,BC 的中点,BD 与EF 交于点H ,点G,R 分别在线段DH ,HB 上,且DGGH =BRRH .将△AED ,△CFD ,△BEF 分别沿DE ,DF ,EF 折起,使点A ,B ,C 重合于点P ,如图2所示,〔I 〕求证:GR ⊥平面PEF ;(Ⅱ)假设正方形ABCD 的边长为4,求三棱锥P- DEF 的切球的半径.(20)〔本小题总分值12分〕 椭圆22:154x y E +=的右焦点为F ,设直线l :x=5与x 轴的交点为E ,过点F 且斜率为k 的直线l 1与椭圆交于A ,B 两点,M 为线段EF 的中点.(I)假设直线l 1的倾斜角为4π,|AB|的值;(Ⅱ)设直线AM 交直线l 于点N ,证明:直线BN ⊥l .(21)〔本小题总分值12分〕函数f(x)=xlnx+(l-k)x+k ,k ∈R.(I)当k=l 时,求函数f(x)的单调区间;(Ⅱ)当x>1时,求使不等式f(x)>0恒成立的最大整数k 的值.请考生在第(22)、(23)题中任选一题作答,如果多做,那么按所做的第一题计分.(22)〔本小题总分值10分〕选修4-4:坐标系与参数方程在平面直角坐标系xOy 中,倾斜角为α(α≠2π〕的直线l 的参数方程为1cos ,sin ,x t y t αα=+⎧⎨=⎩〔t 为参数〕.以坐标原点为极点,以x 轴的正半轴为极轴,建立极坐标系,曲线C 的极坐标方程是ρcosx θ - 4sin θ=0.(I)写出直线l 的普通方程和曲线C 的直角坐标方程;(Ⅱ)点P(1,0).假设点M 的极坐标为〔1,2π〕,直线l 经过点M 且与曲线C 相交于A ,B 两点,设线段AB 的中点为Q ,求|PQ|的值.(23)〔本小题总分值10分〕选修4-5:不等式选讲函数f(x 〕=x +1+ |3 -x|,x ≥-1.(I)求不等式f(x 〕≤6的解集;(Ⅱ)假设f(x 〕的最小值为n ,正数a ,b 满足2nab =a+2b ,求2a+b 的最小值.。