高二数学试题-2018级高一数学练习题(五) 最新
- 格式:doc
- 大小:116.47 KB
- 文档页数:1


江苏省泰州中学2005—2018年度秋学期期终考试高一数学试题本场考试时间为120分钟,满分为150分。
试卷分第I 卷和第II 卷两个部分,其中第I 部分为客观题部分,第II 部分为主观题部分,答案全部答在答题纸上,答在草稿纸上或其它地方的无效。
第I 卷(选择题 共60分)一、本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一个选项是正确的。
1、已知正方形ABCD 的三个顶点分别为A( 1, 1 ), B( 3, 2 ), C( 2, 4 ), 则顶点D 的坐标为A 、(1,3)B 、(2,3)C 、(3,2)D 、( 0, 3 )2、已知),1,(),3,1(-=-=x 且∥b ,则x 等于()A .3B .3-C .31D .31-3、若),12,5(),4,3(==则与的夹角的余弦值为()A .6563 B .6533 C .6533-D .6563-4、点)4,3(-关于点)5,6(-B 的对称点是() A .)5,3(-B .)29,0(C .)6,9(-D .)21,3(-5、在平行四边形ABCD =+()A .=B .=或=C .ABCD 是矩形D .ABCD 是正方形6、已知点C 在线段AB 的延长线上,且λλ则,==等于()A .3B .31C .3-D .31-7、将向量x y 2sin =按向量)1,6(π-=平移后的函数解析式是()A .1)32sin(++=πx y B .1)32sin(+-=πx y C .1)62sin(++=πx yD .1)62sin(+-=πx y8、数)3sin()3cos(3)(θθ---=x x x f 是奇函数,则θ等于( )A 、k π (k ∈Z)B 、k π+6π(k ∈Z) C 、k π+3π(k ∈Z) D 、k π-3π(k ∈Z) 9、函数)32sin()(π-=x x f 的图象向左平移3π个单位,再将图象上各点的横坐标压缩为原来的21,那么所得图象的函数表达式为 )3sin()34sin()324sin(sin πππ+=+=+==x y D x y C x y B x y A10、函数)3cos()33cos()6cos()33sin(ππππ+++-+=x x x x y 的图象的一条对称轴的方程是 2484ππππ-=-===x Dx Cx B x A11、如果直线l 上的一点A 沿x 轴负方向平移3个单位,再沿y 轴正方向平移1个单位后,又回到直线l 上,则l 的斜率是( )A .3B .13 C .-3 D .-1312、设f(x)=xsinx ,若x 1,x 2∈]2,2[ππ-,且f(x 1)>f(x 2),则下列列结论中,必成立的是( ) A 、x 1>x 2 B 、x 1+x 2>0 C 、x 1<x 2 D 、x 12>x 22第II 卷(非选择题 共90分)二、填空题:本题共4小题,每题4分,共16分。
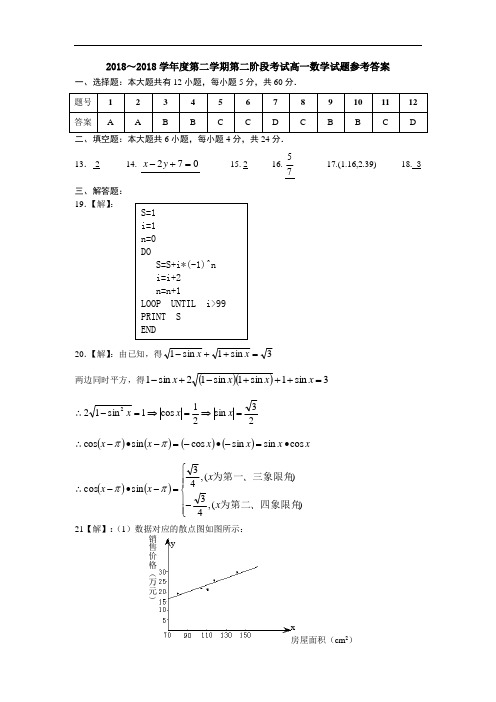
2018~2018学年度第二学期第二阶段考试高一数学试题参考答案一、选择题:本大题共有12小题,每小题5分,共60分.二、填空题:本大题共6小题,每小题4分,共24分. 13.-2 14. 072=+-y x 15. 2 16.75 17.(1.16,2.39) 18. 3三、解答题: 19.【解】:20.【解】:由已知,得3sin 1sin 1=++-x x两边同时平方,得()()3sin 1sin 1sin 12sin 1=+++-+-x x x x∴23sin 21cos 1sin 122=⇒=⇒=-x x x ∴()()()()x x x x x x cos sin sin cos sin cos∙=-∙-=-∙-ππ∴()()⎪⎪⎩⎪⎪⎨⎧-=-∙-)(,43)(,43sin cos 四象限角为第二三象限角为第一、x 、x x x ππ21【解】:(1)数据对应的散点图如图所示:x 房屋面积(cm 2)销售价格(万元)y(2)1095151==∑=i i x x ,1570)(251=-=∑=x x l i i xx ,308))((,2.2351=--==∑=y y x x l y i i i xy设所求回归直线方程为a bx y +=,则1962.01570308≈==xxxy l l b 8166.115703081092.23≈⨯-=-=x b y a 故所求回归直线方程为8166.11962.0+=x y(3)据(2),当x=150(㎡)时,销售价格的估计值为:2466.318166.11501962.0=+⨯=y(万元)22.【解】: (1)324=243×1+81243=81×3+0则 324与 243的最大公约数为 81又 135=81×1+5481=54×1+27 54=27×2+0则 81 与 135的最大公约数为27所以,三个数 324、243、135的最大公约数为 27.(2)先把二进制数()211001化为十进制数:()()104321225168001212120202111001=++++=⨯+⨯+⨯+⨯+⨯= 再把十进制数()1025化为八进制数:所以()()823111001=23.分析:(1)设从4个白球,5个黑球中,任取3个的所有结果组成的集合为I ,所求结果种数n 就是I 中元素的个数;(2)设事件A :取出的3球中2个是白球,1个是黑球,所以事件A 中的结果组成的集合是I 的子集。

2017—2018学年度第二学期数学期末考试试题班级 姓名 座号 评分 .第一部分 选择题(共75分)一、选择题(每题5分,共15题,75分)1.已知}5,4,3,2,1,0{=U ,}0,2,5{=A ,}1,2,3{=B 则=B C A C U U( )A.}2,1,0{B.}5,4,3,1,0{C.}5,3,2,1,0{D.}5,4,3,1{ 2.若条件p :3-<x ,q :5>x ,则p 是q 的( )A.充分条件B.必要条件C.充要条件D.非充分非必要条件 3.已知不等式412>-x ,则x 的范围是( ) A.()1-∞-,B.()∞+,3C.()()∞+-∞-,,31D.φ 4.下列函数在定义域内单调递增的是( )A.2+=x yB.xy )21(=C.2x y =D.x y 31log =5.不等式0652<--x x 的解集是( )A.}32|{<<-x xB.}61|{<<-x xC.}16|{<<-x xD.}61{>-<x x 或6.函数xxy -=2的定义域是 ( )A.}2|{≤x xB.}2|{≥x xC.}02|{≠≤x x x 且D.}0|{<x x 7.是第几象限角01230( )A.第一象限B.第二象限C.第三象限D.第四象限8.下列说法正确的是( )A.040sin 30sin < B.oo110sin 100sin < C.oo40cos 30cos <D.oo110cos 100cos >9.已知角α是第二象限角,21sin =α,则=αtan ( )A.33B.33-C.33±D.3-10.已知函数x x y 22+=,则该函数在区间[]2,2-上最小值为( )A.-2B.-1C.0D.2 11.已知2lg(3)lg lg 4x x -=+,则=2x( )A.1B.9C.1,9D.1,81 12.已知等差数列31=a ,115=a ,则公差=d( )A.1B.2C.3D.413.在等比数列中,已知21=a ,21=q ,则=4a ( )A.21 B.41C.81D.161 14. 已知函数)(x f 是奇函数,且1)2(=f ,则[]=-3)2(f( )A.8-B.1-C.1D.815.已知)(x f 为偶函数,且图像经过点()42-,,则下列等式恒成立的是 ( ) A.2)4(=-f B.()24-=-fC.4)2(=-fD.4)2(-=-f第二部分 非选择题(共75分)二、填空题(每小题5分,共25分) 16.若函数12)(2++=x x x f ,则=)1(f 。

2018级高二数学《数列》测试试卷(2019.10.21)(考试时间:18:40-20:40)一:选择题(共12小题,每小题5分,共60分)1、已知{a n }是等差数列,a 10=10,其中前10项和S 10=70,则其公差d 等( )A .-23B .-13 C.13 D.232、设S n 为等比数列{a n }的前n 项和,8a 2+a 5=0,则S 5S 2=( )A .11B .5C .-8D .-11 3.已知等比数列{}n a 各项都为正数,并且有294a a ⋅=,则2122210log log log a a a +++的值为( )A .10B .20C .30D .404.一张报纸,其厚度为a ,面积为b ,将此报纸对折7次,这时报纸的厚度和面积分别是( )A .b a 81,8B .b a 641,64C .b a 1281,128D .b a 2561,2565、若数列{a n }为等比数列,且a 1=1,q =2,则T n =1a 1a 2+1a 2a 3+…+1a n a n +1的结果可化为( )A .1-14nB .1-12n C.23(1-14n )D.23(1-12n ) 6、数列{a n }中,a 1=1,对所有n ≥2,都有a 1a 2a 3…a n =n 2,则a 3+a 5=( )A.6116 B.259 C.2516 D.31157、已知{a n }为等差数列,a 1+a 3+a 5=105,a 2+a 4+a 6=99.以S n 表示{a n }的前n 项和,则使得S n 达到最大值的n 是( )A .21B .20C .19D .18 8.数列{a n }中,a 1=1,a n +1=22+n n a a (n ∈N *),则1012是这个数列的第几项() A.100项 B.101项 C.102项 D.103项 9.数列{a n }满足递推公式a n =3a n -1+3n-1(n ≥2),又a 1=5,则使得{a n +λ3n}为等差数列的实数λ=( )A .2B .5C .-12 D.1210.数列{a n }满足a n+1=,若a 1=,则a 2014=( )A. B. C. D.11、将数列{3n -1}按“第n 组有n 个数”的规则分组如下:(1),(3,9),(27,81,243),…,则第100组中的第1个数是( )A .34950B .35000C .35010D .3505012、已知数列{}n a 满足:111,().2n n n a a a n N a *+==∈+若11()(1)(),n nb n n N a λ*+=-+∈ 1,b λ=-且数列{}n b 是单调递增数列,则实数λ的取值范围为 ( )A .2λ> B.3λ> C.2λ< D.3λ< 二:填空题:(共4小题,每小题5分,共20分)13.数列{}n a 的前n 项和记为n S ,111,21(1)n n a a S n +==+≥,则{}n a 的通项公式为______。

2018年全国高中数学联赛河北省预赛高二数学试题一、填空题1.已知集合,且A=B,那么_______.【答案】2【解析】【详解】由B中有三个元素知,且,故A中,即有,又若,则.此时.若,则,或,或,不满足互异性,舍去.故,,所以.2.规定:对任意,当且仅当时,,则的解集为__________.【答案】【解析】【详解】由已知得,那么,所以,故所求解集为.3.在平面直角坐标系中,若与点A(2,2)的距离为1,且与点B(m,0)的距离为3的直线恰有三条,则实数m的取值集合是________.【答案】【解析】【详解】以A为圆心,1为半径的圆,和以B为圆心,3为半径的圆相外切时,恰有三条公切线.利用AB=1+3,可得,即实数m的取值集合是.4.在矩形ABCD中,已知AB=3,BC=1,动点P在边CD上.设,,则的最大值为________.【答案】-3【解析】【详解】因为,所以问题转化为求的最小值.由等面积法可得.所以.当,即时,所求最大值为-3.5.已知且,则的最大值为________.【答案】【解析】【详解】由已知得.所以.因为,所以,设,则有点(s,t)在以(1,1)为圆心,2为半径的圆弧(第一象限及坐标轴)上.由线性规划知识直线与圆弧相切于点时,.6.若的三边长分别为8、10、12,三条边的中点分别是B、C、D,将三个中点两两连结得到三条中位线,此时所得图形是三棱锥A-BCD的平面展开图,则此三棱锥的外接球的表面积是________.【答案】【解析】【详解】由已知,四面体A-BCD的三组对棱的长分别是4、5、6.构造长方体使其面对角线长分别为4、5、6,设长方体的长、宽、高分别为x、y、z,外接球半径为R,则,得,故,所以.7.已知.则的取值范围是________.【答案】【解析】【详解】由条件知点表示单位圆上的动点与点连线的斜率大于.作图可得点P在圆弧与上运动,含点和点,不含点和点.如图:而表示原点与点P连线的斜率,由图计算得.故答案为:8.在△ABC中,,,则△ABC的面积最大值为_____.【答案】3【解析】【详解】由正弦定理将变形为,其中.以线段AC所在直线为x轴,以AC的中点O为坐标原点建立平面直角坐标系,则,,由得两边平方整理得因为,所以上述方程可化为为由此可知点B的轨迹是以为圆心,以为半径的圆.所以当点B在圆上运动时,点B到x轴的最大距离为半径,所以的面积在上单调递减,所以.二、解答题9.已知O是的外心,且,求的值.【答案】【解析】【详解】设的外接圆半径r=1,由已知得,两边平方得同理可得,所以故有所以10.设,证明:【答案】见解析【解析】【详解】因为当且仅当,即时等号成立,故原不等式得证.11.若a、b、c为正数且a+6+c=3,证明:【答案】见解析【解析】【详解】因为,同理三式相加得所以故又,所以综上可得.12.若函数的定义域为且满足条件:①存在实数,使得;②当且时,有恒成立.(1)证明:(其中);(2)判断在上的单调性,并证明你的结论;(3)当时,不等式恒成立,求实数a的取值范围.【答案】(1)见解析(2)见解析(3)【解析】【详解】因均为正数,故总存在实数使得,,所以又,所以(2)设,且,则,故可令则由(1)知即,所以在上单调递增.因为,故原不等式可化为,又在上单调递增,所以对于恒成立.因为(当且仅当时等号成立),所以,又,故.13.已知数列中,(1)求数列的通项公式;(2)求数列的前n项和.【答案】(1)(2)【解析】【详解】(1)由知令,则且由得.(2)由题意知所以两式相减得设,再利用错位相减法求得所以.14.如图,设的外接圆为,的角平分线与BC交于点D,M为BC的中点.若的外接圆分别与AB、AC交于P、Q、N为PQ的中点.证明:(1)BP=CQ;(2).【答案】(1)见解析(2)见解析【解析】【详解】(1)设在中,为的平分线,所以,故有,因此有,所以,又,由得由,得因此.(2)连结BQ、PC,并设X、Y分别为BQ、PC的中点,易证XN平行且等于MY,所以四边形为NXMY平行四边形,由CQ=BP知NX=NY,所以四边形为NXMY菱形,从而MN平分,又AD平分,,,所以.。
2018学年度第一学期高一数学期末考试试题2018年1月完卷时间为90分钟,答案请写在答题纸上一、填空题(每小题3分,共33分)1、若集合A ={x |2x –5>0},集合B ={x | x 2–2x –3<0},则集合A ∩B = 。
2、不等式的122+-x x <0的解集是 。
3、函数f (x )=112-+x x (x ≠1)的反函数是=-)(1x f 。
4、函数x y 3log =的定义域是 。
5、方程442log =x的解为 。
6、已知lg2=m ,则lg25= 。
(用含m 的代数式表示)7、若x >0,y >0,且41=xy ,则yx 11+的最小值是___________。
8、设集合A ={x | |x –a |<2},B ={y | y= –x –1,–4<x <1},若A ⊆B ,则实数a 的取值范围 。
9、已知集合{关于x 的方程ax 2 +2x+1=0的解}只含有一个元素,则实数a 的值为_____。
10、指数函数y=(a 2 –1)x 在R 上为单调递减函数,则实数a 的取值范围是 。
11、试构造一个函数f (x ),x ∈D ,使得对一切x ∈D 有|f (–x )| = |f (x )|恒成立,但是f (x )既不是奇函数又不是偶函数,则()x f 可以是 。
二、选择题(每小题3分,共12分)12、a >1且b >1是log a b >0的 ( ) (A )仅充分条件 (B )仅必要条件 (C )充要条件 (D )既非充分也非必要条13、函数y=x+a 与y=log a x 的图像可能是 ( )14、下列函数中值域为+R 的是 ( )x(A ) y = x 3 (B ) y= x –2 (C ) y=x –1 (D ) y=x15、由不全相等的正数),,2,1(n i x i =形成n 个数:,1,,1,113221nn x x x x x x +++- ,11x x n +关于这n 个数,下列说法正确的是 ( ) (A ) 这n 个数都不大于2 (B ) 这n 个数都不小于2 (C ) 至多有1-n 个数不小于2 (D ) 至多有1-n 个数不大于2 三、解答题(本大题要求写出解题步骤,共55分)16、(本题8分)已知点A (10,1)在函数f (x )=log a x 上。
上学期高二数学11月月考试题05考试时间:120分钟总分:150分选择题:(本大题共10小题,每题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列给出的赋值语句中正确的是()A.3=A B. M= -M C. B=A=2 D. x+y=02.对于程序:试问,若输入m=-4,则输出的数为()A.9 B.-7C.5或-7 D.53.图1中的程序框图的循环体执行的次数是()A.49 B.50 C.100 D.994、从装有2个红球和2个白球的口袋里任取2个球,那么互斥而不对立的两个事件是( )(A) 至少1个白球,都是白球(B) 至少1个白球,至少1个红球(C) 至少1个白球,都是红球(D) 恰好1个白球,恰好2个白球5、用秦九韶算法求多项式654323567983512)(xxxxxxxf++++-+=的值,当4-=x图1时,4v 的值为 ( ) A .220 B .124 C .-845D .-576、某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.每组命中个数的茎叶图如下.则下面结论中错误的一个是( ) A .甲的极差是29 B .乙的众数是21 C .甲罚球命中率比乙高 D .甲的中位数是247.是由一个圆、一个三角形和一个长方形构成的图形,现用红、蓝两种颜色为其涂色,每个图形只能涂一种颜色,则相邻两个图形颜色不相同的概率为( ) A.34B.38C.14D.188.一个十字路口的交通信号灯,红灯、黄灯、绿灯亮的时间分别为30秒、5秒、60秒, 则某辆车到达路口,遇见绿灯的概率为( )A. 951B. 1912C. 1910D. 1919、下面有三个游戏规则,袋子中分别装有球,从袋中无放回地取球,问其中不公平的游戏是 A. 游戏1和游戏3 B.游戏1 C. 游戏2 D. 游戏310、甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为,再由乙猜甲刚才所想的数字,把乙猜的数字记为b,其中{},1,2,3,4,5,6a b∈,若1a b-≤,就称甲乙“心有灵犀”.现任意找两人玩这个游戏,则他们“心有灵犀”的概率为( )A. 49 B.29 C.718 D.19二.填空题:(每小题5分,共25分)11、已知程序如下,若 a = 35 ,则程序运行后结果是。
(第15题图)江苏省滨海中学高一年级第三次考试数学试题(考试时间:120分钟,共150分)2005-12-14一、选择题:1.已知MP 、OM 、AT 分别为θ(42ππθ<<)的正弦线、余弦线、正切线,则一定有( )A .MP OM AT << B.OM MP AT << C.AT OM MP << D.OM AT MP <<2.半径为3cm 的圆中,有一条弧,长度为2πcm ,则此弧所对的圆心角为 ( ) A. 30 B .15 C .40 D .203.设34sin ,cos 55αα=-=,那么下列各点在角α终边上的是 ( )A .(3,4)-B .(4,3)-C .(4,3)-D .(3,4)-4.设集合,{|0},A B x x ==>R 则从集合A 到集合B 的映射f 只可能是 ( ) A .||x y x =→ B .xy x 2=→ C .x y x 2log =→ D .22x y x x →=-5.若1tan 2α=-,则2212sin cos sin cos αααα+-的值为 ( )A .3-B .13-C .13D .36.已知α为第四象限角,则πα-是第几象限角 ( )A.一 B .二 C .三 D .四 7.已知函数()sin,()tan()2x f x g x x ππ+==-,则 ( ) A .()f x 与()g x 都是奇函数 B .()f x 与()g x 都是偶函数C .()f x 是奇函数,()g x 是偶函数D .()f x 是偶函数,()g x 是奇函数8.要得到y=tan2x 的图像,只需把y=tan(2x+6π)的图像 ( ) A.向左平移6π个单位 B.向右平移6π个单位C.向左平移12π个单位 D.向右平移12π个单位9.已知θ为第二象限角,则下列四个值中,一定大于0的是 ( )A. sin 2θ B.cos 2θ C.tan 2θ D.sin 2θ10.函数x y a =≠-b(a>0且a 1)的图像不经过第一象限,则 ( )A 、11><-a b 且B 、11<<-a b 且C 、11<≥a b 且D 、11<≤a b 且11.实数x 满足θsin 1log 3+=x ,则|)9||1(|log 2-+-x x 的值为 ( ) A .22B .3C .4D .与θ有关12.若函数1()log ()(011a f x a a x =>≠+且)的定义域和值域都是[0,1],则a= ( )A .12 B C .2D .2 二、填空题:13.函数1x sin 2y -=的定义域为_____________________________. 14.函数2sin cos 1y x x =-+最小值为_________________________ .15.电流强度I (安培)随时间t (秒)变化的函数I = A sin (ωt+ϕ))0,0(>>A ω的图象如图所示,则当t = 1207(秒)时的电流强度为_______.16.设)(x f 是定义域为R,且最小正周期为π25的函数,并且 ⎩⎨⎧<<-<≤=)0(cos )0(sin )(x x x x x f ππ则)411(π-f =_______________________.江苏省滨海中学高一年级第三次考试数学试题(考试时间:120分钟,共150分)2005-12-14一、请把选择题答案填在下面的表格内:(每题5分,共60分)二、请把填空题答案填在下面的横线上:(每题4分,共16分)13. 14. 15. 16.三、解答题:本题17—21小题每题12分,22小题14分,共74分,解答应写出文字说明、证明过程或演算步骤.17.已知1cos(75),180903αα+=-<<-其中,求sin(105)cos(375)αα-+- 的值.18.已知关于221)0sin cos .x x x m θθ-+=的方程的两个根为、(1) 求m ; (2) 求sin cos 11tan 1tan θθθθ+--的值.19.已知方程2212x x x -+=-(1)请用二分法求出方程的正的近似解.(精确到0.1) (2)请用(1)的一种思想方法求解不等式2212x x x -+≥-.20.阅读与理解:给出公式:sin()sin cos cos sin αβαβαβ+=+;cos()cos cos sin sin αβαβαβ-=+; 我们可以根据公式将函数x x x g cos 3sin )(+=化为:)3sin(2)3sin cos 3cos (sin 2)cos 23sin 21(2)(πππ+=+=+=x x x x x x g(1)根据你的理解将函数()sin cos()6f x x x π=+-化为()sin()f x A x ωϕ=+的形式.(2)求出上题函数()f x 的最小正周期、对称中心及单调递增区间.21.设函数()2sin()(0,)22f x x ππωϕωϕ=+>-<<,给出三个论断:①它的图象关于8π=x 对称;②它的最小正周期为π;③它在区间]83,4[ππ以其中的两个论断作为条件,另一个作为结论,试写出你认为正确的一个命题并给予证明.22.已知函数1()log 1amxf x x -=-(0,1,1)a a m >≠≠是奇函数. (1)求实数m 的值;(2)判断函数()f x 在(1,)+∞上的单调性,并给出证明;(3)当(,2)x n a ∈-时,函数()f x 的值域是(1,)+∞,求实数a 与n 的值江苏省滨海中学高一年级第三次考试数学参考答案(考试时间:120分钟,共150分)2005-12-14一、请把选择题答案填在下面的表格内:(每题5分,共60分)二、请把填空题答案填在下面的横线上:(每题4分,共16分)13.52,2,()66k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦14.0 15.0安培 16.2 三、解答题:本题17—21小题每题12分,22小题14分,共74分,解答应写出文字说明、证明过程或演算步骤.17. 18.①2② 1219.① x 1.6≈ ② ⎛⎫-∞+∞ ⎪ ⎪⎝⎦⎣⎭20.①())6f x x π=+② T=2π,中心(,0),()6k k Z ππ-∈,递增区间22,2,()33k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦ 21.①② ⇒ ③ 解略22.解:(1)由已知条件得()()0f x f x -+=对定义域中的x 均成立.…………………………………………1分∴11log log 011aa mx mxx x +-+=--- 即11111mx mxx x +-⋅=--- …………………………………………2分 ∴22211m x x -=-对定义域中的x 均成立. ∴21m =即1m =(舍去)或1m =-. …………………………………………4分(2)由(1)得1()log 1axf x x +=- 设11221111x x t x x x +-+===+---, ∴当121x x >>时,211212122()2211(1)(1)x x t t x x x x --=-=---- ∴12t t <. …………………………………………6分当1a >时,12log log a a t t <,即12()()f x f x <.……………………………………7分∴当1a >时,()f x 在(1,)+∞上是减函数. …………………………………………8分同理当01a <<时,()f x 在(1,)+∞上是增函数. …………………………………9分 (3) 函数()f x 的定义域为(1,)(,1)+∞⋃-∞-,∴①21n a <-≤-,∴01a <<.∴()f x 在(,2)n a -为增函数, 要使值域为(1,)+∞,则1log 1121a n n a +⎧=⎪-⎨⎪-=-⎩(无解) …………………………………………11分 ②12n a ≤<-, ∴3a >.∴()f x 在(,2)n a -为减函数,要使()f x 的值域为(1,)+∞, 则11log 13a n a a =⎧⎪-⎨=⎪-⎩∴2a =1n =. …………………………………………14分。