黑龙江省哈尔滨市道里区2018-2019学年度第二学期 八年级期末质量检测 数学试题

2018-2019学年黑龙江省哈尔滨市道里区八年级（下）期末化学试卷（五四学制）1.太阳岛风景区绿道是2019年首个即将投入使用的绿道工程，已于6月20日全部完工。

下列说法错误的是()A. “绿道”的建设和使用，创造了怡人的环境B. 铺路的沥青是将石油分解得到的产品C. 绿色植物的光合作用可以把二氧化碳转化为氧气D. 建设绿道，倡导“低碳”出行，“低碳”指的是较低的二氧化碳排放2.下列实验基本操作错误的是()A. 倾倒二氧化碳B. 滴加少量液体C. 天平的使用D. 氧气的检验3.下列结构示意图中属于离子的一组是()A. ①③B. ①②C. ③④D. ②⑤4.下列情况，不发生化学变化的是()A. 霓虹灯通电发光B. 铁钉加入到硫酸铜溶液C. 检验氢气纯度D. 蜡烛燃烧生成炭黑5.下列说法正确的是()A. 用过滤的方法可以使硬水软化B. 存放易燃物和易爆物时，堆与堆之间要留有一定距离的通道C. 铜粉在空气中加热质量增加，说明该反应不遵循质量守恒定律D. 人类所需能量主要来自于风能6.下列实验现象的描述正确的是()A. 电解水：正极、负极收集到的氧气与氢气的体积比为2：1B. 硫在氧气中燃烧：淡黄色固体燃烧，放热，发出明亮的蓝紫色火焰C. 氢气还原氧化铜：黑色固体逐渐变红，试管中有气泡冒出，无色液体变白色浑浊D. 木炭在空气中燃烧：发白光，放热7.下列应用、化学方程式及基本反应类型正确的是()A. 一氧化碳用作燃料：2CO+O2− 点燃 2CO2化合反应B. 用过氧化氢溶液制氧气：2H2O2− MnO2 2H2↑+O2↑分解反应C. 用氢气冶炼金属铜：H2+CuO− △ Cu+H2O还原反应D. 用二氧化碳制汽水：CO2+H2O=H2CO3分解反应8.下列物质的用途不正确的是()A. 活性炭−防毒面具B. 氧气−气割C. 木炭−铅笔芯D. CO2−气体肥料9.下列观点解释不正确的是()选项事实解释A一氧化碳和二氧化碳性质有不同分子构成不同B金刚石和石墨性质有差异碳原子的结构不同C加油站附近能闻到汽油味分子是不断运动的D架在高处的电线夏季变得比冬季长原子间隔随温度的改变而改变A. AB. BC. CD. D10.玉米、高粱经过发酵、蒸馏可制得乙醇。

黑龙江省哈尔滨市道里区2018-2019学年八年级下学期期末数学试题学校:___________姓名：___________班级：___________考号：___________1．由线段a b c 、、组成的三角形是直角三角形的是（ ）A ．1,1,a b c ===B ．13,14,15a b c ===C ．6,8,10a b c ===D ．1,2,3a b c ===2．下列图形中，不是轴对称图形的是（ ）A ．矩形B ．菱形C ．平行四边形D ．正方形 3．用配方法解方程2230x x --=，下列配方正确的是（ ）A ．2(1)1x -=B ．2(1)1x +=C ．2(1)4x -=D ．2(1)4x += 4．在□ABCD 中，:::A B C D ∠∠∠∠的值可以是（ ）A ．1:2:3:4B ．3:2:2:3C ．2:3:2:3D ．2:2:3:3 5．下列图象中，表示y 不是x 的函数的是（ ）A ．B ．C ．D ． 6．对角线的夹角为60°的矩形，且这个角所对的边长为5cm ，则矩形的对角线长是（ ）A ．B ．20cmC ．10cmD ．7．关于x 的一元二次方程22(1)10a x x a -++-=的一个根为0，则a 为（ ）8．下列命题是真命题的是( )A ．对角线互相平分且相等的四边形是菱形B ．对角线互相平分且垂直的四边形是矩形C ．对角线互相垂直且相等的四边形是正方形D ．对角线互相平分的四边形是平行四边形9．如图，矩形纸片ABCD ，对角线为BD ，沿过点D 的直线折叠，使点A 落在对角线BD 上的点E 处，折痕DG ，若4,3AB BC ==，则AG 的长是（ ）A ．43B ．32C ．125D ．2310．甲、乙两人进行1500米比赛，在比赛过程中，两人所跑的路程y （米）与所用的时间x （分）的函数关系如图所示，则下列说法：①甲先到达终点；②完成比赛，乙比甲少用30秒；③出发2分钟后乙比甲速度快；④2分时甲、乙相距300米．其中错误的个数是（ ）A ．1个B ．2个C ．3个D ．4个 11．函数23x y x =+中，自变量x 的取值范围是______． 12．命题：如果两个实数的绝对值相等，那么这两个实数相等．此命题的逆命题是_____． 13．已知□ABCD 的周长是40,:3:1cm AB BC =，则AB 的长是_____cm ． 14．四边形ABCD 的对角线9,5AC cm BD cm ==，顺次连接四边形ABCD 各边中点所得四边形的周长等于______cm ．15．如图，一次函数y kx b =+的图象与x 轴交于点(4,0)，与y 轴交于点(0,2)，则不等式0kx b +>的解集为______．16．已知关于x 的一元二次方程2530kx x -+=有两个不相等的实数根，则k 的取值范围是__________．17．某足球比赛，要求每两支球队之间都要比赛一场，若共比赛45场，则有______支球队参加比赛．18．如图，在ABC 中901520BAC AB AC AD BC ∠=︒==⊥，，， ，垂足为D ，则BD 的长为_____．19．在△ABC 中，AB=15，AC=13，高AD=12，则ABC ∆的周长为_______________． 20．如图，矩形,ABCD ABC ∠平分线AD 交于点E ，连接CE ，过点A 作AF CE ⊥交CE 的延长线于点F ，连接,8,6DEF DF S CD ∆==，则AF 的长为______．21．（1）用因式分解法解方程：(4)312x x x +=+；（2）用公式法解方程：24630x x --=．22．方格纸中的每个小正方形的边长均为1，请分别画出符合下列要求的图形．并所画图形的各顶点必须与方格纸中的小正方形的顶点重合．（1）在图1中画一个菱形ABCD ，使得菱形ABCD 的面积为24；（2）在图2中画一个直角三角形,EFG EFG ∠为直角，其面积等于（1）中菱形ABCD 的面积，画一条线段（两端点与小正方形的顶点重合）将此直角三角形EFG 分成两个等腰三角形，并直接写出分割线段的长．23．某地区为了开发农业，决定在公路上相距25km 的A ，B 两站之间E 点修建一个土特产加工基地，使E 点到C ，D 两村的距离相等．如图，DA AB ⊥于点A ，CB AB ⊥于点B ，15km DA =，10km CB =，土特产加工基地E 应建在距离A 站多少千米的地方？24．在□ABCD 中，点E 在CD 上，点F 在AB 上，连接,AE BE CF DF DAE BCF ∠=∠、、、．（1）如图1，求证：四边形DFBE 是平行四边形；（2）如图2，连接,EF EF 平分AEC ∠，且3AB DE =，请直接写出长度等于DE 长度的2倍的线段．25．某超市销售甲、乙两种商品，乙种商品每件进价是甲种商品每件进价的3倍，购进30件甲种商品比购进15件乙种商品少花150元．（1）求甲、乙两种商品的每件进价分别是多少？（2）甲、乙两种商品每件售价分别为15元和40元，超市购进甲、乙两种商品共80件，并且购买甲种商品不多于25件，设购进a 件甲种商品，获得的总利润为W 元，求W 与a 的函数关系式，并写出自变量a 的取值范围；（3）在（2）的条件下，购买两种商品总进价不超过2000元，问该超市会有多少种进货方案？并求出获利最大的进货方案．26．已知：在正方形ABCD 中，点M 在直线BC 上，连接AM ，作CH AM ⊥交直线AM 于点H ，点N 在直线CH 上，连接MN ，且AMB NMB ∠=∠，（1）如图1，当点M 在BC 边上，求证：N BCN DAH ∠+∠=∠；（2）如图2，当点M 在BC 的延长线上，求证：CN MN AM +=；（3）如图3，在（2）的条件下，连接BH ，若2,MN CN CH ==BH 的长．27．在平面直角坐标系中，O 为坐标原点，菱形AOCB 的对角线OB 在x 轴上，A C 、两点分别在第一象限和第四象限.直线AB 的解析式为142y x =-+．（1）如图1，求点A 的坐标；（2）如图2，P 为射线OA 上一动点（不与点O 和点A 重合），过点P 作//PQ x 轴交直线AB 于点Q .设线段PQ 的长度为d ，点P 的横坐标为m ，求d 与m 的函数关系式，并直接写出自变量m 的取值范围；（3）如图3，在（2）的条件下，当点P 运动到线段OA 的延长线上时，连接PC 交x 轴于点M，连接AM，1452MAB AOB∠+∠=，延长MA交PQ于点E，过E作EF AM⊥交y轴于点,F FEM∠，的角平分线ES交x轴于点S，求点S的坐标．参考答案1．C2．C3．C4．C5．A6．C7．B8．D9．B10．A11．x ≠−312．如果两个实数相等，那么这两个实数的绝对值相等．13．15．14．1415．x ＜416．k ＜2512且k≠0． 17．1018．919．32或4220．21．（1）x 1=-4，x 2=3；（2）x 14，x 24．22．图见解析23．土特产加工基地E 应建在距离A 站10千米的地方．24．（1）见解析；（2）有：AE ，AF ，CE ，CF ，理由见解析；25．（1）甲的进价为10元，乙的进价为30元；（2）W=-5a+800，0≤a≤25，且a 为正整数；（3）有6种进货方案，且当甲购进20件，乙购进60件时，获利最大．26．（1）见解析；（2）见解析；（3）BH=．27．（1）A（4，2）；（2）d=82(04)28(4)m mm m-⎧⎨-⎩＜＜＞；（3）S（209，0）．。

2018—2019学年度（下）初中期末教学质量监测八年级数学参考答案选择题（每小题2分，共18分）二、填空题（每小题2分，共18分）10. 2021 11. −2 12. 十 13. 80°或20° 14. −415. 4 16. 2.6cm 17. 1 18.3 三、(每小题4分,共8分)19. （1）因式分解：32296y y x xy ++=)96(22x xy y y ++ ……2分 =2)3(x y y + ……4分（2）解不等式组：解：解不等式①，得 x ≤1 ……1分解不等式②，得 x<4……2分在同一数轴上表示不等式①②的解集，如图.……3分∴原不等式组的解集为：x ≤1 ……4分① ② ≥4, ⎪⎩⎪⎨⎧->+--.1321)2(3x x x x四、（每小题５分，共10分）20.（1）39631122-+÷+---+x xx x x x x =)1(3)3(3112+-⋅--++x x x x x x ……2分 =)1(111+++x x x =x1……4分 当23-=x 时,原式=231-=32- ……5分（2）解方程：14143=-+--xx x 解：方程两边都乘以4-x ,得 ……1分413-=--x x ……2分 解这个方程，得3=x ……3分 检验：将3=x 代入原方程 ……4分左边=右边=1∴原方程的根是3=x ……5分五、（每小题６分，共12分）21. （1）平移如图，△A 1B 1C 1即为所求.A 1的坐标（1,2）……3分（2） 如图，△A 2B 2C 2即为所求.A 2的坐标（−1,−2）……6分（第21题图）22.解：连接AD∵DF 垂直平分AB ，∴AD =BD =26∴∠DAB =∠B =22.5°，∠ADE =45°∵AE ⊥BC ，∴∠AED =90°∴∠EDA =∠EAD =45°∴AE = DE ，设AE= DE =a ，则222)26(=+a a∴a =6，即AE =6， ……4分在Rt △AEC 中，∵∠C =60°，∴∠EAC =30° 设EC =b ，则AC =2b ，∴36)2(22=-b b∴32=b ，即CE =32 ……6分六、(23题7分,24题8分，共15分)23.解：设摩托车速度为x 千米/时，抢修车速度是1.5x 千米/时， ……1分根据题意得：60155.13030+=x x ……3分 解这个方程得40=x ……4分 经检验：40=x 是原方程的根 ……5分 60405.15.1=⨯=x （千米/时） ……6分答：摩托车的速度为40千米/时，抢修车速度是60千米/时 ……7分 24.证明：（1）∵AO =CO ，OE =OF ，∠AOE =∠COF∴△AOE ≌△COF ，∴∠OAE =∠OCF ……2分∴AD ∥BC ，∴∠EDO =∠FBO∵OE =OF ，∠EOD =∠FOB∴△EOD ≌△FOB ， ……4分 ∴OB =OD∴四边形ABCD 是平行四边形. ……5分 （2）∵EF ⊥AC ，AO =CO ，∴AF =FC∴AB +BF +AF =AB +BF +FC =15即AB +BC =15 ……7分 ∵□ABCD 中AD =BC ，AB =CD∴□ABCD 的周长是15×2=30. ……8分七、(本题9分)A25.由)100%(801001-+=x y 得，208.01+=x y 由)50%(90502-+=x y 得，59.02+=x y∴y 1，y 2与x 的函数关系式208.01+=x y ，59.02+=x y ……2分 由y 1>y 2得 59.0208.0+>+x x 150<x ……4分 由y 1=y 2得 59.0208.0+=+x x 150=x ……6分 由y 1<y 2得 59.0208.0+<+x x 150>x ……8分∴当小明购物金额少于150元时，去乙超市合算，等于150元时去两家超市一样，多于150元时去甲超市合算. ……9分八、(本题10分)26.（1）①AE CF CP =- ……1分证明：∵AB PD ⊥∴︒=∠=∠90C PDE ， ∵BP 平分∠ABC ∴PD =PC 又∵PE =PF∴Rt △PDE ≌Rt △PCF ……2分 ∴DE =CF∵△ABC 中，∠C =90°，AC =BC ∴∠A =∠ABC =45° ∴∠APD =∠A =45° ∴AD =PD ∴AD =CP∵AD －DE =AE∴CP －CF =AE ……4分②∵△PCF ≌△PDE ∴∠DPE =∠CPF ∴∠EPF =∠DPC ∵∠ABC =45° ∴∠DPC =360°－90°－90°－45°=135°∴∠EPF =135° ……6分（2）∵∠EPF =135°，∠DPC =135°∴∠DPE =∠CPF又∵∠PCF =∠PDE =90°，PC =PD ∴△PDE ≌△PCF ∴DE =CF∵PC =PD ，∠PDB =∠PCB =90°，BP =BP ∴Rt △PCB ≌Rt △PDB∴BC =BD ……8分设DE =CF =x ，则BD =BC =x +-+163 AB =2BC =)163(2x +-+ ∵∠CFP =60°，∴∠CPF =30° ∴PF =2x ，x x x PC 3)2(22=-= ∴x PC AD PD 3===∴1633-+++=+=x x BE AE AB ∴1633)163(2-+++=+-+x x x ∴1=x ∴13+=AE ∴2332)13(321+=+=⨯=∆PD AE S AEP ……9分 （3）2)13(2m S AEP -=∆。

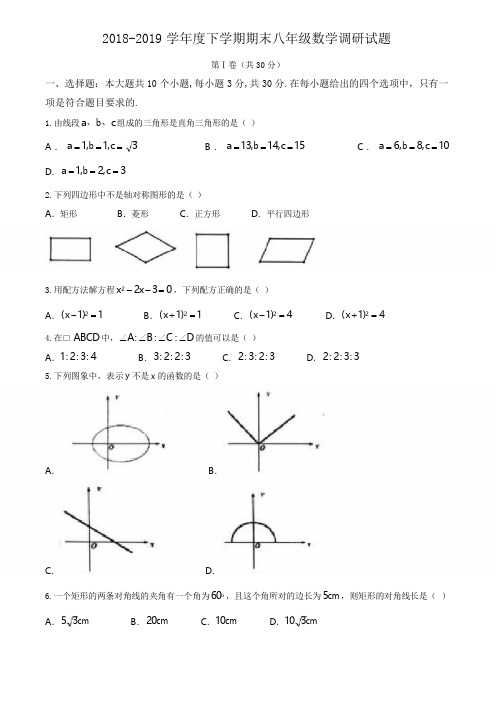
2018-2019学年度下学期期末八年级数学调研试题第Ⅰ卷（共30分）一、选择题：本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.由线段a、b、c组成的三角形是直角三角形的是（）A．a=1,b=1,c=3B．a=13,b=14,c=15C．a=6,b=8,c=10 D．a=1,b=2,c=32.下列四边形中不是轴对称图形的是（）A．矩形B．菱形C．正方形D．平行四边形3.用配方法解方程x2-2x-3=0，下列配方正确的是（）A．(x-1)2=1B．(x+1)2=1C．(x-1)2=4D．(x+1)2=44.在□ABCD中，∠A:∠B:∠C:∠D的值可以是（）A．1:2:3:4B．3:2:2:3C．2:3:2:3D．2:2:3:35.下列图象中，表示y不是x的函数的是（）A．B．C．D．6.一个矩形的两条对角线的夹角有一个角为60ο，且这个角所对的边长为5cm，则矩形的对角线长是（）A．53cm B．20cm C．10cm D．103cmA．47.关于x的一元二次方程(a-1)x2+x+a2-1=0的一个根为0，则a为（）A．1B．-1C．1或-1D．28.下列命题中正确的是（）A．对角线互相垂直且相等的四边形是正方形B．对角线互相垂直的平行四边形是矩形C．对角线互相平分且相等的四边形是菱形D．对角线互相平分的四边形是平行四边形9.如图，矩形纸片ABCD，对角线为BD，沿过点D的直线折叠，使点A落在对角线BD上的点E处，折痕DG，若AB=4,BC=3，则AG的长是（）3122B．C．D．325310.甲、乙两人进行1500米比赛，在比赛过程中，两人所跑的路程y（米）与所用的时间x（分）的函数关系如图所示，则下列说法：①甲先到达终点；②完成比赛，乙比甲少用30秒；③出发2分钟后乙比甲速度快；④2分时甲、乙相距300米.其中错误的个数是（）A．1个B．2个C．3个D．4个第Ⅱ卷（共90分）二、填空题（每题3分，满分30分，将答案填在答题纸上）11.函数y=2xx-3中，自变量x的取值范围是．12.命题：如果两个实数的绝对值相等，那么这两个实数相等.此命题的逆命题是．13.已知□ABCD的周长是40cm,AB:BC=3:1，则AB的长是cm．14.四边形ABCD的对角线AC=9cm,BD=5cm，顺次连接四边形ABCD各边中点所得四边形的周长等于cm．15.如图，一次函数y=kx+b的图象与x轴交于点(4,0)，与y轴交于点(0,2)，则不等式kx+b>0的解集为．16.已知关于x的一元二次方程kx2-4x+2=0有两个不相等的实数根，则k的取值范围是．17.某足球比赛，要求每两支球队之间都要比赛一场，若共比赛45场，则有支球队参加比赛.18.如图，在Rt∆ABC中，∠BAC=90ο,AB=15,AC=20,D、E分别是上的两点，CD=CA,BE=BA,C M⊥AD,BN⊥AE，垂足分别为M和N.则MN的长为．19.在∆ABC中，AB=15,AC=13高AD=12，则∆ABC的周长等于．20.如图，矩形ABCD,∠ABC平分线AD交于点E，连接CE，过点A作AF⊥CE交CE的延长线于点F，=8,C D=6，则AF的长为．连接DF,S∆DEF三、解答题：共60分.解答应写出文字说明、证明过程或演算步骤.第17～21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.21.（1）用因式分解法解方程：x(x+4)=3x+12；（1）用公式法解方程：4x2-6x-3=0.22.方格纸中的每个小正方形的边长均为1，请分别画出符合下列要求的图形.并所画图形的各顶点必须与方格纸中的小正方形的顶点重合.（1）在图1中画一个菱形ABCD，使得菱形ABCD的面积为24；（2）在图2中画一个直角三角形EFG,∠EFG为直角，其面积等于（1）中菱形ABCD的面积，画一条线段（两端点与小正方形的顶点重合）将此直角三角形EFG分成两个等腰三角形，并直接写出分割线段的长.图1图223.某地区为了开发农业，决定在公路上相距25km的A,B两站之间E点修建一个土特产加工基地，使E点到C、D两村的距离相等，如图，DA⊥AB于点A,C B⊥AB于点B,DA=15km,C B=10km，.求土特产加工基地E应建在距离A站多少的地方？24.在□ABCD中，点E在CD上，点F在AB上，连接AE、BE、CF、DF,∠DAE=∠BCF.（1）如图1，求证：四边形DFBE是平行四边形；（2）如图2，连接EF,EF平分∠AEC，且AB=3DE，请直接写出长度等于DE长度的2倍的线段.图1图225.某超市销售甲、乙两种商品，乙种商品每件进价是甲种商品每件进价的3倍，购进30件甲种商品比购进15件乙种商品少花150元.（1）求甲、乙两种商品的每件进价分别是多少？（2）甲、乙两种商品每件售价分别为15元和40元，超市购进甲、乙两种商品共件，并且购买甲种商品不多于25件，设购进a件甲种商品，获得的总利润为W元，求W与a的函数关系式，并写出自变量a的取值范围；（3）在（2）的条件下，购买两种商品总进价不超过2000元，问该超市会有多少种进货方案？并求出获利最大的进货方案.26.已知：在正方形ABCD中，点M在直线BC上，连接AM，作CH⊥AM交直线AM于点H，点N 在直线CH上，连接MN，且∠AMB=∠NMB，（1）如图1，当点M在BC边上，求证：∠N+∠BCN=∠DAH；（2）如图2，当点M在BC的延长线上，求证：C N+MN=AM；（3）如图3，在（2）的条件下，连接BH，若MN=2CN,C H=25，求线段BH的长.图1图2图327.在平面直角坐标系中，O为坐标原点，菱形AOCB的对角线OB在x轴上，A、C两点分别在第一象限和第四象限.直线AB的解析式为y=-12x+4.（1）如图1，求点A的坐标；（2）如图2，P为射线OA上一动点（不与点O和点A重合），过点P作PQ//x轴交直线AB于点Q.设线段PQ的长度为d，点P的横坐标为m，求d与m的函数关系式，并直接写出自变量m的取值范围；（3）如图3，在（2）的条件下，当点P运动到线段O A的延长线上时，连接PC交x轴于点M，连接AM，12∠MAB+∠AOB=45ο，延长M A交PQ于点E，过E作EF⊥AM交y轴于点F,∠FEM，的角平分线ES交x轴于点S，求点S的坐标.图1图2图3。

2018——2019学年度第二学期八年级期末质量检测试卷一、选择题1．下列图案中，不是中心对称图形的是（）A．B． C．D．2．如果a＜0，则下列式子错误的是（）A．5+a＞3+a B．5﹣a＞3﹣a C．5a＞3a D．3．下列因式分解错误的是（）A．x2﹣y2=（x+y）（x﹣y）B．x2+6x+9=（x+3）2C．x2+xy=x（x+y）D．x2+y2=（x+y）24．如图所示，在四边形ABCD中，AD∥BC，要使四边形ABCD成为平行四边形还需要条件（）A．AB=DC B．∠1=∠2 C．AB=AD D．∠D=∠B5．某地震导致某铁路隧道被严重破坏．为抢修其中一段120米的铁路，施工队每天比原计划多修5米，结果提前4天开通了列车．若原计划每天修x米，则所列方程正确的是（）A．B．C．D．6．不等式组的整数解是（）A．﹣1，0，1 B．0，1 C．﹣2，0，1 D．﹣1，17．如图，△ABC中，DE是AB的垂直平分线，AE=4，△ACD的周长为18，则△ABC的周长为（）A．18 B．22 C．24 D．268．如图，已知直角坐标系中的点A、B的坐标分别为A（2，4）、B（4，0），且P为AB的中点．若将线段AB向右平移3个单位后，与点P对应的点为Q，则点Q的坐标是（）A．（3，2） B．（6，2） C．（6，4） D．（3，5）9．如图，△ABC以点O为旋转中心，旋转180°后得到△A′B′C′．ED是△ABC的中位线，经旋转后为线段E′D′．已知BC=4，则E′D′=（）A．2 B．3 C．4 D．1.510．已知x+y=12，xy=9，则的值等于（）A．B．C．D．11．如图，平行四边形ABCD中，AB：BC=3：2，∠DAB=60°，E在AB上，且AE：EB=1：2，F是BC的中点，过D分别作DP⊥AF于P，DQ⊥CE于Q，则DP：DQ 等于（）A．3：4 B．：2C．：2D．2：12．在Rt△ABC中，AC=BC，点D为AB中点．∠GDH=90°，∠GDH绕点D旋转，DG，DH分别与边AC，BC交于E，F两点．下列结论：①AE+BF=AC，②AE2+BF2=EF2，=S△ABC，④△DEF始终为等腰直角三角形．其中正确的是（）③S四边形CEDFA．①②③④B．①②③C．①④D．②③二、填空题13．一个n边形的每个外角都等于36°，则n=．14．若分式的值为零，则m=．15．如图，△ABC中，AB=AC，D是BC边上任意一点，DF⊥AC于点F，E在AB 边上，ED⊥BC于点D，∠AED=155°，则∠EDF等于．16．如图，平行四边形ABCD绕点A逆时针旋转30°，得到平行四边形AB′C′D′（点B′与点B是对应点，点C′与点C是对应点，点D′与点D是对应点），点B′恰好落在BC边上，则∠C=度．17．如图，函数y=2x和y=ax+5的图象相交于A（m，3），则不等式2x＜ax+5的解集为．18．如图，在直线m上摆放着三个正三角形：△ABC、△HFG、△DCE，已知BC=CE，F、G分别是BC、CE的中点，FM∥AC，GN∥DC．设图中三个平行四边形的面积依次是S1，S，S3，若S1+S3=10，则S=．三、解答题19．分解因式：(1)2（m﹣n）2+m（n﹣m）；(2)（2x+y）2﹣（x+2y）2．20．并将解集在数轴上表示出来．21．计算，其中．22．某市政府计划修建一处公共服务设施，使它到三所公寓A、B、C的距离相等．(1)若三所公寓A、B、C的位置如图所示，请你在图中确定这处公共服务设施（用点P表示）的位置（尺规作图，保留作图痕迹，不写作法）；(2)若∠BAC=56°，则∠BPC=°．23．如图，在△ABC中，点D是边BC的中点，点E在△ABC内，AE平分∠BAC，CE⊥AE，点F在边AB上，EF∥BC．(1)求证：四边形BDEF是平行四边形；(2)线段BF、AB、AC的数量之间具有怎样的关系？证明你所得到的结论．24．如图，在等腰Rt△ABC中，∠ACB=90°，D为BC的中点，DE⊥AB，垂足为E，过点B作BF∥AC交DE的延长线于点F，连接CF．(1)求证：AD⊥CF；(2)连接AF，试判断△ACF的形状，并说明理由．25．为了迎接“十•一”小长假的购物高峰．某运动品牌专卖店准备购进甲、乙两种运动鞋．其中甲、乙两种运动鞋的进价和售价如下表：已知：用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同．(1)求m的值；(2)要使购进的甲、乙两种运动鞋共200双的总利润（利润=售价﹣进价）不少于21700元，且不超过22300元，问该专卖店有几种进货方案？(3)在(2)的条件下，专卖店准备对甲种运动鞋进行优惠促销活动，决定对甲种运动鞋每双优惠a（50＜a＜70）元出售，乙种运动鞋价格不变．那么该专卖店要获得最大利润应如何进货？26．在▱ABCD中，∠ADC的平分线交直线BC于点E、交AB的延长线于点F，连接AC．(1)如图1，若∠ADC=90°，G是EF的中点，连接AG、CG．①求证：BE=BF．②请判断△AGC的形状，并说明理由；(2)如图2，若∠ADC=60°，将线段FB绕点F顺时针旋转60°至FG，连接AG、CG．那么△AGC又是怎样的形状．（直接写出结论不必证明）答案一、选择题1．B．2. C．3．D．4．D．5．B．6．A．7．D．8．B．9．A．10．A 11．解：连接DE、DF，过F作FN⊥AB于N，过C作CM⊥AB于M，=S△DFA=S平行四边形ABCD，∵根据三角形的面积和平行四边形的面积得：S△DEC即AF×DP=CE×DQ，∴AF×DP=CE×DQ，∵四边形ABCD是平行四边形，∴AD∥BC，∵∠DAB=60°，∴∠CBN=∠DAB=60°，∴∠BFN=∠MCB=30°，∵AB：BC=3：2，∴设AB=3a，BC=2a，∵AE：EB=1：2，F是BC的中点，∴BF=a，BE=2a，BN=a，BM=a，由勾股定理得：FN=a，CM=a，AF==a，CE==2a，∴a•DP=2a•DQ∴DP：DQ=2：．故选：D．12．解：连接CD，如图，∵AC=BC，点D为AB中点．∠GDH=90°，∴CD=BD，∠B=∠DCA=45°，CD⊥AB，∵∠GDF=90°，即∠CDE+∠CDF=90°，而∠CDF+∠BDF=90°，∴∠CDE=∠BDF，在△CDE和△BDF中，，∴△CDE≌△BDF（AAS），∴CE=BF，DE=DF，∴AE+BF=AE+CE=AC，故①正确；∵∠EDF=90°，∴△DEF始终为等腰直角三角形，故④正确；∵△CDE≌△BDF，∴S=S△BDF，△CDE=S△CDB=S△ABC，故③正确；∴S四边形CEDF∵CE=BF，AC=BC，∴AE=CF，∵CF2+CE2=EF2，∴AE2+BF2=EF2，故②正确．故选：A．13．解：根据题意，得m+2=0，且m﹣2≠0、m+3≠0；解得m=﹣2；故答案是：﹣2．15．解：∵∠B=∠AED﹣∠BDE=155°﹣90°=65°，又∵AB=AC，∴∠C=∠B=65°，∵DF⊥AC，ED⊥BC，∴∠EDF=∠C=65°，故答案为：65°．16解：∵平行四边形ABCD绕点A逆时针旋转30°，得到平行四边形AB′C′D′（点B′与点B是对应点，点C′与点C是对应点，点D′与点D是对应点），∴AB=AB′，∠BAB′=30°，∴∠B=∠AB′B=（180°﹣30°）÷2=75°，∴∠C=180°﹣75°=105°．故答案为：105．17．解：∵点A（m，3）在函数y=2x的图象上，∴3=2m，解得m=，∴A（，3），由函数图象可知，当x＜时，函数y=2x的图象在函数y=ax+5图象的下方，∴不等式2x＜ax+5的解集为：x＜．故答案为：x＜．18．解：根据正三角形的性质，∠ABC=∠HFG=∠DCE=60°，∴AB∥HF∥DC∥GN，设AC与FH交于P，CD与HG交于Q，∴△PFC、△QCG和△NGE是正三角形，∵F、G分别是BC、CE的中点，∴BF=MF=AC=BC，CP=PF=AB=BC∴CP=MF，CQ=BC，QG=GC=CQ=AB，∴S1=S，S3=2S，∵S1+S3=10，∴S+2S=10，∴S=4，故答案为：4．19．解：(1)原式=2（m﹣n）2﹣m（m﹣n）=（m﹣n）（2m﹣2n﹣m）=（m﹣n）（m﹣2n）；(2)原式=（2x+y+x+2y）（2x+y﹣x﹣2y）=3（x+y）（x﹣y）．20．解：∵解不等式①得：x≤0，解不等式②得：x＞﹣5，∴不等式组的解集为：﹣5＜x≤0，在数轴上表示不等式组的解集为：21解：原式=÷=×=，当x=2+时，原式==．22．解：(1)如图：．(2)连接点P和各顶点，延长AP到D交BC于D，∵PA=PB，∴∠PAB=∠PBA，同理∠PAC=∠PCA，∵∠BAP+∠PAC=∠BAC=56°，∴∠PAB+∠PBA+∠PAC+∠PCA=112°，∵∠BPD=∠PAB+∠PBA，∠CPD=∠PAC+∠PCA，∴∠BPC=∠BPD+∠CPD=∠PAB+∠PBA+∠PAC+∠PCA=112°．故答案为：112．23．(1)证明：延长CE交AB于点G，∵AE⊥CE，∴∠AEG=∠AEC=90°，在△AEG和△AEC中，∴△AGE≌△ACE（ASA）．∴GE=EC．∵BD=CD，∴DE为△CGB的中位线，∴DE∥AB．∵EF∥BC，∴四边形BDEF是平行四边形．(2)解：BF=（AB﹣AC）．理由如下：∵四边形BDEF是平行四边形，∴BF=DE．∵D、E分别是BC、GC的中点，∴BF=DE=BG．∵△AGE≌△ACE，∴AG=AC，∴BF=（AB﹣AG）=（AB﹣AC）．24．(1)证明：在等腰直角三角形ABC中，∵∠ACB=90°，∴∠CBA=∠CAB=45°．又∵DE⊥AB，∴∠DEB=90°．∴∠BDE=45°．又∵BF∥AC，∴∠CBF=90°．∴∠BFD=45°=∠BDE．∴BF=DB．又∵D为BC的中点，∴CD=DB．即BF=CD．在△CBF和△ACD中，，∴△CBF≌△ACD（SAS）．∴∠BCF=∠CAD．又∵∠BCF+∠GCA=90°，∴∠CAD+∠GCA=90°．即AD⊥CF．(2)△ACF是等腰三角形，理由为：连接AF，如图所示，由(1)知：△CBF≌△ACD，∴CF=AD，∵△DBF是等腰直角三角形，且BE是∠DBF的平分线，∴BE垂直平分DF，∴AF=AD，∵CF=AD，∴CF=AF，∴△ACF是等腰三角形．25．解：(1)依题意得，=，整理得，3000（m﹣20）=2400m，解得m=100，经检验，m=100是原分式方程的解，所以，m=100；(2)设购进甲种运动鞋x双，则乙种运动鞋（200﹣x）双，根据题意得，，解不等式①得，x≥95，解不等式②得，x≤105，所以，不等式组的解集是95≤x≤105，∵x是正整数，105﹣95+1=11，∴共有11种方案；(3)设总利润为W，则W=（240﹣100﹣a）x+80（200﹣x）=（60﹣a）x+16000（95≤x≤105），①当50＜a＜60时，60﹣a＞0，W随x的增大而增大，所以，当x=105时，W有最大值，即此时应购进甲种运动鞋105双，购进乙种运动鞋95双；②当a=60时，60﹣a=0，W=16000，(2)中所有方案获利都一样；③当60＜a＜70时，60﹣a＜0，W随x的增大而减小，所以，当x=95时，W有最大值，即此时应购进甲种运动鞋95双，购进乙种运动鞋105双．26．(1)证明：①∵四边形ABCD是平行四边形，∠ABC=90°，∴四边形ABCD是矩形，∴∠ABC=90°，AB∥DC，AD∥BC，∴∠F=∠FDC，∠BEF=∠ADF，∵DF是∠ADC的平分线，∴∠ADF=∠FDC，∴∠F=∠BEF，∴BF=BE；②△AGC是等腰直角三角形．理由如下：连接BG，由①知，BF=BE，∠FBC=90°，∴∠F=∠BEF=45°，∵G是EF的中点，∴BG=FG，∠F=∠CBG=45°，∵∠FAD=90°，∴AF=AD，又∵AD=BC，∴AF=BC，在△AFG和△CBG中，，∴△AFG≌△CBG（SAS），∴AG=CG，∴∠FAG=∠BCG，又∵∠FAG+∠GAC+∠ACB=90°，∴∠BCG+∠GAC+∠ACB=90°，即∠GAC+∠ACG=90°，∴∠AGC=90°，∴△AGC是等腰直角三角形；(2)连接BG，∵FB绕点F顺时针旋转60°至FG，∴△BFG是等边三角形，∴FG=BG，∠FBG=60°，又∵四边形ABCD是平行四边形，∠ADC=60°，∴∠ABC=∠ADC=60°∴∠CBG=180°﹣∠FBG﹣∠ABC=180°﹣60°﹣60°=60°，∴∠AFG=∠CBG，∵DF是∠ADC的平分线，∴∠ADF=∠FDC，∵AB∥DC，∴∠AFD=∠FDC，∴∠AFD=∠ADF，∴AF=AD，在△AFG和△CBG中，，∴△AFG≌△CBG（SAS），∴AG=CG，∠FAG=∠BCG，在△ABC中，∠GAC+∠ACG=∠ACB+∠BCG+∠GAC=∠ACB+∠BAG+∠GAC=∠ACB+∠BAC=180°﹣60°=120°，∴∠AGC=180°﹣（∠GAC+∠ACG）=180°﹣120°=60°，∴△AGC是等边三角形．。

2019-2019学年黑龙江省哈尔滨市道里区八年级（下）期末数学试卷一、选择题（本题有10个小题，每小题3分，共30分）1．在4（x﹣1）（x+2）=5，x2+y2=1，5x2﹣10=0，2x2+8x=0，=x2+3中，是一元二次方程的个数为（）A．2个 B．3个 C．4个 D．5个2．下列四组线段中，能组成直角三角形的是（）A．a=1，b=2，c=3 B．a=2，b=3，c=4 C．a=2，b=4，c=5 D．a=3，b=4，c=5 3．函数y=kx+b的图象如图所示，则（）A．k＞0，b＞0 B．k＞0，b＜0 C．k＜0，b＞0 D．k＜0，b＜04．下列命题中，真命题的个数有（）①对角线相等的四边形是矩形；②三条边相等的四边形是菱形；③一组对边平行且相等的四边形是平行四边形．A．3个 B．2个 C．1个 D．0个5．如图，把矩形ABCD沿EF对折后使两部分重合，若∠1=50°，则∠AEF=（）A．110°B．115°C．120° D．130°6．三角形的三边长为a，b，c，且满足（a+b）2=c2+2ab，则这个三角形是（）A．等边三角形B．钝角三角形C．直角三角形D．锐角三角形7．关于x的一元二次方程x2﹣2x+2k=0有实数根，则k的取值范围是（）A．B．k≤C．D．k≥8．若把一次函数y=2x﹣3的图象向上平移3个单位长度，得到图象对应的函数解析式为（）A．y=2x B．y=2x﹣6 C．y=4x﹣3 D．y=﹣x﹣39．如图，在正方形ABCD外侧，作等边三角形ADE，AC，BE相交于点F，则∠BFC为（）A．75°B．60°C．55°D．45°10．小明的爸爸早晨出去散步，从家走了20分到达距离家800米的公园，他在公园休息了10分，然后用30分原路返回家中，那么小明的爸爸离家的距离S（单位：米）与离家的时间t（单位：分）之间的函数关系图象大致是（）A．B．C．D．二、填空题：每题3分，共30分．11．在函数y=中，自变量x的取值范围是．12．若x=2是一元二次方程x2+x+c=0的一个解，则c2=．13．正比例函数y=kx的图象经过点（﹣2，4），则k=．14．如图，在▱ABCD中，∠B=60°，∠BCD的平分线交AD点E，若CD=3，四边形ABCE的周长为13，则BC长为．15．一次函数y=2x﹣3的图象不经过第象限．16．一个凸多边形共有35条对角线，它是边形．17．四边形ABCD为菱形，该菱形的周长为16，面积为8，则∠ABC为度．18．某厂前年的产值为50万元，今年上升到72万元，这两年的年平均增长率是．19．如图，BD为矩形ABCD的对角线，点E在BC上，连接AE，AE=5，EC=7，∠C=2∠DAE，则BD=．20．如图，△ABC，AB=AC，∠BAC=90°，点D，E分别在AC，AB上，AD=AE，△ABC的高AF交BD于G，过点E作BD的垂线交BC于点H，若GF=3，CH=4，则点A到BD的距离为．三、解答题：第21题8分，第22题6分，第23-25题每题8分，第26、27题每题10分，共60分．21．解下列方程：（1）x（x﹣1）=2（x﹣1）（2）2x2﹣x﹣4=0．22．如图所示网格是由边长为1的小正方形组成，点A，B，C位置如图所示，在网格中确定点D，使以A，B，C，D为顶点的四边形的所有内角都相等．（1）确定点D的位置并画出以A，B，C，D为顶点的四边形；（2）直接写出（1）中所画出的四边形的周长和面积．23．如图，点E，F为▱ABCD的对角线BD上的两点，连接AE，CF，∠AEB=∠CFD，求证：AE=CF．24．如图，△ABC中，∠C=90°，BC=5厘米，AB=5厘米，点P从点A出发沿AC边以2厘米/秒的速度向终点C匀速移动，同时，点Q从点C出发沿CB边以1厘米/秒的速度向终点B匀速移动，P、Q两点运动几秒时，P、Q两点间的距离是2厘米？25．利民商店经销某种商品．该种商品的进价为每件80元，该商店销售商品每件售价高于进价但每件售价不超过120元，当售价定为每件120元时每天可售出200件，该商品销售单价在120元的基础上，每降1元，该种商品每天可多售出10件，设该商品的销售单价为x元，每天售出商品的数量为y件．（1）求y与x之间的函数关系式；（不必写出自变量x的取值范围）（2）利民商店在销售该商品时除成本外每天还需支付各种费用1000元，该商店某天销售该商品共获利8000元，求这一天的销售单价为多少元？26．点E在正方形ABCD的边BC上，点F在AE上，连接FB，FD，∠ABF=∠AFB．（1）如图1，求证：∠AFD=∠ADF；（2）如图2，过点F作垂线交AB于G，交DC的延长线于H，求证：DH=2AG；（3）在（2）的条件下，若EF=2，CH=3，求EC的长．27．在平面直角坐标系内，点O为坐标原点，直线y=x+3交x轴于点A，交y 轴于点B，点C在x轴正半轴上，△ABC的面积为15．（1）求直线BC的解析式；（2）横坐标为t的点P在直线AB上，设d=OP2，求d与t之间的函数关系式．（不必写出自变量取值范围）（3）在（2）的条件下，当∠BPO=∠BCA时，求t的值．2019-2019学年黑龙江省哈尔滨市道里区八年级（下）期末数学试卷参考答案与试题解析一、选择题（本题有10个小题，每小题3分，共30分）1．在4（x﹣1）（x+2）=5，x2+y2=1，5x2﹣10=0，2x2+8x=0，=x2+3中，是一元二次方程的个数为（）A．2个 B．3个 C．4个 D．5个【考点】一元二次方程的定义．【分析】根据一元二次方程的定义：只含有一个未知数，并且未知数的最高次数是2的整式方程叫一元二次方程进行分析即可．【解答】解：4（x﹣1）（x+2）=5，5x2﹣10=0，2x2+8x=0，是一元二次方程，共3个，故选：B．2．下列四组线段中，能组成直角三角形的是（）A．a=1，b=2，c=3 B．a=2，b=3，c=4 C．a=2，b=4，c=5 D．a=3，b=4，c=5【考点】勾股定理的逆定理．【分析】根据勾股定理的逆定理对各选项进行逐一分析即可．【解答】解：A、∵12+22=5≠32，∴不能构成直角三角形，故本选项错误；B、∵22+32=13≠42，∴不能构成直角三角形，故本选项错误；C、∵22+42=20≠52，∴不能构成直角三角形，故本选项错误；D、∵32+42=25=52，∴能构成直角三角形，故本选项正确．故选D．3．函数y=kx+b的图象如图所示，则（）A．k＞0，b＞0 B．k＞0，b＜0 C．k＜0，b＞0 D．k＜0，b＜0【考点】一次函数图象与系数的关系．【分析】根据函数y=kx+b的图象所经过的象限与单调性回答．【解答】解：根据图象知，函数y=kx+b的图象经过第一、二、四象限，∴k＜0，b＞0．故选C．4．下列命题中，真命题的个数有（）①对角线相等的四边形是矩形；②三条边相等的四边形是菱形；③一组对边平行且相等的四边形是平行四边形．A．3个 B．2个 C．1个 D．0个【考点】命题与定理．【分析】利用矩形的判定方法、菱形的判定方法及平行四边形的判定方法分别判断后即可确定正确的选项．【解答】解：①对角线相等且平分的四边形是矩形，故错误，错误，是假命题；②三条边相等的四边形是菱形，错误，是假命题；③一组对边平行且相等的四边形是平行四边形，正确，是真命题，故选C．5．如图，把矩形ABCD沿EF对折后使两部分重合，若∠1=50°，则∠AEF=（）A．110°B．115°C．120° D．130°【考点】翻折变换（折叠问题）．【分析】根据折叠的性质，对折前后角相等．【解答】解：根据题意得：∠2=∠3，∵∠1+∠2+∠3=180°，∴∠2=÷2=65°，∵四边形ABCD是矩形，∴AD∥BC，∴∠AEF+∠2=180°，∴∠AEF=180°﹣65°=115°．故选B．6．三角形的三边长为a，b，c，且满足（a+b）2=c2+2ab，则这个三角形是（）A．等边三角形B．钝角三角形C．直角三角形D．锐角三角形【考点】勾股定理的逆定理．【分析】对等式进行整理，再判断其形状．【解答】解：化简（a+b）2=c2+2ab，得，a2+b2=c2所以三角形是直角三角形，故选：C．7．关于x的一元二次方程x2﹣2x+2k=0有实数根，则k的取值范围是（）A．B．k≤C．D．k≥【考点】根的判别式．【分析】判断上述方程的根的情况，只要看根的判别式△=b2﹣4ac的值的符号就可以了．【解答】解：∵a=1，b=﹣2，c=2k，∴△=b2﹣4ac=22﹣4×1×（2k）=4﹣8k，关于x的一元二次方程x2﹣2x+2k=0有实数根，∴4﹣8k≥0，解得k≤．故选B．8．若把一次函数y=2x﹣3的图象向上平移3个单位长度，得到图象对应的函数解析式为（）A．y=2x B．y=2x﹣6 C．y=4x﹣3 D．y=﹣x﹣3【考点】一次函数图象与几何变换．【分析】根据上下平移k不变，b值加减即可得出答案．【解答】解：将直线y=2x﹣3向上平移3个单位后的直线解析式y=2x﹣3+3=2x．故选A9．如图，在正方形ABCD外侧，作等边三角形ADE，AC，BE相交于点F，则∠BFC为（）A．75°B．60°C．55°D．45°【考点】正方形的性质；全等三角形的判定与性质；等边三角形的性质．【分析】由正方形的性质和等边三角形的性质得出∠BAE=150°，AB=AE，由等腰三角形的性质和内角和得出∠ABE=∠AEB=15°，再运用三角形的外角性质即可得出结果．【解答】解：∵四边形ABCD是正方形，∴∠BAD=90°，AB=AD，∠BAF=45°，∵△ADE是等边三角形，∴∠DAE=60°，AD=AE，∴∠BAE=90°+60°=150°，AB=AE，∴∠ABE=∠AEB==15°，∴∠BFC=∠BAF+∠ABE=45°+15°=60°；故选：B．10．小明的爸爸早晨出去散步，从家走了20分到达距离家800米的公园，他在公园休息了10分，然后用30分原路返回家中，那么小明的爸爸离家的距离S（单位：米）与离家的时间t（单位：分）之间的函数关系图象大致是（）A．B．C．D．【考点】函数的图象．【分析】本题是分段函数的图象问题，要根据行走，休息，回家三个阶段判断．【解答】解：第10﹣20分，离家的距离随时间的增大而变大；20﹣30分，时间增大，离家的距离不变，函数图象与x轴平行；30﹣60分，时间变大，离家越来越近．故选：D．二、填空题：每题3分，共30分．11．在函数y=中，自变量x的取值范围是x≠﹣2．【考点】函数自变量的取值范围．【分析】根据分式有意义，分母不等于0列式计算即可得解．【解答】解：由题意得，x+2≠0，解得x≠﹣2．故答案为：x≠﹣2．12．若x=2是一元二次方程x2+x+c=0的一个解，则c2=36．【考点】一元二次方程的解．【分析】根据一元二次方程的解的定义，把x=2代入方程x2+x+c=0即可求得c 的值，进而求得c2的值．【解答】解：依题意，得22+2+c=0，解得，c=﹣6，则c2=（﹣6）2=36．故答案为：36．13．正比例函数y=kx的图象经过点（﹣2，4），则k=﹣2．【考点】一次函数图象上点的坐标特征．【分析】直接把点（﹣2，4）代入y=kx，然后求出k即可．【解答】解：把点（﹣2，4）代入y=kx得解得：k=﹣2，故答案为：﹣214．如图，在▱ABCD中，∠B=60°，∠BCD的平分线交AD点E，若CD=3，四边形ABCE的周长为13，则BC长为5．【考点】平行四边形的性质．【分析】利用平行四边形的对边相等且互相平行，进而得出DE=CD=3，再求出AE+BC=7，BC﹣AE=3，即可求出BC的长．【解答】解：∵CE平分∠BCD交AD边于点E，∴∠ECD=∠ECB，∵在平行四边形ABCD中，AD∥BC，AB=CD=3，AD=BC，∠D=∠B=60°，∴∠DEC=∠ECB，∴∠DEC=∠DCE，∴DE=CD=3，∴△CDE是等边三角形，∴CE=CD=3，∵四边形ABCE的周长为13，∴AE+BC=13﹣3﹣3=7①，∵AD﹣AE═DE=3，即BC﹣AE=3②，由①②得：BC=5；故答案为：5．15．一次函数y=2x﹣3的图象不经过第二象限．【考点】一次函数的性质．【分析】先根据一次函数的性质判断出此函数图象所经过的象限，再进行解答即可．【解答】解：∵一次函数y=2x﹣3中，k=2＞0，∴此函数图象经过一、三象限，∵b=﹣3＜0，∴此函数图象与y轴负半轴相交，∴此一次函数的图象经过一、三、四象限，不经过第二象限．故答案为：二．16．一个凸多边形共有35条对角线，它是十边形．【考点】一元二次方程的应用；多边形的对角线．【分析】设它是n边形，从任意一个顶点发出的对角线有n﹣3条，则n边形共有对角线条，即可列出方程：，求解即可．【解答】解：设它是n边形，根据题意得：=35，解得n1=10，n2=﹣7（不符题意，舍去），故它是十边形，故答案为：十．17．四边形ABCD为菱形，该菱形的周长为16，面积为8，则∠ABC为30或150度．【考点】菱形的性质．【分析】此题菱形的形状不确定所以要分当∠A为钝角和锐角时分别求出∠ABC 的度数即可．【解答】解：如图1所示：当∠A为钝角，过A作AE⊥BC，∵菱形ABCD的周长为l6，∴AB=4，∵面积为8，∴AE=2，∴∠ABE=30°，∴∠ABC=60°，当∠A为锐角是，过D作DE⊥AB，∵菱形ABCD的周长为l6，∴AD=4，∵面积为8，∴DE=2，∴∠A=30°，∴∠ABC=150°，故答案为：30或150．18．某厂前年的产值为50万元，今年上升到72万元，这两年的年平均增长率是20%．【考点】一元二次方程的应用．【分析】由于设每年的增长率为x，那么去年的产值为50（1+x）万元，今年的产值为50（1+x）（1+x）万元，然后根据今年上升到72万元即可列出方程．【解答】解：设每年的增长率为x，依题意得50（1+x）（1+x）=72，即50（1+x）2=72．解得：x=0.2，x=﹣2.2（舍去）故答案为：20%19．如图，BD为矩形ABCD的对角线，点E在BC上，连接AE，AE=5，EC=7，∠C=2∠DAE，则BD=13．【考点】矩形的性质．【分析】直接利用矩形的性质结合等腰直角三角形的性质得出AB，BE的长，再利用勾股定理得出BD的长．【解答】解：∵四边形ABCD是矩形，∴∠ABC=∠C=90°，AD∥BC，∵∠C=2∠DAE，∴∠DAE=45°，∴AB=BE，∵AE=5，∴AB=BE=5，∵EC=7，∴AD=BC=12，∴BD==13．故答案为：13．20．如图，△ABC，AB=AC，∠BAC=90°，点D，E分别在AC，AB上，AD=AE，△ABC的高AF交BD于G，过点E作BD的垂线交BC于点H，若GF=3，CH=4，则点A到BD的距离为．【考点】全等三角形的判定与性质；等腰直角三角形．【分析】如图，作AM⊥EH于M，AN⊥BD于N交BC于T，CK⊥AT于K交EH 的延长线于P，BD交EH于Q．连接AQ．首先证明AQ平分∠EQD，推出四边形AMQN是正方形，由△ABN≌△CAK，推出AM=CK，PK=CK，由TK∥PH，推出CT=TH=2，由△BFN≌△AFT，推出NF=TF=3，FH=1，BF=CF=5，在Rt△BNF中，可得BN==，由△CTK∽△BNF，得到=，求出CK即可解决问题．【解答】解：如图，作AM⊥EH于M，AN⊥BD于N交BC于T，CK⊥AT于K交EH的延长线于P，BD交EH于Q．连接AQ．∵AE=AD，∠EAD=90°，∴∠ADE=∠AED=45°，∵EH⊥BD，∴∠EQD=90°，∴∠EQD+∠EAD=180°，∴A、E、Q、D四点共圆，∴∠AQE=∠ADE=45°，∠AQD=∠AED=45°，∴AQ平分∠EQD，∵AM⊥MQ，AN⊥QD，∴AM=AN，则易知四边形AMQN是正方形，四边形AMPK是矩形，∴AM=PK，在△ABN和△CAK中，，∴△ABN≌△CAK，∴AM=CK，∴PK=CK，∵TK∥PH，∴CT=TH=2，在△BFN和△AFT中，，∴△BFN≌△AFT，∴NF=TF=3，∴FH=1，∴BF=CF=5，在Rt△BNF中，BF=5，FN=3，∴BN==，由△CTK∽△BNF，∴=，∴=，∴CK=．∴AN=CK=．故答案为．三、解答题：第21题8分，第22题6分，第23-25题每题8分，第26、27题每题10分，共60分．21．解下列方程：（1）x（x﹣1）=2（x﹣1）（2）2x2﹣x﹣4=0．【考点】解一元二次方程﹣因式分解法；解一元二次方程﹣公式法．【分析】（1）方程移项后，提取公因式，利用两数相乘积为0两因式中至少有一个为0转化为两个一元一次方程来求解；（2）方程利用公式法求出解即可．【解答】解：（1）方程移项得：x（x﹣1）﹣2（x﹣1）=0，分解因式得：（x﹣1）（x﹣2）=0，解得：x1=1，x2=2；（2）这里a=2，b=﹣1，c=﹣4，∵△=1+32=33，∴x=．22．如图所示网格是由边长为1的小正方形组成，点A，B，C位置如图所示，在网格中确定点D，使以A，B，C，D为顶点的四边形的所有内角都相等．（1）确定点D的位置并画出以A，B，C，D为顶点的四边形；（2）直接写出（1）中所画出的四边形的周长和面积．【考点】勾股定理．【分析】（1）根据题意可知以A，B，C，D为顶点的四边形是矩形，作出矩形ABCD 即为所求；（2）根据勾股定理可求AB、CD的长度，再根据进行的周长公式和面积公式计算即可求解．【解答】解：（1）如图所示：（2）AB==，BC==2，周长为（2+）×2=6，面积为2×=10．23．如图，点E，F为▱ABCD的对角线BD上的两点，连接AE，CF，∠AEB=∠CFD，求证：AE=CF．【考点】平行四边形的性质．【分析】由平行四边形的性质得出AB=CD，∠BAE=∠CDF，由AAS证明证得△ABE ≌△CDF，继而证得结论．【解答】证明：∵四边形ABCD是平行四边形，∴AB=CD，AB∥CD．∴∠BAE=∠DCF，在△ABE和△CDF中，，∴△ABE≌△CDF（AAS）．∴AE=CF．24．如图，△ABC中，∠C=90°，BC=5厘米，AB=5厘米，点P从点A出发沿AC边以2厘米/秒的速度向终点C匀速移动，同时，点Q从点C出发沿CB边以1厘米/秒的速度向终点B匀速移动，P、Q两点运动几秒时，P、Q两点间的距离是2厘米？【考点】一元二次方程的应用．【分析】首先表示出PC和CQ的长，然后利用勾股定理列出有关时间t的方程求解即可．【解答】解：设P、Q两点运动x秒时，P、Q两点间的距离是2厘米．在△ABC中，∠C=90°，BC=5厘米，AB=5厘米，∴AC===10（厘米），∴AP=2x 厘米CQ=x厘米CP=（10﹣2x）厘米，在Rt△CPQ内有PC2+CQ2=PQ2，∴（10﹣2x）2+x2=（2）2，整理得：x2﹣8x+12=0，解得：x=2或x=6，当x=6时CP=10﹣2x=﹣2＜0，∴x=6不合题意舍去．∴P、Q两点运动2秒时，P、Q两点间的距离是2厘米．25．利民商店经销某种商品．该种商品的进价为每件80元，该商店销售商品每件售价高于进价但每件售价不超过120元，当售价定为每件120元时每天可售出200件，该商品销售单价在120元的基础上，每降1元，该种商品每天可多售出10件，设该商品的销售单价为x元，每天售出商品的数量为y件．（1）求y与x之间的函数关系式；（不必写出自变量x的取值范围）（2）利民商店在销售该商品时除成本外每天还需支付各种费用1000元，该商店某天销售该商品共获利8000元，求这一天的销售单价为多少元？【考点】一次函数的应用；一元二次方程的应用．【分析】（1）首先利用当售价定为每件120元时每天可售出200件，该商品销售单价在120元的基础上，每降1元，该种商品每天可多售出10件，进而求出每天可表示出销售商品数量；（2）设商场日盈利达到8000元时，每件商品售价为x元，根据每件商品的盈利×销售的件数=商场的日盈利，列方程求解即可．【解答】解：（1）由题意得：y=200+10=﹣10x+1400；（2）由题意可得：（﹣10x+1400）（x﹣80）﹣1000=8000，整理得：x2﹣220x+12100=0，解得：x1=x2=110，答：这一天的销售单价为110元．26．点E在正方形ABCD的边BC上，点F在AE上，连接FB，FD，∠ABF=∠AFB．（1）如图1，求证：∠AFD=∠ADF；（2）如图2，过点F作垂线交AB于G，交DC的延长线于H，求证：DH=2AG；（3）在（2）的条件下，若EF=2，CH=3，求EC的长．【考点】四边形综合题．【分析】（1）利用等腰三角形的性质结合正方形的性质得出AF=AD，则∠AFD=∠ADF；（2）首先得出四边形AGHN为平行四边形，得出FM=MD，进而NF=NH，ND=NH，即可得出答案；（3）首先得出△ADN≌△DCP（ASA），进而PC=DN，再利用在Rt△ABE中，BE2+AB2=AE2，求出答案．【解答】（1）证明：∵∠ABF=∠AFB，∴AB=AF，∵四边形ABCD为正方形，∴AB=AD，∴AF=AD，∴∠AFD=∠ADF；（2）证明：如图1所示：过点A作DF的垂线分别交DF，DH于M，N两点∵GF⊥DF，∴∠GFD=∠AMD=90°，∴AN∥GH，∵四边形ABCD为正方形，∴AG∥NH，∴四边形AGHN为平行四边形，∴AG=NH，∵AF=AD，AM⊥FD，∴FM=MD，连接NF，则NF=ND，∴∠NFD=∠NDF，∵∠NFD+∠NFH=∠NDF+∠H，∴∠NFH=∠H，∴NF=NH，∴ND=NH，∴DH=2NH=2AG；（3）解：延长DF交BC于点P，如图2所示：∵四边形ABCD为正方形，∴AD∥BC，∴∠ADF=∠FPE，∴∠PFE=∠AFD=∠ADF=∠FPE，∴EF=EP=2，∵∠DAM+∠ADM=∠ADM+∠PDC，∴∠DAM=∠PDC，∵四边形ABCD为正方形，∴AD=DC，∠ADN=∠DCP，在△ADN和△DCP中，∴△ADN≌△DCP（ASA），∴PC=DN，设EC=x，则PC=DN=x+2，DH=2x+4，∵CH=3，∴DC=AB=BC=AF=2x+1∴AE=2x+3，BE=x+1，在Rt△ABE中，BE2+AB2=AE2，∴（x+1）2+（2x+1）=（2x+3）2．整理得：x2﹣6x+7=0，解得：x1=7，x2=﹣1（不合题意，舍去）∴EC=7．27．在平面直角坐标系内，点O为坐标原点，直线y=x+3交x轴于点A，交y轴于点B，点C在x轴正半轴上，△ABC的面积为15．（1）求直线BC的解析式；（2）横坐标为t的点P在直线AB上，设d=OP2，求d与t之间的函数关系式．（不必写出自变量取值范围）（3）在（2）的条件下，当∠BPO=∠BCA时，求t的值．【考点】一次函数综合题．【分析】（1）先求出点A，B坐标，用△ABC的面积为15，求出点C的坐标，用待定系数法求出直线BC解析式；（2）在Rt△OPD中，有OP2=OD2+PD2，代入化简得d=t2+3t+9，（3）先判断出∠EBA=∠OBA，再分两种情况，①点P在第一象限，用PD=OD建立方程求出t，②当点P位于如图2所示P1位置时，用P1O=PO，建立方程求解即可．【解答】解：直线y=x+3交x轴于点A，交y轴于点B，当x=0时y=3，当y=0时，x=﹣6，∴A（﹣6，0）B（0，3），∴OA=6，OB=3，=AC×OB=（OA+OC）×OB．∴S△ABC∴15=（6+OC）×3∴OC=4，∴C（4，0），设直线BC的解析式为y=kx+b，则：∴k=∴直线BC的解析式为y=﹣x+3．（2）横坐标为t的点P在直线AB上，∴P（t，t+3）过点P作x轴的垂线，点D为垂足，如图1，∴D（t，0）在Rt△OPD中，有OP2=OD2+PD2∴d=t2+（t+3）2=t2+3t+9，（3）在在Rt△OBC内有BC2=OB2+OC2∴BC==5过点A作BC的垂线，点E为垂足，如图2S△ABC=BC•AE=15，∴AE=6∴AO=AE，∵∠AEB=∠AOB=90°∴∠EBA=∠OBA当点P位于第一象限时，∠BOP=∠ABO﹣∠APO=∠EBO﹣∠BCO=（∠EBO﹣∠BCO）=∠BOC=45°∴∠POD=∠PDO=45°， ∴PD=OD ，∴t +3=t ，∴t=6当点P 位于如图2所示P 1位置时，∠BP 1O=∠BCA=∠BPO ∴P 1O=PO ，∴P 1O 2=PO 2，∴t 2+3t +9=×62+3×6+9，解得：t=﹣或t=6（舍去）综上所述：当∠BPO=∠BCA 时t 的值为6或﹣．2019年3月13日。

2019学年黑龙江省哈尔滨市道里区八年级下期末物理试卷【含答案及解析】姓名___________ 班级____________ 分数__________一、选择题1. 下列数据估测不符合实际的是（）A．托起两个鸡蛋用的力约1NB．起重机的机械效率是100%C．海平面上的大气压强约1000hPaD．中学生站立时对地面的压力约500N2. 如图所示的做法中，目的是为了减小摩擦的是（）A．运动鞋底装鞋钉B．轴承中装有滚珠C．汽车轮胎刻有花纹D．用力握紧球拍3. 如图所示的用具中，属于费力杠杆的是（）A．镊子B．钳子C．起子D．剪子4. 下列实例中，应用了减小压强的是（）A．“森林医生”啄木鸟有尖锐的喙B．剪刀有锋利的刃C．沙漠中的越野汽车装有非常宽大的轮子D．订书机锋利的订书订5. 下列事例中，属于连通器的是（）A．船闸 B．微小压强计 C．轮船 D．飞机的机翼6. 下列有关力的说法中，正确的是（）A．手拍桌子时，手对桌子施加了力，桌子对手没有施加力B．力的作用效果与力的大小、方向和作用点都有关系C．弹簧被拉伸时产生的力是弹力，钢丝绳悬挂重物的力不是弹力D．重力的方向总是垂直向下7. 大量的实验和理论研究表明，使用任何机械都不能省功，这个结论是（）A．阿基米德原理 B．伯努利原理C．功的原理 D．杠杆平衡原理8. 下列图象中正确表示大气压与高度的关系的是（）A． B．C． D．9. 下列物理知识的叙述错误的是（）A．自然界的流水和风都是大量机械能的天然资源B．水轮机带动发电机可以将水的机械能转化为电能C．汽车方向盘是常见的轮轴，可以达到省力的作用D．定滑轮的作用是省力，但不改变动力的方向10. 借助简单机械将重物提升，若不计滑轮重量及摩擦，以下装置最省力的是（）A． B．C． D．11. 把两个体积相同的小球分别放入盛满水的两个溢水杯中．当小球静止时如图所示，甲杯中溢出50g水，乙杯中溢出30g水，下列结论中不正确的是（）A．在甲、乙两杯中小球排开水的质量之比5：3B．在甲、乙两杯中小球受到的浮力之比5：3C．甲球的质量是50gD．乙球的质量是30g12. 如图，用滑轮组提升重物时，重800N的物体在10s内匀速上升了1m．已知拉绳子的力F为500N，则提升重物的过程中（）A．绳子自由端被拉下3m B．做的有用功是1000JC．拉力F的功率是80W D．滑轮组的机械效率是80%二、填空题13. 汽车刹车后不会立即停下，这是因为汽车具有，车速会逐渐变小，是由于受到地面摩擦力的作用，这说明力可以改变物体的．14. 如图所示，两只纸船浮在水面上静止不动，用大注射器向两船之间的水面快速注水，两船将会（选填“分开”或“靠近”），原因是两船中间的水流动．15. 如图甲所示，物体甲重40N，被50N的水平压力F甲压在竖直墙壁上保持静止．如图乙所示，物体乙重60N，在35N的水平拉力F乙作用下，沿水平桌面匀速向右运动．则物体甲受到的摩擦力f甲为 N，物体乙受到的摩擦力f乙为 N．16. 如图是测大气压值的实验，最早测出大气压数值的科学家是托里拆利，实验中玻璃管竖直放置的优点是便于测量玻璃管内外水银面的差（选填“高度”或“长度”）．高压锅的原理是锅内气压增大，水的沸点（选填“升高”、“不变”或“降低”）．17. “神州七号”载人飞船的返回舱下落到地面附近时，由于受到阻力而做减速运动，在减速下降的过程中，动能，机械能．（填“增大”、“减小”或“不变”）．18. 如图所示，甲、乙两支完全相同的试管，分别装有质量相等的不同液体．甲试管竖直放置，乙试管倾斜放置，两试管液面相平．则甲、乙两试管内液体的密度ρ甲ρ乙，液体对两试管底的压强p甲 p乙．（两空均填“＞”、“＜”、“=”）19. “青岛号”导弹驱逐舰满载时的排水量是4800吨，表示它浮在海平面上，排开的海水质量是4800吨，此时舰所受的浮力是 N．当舰从海洋驶入长江时，所受的浮力（选填“变大”“变小”或“不变”）（ρ海水＞ρ江水）20. 小华同学用60N的水平推力，推放在水平地面上重500N的物体，使其做匀速直线运动．若该物体在10s内移动了5m，则在此过程中它的速度为 m/s，小华做的功是J，功率是 W．21. 小明要把重100N的沙子运到6m高的三楼上，手拉绳子的功率为72W，拉动时间为10s．此过程中小明对沙子做的有用功是 J，滑轮组的机械效率．三、作图题22. 图中木球漂浮在水中，请画出该球的受力示意图．23. 如图所示的是汽车液压刹车装置的一部分，该装置中AOB实为一个杠杆，O是杠杆的支点，B为阻力作用点，画出刹车时B点所受的阻力F2示意图和动力臂L1．四、实验题24. 小明正在对比复习“探究液体压强与哪些因素有关”的实验和“探究影响浮力大小的因素”实验．（1）图1是小明用微小压强计探究“影响液体压强因素”的三个实验装置：①要探究液体深度相同时，液体的压强与液体的密度是否有关，应选取装置乙和装置（选填“甲”或“丙”）来进行研究．②要探究液体密度相同时，液体的压强与液体的深度是否有关，应选取装置甲和装置乙来进行研究；得出的结论是．（2）图2是小明用弹簧测力计探究“影响浮力大小强的因素”的实验装置图．物体静止时，弹簧测力计示数分别如图所示．①物体A浸没在水、盐水中所受浮力大小之比为．②对比实验序号①②③可得出的实验结论是．（3）两个实验对比，小明加深了对液体压强和浮力的理解，浸没在液体中的物体浸入越深，受到液体压强，受到的浮力．25. 小明同学回顾“探究杠杆的平衡条件”的实验时的情景．（1）小明将杠杆中点置于支架上，当杠杆静止时，发现杠杆的左端上翘，此时，他应将杠杆两端的平衡螺母向（选填“左”或“右”）调节，使杠杆在水平位置平衡．杠杆这样放置是为了在挂上钩码后，便于在杠杆上直接读出．（2）如图1所示，若每个钩码重0.5N，且杠杆上每格相等，小明在杠杆左端图示位置处挂上3个钩码，为使杠杆在水平位置平衡，他在图中A处用弹簧测力计施加一个方向向上的力F1，此弹簧测力计的示数至少是 N．（3）如图2，小明用弹簧测力计拉杠杆的C点，使杠杆在水平位置保持平衡．当弹簧测力计由位置1转至位置2的过程中，杠杆在水平位置始终保持平衡，测力计示数变化情况是．（4）第（2）问“探究杠杆的平衡条件”和探究”滑动摩擦力的影响因素”实验中都用到了弹簧测力计，小明对比总结了弹簧测力计使用方法和注意事项，在测力前，前者和后者两个实验中弹簧测力计使用不同之处是，在测力时，两个实验中弹簧测力计使用相同之处是．参考答案及解析第1题【答案】第2题【答案】第3题【答案】第4题【答案】第5题【答案】第6题【答案】第7题【答案】第8题【答案】第9题【答案】第10题【答案】第11题【答案】第12题【答案】第13题【答案】第14题【答案】第15题【答案】第16题【答案】第17题【答案】第18题【答案】第19题【答案】第20题【答案】第21题【答案】第22题【答案】第23题【答案】第24题【答案】第25题【答案】。