第一学期初二数学期中测试卷

第一学期八年级数学期中考试试卷我们要多多参考一下数学题目，可能看多就会了呢，今天小编就给大家来看看八年级数学，欢迎大家学习一下哦第一学期八年级数学期中试卷一.选择题(本大题共 10 小题，每小题 4 分，满分 40 分)1. 下列图形中为轴对称图形的是( )2. 下列各组线段中,能组成三角形的是( )A. 4,5,6B. 6,8,15C. 5,7,12D. 3,9,133. 点 M(3，﹣4)关于 x 轴的对称点M′的坐标是( ) A.(3，4) B.(﹣3，﹣4) C.(﹣3，4) D.(﹣4，3)4. 如图的伸缩门，其原理是( )A.三角形的稳定性B.四边形的不稳定性C.两点之间线段最短D.两点确定一条直线5. 如图,AD 是△ABC 的角平分线,AE⊥BC 于点 E,若∠BAC=110°,∠B=24°,则∠DAE 的度数是( ) A. 10° B. 11° C. 14° D. 16°6. 如图，已知 AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC 的是( )A.CB=CDB.∠BAC=∠DACC.∠BCA=∠DCAD.∠B=∠D=90°(第 5 题图)7. 如图，在△ABC 中，AD 是它的角平分线，AB=8cm，AC=6cm，则S△ABD：S△ACD=( )A.3：4B.4：3A. 16：9 D.9：168. 如图，用尺规作图“过点 C 作CN∥OA”的实质就是作∠DOM=∠NCE，其作图依据是( ) A.SAS B.SSS C.ASA D.AAS9. 如图示，把长方形纸片 ABCD 纸沿对角线折叠，设重叠部分为△EBD，那么，有下列说法：①△EBD 是等腰三角形，EB=ED;②折叠后∠ABE 和∠CBD 一定相等;③折叠后得到的图形是轴对称图形;④△EBA 和△EDC 一定是全等三角形.其中正确的有( ) A.1 个 B.2 个C.3 个D. 4 个10. 如图,坐标平面内一点 A(2,-1),O 为原点,P 是 x 轴上的一个动点,如果以点 P,O,A 为顶点的三角形是等腰三角形,那么符合条件的动点P 的个数为( )A. 2B. 3C. 4D. 5二.填空题(本大共 4 小题，每小题 5 分，满分 20 分)11. 一辆汽车的车牌号在水中的倒影是，那么它的实际车牌号是： .12.等腰三角形的一个角是50°，则它一腰上的高与底边的夹角为 .13. 如图，∠A+∠B+∠C+∠D+∠E= 。

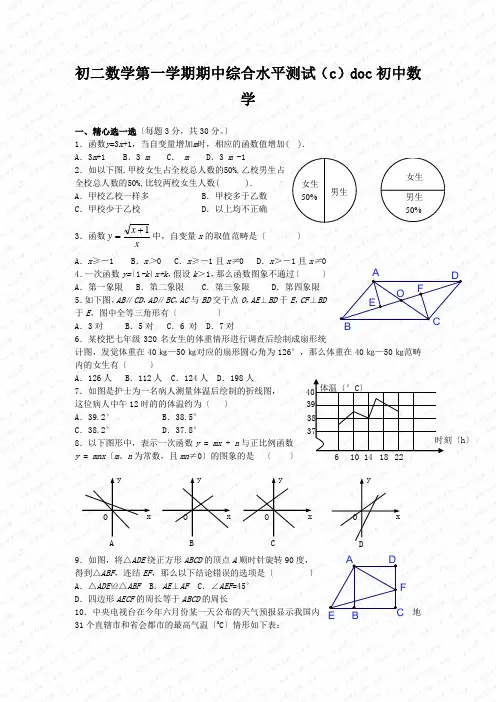
37 38 39 40 体温〔°C 〕 时刻〔h 〕6 10 14 18 22女生 50% 男生男生 50%女生 初二数学第一学期期中综合水平测试（c ）doc 初中数学一、精心选一选〔每题3分，共30分。

〕1．函数y =3x +1，当自变量增加m 时，相应的函数值增加( ). A ．3m +1 B ．3 m C ． m D ．3 m -12．如以下图,甲校女生占全校总人数的50%,乙校男生占全校总人数的50%,比较两校女生人数( ). A ．甲校乙校一样多 B ．甲校多于乙数 C ．甲校少于乙校 D ．以上均不正确 3．函数xx y 1+=中，自变量x 的取值范畴是〔 〕 A ．x ≥－1 B ．x ＞0 C ．x ≥－1且x≠0 D ．x ＞－1且x≠04．一次函数y=〔1-k 〕x+k ，假设k ＞1，那么函数图象不通过〔 〕A ．第一象限B ．第二象限C ．第三象限D ．第四象限5．如下图，AB ∥CD ，AD ∥BC ，AC 与BD 交于点O ，AE ⊥BD 于E ，CF ⊥BD 于E ，图中全等三角形有〔 〕 A ．3对 B ．5对 C ．6 对 D ．7对 6．某校把七年级320名女生的体重情形进行调查后绘制成扇形统计图，发觉体重在40㎏—50㎏对应的扇形圆心角为126°，那么体重在40㎏—50㎏范畴内的女生有〔 〕A ．126人B ．112人C ．124人D ．198人7．如图是护士为一名病人测量体温后绘制的折线图， 这位病人中午12时的的体温约为〔 〕 A ．39.2° B ．38.5° C ．38.2° D ．37.8° 8．以下图形中，表示一次函数y = mx + n 与正比例函数 y = mnx 〔m 、n 为常数，且mn ≠0〕的图象的是 〔 〕9．如图，将△ADE 绕正方形ABCD 的顶点A 顺时针旋转90度，得到△ABF ，连结EF ，那么以下结论错误的选项是〔 〕 A ．△ADE ≌△ABF B ．AE ⊥AF C ．∠AEF =45° D ．四边形AECF 的周长等于ABCD 的周长10．中央电视台在今年六月份某一天公布的天气预报显示我国内地31个直辖市和省会都市的最高气温〔0C 〕情形如下表：A O y xB O y xC O y xD O y x F D CE A B 第3题O A B DCE FADB E CF5060 70 80 9010 20 30 ℃℉气温〔0C 〕 18 21 22 23 24 25 27 28 29 30 32 33 35 36 都市数 11131315431412那么能够显示这些都市在这一天数据的分布情形，可绘制〔 〕 A ．条形图 B ．扇形图 C ．折线图 D ．直方图 二、耐心填一填〔每题3分，共30分〕1．如下图是温度计的示意图，左边的刻度表示摄氏温度，℉右边的刻度表示华氏温度华氏〔℉〕温度y 与摄氏〔℃〕温度x 之间的函数关系式为___ _. 2．弹簧挂上物体后会伸长，测得一弹簧的长度y (cm)与所挂物体的重量x (kg)有关系：x 0 1 2 3 4 5 6 7 8y1212.5 13 13.5 14 14.5 15 15.5 16那么弹簧总长y (cm)与所挂物体质量x (kg)之间的函数关系式为 ． 3．直线32-=x y 可由直线x y 2=向 平移 得到．4．如图，∠ABC =∠DEF ，AB =DE ，要讲明△ABC ≌△DEF 假设以〝SAS 〞为依据，还要添加的条件为______________． 5．一次函数1)2(++=x m y ，函数y 的值随x 值的增大而增大，那么m 的取值范畴是 ．6．如下图：要测量河岸相对的两点A 、B 之间的距离，先从B 处动身与AB 成90°角方向，向前走50米到C 处立一根标杆，然后方向不变连续朝前走50米到D 处，在D 处转90°沿DE 方向再走17米，到达E 处，使A 、C 与E 在同一直线上，那么测得A 、B 的距离为_____米．7．把一组64个数据的样本分成8组，从第一组到第四组的频数分不为5、7、11、13，第五组到第七组的频率差不多上0.125，那么第八组的频率为 ． 8．如图是某校九年级一班50名学生的一次数学测验成绩的扇形统计图，按图中划分的分数段，这次测验成绩中所占百分比最大的分数段是_________________．9．点A(2，4)在正比例函数的图象上，那个正比例函数的解析式是 ． 10．直线6+=x y 与x 轴,y 轴围成一个三角形,那么那个三角形面积为 (平方单位)． 三、认真答一答〔只要你认真摸索, 认真运算, 一定会解答正确的!〕60分—69分70分—79分80分—84分85分以上22%28%36%14%1234551015206t/时s/千米l l 121．〔8分〕如图是小陈同学骑自行车内学的路程与时刻的关系图，请你依照图像描述他上学路上的情形．2、〔10分〕为了了解某初中学生的体能情形，抽取假设干名学生在单位时刻内进行引体向上测试，将所得数据整理后，画出频数分布直方图〔如图〕，图中从左到右依次为第1、2、3、4、5组．（1） 求抽取多少名学生参加测试？（2） 处于哪个次数段的学生数最多？〔答出是第几组即可〕 （3） 假设次数在5次〔含5次〕以上为达标， 求这次测试的达标率． 3、〔8分〕：AB 平分∠CAD ，AC =AD ．求证：BC =BD ．4、〔10分〕如图，1l 反映了甲离开A 的时刻与离A 地的距离的关系，2l 反映了乙离开A 地的时刻与离A 地的距离之间的关系，依照图象填空：〔1〕当时刻为2小时时，甲离A 地 千米，乙离A 地 千米。

专业课原理概述部分一、选择题（每题1分，共5分）1. 下列哪个数是质数？A. 21B. 23C. 27D. 302. 如果一个三角形的两边长分别是8厘米和15厘米，那么第三边的长度可能是多少？A. 3厘米B. 23厘米C. 17厘米D. 25厘米3. 下列哪个数是偶数？A. 101B. 102C. 103D. 1044. 下列哪个数是负数？A. 5B. 0C. 3D. 85. 下列哪个数是立方数？A. 8B. 27C. 64D. 125二、判断题（每题1分，共5分）1. 两个质数的和一定是偶数。

（）2. 所有的偶数都是2的倍数。

（）3. 1是质数。

（）4. 任何数乘以0都等于0。

（）5. 所有的奇数都是质数。

（）三、填空题（每题1分，共5分）1. 1的相反数是______。

2. 9的平方根是______。

3. 2的立方是______。

4. 24的因数有______。

5. 一个等边三角形的内角是______度。

四、简答题（每题2分，共10分）1. 解释什么是质数。

2. 解释什么是偶数。

3. 解释什么是因数。

4. 解释什么是等边三角形。

5. 解释什么是立方数。

五、应用题（每题2分，共10分）1. 一个长方形的周长是18厘米，长是7厘米，求宽。

2. 一个等腰三角形的底边长是8厘米，腰长是5厘米，求周长。

3. 一个数的平方是36，求这个数。

4. 一个数的立方是27，求这个数。

5. 一个数的因数有1、2、3、4，求这个数。

六、分析题（每题5分，共10分）1. 分析一个数的因数和倍数的关系。

2. 分析一个等边三角形的内角和为180度的原因。

七、实践操作题（每题5分，共10分）1. 用直尺和圆规画一个等边三角形。

2. 用直尺和圆规画一个正方形。

八、专业设计题（每题2分，共10分）1. 设计一个实验，验证“两个质数的和一定是偶数”这个命题。

2. 设计一个实验，验证“所有的偶数都是2的倍数”这个命题。

3. 设计一个实验，验证“1是质数”这个命题。

1 二OO 三学年第一学期初二数学期中质量抽测试卷一．填空题。

（每题3分，共30分）1．81的平方根是 。

2．等腰三角形中两边长分别为3cm 和7cm ，则周长为 cm 。

3．在空格中填入“＜”或“＞”或“=”3。

4．的计算结果是 。

5．如图1，已知D 、E 是△ABC 中BC 边上的两点，AD=AE ， 请你再附加一个条件 ，使△ABE ≌△ACD 。

6．正三棱锥中，过三个侧面的公共顶点P 作底面的垂线，垂足应该是底面正三角形 线的交点。

7．已知33.7=1.940，且3a =－19.40，则a = 。

8．若等腰三角形一腰上的高线长是腰长的一半，则底角等于 度。

9．某人到海岛上去探宝，登陆后先往东走8千米，又往北走2千米，遇到障碍又往西走3千米，再折向北走到6千米处往东一拐，仅走1千米找到了宝藏，则登陆点与宝藏 埋藏处的线段长为 千米。

10．如图2，△ABC 是Rt △，BC 是斜边，P 为△ABC 内一点， 将△ABP 绕点A 逆时针旋转后得到△ACP ’，连结PP ’。

若AP=3，则PP ’的长等于 。

二．选择题（每小题3分，共30分）11．实数31，42，6中，无理数的个数是 （ ） A ．0个 B ．1个 C ．2个 D ．3个12．若下列各组数为边长，不能组成直角三角形的是 （ ）A ．3，4，5，B ．5，12，13C ．8，15，17D ．6，8，913．若a 满足2a ＋a =0，则 （ ）A ．a ＞0B ．a ≥0C ．a ＜0D ．a ≤014．用反证法证明“三角形的内角中，至少有一个不大于60°”时应假设 （ ）A ．其中一个小于或等于60°B ．其中一个角大于60°C ．三个角都大于60°D ．三个角都小于或等于60°15．下列定理中没有逆定理的是 （ ）A ．等腰三角形的底角相等B ．全等三角形对应边相等C ．全等三角形的对应角相等D ．若a＞b ，则a ＞b ≥016．如图3，在△ABC 中，已知∠B 和∠C 的平分线相交于点F ，过点F 作DE ∥BC ，交AB 于点D ，交AC 于点E ，若BD ＋CE=9，则线段DE 的长为 （ ） A B DE C 图1图2A。

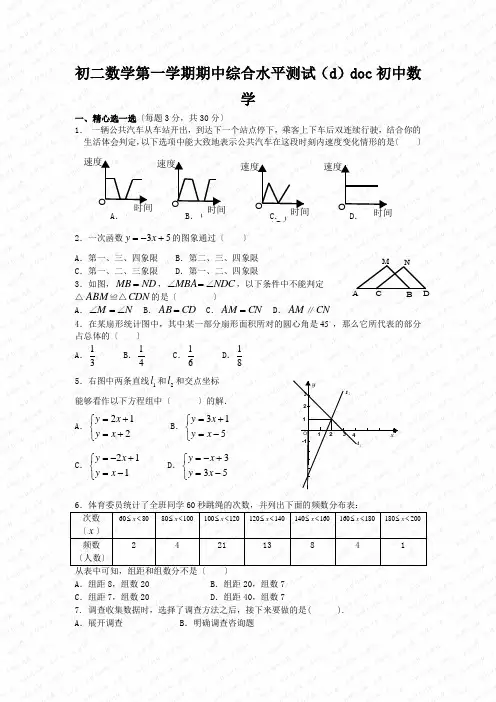
初二数学第一学期期中综合水平测试（d）doc初中数学 一、精心选一选〔每题3分，共30分〕 1． 一辆公共汽车从车站开出，到达下一个站点停下，乘客上下车后双连续行驶，结合你的生活体会判定，以下选项中能大致地表示公共汽车在这段时刻内速度变化情形的是〔 〕

2．一次函数53xy的图象通过〔 〕 A．第一、三、四象限 B．第二、三、四象限 C．第一、二、三象限 D．第一、二、四象限 3．如图，NDMB，NDCMBA，以下条件中不能判定 △ABM≌△CDN的是〔 〕 A．NM B．CDAB C．CNAM D．AM∥CN 4．在某扇形统计图中，其中某一部分扇形面积所对的圆心角是45，那么它所代表的部分占总体的〔 〕

A．31 B．41 C．61 D．81

5．右图中两条直线1l和2l和交点坐标 能够看作以下方程组中〔 〕的解．

A．212xyxy B．513xyxy

C．112xyxy D．533xyxy 6．体育委员统计了全班同学60秒跳绳的次数，并列出下面的频数分布表： 次数 〔x〕 8060x 10080x 120100x 140120x 160140x 180160x 200180x

频数 〔人数〕 2 4 21 13 8 4 1 从表中可知，组距和组数分不是〔 〕 A．组距8，组数20 B．组距20，组数7 C．组距7，组数20 D．组距40，组数7 7. 调查收集数据时，选择了调查方法之后，接下来要做的是( ). A．展开调查 B．明确调查咨询题

ABDC

MN

12

l1

4321

321O

y

x-1

O时间

速度O时间

速度O时间

速度O时间

速度

（A）（B）（C）（D）

A． B． C． D． A B C E

F

A

B C

D

中国20%印度

18%

其他国家62%

C．记录调查结果 D．确定调查对象 8. 如图，△ABC≌△AEF，AB与AE，AC与AF是对应边，那么∠EAC等于〔 〕 A．∠ACD B．∠BAF C．∠CAF D．∠BAC

初二上册数学期中考试试卷一、选择题（每题3分，共30分）1. 下列哪个选项是正数？A. -3B. 0C. 2D. -22. 计算下列哪个表达式的结果是负数？A. 5 - 3B. 3 + (-2)C. 4 × 2D. 6 ÷ 23. 下列哪个图形是轴对称图形？A. 平行四边形B. 梯形C. 等腰三角形D. 不规则多边形4. 一个数的相反数是-7，那么这个数是？A. 7B. -7C. 0D. 145. 以下哪个选项是不等式？A. 3x + 2 = 11B. 4y - 6 > 0C. 5z - 3 < 0D. 所有选项都是6. 计算下列哪个表达式的结果是0？A. 3 × 0B. 0 ÷ 5C. 0 - 0D. 0 + 07. 一个数的绝对值是5，那么这个数可能是？A. 5B. -5C. 5或-5D. 都不是8. 下列哪个选项是二次根式？A. √4B. √(-4)C. √0D. √(2/3)9. 一个数的平方是16，那么这个数是？A. 4B. -4C. 4或-4D. 都不是10. 计算下列哪个表达式的结果是正数？A. (-3) × (-2)B. (-4) ÷ 2C. (-5) + (-3)D. (-6) - (-8)二、填空题（每题3分，共30分）11. 一个数的立方是-8，那么这个数是______。

12. 一个数的平方根是2，那么这个数是______。

13. 一个数的倒数是1/3，那么这个数是______。

14. 一个数的绝对值是3，那么这个数可能是______或______。

15. 计算2的平方根是______。

16. 计算(-5)的相反数是______。

17. 计算3的平方是______。

18. 计算4的立方根是______。

19. 计算5的绝对值是______。

20. 计算6的倒数是______。

三、解答题（每题10分，共40分）21. 解下列方程：2x - 5 = 922. 解下列不等式：3y + 7 > 1123. 计算下列表达式的值：(-2)³ + 4 × (-3)² - 524. 证明：如果一个角的补角是120°，那么这个角是60°。

中学八年级第一学期数学期中试卷双向细目表命题人：王**新泾中学2013学年度第一学期八年级数学期中试卷 考试时间：90分钟 满分：100分 、填空题（本大题共 题，每题分，共分）1.计算：122 33 =2.当x 时，J2x 1有意义 3 .化简： x 2y(x 0)=.4 .如图1,数轴上点A 所对应的数为a ,化简：J （1 ―才45 .分母有理化：1136 .不等式2V2x 拆 0的解集是 .7 .如果J x 5与J 2是同类二次根式，那么 x 的值可以是 （只需写出一个）. 8 .如果方程（m 1）x 2mx 10是一元二次方程，那么 m 的取值范围是、…2一9 .万程x 1 4 0的根是A-'1 0 1 2 a■ 图110.如果关于x的一元二次方程x23（m 1）x m 3 0有一个根是0,那么m15 . ,'x y 的一个有理化因式是16 .下列二次根式中，最简二次根式是211 .在实数范围内因式分解：2x 3x112 .有一块面积为 1000平方米的长方形草地，它的长比宽多30米，那么这块草地的宽为米.13 .将命题“全等三角形对应边上的中线相等”改写成“如果……，那么”的形队：14 .如图2,已知0比 AOB 勺平分线，DC OB 那么△ DOC .定是 三角形，若 AOB=12度，则△DO)定是(填按边分类的所属类型)二、选择题(本大题共 4题，每题3分，共12分)(A) xx y(B) Vx 旧 (C)7x 7y(D)Jx y“2(B) 26x (C) ...x 3y(D) x 2 2xy y 217.下列各组二次根式中，属于同类二次根式的是V18(A) '2；(C) 133；18.下列命题中，假命题是 (B )河与河;(D) 3.5和 15(A) 三条直线相交，最多有 3个交点; (B) 两条直线被第三条直线所截，内错角相等;(0 在同一平面内, 平行于同一条直线的两条直线平行;(D) 在同一平面内, 垂直于同一条直线的两条直线平行.三、简答题(本大题共5题，每题6分，共30分)m19.化简：2n— ,n20.计算：(.0.5 2, 3)(18 .27).21.用配方法解方程：x24x 2 0. 22 ,解方程：(x 2)(x 1) 10.23.已知：如图3,在△ABC^, AB=AC点H E分别在边AB BC上，DE// AC求证：DB=DE四、解答题：(本大题共3题，每题7分，共21分)24.已知关于x的一元二次方程x2 2mx (m 2)(m 1) 0 (m为常数)(1)如果方程有两个不相等的实数根，求m的取值范围；(2)如果方程有两个相等的实数根，求m的值；(3)如果方程没有实数根，求m的取值范围.25 .恒利商厦九月份的销售额为 200万元，十月份的销售额下降了 20%商厦从十一月份起 加强管理，改善经营，使销售额稳步上升，十二月份的销售额达到了万元， 求这两个月的平均增长率.26 .已知：如图4,在△ABC43, BE 、CF 分别是边 AC AB 上的高，BP = AC, CQ = AB , 求证：AP = AQ.五、证明题［本大题只有1题，第(1)小题2分，第(2)小题7分，共9分］27 .如图5,在△ABC 3, AB= AC D 是CB 延长线上的一点，/ D= 60° , E 是AD上的一点,DE= DB(2)试添加辅助线，猜想线段 AE 、BE 和BC之间的大小关系，并加以证(1)求证: △ DEB 是等边三角形。

2021学年第一学期八年级期中质量监测参考答案一、选择题1.C2.C3.B4.A5.B6.A二、填空题7. 1≥x 8.a -3 9.5,021==x x 10.3-2-＞x 11.1-12. 二、四 13.2- 14. 41≤a 15.)21)(2(2--x x 16.%20 17.6 18.6230＞或＜＜k k 三、计算题.19解：原式=12432223+-++-----------1分+2分+2分 332221++=----------1分 .20解：原式=x yx y x ⋅⋅⨯⨯224552----------------1分+1分 =4x ---------------1分+1分=2x ---------------2分.21解：4)3(232=--x x -------------1分02322=--x x -----1分0)12)(2(=+-x x -----1分解得：21=x 或212-=x -----2分 ∴原方程的根是21=x 或212-=x -----1分 .22解： 22470x x --=7422=-x x2722=-x x …………………………1分 127122+=+-x x()2712=-x ……………… 2分 2231±=-x 22311+=x ，22312-=x …………………………2分 所以原方程的根是13211-=x ，13211--=x ---------------1分 .23 （1） △=()4412k k k ⋅-+=12+k ∵方程有两个不相等的实数根∴012>+k 解的21->k ………………2分 又∵关于x 的一元二次方程04)1(2=+++k x k kx ∴0≠k∴k 的取值范围：21->k 且0≠k ………………1分 （2）由题意得312=+k ，解得k=1……………………………1分 原方程04122=++x x 解得2321+-=x ，2322--=x ……………………………2分四、解答题.24解：设农产品礼包每包降价x 元时，这种农产品在4月份可获利4620元--------1分根据题意，可列方程为：4620)5400)(15(=+-x x ---------------3分0276652=-+x x --- ---1分解得：4),(6921=-=x x 舍去------------2分答：设农产品礼包每包降价4元时，这种农产品在4月份可获利4620元----1分.25（1）50 …………1分（2）40 …………1分（3）8 …………1分（4） 740…………2分 （5）t S 8=（500≤≤t ）…………2分+1分.2628.（1）21=k …………2分 （2）5)1,2,//=∴BM M M OA y BM B （则于点轴，交直线作过点…………1分 2515212521=⨯⨯-⨯⨯=-=∴∆∆∆ABM OBM OAB S S S …………2分 （3）当点C 在点A 的右侧时或)1时（当>a 255-=∴∆a S ABC 当点C 在点A 的左侧时或)1时（当<a 255aS ABC -=∴∆ （共3分，答对一个给2分）.27（1）∵点)8,6(A 在正比例函数上∵设正比例函数的解析式为)0(≠=k kx y 即k 68=---------------1分 解得34=k ---------------1分∵正比例函数的解析式为x y 34=---------------1分 （2）∵点B 的坐标为)0,12(∵OB=12---------------1分 ∵点Q 在直线AO 上运动 且OBQ ∆的面积为6过点Q 向x 轴作垂线段，垂足为H 则621=⋅⋅=∆QH OB S OBQ 解得1=QH ---------------1分∵点Q 的坐标为)1,43(),1,43(21--Q Q ---------------1分+1分 （2）∵AO=AB∵∵QOP=∵CBP∵∵OPQ 与∵BPC 全等∴∵当OP=BC=5,QO=BP 时， ∵OP=5∵12-2t=5 解得27=t ---------------1分∵OP=5,∵OQ=BP=7∵AQ=3 ∵327=v 解得76=v ---------------1分即点Q 运动的速度是76个单位/秒②当6,5====PB OP BC OQ 时， ∵621===OB PB OP∵62=t解得3=t ---------------1分 ∵5=OQ∵5510=-=-=OQ OA AQ ∵53=v 解得35=v ---------------1分即点Q 运动的速度是35个单位/秒综上，当点Q 的运动速度为76或35个单位/秒时，OPQ ∆与BPC ∆会全等。

初二数学第一学期期中综合水平测试（a ）doc 初中数学一、耐心填一填〔每题3分，共30分〕1．假如3(2)k y k x -=-是正比例函数，那么k =______，且y 随x 的增大而______． 2．一次函数22y mx x =+-，y 随x 的增大而增大，那么m 的取值范畴是______． 3．要了解一天的气温变化情形，可采纳______统计图．4．七〔1〕班一次数学测试成绩优秀的有20人，良好的有15人，及格的有5人，没有不及格的同学，制成扇形统计图时，成绩优秀的所占圆心角的度数是______，良好的所占圆心角的度数是______．5．如图1，△ABC 中，AB AC =，EB EC =，那么由〝SSS 〞能够判定______≌______．6．一次函数24y x =-+的图象通过的象限是______，它与x 轴的交点坐标是______，与y 轴的交点坐标是______，y 随x 的增大而______． 7．〝两个锐角对应相等〞_______〔填〝能〞或〝不能〞〕判不两个直角三角形全等．8．按照年龄把某校七~九年级学生分为四种情形：①13岁与不足13岁的；②14岁的；③15岁的；④16岁与大于16岁的． 只要明白其中______种情形显现的频率，就能够画出扇形统计图．9．如图2，AE ⊥BD 于C ，AB ED =，AC EC =，那么AB 与ED 的关系是______．10．2y -与3x +成正比例，且当x =1时，2y =-，那么y 与x 之间的函数解析式为______．二、精心选一选〔每题3分，共30分〕1．在圆的面积公式2πS r =中，不是变量的是〔 〕． A ．S ，r B ．r C ．π D ．S2．一次函数24y mx m =+-的图象通过原点，那么m 的值为〔 〕． A ．0 B ．4 C ．4- D ．4或4-3．最适合用来描述全校各年级男、女生人数情形的统计图是〔 〕． A ．直方图 B ．条形统计图 C ．扇形统计图 D ．以上均能够 4．某中学举行一次演讲竞赛，分段统计参赛同学的成绩，结果如下表：分数段/分 60~69 70~79 80~89 90~100 人数/名2864成绩在90分~100分的同学为优胜者，那么优胜率为〔 〕． A ．5% B ．10% C ．15% D ．20% 5．以下讲法中正确的有〔 〕． ①三边对应相等的两个三角形全等； ②两个等边三角形全等； ③两个等腰三角形全等； ④两个直角三角形全等； ⑤全等三角形的对应边相等．ADE C图1B ADECB 图2A ．1个B ．2个C ．3个D ．4个6．在△ABC 和A B C '''△中，假设从条件：①AB A B ''=;②BC B C ''=;③AC A C ''=;④A A '=∠∠;⑤B B '=∠∠;⑥C C '=∠∠．选取三个为条件，那么不能保证ABC A B C '''△≌△的是〔 〕．A ．①②③B ．①③④C ．①④⑤D ．④⑤⑥7．如图3，DE ⊥AB 于E ，DF ⊥AC 于F ，AE AF =，那么以下结论成立的是〔 〕． A ．BD=CD B ．DE=DF C ．∠B =∠C D ．AB =AC8．如图4，直线y=kx+b 与x 轴交于点(4-，0)，那么0y >时，x 的取值范畴是〔 〕． A ．4x >- B ．x ＞0 C ．x ＜4- D ．x ＜9．弹簧的长度与所挂物体的质量的关系为一次函数，如图5所示，由图可知不挂物体时弹簧的长度为〔 〕．A ．7cmB ．8cmC ．9cmD ．10cm10．如图6，向放在水槽底部的烧杯注水〔流量一定〕，注满烧杯后，连续注水，直至注满水槽，水槽中水面上升高度h 与注水时刻t 之间的函数关系大致是以下图象中的〔 〕．三、用心想一想〔本大题共60分〕1．(此题10分)一次函数114y k x =-与正比例函数22y k x =的图象都通过点(2，1-)，求这两个函数图象与y 轴围成的三角形的面积．2．(此题11分)用四根小木棒扎风筝，要求:风筝的两脚的大小相同，即∠B =∠C ．小红是如此扎的：取AC =BD ，AB =CD 的四根小木棒，扎成如图7的形状．如此做行吗?什么缘故?3．(此题12分)如图8，是一个路程随时刻变化的图象，请你依照图中所提供的信息，结合实际写出一个生活片断．(你能够在s 轴上标出一些数据)A DC B 图3 E F y x 图4 O 4- y x 图5 O 2012.55 20图6A D C 图7B4．(此题12分)为加强公民节约用水，减少污水排放的环保意识，某都市制定了以下用水收费标准〔含都市污水处理费〕：每户每月用水未超过28m时，按1.2元/3m收费；每户每月用水超过83m收费．设某户每月m仍按原标准收费，超过部分按1.9元/3m时，其中的83用水量为x(3m)，应交水费为y(元)．〔1〕分不写出用水未超过83m时，y与x之间的函数关系式；m和超过83〔2〕某用户五月份共交水费13.4元，咨询该用户五月份用水多少立方米．5．(此题15分)〔1〕如图9，△ABC中，AB=AC，∠BAC=90°，分不过B，C向过点A的直线做垂线，垂足分不为E，F，那么EF和BE，CF有什么关系呢？请讲明理由．〔2〕如图10，假设过点A的直线与斜边相交时，其他条件不变，你能得到什么结论？请讲明理由．参考答案：一、1．4，增大 2．>2m - 3．折线 4．180°，135° 5．△ABE ，△ACE 6．一、二、四，〔2，0〕，〔0，4〕，减小 7．不能 8．三 9．平行且相等 10．1y x =-- 二、1．C 2．B 3．B 4．D 5．B 6．D 7．B 8．A 9．D 10．B 三、1．解：在坐标系中画出这两个函数的图象如图： 图中两个函数图象与y 轴围成的三角形的底可看作4，高看作2，因此1S =42=42⨯⨯△．2．行．证明：连接AD ，在△ABD 和△DCA 中，AB DC AC DB AD DA =⎧⎪=⎨⎪=⎩，，，∴△ABD ≌△DCA (SSS)． ∴∠B =∠C ． 3．略．4．解：〔1〕当用水未超过38m 时：y =1.2x (0≤x ≤8)； 当用水超过38m 时： 1.9 5.6( 8)y x x =->；〔2〕明显此用户用水超过38m ，代入 1.9 5.6y x =-，得13.4 1.9 5.6x =-． 解得x =10．因此该用户五月份用水310m ． 5．〔1〕有EF BE CF =+． 证明：∵∠BAC =90°, ∴∠EAB +∠CAF =90°． 又∵BE EF CF EF ⊥⊥，， ∴∠EAB =∠FCA ，∠EBA =∠FAC ． 在△ABE 和△CAF 中， EAB FCA AB CA EBA FAC =⎧⎪=⎨⎪=⎩，，， ∴△ABE ≌△CAF (ASA)． ∴BE AF AE CF ==，． ∴EF AF AE BE CF =+=+． 〔2〕有EF BC CF =-． 证明:∵∠BAC =90°, ∴∠BAE +∠CAF =90°． ∵BE AF CF AF ⊥⊥，， ∴∠BAE =∠ACF ，∠ABE =∠CAF ．在△ABE和△CAF中，BAE ACF AB CA ABE CAF=⎧⎪=⎨⎪=⎩，，，∴(ASA)ABE CAF△≌△．∴BE AF AE CF==，．∴EF AF AE BE CF=-=-．。