分数除法解决问题例2
- 格式:ppt
- 大小:2.91 MB
- 文档页数:27

分数除法解决问题专项训练1.甲乙两人从相距13千米的两地同时出发相向而行,经过3小时相遇。
甲每小时行5千米,求乙每小时行多少千米。
2.一个水果店分两次运一批水果,第一次运了50千克,第二次运了70千克,两次正好运完这批水果,求这批水果的总重量。
3.六年级一班男生23人,女生22人,全班学生占六年级学生总数的十分之一,求六年级学生总数。
4.一个饲养小组养了白兔和黑兔共18只,其中黑兔的只数是白兔的五分之一,求白兔和黑兔各有多少只。
5.XXX买了一枝圆珠笔和一枝钢笔,共用去12元,圆珠笔的单价是钢笔的五分之三,求圆珠笔和钢笔的单价各是多少元。
6.一套西装160元,其中裤子的价格是上衣的五分之三,求上衣和裤子的价钱各是多少元。
7.打字员打了一部书稿,第一天打了12页,第二天打了13页,这两天打的页数占这部书稿的五分之十二,求这部书稿的总页数。
8.XXX收集的火柴盒上的画比XXX收集的多60枚,XXX收集的火柴盒上的画是XXX的五分之一,求XXX和XXX收集的火柴盒上的画各是多少枚。
9.一个建筑工地九月份上半月用水泥18吨,下半月用的水泥是上半月的九分之一,求九月份一共用了多少水泥。
10.一支工程队修一条公路,第一天修了38米,第二天修了42米,第二天比第一天多修的是这条路全长的二十八分之一,求这条路的全长。
11.一张课桌比一把椅子贵10元,如果椅子的单价是课桌单价的五分之三,求课桌和椅子的单价各是多少元。
12.一条水渠修了五分之三,还剩240米没有修,求这条水渠的总长。
13.一根电线杆,埋在地下的部分是全长的十三分之一,露出地面的部分是5米,求这根电线杆的总长。
14.人造地球卫星每秒运行8千米,比宇宙飞船的速度慢57倍,求宇宙飞船每秒运行多少千米。
15.一个县去年绿色蔬菜总产量是720万千克,今年比去年增产十分之一,求今年全县绿色蔬菜总产量是多少万千克。
16.一个畜牧场卖出肉牛头数的,还剩250头,求这个畜牧场原有多少头肉牛。

二、解决问题
1、全世界有60亿人,全世界约有53
的人没有充足的淡水保障。
全世
界没有充足淡水保障的人有多少亿。
2、学校买了900本书,其中六年级分得这些书的9
2,五年级分的本数是六年级的5
4,五年级分得多少本?
3、食堂买回54吨大米,第一周吃了它的31,第二周又吃了5
1吨,两周一共吃了多少吨?
4、人体共有206块骨头,其中手骨的块数占全身骨头的103
27
,手指骨的块数又占手骨的27
14
,人体手指骨头共有多少块?
5、某车间有三个小组,甲组生产了120个零件,乙组生产的零件数是甲组的4
5倍,丙组生产的零件是乙组的6
5,丙组生产了多少个零件?
6、小芳有36张邮票,小华的邮票张数比小芳多3
1,小华比小芳多多少张邮票?小华有多少张邮票?
7、中央电视塔高405米,东方明珠电视塔碧中央电视塔高45
7
,东方明珠电视塔高多少米?
8、张老师是集邮爱好者,他收集了270张中国邮票,收集的外国邮票比中国邮票少9
1,收集的外国邮票有多少张?
9、人的血液大约占体重的3
1,血液里大约有3
2是水。
小东的体重是39千克,他的血液里大约含水多少千克?
10、小明的体重是30千克,小青的体重比小明轻6
1,小青体重是多少千克?。
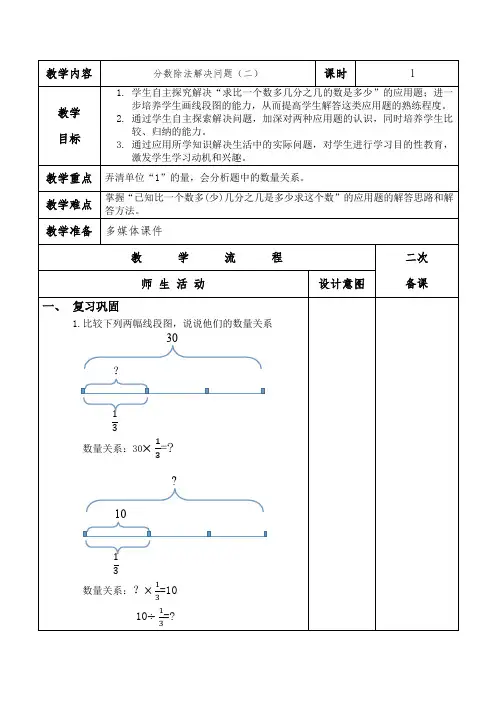
教学内容 分数除法解决问题(二) 课时 1教学 目标1. 学生自主探究解决“求比一个数多几分之几的数是多少”的应用题;进一步培养学生画线段图的能力,从而提高学生解答这类应用题的熟练程度。
2. 通过学生自主探索解决问题,加深对两种应用题的认识,同时培养学生比较、归纳的能力。
3. 通过应用所学知识解决生活中的实际问题,对学生进行学习目的性教育,激发学生学习动机和兴趣。
教学重点 弄清单位“1”的量,会分析题中的数量关系。
教学难点 掌握“已知比一个数多(少)几分之几是多少求这个数”的应用题的解答思路和解答方法。
教学准备 多媒体课件教 学 流 程 二次备课师 生 活 动设计意图一、 复习巩固1.比较下列两幅线段图,说说他们的数量关系数量关系:30×13=?数量关系:×13=1010÷13=?13 301013比较以上两幅图,他们的数量关系能否用一个式子表示:单位“1”×比较量的分率=比较量2.爸爸的体重是75千克,小明的体重比爸爸轻815,小明的体重是多少千克?方法一:75×(1-815)=35(kg ) 方法二:75-75×815=35(kg )二、 新知探究1.出示例题,比较两题的区别和联系。
爸爸的体重是75千克,小明的体重比爸爸轻815,小明的体重是多少千克?小明的体重是35千克,小明的体重比爸爸轻815,爸爸的体重是多少千克?相同点:关键句不变,所以单位“1”不变,数量关系也不行。
不同点:前者已知单位“1”,求比较量;后者已知比较量,求单位“1”。
2.画线段图。
你能画出线段图吗?(可以在上一题的图上进行修改)比较两幅图,你发现什么?75kgkg轻815kg 35kg 轻8155. 出示题目。
这就是今天我们要学习的题型“已知比一个数多(或少)几分之几的数是多少,求这个数”1.(1)某厂计划生产化肥480万吨,实际比计划多14,实际生产化肥多少万吨?(2)某厂实际生产化肥600万吨,比计划多14,计划生产化肥多少万吨?方法一:480×(1+14)=600(吨) 方法二:480+480×14 =600(吨)解:设实际计划生产化肥X 吨。

使用分数除法解决问题带答案分数除法是解决数学问题中常用的方法之一,特别适用于需要精确计算的情况。
本文将介绍使用分数除法解决问题的步骤,并给出一些实际问题的答案作为示例。
步骤使用分数除法解决问题的步骤如下:1. 将被除数和除数写成分数的形式。
确保分数的分子和分母都是整数。
2. 求出除数的倒数,即将除数的分子和分母交换位置。
3. 将被除数和除数的倒数相乘,得到一个新的分数。
4. 化简新的分数。
如果分子和分母有公因子,则可以约分。
5. 得到最终的商,即新的分数的值。
示例问题及答案问题一玛丽有7个苹果,她要将这些苹果平均分给她的3个朋友,每人分到几个苹果?解答:1. 将被除数7和除数3写成分数的形式:- 被除数:7/1- 除数:3/12. 求除数的倒数:- 除数的倒数:1/33. 将被除数和除数的倒数相乘:- 7/1 * 1/3 = 7/34. 化简新的分数:- 7/3 无法再化简,保留原样。
5. 得到最终的商:- 最终的商为7/3。
答案:每个朋友分到的苹果数为7/3个。
问题二小明有13块巧克力,他要将这些巧克力平均分给他的4个朋友,每人分到几块巧克力?解答:1. 将被除数13和除数4写成分数的形式:- 被除数:13/1- 除数:4/12. 求除数的倒数:- 除数的倒数:1/43. 将被除数和除数的倒数相乘:- 13/1 * 1/4 = 13/44. 化简新的分数:- 13/4 无法再化简,保留原样。
5. 得到最终的商:- 最终的商为13/4。
答案:每个朋友分到的巧克力数为13/4块。
以上是使用分数除法解决问题的步骤和示例问题的答案。
通过掌握这些方法,你可以更好地解决涉及分数除法的数学问题。


分数除法1、加工一批零件,第一天加工200个,第二天加工250个,这两天共加工了这批零件的3/5。
这批零件共有多少个?2、超市运进水果,第一批运进320千克,第二批运进400千克,这两批运进水果的重量占超市现在所有水果的2/3,超市现在一共有水果多少千克?3、一条铁路,修完900千米后,剩余部分比全长的3/4少300千米,这条铁路长多少千米?4、李楠三天看完一本书,第一天看了全书的3/10,第二天看了24页,还剩下全书的2/5未看。
这本书共有多少页?5、电脑公司要修一批电脑,已经修了这批电脑的1/3,再修24台正好修了这批电脑的一半。
这批电脑有多少台?6、一筐萝卜卖掉1/5以后,又卖出6千克,这时卖出的正好是剩下萝卜的1/2。
这筐萝卜原有多少千克?7、修路队三天修好一条马路,第一天修了全长的1/4,第二天修了全长的2/5,第一天比第二天少修90米,这条马路全长多少米?1、一捆电线,第一次用去全长的1/4,第二次用去余下的1/5,这时还剩108米。
这捆电线共长多少米?2、工厂进了一批原料,第一个星期用去总数的2/5,第二个星期用去总数的4/9,这时用去的比剩下的多31吨,这批原料共有多少吨?3、王师傅计划做一批零件,第一天做了计划的4/7,第二天又做了余下的3/5,这时还剩42个零件没做。
王师傅计划做多少个零件?4、一批木料,先用去总数的2/7,又用去剩下的2/5,这时用去的比剩下的多10立方米,这批木料共有多少立方米?5、学校植树,第一天完成了计划的3/8,第二天完成了计划的5/12,第三天植树55棵,结果超过计划的1/4,学校计划植树多少棵?6、服装厂计划两周生产一批服装,第一周完成计划的3/10,第二周完成计划的4/5,结果比计划多生产了200件。
服装厂计划生产多少件服装?7、一堆砖,用去它的3/10后,又增加了340块,这时砖的总块数是原来没有用时的块数的9/8。
这堆砖原有多少块?一、判断1、自然数a除以4/5,所得的商一定大于a。

用分数除法解决问题的过程和方法一、工程问题类。
1. 一项工程,甲队单独做需要10天完成,甲队的工作效率是多少?过程:把这项工程的工作量看作单位“1”,根据工作效率 = 工作量÷工作时间,甲队单独做需要10天完成,所以甲队的工作效率为1÷10=(1)/(10)。
解析:在工程问题中,通常将工作量设为单位“1”,工作效率就是单位时间内完成的工作量。
这里用工作量1除以甲队完成工作的时间10天,就得到甲队的工作效率(1)/(10)。
2. 一项工程,甲队单独做12天完成,乙队单独做15天完成。
甲队每天完成这项工程的几分之几?乙队每天完成这项工程的几分之几?过程:甲队:把工程总量看作单位“1”,甲队单独做12天完成,甲队每天完成1÷12 = (1)/(12)。
乙队:同理,乙队单独做15天完成,乙队每天完成1÷15=(1)/(15)。
解析:对于工程问题,用单位“1”除以工作时间就得到工作效率。
这里分别用1除以甲队的工作时间12天和乙队的工作时间15天,得到甲队和乙队每天完成工程的比例(1)/(12)和(1)/(15)。
3. 一项工程,甲队单独做8天完成,乙队单独做10天完成。
甲队的工作效率是乙队工作效率的多少倍?过程:甲队工作效率:1÷8=(1)/(8)乙队工作效率:1÷10=(1)/(10)倍数关系:(1)/(8)÷(1)/(10)=(1)/(8)×10=(5)/(4)解析:先分别求出甲队和乙队的工作效率,然后用甲队的工作效率除以乙队的工作效率,得到倍数关系。
在除法运算中,除以一个分数等于乘以它的倒数,所以(1)/(8)÷(1)/(10)=(1)/(8)×10=(5)/(4)。
二、已知一个数的几分之几是多少,求这个数类。
4. 已知一个数的(2)/(3)是10,求这个数。
过程:设这个数为x,根据题意可得(2)/(3)x = 10,则x=10÷(2)/(3)=10×(3)/(2) = 15。

分数除法解决问题2班级 姓名一、比一比,算一算1、某超市一月份的营业额是30万元,比二月份多41,二月份营业额是多少元?2、某超市一月份的营业额是30万元,二月份比一月份多41,二月份的营业是多少?3、某超市一月份的营业是30万元,比二月份少41,二月份的营业额是多少?4、某超市一月份的营业额是30万元,二月份比一月份少41,二月分的营业额是多少?二、解决问题1、松树有360棵,比棵树多31,杨树有多少棵?2、苹果树有300棵,比李子树少41,李子树有多少棵?3、小明上学,妈妈给他一些零花钱。
他早餐花了6元,中午吃饭花了9元,这两笔钱是妈妈给小明钱数的43,妈妈给他多少钱?4、讲台上有红色粉笔16支,白色粉笔的支数是红色粉笔的45,又是蓝色粉笔的1110,蓝色粉笔有多少支?5、一条铁路,修完了800千米后,剩余部分比全长的53少200米,这条铁路长多少千米?6、一辆客车从甲城开往乙城,前3小时行驶了全程的21多35千米。
后2小时行驶了全程的31多20千米,正好到达乙城,甲、乙两地相距多少千米?7、某车间的女工人数是男工人数的21,若调走21个男工,那么男工人数是女工人数的21,这个车间的女工有多少人?8、一根绳子,第一次用去全长的92,第二次比还第一次多用8米,还剩12米,它全长多少米?9、一辆汽车以每小时45千米的速度从甲地到乙地,3小时行了全程的75。
这辆汽车还要行多少千米才能到达乙地?10、某车间加工一批零件,每天加35个,加工了5天后,这批零件还剩下72。
这批零件有多少个?11、有一捆铁丝,第一次用去它的52,第二次用去它的31,第三次用去40米,正好用去40米,正好用完。
这捆铁丝长多少米?。

《分数除法解决问题(二)》教学反思石嘴山市第十中学杨京强“已知一个数的几分之几是多少,求这个数”的应用题,是由分数乘法意义扩展到除法意义而产生的应用题,这类应用题历来是教学中的难点。
这类应用题是求“一个数的几分之几是多少”应用题的逆解题。
因此,紧扣已掌握的分数乘法应用来组织教学显得比较重要。
此外,由于分数除法应用题和乘法应用题都存在着“单位‘1’的量×几分之几=对应数量”这样的数量关系,不同的仅是一个条件和问题不同,因此教材强化用列方程的方法解,这样做就能利用分数乘除法之间的内在联系,统一分数乘除法应用题的解题思路。
因此,在教学中我注重已下几点:一、重视新旧知识的内在联系。
分数除法应用题和乘法应用题都存在着“单位‘1’的量×几分之几=对应数量”这样的数量关系,因此在探索新知之前,精心设计复习练习。
一是找单位“1”和写数量关系式练习;二是出示与例题有关的分数乘法应用题。
复习与新知有密切联系的旧知,为新知的探究铺路搭桥,为学生更好地从旧知迁移到新知做准备,起到水到渠成的作用。
二、重视思路教学。
思路,是学生确定解题方法的分析、思考过程,这个过程应是有条有理的,有要有据的。
本课分析、具体地设计了使学生形成思路的过程:首先,分步思考;接着,引导学生完整地复述思考过程;最后,通过个别、集体训练,使学生形成完整思路。
三、重视训练学生讲题。
应用题教学重在分析数量关系。
学生只有理解了题目中的数量关系,才会进一步进行思考。
若在学生不理解题目中的数量关系的情况下进行分析,则思无源,想无据。
所以,讲清题目中的数量关系是分析的基础,必须给予足够的重视。
四、重视列方程解答。
本节课没有设计算术思路,因为用列方程解答分数应用题是有限的,能比较熟练地解答,但达不到熟练的程度,发现不了解答规律。
本堂课我设计了“题目——线段图——等量关系式——解决问题”这样四个环节来教学例(1)的2个问题,本是很清晰的一个教学思路,意在引导学生解决问题的同时教给他们此类问题的解决方法。

分数除法解决问题(简单问题一)1、学校有故事书320本,占图书总数的25 .全校有图书多少本?2、一条裤子的价格是75元,是一件上衣的23 ,一件上衣多少元?3、水果店原来苹果28箱,正好是运来梨的47 ,运来梨多少箱?4、从甲地到乙地,已行240千米,占全长的34 ,。
甲乙两地相距多少千米?5、某班有男生20人,相当于女生人数的45 。
女生有多少人?6、男生30人,是女生人数的23 ,女生有多少人?全班共有多少人?例:(1)、六一班有男生25人 ,女生20人。
女生人数占男生人数的几分之几?(2)、六一班有男生25人 ,女生20人。
女生人数占全班人数的几分之几?(3)、六一班有学生45人,女生占49 。
女生有多少人?(4)、六一班有学生45人,女生占49 。
男生有多少人?(5)、六一班有男生25人 ,占全班的59 。
全班共有多少人?1、(1)、林庄有3公顷苹果树,占果园总面积的34 。
果园总面积是多少公顷?(2)、林庄有一块4公顷果园,苹果树占果园总面积的34 。
苹果树占地多少公顷?2、甲数是乙数的23 ,已知甲数12,乙数是多少?3、某村种玉米12公顷,种玉米的面积是小麦面积的34 小麦面积是多少公顷?4、某校有女生160人,正好是男生人数的89 。
全校有多少人?5、建筑工地有一批黄沙,甲工程队运走全部的14 ,乙工程队运走全部的13 ,甲工程队运12吨。
乙工程队运走多少吨?6、某校六年级有男生118人,女生122人。
六年级的学生人数正好是全校学生人数的16 ,全校有学生多少人?7、六年级有学生111人,相当于五年级的学生人数的34 ,五年级和六年级一共有多少人?8、小刚家买来一袋面粉,吃了15千克,正好是这袋 面粉的58 。
这袋 面粉还剩多少千克?9、小丽比小兰多12张彩色图片,这个数目正好相当于小兰图片张数310 。
小兰有多少张彩色图片?小丽有多少张彩色图片?10、一筐梨,连筐重52千克,卖出25 以后,连筐重32千克。

六年级上册分数除法解决问题分类练习班级:学号:姓名:一、明确具体量对应的分率。
例题1:一条公路已经修了它的35,再修800米正好修完,这条公路全长多少米?例题2:阳光农场有稻田和鱼塘共32公顷,占农场全部土地的811。
(1)阳光农场共有多少公顷土地?(2)如果稻田为11公顷,稻田占农场全部土地的几分之几?【巩固练习】1、小明读一本书,读了36页,正好读了全书的49,这本书一共有多少页?2、一套书现价240元,是原价的45。
现价比原价便宜多少元?3、电脑员要录入一篇文章,已经录入了1600个字,正好录入了全文的25,还有多少字未录入?4、果园里苹果树的棵数是梨树的57,桃树的棵数是梨树的45,桃树有280棵,苹果树有多少棵?5、三个同学跳绳。
小明跳了120个,小军跳的是小明跳的56,是小强跳的45,小军跳了多少个?6、李强看一本故事书,已经看了全书的35,正好是 45 页。
这本书一共有多少页?7、修一条水渠,已经修了34,剩下18千米,这条水渠有多长?8、小红录入一份稿件,录入了57后还剩700字,这份稿件共有多少字?9、一辆汽车从甲地开往乙地,已经行驶了全程的25,这时离乙地还有144千米。
甲、乙两地相距多少千米?10、一条公路已经修了它的35,再修800米正好修完,这条公路全长多少米?二、转化具体量所对应的分率。
例题1:一桶油,吃了710,又添进去15千克,这时桶中的油正好是这桶油的一半,这桶油重多少千克?例题2:一条公路,第一天修了全长的15,第二天修了600米,这时还剩下全长的一半没有修。
这条公路全长是多少米?例题3:修路队修一条路,第一天修了全长的14,第二天修了全长的320,还剩下1200米没有修完,这条路一共长多少米?例题4:小路周末做一些计算题,上午做了全部题目的25,下午又做了余下题目的56,这时还剩下10道题,这些计算题一共有多少道?【巩固练习】1、小强看一本科技书,第一天看了20页,第二天看了25页,两天正好看了全书的35.这本科技书有多少页?2、某汽车厂上半月完成计划任务的35,下半月完成计划任务的12,结果超产 160辆,该厂本月计划生产汽车多少辆?3、库房有一批货物,第一天运走15,第二天比第一天多运8吨,还剩这批货物总重量的1425,这批货物有多少吨?4、果园里有桃树、梨树、苹果树.已知桃树棵数占总棵数的15,梨树棵数占总棵数的14,这两种树一共有180棵.果园里共有多少棵果树?5、黄叔叔将驾驶的汽车加满油后,第一天用去了全部的12,第二天用去了全部的13,这时油箱里还剩下12 L油。
分数除法解决问题练习
班级:__________ 姓名:__________
1、小明沿着操场跑一圈(360米)需要7分钟,小明平均每分钟跑多少米?照这样的速度,他5
42分钟能跑多少圈?
2、一张纸的9
5能做25双小鞋,照这样计算,做一双小鞋要多少张纸?1张纸能做多少双小鞋?
3、小红从家到图书馆有4.5千米,小红走了12分钟,还有5
1的路没走完,小红每分钟走多少千米?
4、把一根长9
71米的钢管锯成若干段相等的小段,一共锯了8次,平均每段钢管长多少米?
5、某设备厂使用一种自动检测仪来检测零件是否有缺陷,检测1个零件使用的时间是40
3秒,半秒钟可以检测多少个零件?3分钟可以检测多少个零件?
6、一个等腰梯形的宣传牌,上底是83米,下底是54米,高是3
2米,这块宣传牌的面积是多少平方米?
7、王叔叔打一份36000字的文件,他6小时打了12
7,他平均每小时打多少个子?
8、某市教育局共有16层,高度是52米,局长办公室设在13楼,局长办公室的地板距离地面有多少米?
9、有280千克盐,每254千克装一袋,已经包装了总量的7
5,已经包装了多少袋?
10、用一根长54米的绳子捆绑一些树木,已知捆绑一棵树用去4
3米,一共用去了绳子的一半,问:捆绑了多少棵树木?
11、学校有梧桐树15棵,杨树的棵树是梧桐树的32,又是柳树的7
2,柳树有多少棵?
12、妈妈今年40岁,小红的年龄是妈妈的103,又正好是外婆的6
1,小红的外婆今年多少岁?
13、合唱团有女生32名,比男生少9
1,男生有多少人?
14、一根电缆,第一次用去全长的31,第二次用去全长的5
2,还剩下80米,这根电缆长多少米?。
分数除法解决问题(重难点)(1)求A 是B 的几分之几(或百分之几) 方法:确定谁是单位“1” B 是单位“1” A÷B 例:六(1)班男生25人,女生20人。
男生人数是女生的几分之几(百分之几)? 25÷20 男生人数占全班的几分之几(百分之几)? 25÷(25+20)(2)求A 比B 多(少、增加、减少、提高、降低)百分之几? 方法:(多、少、增加、减少、提高、降低)的量÷单位“1” 例:现在买一台收音机用160元,比过去少用85元,收音机售价降低了百分之几 ?想:求降低百分之几就是求降低的价钱占原价的百分之几 即降低的价钱÷原价85÷(160+85)(3)已知A 的几分之几(或百分之几)是多少,求A 方法:对应数量÷对应分率=单位“1”的量①一袋面粉,2天吃了25,正好吃了16千克,这袋面粉多少千克?16÷25 ②一袋面粉,2天吃了25,还剩下6千克,这袋面粉多少千克? 6÷(1-25)分数除法解决问题(重难点) (4)已知A 比B 多几分之几,求B 比A 少几分之几? 方法:先明确前句和后句的单位“1”不一致,前句的单位“1”是B ,后句的单位“1”是 A ;例:甲比乙多1/7,乙比甲少几分之几?解题思路1:前句的单位“1”是乙,则甲是乙的(1+1/7)=8/7;后句单位“1”变为甲,则乙比甲少1/7÷8/7=1/8解题思路2:运用倍数的知识进行解答,如果把前句的单位“1”——乙看作7份,则甲就是8份,最后用少的份数除以后句的单位“1”——甲即可:(8-7)÷8=1/8(5)已知A 和B 的总量,A 是B 的几分之几,求A 和B 各是多少?例:图书室有故事书和文艺书共440册,文艺书是故事书的65,文艺书、故事书各有多少册?解题思路:对应总量÷对应总分率=单位“1”的量:故事书440÷(1+65);文艺书440÷(1+65)×65;(6)已知A 和B 的总量,A 比B 多/少几分之几,求A 和B 各是多少?分数除法解决问题(重难点) 例:图书室有故事书和文艺书共450册,故事书比文艺书多14,文艺书、故事书各有多少册?解题思路:对应量÷对应分率=单位“1”的量:文艺书440÷(1+14);故事书440÷(1+14)×(1+14)(7)已知A 比B 少多少,A 是B 的几分之几,求A 和B 各是多少?例:学校图书室故事书比文艺书少40册,文艺书是故事书的65 ,文艺书、故事书各有多少册?解题思路:对应量÷对应分率=单位“1”的量文艺书40÷(65-1)×65;故事书40÷(65-1)(8)已知A 比B 少多少,B 比A 多几分之几,求A 和B 各是多少?例:学校图书室故事书比文艺书少40册,文艺书比故事书多15,文艺书、故事书各有多少册?分数除法解决问题(重难点) 解题思路:对应量÷对应分率=单位“1”的量文艺书40÷15×(1+15);故事书40÷15(9)已知A 比B 少多少,A 比B 少几分之几,求A 和B 各是多少?例:学校图书室故事书比文艺书少40册,故事书比文艺书少15 ,文艺书、故事书各有多少册?解题思路:对应量÷对应分率=单位“1”的量文艺书40÷15;故事书40÷15×(1-15)(10)单位“1”在原有的基础上发生了变化例:某工厂原有工人450人,其中女工占925。
例1如果曹操率领大军攻打刘备,刘备的有10万守城将士,只占曹操大军的51,那么曹操带了多少军队攻城?例2张学友开演唱会之前去买了一套衣服,其中裤子的价格是鞋子的32,鞋子的价格是衣服的52,而买裤子花了1200元,那么他买衣服用了多少钱?例3六(1)班有60人, 比六二班多51,六(2)班有多少人?例4胡总今年有100位保镖,比去年少211,去年有多少为保镖呢?例5成龙看一本功夫秘籍,第一天看了全书的51,第二天看了50页,还有全书的52没看,这本功夫秘籍共有多少页?例6假设中国有450艘战舰,比日本的54多180艘,你说日本鬼子有多少战舰呢?例7学校运进一批煤,第一个月用去全部的51,第二个月比第一个月少用2吨,还剩14吨,你帮学校算算总共运进了多少煤?例8如果你的钱比你的弟弟多200元,而你的弟弟的钱比你少51,你们两兄弟各有多少钱?例9修一条路,第一天修了全长的31,第二天修了全长的41,第一天比第二天多修200米。
这条路长多少米?随堂练习:1、今年妈妈36岁,小明年龄是妈妈的31。
小明今年多少岁?2、今年小明12岁,是妈妈年龄的31。
妈妈今年多少岁?3、今年小明12岁,比妈妈年龄小32。
妈妈今年多少岁?4、今年妈妈36岁,比小明年龄大31。
小明今年多少岁?5、修一条公路,已修的是未修的43。
没有修的还有120米,这条路全长多少米?6、修一条公路,已修的是未修的43。
已经修了120米,这条路全长多少米?7、一堆货物,甲车运走24吨,是乙车的54,乙车运的是丙车的32。
丙车运了多少吨?8、一堆货物,甲车运走24吨,是乙车的54,丙车运的是乙车的32。
丙车运了多少吨?9、一堆货物,甲车运走24吨,乙车运的是甲车的43,乙车运的是丙车的32。
丙车运了多少吨?10、一堆货物,甲车运走24吨,乙车运的是甲车的43,丙车运的是乙车的32。
丙车运了多少吨?11、西门吹雪的剑重41kg ,比冯七公的打狗棒的54重5kg ,那么冯七公的打狗棒中多少啊?12、喜洋洋买了一些大米回来,第一天吃了201,第二天比第一天多吃1kg ,还剩35kg ,他一共买了多少千克大米?13、灰太狼比喜洋洋重5kg ,而喜洋洋比灰太狼轻61,他们各重多少千克?14、两兄弟拿了一些钱去买吃的 ,哥哥用了其中的41,弟弟用了其中的51,哥哥比弟弟多用20元,他们一共拿了多少钱去买吃的?。