当前位置：文档之家 › 2-2逆矩阵及其运算

2-2逆矩阵及其运算

  • 格式：pps
  • 大小：1.18 MB
  • 文档页数：54

下载文档原格式

  / 54

合集下载

2-2逆矩阵

2-2逆矩阵
11
解
西安交通大学
线性代数与空间解析几何
Cramer法则(定理1.3.1)的证明：
方程组有唯一解，
xj Dj D ( j 1, 2, , n)，
12
西安交通大学
线性代数与空间解析几何
证明 记
则方程组为Ax=b, D=|A|≠0, 所以A可逆, 1 * 1 A b, x A b A
西安交通大学
线性代数与空间解析几何
第二节 逆矩阵
作业 习题2.2(A) 1，4,7,10
1
西安交通大学
线性代数与空间解析几何
一、背景
1、数 在数的运算中，当a≠０时， 有 aa 1 a 1a 1, 1 1 则 a 称为 a 的倒数， （或称为 a 的逆）； a 在矩阵的运算中， 单位阵I 相当于数的
1 1 记作 A , 即A B .
1 2 1 1 ,B 例如 A 1 1 1 2 AB BA I ,
1 2 , 1 2
B 是 A 的逆矩阵.
3
西安交通大学
线性代数与空间解析几何
结论 证明
若 A 是可逆矩阵，则 A的逆矩阵唯一. 若设 B 和 C 是 A 的逆矩阵， 则有
B均是 n 阶可逆方阵） （设 A，
-1 T (2) AT 可逆，且（AT） （A-1 ） 1 -1 -1 (3)kA可逆，且（kA ） A k -1 -1 -1 (4) AB可逆，且（AB ）B A
推广
-1
A1 A2 Am
1
Am A2 A1 .
1
1
1
1 (5) A A
1

A

1
1
A A

二阶方阵的逆矩阵的计算

二阶方阵的逆矩阵的计算

二阶方阵的逆矩阵的计算在线性代数中，矩阵是一种经常使用的工具，用于表示线性方程组的系数矩阵或线性变换的矩阵。

在矩阵运算中，逆矩阵是一种非常重要的概念。

本文将重点讨论二阶方阵的逆矩阵的计算方法。

一、逆矩阵的定义对于一个n阶方阵A，如果存在一个n阶方阵B，使得AB=BA=I，其中I为n阶单位矩阵，则称矩阵B为矩阵A的逆矩阵，记作A-1。

如果不存在逆矩阵，则称矩阵A为奇异矩阵，否则称为非奇异矩阵。

二、二阶方阵的逆矩阵的计算对于一个2阶方阵A，其逆矩阵A-1的计算方法如下：A = [ a11 a12 ][ a21 a22 ]1. 计算矩阵A的行列式：|A| = a11*a22 - a12*a21如果|A|≠0，则矩阵A存在逆矩阵，否则不存在逆矩阵。

2. 计算矩阵A的伴随矩阵：adj(A) = [ a22 -a12 ][ -a21 a11 ]伴随矩阵是由矩阵A的代数余子式构成的矩阵的转置矩阵。

3. 计算矩阵A的逆矩阵：A-1 = (1/|A|) * adj(A)其中，(1/|A|)为矩阵A的行列式的倒数。

例如，对于一个2阶方阵A = [ 1 2 ; 3 4 ]，其逆矩阵的计算过程如下：|A| = 1*4 - 2*3 = -2因为|A|≠0，所以矩阵A存在逆矩阵。

adj(A) = [ 4 -2 ][ -3 1 ]A-1 = (1/|A|) * adj(A) = (-1/2) * [ 4 -2 ; -3 1 ] = [ -2 1 ; 3/2 -1/2 ]因此，矩阵A的逆矩阵为A-1 = [ -2 1 ; 3/2 -1/2 ]。

三、逆矩阵的应用逆矩阵在矩阵运算中有着广泛的应用，例如：1. 解线性方程组：对于一个线性方程组Ax=b，如果矩阵A是非奇异矩阵，则可以通过求解逆矩阵来求解方程组的解，即x=A-1b。

2. 矩阵变换的求逆：对于一个线性变换A，如果其矩阵是非奇异矩阵，则可以通过求解逆矩阵来求解逆变换的矩阵，即A-1。

2-2,3_矩阵的运算,逆矩阵(第五次)

2-2,3_矩阵的运算,逆矩阵(第五次)

矩阵乘法的性质 (1) (AB)C=A(BC)； = ； (2) (A+B)C=AC+BC； + = + ； (3) C(A+B)=CA+CB； + = + ； (4) k(AB)=(kA)B=A(kB) . = =
应注意的问题 (1) AB≠BA ； ≠ (2) AC=BC ⇒ A=B； = / = ； (3) AB=O ⇒ A=O或B=O ； / = 或 = = (4) AA=A ⇒ A=E或A=O . = 或 = = /
2 3 1 −2 −3 例3．设 A= 1 −2 ， B = ，求AB及BA . 求 2 −1 0 3 1 8 −7 −6 解： AB = −3 0 −3 , BA= −9 4 . = 3 8 5 −7 −9 −2 4 2 4 例4．设 A= ， B= ，求AB及BA . 注意： 求 注意：左乘右乘的不同 −2 −3 −6 − − 1− −16 −32 0 0 解： AB= ， BA= 8 16 0 0
显然AC=BC，但A≠B . ， 显然 ≠
1 , 0
1 . 0
矩阵乘法不满足消去律. 注4： 矩阵乘法不满足消去律
对于任意矩阵A及相应的矩阵 及相应的矩阵O， ， 例7． 对于任意矩阵 及相应的矩阵 ，E，有 AO=O， OA=O； ， ； AE=A， EA=A， EE=E. ， ， 例8 . 设A = 1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0 0 0 = 1 1 0 0 0 0 0 0 0 1
那么, 那么,F 矩阵 是怎么得到 的呢？ 的呢？
0 x1 1 = 1 x2 2
从而得方程组的解: 从而得方程组的解 x1 = 1 , x2 = 2.

2-2逆矩阵

2-2逆矩阵

A −1
2 6 −4 1 3 −2 1 ∗ 1 = A = −3 −6 5 = − 3 2 −3 5 2 . A 2 2 2 −2 1 1 −1
14
三、逆矩阵的求法及应用
用可逆矩阵求解矩阵方程 矩阵方程AX=B的矩阵 其中 的矩阵X,其中 例3：求满足矩阵方程 ：求满足矩阵方程 的矩阵
左乘方程AX=B两边得： 两边得： 用A-1左乘方程 两边得
15
三、逆矩阵的求法及应用
1 1 X = A −1 B = 2 9 2 2 1 −2 2 8 − 2 − 5 1 2
2 3 9 = 7 9 9 28 15 9
第二章 矩阵及其运算
第二节 逆矩阵 (Inverse matrix) 一、逆矩阵的定义及性质
二、方阵可逆的充要条件 三、逆矩阵的求法及应用 四、小结 思考题
1
一、逆矩阵的定义及性质
1、数 、
−1
在数的运算中，当数α≠０时， 在数的运算中，当数 ０
有
aa −1 = a −1a = 1,
1 的倒数， 则 a = 称为 a 的倒数， a
17 3 − 5 3 1 3
注: 1)上例中X≠BA-1; 1)上例中 2)若矩阵方程为XB=C 或 AXB=C,其中矩阵A与B是可逆 2)若矩阵方程为XB=C 若矩阵方程为 方阵, 方阵,则 X=CB-1或 X=A-1CB-1; 注：若Ａ不是可逆阵，或者不是方阵，矩阵方程不能 不是可逆阵，或者不是方阵， 用可逆矩阵求解
A11 = ( −1)
2
2 1 4 3
= 2,
A12 = ( −1)
3
2 1 3 3

逆矩阵 算法-概述说明以及解释

逆矩阵 算法-概述说明以及解释

逆矩阵算法-概述说明以及解释1.引言1.1 概述逆矩阵是矩阵理论中一个非常重要的概念，它在线性代数、数值计算等领域中都有广泛的应用。

简单来说，对于一个可逆的方阵A，存在另一个方阵B，使得A与B的矩阵乘积等于单位矩阵I，那么我们称B为A的逆矩阵。

逆矩阵在很多实际问题中起到了至关重要的作用。

本文将主要介绍逆矩阵的定义、性质以及计算方法。

首先，我们将给出逆矩阵的定义，并讨论什么样的矩阵会存在逆矩阵以及如何判断一个矩阵是否可逆。

然后，我们将深入探讨逆矩阵的性质，比如逆矩阵的唯一性以及逆矩阵与矩阵的乘法规则等。

接下来，我们将介绍一些常见的逆矩阵计算方法，包括伴随矩阵法、初等变换法以及利用矩阵的特征值和特征向量来求逆矩阵等。

逆矩阵算法在数值计算中具有广泛的应用领域。

例如，在线性方程组的求解中，我们可以利用逆矩阵的性质来求解未知数向量。

此外，在图像处理、信号处理、网络优化等领域也都可以看到逆矩阵算法的应用。

逆矩阵算法的发展前景非常广阔，随着计算机计算能力的不断提升，逆矩阵算法将能够承担更加复杂和庞大的计算任务。

总之，逆矩阵算法是一项重要且充满潜力的计算方法，它在线性代数和数值计算领域具有重要的地位。

通过深入研究和应用逆矩阵算法，我们可以更好地理解矩阵的性质和应用，从而为实际问题的求解提供有效的数学工具。

在接下来的正文中，我们将详细介绍逆矩阵的定义、性质以及计算方法，以期帮助读者更好地理解和应用逆矩阵算法。

文章结构部分的内容如下所示：1.2 文章结构本文将按照以下结构组织内容：引言部分将首先概述逆矩阵算法的背景和重要性，介绍本文的目的，并对整篇文章进行总结。

正文部分将着重介绍逆矩阵的定义，包括数学上对逆矩阵的准确描述。

随后，我们将详细探讨逆矩阵的性质，包括逆矩阵与原矩阵之间的关系，以及逆矩阵的特点和作用。

最后，我们将介绍逆矩阵的计算方法，包括传统的高斯消元法和基于分解的LU分解法等。

结论部分将重点探讨逆矩阵算法的重要性，阐述逆矩阵算法在实际问题中的应用领域，如线性方程组的求解、图像处理和机器学习等。

矩阵求逆方法大全-1

矩阵求逆方法大全-1

求逆矩阵的若干方法和举例苏红杏广西民院计信学院00数本（二）班[摘 要] 本文详细给出了求逆矩阵的若干方法并给出相应的例子，以供学习有关矩阵方面的读者参考。

[关键词] 逆矩阵 初等矩阵 伴随矩阵 对角矩阵 矩阵分块 多项式等引 言 在我们学习《高等代数》时，求一个矩阵的逆矩阵是一个令人十分头痛的问题。

但是，在研究矩阵及在以后学习有关数学知识时，求逆矩阵又是一个必不可缺少的知识点。

为此，我介绍下面几种求逆矩阵的方法，供大家参考。

定义: n 阶矩阵A 为可逆，如果存在n 阶矩阵B ，使得E BA AB ==，这里E 是n 阶单位矩阵，此时，B 就称为A 的逆矩阵，记为1-A ，即：1-=A B方法 一. 初等变换法（加边法）我们知道，n 阶矩阵A 为可逆的充分必要条件是它能表示成一系列初等矩阵的乘积A=m Q Q Q 21， 从而推出可逆矩阵可以经过一系列初等行变换化成单位矩阵。

即，必有一系列初等矩阵 m Q Q Q 21使E A Q Q Q m m =-11 （1） 则1-A =E A Q Q Q m m =-11 （2）把A ，E 这两个n 阶矩阵凑在一起，做成一个n*2n 阶矩阵（A ，E ），按矩阵的分块乘法，（1）（2）可以合并写成11Q Q Q m m -（A ，E ）=（11Q Q Q m m -，A ，E Q Q Q m m 11 -）=（E ，1-A ） （3） 这样就可以求出矩阵A 的逆矩阵1-A 。

例 1 . 设A= ⎪⎪⎪⎭⎫ ⎝⎛-012411210 求1-A 。

解：由（3）式初等行变换逐步得到：⎪⎪⎪⎭⎫ ⎝⎛-100012010411001210→ ⎪⎪⎪⎭⎫ ⎝⎛-100012001210010411 →⎪⎪⎪⎭⎫ ⎝⎛----123200124010112001→⎪⎪⎪⎪⎭⎫ ⎝⎛----21123100124010112001于是1-A = ⎪⎪⎪⎪⎭⎫ ⎝⎛----21123124112说明：此方法适用于求元素为具体数字的矩阵的逆矩阵，比较简便，特别是当阶数较高时，使用初等变换法的优点更明显。

逆矩阵的十种求法

逆矩阵的十种求法
华北水利水电大学
.矩阵可逆的判定及求解
课程名称：线性代数
专业班级：工程力学2012054
成员组成：姓名：马原响学号：*******01
姓名：董迪学号：********6
姓名：霍帅磊学号：*********
联系方式：13017682997 130****3523 130****3589
2013年11月12日
利用公式得
W-1=
方法四初等变化法:因为当n级方阵A可逆时，A可由初等行变换化成单位矩阵，即PnPn-1…P1A=E
于是PnPn-1…P1AE=A-1，这里PnPn-1…P1A都是初等矩阵，可见A-1=PnPn-1…P1A
即有【A,E】 （PnPn-1…P1A，PnPn-1…P1E）=(E,A)
根据上面的分析可得到，令B=A-1，则 =
②对于分块矩阵 不能按上述规律求伴随矩阵.
例2：已知 ，求A-1.
解∵| A | = 2≠0
∴A可逆.由已知得
A-1= A* =
方法三矩阵分块求逆法；由于计算和讨论问题的需要，在处理大型矩阵时，常常采用对矩阵分块的方法。因为把矩阵分块，可以事型号大的矩阵的运算化为型号小的矩阵的运算，即只需要把字块当做元素来进行运算，并按照通常矩阵的加减法、数乘、乘法等法则来运算，这种运算上的抽象性及究竟如何对矩阵进行分块等问题，就使得分块矩阵形成了学习上的一个难点。特别注意的是，在做分块的乘法时，应使左矩阵上列的分块方式与右矩阵上的分块方式一致。对于某些特殊矩阵，利用分块矩阵求其逆矩阵，有时是很方便的，比用其他方法要快，要准确。若遇到以下形式矩阵，我们可以采取以下方法。
.矩阵可逆的判定及求解
摘要：为了更便捷地解决求矩阵的逆,本文根据不同矩阵的不同特点简单介绍了几种求逆矩阵的方法.定义法、伴随矩阵法、初等变换法、分块矩阵法、解方程组法、多项式法、“和化积”法、Hamilton-Caley定理法、公式法等多种方法求逆矩阵,并对部分进行了简要论证

2-2可逆矩阵与分块矩阵

2-2可逆矩阵与分块矩阵

例2.5 n阶方阵A满足A2-3A-4I=0且|A|=2, 求|A-2A*|. 解 :由A2 3 A 4 I 0可知 A2 3 A 4 I . 即 1 4 ( A 3I ) A I . 1 从而 A 1 ( A 3 I ). 由A* | A | A1可知 4 A 2 A* A 2 | A | A1 A 4 A1 3 I | A 2 A* || 3 I | 3n. 因此 例2.6 设A2=B2=I 且|A|+|B|=0, 证明A+B不可逆. 证明 由A2 B 2 I及 | A | | B | 0可知 | A | | B | 0 又因为 A( A B ) A2 AB B 2 AB ( A B ) B 所以 | A || A B || B || A B | | A || A B | . 故 2 | A || A B | 0 即 | A B | 0. 所以A B不可逆.
4 分块矩阵的运算规则
A11 A1r A11 A1r 1 A , 为数, 那末 A . As1 Asr As1 Asr
( 2) 设矩阵A与B的行数相同, 列数相同, 采用相同的分 块法, 有
A11 A1r B11 B1r , B A As1 Asr Bs1 Bsr
其中Aij 与Bij的行数相同, 列数相同, 那末 A11 B11 A1r B1r . A B As1 Bs1 Asr Bsr
证明:只需要证明充分条件 此时 | A | 0, 因此 . 1 * 1 1 * * A A I AA A( A ). | A| | A| | A| 1 因此A可逆且A1 | A| A* . 即 | A | A1 A*

2-2可逆矩阵和分块矩阵

2-2可逆矩阵和分块矩阵

1 0
2 1
使得
AB
1 0
10
BA
因而A可逆. A1 B
注: 逆矩阵唯一.
事实上,若B,C均为A的逆矩阵, 则有
BA AB I; CA AC I. 因而 B BI BAC IC C.
定义2.2: 若n阶方阵A的行列式满足|A|0, 则称A 是非奇异的, 否则称为奇异的.
注: 可逆矩阵必是非奇异矩阵 因为,若A可逆,则存在B使得AB I 从而
定理2.1 n阶方阵A可逆的充要条件是A非奇异, 即 |A|0. 此时 A1 1 A*
| A|
证明:只需要证明充分条件. 此时 | A | 0, 因此
1 A* A I 1 AA* A( 1 A* ).
| A|
| A|
| A|
因此A可逆且A1
1 |A|
A*
.
即|
A|
A1
A*
推论2.2 若方阵AB=I, 则A, B均可逆且A-1=B, B-1=A.
A
5 0 0
0 3 2
110
A1 O
O A2
,
其中
A1 5,
A2
3 2
11,
由
A11
1 5
;
A21
1 2
31 可知
A1
Btr
,
其中Ai1 , Ai2 , , Ait的列数分别等于B1 j , B2 j , , Btj
的行数, 那末 AB
C11
C s1
C1r
C sr
其中Cij
t
Aik Bkj
i 1, , s; j 1, , r .
k 1
例2.9
设A

线性代数课件2-2方阵的逆阵

线性代数课件2-2方阵的逆阵
不是所有矩阵都有逆阵，只有方 阵才可能有逆阵。一个方阵A的 逆阵存在当且仅当A是可逆矩阵，
即A的行列式值不为零。
逆阵的求法
求一个方阵的逆阵，需要先计算 该方阵的行列式值，然后通过特
定的公式计算出逆阵的元素。
利用逆阵进行矩阵乘法运算
矩阵乘法运算
01
矩阵乘法是线性代数中基本的运算之一，通过矩阵乘法可以解
逆矩阵存在条件
一个方阵存在逆矩阵的充分必要条件是该矩阵非奇异（即行列 式值不为0）。
逆阵的性质
逆矩阵的唯一性
一个方阵的逆矩阵是唯一的。
逆矩阵与转置矩阵的关系
如果$A^{-1}$是矩阵$A$的逆矩阵，那么$(A^{-1})^{-1} = A$。
逆矩阵与行列式的关系
如果$A^{-1}$是矩阵$A$的逆矩阵，那么$det(A^{-1}) = frac{1}{det(A)}$。
决许多实际问题。
逆阵在矩阵乘法中的作用
02
在矩阵乘法中，如果一个矩阵与其逆阵相乘，结果是一个单位
矩阵。因此，利用逆阵可以简化矩阵乘法运算。
逆阵在矩阵乘法中的优势
03
利用逆阵进行矩阵乘法运算可以大大简化计算过程，提高运算
效率。
逆阵在矩阵运算中的重要性
1 2
逆阵的应用范围
逆阵在许多领域都有广泛的应用，如线性方程组 的求解、矩阵的分解、特征值的计算等。
中的应用
线性方程组的解法
01
02
03
高斯消元法
通过消元和回代步骤求解 线性方程组，但当系数矩 阵的行列式为零时，该方 法失效。
克拉默法则
适用于线性方程组系数行 列式不为零的情况，通过 求解方程组得到解。
迭代法
通过迭代过程逐步逼近方 程组的解，适用于大规模 线性方程组。

难忘一课 2-2逆矩阵

难忘一课 2-2逆矩阵
行列式性质：
i1 j1 i2 j2
A1n A2n
in
jn
Ann
伴随矩阵Adjoint matrix
9
三、方阵可逆的充要条件
a11 a 21 AA a n1 a12 a1n A11 A21 a22 a2 n A12 A22 an 2 ann A1n A2 n An1 An 2 Ann
四、逆矩阵的求法及应用
例2 求方阵
第二节
逆矩阵
1 2 3 A 2 2 1 3 4 3
1 2 3
的逆矩阵.
解
A2 2 1 3 4 3
2 1 4 3
A1存在. 2,
A11 ( 1) M11 ( 1)
2
2
2,
A12 3,
A13 2,
1
ax b(a 0)
a ax a b x a 1b
对于 a ，能找到 a 的倒数
1
1
1
EX A1B
X A1B
B
对于 A ，如果能找到一个
1
a （或称为 a的逆），满足： 矩阵 A 满足：
a a aa 1
1
1
A 1 A E ,
AA1 E
AA A A A E
如果
引理2.1
第二节
逆矩阵
A A , A 0, 则 A( ) ( ) A E A A
A 1 . 按逆矩阵的定义得：A 可逆，且 A A 【定理２.２】 设A是n阶方阵，则A可逆的充要条件是 A 0. 当 A 0 有 1 1 A A A 【证】充分性（已证）

2-2,3 矩阵的运算,逆矩阵(第五次)

2-2,3 矩阵的运算,逆矩阵(第五次)

转置矩阵有Leabharlann 列性质 (1)(AT)TA； (2)(AB)TATBT； (3)(kA)TkAT； (4)(AB)TBTAT .
定义5 设A 为n阶方阵，若AT=A，则称A为对称矩阵，如 果AT= - A，则称A为反对称矩阵. 显然：A为对称矩阵的充分必要条件是aij=aji ; A为反对称矩阵的充分必要条件是 aij=-aji . 如： 1 -1 2 0 1 -2 A -1 3 4 , B -1 0 -4 2 4 -2 2 4 0 分别是三阶对称矩阵和三阶反对称矩阵.
注2：矩阵乘法一般不满足交换律，即ABBA ; 注 3 ： 两个非零矩 阵 相乘 ， 乘 积可能 是 零矩阵 ， 但不能从 AB=O，推出A=O或B=O .
1 2 1 0 1 1 例5 ．设 A , B , C , 则 0 3 0 4 0 0 1 AC 0 1 BC 0 2 1 3 0 0 1 4 0 1 1 0 0 1 1 0 0 1 , 0 1 . 0
注2：矩阵乘法一般不满足交换律，即ABBA ; 注 3 ： 两个非零矩 阵 相乘 ， 乘 积可能 是 零矩阵 ， 但不能从 AB=O，推出A=O或B=O .
2 3 1 -2 -3 例3．设 A 1 -2 ， B = ，求AB及BA . 2 -1 0 3 1 8 -7 -6 解： AB -3 0 -3 , BA -9 4 . 3 8 5 -7 -9 -2 4 2 4 例 4 ． 设 A ， B ，求AB及BA . -3 -6 1 -2 -16 -32 0 0 解： AB ， BA 8 16 0 0
cij (ai1 ai2
因此， cij 可表示为 A 的第 i 行与 B 的第 j 列的乘积.

矩阵的乘法及求逆运算 最终版

矩阵的乘法及求逆运算 最终版

(1)
a31x1 a32 x2 a33 x3 b3
记
a11
A


a21 a31
a12 a22 a32
a13
a23 a33

,
x1
x


x2 x3
,
b1
b


b2 b3

则方程组(1)可表示为 Ax b.
二.矩阵的求逆
一、逆矩阵的概念 二、方阵可逆的判别定理 三、逆矩阵的基本性质 四、用矩阵的初等变换求逆矩阵
若Ak 0，即（I A）可逆，且有（I-A）1 I A A2 L AK 1 我们通过上式，求出 A1
例 .求下面矩阵的逆矩阵，已知：
1 1 2 3 4

0
1
1
2
3

A 0 0 1 1 2

0
0
0
1
1
0 0 0 0 1
0 L


,
Aii
是矩阵。(i

1,
2,L
n
)
Ann
其求逆的方法：
可以证明：如果A11, A22 ,L , Ann都可逆，则准对角矩阵也可逆，且
A11 0 L

0
A22 L
L L L

0
0L
0 0 L
1







A1 11 0
L
Ann
0
0L
A1 22
矩阵的乘法及求逆的运算
小组成员：王沛竣 曾杨帆 兰军 卓磊 曹诗瑶
一、矩阵乘法的定义

矩阵求逆方法大全

矩阵求逆方法大全

求逆矩阵的若干方法和举例苏红杏广西民院计信学院00数本（二）班[摘 要] 本文详细给出了求逆矩阵的若干方法并给出相应的例子，以供学习有关矩阵方面的读者参考。

[关键词] 逆矩阵 初等矩阵 伴随矩阵 对角矩阵 矩阵分块 多项式等引 言 在我们学习《高等代数》时，求一个矩阵的逆矩阵是一个令人十分头痛的问题。

但是，在研究矩阵及在以后学习有关数学知识时，求逆矩阵又是一个必不可缺少的知识点。

为此，我介绍下面几种求逆矩阵的方法，供大家参考。

定义: n 阶矩阵A 为可逆，如果存在n 阶矩阵B ，使得E BA AB ==，这里E 是n 阶单位矩阵，此时，B 就称为A 的逆矩阵，记为1-A ，即：1-=A B方法 一. 初等变换法（加边法）我们知道，n 阶矩阵A 为可逆的充分必要条件是它能表示成一系列初等矩阵的乘积A=m Q Q Q 21， 从而推出可逆矩阵可以经过一系列初等行变换化成单位矩阵。

即，必有一系列初等矩阵 m Q Q Q 21使E A Q Q Q m m =-11 （1）则1-A =E A Q Q Q m m =-11 （2）把A ，E 这两个n 阶矩阵凑在一起，做成一个n*2n 阶矩阵（A ，E ），按矩阵的分块乘法，（1）（2）可以合并写成11Q Q Q m m -（A ，E ）=（11Q Q Q m m -，A ，E Q Q Q m m 11 -）=（E ，1-A ） （3） 这样就可以求出矩阵A 的逆矩阵1-A 。

例 1 . 设A= ⎪⎪⎪⎭⎫⎝⎛-012411210 求1-A 。

解：由（3）式初等行变换逐步得到：⎪⎪⎪⎭⎫ ⎝⎛-1012010411001210→ ⎪⎪⎭⎫ ⎝⎛-1012001210010411→⎪⎪⎪⎭⎫ ⎝⎛----12320124010112001→⎪⎪⎪⎪⎭⎫ ⎝⎛----211231124010112001于是1-A = ⎪⎪⎪⎪⎭⎫ ⎝⎛----21123124112说明：此方法适用于求元素为具体数字的矩阵的逆矩阵，比较简便，特别是当阶数较高时，使用初等变换法的优点更明显。

线性代数课件-ch-2-2逆矩阵

线性代数课件-ch-2-2逆矩阵

用中，可以根据具体情况选择适合的计算方法。
判断矩阵是否可逆
可逆矩阵的定义
如果一个矩阵A存在逆矩阵，则称A为可逆矩阵。
可逆的条件
一个矩阵可逆的条件是其行列式值不为零。此外，还需要满足其他条件，如矩阵的秩等于 其阶数等。
判断方法
判断一个矩阵是否可逆的方法有多种，包括计算行列式值、观察矩阵的秩等。在实际应用 中，可以根据具体情况选择适合的方法进行判断。
记A的逆矩阵为$A^{-1}$。
性质
唯一性
如果矩阵A有逆矩阵，则其逆矩阵 是唯一的。
交换律
如果矩阵A和B满足交换律，即 $AB=BA$，则A和B都是可逆的， 并且$A^{-1}=B^{-1}$。
结合律
如果矩阵A、B和C满足结合律，即 $ABC=BCA=CAB$，则$(AB)^{1}=B^{-1}A^{-1}$，$(A^{-1})^{1}=A$。
计算行列式
01
行列式的定义
行列式是线性代数中的基本概念之一，它是一个数值，由一个n阶方阵
的元素按照一定规则计算得出。
02
逆矩阵与行列式的关系
行列式和逆矩阵之间存在一定的关系。如果一个矩阵的行列式值不为零
，则该矩阵可逆。同时，如果一个矩阵可逆，则其行列式值不为零。
03
行列式的计算方法
行列式的计算方法有多种，包括展开法、递推法、分块法等。在实际应
线性代数课件-ch-2-2逆矩阵
contents
目录
• 逆矩阵的定义与性质 • 逆矩阵的运算规则 • 逆矩阵的求法 • 逆矩阵的应用 • 逆矩阵的实例分析
01
逆矩阵的定义与性质
定义
逆矩阵
设矩阵A是一个n阶方阵，如果存在一个n阶方阵B，使得$AB=BA=I$，则称A是 可逆的，B是A的逆矩阵。

矩阵的逆计算方法

矩阵的逆计算方法

矩阵的逆计算方法全文共四篇示例，供读者参考第一篇示例：矩阵是线性代数中非常重要的一个概念，它在各个领域中都有着广泛的应用。

而矩阵的逆是矩阵理论中一个核心的概念，它在很多问题的解决过程中起着非常关键的作用。

在这篇文章中，我们将会介绍矩阵的逆的计算方法，以及一些相关的概念和定理。

矩阵的逆是指对于一个方阵A，如果存在一个矩阵B，使得AB=BA=I，其中I是单位矩阵，那么B就是A的逆矩阵，记作A^{-1}。

逆矩阵的存在性是一个非常重要的问题，因为只有存在逆矩阵的矩阵才能称之为可逆矩阵，可逆矩阵的性质非常重要。

在实际计算中，如何求一个矩阵的逆是一个比较复杂的问题。

下面我们将介绍几种常见的计算方法：1. 初等变换法：这是求逆矩阵最常用的方法之一。

首先将矩阵A与单位矩阵I组合成一个增广矩阵[A|I]，然后通过一系列的初等行变换将左侧的矩阵变为单位矩阵，那么矩阵A就会变成逆矩阵。

2. 初等矩阵法：利用初等矩阵与原矩阵的乘积来求逆矩阵。

首先将矩阵A分解成一系列的初等矩阵的乘积，然后分别求每一个初等矩阵的逆矩阵，最后把它们逆序相乘，就能得到矩阵A的逆矩阵。

3. 行列式法：对于一个方阵A，如果det(A)不为0，那么就可以通过公式A^{-1} = \frac{1}{det(A)}\text{adj}(A)来求得A的逆矩阵，其中adj(A)是A的伴随矩阵。

除了这些常见的方法之外，还有一些特殊的矩阵，如对称矩阵、正交矩阵等，它们的逆矩阵的求解方法可能会有一些特殊的性质和技巧。

在实际的计算过程中，可以根据矩阵的具体性质和条件来选择最合适的方法来求解逆矩阵。

在矩阵逆的计算过程中还有一些需要注意的细节和注意事项，比如矩阵的秩、行列式、伴随矩阵等概念。

我们需要保证矩阵是方阵，而且行列式不为0，才能保证逆矩阵的存在性。

在实际的计算中，可能会遇到矩阵奇异的情况，求不出逆矩阵，这时候需要进行特殊处理。

矩阵的逆是线性代数中一个非常重要的概念，它在很多问题的解决过程中都起着非常关键的作用。

二维矩阵的逆矩阵公式

二维矩阵的逆矩阵公式

二维矩阵的逆矩阵公式二维矩阵的逆矩阵公式是矩阵代数中的重要内容之一。

在线性代数中，矩阵的逆矩阵是指能够与原矩阵相乘得到单位矩阵的矩阵。

逆矩阵的概念在许多领域中都有广泛的应用，如物理学、经济学、计算机科学等。

在二维矩阵中，逆矩阵的计算方法相对简单。

假设有一个二维矩阵A，其逆矩阵记作A^-1。

那么根据逆矩阵的定义，A和A^-1的乘积应该等于单位矩阵I。

即A * A^-1 = I。

要计算A的逆矩阵，可以使用公式A^-1 = (1 / det(A)) * adj(A)，其中det(A)表示矩阵A的行列式，adj(A)表示A的伴随矩阵。

逆矩阵的计算过程并不复杂，但需要一定的数学知识和计算能力。

首先，我们需要计算矩阵A的行列式det(A)。

行列式是一个标量，表示矩阵A的某种性质。

通过计算矩阵A的代数余子式，并按照一定规则进行求和，可以得到行列式的值。

接下来，我们需要计算矩阵A的伴随矩阵adj(A)。

伴随矩阵是通过将矩阵A的每个元素的代数余子式转置得到的。

具体而言，对于矩阵A中的每个元素a_ij，其对应的代数余子式是删去第i行和第j列后剩余元素的行列式。

我们将行列式和伴随矩阵代入逆矩阵的公式A^-1 = (1 / det(A)) * adj(A)中，即可计算出矩阵A的逆矩阵A^-1。

逆矩阵的计算结果是一个与矩阵A维度相同的矩阵，其每个元素都是一个有理数或实数。

逆矩阵在实际应用中有着广泛的用途。

例如，在线性方程组的求解中，可以使用逆矩阵来求解未知数的值。

具体而言，假设有一个线性方程组Ax = b，其中A是一个已知的系数矩阵，x是未知数向量，b是已知的结果向量。

如果矩阵A存在逆矩阵A^-1，那么方程组的解可以表示为x = A^-1 * b。

通过计算逆矩阵，可以快速求解线性方程组的解。

在几何变换中，逆矩阵也有着重要的作用。

例如，对于二维平面上的一个向量，可以通过矩阵A的逆矩阵A^-1来进行逆变换。

具体而言，假设有一个向量v，通过将其与矩阵A相乘可以得到一个新的向量v'，即v' = A * v。

逆矩阵的概念矩阵可逆的条件逆矩阵的求法-毕业论文-全文在线阅读-

逆矩阵的概念矩阵可逆的条件逆矩阵的求法-毕业论文-全文在线阅读-
上页 下页 返回
上页 下页 返回
例10 设
求矩阵X使满足AXB= C。 分析：
若A-1，B -1存在，则由A-1左乘AXB=C，又
用B-1右乘AXB= C，
有
A-1AXBB-1= A-1CB-1，
即
X = A-1CB-1。
上页 下页 返回
解
上页 下页 返回
矩阵的运算小结
一、已定义过的运算：
★ 矩阵与矩阵的加、减法； ★ 矩阵与数的乘积； ★ 矩阵与矩阵的乘积； ★ 方阵的行列式； ★ 逆矩阵； ★ 矩阵的转置。
Ex.4
解
又
上页 下页 返回
于是
上页 下页 返回
也可以直接按定义来验证这一结论。
上页 下页 返回
Ex.5 解
上页 下页 返回
Ex.6 解
上页 下页 返回
上页 下页 返回上页Fra bibliotek返回设给定一个线性变换： 它的系数矩阵是一个 n 阶方阵A，
上页 下页 返回
记
则线性变换(7)可记为 Y =AX.
逆矩阵。
例如
因为AB= BA= E，所以B是A的逆矩阵，同样A也 是B的逆矩阵。
上页 下页 返回
如果方阵A是可逆的，则 A的逆阵一定是唯一 的。 这是因为：设 B、C都是 A的逆矩阵， 则有
B=BE =B（AC）=（BA）C =EC =C， 所以 A的逆阵是唯一的。
A的逆阵记作A-1。 即若AB=BA=E，则 B=A-1。
§3 逆 阵
★ 逆矩阵的概念 ★ 矩阵可逆的条件 ★ 逆矩阵的求法
矩阵之间没有定义除法，而数的运算有 除法，本节相对于实数中的除法运算，引入 逆矩阵的概念。
下页 关闭
逆阵的概念
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

线性代数第二节逆矩阵及其运算一、逆矩阵的概念和性质五、初等变换求逆矩阵四、矩阵的初等变换和初等矩阵二、矩阵可逆的条件三、用伴随矩阵法求逆矩阵线性代数（或称的逆）；其中为的倒数，a 11a a -=a ,111aa a a --==在数的运算中，对于数，有是否存在一个矩阵,.11AA A A E --==在矩阵的运算中,单位矩阵E 相当于数的乘法运算中的1，那么，对于矩阵A ，1A -使得一、逆矩阵的概念和性质0a ≠线性代数对于n 阶矩阵A ，如果有一个n 阶矩阵B ,使得则说矩阵A 是可逆矩阵或非奇异矩阵，并把矩阵B 称为A 的逆矩阵，否则称A 是不可逆矩阵或奇异矩阵。

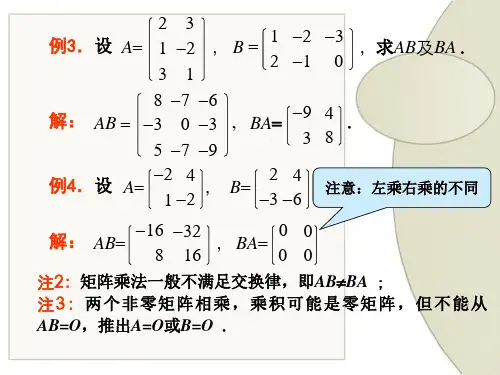
,AB BA E ==例1设,01011010A B -⎛⎫⎛⎫== ⎪ ⎪-⎝⎭⎝⎭,AB BA E ==∴B 是A 的一个逆矩阵。

定义1（可逆矩阵）线性代数例1 设,2110A ⎛⎫= ⎪-⎝⎭解设是A 的逆矩阵,a b B c d ⎛⎫= ⎪⎝⎭则2110a b AB c d ⎛⎫⎛⎫= ⎪⎪-⎝⎭⎝⎭1001⎛⎫= ⎪⎝⎭221001a c b d ab ++⎛⎫⎛⎫⇒= ⎪ ⎪--⎝⎭⎝⎭求A 的逆矩阵线性代数,,,,212001a c b d a b +=⎧⎪+=⎪⇒⎨-=⎪⎪-=⎩,,,.0112a b c d =⎧⎪=-⎪⇒⎨=⎪⎪=⎩又因为⎪⎭⎫ ⎝⎛-01120112-⎛⎫ ⎪⎝⎭⎪⎭⎫ ⎝⎛-0112=0112-⎛⎫ ⎪⎝⎭,1001⎛⎫= ⎪⎝⎭所以.10112A --⎛⎫= ⎪⎝⎭A BA B (待定系数法)线性代数注：不是每个非零矩阵都有逆矩阵。

0102A ⎛⎫= ⎪⎝⎭例如11AA A A E --==不论一个怎样的矩阵的第一列全都是零。

因此，不可能有一个矩阵, 使,B 1A -BA线性代数定理1若A 是可逆矩阵，则A 的逆矩阵是惟一的.,,AB BA E AC CA E ====又B EB =()CA B =()C AB =.CE C ==所以A 的逆矩阵是惟一的,即B C=证明:设B 和C 是A 的逆矩阵，则有以后，把A 的逆矩阵记为。

1A -线性代数逆矩阵的运算性质A ().11A A --=(1)若可逆，则也可逆，且1A -证明可逆，则有逆矩阵，使A 1A -11AA A A E--==成立由定义也可逆，且1A -().11A A --=线性代数().111AB B A ---∴=()()11AB BA --1AEA -=,1AA E -==证明().11111122m m A A A A A A ----=()11A BB A --=()()11B A AB --()11B A A B --=1B EB E -==推广()111B B A A ---=（2）若n 阶矩阵A 、B 均可逆，则AB 也可逆，且线性代数()()11A A A A --'''=E E'==()().11A A --''∴=证明(3) 若可逆，则也可逆，而且A A '()()11A A --''=()()11A A AA E--'''==线性代数二矩阵可逆的条件定义 2 (n 阶矩阵的行列式)111212122212n n n n nna a a a a a a a a 设是一个n 阶矩阵，按诸原来的位置，正好()ij A a ij a 叫做A 的行列式，记为A对应一个n 阶行列式线性代数定理2对任意两个n 阶矩阵A 、B ，恒有AB A B=证明：设()()(),,ij ij ij A a B b C AB c ====111111110000011n n nnn nnna a a a Ab b EBb b =---构造2n 阶方阵线性代数作列的变换将行列式中的B 的元素全部化为000A A C EBE=--由Laplace 定理()(122)1n A B E C+++=--n(2n+1)=(-1)(1)nC-C AB==则有线性代数112111222212n n n nnn A A A A A A A A A A *⎛⎫ ⎪ ⎪= ⎪⎪⎝⎭给定n 阶矩阵111212122212n n n n nn a a a a a a A a a a ⎛⎫ ⎪ ⎪= ⎪⎪⎝⎭中的元素A ij 为中元素a ij 的代数余子式。

A *A 称为A 的伴随矩阵，定义3（伴随矩阵）线性代数A 定理3矩阵可逆的充要条件是，且,11A A A -*=0A ≠其中为矩阵A 的伴随矩阵。

A *A 证明: ( 必要性)若可逆，则有，使1A -,11A AE -∴⋅==.0A ≠.1AA E -=从而线性代数111211121121222122221212n n n n n n nn n nnn a a a A A A a a a A A A AA a a a A A A *⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪= ⎪ ⎪⎪⎪⎝⎭⎝⎭⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭0(充分性)设。

0A ≠A 0A A A A E =AA A A A E **∴==,A A A A E A A **⇒==.1A A A*-=由逆矩阵的定义A 可逆，且证毕同理可以计算A A A E*=,1AB A B E =⋅==,0A ≠故,1A -因而存在于是().1AB E BA E B A -==⇒=若或定理4证明:B EB =()1A AB -=()1AAB -=11A E A--==证毕由于AB E=线性代数三、用伴随矩阵法求逆矩阵根据定理3若A 可逆，则,11A A A-*=其中为矩阵A 的伴随矩阵。

A *线性代数解313413314A =,10=-≠.1A -∴存在,1113114A ==,1243734A =-=-例2 求方阵,313413314A ⎛⎫⎪= ⎪ ⎪⎝⎭1234B ⎛⎫= ⎪⎝⎭的逆矩阵.线性代数同理可得,,,,132122231130A A A A ==-==,,,313233031A A A ===-,110733101A *-⎛⎫ ⎪=- ⎪ ⎪-⎝⎭得故11A A A -*=110733101-⎛⎫ ⎪=-- ⎪ ⎪-⎝⎭.110733101-⎛⎫ ⎪=-- ⎪ ⎪-⎝⎭线性代数122034B ==-≠.1B -∴存在得112112224231B B B B B *-⎛⎫⎛⎫==⎪ ⎪-⎝⎭⎝⎭14211312B B B -*-⎛⎫==- ⎪-⎝⎭()12234B ⎛⎫= ⎪⎝⎭线性代数,,.1112212215321414x x A X B x x -⎛⎫⎛⎫⎛⎫===⎪ ⎪⎪-⎝⎭⎝⎭⎝⎭例3 解方程，其中AX B =解方程两端左乘矩阵,11514--⎛⎫⎪-⎝⎭111515153214141414X -----⎛⎫⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭⎝⎭得E线性代数45321114--⎛⎫⎛⎫= ⎪⎪--⎝⎭⎝⎭.172846--⎛⎫= ⎪--⎝⎭115321414X --⎛⎫⎛⎫∴= ⎪ ⎪-⎝⎭⎝⎭线性代数四、矩阵的初等变换和初等矩阵12312313231(1)425 1 (2)2 21(3)x x x x x x x x -+=⎧⎪++=⎨⎪+=⎩(1)(2)(2), (1)(1)(3)⨯-+⨯-+用消元法解线性方程组1232323231(1)4 2 (4) 5(5)x x x x x x x -+=⎧⎪-=⎨⎪-=⎩解：得线性代数(4)(5)↔1232323231(1) 5 (5)4 2(4)x x x x x x x -+=⎧⎪-=⎨⎪-=⎩(5)(4)(4)⨯-+123233231(1) 2 (5)318(6)x x x x x x -+=⎧⎪-=⎨⎪=-⎩1(6),3⨯123233231(1) 2 (5) 6(6)x x x x x x -+=⎧⎪-=⎨⎪=-⎩线性代数反复做下面三种变换：3 交换某两行。

1 用非零实数乘以某行。

2 将某行的倍数加到另一行。

其实质是对矩阵作如下三种变换：()A b 3 交换两个方程。

1 用非零实数乘以某个方程。

2 将某个个方程的倍数加到另一个方程。

总结：消元的过程实际上是对方程组线性代数定义由单位矩阵经过一次初等变换得到的矩阵称为初等矩阵.定义：将如下变换统称为初等变换3 交换两行（列）。

1 用非零实数乘以某行（列）。

2 将某行（列）的倍数加到另一行（列)。

类型Ⅰ第一类初等矩阵由交换单位阵E 的两行（列）得到。

010100001⎛⎫⎪ ⎪ ⎪⎝⎭类型Ⅱ第二类初等矩阵由单位阵E 的某行（列）乘以一个非零常数得到。

例100010003⎛⎫⎪ ⎪ ⎪⎝⎭12R =12C =R 3③==C 3③例类型Ⅲ第三类初等矩阵由单位阵E 的某行（列）的倍数加到另一行（列)得到。

例103010001⎛⎫ ⎪⎪⎪⎝⎭R 3③+①==C 3①+③线性代数定理5 A 为任意矩阵，则A 的任一初等行变换就相当于A 的左边乘以一个相应的初等矩阵；A 的任一初等列变换就相当于A 的右边乘以一个相应的初等矩阵。

111213212223212223111213313233313233a a a a a a a a a a a a a a a aa a ⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭（1）010100001⎛⎫ ⎪= ⎪ ⎪⎝⎭线性代数111213111112132122232121222331323331313233a a a a a a a a a a a a a a aa a aa a a μμμ+⎛⎫⎛⎫⎪ ⎪+ ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭（3）10010001μ⎛⎫⎪= ⎪ ⎪⎝⎭111213111213212223212223313233313233a a a a a a a a a a a a aa a aa a λλλ⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭（2）10000001λ⎛⎫ ⎪= ⎪ ⎪⎝⎭线性代数设矩阵练习111213212223212223111213313233311132123313,a a a a a a A a a a B a a a a a a a a a a a a ⎛⎫⎛⎫⎪⎪== ⎪ ⎪⎪ ⎪+++⎝⎭⎝⎭12010100100,010001101P P ⎛⎫⎛⎫⎪ ⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭则有12211221(1).(2).(3).(4)AP P B AP P B P P A B P P A B====线性代数定理6 若A 为初等矩阵，则A 是非奇异的，1A -且为一与它同类型的初等矩阵。

下面举例说明100001010A ⎛⎫⎪= ⎪ ⎪⎝⎭②③E100001,010A E ⎛⎫⎪∴= ⎪ ⎪⎝⎭1100001010A -⎛⎫⎪∴= ⎪ ⎪⎝⎭ⅠⅡ020001A ⎪= ⎪ ⎪⎝⎭显然AE②×12即100100,2001A E ⎛⎫⎪ ⎪= ⎪ ⎪⎝⎭故1100102001A -⎛⎫⎪ ⎪= ⎪ ⎪⎝⎭Ⅲ010201A ⎪= ⎪ ⎪⎝⎭AE①()2⨯-+③100010,201A E ⎛⎫⎪= ⎪ ⎪-⎝⎭显然即故1100010201A -⎛⎫⎪= ⎪ ⎪-⎝⎭线性代数定理1n 阶可逆矩阵A 恒为若干个初等矩阵之积。