人教版七年级上册常见立体图形的分类

4。

1 生活中的立体图形1．常见的立体图形(1）柱体①棱柱：有两个面互相平行，其余各面都是四边形，并且每两个相邻的四边形的公共边互相平行，由这些面围成的几何体叫棱柱．如三棱柱、四棱柱、五棱柱等；②圆柱：以矩形的一边所在的直线为旋转轴，其余各边围绕它旋转形成的几何体叫做圆柱．（2）锥体①棱锥:有一个面是多边形,其余各面都是有一个公共顶点的三角形，由这些面围成的几何体叫棱锥．如三棱锥、四棱锥、五棱锥等；②圆锥：以直角三角形一边所在的直线为旋转轴,其余各边围绕它旋转形成的几何体叫做圆锥．(3）球体：半圆以它的直径为旋转轴，旋转而成的几何体叫做球体．【例1】判断下列说法是否正确：(1）柱体的上、下两个面不一样大()．(2)圆柱、圆锥的底面都是圆（）．（3)棱柱的底面不一定是四边形()．(4)圆柱的侧面是平面（）．（5）棱锥的侧面不一定是三角形()．解析：柱体的上、下底面是平行且相等的（形状相同、大小相等），所以(1)错误；圆柱的上、下两个底面都是圆，圆锥的底面是圆,所以(2）正确；棱柱可以是三棱柱、四棱柱、五棱柱等，即棱柱的底面不一定是四边形，所以(3)正确；圆柱的侧面是曲面不是平面,所以(4）错误；棱锥的侧面一定是三角形，所以(5）错误．答案:(1)×(2）√（3）√（4）×（5）×2．立体图形的分类立体图形错误!为便于理解与识记，形象地总结立体图形的分类如下：【例2】下列图形中柱体的个数为（）．A．1 B．2 C．3 D．4解析：柱体的特点是它们的上、下底面是平行且相等的（形状相同、大小相等），由此判断①和②是柱体．答案:B3．多面体（1)多面体的概念:围成棱柱和棱锥的面是平的面,像这样的立体图形叫做多面体．如图，下列图形分别为：棱柱(长方体)、棱锥（三棱锥），它们均为多面体．(2)正四面体:由四个完全一样的正三角形围成的空间图形称为正四面体，这些三角形的顶点、边分别称为正四面体的顶点、棱(相邻的三角形的公共边只算一条棱）．(3)正六面体：类似的,组成正方体的每个正方形的顶点、边分别称为正六面体的顶点、棱(相邻的正方形的公共边只算一条棱）．此外,还有正八面体、正十二面体和正二十面体，如图．谈重点常见的多面体棱柱和棱锥都是多面体，圆柱、圆锥和球不是多面体．【例3】一个棱柱的底面是五边形，它有几条侧棱，几个顶点？共有几个面？分析：由已知易知该立体图形是五棱柱,结合图形回答问题即可．解：它有5条侧棱,10个顶点，共有7个面．析规律棱柱棱数、顶点数和面数的确定底面为n边形的棱柱有n条侧棱,2n个顶点,（n＋2)个面．。

4.1.1 立体图形与平面图形第1课时1.会识别生活中的几何体,并能把它们分类.2.能认识常见的几何图形,并能用自己的语言描述常见的几何图形的特征. 【重点难点】1.会识别生活中的几何体,并能把它们分类.2.用自己的语言描述常见的几何图形的特征.【新课导入】同学们玩过七巧板吗?应用七巧板可以拼出许多有趣的图案,如图所示,你知道这些图案是由哪些基本图形组成的吗?【课堂探究】一、生活中的几何体1.下面物体中,最接近圆柱的是( C )2.想一想我们常用的水杯的形状,下面给出的四类几何体中,与水杯最相近的是( C )3.下列说法不正确的是( C )(A)圆柱体的上、下两个底面一样大(B)正方体的所有棱长都相等(C)球不是几何体(D)圆锥不是平面图形4.日常生活中,我们会遇到很多平面图形,请辨别图中各包含着哪些平面图形?解:国旗是长方形和五角星,五环标志是圆形,香港区旗是长方形,中间图案是紫荆花.二、几何体的特征5.从一个六边形的某个顶点出发,分别连接这个顶点与其余各顶点,可以把这个六边形分割成 4 个三角形.6.如图是由 5 种平面图形组成的,它们分别是平行四边形、三角形、正方形、长方形、圆.平面图形与立体图形的区别1.下列各物体的形状为圆柱的是( C )(A)火力发电厂的烟囱(B)打足气的自行车内胎(C)没有使用的上下两个面都是圆形的铅笔(D)体育用品中的标枪2.如图所示的立体图形中,不是柱体的是( D )3.下列实物中含有棱锥的几何体是( C )4.图中的小猫是由三角形组成的,三角形的个数为( B )(A)8个(B)11个(C)10个(D)6个5.观察下列图形并填空.上面图形中,圆柱是④,棱柱是③⑥,圆锥是①⑦,棱锥是②,圆台是⑧,棱台是⑨,球体是⑤.6.如图所示,下列各标志图形主要由哪些简单的几何图形组成?解:①由圆组成;②由长方形和正方形组成;③由四边形(或菱形)组成;④由圆和圆弧组成.。

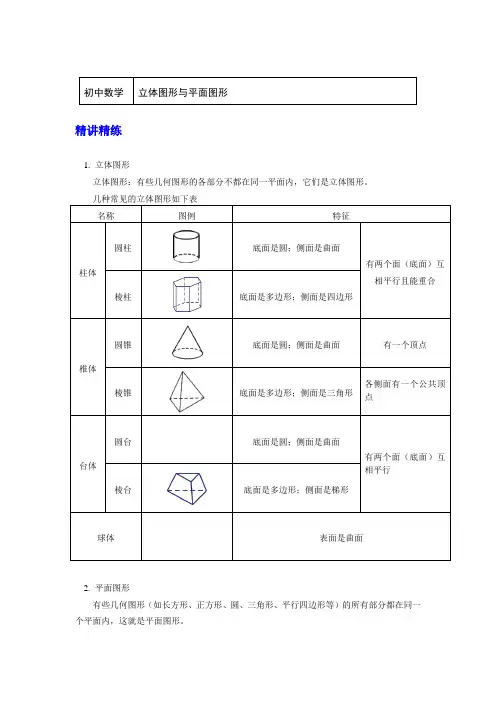
初中数学立体图形与平面图形精讲精练1. 立体图形立体图形：有些几何图形的各部分不都在同一平面内，它们是立体图形。

名称图例特征柱体圆柱底面是圆；侧面是曲面有两个面（底面）互相平行且能重合棱柱底面是多边形；侧面是四边形椎体圆锥底面是圆；侧面是曲面有一个顶点棱锥底面是多边形；侧面是三角形各侧面有一个公共顶点台体圆台底面是圆；侧面是曲面有两个面（底面）互相平行棱台底面是多边形；侧面是梯形球体表面是曲面2. 平面图形有些几何图形（如长方形、正方形、圆、三角形、平行四边形等）的所有部分都在同一个平面内，这就是平面图形。

名称图形直线直线l射线射线OA线段线段AB三角形长方形正方形梯形平行四边形圆扇形3. 几何体的三视图。

立体图形是三维图形，物体的观察方向有上、下、前、后、左、右，其中利用前视图（正视图）、俯视图、左视图即可描述物体的几何形状。

物体的三视图的关系为（如图所示）：主、俯视图：长对正；主、左视图：高平齐；俯、左视图：宽相等。

由三视图想象几何体的形状，首先，应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状，然后综合起来考虑整体形状。

例题1 如图，有一正角锥的底面为正三角形，侧面是等腰三角形，若此正角锥其中两个面的周长分别为27、15，则此正角锥所有边的长度和为多少？（）A. 36B. 42C. 45D. 48思路分析：如图所示：根据题意得：2y+x=27，3x=15，其他都不符合三角形条件，解得：x=5，y=11，∴正角锥所有边的长度和=3x+3y=15+33=48，故选D。

答案：D例题2 如图，在3×3的正方形网格中，含有“梦”字的正方形的个数是（）A. 1个B. 4个C. 6个D. 14个思路分析：如下图所示：由图可知：含有梦字的正方形有第5个，第1，2，4，5组成的正方形，第2，3，5，6组成的正方形，第4，5，7，8组成的正方形，第5，6，8，9组成的正方形，第1，2，3，4，5，6，7，8，9组成的正方形。

立体几何是几何学中的一个分支，研究三维空间中的几何问题，包括各种立体图形的性质、体积、表面积等。

在七年级的学习中，立体几何是一个重要的内容，对学生在几何学习中的能力提升和思维发展具有重要作用。

以下是七年级立体几何知识点的总结：1.立体图形的分类在七年级的学习中，学生将学习到各种立体图形的分类，包括正方体、长方体、棱柱、棱锥、圆柱、圆锥等。

这些立体图形具有各自的特点和性质，学生需要能够准确地识别和描述这些立体图形。

2.立体图形的表面积立体图形的表面积是指该立体图形所有表面的总面积。

在七年级的学习中，学生将学习如何计算各种立体图形的表面积，包括正方体、长方体、棱柱、棱锥、圆柱、圆锥等。

学生需要了解各种立体图形的表面积计算公式，并能够灵活应用到实际问题中。

3.立体图形的体积立体图形的体积是指该立体图形所包围的空间的大小。

在七年级的学习中，学生将学习如何计算各种立体图形的体积，包括正方体、长方体、棱柱、棱锥、圆柱、圆锥等。

学生需要了解各种立体图形的体积计算公式，并能够灵活应用到实际问题中。

4.立体图形的投影在七年级的学习中，学生还将学习立体图形的投影，包括正投影和斜投影。

正投影是指平行于坐标轴的投影，斜投影是指不平行于坐标轴的投影。

学生需要了解如何绘制各种立体图形的正投影和斜投影，并能够根据所给条件求解相应的问题。

5.空间位置关系在七年级的学习中，学生还将学习各种立体图形之间的空间位置关系，包括平行关系、垂直关系、相交位置等。

学生需要了解如何判断各种立体图形之间的空间位置关系，并能够应用到实际问题中。

《立体图形与平面图形》知识全解课标要求1．通过实物和具体模型，了解从物体抽象出来的几何体、平面、直线和点等．2．了解立体图形与平面图形之间的区别和联系，初步建立空间观念．知识结构内容解析1.几何图形各种各样的物体除了具有颜色、质量、材质等性质，还具有形状（如方的、圆的等）、大小（如长度、面积、体积等）和位置关系（如相交、垂直、平行等），物体的形状、大小和位置关系才是我们几何中研究的内容．长方体、圆柱、球、长（正）方形、圆、线段、点等，以及小学学习过的三角形、四边形等，都是从形形色色的物体外形中抽象出来的．我们把从实物中抽象出的各种图形统称为几何图形．几何图形是数学研究的主要对象之一．2.立体图形立体图形：有些几何图形的各部分不都在同一平面内，它们是立体图形.常见的立体图形：（1）柱体：棱柱和圆柱；（2）锥体：棱锥和圆锥；（3）球.说明：（1）圆柱和棱柱的区别：圆柱的底面是圆形，棱柱的底面是多边形；圆柱的侧面是曲面，棱柱的侧面是四边形.（3）球与圆的区别：球是立体图形，而圆是平面图形，这是易误点.3.平面图形平面图形：有些几何图形的各部分都在同一平面内，它们是平面图形.线段、角、长方形、正方形、三角形、圆等都是我们十分熟悉的平面图形.一些简单的平面图形可以组合成许多优美的图案，如某些国家的国旗，各种标志，由各种开关的地砖或瓷砖铺成的漂亮的地面和墙面.重点难点本节内容的重点是：立体图形和平面图形的概念，能从实物的外形中抽象出几何图形． 教学重点的解决方法：要通过教师引导，让学生能充分掌握直观感知，具体操作、确认等实践活动，区分图形，探索出图形的特征和性质，培养空间想象能力，解决重点． 本节内容的难点是：从实物的外形中抽象出几何图形．教学难点的解决方法：突破难点的方法是引导学生欣赏丰富的实物图片，从实物抽象出立体图形，使学生有具体的感性认识；教师通过展示立体图形的模型，让学生观察、触摸，使学生进一步感知每种立体图形的特点，并请学生找生活中各种简单立体图形所对应的实物，进一步巩固学生对立体图形的认知，解决教学难点．教法导引1．充分了解与关注学情在小学阶段，虽然学生没有听说过“几何”，但这部分内容实际上小学阶段已经有了最基础的铺垫，学生学习了常见的立体图形和平面图形，包括长方体（正方体），圆锥体，圆 实物模型 几何图形 立体图形 平面图形 抽象 还原（各部分不都在同一平面内） （各部分都在同一平面内）柱体，球体，三角形（等腰三角形，等边三角形，直角三角形，锐角三角形，钝角三角形），长方形（正方形），梯形，平行四边形，菱形，角，线段，射线，直线等等，知道这些图形在生活中随处可见，并能从具体事物和情景中感知这些常见图形，这些储备都是这节课学习的认知起点．可见这节课不完全是初中“几何”的初始课、引言课，它更是对小学学习的继承与发展．那么教师的教学设计就应该充分利用和重视学生已有的知识储备，完善与发展他们对几何图形的认识．2．充分重视问题设计的生活化由于本节学习内容的特殊性，本节课的设计可以使数学问题生活化，让学生在教师问题的引导下更好地认识身边的图形世界，体验几何图形在生活中的价值，并在熟悉的场景里提炼概括知识，形成系统．如课堂中问题可设计为：你能从中找到熟悉的图形吗？你在生活中还能举出“点、线、面、体”的例子吗？在刚刚接触的实际物体和场景中，哪些面是平的，哪些是曲的？你能说说你对无限延展的理解吗？你能对这些图形分类吗？仔细观察演示，你能在生活中找到类似的揭示点、线、面、体之间关系的例子吗？你能找出图中的平面图形吗？你能找出身边教室里的几何图形吗？3．充分重视学生主体地位、教师主导地位的科学把握自主探究、合作交流的学习方式能充分体现以教师为主导，学生为主体的课程理念．然而探究并不是简单地改“满堂灌”为“满堂问”．因此问题的层次性、有效性在探究活动的激发和引导过程中就比较重要．如本节课的问题可以依次引领学生经历了几何图形的抽象、概括、分类和应用过程，同时在学习活动的设计中充分预留了学生的思考、交流、辨析时间，确保了学生能真正经历知识的发生、发展过程．4．充分重视原始概念与科学概念的甄别学生对几何图形的了解很大部分局限于生活经验，从生活经验中获取的一些原始概念和教师的科学概念之间会有一些冲突和差别，所以在教学中要注意引导和纠正．比如，生活中的图形并不等同于几何中的图形，在抽象的过程中，要引导学生注意甄别．另外生活中的物体的形状不会都是标准的几何图形，还有颜色、材料之分别等，但几何中教师只研究图形的形状、大小和相互位置，几何中点无大小、线无粗细、面无厚薄．这些都需要教师设计好问题，一点点地让学生在学习过程中建立科学的“几何图形”的概念．学法建议在学习过程中，应主动观察、动手操作、大胆猜想、多与同学进行交流自己的看法。

第1页/共3页 2019初一上册数学第四章知识点总结：几何图形分类 成绩的提高是同学们提高总体学习成绩的重要途径，大家一定要在平时的练习中不断积累，小编为大家准备了2019最新初一上册数学第四章知识点总结：几何图形分类，希望同学们不断取得进步! (1)立体几何图形可以分为以下几类： 第一类：柱体; 包括：圆柱和棱柱，棱柱又可分为直棱柱和斜棱柱，棱柱体按底面边数的多少又可分为三棱柱、四棱柱、N棱柱; 棱柱体积统一等于底面面积乘以高，即V=SH， 第二类：锥体; 包括：圆锥体和棱锥体，棱锥分为三棱锥、四棱锥以及N棱锥; 棱锥体积统一为V=SH/3， 第三类：球体; 此分类只包含球一种几何体， 体积公式V=4πR3/3， 其他不常用分类：圆台、棱台、球冠等很少接触到。 大多几何体都由这些几何体组成。 (2)平面几何图形如何分类 a.圆形 第2页/共3页

b.多边形：三角形(分为一般三角形，直角三角形，等腰三角形，等边三角形)、四边形(分为不规则四边形，体形，平行四边形，平行四边形又分：矩形，菱形，正方形)、五边形、六…… 注：正方形既是矩形也是菱形 与当今“教师”一称最接近的“老师”概念，最早也要追溯至宋元时期。金代元好问《示侄孙伯安》诗云：“伯安入小学，颖悟非凡貌，属句有夙性，说字惊老师。”于是看，宋元时期小学教师被称为“老师”有案可稽。清代称主考官也为“老师”，而一般学堂里的先生则称为“教师”或“教习”。可见，“教师”一说是比较晚的事了。如今体会，“教师”的含义比之“老师”一说，具有资历和学识程度上较低一些的差别。辛亥革命后，教师与其他官员一样依法令任命，故又称“教师”为“教员”。 要练说，得练听。听是说的前提，听得准确，才有条件正确模仿，才能不断地掌握高一级水平的语言。我在教学中，注意听说结合，训练幼儿听的能力，课堂上，我特别重视教师的语言，我对幼儿说话，注意声音清楚，高低起伏，抑扬有致，富有吸引力，这样能引起幼儿的注意。当我发现有的幼儿不专心听别人发言时，就随时表扬那些静听的幼儿，或是让他重复别人说过的内容，抓住教育时机，要求他们专心听，用心记。平时我还通过各种趣味活动，培养幼儿边听边记，边听边想，边听边说的能力，如听词对词，听词句说意思，第3页/共3页