当前位置：文档之家 › 自动控制原理_第四章习题集配套答案

自动控制原理_第四章习题集配套答案

  • 格式：doc
  • 大小：581.00 KB
  • 文档页数：10

下载文档原格式

  / 10

合集下载

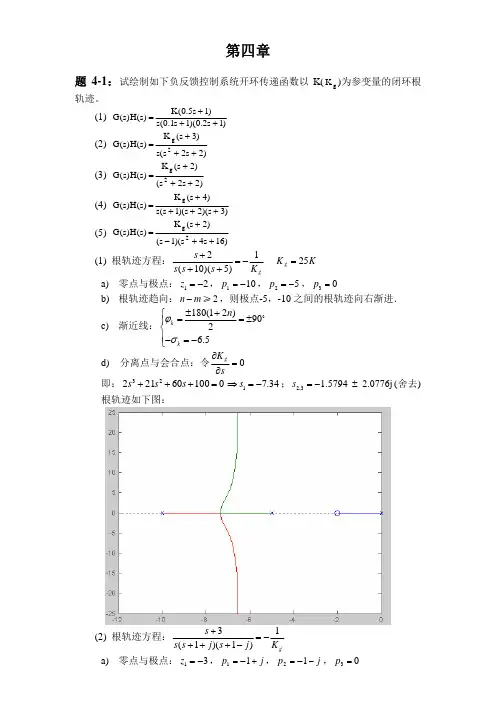
自动控制原理参考答案-第4章

自动控制原理参考答案-第4章

d) 与虚轴交点：
特征方程： s3 + 2s2 + (2 + Kg )s + 3Kg = 0
s3
1
2+ Kg
s2
2
3Kg
s1 2 − 0.5Kg
s0
3Kg
当 Kg = 4 时， 2s2 +12 = 0 ⇒ s = ±2.45 j
e) 出射角： βsc = ±180(1+ 2n) − ∑ β + ∑α
s3
1
7
s2
2
Kg −10
s1 12 − 0.5Kg
s0 Kg −10
当 Kg = 24 时， 2s2 +14 = 0 ⇒ s1,2 = ±2.65 j
劳斯表的 s0 行为正 ⇒ Kg > 10 ，即10 < Kg < 24 根轨迹如下图：
题 4-6：已知负反馈控制系统的开环传递函数为
G(s)H(s)
b) 根轨迹趋向： n − m≥ 2 ，则极点-5，-10 之间的根轨迹向右渐进．
c)
渐近线： ⎧⎪⎨ϕk
=
±180(1 + 2
2n)
=
±90o
⎪⎩−σ k = −6.5
d) 分离点与会合点：令 ∂Kg = 0 ∂s
即： 2s3 + 21s2 + 60s +100 = 0 ⇒ s1 = −7.34 ； s2,3 = −1.5794 ± 2.0776j (舍去) 根轨迹如下图：
(4) 稳态速度误差系数是多少？
(5) 系统指标比该点的二阶指标大还是小？如果要求系统有该点二阶指标
的超调量，能否通过改变阻尼线而获得？是增大阻尼比还是减小它？

广西大学自动控制原理习题答案（本科）第4章

广西大学自动控制原理习题答案（本科）第4章

⼴西⼤学⾃动控制原理习题答案（本科）第4章习题参考答案4-1已知单位反馈系统的开环传递函数为2()(0.21)K G s s s =+试求：⑴使系统增益裕度为10的K 值；⑵使系统相⾓裕度为30?的K 值。

解:系统开环频率特性为2)(+=ωωωKi G (1)求10=m g 的K 值：令180ω为相⾓交越频率，有180arctan 0.245ω=?，5180=ω由10)04.01(|)(|12180180180=+==Ki G g m ωωω可解得K=1。

(2)求30m ?=?的K 值：由定义180()180(902arctan 0.2)30m c c G i ?ωω=?+∠=?+-?-=?=302.0arctan c ω求得系统幅值交越频率c ω=由1)04.01(|)(|2=+=c c c Ki G ωωω85.3)04.01(2=+=c c K ωω注意：涉及相⾓的计算时，可以（1）逐个计算基本环节的相⾓，然后叠加起来。

（2）将频率特性展开为实部和虚部，然后计算相⾓。

计算幅值⼀般将各个基本环节的幅值相乘。

4-2试由幅相频率计算式()90arg tan arg tan arg tan103(5)2G i G i ωωωω∠=-?-+-=确定最⼩相位系统的传递函数。

解:由相频计算式可得出传递函数的形式为(/31)()(1)(101)K s G s s s s +=++由幅频计算式(5)2G i =有2=求得10/3K ω==，所求最⼩相位系统的传递函数为1312(/31)()(1)(101)s G s s s s +=++4-3已知单位反馈系统开环传递函数)2)(5.1)(1()(+++=s s s Ks G 若希望系统闭环极点都具有⼩于-1的实部，试⽤Nyquist 判据确定增益K 的最⼤值。

解：令1u s =+，则“u 平⾯所有极点均处于负平⾯”等价于“s 平⾯所有闭环极点均具有⼩于-1的实部”，并且)1)(5.0()(++=u u u Ku G 可见)(u G 并⽆右半平⾯的开环极点，所以)(u G 的Nyquist 轨线不能包围)0,1(i -点。

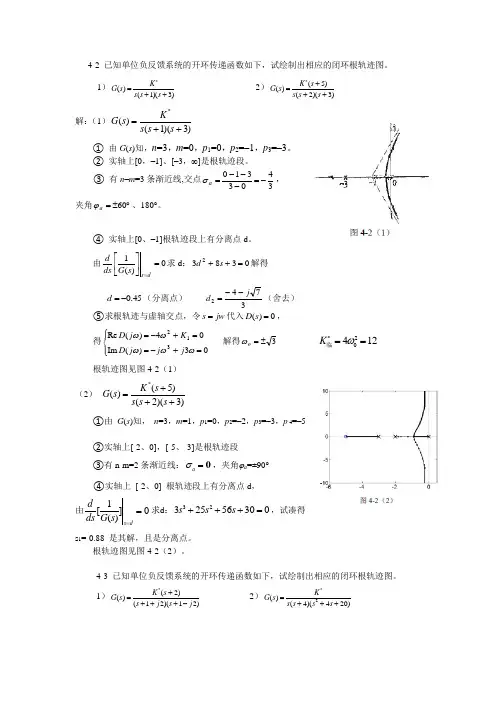
自动控制原理第4章 习题及解析

自动控制原理第4章 习题及解析

4-2 已知单位负反馈系统的开环传递函数如下，试绘制出相应的闭环根轨迹图。

1）*()(1)(3)K G s s s s =++ 2）*(5)()(2)(3)K s G s s s s +=++解：（1）()(1)(3)*K G s s s s =++① 由G (s )知，n =3，m =0，p 1=0，p 2=–1，p 3=–3。

② 实轴上[0，–1]、[–3，∞]是根轨迹段。

③ 有n –m =3条渐近线,交点3403310-=---=a σ， 夹角︒±=60a ϕ、180°。

④ 实轴上[0、–1]根轨迹段上有分离点d 。

由0)(1=⎥⎦⎤⎢⎣⎡=ds s G ds d 求d ：03832=++s d 解得 45.0-=d （分离点） 3742j d --=（舍去） ⑤求根轨迹与虚轴交点，令jw s =代入0)(=s D ，得⎪⎩⎪⎨⎧=+-==+-=03)(Im 04)(Re 312ωωωωωj j j D K j D 解得3±=o ω 20412*K ω==临根轨迹图见图4-2（1）（2） *(5)()(2)(3)K s G s s s s +=++①由 G (s )知， n =3，m =1，p 1=0，p 2=–2，p 3=–3，p 4=–5②实轴上[-2、0]，[-5、-3]是根轨迹段 ③有n-m=2条渐近线：0a σ=，夹角ϕa =±90°④实轴上 [-2、0] 根轨迹段上有分离点d ， 由1[]0()s dd ds G s ==求d ：3232556300s s s +++=，试凑得 s 1=-0.88 是其解，且是分离点。

根轨迹图见图4-2（2）。

4-3 已知单位负反馈系统的开环传递函数如下，试绘制出相应的闭环根轨迹图。

1）*(2)()(12)(12)K s G s s j s j +=+++- 2）*2()(4)(420)K G s s s s s =+++解：（1）*(2)()(12)(12)K s G s s j s j +=+++-根轨迹图见图4-3（1）（2）*2()(4)(420)K G s s s s s =+++① n =4，m =0，p 1=0，p 2=–4，p 3、4=–2±j 4② p 1、p 2连线中点正好是p 3、p 4实部，开环极点分布对称于垂线s=–2，根轨迹也将对称于该垂线。

自控原理第四章书后习题答案

自控原理第四章书后习题答案

4-1 绘制具有下列开环传递函数的负反馈系统的根轨迹1、()()()()54*++=s s s K s H s G解：（1）3个开环极点为：p 1=0，p 2=-4，p 3=-5。

（2）实轴上的根轨迹（-4，0），（-∞，-5）（3）303054011-=----=--=∑∑==mn zp n i mj jiσ()() ,,331212ππππϕ±±=+=-+=k mn k a(4) 分离点：1110d 45d d ++=++ d=-1.47, d=-4.53(舍) （5）与虚轴的交点：在交点处，s=j ω，同时也是闭环系统的特征根，必然符合闭环特征方程，于是有：()020********=++--=+++*=*K j j K s s sj s ωωωω整理得： 0203=-ωω；092=-*ωK 解得01=ω；203,2±=ω；18092==*ωK 最后，根据以上数据精确地画出根轨迹。

2、()()()()11.02*++=s s s K s H s G 解：（1）开环极点有3个，分别为：p 1=p 2=-0，p 3=-1，开环零点为z=-0.1 （2）实轴上的根轨迹为：[-1 -0.1] (3) 渐进线有两条，45.0131.010011-=-+--=--=∑∑==mn zp n i mj jiσ()() ,23,2131212ππππϕ±±=-+=-+=k mn k a (4) 分离点：1111d 10.1d d d ++=++ d=0, d=--0.4(舍), d=0.25(舍)分离角：()() ,23,221212ππππϕ±±=+=+=k lk d 最后，精确地画出根轨迹。

4-3 已知系统的开环传递函数为()()()2*1+=s s K s H s G ① 绘制系统的根轨迹图；② 确定实轴上的分离点及K *的值； ③ 确定使系统稳定的K *值范围。

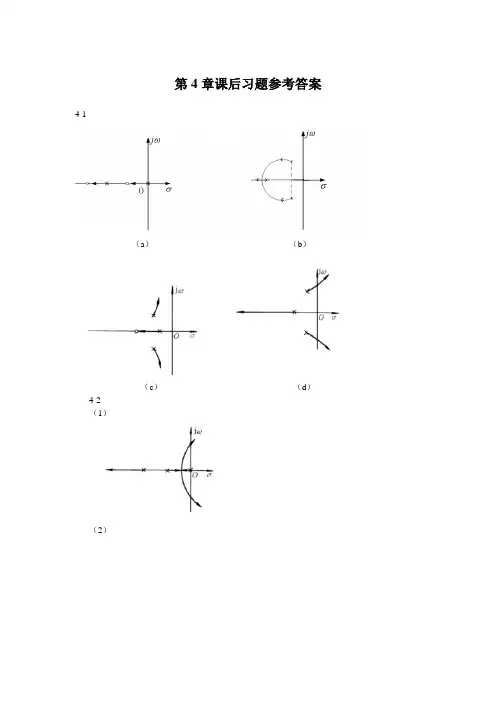
国防《自动控制原理》教学资料包 课后习题答案 第四章

国防《自动控制原理》教学资料包 课后习题答案 第四章

第4章课后习题参考答案4-1（a）（b）（c）（d）4-2（1）（2）4-3（1）（2）（j 24.20 ），K=10.14 4-4 （1）（2）（3）4-5（1）0>K （2）2>K 4-6(1)(2) 闭环极点（j 7.597.0±-），K=34.77 4-7 （1）110222-=+++s s s a（2）130202-=+ss a4-8正反馈 负反馈表明K>0对于正反馈系统不稳定，负反馈系统稳定。

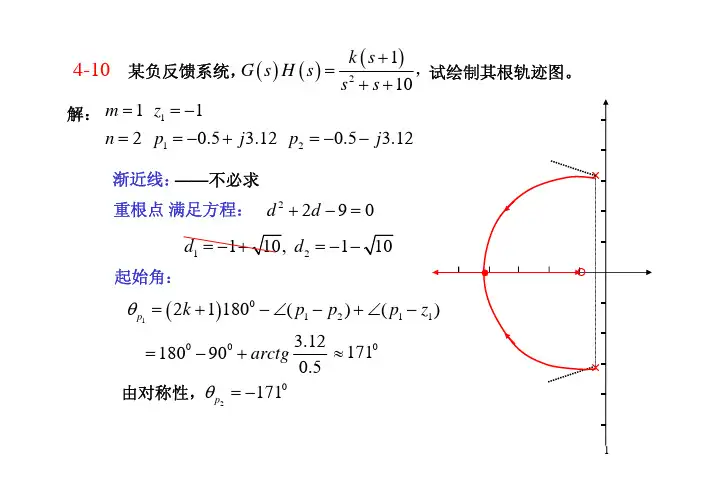
4-90.707ξ=，系统开环传递函数为)4(8)(+=s s s G ，系统的单位阶跃响应为)(t h =)452sin(5.012 +--t e t4-10σωj 007.17-93.2-5-10-（1） K=5；（2）不含有衰减振荡分量的K 值范围为86.00<<K 或29>K 。

4-11 系统的开环极点为0和－p ，开环零点为－z 。

由根轨迹的幅角条件， 得π)12()()(+=+∠-∠-+∠q p s s z s 。

将ωσj s +=代入，整理有pz++︒=-+---σωσωσω111tan 180tan tan取上述方程两端的正切，并利用下列关系yx yx y x tan tan 1tan tan )tan( ±=±有p z z +=++-σωωσσω2)(，则zp z z -=++222)(ωσ，这是一个圆的方程，圆心位于（－z ，j 0）处，而半径等于zp z -2（注意，圆心位于开环传递函数的零点上）。

证毕。

4-12（1）分离点-0.465,对应K=0.88；虚轴的交点j 2± （2）88.00<<K ，阶跃响应不出现超调。

4-13（1）（2）70MAX K =4-14负反馈稳定K 值范围为0<K<73.8，正反馈稳定K 值范围为0<K<35，所以确定根轨迹增益K 的范围为0<K<35。

自动控制原理第二版第四章课后答案

自动控制原理第二版第四章课后答案

自动控制原理第二版第四章课后答案【篇一：《自动控制原理》第四章习题答案】4-1 系统的开环传递函数为g(s)h(s)?k*(s?1)(s?2)(s?4) 试证明点s1??1?j3在根轨迹上，并求出相应的根轨迹增益k*和开环增益k。

解若点s1在根轨迹上，则点s1应满足相角条件?g(s)h(s)??(2k?1)?，如图解4-1所示。

对于s1= -1+j3，由相角条件?g(s1)h(s1)?0??(?1?j3?1)??(?1?j3?2)??(?1?j3?4)? 0??2??3??6???满足相角条件，因此s1= -1+j3在根轨迹上。

将s1代入幅值条件： g(s1)h（s1?k*?1?1?j3?1??1?j3?2??1?j3?4k8*解出： k=12 ，k=*?324-2 已知开环零、极点如图4-2 所示，试绘制相应的根轨迹。

解根轨如图解4-2所示：4-3 单位反馈系统的开环传递函数如下，试概略绘出系统根轨迹。

⑴ g(s)?ks(0.2s?1)(0.5s?1)k(s?5)s(s?2)(s?3)* ⑵ g(s)?⑶ g(s)?k(s?1)s(2s?1)解⑴ g(s)?ks(0.2s?1)(0.5s?1)=10ks(s?5)(s?2)系统有三个开环极点：p1?0,p2= -2,p3 = -5①实轴上的根轨迹：???,?5?, ??2,0?0?2?57?????a??33②渐近线： ????(2k?1)????,?a?33?③分离点：1d?1d?5?1d?2?0解之得：d1??0.88，d2?3.7863(舍去)。

④与虚轴的交点：特征方程为 d(s)=s3?7s2?10s?10k?0?re[d(j?)]??7?2?10k?0令 ? 3im[d(j?)]????10??0?解得?????k?7。

根轨迹如图解4-3(a)所j）与虚轴的交点（0，?示。

⑵根轨迹绘制如下：①实轴上的根轨迹：??5,?3?, ??2,0?0?2?3?(?5)????0a??2②渐近线： ????(2k?1)????a?22?③分离点： 1d?1d?2?1d?3?1d?5用试探法可得 d??0.886。

自动控制原理简明教程第二版课后答案第四章习题答案

自动控制原理简明教程第二版课后答案第四章习题答案
20，ｊ０）。 起始角：
m
n
∑ ∑ θ pi = (2k +1)π +
ϕ − θ z j pi
pi pi
j=1 j=1 ( j≠i)
k = 0,±1,±2,
θ p1 = 1800 θ p2 = 1800 +ϕz1p2 −θ p1p2 −θ = p3p2 1800 + 450 −1350 −
900 = 00 θ p3 = 1800 +ϕz1p3−θ p1p3 −θ p2p3 =1800 − 450 +1350 + 900
（－２＋ｊ０）点在根轨迹上，而（０＋ｊ１）， （－３＋ｊ２）点不在根轨迹上。 4-2 设单位反馈控制系统的开环传递函数
G(s) = K (3s +1) s(2s +1)
试用解析法绘出开环增益 K 从零增加到无穷时的闭环根轨迹图。 解：
系统开环传递函数为 G(s) = 3K /2(s +1/3) = K g (s +1/3) s(s +1/ 2) s(s +1/ 2)
mn
∑ ∑ θ pi = (2k +1)π +
ϕ − θ z j pi
pi pi
j=1 j=1
( j≠i)
k = 0,±1,±2,
θ p1 =1800
θ p2 =−900
θ p3 =+90
θ p4 = 00
根轨迹如图所示。
4-9 已知开环传递函数为
12
胡寿松自动控制原理习题解答第四章 电三刘晓峰制作
取分离点为 d1 =−1.7，d2 =−0.29 K *(s + 5)
(3) G(s) = s(s + 2)(s + 3)

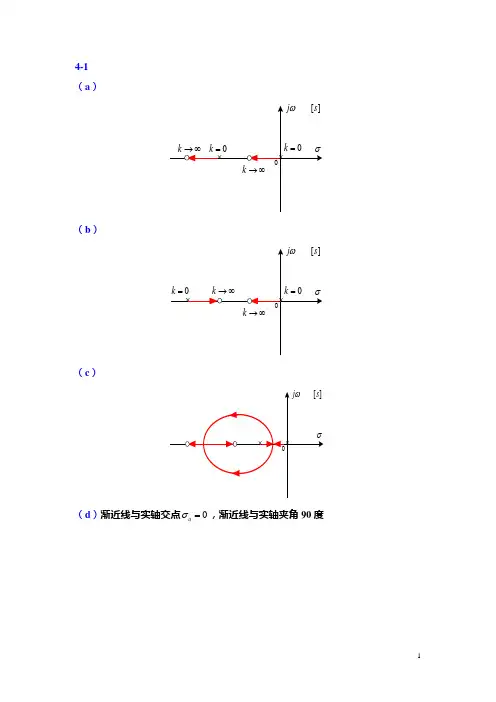
薛安克第二版自动控制原理第四章习题参考答案

薛安克第二版自动控制原理第四章习题参考答案

（a）（b）（c）σ=，渐近线与实轴夹角90度（d）渐近线与实轴交点0a1230, 0, 1p p p ===-1. 实轴上的根轨迹(,1) (0,0)-∞-2. 渐近线：3n m -=3条根轨迹趋向无穷远处的渐近线相角为180(21)60,180 (0,1)3a q q ϕ︒+=±=±︒︒= 渐近线与实轴的交点为11001133n mi ii j a p zn mσ==---===--∑∑ 3. 分离点（会合点）：系统的特征方程为21+()10(1)KG s s s =+=+即 232=(1)K s s s s -+=--2=320dKs s ds--=(32)0s s +=根 10s =，20.667s =-（舍去）4. 与虚轴的交点：令 s j ω= 代入特征方程 21+()10(1)KG s s s =+=+2(1)=0s s K ++2()(1)=0j j K ωω++2(1)=0j K ωω-++2=0K j ωω--2=00K ωω⎧-⎨=⎩=0ω （舍去）与虚轴没有交点，即只有根轨迹上的起点，也即开环极点 1,20p = 在虚轴上。

4.5 开环传递函数为2()(6)(645)K G s s s s s =+++ 开环极点为123,40, 6, 36p p p j ==-=-±1. 实轴上的根轨迹：(6,0)-2. 渐近线：4n m -=，共有4条渐近线，4条根轨迹趋向无穷远处的渐近线相角180(21)45,135 4a q ϕ︒+=±=±︒±︒ 渐近线与实轴的交点为116363634n mi ii j a p zj jn mσ==---+--===--∑∑3. 分离点（会合点）：系统的特征方程为21+()10(6)(645)KG s s s s s =+=+++ 即 2432(6)(645)(1281270)K s s s s s s s s =-+++=-+++=0dKds根 13s =-，2,33s j =- 4. 与虚轴的交点：令 s j ω= 代入特征方程 21+()10(6)(645)KG s s s s s =+=+++4324231281270081012270=0s j j j K K j j ωωωωωωωωω=--++=-+=-+令，得实部： 虚部：解得：=0= 4.74=1316.25K ωω±（舍去），，5. 出射角：出射角公式11,()180(2)()1r nr mj r rp i j i j p z p p k θ==≠=±+∠︒--∠-+∑∑极点23+2s j =-的出射角为 22211,2(63.41180(21)()(0)=16.690)180(21)=90mnp i j i j j k p z p p k θ==≠-︒+︒+=±︒++∠--∠-±︒︒++-︒∑∑Locus of E xample 4-5 in P 72ReI m。

自动控制原理-吴怀宇-课后习题-第四章

自动控制原理-吴怀宇-课后习题-第四章

第四章4-1已知单位反馈系统的开环传递函数为()(1)(2)KG s s s s =++ 试绘制该系统在正、负反馈情况下的根轨迹图。

解：（1）负反馈情况令(1)(2)=0s s s ++，解得 3个开环极点1230,1,2p p p ==-=-根轨迹分支数为3，起点分别为(0,0),(1,0),(2,0)j j j -- 终点均为无穷远处。

在实轴上的根轨迹为(][],2,1,0-∞--两段。

由n=3,m=0得轨迹有3条渐近线，它们在实轴上的交点坐标111n mi ji j a p zn mσ==-==--∑∑渐近线与实轴正方向的夹角为2121=3a k k n m ππϕ++=-（）（），（k=0,1,2）当k=0,1,2时，计算得a ϕ分别为60°，180°，-60° 确定分离点，由111++=012d d d ++解得120.42, 1.58d d =-=-由于2d 不是根轨迹上的点，故不是分离点，分离点坐标为1d确定根轨迹与虚轴的交点：控制系统特征方程3232=0s s s K +++令=s j ω 代入上式得3232=0j j K ωωω--++ 写出实部和虚部方程233=020K ωωω⎧-⎪⎨-=⎪⎩可求得=006K K ωω⎧⎧=⎪⎨⎨==⎪⎩⎩因此，根轨迹在ω=6K =；另外实轴上的根轨迹分支在0ω=处与虚轴相交。

负反馈系统根轨迹如下图所示（2）正反馈情况令(1)(2)=0s s s ++，解得 3个开环极点1230,1,2p p p ==-=-根轨迹分支数为3，起点分别为(0,0),(1,0),(2,0)j j j -- 终点均为无穷远处。

在实轴上的根轨迹为[](]2,1,0,--+∞两段。

由n=3,m=0得轨迹有3条渐近线，它们在实轴上的交点坐标111n mi ji j a p zn mσ==-==--∑∑渐近线与实轴正方向的夹角为2=3a k πϕ，（k=0,1,2）当k=0,1,2时，计算得a ϕ分别为0°，120°，-120° 确定分离点，由111++=012d d d ++解得120.42, 1.58d d =-=-由于1d 不是根轨迹上的点，故不是分离点，分离点坐标为2d确定根轨迹与虚轴的交点：控制系统特征方程3232-=0s s s K ++将=s j ω 代入上式得3232-=0j j K ωωω--+ 写出实部和虚部方程23-3=020K ωωω⎧-⎪⎨-=⎪⎩可求得=00-6K K ωω⎧⎧=⎪⎨⎨==⎪⎩⎩ 因此，根轨迹在0ω=处与虚轴相交。

自动控制原理-第4章习题解答

自动控制原理-第4章习题解答
* K ( s + 1) 10 K s 1 K s + 1) + ( ) ( 解： G ( s ) H ( s ) = = 2 = 2 2 s（0.1 s +1 ） s（ s + 10） s（s + 10）
( K * = 10 K )
⎧ m = 1: z1 = −1 ⎨ ⎩ n = 3 : p1 = 0; p2 = 0; p3 = −10
k ( s + 1) G (s) H (s) = 2 ， 4-10 某负反馈系统， 试绘制其根轨迹图。 s + s + 10 解： m = 1 z1 = −1
n = 2 p1 = −0.5 + j 3.12 p2 = −0.5 − j 3.12
渐近线： ——不必求 重根点 满足方程： d 2 + 2d − 9 = 0
绘制其根轨迹图。
非最小相位系统
解：⎧ ⎨
m = 1: z1 = −1
⎩ n = 2 : p1 = 0; p2 = 3
重根点：d1 = 1 , d 2 = −3 与虚轴交点：
ω=± 3
●
○
其复数部分根轨迹为圆。
-3
-1
×
●
1
×
3
9
4-16
2 已知系统特征方程为： ( s + 1)( s + 3)( s − 1)( s − 3) + k ( s + 4) = 0 绘制其根轨迹图。
●
渐近线： σ a = +0.5
×
ϕ a = ±900
○
起始角：
θ p = 00，θ p = 00
2 3
-2
-1
×

自动控制原理(北大丁红版)第四章习题解答

自动控制原理(北大丁红版)第四章习题解答
运用长除法得另一极点为 s 3 2.35 ， 因为 s 3 0.3 5 ， 所以 s1, 2 0.33 0.572 j 可认为是系统的主导极点。 系统的闭环传递函数可近似地表示为： D ( s )
0.4356 s 0.665s 0.4356
2
可以近似地运用典型二阶系统估算系统的时域性能指标： 超调量： % e 调节时间： t s
当 a 9 时，例如 a 10 ，求得： 根轨迹起于 0，0，-10； 根轨迹终止于-1 和无穷远点； 根轨迹的渐近线与实轴交于-4.5； 根轨迹的渐近线与实轴的夹角为 90 ， 90 ；
o o
实轴上根轨迹区间为：[-10,-1]； 根轨迹的分离点为：-2.5，-4。 系统的根轨迹如下图所示
负反馈系统在 0 K * 12 时是稳定的； 当 K : 0 时，正反馈系统恒不稳定。
*
4.8 解： n 3 ， m 0 ；根轨迹分离点 d 1 交点为
3 0.42 ，对应的 K 0.192 ；与虚轴的 3
2 j ，对应的 K 3 ，根轨迹如图所示。
Im

o o
Re
4.13 解：闭环系统特征方程为：
1 G ( s) H ( s) 0
因为 H ( s ) 1 ，则 1 G ( s ) 0 ， Ts s 3s 2 0
o o o
分离点的计算：
K*
s 2 ( s 2)( s 4) s 1
dK * 令 0 ，求得分离点在-3.08 和 0 处。 ds
根轨迹如下图所示：
Root Locus 3 2 Imaginary Axis 1 0 -1 -2 -3 -5
-4

黄家英自动控制原理第二版第四章习题答案

黄家英自动控制原理第二版第四章习题答案

dG !K (s ) d (s 1) c、 分 离 点 ： [ 2 ] 0 ds ds s (s 2)(s 4) 或： 3s 4 16s 3 26s 2 16s 3s(s 3.08)[(s 1.12) 0.692 ] 0 经 检 验 可 得 分 离 点 为 d 3.08 ： 概 略 绘 制 系 统 的 根 轨如 图 所 示 。 迹
由根轨迹图可见，负馈系统稳定时的开环轨迹 反 根 增 益 临 界 值 为 ： gc 12 即 开 环 增 益 临 界 值c K gc / 8 1.5） K （ K , 而正反馈系统为结构不稳定的。 性
j
0 -4
-2 -1
负反馈
j
0
正反馈
B4.14 设某单位反馈位置随动系统的开环传递函数为
2 2
经检验分离点为： d 1 6 d 2 , 3 6 j 28 6 j5.29
j
-12
-8
-4
0
B4.5 设单位反馈系统的开环传递函数为
要求： (1)绘制系统的根轨迹； (2)确定系统的临界开环增益； (3)当系统的暂态响应为欠阻尼、临界阻尼或过阻尼时， 试分别求其开环增益的取值范围。
241 5 nm 41 3 c、 根 轨 迹 与 虚 轴 的 交 ： 点 a 令 s j,由 特 征 方 程 可 得 ；
4 D（j）（j） 6( j) 3 8( j) 2 jK g K g 0
p 0i Z 0 j
4 8() 2 K g 0 或 联 立 求 解 得 ： 0和 2 3 6() K g 0 于 是 可 概 略 绘 制 系 统根 轨 迹 如 图 所 示 。 的

自动控制原理答案(黄坚)第四章

自动控制原理答案(黄坚)第四章

第四章 根轨迹分析法习题4-2 单位回馈控制系统的开环传递函数1)(+=s K s G r，试用解析法绘出r K 从零变化到无穷时的死循环根轨迹图，并判断-2, j1, (-3+j2)是否在根轨迹上。

解：1-s 01s 0r=⇒=+=时，K2-s 02s 1r=⇒=+=时，K3-s 03s 2r=⇒=+=时，K……-2 在根轨迹上，（-3+j2），j1不在根轨迹上。

4-3 回馈控制系统的开环传递函数如下，0≥r K ，试画出各系统的根轨迹图。

(2) )4)(1()5.1()(+++=s s s s K s G r (3) 2)1()(+=s s K s G r ，解：（2）1）开环零、极点：p 1=0，p 2=-1,p 3=-4,z=-1.0，n=3，m=1 2）实轴上根轨迹段：（0，-1），（-1.5，-4） 3）根轨迹的渐近线：︒±=±=-+±=-=----=902)12(,75.12)5.1(410)2( ππϕσm n k aa夹角交点条渐近线4）分离点和会合点6.05.1141111-=+=++++d d d d d 试探法求得（3）1）开环零、极点：p 1=0，p 2,3=-1，n=32）实轴上根轨迹段：（0，-1），（-1，-∞） 3）根轨迹的渐近线：±=-+±=-=--=3)12(,323110)3( ππϕσm n k aa夹角交点条渐近线4）分离点和会合点310121-=⇒=++d d d 5）与虚轴交点：223++s s4-5 系统的开环传递函数为)1()2()(++=s s s K s G r ，(1) 画出系统的根轨迹，标出分离点和会合点；(2) 当增益r K 为何值时，复数特征根的实部为-2？求出此根。

解： （1）1）开环零、极点：p 1=0，p 22）实轴上根轨迹段：（0，-13）分离点和会合点.3,586.02111121-=-=⇒+=++d d d d d123s s s s r2K -r21 1K rKj,202rr±==⇒=-s K K（2）系统特征方程为02)1(rr2=+++K s K s2j 2322122,1rr±-==-=+-=-s K Ka b ，，得：由4-6 单位回馈系统的前向信道函数为)3)(1()(++=s s s K s G r，为使死循环主导极点具有阻尼比5.0=ξ，试确定r K 的值。

自动控制原理黄坚第二版第四章习题答案

自动控制原理黄坚第二版第四章习题答案

σ根 s=3-K+ω轨4r3--s+p14迹32ω13-+~3ω的3p2==s2=+-分001K.离p3r=3~KK点0θrr-===：012+ωω6012o=,,3+=01±810.7o
ζ=AK0sss(2.3rs1没5====)3B|--s有4.03系3'2+(得|.s|64s位s20统)×5+3.=+23s8于A根.171s2=|'×+根|6(轨s-23s×03=s)=+0轨.B2迹3-.0=332(7迹|-s.6+22)=j.6上201..8，9 舍s去3 p-33。
第四章习题课 (4-1)
4-1 已知系统的零、极点分布如图，大 致绘制出系统的根轨迹。
解: (1)
jω (2)
jω
600
0σ
0σ
(3)
jω
(4)
jω
900
0σ
600
0σ
第四章习题课 (4-1)
(5)
jω
(6)
jω
600
0σ
0σ
(7)
jω
1350
450
0σ
(8)
jω
1080
360
0σ
第四章习题课 (4-2)
p4
5）p4分=-离15点和z1会=-8合点
pp z13 -5.672
p
01 σ
2A）(s实)=轴s4+上25根s3轨+1迹71段s2+3p115~sp2 p3~z1
-6.2
3A）(s根)'=轨4s迹3+的75渐s2+近3线42s+315p4~-∞
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

.. .. . . . . 第四章 根轨迹分析法习题

4-2 单位回馈控制系统的开环传递函数1)(sKsGr，试用解析法绘出rK从零变化到无穷时的死循环根轨迹图，并判断-2, j1, (-3+j2)是否在根轨迹上。 解：1-s01s0r时，K

2-s02s1r时，K 3-s03s2r时，K ……

-2 在根轨迹上，（-3+j2），j1不在根轨迹上。 4-3 回馈控制系统的开环传递函数如下，0rK，试画出各系统的根轨迹图。 (2) )4)(1()5.1()(ssssKsGr (3) 2)1()(ssKsGr， 解：（2） 1）开环零、极点：p1=0，p2=-1,p3=-4,z=-1.0，n=3，m=1 2）实轴上根轨迹段：（0，-1），（-1.5，-4） 3）根轨迹的渐近线：

902)12(,75.12)5.1(410)2( mnkaa夹角交点条渐近线

4）分离点和会合点 6.05.1141111ddddd试探法求得 （3） 1）开环零、极点：p1=0，p2,3=-1，n=3 2）实轴上根轨迹段：（0，-1），（-1，-∞） 3）根轨迹的渐近线： .. .. . . . . 180,603)12(,323110)3( mnkaa夹角交点条渐近线

4）分离点和会合点 310121

ddd

5）与虚轴交点：02r23Ksss

4-5 系统的开环传递函数为)1()2()(sssKsGr， (1) 画出系统的根轨迹，标出分离点和会合点； (2) 当增益rK为何值时，复数特征根的实部为-2？求出此根。

解： （1） 1）开环零、极点：p1=0，p2=-1 z=-2，n=2，m=1 2）实轴上根轨迹段：（0，-1），（-2，-∞） 3）分离点和会合点

414.3,586.02111121ddddd

可以证明该根轨迹是一个半径为1.414，原点在-2处的标准圆 （2）系统特征方程为02)1(rr2KsKs 2j2322122,1rrsKKab，，得：由

0123ssss

r2Kr 21 1K

rKj,202rrsKK.. ..

. . . . 4-6 单位回馈系统的前向信道函数为)3)(1()(sssKsGr，为使死循环主导极点具有阻尼比5.0，试确定rK的值。 解： 系统的根轨迹如图: d=-0.45 在根轨迹图上作射线: β=±60º 与根轨迹相交点为s1和s2 设相应两个复数死循环极点分别为：

nnjs866.05.01

nnjs866.05.02 则死循环特征方程式可表示为 0)()())()((2332233321nnnnssssssssssss

034r23Ksss系统特征方程为

比较系数，得： r2332334Ksssnnnn828.125.375.0r3Ksn

4-7 控制系统的开环传递函数为)4)(2()(sssKsGr (1) 绘出该回馈系统的根轨迹图； (2) 求系统具有阻尼振荡响应的rK取值围； (3) 系统稳定的rK最大为多少？并求等幅震荡的频率； (4) 求使主导极点具有阻尼比5.0时的rK值，并求对应该值时， 零极点形式的死循环传递函数。

解：（1） 1）开环零、极点：p1=0，p2=-2，p3=-4，n=3 2）实轴上根轨迹段：（0，-2），（-4，-∞） .. .. . . . . 3）根轨迹的渐近线：

180,603)12(,23420)3( mnkaa夹角交点条渐近线

4）分离点和会合点 )(732.4,845.004121121舍ddddd

分离点对应的08.3155.3155.1845.0rK 5）与虚轴交点：086r23Ksss

（2）系统具有阻尼振荡响应的rK取值围是：4808.3rK （3）系统稳定的48rK，等幅振荡频率为22 （4）同上题方法可求得： 阻尼比5.0时j1.1567.0,67.4,3.82,13ssKr

)15.1j67.0)(15.1j67.0)(67.4(3.8)(ssss

4-8单位负反馈系统的开环传递函数为)15.0)(1()(sssKsGr，用根轨迹分析系统的稳定性。 解：1）开环零、极点：p1=0，p2=-1，p3=-2，n=3 2）实轴上根轨迹段：（0，-1），（-2，-∞） 3）根轨迹的渐近线：

0123ssss

r84Kr 68 1K

rK2j2,48084rrsK

K.. ..

. . . . 180,603)12(,13210)3( mnkaa夹角交点条渐近线

4）分离点和会合点 )(644.1,356.002111121舍ddddd

5）与虚轴交点：0223r23Ksss

所以，系统稳定的rK取值围是：30rK

4-9 单位负反馈系统的开环传递函数为)02.01)(01.01()(sssKsGr (1) 画出系统的根轨迹图； (2) 确定系统临界稳定时的开环增益； (3) 确定与临界阻尼比相应的开环增益。

解：（1）)50)(100(5000)(sssKsGr

① 实轴上的根轨迹：[0, -50],[-100,-]

0123ssss

r26Kr2 32 1K

r2Kj,30262,1rrsKK.. ..

. . . . ② 分离点：0100d150d1d1

求解得87.78d13.21d21， ③ 渐近线：ooaa1806050，， 根轨迹如图所示。 (2) 系统临界稳定时 150750000*rKK，

(3) 系统临界阻尼比时 62.95.48112*rKK，

4-10 系统的开环传递函数为32)2()(2sssKsGr，试绘制系统在rK0时的根轨迹，并确定系统临界阻尼时的rK值。 解：

1）开环零、极点：2,2j12,1zp，n=2，m=1

2）实轴上根轨迹段：（-2，-∞） 3）分离点和会合点

1)( ,22)(2)( ,32)(2sBssAssBsssA .. .. . . . . )()()()(sAsBsBsA

)22)(2(322ssss s1=-3.732，s2=-0.268（舍）

此时系统即为临界阻尼情况， 对应的46.5732.1732.22732.2222rK

4）出射角7.1447.5490180 4-12 系统结构如图所示，试画出回馈系数k为变数的根轨迹。

解：)110(10)(KsssG 0)110(101)(1KsssG由 01010s2sKs 则，系统等效开环传递函数1010)(2sskssG

1）分离点和会合点 1)( ,12)()( ,10)(2sBssAssBsssA

)()()()(sAsBsBsA )12(102ssss s1=-3.16，s2=3.16（舍）

2）与虚轴无交点：010)110(2sks

3）1.9)1.99(90180

4-14 系统结构如图所示，闭环根轨迹通过(-0.65+j1.07)点，试绘制rK从0变化时系统的根轨迹。

-k110ss

1-)(sR

)(sC .. ..

. . . . 解：)2)(1()1(10)(1ssssTKsG

系统特征方程为：0)1(10)2)(1(1sTKsss 将s=-0.65+j1.07代入上式，可得：667.0,266.01TK

)2)(1()5.1(67.6)(ssssKsG)2)(1()5.1(sss

sK

r

1）根轨迹的渐近线：

902)12(,75.025.1210)2( mnkaa夹角交点条渐近线

2）分离点和会合点 54.05.1121111ddddd试探法求得： 5）与虚轴交点：0.5123rr23KsKss）（

所以，与虚轴无交点。 4-16 单位回馈系统的闭环特征方程为04)1(223rrKsKss。试绘制系统的根轨迹，并求闭环出现重根时的rK值和对应的闭环根。 解： 由系统特征方程可得系统等效开环传递函数2)1()4()(sssKsGr

0123ssss

r.516Krr1.5 32 1K

K

r2K