测绘工程 测量平差(总复习题)
- 格式:doc
- 大小:518.50 KB
- 文档页数:6

复习4一、填空题请在每小题的空格中填上正确答案。
错填、不填均无分。
(一)1.我国目前采用的大地坐标系是_______________。
2.测量平面直角坐标系的X轴指向_______________方向、Y轴指向_______________方向。
3.水准测量中,要消除地球曲率和大气折光的影响,所采用的方法是_______________。
4.水准器的分划值越小,说明其灵敏度就越_______________。
5.根据标准方向的不同,方位角可分为真方位角、_______________和_______________。
6.经纬仪的视准轴应与横轴_______________。
7.观测水平角时,要消除视准轴误差对水平角的影响,所采用的方法是_______________。
8.阐述函数中误差与观测值中误差之间关系的定律称为_______________。
9.坐标反算是根据两点平面直角坐标推算_______________和_______________。
10.已知某地形图上AB线段长度为2.5厘米,其实地水平距离为125米,则该图的比例尺为_______________,比例尺精度为_______________米。
11.地物符号包括依比例符号、_______________和_______________。
12.平整场地时,填挖高度是地面高程与_______________之差。
13.要在AB方向上测设一条坡度为1%的坡度线,已知A点高程为24.050米,AB的实地水平距离为120米,则B点高程应为_______________米。
14.里程桩的桩号表示该桩距离_______________的里程。
15.用钢尺分别丈量了两段距离,AB段长100米,CD段长200米,丈量两段的中误差均为±0.02米,则AB段比CD段丈量精度_______________。
(二)1.在用钢尺量距时,通常用标杆来标定直线的位置,该项工作称为___________ 。

复习题一、名词解释(共58题)1.工程测量:大地水准面:铅垂线:绝对高程:中央子午线:水准测量:望远镜视准轴:水准路线:水准点:高差闭和差:水平角:竖直角:竖盘指标差:照准部偏心差:照准误差:直线定线:端点尺:刻划尺:尺长改正:温度改正:直线定向:方位角:象限角:子午线收敛角:轴北方向:误差:系统误差:偶然误差:误差传播定律:权:平面控制测量:导线:图根点:导线相对闭合差:归零差:比例尺精度:等高线:等高距:地貌特征线:示坡线:视距测量:碎部测量:图廓:接图表:三北方向:坡度比例尺:填挖边界线:中线测量:转点:整桩:中平测量:测设:整桩号测设:整桩距测设:建筑方格网:龙门桩:清基开挖线:施工基面:二、填空题(共103题)1.工程测量是一门的科学,它是通过测定点之间的、和三个基本量来实现的。
2.工程测量的主要任务是、、。
3.通过平均海洋面的水准面称为。
4.^5.地面点沿至的距离称为点的绝对高程,而至的铅垂距离称为它的相对高程。
6.地面上两点M、N之间的高差为h MN= 。
若h MN<0,则点M 于点N。
7.已知某点的横坐标通用值为.31m,则该点是在高斯投影分带的第带号内,其自然值是。
8.测量上采用的平面直角坐标系与数学上的基本相似,它们不同的地方是和。
9.测量中测定地面点位是通过测定三个定位元素、和来实现的。
10.测量工作的基本原则是、。
确定点位的测量方法分为、。
11.水准测量的原理是:。
12.:13.高程测量按采用的仪器和测量方法分有、和三种。
14.水准测量中,调节圆水准气泡居中的目的是;调节管水准气泡居中的目的是。
两者的关系是。
15.由已知点A测量并计算未知点B的高程的方法有两种,一是,其计算公式是;二是;其计算公式是。
16.写出水准仪上3条轴线的定义:1)视准轴;2)水准管轴;3)圆水准器轴。
17.水准仪应满足的几何条件有:^1);2);3)。
18.水准路线的布设形式有、和。
19.三、四等水准路线,必须进行观测或观测;目的是消减的影响。

工程测量复习题含参考答案一、单选题(共50题,每题1分,共50分)1、地面某线段的坡度可用该线段坡度角的()值以百分比形式表示。
A、余切B、正弦C^余弦D、正切正确答案:D2、下列观测量,不是确定地面点的基本要素有()。
A、水平角B、斜距C、高差D、水平距离正确答案:B3^大地高是指()oA、地面点沿法线到大地水准面的距离B、地面点沿铅垂线到参考椭球面的距离C、地面点沿法线到参考椭球面的距离D、地面点沿铅垂线到大地水准面的距离正确答案:C4、一组测量值的中误差越小,表明测量精度越()。
A、高B、无法确定C、低D、精度与中误差没有关系正确答案:A5、使水准仪的圆水准器的气泡居中,应旋转()oA、微倾螺旋B、微动螺旋C、对光螺旋D、脚螺旋正确答案:D6、《工程测量规范》(GB50026-2007)规定:三级导线测量中,测距中误差容许值为()。
A^ 1OmmB、12πunC> 15mmD、18mm正确答案:C7、下列测量工作中,不属于施工测量的是()。
A、轴线投测B、测设建筑基线C、建筑物定位D、建筑物测绘正确答案:D8、竖直指标水准管气泡居中的目的是()。
A、使竖盘指标指向270°B、使竖盘指标指向90°或270°C、使竖盘处于铅垂位置D、使竖盘指标指向90°正确答案:B9、每隔四条首曲线而加粗描绘的一条等高线,称为()oA、助曲线B、计曲线C、间曲线D、辅助等高线正确答案:B10、在比例尺为1:2000、等高距为2m的地形图上,要求从A到B以5% 的坡度选定一条最短的路线,则相邻两条等高线之间的最小平距应为()。
A、20mmB、25mmC、I OmmD、5mm正确答案:A11、等精度观测三角形内角,角度闭合差中误差为±8〃,则测角中误差为()A、±8.0"B、+13.9z,C、±4.6"D、土6. O"正确答案:C12、当钢尺的实际长度大于名义长度时,其丈量的值比实际值要()oA、相等B、大C、小D、不定正确答案:C13、为了计算和用图的方便,每隔四根基本等高线加宽描绘一条并注上高程的等高线,称()。

绪论1.平差问题的函数模型的随机模型,无非以下几种:函数模型中系数阵是列满秩还是秩列亏;待估参数是非随机量还是随机量或者两者兼有;观测量的协方差阵是满秩还是奇异;2.以不同的准则来求定未知参数的最佳估计,得到不同的估计方法,经典的测量平差方法都是以最小二乘估计或者极大似然估计为根据导出的;滤波、配置和动态系统的卡尔曼滤波,最初是以极大验后估计或者最小方差估计导出的。
3.有偏估计是为了克服法方程病态的问题的平差方法,病态又称为法方程的复共线性。
P163(论述题)4.简述引起测量平差法方程系数矩阵病态的原因及其后果,通常采用什么方法解决这一问题,采用何种指标评价参数估值的精度?(在第一章讲过)(秩亏是用秩亏自由网平差,病态用有偏估计)原因:误差方程的系数矩阵存在着很弱的弱相关性,弱相关性也称复共线性。
法方程中系数和常数项存在舍入误差而产生微小变化时,引起的解的很大差异。
这种情况下法方程系数阵的性质不好,称为病态方程。
后果:一旦存在病态性,法方程系数上的微小误差会导致方程的解完全被扭曲。
最小二乘解不稳定。
解决方法:采用有偏估计,包括岭估计、广义岭估计、主成分估计等等有偏估计方法。
评定精度的指标:(在经典平差里面用参数估值的方差评定精度,在广义平差里面用参数估计误差的方差评定精度)在有偏估计中采用均方误差MSE(X尖)来评定精度,均方误差用来衡量参数与其真值的偏离程度。
(参数与数学期望间的偏离程度是方差)5.随着测绘科学技术的变革和不断发展,经典测量平差理论已经不能满足现代测量数据处理,根据自己的理解论述现代测量数据处理的发展方向。
(PPT里面有)1.从法方程系数矩阵满秩扩展到法方程系数矩阵亏秩2.从仅处理静态数据扩展到处理动态数据3.从无偏估计扩展到有偏估计4.从线性模型的参数估计扩展到非线性模型的参数估计5.从待估参数为非随机量扩展到待估参数为随机量6.从观测值仅含偶然误差扩展到含有系统误差和粗差7.从主要研究函数模型扩展到深入研究随机模型经典—非随机广义---随机6.经典平差对观测误差的基本假设是?答:观测误差仅含有偶然误差经典平差的基本假设:(局限性)1)系统是静态的2)有足够的起算数据3)观测值是随机变量,参数是非随机变量4)观测误差为偶然误差5)观测值函数独立6)平差准则为V T PV = min7.经典平差---未知参数为非随机参数;第一章极大似然估计P81、正态分布的极大似然估计与最小二乘估计相同————之间的转换,PPT15/16页2、均无法顾及到参数的先验统计性质。
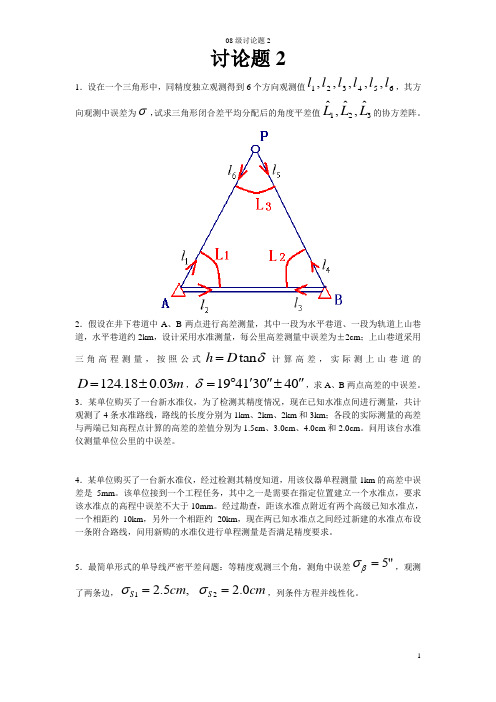
讨论题21.设在一个三角形中,同精度独立观测得到6个方向观测值654321,,,,,l l l l l l ,其方向观测中误差为σ,试求三角形闭合差平均分配后的角度平差值321ˆ,ˆ,ˆL L L 的协方差阵。
2.假设在井下巷道中A 、B 两点进行高差测量,其中一段为水平巷道、一段为轨道上山巷道,水平巷道约2km ,设计采用水准测量,每公里高差测量中误差为±2cm ;上山巷道采用三角高程测量,按照公式δtan D h =计算高差,实际测上山巷道的m D 03.018.124±=,"±"'︒=40304119δ,求A 、B 两点高差的中误差。
3.某单位购买了一台新水准仪,为了检测其精度情况,现在已知水准点间进行测量,共计观测了4条水准路线,路线的长度分别为1km 、2km 、2km 和3km ;各段的实际测量的高差与两端已知高程点计算的高差的差值分别为1.5cm 、3.0cm 、4.0cm 和2.0cm 。
问用该台水准仪测量单位公里的中误差。
4.某单位购买了一台新水准仪,经过检测其精度知道,用该仪器单程测量1km 的高差中误差是5mm 。
该单位接到一个工程任务,其中之一是需要在指定位置建立一个水准点,要求该水准点的高程中误差不大于10mm 。
经过勘查,距该水准点附近有两个高级已知水准点,一个相距约10km ,另外一个相距约20km ,现在两已知水准点之间经过新建的水准点布设一条附合路线,问用新购的水准仪进行单程测量是否满足精度要求。
5.最简单形式的单导线严密平差问题:等精度观测三个角,测角中误差"5=βσ,观测了两条边,cm cm S S 0.2,5.221==σσ,列条件方程并线性化。
6.写出条件平差的基础公式,设观测值的协因数阵为LL Q ,推求L L Q ˆˆ掌握一些概念:观测条件、偶然误差、系统误差、粗差、真误差、方差、中误差、平均误差、或然误差、极限误差、相对误差、误差转播定律、协因数转播定律、权的定义、平差模型、条件方程、改正数方程等。

复习题及参考答案工程测量基础一、判断题:[正确打V 错误打X ]1. 大地水准面所包围的地球形体,称为地球椭球体。
[A ]2. 测量工作的实质就是测量(或测设)点位的工作。
[B ]3. 测量中的坐标轴方向和象限顺序与数学中的坐标轴方向和象限顺序正好相同。
[A ]4. 旋转微倾螺旋可使望远镜连同管水准器作俯仰微量的倾斜,从而使视线精确整平。
因此这种水准仪称为微倾式水准仪。
[B]5. 对于水准支线,应将高程闭合差按相反的符号平均分配在往测和返测所得的高差值上。
[B ]6观测导线右角时,附合导线和闭合导线角度闭合差的分配原则都是将角度闭合差以相反的符号平均分配到各个右角。
[]7. 1: 50000地形图上,求得A点的高程H=418. 3m, B点的高程H B=416. 7m, AB两点图上的长度为15mm,则AB直线的坡度应是-2 %。
[]8. 衡量导线的精度应该以角度闭合差和导线全长闭合差来衡量。
[]9. 地形图上0.1伽长所代表的实际长度称为比例尺的精度。
30 〃则距 ZH 点 40米处的缓和曲线半径为2500米 [ ]除。
17. 当对一个观测量进行同精度多次观测后 , 则观测值的算术平均值就是观测量 的最或然值。
[ ]18. 中误差、 容许误差、 相对误差在测量中都能够作为评定精度的标准。
[ ] 19. 导线计算的目的是算出各导线点的坐标 , 并检验导线测量的精度是否符合要 求。
[ ]20. 支导线由于没有检核条件 , 故只能用于图根控制。
[ ]10.圆曲线半径 R=1000米,缓和曲线总长 L o =100米,直线转向角a =15° 20'11 . 绝 对 高 程 无 负 值 [ ]相对高程有负值12.水准测量中 ,每一站读完后视读数瞄准前视尺时 必须旋转脚螺旋使管水准 泡居中再、+、八视读数13.经纬仪竖轴倾斜引起的误差 , 能够采用盘左、 盘右观测取平均值的方法消 14视差象无法消除15反坐 标方位角 总 是 相 差 180 。
工程测量复习题及答案1. 什么是工程测量?工程测量是应用测量学的原理和方法,对工程对象进行测量、设计、施工和运营管理的一门综合性技术学科。
2. 工程测量的主要任务有哪些?工程测量的主要任务包括:地形图的测绘、施工放样、变形监测、工程定位、测量数据的处理与分析等。
3. 地形图测绘的步骤是什么?地形图测绘的步骤包括:外业测量、内业成图、地形图的校验和出版。
4. 施工放样的方法有哪些?施工放样的方法包括:直接放样法、间接放样法、坐标放样法和极坐标放样法。
5. 变形监测的目的是什么?变形监测的目的是通过对工程结构的位移、倾斜、裂缝等变形现象的监测,评估结构的稳定性和安全性,为工程的维护和加固提供依据。
6. 工程测量中常用的测量仪器有哪些?工程测量中常用的测量仪器包括:全站仪、水准仪、经纬仪、GPS接收机、测距仪等。
7. 测量误差的来源有哪些?测量误差的来源包括:仪器误差、观测误差、环境误差和计算误差。
8. 如何减少测量误差?减少测量误差的方法包括:采用高精度的测量仪器、提高观测者的技术水平、采用合理的观测方法和数据处理方法。
9. 什么是相对误差和绝对误差?相对误差是指测量值与真实值之差与真实值的比值,绝对误差是指测量值与真实值之差。
10. 工程测量中常用的坐标系统有哪些?工程测量中常用的坐标系统包括:笛卡尔坐标系、极坐标系、地理坐标系和投影坐标系。
11. 什么是高程测量?高程测量是指测量地面点相对于某一基准面的高度。
12. 水准测量的原理是什么?水准测量的原理是利用水准仪和水准尺,通过测量两点间的高差来确定两点的高程。
13. GPS测量的基本原理是什么?GPS测量的基本原理是通过接收卫星发射的信号,计算出接收机与卫星之间的距离,进而确定接收机在地球上的位置。
14. 什么是控制测量?控制测量是指在工程测量中,为了提高测量的精度和可靠性,先在测区内建立一个或多个基准点,然后以此为基础进行其他测量工作。
15. 工程测量中如何进行数据处理?工程测量中的数据处理包括:数据的整理、平差、分析和绘图等步骤。
测量平差复习题答案一、单项选择题1. 在测量平差中,观测值的改正数与观测值的符号相反,说明该观测值是()。
A. 正误差B. 负误差C. 系统误差D. 偶然误差答案:B2. 测量平差中,观测值的中误差是指()。
A. 观测值的标准差B. 观测值的均值C. 观测值的偏差D. 观测值的最大误差答案:A3. 测量平差中,单位权中误差的计算公式为()。
A. σ0 = √(Σσ²) / nB. σ0 = Σσ² / nC. σ0 = √(Σσ²) / ΣnD. σ0= Σσ² / Σn答案:A二、多项选择题1. 测量平差中,下列哪些因素会影响观测值的精度()。
A. 观测者的技能水平B. 观测仪器的精度C. 观测环境D. 观测时间答案:ABCD2. 在测量平差中,下列哪些方法可以提高观测精度()。
A. 增加观测次数B. 采用高精度仪器C. 改进观测方法D. 延长观测时间答案:ABC三、填空题1. 测量平差中,观测值的中误差是用来衡量观测值的______。
答案:精度2. 测量平差中,单位权中误差是用来衡量观测值的______。
答案:精度3. 在测量平差中,观测值的改正数是用来______观测值的系统误差。
答案:消除四、简答题1. 简述测量平差中,观测值的中误差与观测值的精度之间的关系。
答案:观测值的中误差是观测值精度的一种度量,中误差越小,说明观测值的精度越高。
2. 测量平差中,如何通过观测值的改正数来判断观测值的误差性质?答案:观测值的改正数与观测值的符号相反,说明该观测值是负误差;如果改正数与观测值的符号相同,则说明该观测值是正误差。
五、计算题1. 已知一组观测值的方差分别为2、3、4,计算该组观测值的单位权中误差。
答案:σ0 = √(2+3+4) / 3 = √9 / 3 = √32. 假设在一次测量中,观测者得到了一组观测值,其改正数分别为-0.1、0.2、-0.3,计算该组观测值的平均改正数。
第十讲 习题作业思考题1你是如何理解观测误差、模型误差是不可避免的?2试述中误差与真误差的概率关系?并说明计算中误差的意义。
3什么是最小二乘原理?4如何理解测量平差这一学科在测绘成果质量控制中的作用?参考答案1你是如何理解观测误差、模型误差是不可避免的?观测不可避免的存在误差,是测量本身固有属性所决定的,一个测量过程离不开观测员的基本操作、仪器工具的使用、观测的环境及其变化等,任何过程都可能产生误差(仪器误差,人为误差,外界条件误差)。
分类:偶然误差(由偶然因素引起的、不是观测者所能控制的一种误差。
采用一定的最优化准则处理,允许存在)、系统误差(在相同的观测条件下作一系列观测,如果误差在大小、符号上表现出系统性,或者在观测过程中按一定的规律变化,或者为某一常数)、粗差(粗大误差,是指比在正常观测条件下所可能出现的最大偶然误差还大的误差)。
用计算机解决科学计算问题首先要建立数学模型,它是对被描述的实际问题进行抽象、简化而得到的,因而是近似的我们把数学模型与实际问题之间出现的这种误差称为模型误差。
任何观测和模型都具有误差,不可避免。
2试述中误差与真误差的概率关系?并说明计算中误差的意义。
中误差是衡量观测精度的一种数字标准,亦称“标准差”或“均方根差”。
在相同观测条件下的一组真误差平方中数的平方根。
因真误差不易求得,所以通常用最小二乘法求得的观测值改正数来代替真误差。
它是观测值与真值偏差的平方和观测次数n比值的平方根。
中误差不等于真误差,它仅是一组真误差的代表值。
中误差的大小反映了该组观测值精度的高低,因此,通常称中误差为观测值的中误差。
在一定置信度下真误差的大小可用中误差大小某种范围来表示,从而误差的传播、预测和控制都可通过计算中误差来完成。
3什么是最小二乘原理?最小二乘法(又称最小平方法)是一种数学优化技术。
它通过最小化误差的平方和寻找数据的最佳函数匹配。
利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
设对一段距离丈量了三次,三次结果分别为9.98m ,10.00m ,10.02m ,试根据测量平差
概念,按独立等精度最小二乘原理(
min 1
2
=∑=n
i i
v
)求这段距离的平差值以及消除矛盾时各次
结果所得的最或然改正数。
设距离的观测值为m 2000,相对中误差为200000/1,试求其绝对中误差。
如图所示,已知相互独立的 三个方向值321L L L 、、的方差 均为2
σ,试求角度α、β、γ 的方差及其协方差。
设有独立观测值1L 、2L ,其方差分别为2
1σ、2
2σ,21L L x +=,21L L y -=,试求x 、
y 的方差及协方差。
已知L X ⎥⎦⎤⎢⎣⎡
-=1111,X Y ⎥⎦⎤⎢⎣⎡--=2112,⎥⎦
⎤⎢⎣⎡=∑2112L
,试求X ∑,Y ∑,XY ∑,YX ∑,XL ∑,
LY ∑。
设i v 的值是按公式i i L x v -=求得,其中)(1
21n L L L n
x +++=
,x 的中误差为x m ,),,1(n i L i =为独立等精度观测值,中误差均为m ,试求i v 的中误差i v m 并证明i v 与x 互
不相关。
已知321L L L 、、的权分别为
25141161、、,求函数45
1
2141321+-+=L L L z 的权。
已知某点平面坐标x 、y 的中误差分别为cm 0.4±、cm 0.3±,
1) 若已知x 、y 的协方差2
0.9cm m xy =,试写出向量[]T
y x
Z =的协方差阵和x 、y 的
相关系数xy ρ;
1
L 2
L 3
L α
β
γ
2) 若已知x 、y 的相关系数5.0-=xy ρ,试写出Z 的协方差阵;
3) 若取2
209cm =σ,试写出1)和2)中Z 的权阵及权逆阵。
已知
L
X ⎥⎦
⎤⎢⎣⎡=1112,
X
Y ⎥⎦
⎤⎢⎣⎡--=1111,
⎥
⎦
⎤
⎢⎣⎡--=2112L Q ,求
YX YL LX XL Y X Q Q Q Q Q Q 、、、、、及21y x p p 、。
已知⎥
⎦
⎤⎢⎣⎡--=4223L P ,82
0=σ,求1L p 、2L p 、L Q 、L ∑。
已知某平差问题(参数平差)的法方程为(L Q 为单位阵):⎪⎪⎩⎪
⎪⎨⎧++-=--=-+-=+=+=6ˆˆˆ 7ˆˆ 8 ˆˆ0 x ˆ 0 ˆ 3215
3242132211x x x v x x v x x v v x
v δδδδδδδδδ,
试求:
1)1ˆx
的权倒数1
ˆ1
x p ; 2)函数32ˆˆx x
+=ϕ的权倒数ϕ
p 1
; 3)
1
ˆ1L p 、3
ˆ
1L p ; 4)
1
1v p 、41v p ; 5)X Q ˆ、V Q 、L Q ˆ的秩)(ˆX Q rk 、)(V Q rk 、)(ˆL Q rk ;
有一模拟三角网如图所示,已知数据为:km x A 2=、km y A 1=,km x B 1=、0=B y ,
0=C x 、km y C 1=,观测角度值及其权逆阵如下,
4000459595447595891000459595443000902
54321'
''='
''='''='
''='
''='''=
L L L L L L ⎥⎥
⎥
⎥⎥⎥
⎥⎥⎦
⎤⎢⎢
⎢⎢⎢
⎢⎢
⎢⎣⎡----=210
00012000000200
0000
21000012000
000
2L Q
若取P 点坐标为未知参数,近似值取为km x P 10
=、km y P 20
=,试计算P 点坐标平差值。
如图所示,已知000085'''=∠
AOB ,各观测角度独立且等精度,观测值如下:
22932453955471023024026012003054321'
''='''='''='''='''= L L L L L
求各角最或然值。
(参数平差)
已知m H A 736.12=,为求1P 、2P 点的高程,进行了四条路线的水准测量,结果如图所示,试用参数平差法求:
1)1P 、2P 点高程最或然值及其中误差; 2)平差后1P 、2P 点间高差中误差。
2
s 537.81s 784.122
s 537.81s 250.444332211========h h h km
m h
在A 、B 、C 三个测站上,以同样精度观测了五个角,观测结果如下:
O
A
1
h 2
h 3
h 4
h 1
P 2
P x
015511401517005934404729123254354321'
''='''='''='''='''= L L L L L 试用参数平差法求:
1) 各角最或然值并比较它们的精度高低,比较结果说明了什么问题;
2) 4
3ˆˆL L +的中误差。
在A 、B 、C 三个测站上,以同样精度观测了五个角度,观测结果为:(条件平差)
015511401517005934404729123254354321'
''='''='''='''='
''= L L L L L 若取观测值的权阵为单位阵,试按条件平差法求: 1) 各角最或然值;
2) 各角最或然值的协方差阵L ˆ∑; 3) V ∑、L ˆ∑的秩。
下图为一简单的水准网,A 为已知水准点,m H A 100.10=,B 、C 、D 为未知水准点,各观测高差及所在距离如下。
试按条件平差法求: 1)B 、C 、D 点高程的最或然值;
2)B 、C 、D 点高程最或然值的权逆阵及其中误差; 3)B 、C 点间高差最或然值及其中误差。
A
B C
P
1L 3
L 2
L 4
L 5L A
B C
P
1L 3
L 2
L 4
L 5L A
1
h 2
h 3
h B
D
6
h 4
h
20
023.720 459.320 564.310
568.410 114.110 455.2665544332211============s h s h s h s h s h km s m h
已知条件平差的观测方程为B BL W W B +==+∆,0,试根据V 与∆的关系证明
r
PV
V T ±
=μ。
已知综合平差模型(又称通用平差模型)为
⎪⎩
⎪⎨⎧+==+++==++⨯⨯⨯⨯⨯⨯⨯⨯0
0110
01
11,0ˆ,0ˆC CX W W X C B X B BL W W X B V B C s C t t s X r t t r X n n r δδ 式中,r B R =)(,t B R X =)(,s C R =)(,
1) 试指出参数平差模型、条件平差模型、具有参数的条件平差模型、具有条件的参数平差模型在本模型中的特例情况; 2) 试推导综合平差模型的法方程。
当观测值仅含偶然误差时,试证明参数平差结果的下列性质:
1)2
0ˆσ
的无偏性;
某三角网中含有一个待定点P ,经参数平差得法方程为:
0394.0534.0ˆˆ762.1411.0411.0287.1=⎥
⎦
⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡y x
δδ 单位权中误差为0.1''±=μ,x
ˆδ、y ˆδ以dm 为单位,试求: 1)E 、F ; 2)1α、2α;
3)坐标中误差x m ˆ、y m ˆ及点位中误差P m 。
某平面网经过平差得待定点P 的坐标权逆阵为:
⎥
⎦⎤⎢⎣⎡=⎥⎦
⎤⎢⎣⎡700.0433.0433.0200.1ˆˆy x Q (单位:2
2)/("dm ) 已知为0.1''±=μ,试求: 1)E 、F 、1α; 2)P 点点位方差。