测量平差试题

2．某单位购买了一台新水准仪，经过检测其精度知道，用该仪器单程测量1km 的高差中误 1. 间接平差公式汇编，设观测值的协因数阵为LL Q ，求未知参数平差值的协因数阵。

3．差是5mm 。

该单位接到一个工程任务，其中之一是需要在指定位置建立一个水准点，要求该水准点的高程中误差不大于10mm 。

经过勘查，距该水准点附近有两个高级已知水准点，一个相距约10km ，另外一个相距约20km ，现在两已知水准点之间经过新建的水准点布设一条附合路线，问用新购的水准仪进行单程测量是否满足精度要求。

（使用间接平差解答）。

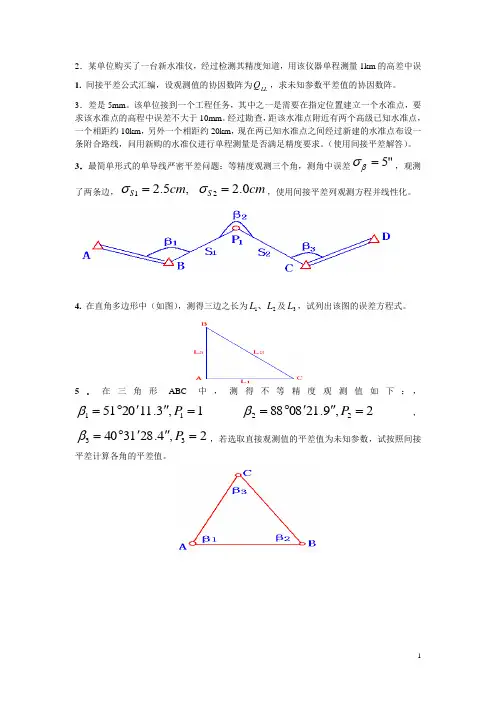
3．最简单形式的单导线严密平差问题：等精度观测三个角，测角中误差"5=βσ，观测了两条边，cm cm S S 0.2,5.221==σσ，使用间接平差列观测方程并线性化。

4. 在直角多边形中（如图），测得三边之长为21L L 、及3L ，试列出该图的误差方程式。

5．在三角形ABC中，测得不等精度观测值如下：，1,3.11205111="'︒=P β2,9.21088822="'︒=P β，2,4.28314033="'︒=P β，若选取直接观测值的平差值为未知参数，试按照间接平差计算各角的平差值。

6．如图所示的直角三角形ABC 中，已知AB=100.00m （无误差），测得边长AC 和角度A ，得观测值为ml 470.1151=，,5559292"'︒=l 其中误差分别为,51mm l ±=σ,42"±=l σ试按间接平差法求三角形ABC中的平差值。

7. 图4.3中,C B A 、、是已知点, 21P P 、为待定点,网中观测了12个角度和6条边长。

已知测角中误差为5.1''±，边长测量中误差为0.2±cm ，起算数据及观测值分别列表于表4.1和表4.2。

误差理论与测量平差基础试题平差练习题及题解第一章1.1.04 用钢尺丈量距离，有下列几种情况使量得的结果产生误差，试分别判定误差的性质及符号：（1）尺长不准确；系统误差。

当尺长大于标准尺长时，观测值小，符号为“+”；当尺长小于标准尺长时，观测值大，符号为“－”。

（2）尺不水平；系统误差，符号为“－”。

（3）估读小数不准确；偶然误差，符号为“+”或“－”。

（4）尺垂曲；系统误差，符号为“－”。

（5）尺端偏离直线方向。

系统误差，符号为“－”。

第二章2.6.17 设对某量进行了两组观测，他们的真误差分别为：第一组：3，－3，2，4，－2，－1，0，－4，3，－2第二组：0，－1，－7，2，1，－1，8，0，－3，1试求两组观测值的平均误差?1、?2＾＾＾＾＾和中＾?1、?2，并比较两组观测值的精度。

＾＾解：?1＝2.4，?2＝2.4，?1＝2.7，?2＝3.6。

两组观测值的平均误差相同，而中误差不同。

由于中误差对大的误差反应灵敏，故通常采用中误差作为衡量精度的指标。

本题中?1＜?2，因此，第一组观测值的精度高。

＾＾第三章3.2.14 已知观测值向量L1、L2和L3及其协方差阵为ｎ1ｎ2ｎ3D11 D12 D13 D21 D22 D23 D31D32 D ,现组成函数：X=AL1+A0,Y=BL2+B0,Z=CL3+C0,式中A、B、C为系数阵，A0、B0、C0为常数阵。

令W=[X Y Z],试求协方差阵DWW 解答：XX DXY DXZ 11A AD12B AD13CDWW = DYX DYY DYZ = BD21A BD22B BD23CZX DZY D 31A CD32B CD33C3.2.19 由已知点A（无误差）引出支点P，如图3-3所示。

其中误差为?0，?0为起算方位角，观测角β和边长S的中误差分别为??和?S，试求P点坐标X、Y的协方差阵。

TTTTTTTTTT图3-1解答：令P点坐标X、Y的协方差阵为2 ?xyx2xy ?2???XAP2222?02 式中：?x=（）?S＋?YAP－2＋?YAP2 ?S?22???YAP2222?02）?S＋?XAP－2＋?XAP2 ?y=（?S?2???XAP?YAP?022）?S－?XAP?YAP2－?XAPYAP2 ?xy=（2?S?2?xy=?yx3.5.62 设有函数F=f1x＋f2y，其中x??1L1??2L2????nLn，y??1L1??2L2????nLn，?i，?i（i?1,2,?n）为无误差的常数，而L1,L2?Ln的权分别为P1,P2?Pn，试求函数F的权倒数1。

武汉⼤学测量平差真题2004年攻读硕⼠学位研究⽣⼊学考试试题考试科⽬：测量平差科⽬代码： 884注意：所有的答题内容必须答在答题纸上，凡答在试题或草稿纸上的⼀律⽆效。

可使⽤计算器。

⼀、填空题（本题共40分，共10个空格，每个空格4分）1．已知观测值向量的协⽅差阵及单位权⽅差。

现有函数，则其⽅差①，协因数②，函数关于观测值向量的协⽅差阵③，协因数阵④。

2．已知观测值向量的权阵，则观测值的权⑤，⑥，观测值的协因数阵⑦。

3．条件平差的函数模型是⑧，附有参数的条件平差的函数模型是⑨，它们的随机模型是⑩。

⼆、问答题（本题共30分，共2⼩题，每⼩题15分）1．在图⼀所⽰测⾓⽹中，A、B为已知点，C、D、E和F为待定点，同精度观测了共16个⾓度。

若按条件平差法对该⽹进⾏平差：（1）共有多少个条件？每种条件各有⼏个？（2）试列出全部⾮线性条件⽅程（不必线性化）。

2．在间接平差中，误差⽅程为。

式中，观测值的权阵为。

已知参数的协因数阵。

现应⽤协因数传播测量平差共3页第1页律由误差⽅程得：。

以上做法是否正确？为什么？三．计算题（本题共60分，共4⼩题，每⼩题15分）1．有⽔准⽹如图⼆所⽰。

图中A、B、C为已知点，、为待定点。

已知点⾼程为，, 。

观测⾼差为，，，，。

设各⽔准路线长度相等。

试按间接平差法求：（1）、两点⾼程的平差值；（2）平差后与两点间⾼差的权。

2．在图三所⽰测⾓⽹中，A、B、C为已知点，P为待定点，为同精度观测值。

其中，。

若按坐标平差法对该⽹进⾏平差，计算得，，，以及坐标⽅位⾓改正数⽅程的系数（见表⼀）。

现设参数改正数、的单位为“cm” ：（1）试列出和的线性化误差⽅程；（2）列出平差后PC边的坐标⽅位⾓的权函数式。

表中：图三3．设某平差问题有以下函数模型（为单位阵）试写出⽤以上函数模型进⾏平差的⽅法的名称并组成法⽅程。

4．为了确定通过已知点（）处的⼀条直线⽅程（见图四），现以等精度量测了处的函数值，分别为，，，，⼜选直线⽅程中的作为参数。

B测量平差基础一、 正误判断（正确“T ”，错误“F ”每题1分，共10 分）。

1．已知两段距离的长度及中误差分别为128.286m ±4.5cm 与218.268m ±4.5cm ，则其真误差与精度均相同（ ）。

2．如果X 与Y 的协方差0xy σ=，则其不相关（ ）。

3．水准测量中，按公式i icp s =（i s 为水准路线长）来定权，要求每公里高差精度相同（ ）。

4．可用误差椭圆来确定待定点与待定点之间的某些精度指标（ ）。

5．在某一平差问题中，观测数为n ，必要观测数为t ，参数个数u ＜t 且不独立，则该平差问题可采用附有参数的条件平差的函数模型。

（ ）。

6．由于同一平差问题采用不同的平差方法得到的结果不同，因此为了得到最佳平差结果，必须谨慎选择平差方法（ ）。

7．根据公式()222220cos sin 0360E F θσθθθ=+≤≤得到的曲线就是误差椭圆（ ）。

8．对于特定的平面控制网，如果按间接平差法解算，则误差方程的个数是一定的（ ）。

9．对于同一个观测值来说,若选定一定权常数0σ，则权愈小，其方差愈小，其精度愈高（ ）。

10．设观测值向量,1n L 彼此不独立，其权为()1,2,,i P i n = ，12(,,,)n Z f L L L = ，则有22211221111Z n nf f f P L P L P L P ⎛⎫⎛⎫⎛⎫∂∂∂=+++ ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭ （ ）。

二、填空题（每空2分，共24分）。

1、设对某三角网进行同精度观测，得三角形角度闭合差分别为：3秒，-3秒，2秒，4秒，-2秒，-1秒，0秒，-4秒，3秒，-2秒，则测角中误差为 秒。

2、某平差问题函数模型)(I Q =为⎪⎪⎩⎪⎪⎨⎧=-=--=+-+=--0ˆ03060515443121x v v v v v v v v ，则该函数模型为平差方法的模型；=n ，=t ，=r ，=c ，=u 。

测量平差复习题答案一、单项选择题1. 在测量平差中，观测值的改正数与观测值的符号相反，说明该观测值是（）。

A. 正误差B. 负误差C. 系统误差D. 偶然误差答案：B2. 测量平差中，观测值的中误差是指（）。

A. 观测值的标准差B. 观测值的均值C. 观测值的偏差D. 观测值的最大误差答案：A3. 测量平差中，单位权中误差的计算公式为（）。

A. σ0 = √(Σσ²) / nB. σ0 = Σσ² / nC. σ0 = √(Σσ²) / ΣnD. σ0= Σσ² / Σn答案：A二、多项选择题1. 测量平差中，下列哪些因素会影响观测值的精度（）。

A. 观测者的技能水平B. 观测仪器的精度C. 观测环境D. 观测时间答案：ABCD2. 在测量平差中，下列哪些方法可以提高观测精度（）。

A. 增加观测次数B. 采用高精度仪器C. 改进观测方法D. 延长观测时间答案：ABC三、填空题1. 测量平差中，观测值的中误差是用来衡量观测值的______。

答案：精度2. 测量平差中，单位权中误差是用来衡量观测值的______。

答案：精度3. 在测量平差中，观测值的改正数是用来______观测值的系统误差。

答案：消除四、简答题1. 简述测量平差中，观测值的中误差与观测值的精度之间的关系。

答案：观测值的中误差是观测值精度的一种度量，中误差越小，说明观测值的精度越高。

2. 测量平差中，如何通过观测值的改正数来判断观测值的误差性质？答案：观测值的改正数与观测值的符号相反，说明该观测值是负误差；如果改正数与观测值的符号相同，则说明该观测值是正误差。

五、计算题1. 已知一组观测值的方差分别为2、3、4，计算该组观测值的单位权中误差。

答案：σ0 = √(2+3+4) / 3 = √9 / 3 = √32. 假设在一次测量中，观测者得到了一组观测值，其改正数分别为-0.1、0.2、-0.3，计算该组观测值的平均改正数。

《误差理论与测量平差基础》期末考试试题A(参考答案)一、名词解释（每题2分，共10分）1、偶然误差——在相同的观测条件系作一系列的观测，如果误差在大小和符号上都表现出偶然性。

即从单个误差看，该误差的大小和符号没有规律性，但就大量误差的总体而言，具有一定的统计规律。

这种误差称为偶然误差。

2、函数模型线性化——在各种平差模型中，所列出的条件方程或观测方程，有的是线性形式，有的是非线性形式。

在进行平差计算时，必须首先把非线性形式的函数方程按台劳公式展开，取至一次项，转换成线性方程。

这一转换过程，称之为函数模型的线性化。

3、点位误差椭圆——以点位差的极大值方向为横轴轴方向，以位差的极值分别为椭圆的长、短半轴，这样形成的一条椭圆曲线，即为点位误差椭圆。

4、协方差传播律——用来阐述观测值的函数的中误差与观测值的中误差之间的运算规律的数学公式。

如，若观测向量的协方差阵为，则按协方差传播律，应有。

5、权——表示各观测值方差之间比例关系的数字特征，。

二、判断正误（只判断）（每题1分，共10分）参考答案：X √X √X X X √√X三、选择题（每题3分，共15分）参考答案：CCDCC四．填空题（每空3分，共15分）参考答案：1. 6个2. 13个3.1/n4. 0.45. ,其中五、问答题（每题4分，共12分）1. 几何模型的必要元素与什么有关？必要元素数就是必要观测数吗？为什么？答：⑴几何模型的必要元素与决定该模型的内在几何规律有关；（1分） ⑵必要元素数就是必要观测数；（1分）⑶几何模型的内在规律决定了要确定该模型，所必须具备的几何要素，称为必要元素，必要元素的个数，称为必要元素数。

实际工程中为了确定该几何模型，所必须观测的要素个数，称为必要观测数，X F E 、0K KL Z +=LL D T LL ZZ K KD D =220ii P σσ=0)()()()(4320020=''+∆+∆+-''+-''-W y SX X x SY Y C ACA C C ACA C ρρABAC AC X X Y Y W αββ-++--=''4300arctan其类型是由必要元素所决定的，其数量，必须等于必要元素的个数。

为边长观测值，若按条件图27BC α654321D CBA 武汉大学 测绘学院误差理论与测量平差基础 课程试卷（A 卷）出题者：黄加纳 审核人：邱卫宁一.已知观测值向量的协方差阵为，又知协因数，试求观测值的权阵及观测值的权和。

（10分）二.在相同观测条件下观测A 、B 两个角度，设对观测4测回的权为1，则对观测9个测回的权为多少？（10分）三.在图一所示测角网中，A 、B 为已知点，为已知方位角，C 、D 为待定点，为同精度独立观测值。

若按条件平差法对该网进行平差：(1).共有多少个条件方程？各类条件方程各有多少个？(2).试列出全部条件方程（非线性条件方程要求线性化）。

（15分）图一四.某平差问题有以下函数模型21L ⎥⎦⎤⎢⎣⎡--=3112LL D 5112-=Q LL P 1L P 2L P A ∠B ∠BC α721,,,L L L )(I Q =⎪⎪⎩⎪⎪⎨⎧=-=--=+-+=--0ˆ03060515443121x v v v v v v v v57624312P 2(1.732,3.000P 1(1.732,1.000A(0,0)B(0,2)Ah 5h 4h 1h 3h 2C DB 试问：(1).以上函数模型为何种平差方法的模型？(2).本题中， ， ， ， ， ， 。

(10分)五.在图二所示测角网中，已知A 、B 两点的坐标和P 1、P 2两待定点的近似坐标值（见图二，以“km ”为单位），以及，，，，为同精度观测值，其中。

若按坐标平差法对该网进行平差，试列出观测角的误差方程(设，、图二 以dm 为单位)。

(10分)六.有水准网如图三所示，网中A 、B 为已知点，C 、D 为待定点，为高差观测值，设各线路等长。

已知平差后算得，试求平差后C 、D两点间高差的权及中误差。

（10分）=n =t =r =c =u =s 0000330001'''=BP α000030002'''=BP αkm S BP 0.201=km S BP 0.202=721,,,L L L 65955906'''=L 6L 5102⨯=ρxˆyˆ51~h h )(482mm V V T =5ˆhABP 2h 5h 4h 1h 3h 2P 17654321PCBA图三七.在间接平差中，参数与平差值是否相关？试证明之。

平差期末试题及答案一、选择题1. 以下哪项不是平差的基本原理？A. 最小二乘法B. 应力平衡法C. 非平衡调整法D. 平差法答案：B2. 平差的基本任务是什么？A. 求出各个未知量的近似值B. 求出各观测值的精确值C. 求出各个未知量的精确值D. 检验各观测值的合理性答案：C3. 以下哪项不是平差的基本要求？A. 观测条件要满足平差要求B. 观测值的精度应满足精度要求C. 未知量的个数应大于观测值的个数D. 观测量之间应相互独立答案：C4. 平差中的误差分析和检验是为了什么？A. 评估观测数据的可靠性B. 评估平差结果的可靠性C. 检查未知量的合理性D. 检查观测装置的准确性答案：B二、填空题1. 平差的基本原理是利用 ________ 求解未知量的最优估计值。

答案：最小二乘法2. 平差的核心思想是达到观测 ________ 和观测 ________ 的双重平衡。

答案：方程、误差3. 平差中，误差方程的个数应大于等于 ________ 方程数量。

答案：未知量4. 平差中，未知量的个数应大于等于 ________ 数量。

答案：观测值三、解答题1. 试述平差的基本步骤及其适用范围。

平差的基本步骤如下：1）建立观测方程，将观测值与未知量之间的关系用数学方程表示。

2）编写误差方程，将观测方程中的观测值与未知量的函数关系转化为观测值和未知量的误差关系。

3）求解误差方程，利用最小二乘法求解未知量的最优估计值。

4）误差分析和检验，评估平差结果的可靠性。

平差适用的范围包括但不限于以下情况：- 大地测量中的测量数据处理；- 工程测量中的控制网调整；- 精密工程测量中的测量结果分析；- 地质勘探中的断层滑坡分析等。

2. 举例说明平差中的最小二乘法原理及其应用。

最小二乘法原理是平差中常用的处理方法之一，其核心思想是使平差结果使得所有观测值的残差平方和最小。

例如，我们进行了一组斜距观测，并欲求解各个未知点的坐标。

根据最小二乘法原理，我们可以建立观测方程和误差方程，并通过求解误差方程得到未知点的最优估计值。