麻将牌型概率算法

麻将专家告诉你，打麻将也需要懂概率论！以上我们从定性方面，列举了多个牌例来说明人手牌的好、中、差。

那么，对一副起手牌可不可以从数学角度，即定量方面来判断它的好、中、差呢?应该说是可以的。

定量分析的尺子和出发点就是麻将牌听、和牌的标准形式。

根据国家体委规定。

麻将牌基本和牌形式有以下5种:①11、123、123、123、123②1一、123、123、123、111(11、123、123、123、1111)311、123、123、111、111.11、123、111、111、ill⑤ll、ill、Ill、111、111特殊和牌形式有以下3种:①I l、11、11、11、11、11、I1M1、1、I、1、1、I、1、I、1、I、1、I、11③1、1、I、I、I、1、I、1、1、I、1、1、1、1{1二单张11二将牌11!二刻子1111二杠123二顺子)由于目前全国各地流行的麻将和牌方式大多属5种基本和牌范围，所以我们从这S种和牌标准形式出发来对入手牌进行分析。

5种基本和牌形式，均为4组1对。

4组中，除1对外，或是刻子，或是顺子，我们就从这4组1对原则出发来对人手牌优劣进行定量分析判断。

因为起手牌无论什么情况，和牌最终都要实现这4组1对，那么，离组成这4组I对越近，显然听牌和牌就快，自然称之为好牌。

而离组成这4组I对越远，听牌、和牌就越慢，自然称为坏牌。

但是，无论是谁，无论在什么情况下，起手牌就会抓到这样的4组1对几乎是不可能的，即使有，也是极为罕见的。

起于抓到的牌大多数情况是包括单张，如么饼、五万，对子，如对么万、六条，相互连络或隔张连络，或带对联络的牌.如五、六万，四、六饼，二、二、三条等，我们称这样的有连络性的牌组为搭子。

显然，人手牌中的搭子越多，组成顺子、刻子这样的3张1组的牌组就越快。

如我们列举的起手牌中四、五万，如下一轮摸入或吃进上家舍出的三、六万，就可立即组成三、四、五万或四、五、六万牌组。

上碰下胡概率碰碰胡是一种在中国流行的麻将胡牌方式，玩家需要将手中的牌组成特定的牌型才能胡牌。

以上碰下胡概率作为标题，本文将探讨碰碰胡的胡牌概率以及相关的胡牌技巧。

我们需要了解碰碰胡的牌型要求。

碰碰胡的牌型要求是由四副刻子（三张相同的牌）和一对将牌（两张相同的牌）构成。

在一副完整的麻将牌中，共有136张牌，其中包括4副万、4副筒、4副条各9张，以及4张东南西北中发白。

因此，我们可以计算出碰碰胡的牌型数量。

我们从万、筒、条三种花色中选择一种，共有3种选择。

然后，我们从已选择的花色中选择3张牌作为刻子，共有C(9,3) = 84种选择。

最后，我们从剩下的6张牌中选择2张作为将牌，共有C(6,2) = 15种选择。

综上所述，碰碰胡的牌型数量为3 × 84 × 15 = 3780种。

接下来，我们来计算碰碰胡的胡牌概率。

在一局麻将中，每位玩家初始手牌为13张牌，然后通过摸牌和其他玩家的弃牌来逐渐组成牌型。

因此，我们需要计算在13张牌中能够组成碰碰胡牌型的概率。

我们从136张牌中选择13张牌，共有C(136,13)种选择。

然后，我们计算在这13张牌中能够组成碰碰胡牌型的数量。

我们可以按照以下步骤进行计算：1. 选择一种花色：共有3种选择。

2. 从已选择的花色中选择3张牌作为刻子：共有C(9,3)种选择。

3. 从剩下的6张牌中选择2张作为将牌：共有C(6,2)种选择。

能够组成碰碰胡牌型的数量为3 × C(9,3) × C(6,2)。

因此，碰碰胡的胡牌概率为(3 × C(9,3) × C(6,2)) / C(136,13)。

除了计算胡牌概率，玩家在实际的麻将游戏中还可以通过一些技巧提高胡牌的机会。

玩家需要时刻关注其他玩家的弃牌情况。

如果其他玩家弃牌中出现了需要的牌，那么玩家可以根据这些信息调整自己的打牌策略，尽量避免打出对手需要的牌。

玩家可以根据自己手中的牌型进行适当的策略调整。

运用概率科学赢牌技巧概率,是概率论中最根本的概念。

在社会和自然界中，某一类事情在相同的条件下，可以发作也可以不发作，这类事情称为“随机事情”，概率就是用来表明随机事情发作的可以性巨细的一个量。

很自然地把必定发作的事情的概率规定为1 。

并把不可以发作的事情的概率规定为。

而普通随机事情的概率是介于0与1之间的一个数.愈接近于1，这事情发作的可以性愈大。

打麻将是颠末换牌来对本人的牌列，作四放一对的排列组合.使用概率来挑选牌张，即要挑选简单到手的牌张和对我效果大的牌张，可是.实际状况往往是.简单到手的牌张对我的牌(指具体的这一牌的牌架子)效果不大〔牌架子，刚刚起完了13弓长牌，没有翻开，这起完的13张牌，就叫做这一牌的牌架子。

若是颠末摸牌换牌后的13张牌，通称一副牌或这付牌。

我所需求的效果大的牌张，(指具体的这一牌的牌架子需求)又不简单到手。

这里，就需求先知道麻将牌张在排列组合中的异样效果及其效果的巨细，才有可以较好地处理简单到手的牌张也是对我效果大的牌张，做到合二而一然后优化组合咱们的四放一对，即组合较快.符牌机缘较大，也就是处理一个优化组合何题。

麻将牌136张，用了从1至.9九个数字和七个字头，从1至9分简、索、万三色，异样的把戏间的数字自成系列，所以便构成了34个异样的数字色样及字头，而每一个数字色样及字头有相同的牌4张。

麻将的输赢是谁先组成“放”，一放牌3张，只要两种联接方法，一是本人成坎。

二是靠吃、碰。

所以，数字便在联接中发作巨细异样的效果，从1至9.不分筒、索、万，它们可以构成123,234,345,456,567,678,789七种组合，若是加上本身成坎、九个数字中的3,4,5,6,7可以有四种方法组进一放牌，字头则只要本身成坎一种方法。

熟习麻将的人，在思维知道上，普通都把119和字头归作一类，统称为“么”，而对其他的牌，则统称为中间张子.固然1、9和字头略有异样，它们可以组进123和789的放子，但还它们得碰的时机又较字头为少.相同的道理，2和8归入中间张子也略胜一筹，但得碰的时机要多一点。

[教学研究]麻将与概率论 麻将与概率论 麻将与概率论 简介: 麻将牵涉到全方位思考，是一种以运气为主、技术为辅的游戏，因此，任何一张留牌或舍牌 都必须考虑清楚，不可轻忽。有时候，难免会因为一张牌打得不好，导致全局皆输。 ?理论上来说，舍牌的先后顺序如下: 没有构成番数的风向牌。 没有抓对的三元牌。有构成番数， 可惜没有抓对的风向牌。没有连络性的边张(幺九牌)。没有连络性的二、八孤张(筒、万、条)。没有连络 性的中张牌(三、四、五、六、七)。久久拆不出的宇牌对于。拆难以碰到的中张牌对子。拆难以碰到的二 、八数牌对子。久久拆不出的边张对子(幺九对子)。拆偏张搭子(一、二或八、九数牌)。 拆中张牌所构成的嵌张(三、五或六、八数牌)。拆边张牌所构成的嵌张(一、三或七、九数牌)。 拆中张 牌所构成的两面搭子(四、五或六、七数牌)。拆二、八所构成的两面搭子(二、三或七、八数牌)。 以上所列的舍牌顺序，诚然是就整副牌发展的角度而论，是一种几率学的参考，但打麻将重点在于攻 守兼顾，仍须视海底牌，以及各字碰牌、吃牌等等实际状况，来调整舍牌的方向。 ?就孤张而言，假若手底牌有九条、五条、一条、四筒，这四张孤张，您会先打哪一张呢?我想，一 定会有人说，那还不简单，先打边张一条或九条就对了嘛!然而请恕笔者直言:错了～应该把四筒打掉比 较合理。怎么说呢,因为四筒必须摸进六、五、四、三、二筒才能跟自己产声联络性，推算结果，共有19 牌(20—1张)的机会。反观一、五、九条，只要摸进一至九条都能跟本身持牌产生连络性，共有33张牌之 多 (36—3张)，就几率而言，当然是四筒先溜咯! ?舍弃任何孤张之前，务必先就它对这把牌的贡献度，以及牌局本身的发展，作一个全盘考虑。换言 之，就算是上家、对家舍弃过的张，也许下家正求之不得也说不定呢!例如:对家、上家在牌局开始没多 久，便相继打了九万，这时，阁下若没有七、八万可以吃，而且手底牌也同样握有一张九万，试想，这只 九万能跟打吗?笔者的建议是，如果阁下的牌姿还不错，决心拼斗下去，那么您应该马上跟着溜。免得留 到后来放炮，而假若阁下拿到的是大烂牌，那就绝对没必要跟着打出去-——因为，上家、对家显然没有 七、八万搭子所以才舍弃九万的，而你也没有，这样一来，下家拿到七、八万的可能性必然相对提高了， 如果盲目地跟着打九万的话，不等于白白送给下家一次吃进牌的机会吗? ?拆牌的先后次序也是有学问的，例如拆除一、二万，您会先打一万呢?还是二万?应先打一万。因为 ，下一手若不小心摸到三万，便会形成二、三万双面搭子，也就是回头张(一万自己曾打过)，极容易吃到 上家的舍牌。先打二万另一个缺点是，万一下家有一、二、三、三万，他自然会拆出一、三万吃二万，预 留二、三万还可吃你准备要舍出的一万，等于让下家有连吃两组顺子的机会，可说赔大了!先丢一万则无 此项困扰。 ?假若手底牌有一、二、四、五万两个搭子，因为都出现重复求进三万的现象，因此，拆除一、二万 搭子是绝对可行的。 ?两个搭子，以求进一、四或六、九这两种最美，其次是二、五或五、八，至于中张牌，因为大家都 扣得很紧，所以比较难进牌。 ?如果对子过多，而且都是很难碰到的中张牌，选择边跑边玩，甚至放弃该把牌，也是可行的。因为 如果拆除的对子都是中张或生张，只会增加另三家进牌的机会。 ?如果搭子过多，而且几乎都是中张牌所形成的嵌张，也是要以明哲保身为要，紧紧盯住下家，不喂 他吃牌方是上策。 ?留下“上家”一开始就打过的中张牌，是可以发挥相当大的作 用的。例如:上家打过六万，你的手 底牌恰巧也有一孤张六万，这时最好能够将它留下来，怎么说呢?倘使你随后摸到五万，可形成五、六万 双面搭子，倘若摸到七万，则可形成六、七万搭子，就算摸到八万，至少也可形成六、八万嵌张，而上家 既然一开始就舍弃六万，表示需要七、八万的可能性不大，一旦随后让他摸到了，也会以废牌打出，这样 一来，等于两个人在摸牌，无疑大大增加你组成“六、七、八万”一顺子或“五、六、七万”一顺子的机 会。同理可推，如果你手心早已经有了六、九万复合面子， 上家舍出六万，你也不必急着跟打六、九万 出去，毕竟他后来若摸到了七万，即可能还是废牌，不得不打出，这时你便可以用八九万吃他舍出的七万 ，预留六、七万双面搭子，继续守候上家可能还会摸到进而舍出的八万了。 ?必须拆除某某搭子的时候，务必要先推算可进张数的多寡，再决定拆哪一搭。举例来说，三家已有 人先后碰走了一、三万各一坎，尸牌也出现过一张二万了，这时，如果你的手底仍有一、三万搭子，当然 不能拆掉。毕竟，二万无人抓对，一、三万已经叫绝，另三家等于帮着你摸二万，进张的可能性不是大大 提高了吗?这种情形甚至比一般的双面搭子还要容进张。 ?仍需再度强调，有时候拆牌打，绝对要比一味打出单只中张牌来得有利。例如:阁下手内牌有一、 二、四、五筒及三万，试想，两个搭子同时要连三筒的话，不是有些困难且多此一举吗?这时，不妨将偏 张拆除，留下四、五筒求进三、六筒就好。至于三万，由于连络性佳，会让你摸进更好的搭子也未可知。 ?熟记下家的舍牌顺序，大可让自己不会因为打错牌而捶胸顿足。例如:下家曾打过七、九万，你手 底牌有三、四、五、六万复合面子，必须舍出五万或六万才可听牌，这时，打六万绝对比三万安全。 ?孤张的取舍，在缺少对子的情况下，尽量留下尸牌不见的生张，可增加配对的机会。 ?孤张的取舍，在搭子不够的情况下，尽量留下连络性较佳的中张牌。 ?孤张的取舍，在牌面搭子已经完备的情况下，生张先溜，再打熟张。 ?麻将比赛，环环相扣，进人中局以后，拆牌行为就要开始小心了，避免“意外放炮”绝对是您优先 的考虑。 ?在阁下求和有望的情况下，倘若认定拆掉的牌不至于造成放炮，尽管极可能会喂到下家，当然还是 值得打出的(再怎么说，你都比他先摸牌，当然可以力拼)。 ?明知不可为的牌局，必须毅然决定下车，不要心存幻想，死到临头还硬拼——总之，扣下任何生张 牌“堵下家”，并且防止对家、上家碰出，都是减缓敌方进牌速度最有效的必然手段。同理，拿到漂亮的 起手牌之后，该跑的生张就该快速脱手，祈求另三家吃、碰，使牌势因此急速运转，有利于自己的听牌进 度。

麻将算牌方法和规律麻将是一种古老而又深受人们喜爱的游戏，而在麻将游戏中，算牌方法和规律是非常重要的。

掌握了麻将的算牌方法和规律，可以帮助玩家更好地制定策略，提高胜率。

下面我们就来详细了解一下麻将的算牌方法和规律。

首先，对于麻将的算牌方法，最基本的就是要了解麻将的牌型和牌面的点数。

麻将一共有136张牌，包括万、条、筒、字牌四种花色，每种花色都有1-9共计36张牌。

在算牌时，要对每一张牌进行点数的计算，并且要根据手中的牌来进行相应的加减法运算，以便更好地掌握牌的情况。

其次，麻将的算牌方法还包括对手牌的分析和推演。

在游戏过程中，要根据自己手中的牌和已经打出的牌来进行推演，猜测其他玩家的牌型和可能的组合。

这样可以更好地制定出下一步的策略，提高自己的胜率。

另外，麻将的算牌方法还包括对牌的搭配和组合的分析。

在游戏中，要根据手中的牌来进行搭配和组合，尽可能地组成胡牌的形式。

这就需要对不同的牌型和组合进行深入的分析和研究，找出最佳的搭配和组合方式。

除了算牌方法，麻将的规律也是非常重要的。

首先，要了解麻将游戏中的基本规则，包括吃、碰、杠、胡等各种动作的规定。

只有深入了解了这些规则，才能更好地运用在实际的游戏中。

其次，要了解麻将游戏中的牌的分布规律。

在游戏过程中，要根据已经打出的牌和其他玩家的动作来推测牌的分布情况，从而更好地制定出自己的策略。

最后，要了解麻将游戏中的对局规律。

不同的对局可能会有不同的规律，要根据实际情况来灵活应对，制定出最佳的策略。

总的来说，麻将的算牌方法和规律是非常重要的，它可以帮助玩家更好地制定出策略，提高胜率。

希望大家能够认真学习和掌握这些方法和规律，成为一名优秀的麻将玩家。

麻将公式一定要背下来麻将，作为一种深受大众喜爱的棋牌游戏，不仅需要运气，更需要技巧和策略。

在麻将的世界里，掌握一些实用的公式，可以大大提高我们的获胜几率。

接下来，就为大家详细介绍一些一定要背下来的麻将公式。

首先，“听牌公式”是重中之重。

听牌是麻将中决定胜负的关键阶段，正确判断听牌的可能性和选择最佳的听牌方式至关重要。

常见的听牌公式之一是“顺子＋对子＋刻子”。

顺子，如 123 万、456 条；对子，像两个东风；刻子，例如三个八万。

通过合理组合这些牌型，增加听牌的张数和成功率。

另一个重要的公式是“进张数计算”。

在麻将游戏中，要时刻关注自己手中的牌以及桌面上已经出现的牌，通过计算进张数来判断自己手牌的价值和潜在的胡牌可能性。

比如，手中有一对五万，三万和七万已经出现较多，那么此时五万的进张数就相对较少，可能需要重新考虑这对五万在牌局中的作用。

“牌效率公式”也不容忽视。

这主要是指在摸牌和出牌的过程中，优先处理价值较低的牌，保留能够组成有效牌型的牌。

比如，有一张单独的九条，而手中还有顺子的边张一、二万等着组成顺子，那么九条就应该先打出，以提高牌的效率。

还有“防守公式”。

当自己的牌型不太理想，或者判断其他玩家可能即将胡牌时，防守就变得尤为重要。

这时候要避免打出危险牌，比如桌面上已经出现了两张东风，而自己手中还有一张东风，此时打出东风就很可能点炮，应该谨慎处理。

“吃碰杠公式”同样有讲究。

吃牌要考虑是否能够加快自己的听牌速度；碰牌则要思考是否能够破坏其他玩家的牌型或者增加自己的进张；杠牌更是要权衡利弊，因为杠牌会暴露自己的牌型，同时也可能会影响牌局的走势。

“舍牌公式”也很关键。

一般来说，先舍出孤张和边张，比如单独的九筒或者一、九条。

然后再根据牌局的进展和其他玩家的出牌情况，逐步舍弃价值较低的中张牌。

在实际的麻将游戏中，灵活运用这些公式是取得胜利的关键。

但同时也要记住，麻将是一种充满变数的游戏，不能仅仅依靠公式，还需要结合牌局的具体情况、其他玩家的表情和动作等因素进行综合判断。

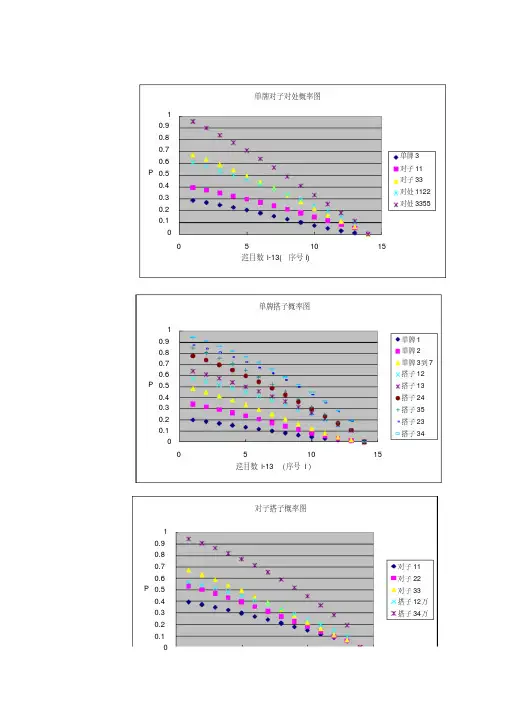
0.10.20.30.40.50.60.70.80.91051015P 巡目数i-13(序号i)单牌对子对处概率图单牌3对子11对子33对处1122对处33550.10.20.30.40.50.60.70.80.91051015P 巡目数i-13（序号i ）单牌搭子概率图单牌1单牌2单牌3到7搭子12搭子13搭子24搭子35搭子23搭子3400.10.20.30.40.50.60.70.80.91P 对子搭子概率图对子11对子22对子33搭子12万搭子34万搭子对子概率图分析：记号说明，记号“12万<23万”意思是12万成顺成坎的概率小于23万成顺1、12万<1122万<13万，特别是1122万和13万的对应曲线靠的很近，说明它们成顺成坎的概率接近.或说从12，1122，13对应的曲线可以看出，它们属于同一组，故它们的行牌特征相近。

2、1133万<24万<2233万<2244<35万，这5条曲线为一组，它们的概率变化规律相同.行牌特征相近．3、从第5手牌起（即进入中盘起），3344万<3355万<23万<34万，在前5手中，23搭子的效率是最低的。

搭子与关联对处曲线被划分为了3组，前两组的特征相似，第3组的特征差异大，究其原因是因为第三组要注意2233不如2244效率高，同样3344不如3355效率高．4.由数据分析可以看出对处不如一卡在一定程度上是对的。

边张12万无论从什么角度看效率都是最低的注：本页数据来自于前面的单牌表，搭子表，对子表，关联对处表，改动前面的数据，这里的图表会动结束语：用序列模型可以很好的研究麻将概率，打麻将抛开人的斗智斗勇，从纯数学观点看，玩麻将就抽签游戏，或不放回摸球游戏.研究各轮的概率可以用独立重复试验来研究，但对同一轮内的概率研究却试验。

常听到这样一个问题手拿1、3万，问摸四万的概率多大？大多数人的回答是4/108=0.037.这个说因为古典概型的等可能性是在一定条件下描述的。

我们都知道比的是相对大小，不是绝对大小。

你的牌赢不赢，并不取决于你的牌多大，而是取决于你和对手的牌相对来讲谁大谁小。

但尽管如此，人们还是希望自己来一副“大牌”。

何谓“大牌”？从概率学讲，大牌是那种不易出现的，用一些花色和数码特殊排列组合而成的牌。

如豹子、同华顺、金、顺等，比它们更小一些的是一对带单，再次就是单打了。

备注：（1）由于概率太小，本统计资料未显示豹子、同花顺、金、顺的具体概率。

（2）大对代单指A、K、Q、J的对、中对代单指10、9、8、7、6的对、小对代单指5、4、3、2对。

由以上统计不难看出，同花顺出现的概率比豹子要小，顺出现的概率比金要小。

也就是我们常用的大小尺度有不合理的地方。

但以上两对的概率相差很小，所以我们姑且按老规矩比大小。

拿了顺以上的牌，一般就很不容易了（8.67％），其实拿到对儿以上就很不错了（25.61％）。

四个人诈金花，每局都有顺以上大牌出现的概率是34.7％，五个人此概率为43.3％，六个人则为52％，七个人就能达到60％以上，所以“人多出大牌”就是这个道理。

我想先对单打牌做些分析，因为它们占了大部分牌型，且它们往往在实力和诈骗之间扮演不同角色。

一副牌没看，那它有多大我们就对它不会失望呢？也就是我们对它的数学期望是多少呢？从以上表中可看出，牌的数学期望在K带队的牌之中，确切说是大概K带一个9和一个8。

也就是说，两个人互不知道对方牌，若自己拿着这样一副牌，对方比你大或比你小的概率是一样的。

所以人们常说的：“你丫暗的有啥了不起，我有个尖儿（A）就开你！”甚至有人还说，“我有个人儿（JQK）就开你”。

那我们就看看拿这些单打中的牛牌开，结果如何?上表显示比A带队大的概率为25.61％，所以有尖儿必然要开，尤其是尖儿代KQJ等所谓单打冠亚军们，毫不犹豫。

K带队就不一定了，因为数学期望值就在当中。

这是一个分水岭。

K代大牌的赢率约一半，上面讲了K 9 8是恰好一半。

而Q带队和J带队赢的几率就小于一半了。

一分钟学会算抽牌的概率
“四二法则”是一种估算概率的方法，让你能快速计算你想要的牌出现的概率。

比如：桌子上的牌是A-6-7-Q，而你的手牌是8-9。

你想要再来一张5或者10来凑成顺子，但你只剩最后一轮机会。

严格来计算概率应该这样：
一副牌52张，去掉翻牌3张，转牌1张，手牌2张，剩下52-3-2-1=46张；
你想要的牌是4张5和4张10，共4+4=8张。

那么此时，你在河牌中顺子的概率为：8/46=0.1739，即17%。

你可能觉得这样计算会比较麻烦，于是就有了四二法则，即：你
想要的牌有4+4=8张，
只剩最后一轮机会，所以让8*2=16，即你有约16%的机会中顺子，与上述17%基本近似。

这是四二法则中的“二”。

当然，如果你还有两轮机会的话，即河牌圈与转牌圈，情况是这样的。

比如桌子上翻牌为A-6-7，你的手牌依旧是8,9。

不一样的是，你有两轮机会来等5或者10，共8张想要的牌
那么两轮内你中顺子的概率为：
1-(47-8)/47*(46-8)/46=0.3145,即约为31%。

那么利用四二法则，8*4=32，即你约有32%的机会中顺子，是不是跟理论值也很接近。

这就是四二法则中的“四”。

总之就是，先想好自己想要的牌的张数，然后，还有两轮机会就乘4，还有一轮机会就乘2，得到的就是你想要的牌接下来会出现的概率。

接着，根据赔率以及战况来决定接下来该怎么办。

利用好四二法则，可以帮你快速估算概率。

麻将公式一定要背下来（麻将胡牌的万能公式）麻将公式一定要背下来（麻将胡牌的万能公式）你还在为打麻将胡牌难而苦恼吗?尤其是刚学打麻将的新手们对于胡牌的阵型总是有的迷糊。

那么这个万能的麻将胡牌公式你一定要记住了，让你一分钟Get麻将胡牌的正确姿势。

麻将胡牌万能公式长啥样?n*AAA+m*ABC+DD看起来是不是有点蒙，其实这个公式非常好理解，AAA就是三个一样的牌(刻子)，ABC就是顺子，DD就是对子。

mn可以为0，加起来一共14张牌即为和牌，少任何一张即为听牌。

•当m=0且n=0时，此时和牌的牌型就是7小对，7个对子少一张牌，独听那张单牌。

•当n=0时，m=4，除了1个对子外有4个顺子，此时和牌的牌型属于平和，是较为普通的牌型。

•当m=0时，n=4，除了1个对子外有4个刻子，此时听牌一般听两个对子，摸到其中一个对子的牌，凑足4个刻子，即可和牌。

刻子可以是碰来的，也可以是摸来的，如果都是碰来的，就叫“碰碰和”。

•n和m都不为0时，n+m=4，除特殊情况外，基本属于平和的状态。

学会了正确的打牌姿势后，赢麻将的招数自然很多。

1、猜牌算牌不能少。

根据对方打出的牌和牌面结合猜测TA手中的牌。

比如说打3万，可能没有一二万，打五条可能没有4、6条，因为一般打出去的牌基本都是闲张或者是孤张，所以在猜牌的时候可以结合牌面和此类规律进行猜测。

2.忌危险牌，即忌出手。

这个也要结合卡面来分析。

如果觉得有人会要、吃、碰你手里的闲牌，可以在不影响自己牌面的情况下，尽早打出来。

但如果到了游戏中后期，就需要尽可能的扣牌，避免危险牌，防炮。

3.注意选座。

打麻将也有很多运气成分，有些位置不利于财运的聚集，所以打麻将要注意避开，比如背后的窗户或者书柜，头顶的横梁，卫生间的门等等。

4、虚拟现实，在做大牌的时候，为了防止被扣分，你需要故意打出一些牌，摸摸，让别人察觉不到你的真实意图，诱导别人把你需要的牌给你。

这是一个非常聪明的做法。

运用概率科学赢牌技巧概率,是概率论中最根本的概念。

在社会和自然界中，某一类事情在相同的条件下，可以发作也可以不发作，这类事情称为“随机事情”，概率就是用来表明随机事情发作的可以性巨细的一个量。

很自然地把必定发作的事情的概率规定为1 。

并把不可以发作的事情的概率规定为。

而普通随机事情的概率是介于0 与1之间的一个数 .愈接近于1，这事情发作的可以性愈大。

打麻将是颠末换牌来对本人的牌列，作四放一对的排列组合.使用概率来挑选牌张，即要挑选简单到手的牌张和对我效果大的牌张，可是.实际状况往往是 .简单到手的牌张对我的牌(指具体的这一牌的牌架子)效果不大〔牌架子，刚刚起完了13 弓长牌，没有翻开，这起完的13 张牌，就叫做这一牌的牌架子。

若是颠末摸牌换牌后的13 张牌，通称一副牌或这付牌。

我所需求的效果大的牌张，(指具体的这一牌的牌架子需求)又不简单到手。

这里，就需求先知道麻将牌张在排列组合中的异样效果及其效果的巨细，才有可以较好地处理简单到手的牌张也是对我效果大的牌张，做到合二而一然后优化组合咱们的四放一对，即组合较快.符牌机缘较大，也就是处理一个优化组合何题。

麻将牌 136 张，用了从 1 至.9 九个数字和七个字头，从1 至9 分简、索、万三色，异样的把戏间的数字自成系列，所以便构成了34 个异样的数字色样及字头，而每一个数字色样及字头有相同的牌 4 张。

麻将的输赢是谁先组成“放”，一放牌3 张，只要两种联接方法，一是本人成坎。

二是靠吃、碰。

所以，数字便在联接中发作巨细异样的效果，从 1 至9.不分筒、索、万，它们可以构成 123,234,345,456,567,678,789七种组合，若是加上本身成坎、九个数字中的3,4,5,6,7可以有四种方法组进一放牌，字头则只要本身成坎一种方法。

熟习麻将的人，在思维知道上，普通都把119 和字头归作一类，统称为“么”，而对其他的牌，则统称为中间张子 .固然1、9 和字头略有异样，它们可以组进123和789 的放子，但还它们得碰的时机又较字头为少.相同的道理，2 和8 归入中间张子也略胜一筹，但得碰的时机要多一点。

麻将基础知识1—麻将的牌理及数理特性关于麻将牌理与数理特性，是麻将知识最基础的部分，但同时也是最容易被初学玩家忽视的一部分。

之所以我们要研究数理特性，是因为在这里能够发现麻将的机率与牌理。

麻将的牌理根据牌理打牌。

牌理指的就是为了有效率地完成手牌4面子+一组雀头的理论。

这是麻将中做牌的最根本的想法。

和牌理有相同意义的词语就是我们常说的“牌效率”了。

以一局作为单位来说的话，麻将就是比赛“对局4人中谁能够最快的组成4面子+一组雀头”的游戏。

因此，根据牌理选择舍牌（就是打出的牌）是基础。

麻将手牌有“速度”（和牌速度）、“高度”（得点多少）、“防御力”三个要素。

其中“速度”是最重要的。

天下武功，唯快不破，这句话同样适用于麻将对局。

所谓“速度”，就是快速听牌，在麻将对局中超过对手，以最快速度最先听牌。

快速听牌，就是对对手的威胁，就能造成对手“受迫性失误”，该听牌的不敢听，该冲张的不敢冲，该和牌的没和到，气势就在这之中微妙的改变了。

所以说，“速度”能够给予“高度”和“防御力”以掩护。

无论多么大的牌只要和不了就不能增加点数。

尽早和牌就可以阻止对手可能和出的牌，实际的收益也可以看作“和了的点数”+“各种未知的收益”。

而且在对手听牌之前就和牌的话还可以避免放炮。

“速度”是手牌的生命线。

一定要切记：被其它因素迷惑双眼而不去和牌是非常不可取的行为。

下面来说说根据牌理打牌到底是怎么一回事。

这个手牌会有什么想法呢？有全带幺九的机会，要是索子能够上张的话，也可以做三色同顺。

初学者总是容易有“到底应该去做自己记得的那一个牌型呢？”这种想法。

因此，像这样：当摸到中的时候，往往会选择打掉9万这样的错招。

从13（14）张手牌的结构方面去考虑是非常重要的。

手牌的结构如上图，4面子1雀头（北风对），我们到底缺什么呢？目前已经完成了2面子和1雀头，把78饼算作一个面子的话，我们就还差一组面子了。

既然没有其他的搭子，那么就只能用剩下的9万、5索、3饼和中来构成了。

麻将规则全面解析：牌型组合技巧与胡牌算法麻将是一种古老而受欢迎的桌上游戏，它结合了策略、技巧和运气。

在这篇文章中，我们将全面解析麻将的规则，包括牌型组合技巧与胡牌算法。

一、麻将的基本规则麻将的基本规则非常简单。

游戏中有136张牌，分为万、筒、索三种花色，每种花色有序数1到9。

此外，还有风牌和箭牌。

每个玩家初始时会获得13张牌，通过摸牌和弃牌的方式进行游戏。

在麻将中，玩家可以通过组合自己手中的牌来获取最大的利益。

不同的组合形成不同的牌型，而牌型决定了游戏的结果。

二、常见的牌型组合技巧1. 刻子：刻子是指由三张相同数字的牌组成的组合，比如三张“一万”或三张“二索”。

刻子是麻将中最基本的组合形式，能够增加你的得分。

2. 顺子：顺子是指由连续三张数字相邻的牌组成的组合，比如“一万、二万、三万”或“四索、五索、六索”。

在游戏中，顺子是非常重要的组合形式，可以帮助你更快地胡牌。

3. 对子：对子是指由两张相同数字的牌组成的组合，比如两张“八筒”或两张“红中”。

对子在游戏中也很常见，有时也可以帮助你胡牌。

4. 雀头：雀头是指由一对相同数字的牌组成的组合，在麻将中用来判断是否可以胡牌。

只有有雀头，才能进行更复杂的组合。

以上是麻将中常见的牌型组合技巧，熟练掌握并合理运用这些技巧，能够提高你在游戏中的胜率。

三、胡牌算法1. 基本胡牌算法：胡牌是麻将游戏中的终极目标。

胡牌的判定方式通常有两种：七对和十三幺。

- 七对：如果你的手牌中有七对（即七个对子），则可以胡牌。

这是最简单的胡牌方式，但并非所有局面都能胡。

- 十三幺：如果你的手牌中有一张万、一张筒、一张索各一、以及一对风牌和箭牌（例如东南西北中发白等），则可以胡牌。

这是最复杂的胡牌方式，也是麻将中最高级别的胡牌方式。

2. 特殊胡牌算法：除了基本胡牌算法外，麻将中还有一些特殊的胡牌方式。

- 平胡：除了七对和十三幺之外，还有一种胡牌方式叫做平胡。

平胡是指手牌中存在组合满足基本规定的胡牌方式，但不足以构成七对或十三幺的情况。

桥牌竞技中的概率问题桥牌是一种概率游戏，其叫牌体系和打牌路线的设计要以概率计算为基础，牌力与控制力的估算标准也要靠概率分析作科学论证，概率常识已经成了牌手们掌握胜算的诀窍。

1.常见牌型概率：桥牌数学原理中的概率计算公式是C(m,n)=m!/(m-n)!*n!，依据概率计算，常见牌型概率如下：整理上表：①无5张套的均牌(4-4-3-2与4-3-3-3)占32.08%。

②无5张套的三色套(4-4-4-1)占2.99%。

有5张以上套的5高(低)花占64.93%。

在5高(低)花中：③三色套(5-4-4-0)占1.34%；双色套占35.77%；单色套占27.82%。

在双色套中：④5-4双套(5-4-3-1与5-4-2-2)占23.51%; ⑤5-5以上双套占5.62% (其中5-5-3-0与5-5-2-1占4.05%，6-5占1.36%，6-6、7-5、7-6等只占0.19%)；⑥4-6以上双套占6.83% (其中4-6-3-0与4-6-2-1占6.03%，4-7占0.75%，4-8等只占0.05%）。

在单色套中：⑦5张单套(5-3-3-2)占15.52%；⑧6张单套(6-3-3-1与6-3-2-2)占9.09%；⑨7张以上单套占3.11% (其中7-3-2-1与7-2-2-2和7-3-3-0占2.66%，而8-2、8-3、9-2等只占0.45%)。

以上总概率99.3%的3组9类18种牌型就是本体系所应该(能够)描述的牌型。

2.防守方牌张分配概率：依据机会均等原则，防守方在某一门花色上的牌张分配似乎总是理当趋近于均匀，但桥牌分牌竟必不同于扔硬币，概率测算结果自然会有些异常：牌张数=奇数(3,5,7)时，均匀分配(2-1,3-2,4-3)概率均大于50%，对庄家有利。

牌张数=偶数(4,6,8)时，平均分配概率均小于50%，非均匀分配(3-1,4-2,5-3)概率反而更大，对庄家不利。

唯牌张数=2例外，1-1分配概率52%，2-0分配概率48%。