武汉中考第24题二次函数与垂直定点问题
- 格式:pdf
- 大小:318.02 KB
- 文档页数:7

初三数学 二次函数 知识点总结一、二次函数概念:1.二次函数的概念:一般地,形如2y ax bx c =++(a b c ,,是常数,0a ≠)的函数,叫做二次函数。
这里需要强调:和一元二次方程类似,二次项系数0a ≠,而b c ,可以为零.二次函数的定义域是全体实数.2. 二次函数2y ax bx c =++的结构特征:⑴ 等号左边是函数,右边是关于自变量x 的二次式,x 的最高次数是2. ⑵ a b c ,,是常数,a 是二次项系数,b 是一次项系数,c 是常数项.二、二次函数的基本形式1. 二次函数基本形式:2y ax =的性质: a 的绝对值越大,抛物线的开口越小。
2. 2y ax c=+上加下减。
3. ()2y a x h =-的性质:左加右减。
4. ()2y a x h k =-+的性质:三、二次函数图象的平移1. 平移步骤:⑴ 将抛物线解析式转化成顶点式()2y a x h k =-+,确定其顶点坐标()h k ,; ⑵ 保持抛物线2y ax =的形状不变,将其顶点平移到()h k ,处,具体平移方法如下:2. 平移规律在原有函数的基础上“h 值正右移,负左移;k 值正上移,负下移”. 概括成八个字“左加右减,上加下减”. 四、二次函数()2y a x h k =-+与2y ax bx c =++的比较【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位从解析式上看,()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式,后者通过配方可以得到前者,即22424b ac b y a x a a -⎛⎫=++ ⎪⎝⎭,其中2424b ac b h k a a -=-=,. 六、二次函数2y ax bx c =++的性质1. 当0a >时,抛物线开口向上,对称轴为2bx a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,.当2bx a<-时,y 随x 的增大而减小; 当2bx a>-时,y 随x 的增大而增大; 当2bx a=-时,y 有最小值244ac b a -.2. 当0a <时,抛物线开口向下,对称轴为2b x a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,.当2bx a <-时,y 随x 的增大而增大;当2b x a >-时,y 随x 的增大而减小;当2bx a=-时,y 有最大值244ac b a -.七、二次函数解析式的表示方法1. 一般式:2y ax bx c =++(a ,b ,c 为常数,0a ≠);2. 顶点式:2()y a x h k =-+(a ,h ,k 为常数,0a ≠);3. 两根式(交点式):12()()y a x x x x =--(0a ≠,1x ,2x 是抛物线与x 轴两交点的横坐标). 注意:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可以写成交点式,只有抛物线与x 轴有交点,即240b ac -≥时,抛物线的解析式才可以用交点式表示.二次函数解析式的这三种形式可以互化.八、二次函数的图象与各项系数之间的关系1. 二次项系数a⑴ 当0a >时,抛物线开口向上,a 的值越大,开口越小,反之a 的值越小,开口越大; ⑵ 当0a <时,抛物线开口向下,a 的值越小,开口越小,反之a 的值越大,开口越大. 2. 一次项系数b在二次项系数a 确定的前提下,b 决定了抛物线的对称轴.(同左异右 b 为0对称轴为y 轴) 3. 常数项c⑴ 当0c >时,抛物线与y 轴的交点在x 轴上方,即抛物线与y 轴交点的纵坐标为正; ⑵ 当0c =时,抛物线与y 轴的交点为坐标原点,即抛物线与y 轴交点的纵坐标为0; ⑶ 当0c <时,抛物线与y 轴的交点在x 轴下方,即抛物线与y 轴交点的纵坐标为负. 总结起来,c 决定了抛物线与y 轴交点的位置.十、二次函数与一元二次方程:1. 二次函数与一元二次方程的关系(二次函数与x 轴交点情况):一元二次方程20ax bx c ++=是二次函数2y ax bx c =++当函数值0y =时的特殊情况. 图象与x 轴的交点个数:① 当240b ac ∆=->时,图象与x 轴交于两点()()1200A x B x ,,,12()x x ≠,其中的12x x ,是一元二次方程()200ax bx c a ++=≠的两根.. ② 当0∆=时,图象与x 轴只有一个交点; ③ 当0∆<时,图象与x 轴没有交点.1' 当0a >时,图象落在x 轴的上方,无论x 为任何实数,都有0y >; 2' 当0a <时,图象落在x 轴的下方,无论x 为任何实数,都有0y <.2. 抛物线2y ax bx c =++的图象与y 轴一定相交,交点坐标为(0,)c ;二次函数对应练习试题一、选择题1. 二次函数247y x x =--的顶点坐标是( )A.(2,-11)B.(-2,7)C.(2,11)D. (2,-3) 2. 把抛物线22y x =-向上平移1个单位,得到的抛物线是( )A. 22(1)y x =-+ B. 22(1)y x =-- C. 221y x =-+ D. 221y x =--3.函数2y kx k =-和(0)ky k x=≠在同一直角坐标系中图象可能是图中的( )4.已知二次函数2(0)y ax bx c a =++≠的图象如图所示,则下列结论: ①a,b 同号;②当1x =和3x =时,函数值相等;③40a b +=④当2y =-时, x 的值只能取0.其中正确的个数是( )A.1个B.2个C. 3个D. 4个5.已知二次函数2(0)y ax bx c a =++≠的顶点坐标(-1,-3.2)及部分图象(如图),由图象可知关于x 的一元二次方程20ax bx c ++=的两个根分别是121.3x x ==和( )A.-1.3 B.-2.3 C.-0.3 D.-3.36. 已知二次函数2y ax bx c =++的图象如图所示,则点(,)ac bc 在( )A .第一象限B .第二象限C .第三象限D .第四象限 7.方程222x x x-=的正根的个数为( ) A.0个 B.1个 C.2个. 3 个8.已知抛物线过点A(2,0),B(-1,0),与y 轴交于点C,且OC=2.则这条抛物线的解析式为A. 22y x x =-- B. 22y x x =-++C. 22y x x =--或22y x x =-++ D. 22y x x =---或22y x x =++二、填空题9.二次函数23y x bx =++的对称轴是2x =,则b =_______。

2020-2021武汉中考数学二次函数综合试题一、二次函数1.如图,抛物线y=ax2+bx+3(a≠0)的对称轴为直线x=﹣1,抛物线交x轴于A、C两点,与直线y=x﹣1交于A、B两点,直线AB与抛物线的对称轴交于点E.(1)求抛物线的解析式.(2)点P在直线AB上方的抛物线上运动,若△ABP的面积最大,求此时点P的坐标.(3)在平面直角坐标系中,以点B、E、C、D为顶点的四边形是平行四边形,请直接写出符合条件点D的坐标.【答案】(1)y=﹣x2﹣2x+3;(2)点P(32-,154);(3)符合条件的点D的坐标为D1(0,3),D2(﹣6,﹣3),D3(﹣2,﹣7).【解析】【分析】(1)令y=0,求出点A的坐标,根据抛物线的对称轴是x=﹣1,求出点C的坐标,再根据待定系数法求出抛物线的解析式即可;(2)设点P(m,﹣m2﹣2m+3),利用抛物线与直线相交,求出点B的坐标,过点P作PF∥y 轴交直线AB于点F,利用S△ABP=S△PBF+S△PFA,用含m的式子表示出△ABP的面积,利用二次函数的最大值,即可求得点P的坐标;(3)求出点E的坐标,然后求出直线BC、直线BE、直线CE的解析式,再根据以点B、E、C、D为顶点的四边形是平行四边形,得到直线D1D2、直线D1D3、直线D2D3的解析式,即可求出交点坐标.【详解】解:(1)令y=0,可得:x﹣1=0,解得:x=1,∴点A(1,0),∵抛物线y=ax2+bx+3(a≠0)的对称轴为直线x=﹣1,∴﹣1×2﹣1=﹣3,即点C(﹣3,0),∴309330a ba b++⎧⎨-+⎩==,解得:12ab-⎧⎨-⎩=,=∴抛物线的解析式为:y=﹣x2﹣2x+3;(2)∵点P在直线AB上方的抛物线上运动,∴设点P(m ,﹣m 2﹣2m+3),∵抛物线与直线y =x ﹣1交于A 、B 两点,∴2231y x x y x ⎧--+⎨-⎩== ,解得:1145x y -⎧⎨-⎩==,2210x y =,=⎧⎨⎩∴点B(﹣4,﹣5),如图,过点P 作PF ∥y 轴交直线AB 于点F ,则点F(m ,m ﹣1),∴PF =﹣m 2﹣2m+3﹣m+1=﹣m 2﹣3m+4, ∴S △ABP =S △PBF +S △PFA =12(﹣m 2﹣3m+4)(m+4)+12(﹣m 2﹣3m+4)(1﹣m) =-52(m+32 )2+1258, ∴当m =32-时,P 最大, ∴点P(32-,154). (3)当x =﹣1时,y =﹣1﹣1=﹣2, ∴点E(﹣1,﹣2),如图,直线BC 的解析式为y =5x+15,直线BE 的解析式为y =x ﹣1,直线CE 的解析式为y =﹣x ﹣3,∵以点B 、C 、E 、D 为顶点的四边形是平行四边形,∴直线D 1D 3的解析式为y =5x+3,直线D 1D 2的解析式为y =x+3,直线D 2D 3的解析式为y =﹣x ﹣9,联立533y x y x +⎧⎨+⎩== 得D 1(0,3), 同理可得D 2(﹣6,﹣3),D 3(﹣2,﹣7),综上所述,符合条件的点D 的坐标为D 1(0,3),D 2(﹣6,﹣3),D 3(﹣2,﹣7).【点睛】本题考查二次函数的综合应用,解决第(2)小题中三角形面积的问题时,找到一条平行或垂直于坐标轴的边是关键;对于第(3)小题,要注意分类讨论、数形结合的运用,不要漏解.2.已知,点M为二次函数y=﹣(x﹣b)2+4b+1图象的顶点,直线y=mx+5分别交x轴正半轴,y轴于点A,B.(1)判断顶点M是否在直线y=4x+1上,并说明理由.(2)如图1,若二次函数图象也经过点A,B,且mx+5>﹣(x﹣b)2+4b+1,根据图象,写出x的取值范围.(3)如图2,点A坐标为(5,0),点M在△AOB内,若点C(14,y1),D(34,y2)都在二次函数图象上,试比较y1与y2的大小.【答案】(1)点M在直线y=4x+1上;理由见解析;(2)x的取值范围是x<0或x>5;(3)①当0<b<12时,y1>y2,②当b=12时,y1=y2,③当12<b<45时,y1<y2.【解析】【分析】(1)根据顶点式解析式,可得顶点坐标,根据点的坐标代入函数解析式检验,可得答案;(2)根据待定系数法,可得二次函数的解析式,根据函数图象与不等式的关系:图象在下方的函数值小,可得答案;(3)根据解方程组,可得顶点M的纵坐标的范围,根据二次函数的性质,可得答案.【详解】(1)点M为二次函数y=﹣(x﹣b)2+4b+1图象的顶点,∴M的坐标是(b,4b+1),把x=b代入y=4x+1,得y=4b+1,∴点M在直线y=4x+1上;(2)如图1,直线y=mx+5交y轴于点B,∴B点坐标为(0,5)又B在抛物线上,∴5=﹣(0﹣b)2+4b+1=5,解得b=2,二次函数的解析是为y=﹣(x﹣2)2+9,当y=0时,﹣(x﹣2)2+9=0,解得x1=5,x2=﹣1,∴A(5,0).由图象,得当mx+5>﹣(x﹣b)2+4b+1时,x的取值范围是x<0或x>5;(3)如图2,∵直线y=4x+1与直线AB交于点E,与y轴交于F,A(5,0),B(0,5)得直线AB的解析式为y=﹣x+5,联立EF,AB得方程组415 y xy x=+⎧⎨=-+⎩,解得45215xy⎧=⎪⎪⎨⎪=⎪⎩,∴点E(45,215),F(0,1).点M在△AOB内,1<4b+1<215,∴0<b<45.当点C,D关于抛物线的对称轴对称时,b﹣14=34﹣b,∴b=12,且二次函数图象开口向下,顶点M在直线y=4x+1上,综上:①当0<b<12时,y1>y2,②当b=12时,y1=y2,③当12<b<45时,y1<y2.【点睛】本题考查了二次函数综合题,解(1)的关键是把点的坐标代入函数解析式检验;解(2)的关键是利用函数图不等式的关系:图象在上方的函数值大;解(3)的关键是解方程组得出顶点M 的纵坐标的范围,又利用了二次函数的性质:a <0时,点与对称轴的距离越小函数值越大.3.如图,抛物线212222y x x =-++与x 轴相交于A B ,两点,(点A 在B 点左侧)与y 轴交于点C.(Ⅰ)求A B ,两点坐标.(Ⅱ)连结AC ,若点P 在第一象限的抛物线上,P 的横坐标为t ,四边形ABPC 的面积为S.试用含t 的式子表示S ,并求t 为何值时,S 最大.(Ⅲ)在(Ⅱ)的基础上,若点,G H 分别为抛物线及其对称轴上的点,点G 的横坐标为m ,点H 的纵坐标为n ,且使得以,,,A G H P 四点构成的四边形为平行四边形,求满足条件的,m n 的值.【答案】(Ⅰ)(2,0),2,0)A B ;(Ⅱ)22(2)42(022)2S t t =--+<<,当2t =时,42S =最大;(Ⅲ)满足条件的点m n 、的值为:2324m n =-=,或52154m n ==-,或3214m n == 【解析】 【分析】(Ⅰ)令y=0,建立方程求解即可得出结论;(Ⅱ)设出点P 的坐标,利用S=S △AOC +S 梯形OCPQ +S △PQB ,即可得出结论;(Ⅲ)分三种情况,利用平行四边形的性质对角线互相平分和中点坐标公式建立方程组即可得出结论. 【详解】解:(Ⅰ)抛物线212222y x x =-++, 令0y =,则2122022x x -++=, 解得:2x =-或22x =, ∴()()2,0,22,0A B - (Ⅱ)由抛物线212222y x x =-++,令0x =,∴2y =,∴()0,2C , 如图1,点P 作PQ x ⊥轴于Q , ∵P 的横坐标为t ,∴设(),P t p , ∴2122,22,22p t t PQ p BQ t OQ t =-++==-=, ∴()()11122222222AOCPQBOCPQ S SS Sp t t p =++=⨯⨯++⨯+⨯-⨯梯形 11222222t pt p pt p t =+++-=++ 21222222t t t ⎛⎫=-++++ ⎪ ⎪⎝⎭ ()22242(022)2t t =--+<<,∴当2t =时,42S =最大;(Ⅲ)由(Ⅱ)知,2t =,∴)2,2P,∵抛物线21222y x x =-++的对称轴为2x =,∴设21,2,222G m m m H n ⎛⎫⎛⎫-++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭以,,,A G H P 四点构成的四边形为平行四边形,()A , ①当AP 和HG 为对角线时,∴()211111,20222222m m n ⎛⎛⎫=++=-+++ ⎪ ⎪⎝⎭⎝⎭,∴324m n =-=, ②当AG 和PH 是对角线时,∴(()211111,20222222m m n ⎛⎫=-++=+ ⎪ ⎪⎭⎝⎭,∴154m n ==-, ③AH 和PG 为对角线时,∴(()211111,22022222m m n ⎛⎛⎫=+-+++=+ ⎪ ⎪⎝⎭⎝⎭,∴14m n ==, 即:满足条件的点m n 、的值为:324m n =-=,或15,24m n ==-,或124m n =-= 【点睛】此题是二次函数综合题,主要考查了坐标轴上点的特点,三角形的面积公式,梯形的面积公式,平行四边形的性质,中点坐标公式,用方程的思想解决问题是解本题的关键.4.已知,抛物线y =﹣x 2+bx +c 经过点A (﹣1,0)和C (0,3). (1)求抛物线的解析式;(2)在抛物线的对称轴上,是否存在点P ,使PA +PC 的值最小?如果存在,请求出点P 的坐标,如果不存在,请说明理由;(3)设点M 在抛物线的对称轴上,当△MAC 是直角三角形时,求点M 的坐标.【答案】(1)223y x x =-++;(2)当PA PC +的值最小时,点P 的坐标为()1,2;(3)点M 的坐标为()1,1、()1,2、81,3⎛⎫ ⎪⎝⎭或21,3⎛⎫- ⎪⎝⎭. 【解析】 【分析】()1由点A 、C 的坐标,利用待定系数法即可求出抛物线的解析式;()2连接BC 交抛物线对称轴于点P ,此时PA PC +取最小值,利用二次函数图象上点的坐标特征可求出点B 的坐标,由点B 、C 的坐标利用待定系数法即可求出直线BC 的解析式,利用配方法可求出抛物线的对称轴,再利用一次函数图象上点的坐标特征即可求出点P 的坐标;()3设点M 的坐标为()1,m ,则22CM (10)(m 3)=-+-,()22AC [01](30)10=--+-=,()22AM [11](m 0)=--+-,分AMC 90∠=、ACM 90∠=和CAM 90∠=三种情况,利用勾股定理可得出关于m 的一元二次方程或一元一次方程,解之可得出m 的值,进而即可得出点M 的坐标. 【详解】解:()1将()1,0A -、()0,3C 代入2y x bx c =-++中,得:{103b c c --+==,解得:{23b c ==,∴抛物线的解析式为223y x x =-++.()2连接BC 交抛物线对称轴于点P ,此时PA PC +取最小值,如图1所示.当0y =时,有2230x x -++=, 解得:11x =-,23x =,∴点B 的坐标为()3,0.抛物线的解析式为2223(1)4y x x x =-++=--+,∴抛物线的对称轴为直线1x =.设直线BC 的解析式为()0y kx d k =+≠, 将()3,0B 、()0,3C 代入y kx d =+中, 得:{303k d d +==,解得:{13k d =-=,∴直线BC 的解析式为3y x =-+.当1x =时,32y x =-+=,∴当PA PC +的值最小时,点P 的坐标为()1,2.()3设点M 的坐标为()1,m ,则22(10)(3)CM m =-+-,()22[01](30)10AC =--+-=,()22[11](0)AM m =--+-.分三种情况考虑:①当90AMC ∠=时,有222AC AM CM =+,即22101(3)4m m =+-++,解得:11m =,22m =,∴点M 的坐标为()1,1或()1,2;②当90ACM ∠=时,有222AM AC CM =+,即224101(3)m m +=++-,解得:83m =, ∴点M 的坐标为81,3⎛⎫⎪⎝⎭;③当90CAM ∠=时,有222CM AM AC =+,即221(3)410m m +-=++,解得:23m =-, ∴点M 的坐标为21,.3⎛⎫- ⎪⎝⎭综上所述:当MAC 是直角三角形时,点M 的坐标为()1,1、()1,2、81,3⎛⎫ ⎪⎝⎭或21,.3⎛⎫- ⎪⎝⎭【点睛】本题考查待定系数法求二次(一次)函数解析式、二次(一次)函数图象的点的坐标特征、轴对称中的最短路径问题以及勾股定理,解题的关键是:()1由点的坐标,利用待定系数法求出抛物线解析式;()2由两点之间线段最短结合抛物线的对称性找出点P 的位置;()3分AMC 90∠=、ACM 90∠=和CAM 90∠=三种情况,列出关于m 的方程.5.已知抛物线2y ax bx c =++上有两点M (m +1,a )、N (m ,b ). (1)当a =-1,m =1时,求抛物线2y ax bx c =++的解析式; (2)用含a 、m 的代数式表示b 和c ;(3)当a <0时,抛物线2y ax bx c =++满足24b ac a -=,2b c a +≥,34m ≤-, 求a 的取值范围. 【答案】(1)11b c =⎧⎨=⎩;(2)b=-am ,c=-am ;(3)161393a -≤≤- 【解析】 【分析】(1)根据题意得到M (2,-1)、N (1,b ),代入抛物线解析式即可求出b 、c ;(2)将点M (m +1,a )、N (m ,b )代入抛物线2y ax bx c =++,可得22(1)(1)a m b m c aam bm c b⎧++++=⎨++=⎩,化简即可得出;(3)把b am =-,c am =-代入24b ac a -=可得214a m m=+,把b am =-,c am =-代入2b c a +≥可得1m ≥-,然后根据m 的取值范围可得a 的取值范围.【详解】解:(1)∵a =-1,m =1,∴M (2,-1)、N (1,b )由题意,得4211b c b c b -++=-⎧⎨-++=⎩,解,得11b c =⎧⎨=⎩(2) ∵点M (m +1,a )、N (m ,b )在抛物线2y ax bx c =++上22(1)(1)a m b m c a am bm c b ⎧++++=⎨++=⎩①②①-②得,2am b b +=-,∴b am =-把b am =-代入②,得c am =-(3)把b am =-,c am =-代入24b ac a -=得2224a m a m a +=0a <,22141,4am am a m m∴+=∴=+把b am =-,c am =-代入2b c a +≥得22am a -≥,1m ∴≥-34m ≤-,314m ∴-≤≤-224(2)4m m m +=+-,当2m >-时,24m m +随m 的增大而增大2393416m m ∴-≤+≤-216113943m m ∴-≤≤-+ 即161393a -≤≤- 【点睛】本题考查待定系数法求函数解析式以及二次函数的图像和性质,由函数图像上点的坐标特征求出b am =-,c am =-是解题关键.6.在平面直角坐标系xOy 中(如图).已知抛物线y=﹣12x 2+bx+c 经过点A (﹣1,0)和点B (0,52),顶点为C ,点D 在其对称轴上且位于点C 下方,将线段DC 绕点D 按顺时针方向旋转90°,点C 落在抛物线上的点P 处. (1)求这条抛物线的表达式; (2)求线段CD 的长;(3)将抛物线平移,使其顶点C 移到原点O 的位置,这时点P 落在点E 的位置,如果点M 在y 轴上,且以O 、D 、E 、M 为顶点的四边形面积为8,求点M 的坐标.【答案】(1)抛物线解析式为y=﹣12x 2+2x+52;(2)线段CD 的长为2;(3)M 点的坐标为(0,72)或(0,﹣72). 【解析】【分析】(1)利用待定系数法求抛物线解析式; (2)利用配方法得到y=﹣12(x ﹣2)2+92,则根据二次函数的性质得到C 点坐标和抛物线的对称轴为直线x=2,如图,设CD=t ,则D (2,92﹣t ),根据旋转性质得∠PDC=90°,DP=DC=t ,则P (2+t ,92﹣t ),然后把P (2+t ,92﹣t )代入y=﹣12x 2+2x+52得到关于t 的方程,从而解方程可得到CD 的长;(3)P 点坐标为(4,92),D 点坐标为(2,52),利用抛物线的平移规律确定E 点坐标为(2,﹣2),设M (0,m ),当m >0时,利用梯形面积公式得到12•(m+52+2)•2=8当m <0时,利用梯形面积公式得到12•(﹣m+52+2)•2=8,然后分别解方程求出m 即可得到对应的M 点坐标.【详解】(1)把A (﹣1,0)和点B (0,52)代入y=﹣12x 2+bx+c 得 10252b c c ⎧--+=⎪⎪⎨⎪=⎪⎩,解得252b c =⎧⎪⎨=⎪⎩,∴抛物线解析式为y=﹣12x 2+2x+52; (2)∵y=﹣12(x ﹣2)2+92, ∴C (2,92),抛物线的对称轴为直线x=2, 如图,设CD=t ,则D (2,92﹣t ),∵线段DC 绕点D 按顺时针方向旋转90°,点C 落在抛物线上的点P 处, ∴∠PDC=90°,DP=DC=t ,∴P (2+t ,92﹣t ), 把P (2+t ,92﹣t )代入y=﹣12x 2+2x+52得﹣12(2+t )2+2(2+t )+52=92﹣t ,整理得t 2﹣2t=0,解得t 1=0(舍去),t 2=2, ∴线段CD 的长为2;(3)P 点坐标为(4,92),D 点坐标为(2,52), ∵抛物线平移,使其顶点C (2,92)移到原点O 的位置,∴抛物线向左平移2个单位,向下平移92个单位,而P点(4,92)向左平移2个单位,向下平移92个单位得到点E,∴E点坐标为(2,﹣2),设M(0,m),当m>0时,12•(m+52+2)•2=8,解得m=72,此时M点坐标为(0,72);当m<0时,12•(﹣m+52+2)•2=8,解得m=﹣72,此时M点坐标为(0,﹣72);综上所述,M点的坐标为(0,72)或(0,﹣72).【点睛】本题考查了二次函数的综合题,涉及到待定系数法、抛物线上点的坐标、旋转的性质、抛物线的平移等知识,综合性较强,正确添加辅助线、运用数形结合思想熟练相关知识是解题的关键.7.课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长是多少mm?小颖解得此题的答案为48mm,小颖善于反思,她又提出了如下的问题.(1)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少mm?请你计算.(2)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.【答案】(1)2407mm,4807mm;(2)PN=60mm,40PQ mm.【解析】 【分析】(1)、设PQ=y (mm ),则PN=2y (mm ),AE=80-y (mm ),根据平行得出△APN 和△ABC 相似,根据线段的比值得出y 的值,然后得出边长;(2)、根据第一题同样的方法得出y 与x 的函数关系式,然后求出S 与x 的函数关系式,根据二次函数的性质得出最大值. 【详解】(1)、设PQ=y (mm ),则PN=2y (mm ),AE=80-y (mm ) ∵PN ∥BC, ∴=,△APN ∽△ABC∴= ∴=∴=解得 y=∴2y=∴这个矩形零件的两条边长分别为mm ,mm(2)、设PQ=x (mm ),PN=y (mm ),矩形面积为S ,则AE=80-x (mm ).. 由(1)知=∴=∴ y=则S=xy===∵∴ S 有最大值∴当x=40时,S 最大=2400(mm 2) 此时,y==60 .∴面积达到这个最大值时矩形零件的两边PQ 、PN 长分别是40 mm ,60 mm . 考点:三角形相似的应用8.如图,抛物线2y ax bx c =++的图象过点(10)(30)(03)A B C ﹣,、,、,.(1)求抛物线的解析式;(2)在抛物线的对称轴上是否存在一点P ,使得△PAC 的周长最小,若存在,请求出点P 的坐标及△PAC 的周长;若不存在,请说明理由;(3)在(2)的条件下,在x 轴上方的抛物线上是否存在点M (不与C 点重合),使得PAM PAC S S ∆∆=?若存在,请求出点M 的坐标;若不存在,请说明理由.【答案】(1)223y x x =++-;(2)存在,点(12)P ,1032;(3)存在,点M 坐标为(14), 【解析】 【分析】(1)由于条件给出抛物线与x 轴的交点1030A B (﹣,)、(,),故可设交点式13y a x x +=()(﹣),把点C 代入即求得a 的值,减小计算量.(2)由于点A 、B 关于对称轴:直线1x =对称,故有PA PB =,则PAC C AC PC PA AC PC PB ∆++++==,所以当C 、P 、B 在同一直线上时,PAC C AC CB ∆+=最小.利用点A 、B 、C 的坐标求AC 、CB 的长,求直线BC 解析式,把1x =代入即求得点P 纵坐标.(3)由PAM PAC S S ∆∆=可得,当两三角形以PA 为底时,高相等,即点C 和点M 到直线PA 距离相等.又因为M 在x 轴上方,故有//CM PA .由点A 、P 坐标求直线AP 解析式,即得到直线CM 解析式.把直线CM 解析式与抛物线解析式联立方程组即求得点M 坐标. 【详解】解:(1)∵抛物线与x 轴交于点1030A B (﹣,)、(,)∴可设交点式13y a x x +=()(﹣) 把点03C (,)代入得:33a ﹣=1a ∴=﹣21323y x x x x ∴+++=-()(﹣)=﹣∴抛物线解析式为223y x x ++=-(2)在抛物线的对称轴上存在一点P ,使得PAC ∆的周长最小. 如图1,连接PB 、BC∵点P 在抛物线对称轴直线1x =上,点A 、B 关于对称轴对称PA PB ∴=PAC C AC PC PA AC PC PB ∆∴++++==∵当C 、P 、B 在同一直线上时,PC PB CB +=最小103003A B C (﹣,)、(,)、(,)AC BC ∴===PAC C AC CB ∆∴+=设直线BC 解析式为3y kx +=把点B 代入得:330k +=,解得:1k =﹣ ∴直线BC :3y x +=﹣132P y ∴+=﹣=∴点12P (,)使PAC ∆. (3)存在满足条件的点M ,使得PAM PAC S S ∆∆=. ∵PAM PAC S S ∆∆=S △PAM =S △PAC ∴当以PA 为底时,两三角形等高 ∴点C 和点M 到直线PA 距离相等 ∵M 在x 轴上方//CM PA ∴1012A P (﹣,),(,),设直线AP 解析式为y px d += 02p d p d -+=⎧∴⎨+=⎩ 解得:p 1d 1=⎧⎨=⎩∴直线1AP y x +:=∴直线CM 解析式为:3y x +=2323y x y x x =+⎧⎨=-++⎩ 解得:1103x y =⎧⎨=⎩(即点C ),2214x y =⎧⎨=⎩∴点M 坐标为14(,)【点睛】考查了待定系数法求二次函数解析式、一次函数解析式,轴对称的最短路径问题,勾股定理,平行线间距离处处相等,一元二次方程的解法.其中第(3)题条件给出点M 在x 轴上方,无需分类讨论,解法较常规而简单.9.已知,m ,n 是一元二次方程x 2+4x +3=0的两个实数根,且|m |<|n |,抛物线y =x 2+bx +c 的图象经过点A (m ,0),B (0,n ),如图所示. (1)求这个抛物线的解析式;(2)设(1)中的抛物线与x 轴的另一个交点为抛物线的顶点为D ,求出点C ,D 的坐标,并判断△BCD 的形状;(3)点P 是直线BC 上的一个动点(点P 不与点B 和点C 重合),过点P 作x 轴的垂线,交抛物线于点M ,点Q 在直线BC 上,距离点P 为2个单位长度,设点P 的横坐标为t ,△PMQ 的面积为S ,求出S 与t 之间的函数关系式.【答案】(1)223y x x =--;(2)C (3,0),D (1,﹣4),△BCD 是直角三角形;(3)2213(03)2213(03)22t t t S t t t t ⎧-+⎪⎪=⎨⎪-⎪⎩<<<或>【解析】试题分析:(1)先解一元二次方程,然后用待定系数法求出抛物线解析式;(2)先解方程求出抛物线与x 轴的交点,再判断出△BOC 和△BED 都是等腰直角三角形,从而得到结论;(3)先求出QF=1,再分两种情况,当点P 在点M 上方和下方,分别计算即可. 试题解析:解(1)∵2+430x x +=,∴11x =-,23x =-,∵m ,n 是一元二次方程2+430x x +=的两个实数根,且|m|<|n|,∴m=﹣1,n=﹣3,∵抛物线223y x x =--的图象经过点A (m ,0),B (0,n ),∴10{3b c c -+==-,∴2{3b c =-=-,∴抛物线解析式为223y x x =--;(2)令y=0,则2230x x --=,∴11x =-,23x =,∴C (3,0),∵223y x x =--=2(1)4x --,∴顶点坐标D (1,﹣4),过点D 作DE ⊥y 轴,∵OB=OC=3,∴BE=DE=1,∴△BOC 和△BED 都是等腰直角三角形,∴∠OBC=∠DBE=45°,∴∠CBD=90°,∴△BCD 是直角三角形;(3)如图,∵B (0,﹣3),C (3,0),∴直线BC 解析式为y=x ﹣3,∵点P 的横坐标为t ,PM ⊥x 轴,∴点M 的横坐标为t ,∵点P 在直线BC 上,点M 在抛物线上,∴P (t ,t ﹣3),M (t ,223t t --),过点Q 作QF ⊥PM ,∴△PQF 是等腰直角三角形,∵PQ=2,∴QF=1.①当点P 在点M 上方时,即0<t <3时,PM=t ﹣3﹣(223t t --)=23t t -+,∴S=12PM×QF=21(3)2t t -+=21322t t -+,②如图3,当点P 在点M 下方时,即t <0或t>3时,PM=223t t --﹣(t ﹣3)=23t t -,∴S=12PM×QF=12(23t t -)=21322t t -.综上所述,S=2213(03)22{13 (03)22t t t t t t t 或-+<<-.考点:二次函数综合题;分类讨论.10.如图,抛物线y=﹣(x ﹣1)2+c 与x 轴交于A ,B (A ,B 分别在y 轴的左右两侧)两点,与y 轴的正半轴交于点C ,顶点为D ,已知A (﹣1,0).(1)求点B ,C 的坐标;(2)判断△CDB 的形状并说明理由;(3)将△COB 沿x 轴向右平移t 个单位长度(0<t <3)得到△QPE .△QPE 与△CDB 重叠部分(如图中阴影部分)面积为S ,求S 与t 的函数关系式,并写出自变量t 的取值范围. 【答案】(Ⅰ)B(3,0);C(0,3);(Ⅱ)CDB ∆为直角三角形;(Ⅲ)22333(0)221933(3)222t t t S t t t ⎧-+<≤⎪⎪=⎨⎪=-+<<⎪⎩.【解析】 【分析】(1)首先用待定系数法求出抛物线的解析式,然后进一步确定点B ,C 的坐标. (2)分别求出△CDB 三边的长度,利用勾股定理的逆定理判定△CDB 为直角三角形. (3)△COB 沿x 轴向右平移过程中,分两个阶段: ①当0<t≤32时,如答图2所示,此时重叠部分为一个四边形; ②当32<t <3时,如答图3所示,此时重叠部分为一个三角形. 【详解】解:(Ⅰ)∵点()1,0A -在抛物线()21y x c =--+上,∴()2011c =---+,得4c =∴抛物线解析式为:()214y x =--+,令0x =,得3y =,∴()0,3C ; 令0y =,得1x =-或3x =,∴()3,0B . (Ⅱ)CDB ∆为直角三角形.理由如下: 由抛物线解析式,得顶点D 的坐标为()1,4. 如答图1所示,过点D 作DM x ⊥轴于点M ,则1OM =,4DM =,2BM OB OM =-=.过点C 作CN DM ⊥于点N ,则1CN =,1DN DM MN DM OC =-=-=. 在Rt OBC ∆中,由勾股定理得:22223332BC OB OC =+=+=; 在Rt CND ∆中,由勾股定理得:2222112CD CN DN =+=+=; 在Rt BMD ∆中,由勾股定理得:22222425BD BM DM =+=+=.∵222BC CD BD +=, ∴CDB ∆为直角三角形.(Ⅲ)设直线BC 的解析式为y kx b =+, ∵()()3,0,0,3B C ,∴303k b b +=⎧⎨=⎩,解得1,3k b =-=,∴3y x =-+,直线QE 是直线BC 向右平移t 个单位得到,∴直线QE 的解析式为:()33y x t x t =--+=-++; 设直线BD 的解析式为y mx n =+, ∵()()3,0,1,4B D , ∴304m n m n +=⎧⎨+=⎩,解得:2,6m n =-=,∴26y x =-+.连续CQ 并延长,射线CQ 交BD 交于G ,则3,32G ⎛⎫ ⎪⎝⎭. 在COB ∆向右平移的过程中: (1)当302t <≤时,如答图2所示:设PQ 与BC 交于点K ,可得QK CQ t ==,3PB PK t ==-. 设QE 与BD 的交点为F ,则:263y x y x t=-+⎧⎨=-++⎩.解得32x ty t=-⎧⎨=⎩,∴()3,2F t t -.111222QPE PBK FBE F S S S S PE PQ PB PK BE y ∆∆∆=--=⋅-⋅-⋅ ()221113333232222t t t t t =⨯⨯---⋅=-+. (2)当332t <<时,如答图3所示:设PQ 分别与BC BD 、交于点K 、点J . ∵CQ t =,∴KQ t =,3PK PB t ==-.直线BD 解析式为26y x =-+,令x t =,得62y t =-, ∴(),62J t t -.1122PBJ PBK S S S PB PJ PB PK ∆∆=-=⋅-⋅ ()()()211362322t t t =---- 219322t t =-+. 综上所述,S 与t 的函数关系式为:2233302219333222t t t S t t t ⎧⎛⎫-+<≤ ⎪⎪⎪⎝⎭=⎨⎛⎫⎪=-+<< ⎪⎪⎝⎭⎩.11.已知,如图,抛物线2(0)y ax bx c a =++≠的顶点为(1,9)M ,经过抛物线上的两点(3,7)A --和(3,)B m 的直线交抛物线的对称轴于点C .(1)求抛物线的解析式和直线AB 的解析式.(2)在抛物线上,A M 两点之间的部分(不包含,A M 两点),是否存在点D ,使得2DAC DCM S S ∆∆=?若存在,求出点D 的坐标;若不存在,请说明理由.(3)若点P 在抛物线上,点Q 在x 轴上,当以点,,,A M P Q 为顶点的四边形是平行四边形时,直接写出满足条件的点P 的坐标.【答案】(1)抛物线的表达式为:228y x x =-++,直线AB 的表达式为:21y x =-;(2)存在,理由见解析;点P (6,16)-或(4,16)--或(17,2)+或(17,2).【解析】 【分析】(1)二次函数表达式为:y=a (x-1)2+9,即可求解; (2)S △DAC =2S △DCM ,则()()()()()21112821139112222DACC A SDH x x x x x x =-=-++-++=--⨯,,即可求解;(3)分AM 是平行四边形的一条边、AM 是平行四边形的对角线两种情况,分别求解即可. 【详解】解:(1)二次函数表达式为:()219y a x =-+, 将点A 的坐标代入上式并解得:1a =-, 故抛物线的表达式为:228y x x =-++…①, 则点()3,5B ,将点,A B 的坐标代入一次函数表达式并解得: 直线AB 的表达式为:21y x =-; (2)存在,理由:二次函数对称轴为:1x =,则点()1,1C , 过点D 作y 轴的平行线交AB 于点H ,设点()2,28D x x x -++,点(),21H x x -,∵2DAC DCM S S ∆∆=, 则()()()()()21112821139112222DACC A SDH x x x x x x =-=-++-++=--⨯, 解得:1x =-或5(舍去5), 故点()1,5D -;(3)设点(),0Q m 、点(),P s t ,228t s s =-++, ①当AM 是平行四边形的一条边时,点M 向左平移4个单位向下平移16个单位得到A ,同理,点(),0Q m 向左平移4个单位向下平移16个单位为()4,16m --,即为点P , 即:4m s -=,6t -=,而228t s s =-++, 解得:6s =或﹣4, 故点()6,16P -或()4,16--; ②当AM 是平行四边形的对角线时,由中点公式得:2m s +=-,2t =,而228t s s =-++,解得:17s =±,故点()17,2P +或()17,2-;综上,点()6,16P -或()4,16--或()17,2+或()17,2-. 【点睛】本题考查的是二次函数综合运用,涉及到一次函数、平行四边形性质、图形的面积计算等,其中(3),要注意分类求解,避免遗漏.12.如图①,抛物线2(1)y x a x a =-++-与x 轴交于A 、B 两点(点A 位于点B 的左侧),与y 轴交于点C ,已知ABC ∆的面积为6. (1)求a 的值;(2)求ABC ∆外接圆圆心的坐标;(3)如图②,P 是抛物线上一点,点Q 为射线CA 上一点,且P 、Q 两点均在第三象限内,Q 、A 是位于直线BP 同侧的不同两点,若点P 到x 轴的距离为d ,QPB ∆的面积为2d ,且PAQ AQB ∠=∠,求点Q 的坐标.【答案】(1)-3;(2)坐标(-1,1);(3)Q ()4,1-. 【解析】 【分析】(1)利用抛物线解析式得到A 、B 、C 三点坐标,然后利用三角形面积公式列出方程解出a ;(2)利用第一问得到A 、B 、C 三点坐标,求出AC 解析式,找到AC 垂直平分线的解析式,与AB 垂直平分线解析式联立,解出x 、y 即为圆心坐标;(3)过点P 做PD ⊥x 轴,PD =d ,发现△ABP 与△QBP 的面积相等,得到A 、D 两点到PB 得距离相等,可得AQ PB ∥,求出PB 解析式,与二次函数解析式联立得到P 点坐标,又易证ABQ QPA ∆∆≌,得到BQ =AP 26Q 点坐标,点与点的距离列出方程,解出Q 点坐标即可 【详解】(1)解:由题意得()()1y x x a =--- 由图知:0a <所以A (,0a ),()10B ,,()0,C a - ()()112ABC S a a ∆=-⋅-=634()a a =-=或舍∴3a =-(2)由(1)得A (-3,0),()10B ,,()0,3C ∴直线AC 得解析式为:3y xAC 中点坐标为33,22⎛⎫-⎪⎝⎭∴AC 的垂直平分线为:y x =-又∵AB 的垂直平分线为:1x =-∴1y x x =-⎧⎨=-⎩ 得11x y =-⎧⎨=⎩ABC ∆外接圆圆心的坐标(-1,1). (3)解:过点P 做PD ⊥x 轴 由题意得:PD =d ,∴12ABP S PD AB ∆=⋅=2d∵QPB ∆的面积为2d∴ABP BPQ S S ∆∆=,即A 、D 两点到PB 得距离相等 ∴AQ PB ∥设PB 直线解析式为;y x b =+过点(1,0)B ∴1y x =-∴2123y x y x x =-⎧⎨=--+⎩易得45x y =-⎧⎨=⎩ 1()0x y =⎧⎨=⎩舍 所以P (-4,-5),由题意及PAQ AQB ∠=∠ 易得:ABQ QPA ∆∆≌∴BQ=AP=26设Q(m,-1)(0m<)∴()221126m-+=4m=-∴Q()4,1-.【点睛】本题考查二次函数综合性问题,涉及到一次函数、三角形外接圆圆心、全等三角形等知识点,第一问关键在于用a表示出A、B、C三点坐标;第二问关键在于找到AC垂直平分线的解析式,与AB垂直平分线解析式;第三问关键在于能够求出PB的解析式13.如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P做x轴的垂线l交抛物线于点Q,交直线BD于点M.(1)求该抛物线所表示的二次函数的表达式;(2)已知点F(0,12),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?(3)点P在线段AB运动过程中,是否存在点Q,使得以点B、Q、M为顶点的三角形与△BOD相似?若存在,求出点Q的坐标;若不存在,请说明理由.【答案】(1)y=﹣12x2+32x+2;(2)m=﹣1或m=3时,四边形DMQF是平行四边形;(3)点Q的坐标为(3,2)或(﹣1,0)时,以点B、Q、M为顶点的三角形与△BOD相似.【解析】分析:(1)待定系数法求解可得;(2)先利用待定系数法求出直线BD解析式为y=12x-2,则Q(m,-12m2+32m+2)、M(m,12m-2),由QM∥DF且四边形DMQF是平行四边形知QM=DF,据此列出关于m的方程,解之可得;(3)易知∠ODB=∠QMB ,故分①∠DOB=∠MBQ=90°,利用△DOB ∽△MBQ 得12DO MB OB BQ ==,再证△MBQ ∽△BPQ 得BM BP BQ PQ=,即214 132222mm m -=-++,解之即可得此时m 的值;②∠BQM=90°,此时点Q 与点A 重合,△BOD ∽△BQM′,易得点Q 坐标.详解:(1)由抛物线过点A (-1,0)、B (4,0)可设解析式为y=a (x+1)(x-4), 将点C (0,2)代入,得:-4a=2, 解得:a=-12, 则抛物线解析式为y=-12(x+1)(x-4)=-12x 2+32x+2;(2)由题意知点D 坐标为(0,-2), 设直线BD 解析式为y=kx+b ,将B (4,0)、D (0,-2)代入,得:402k b b +⎧⎨-⎩==,解得:122k b ⎧⎪⎨⎪-⎩==, ∴直线BD 解析式为y=12x-2, ∵QM ⊥x 轴,P (m ,0),∴Q (m ,--12m 2+32m+2)、M (m ,12m-2),则QM=-12m 2+32m+2-(12m-2)=-12m 2+m+4,∵F (0,12)、D (0,-2), ∴DF=52, ∵QM ∥DF ,∴当-12m 2+m+4=52时,四边形DMQF 是平行四边形, 解得:m=-1(舍)或m=3,即m=3时,四边形DMQF 是平行四边形; (3)如图所示:∵QM∥DF,∴∠ODB=∠QMB,分以下两种情况:①当∠DOB=∠MBQ=90°时,△DOB∽△MBQ,则21=42 DO MBOB BQ==,∵∠MBQ=90°,∴∠MBP+∠PBQ=90°,∵∠MPB=∠BPQ=90°,∴∠MBP+∠BMP=90°,∴∠BMP=∠PBQ,∴△MBQ∽△BPQ,∴BM BPBQ PQ=,即214132222mm m-=-++,解得:m1=3、m2=4,当m=4时,点P、Q、M均与点B重合,不能构成三角形,舍去,∴m=3,点Q的坐标为(3,2);②当∠BQM=90°时,此时点Q与点A重合,△BOD∽△BQM′,此时m=-1,点Q的坐标为(-1,0);综上,点Q的坐标为(3,2)或(-1,0)时,以点B、Q、M为顶点的三角形与△BOD相似.点睛:本题主要考查二次函数的综合问题,解题的关键是掌握待定系数法求函数解析式、平行四边形的判定与性质、相似三角形的判定与性质及分类讨论思想的运用.14.如图,抛物线与x轴交于点A(,0)、点B(2,0),与y轴交于点C(0,1),连接BC.(1)求抛物线的函数关系式;(2)点N为抛物线上的一个动点,过点N作NP⊥x轴于点P,设点N的横坐标为t (),求△ABN的面积S与t的函数关系式;(3)若且时△OPN∽△COB,求点N的坐标.【答案】(1);(2);(3)(,)或(1,2).【解析】试题分析:(1)可设抛物线的解析式为,用待定系数法就可得到结论;(2)当时,点N在x轴的上方,则NP等于点N的纵坐标,只需求出AB,就可得到S与t的函数关系式;(3)由相似三角形的性质可得PN=2PO.而PO=,需分和0<t<2两种情况讨论,由PN=2PO得到关于t的方程,解这个方程,就可得到答案.试题解析:(1)设抛物线的解析式为,把C(0,1)代入可得:,∴,∴抛物线的函数关系式为:,即;(2)当时,>0,∴NP===,∴S=AB•PN==;(3)∵△OPN∽△COB,∴,∴,∴PN=2PO.①当时,PN===,PO==,∴,整理得:,解得:=,=,∵>0,<<0,∴t=,此时点N的坐标为(,);②当0<t<2时,PN===,PO==t,∴,整理得:,解得:=,=1.∵<0,0<1<2,∴t=1,此时点N的坐标为(1,2).综上所述:点N的坐标为(,)或(1,2).考点:1.二次函数综合题;2.待定系数法求二次函数解析式;3.相似三角形的性质.15.如图,在平面直角坐标系中,已知抛物线y=12x2+32x﹣2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,直线l经过A,C两点,连接BC.(1)求直线l的解析式;(2)若直线x=m(m<0)与该抛物线在第三象限内交于点E,与直线l交于点D,连接OD.当OD⊥AC时,求线段DE的长;(3)取点G(0,﹣1),连接AG,在第一象限内的抛物线上,是否存在点P,使∠BAP=∠BCO﹣∠BAG?若存在,求出点P的坐标;若不存在,请说明理由.【答案】(1)y=122x--;(2)DE=3225;(3)存在点P(139,9881),使∠BAP=∠BCO﹣∠BAG,理由见解析.【解析】【分析】(1)根据题目中的函数解析式可以求得点A和点C的坐标,从而可以求得直线l的函数解析式;(2)根据题意作出合适的辅助线,利用三角形相似和勾股定理可以解答本题;(3)根据题意画出相应的图形,然后根据锐角三角函数可以求得∠OAC=∠OCB ,然后根据题目中的条件和图形,利用锐角三角函数和勾股定理即可解答本题.【详解】(1)∵抛物线y=12x 2+32x-2, ∴当y=0时,得x 1=1,x 2=-4,当x=0时,y=-2,∵抛物线y=12x 2+32x-2与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C , ∴点A 的坐标为(-4,0),点B (1,0),点C (0,-2), ∵直线l 经过A ,C 两点,设直线l 的函数解析式为y=kx+b , 402k b b -+⎧⎨-⎩==,得122k b ⎧-⎪⎨⎪-⎩==, 即直线l 的函数解析式为y=−12x−2; (2)直线ED 与x 轴交于点F ,如图1所示,由(1)可得,AO=4,OC=2,∠AOC=90°,∴5∴4525=, ∵OD ⊥AC ,OA ⊥OC ,∠OAD=∠CAO ,∴△AOD ∽△ACO ,∴AD AO AO AC =, 即425AD =,得AD=855, ∵EF ⊥x 轴,∠ADC=90°,∴EF ∥OC ,∴△ADF ∽△ACO ,∴AF DF AD AO OC AC ==, 解得,AF=165,DF=85, ∴OF=4-165=45, ∴m=-45, 当m=-45时,y=12×(−45)2+32×(-45)-2=-7225, ∴EF=7225, ∴DE=EF-FD=7225−85=3225; (3)存在点P ,使∠BAP=∠BCO-∠BAG ,理由:作GM ⊥AC 于点M ,作PN ⊥x 轴于点N ,如图2所示,∵点A (-4,0),点B (1,0),点C (0,-2),∴OA=4,OB=1,OC=2,∴tan ∠OAC=2142OC OA ==,tan ∠OCB=12OB OC =,5, ∴∠OAC=∠OCB ,∵∠BAP=∠BCO-∠BAG ,∠GAM=∠OAC-∠BAG ,∴∠BAP=∠GAM , ∵点G (0,-1),5OA=4,∴OG=1,GC=1,∴17,••22AC GM CG OA =,即51422GM ⨯=, 解得,25, ∴22AG GM -222595(17)()55-=,∴tan∠GAM=29GMAM=,∴tan∠PAN=29,设点P的坐标为(n,12n2+32n-2),∴AN=4+n,PN=12n2+32n-2,∴21322 2249n nn+-+=,解得,n1=139,n2=-4(舍去),当n=139时,12n2+32n-2=9881,∴点P的坐标为(139,9881),即存在点P(139,9881),使∠BAP=∠BCO-∠BAG.【点睛】本题是一道二次函数综合题,解答本题的关键是明确题意,作出合适的辅助线,找出所求问题需要的条件,利用三角形相似、锐角三角函数和二次函数的性质解答.。

二次函数的最值与图像过定点问题对于二次函数:y=-x 2+4x-1/2(1)当x 取任意实数时,该函数有最 值,最 值是(2)当-1≤x≤1时,该函数的最大值是 ;最小值是(3)当3≤x≤4时,该函数的最大值是 ;最小值是(4)当0≤x≤3时,该函数的最大值是 ;最小值是求二次函数最值的一般方法: 1画出函数图像找对称轴; 2分清自变量范围找区间; 3数形结合找对应函数值例1、对于二次函数y=-x 2+2bx-0.5(1)若b<-1,当-1≤x≤1时,求该函数的最大或最小值(用含b 的式子表示)。
(2)若0﹤b ﹤1时,当-1≤x≤1,求该函数的最大或最小值。
1.如图,抛物线22y x x p =--与直线x y =交于点A(-1,m)、B(4,n),点M 是抛物线上的一个动点,连接OM(1)求m,n,p 。
(2)当M 为抛物线的顶点时,求M 坐标和⊿OMB 的面积;(3)当点M 在直线AB 的下方抛物线上,M 运动到何处时,⊿AMB 的面积最大。
2.抛物线y=ax 2和直线y=kx+b(k 为正常数)交于点A 和点B,其中点A 的坐标是(-2,1),过点A 作x 轴的平行线交抛物线于点E,点D 是抛物线上B,E 之间的一个动点,设其横坐标为t,经过点D 作两坐标轴的平行线分别交直线AB 于点C,M,设CD=r,MD=m.(1)根据题意可求出a= ,点E 的坐标是 ;(2)当点D 可与B,E 重合时,若k=0.5,求t 的取值范围,并确定t 为何值时,r 的值最大;(3)当点D 不与B,E 重合时,若点D 运动过程中可以得到r 的最大值,求k 的取值范围,并判断当r 为最大值时m 的值是否最大,说明理由(下图供分析参考用).yxCME AO BD24.(12分) 如图1,平面之间坐标系中,等腰直角三角形的直角边BC 在x 轴正半轴上滑动,点C 的坐标为(t ,0),直角边AC=4,经过O ,C 两点做抛物线y 1=ax(x ﹣t)(a 为常数,a >0),该抛物线与斜边AB 交于点E ,直线OA :y 2=kx(k 为常数,k >0)(1)填空:用含t 的代数式表示点A 的坐标及k 的值:A_________,k=_________;(2)随着三角板的滑动,当a=14时:①请你验证:抛物线y 1=ax(x ﹣t)的顶点在函数y=﹣14x 2的图象上;②当三角板滑至点E 为AB 的中点时,求t 的值;(3)直线OA 与抛物线的另一个交点为点D ,当t≤x≤t+4,|y 2﹣y 1|的值随x 的增大而减小,当x≥t+4时,|y 2﹣y 1|的值随x 的增大而增大,求a 与t 的关系式及t 的取值范围.抛物线过定点的问题集锦解法步骤第一步:对含有变系数的项集中第二步:然后将这部分项分解因式,使其成为一个只含系数和常数的因式与一个只含x 和常数的因式之积的形式 第三步:令后一因式等于0,得到一个关于自变量x 的方程(这时系数如何变化,都“失效”了)第四步:解此方程,得到x 的值x0(定点的横坐标),将它代入原函数式(也可以是其变式),即得到一个y 的值y0(定点的纵坐标),于是,函数图象一定过定点(x0,y0); 第五步:反思回顾,查看关键点、易错点,完善解题步骤1.某二次函数y =ax 2-(a +c)x +c 必过定点__________2.无论m 为任何实数,二次函数y =x 2+(2-m)x +m 的图像总过的点是( )A. (1,3)B. (1,0)C. (-1,3)D. (-1,0)3.不论a 取何值,抛物线y =-12x 2+5-a 2x +2a -2 经过x 轴上一定点Q ,则点Q 坐标为 4.抛物线y =ax 2+ax -2过直线y =mx -2m +2上的定点A ,求抛物线的解析式。

中考专题:二次函数一题多问【类型1】求解析式与顶点 (2)【类型2】线段相关 (2)【题型1】垂线段 (2)【题型2】斜线段 (3)【题型3】中点问题 (4)【题型4】定值问题 (4)【题型5】最值问题 (5)【题型6】条件求值问题 (6)【题型7】最短路径 (6)【类型3】面积相关 (8)【题型5】角度问题 (10)【题型6】45°角 (14)【题型7】等腰直角三角形存在性问题 (15)【题型8】直角三角形存在性问题 (17)【题型9】等腰三角形存在性问题 (19)【题型10】等边三角形存在性问题 (21)【题型11】平行四边形存在性问题 (22)【题型12】正方形存在性问题 (23)【题型13】菱形存在性问题 (24)【题型14】梯形存在性问题 (25)【题型15】相似存在性问题 (25)【题型16】全等存在性问题 (27)【题型17】平移问题 (27)【题型18】折叠问题 (28)【题型19】旋转问题 (29)【题型20】与圆结合 (30)【题型21】定值问题 (31)二次函数一题多问【例题】如图,在平面直角坐标系中,OB=OC=3,OA=1,抛物线C:c bx ax y ++=2(0≠a )过点A 、B 、C.【类型1】求解析式与顶点1.求抛物线C 的表达式和顶点D 的坐标;【类型2】线段相关【题型1】垂线段2.点P 为抛物线上一点,过点P 做直线PF⊥x 轴于点F ,交直线BC 于点E ,若5=EFPF,求点P 的横坐标;3.直线l :121+-=x y 与y 轴交于点N ,点P 是x 轴上方抛物线上一点,过点P 作直线PF⊥x 轴于点F ,交直线l 于点E ,设点P 横坐标为m ,当PE=5EF 时,求m 的值;【题型2】斜线段4.若点P是直线BC上方抛物线上一点,连接PO交线段BC于点E,求PE:EO的最大值;5.若点P是直线BC上方抛物线上一点,连接PA交线段BC于点E,求PE:EA的最大值;6.设抛物线对称轴与x轴交于点F,点M(m,n)是抛物线上的一个动点,连接MF,把MF2表示成自变量n的函数,并求出MF2取得最小值时点M的坐标.7.E是线段AC上的一点,EF⊥x轴交BC于点F,FG⊥X轴,求线段EG的最小值.8.将直线CD 向下平移,交x 、y 轴分别于S 、T ,交抛物线于点P ,若34=PT PS 时,求P 点坐标.9.已知直线L 为434+=x y ,P 为抛物线上一点,则点P 到直线L 的距离的最小值为多少?【题型3】中点问题10.点E (0,1),P 为BC 上方抛物线上一动点,连接PE 交BC 于点G ,若点G 恰好平分PE ,求点P 坐标.【题型4】定值问题11.过抛物线顶点D 作直线DE⊥y 轴,交x 轴于点E ,点P 是抛物线上B 、D 两点间的一个动点(点P 不与B 、D 两点重合),PA 、PB 与直线DE 分别交于点F 、G ,当点P 运动时,EF +EG 是否为定值?若是,试求出该定值;若不是,请说明理由.12.过点M (-3,0)做直线交抛物线于G 、H 两点,过G 、H 两点分别作x 轴的垂线,垂足分别为E 、F ,求证:ME×MF 为定值.【题型5】最值问题13.点M (m ,0)为线段AB 上一点(不与点A 、B 重合),过点M 作x 轴的垂线,与直线BC 交于点E ,与抛物线交于点P ,过点P 作PQ⊥AB 交抛物线于点Q ,过点Q 作QN⊥x 轴于点N ,可得矩形PQNM .如图,点P 在点Q 左边.⊥试用含m 的式子表示矩形PQNM 的周长;当矩形PQNM 的周长最大时,m 的值是多少?并求出此时的⊥AEM 的面积;⊥在⊥的条件下,当矩形PMNQ 的周长最大时,连接DQ ,过抛物线上一点F 作y 轴的平行线,与直线BC 交于点G(点G 在点F 的上方).若FG =22DQ ,求点F 的坐标.14.在直线BC 上方的抛物线上有一点E ,作EF⊥x 轴,与抛物线交于点F ,作EN⊥x 轴于N ,作FM⊥x 轴于M ,长度为22的线段PQ 在直线AC 上运动(点P 在点Q 左侧),当四边形ENMF 的周长取最大值求四边形DPQE 的周长的最小值及对应的点Q 的坐标;15.将直线BC 向上平移t 个单位,得到直线与抛物线交于P 、Q 两点,过P 、Q 分别作y 轴的平行线交BC 于点E 、F ,则 PQFE 周长的最大值为多少,求出此时直线PQ.16.若在第一象限的抛物线下方有一动点M ,满足MB=OB ,过M 作MG⊥X 轴于点G ,设⊥MBG 的内心为I ,试求CI 的最小值.【题型6】条件求值问题17.若直线l :n mx y +=与抛物线有两个交点M ,N (M 在N 的左边),P 为抛物线上一动点(不与M ,N 重合).过P 作PH 平行于y 轴交直线l 于点H ,若5=⋅HPHNHM ,求m 的值.18.M (m ,0)为线段OB 上一个动点(与点B ,O 不重合),过点M 作x 轴的垂线与线段BC 交于点Q ,与抛物线交于点P ,连接AQ ,与y 轴交于点F ,连接CP ,当线段QF =CP 时,求m 的值.【题型7】最短路径19.(1)若E 为C 点关于对称轴的对称点,在对称轴上是否存在点Q 使得QB+QE 的值最小,若存在,求出最小值,并求出点此时点Q的坐标;(2)设点M(3,m),求使MC+MD最小时m的值;MB 的值最大,若存在,求出最大值,并求出点此时点M的坐标;20.在对称轴上是否存在点M,使得MC21.若E为C点关于对称轴的对称点,点M在x轴上,点N在y轴上,若四边形DEMN的周长最小为多少,此时M,N的坐标分别为多少;22.点M为线段OC上任一点(不与O、C重合),求MA+MC的最小值及此时M点的坐标.23.将BO绕点B旋转至BO1使得O1在⊥OBC内,E、F分别为x轴和线段BC上的任意一点,则⊥O1EF的周长最小值为多少?24.在直线AD上,是否存在一点M,使BM+CM最小,若存在,求出M点坐标;若不存在,请说明理由.【类型3】面积相关25.(1)若⊥PAB与四边形ABDC的面积相等,求点P的坐标;(2)若以点P和B、C以及另一点Q为顶点的平行四边形BCQP的面积为3,求P两点的坐标;(3)抛物线上是否存在异于点D的一点P,使⊥PBC与⊥DCB的面积相等,若存在,求出点P的坐标;若不存在,说明理由.26.若点P为直线BC上方的点,求⊥PCB面积的最大值(或四边形PCOB、四边形PCAB);27.已知点E(2,3),若点P为直线AE上方的点,求⊥PAE面积的最大值(或四边形PEOA);28.设抛物线对称轴与x轴交于点F,连接CF,点P为第一象限的点,求⊥PCF面积的最大值;29.P为抛物线第一象限部分上的一动点,连接PA分别交BC,y轴于点E、F,若⊥PEB,⊥CEF的面积分别用S1、S2表示,求S1—S2的最大值,请求出此时P点坐标.30.连接BD,若点M是线段OC上的一动点,过点M作线段BD的垂线,分别与线段BD、抛物线相交于点E、F (点E、F都在抛物线对称轴的右侧),当EF最大时,求⊥MOF的面积.31.⊥如图1,连接OD,作CE⊥OD交BD的延长线于点E,连接OE交CD于点F,M是BE的中点,则OM是否将四边形OBDC 分成面积相等的两部分?请说明理由,⊥如图2,P (m ,n )是抛物线在第四象限的图象上的点,且1-=+n m ,连接PA .PD ,在线段PA 上确定一点N ,使DN 平分四边形APDC 的面积,求点N 的坐标.图1 图232.抛物线上一点P ,连接PC 交线段BD 于点Q,满足CDQ BPQ s s △△=,请求出P 点坐标.33.当点P 从C 点出发沿线段CB 上方的抛物线向终点B 移动,在移动中,点P 的横坐标以每秒1个单位长度的速度变动;与此同时点M 以每秒1个单位长度的速度沿CO 向终点O 移动,点P ,M 移动到各自终点时停止,当两个动点移动t 秒时,求四边形PCMB 的面积S 关于t 的函数表达式,并求t 为何值时,S 有最大值,最大值是多少?【题型5】角度问题34.(角度相等)求⊥CBD 和⊥ACO 的正切值;⊥ACB 与⊥ABD 是否相等?请证明你的结论;35.已知点E(2,3),且⊥PCE=⊥ACO,求点P的坐标;36.若E为C点关于对称轴的对称点,过点E作X轴的垂线垂足为F,H为OC中点,M为BE上一动点,满足⊥HMF=⊥ABE,求点M的坐标.37.(二倍角)若P在直线BC上方,过点P作PF⊥线段BC于点F,若⊥PCF中有1个锐角等于⊥ACO的2倍,求点P的坐标;38.若M时直线BC上一点,当直线DM与直线BC的夹角为⊥CBD的2倍时,求点M的坐标;39.(角平分线)P 为抛物线对称轴上的一点,若PD 恰好为⊥PBC 的角平分线,求点P 的坐标.40.点M 为直线x y -=上一点,若MO 恰好为⊥MAB 的角平分线,求点M 的坐标.41.若E 为C 点关于对称轴的对称点,连接AC 、AE ,抛物线上有一点P ,点C 关于直线AE 的对应点C '落在直线AP 上,求P 点坐标.42.将直线BC 绕点B 逆时针旋转与线段AC 交于点E (不包括端点A 、C ),过点E 作EF⊥x 轴,垂足为F ,过点E 作EG⊥BC ,垂足为G ,H 为BE 中点,连接FH 、HG ,在直线BC 旋转过程中⊥FHG 是否发生变化,并说明理由.43.在BC上方的抛物线上是否存在一点P使得⊥ACP+⊥ABC=180°,若存在请求出点P的坐标,若不存在请说明理由.44.当点P移动到抛物线的什么位置时,使得⊥PAB=75°,求出此时点P的坐标;45.点P为抛物线第一象限上的点,过点A作CP的平行线交y轴上一点F,连接BF,在AF的延长线上取点E,连接PE,若PE=BF,⊥BFE+⊥AEP=180°,求点P的坐标.46.在抛物线上是否存在点P,使得∠CPO=∠BPO?若存在,请求出点P的坐标,若不存在,请说明理由.【题型6】45°角47.(45°角)若⊥PBD=45°,求点P 的坐标;48.点M 为抛物线于对称轴的交点,连接CM ,若⊥PMC=45°求点P 的坐标;49.点E 为横坐标为21的抛物线上的点,若⊥PBE=45°,求点P 的坐标;50.(角度之和)连接BC ,且满足⊥ACO+⊥PCB=45°,求点P 的坐标;51.点M在y轴上,满足⊥ACO+⊥AMO=45°,求点M的坐标.【题型7】等腰直角三角形存在性问题52..点P为对称轴右侧抛物线上一点,以BP为斜边作等腰直角三角形,直角顶点M落在对称轴上,求P点的坐标53.直线L平行于X轴交抛物线于E、F两点,点P为X轴上的任一点,若⊥PEF为等腰直角三角形,求P点坐标.54.已知点M(0,1),点N为直线BM上任一点,点P为抛物线上的任一点,若⊥BPN为等腰直角三角形,则求P点坐标.55.设点P从点A出发,以每秒1个单位长度的速度沿x轴向右运动,运动时间为t s,点M为射线AC上一动点,过点M作MN⊥x轴交抛物线对称轴右侧部分于点N.试探究点P在运动过程中,是否存在以P,M,N为顶点的三角形为等腰直角三角形?若存在,求出t的值;若不存在,请说明理由.56.若D为抛物线的顶点,点Q在直线BC上,点N在直线BD上,Q、D、N三点构成以DN为底边的等腰直角三角形,求点N的坐标.57.点F为直线BC上的动点,在抛物线上是否存在点P,使得⊥BFP为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.58.若E为C点关于对称轴的对称点,连接AE交y轴于点F,直线AE上方的抛物线上有动点P,在直线AE上是否存在一点H,使⊥PDH为等腰直角三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.59.若E为C点关于对称轴的对称点,在线段PQ最长的条件下,点M在直线PQ上运动,点N在x轴上运动,当以点E、M、N为顶点的三角形为等腰直角三角形时,请求出此时点N的坐标.60.点M为抛物线对称轴上的点,问:在抛物线上是否存在点P,使⊥MPO是以⊥MPO为直角的为等腰直角三角形?若存在,请直接写出点N的坐标;若不存在,请说明理由.【题型8】直角三角形存在性问题61.(1动点)连接BC,若⊥PBC为直角三角形,求点P的坐标;62.(2动点)连接BC,过点P作PM⊥x轴交直线BC于点M,若⊥CPM为直角三角形,则P点坐标;63.过点B作BC的垂线交y轴于点M,平移直线AM交抛物线于点E、F两点,连结EO、FO.若⊥EFO为以EF 为斜边的直角三角形,求平移后的直线的解析式.64.能否在抛物线上找到一点Q,使⊥BDQ为直角三角形?如能,求出Q点的坐标,若不能,请说明理由.65.若R为抛物线对称轴上一点(R在D点下方),过R的直线与抛物线交于E、F两点,若⊥DEF的外心在直线EF上则求出R点坐标.66.对称轴与抛物线相交于点D,与x轴相交于点F.点Q是线段MN上的一动点,过点Q作QE⊥CQ交x轴于点E.(1)当点E与点O(原点)重合时,求点Q的坐标.(2)点Q从D运动到F的过程中,求动点E的运动的路径长.67.抛物线顶点为D,ED⊥x轴于E点,N是线段DE上一动点,M(m,0)是x轴上一动点,若⊥MNC=90°,直接写出实数m的取值范围.68.若E为C点关于对称轴的对称点,点M是线段AB上的动点(点M不与点A、B重合),过点M作PM⊥x轴交该抛物线于点P,连接AP、EP,当⊥AEP是直角三角形时,求出所有满足条件的点P的坐标.【题型9】等腰三角形存在性问题69.(1动点)连接BD,若点Q为x轴上的动点,且⊥QBD为等腰三角形,求点Q的坐标;70.以点B为直角顶点,BC为直角边作RT⊥BCE,CE交抛物线于点P,若PC=PE,求P的坐标.71.点P在BC上方的抛物线上一点,过点P做PM⊥x轴于点M,交BC于点F,过点P做PN⊥AC交x轴于点N,交BC于点E.⊥若A、C、F构成的三角形为等腰三角形,则求P点坐标;⊥求出EF的最大值,此时P点坐标.72.若P为抛物线第一象限上任意一点,PH⊥x轴于点H,与BC交于点M,连接PC.当⊥PCM是以PM为一腰的等腰三角形时,求点P的坐标.73.(2动点)对称轴交x轴于点F,点E(3,4),在如图所示的矩形DFBE中,动点M从点D出发,沿线段DF 向终点F运动,同时点G从点B出发,沿线段BE向终点E运动,速度均为每秒1个单位长度,运动时间为t秒.过点M作QM⊥DF交DB于点Q.连接QG.在点M、G运动的过程中,判断有几个时刻使得⊥BQG是等腰三角形?请求出相应的t值.74.连接BC,过点P作PM⊥x轴交直线BC于点M,沿PM折叠⊥CPM得到四边形CPC′M为菱形,则P点坐标;75点E 从C 出发,沿线段CO 以1个单位/秒的速度向终点O 运动,过点E 作OC 的垂线交BC 于点F ,作FP⊥OC ,交抛物线于点P ,连接CP 、EP ,当⊥CEP 为等腰三角形时求出所有t 的值.76.直线kx y =(0<k )交直线3-=x y 于点M ,交抛物线于点P ,过点P 作x 轴的垂线,垂足为H ,交直线3-=x y 于点N ,则⊥MPN 能否为等腰三角形若能求出k 值,若不能请说明理由.【题型10】等边三角形存在性问题77.设P 是抛物线上位于对称轴右侧的一点,点Q 在抛物线的对称轴上,当⊥BPQ 为等边三角形时,求直线AP 的函数表达式.78.已知F (1,415)和直线l :417 y ,点P 为抛物线上任意一点,过点P 做PM⊥l 于点M ,是否存在这样的P 点使得⊥PFM 为等边三角形,若存在,求出点P 的坐标;若不存在,请说明理由.【题型11】平行四边形存在性问题79.(1)若点E 在x 轴上,当P 、C 、E 、B 四点构成平行四边形时,求点P 的坐标;(2)若点E 在抛物线对称轴上,当P 、C 、E 、B 四点构成平行四边形时,求点P 的坐标;80.若点E 在x 轴上,当C 、D 、P 、E 四点构成平行四边形时,求点P 的坐标;81.已知点E (2,3),过点E 作直线BC 的垂线垂足为F ,PQ⊥BC 于点Q ,若P 、Q 、E 、F 四点构成平行四边形,求点P 的坐标;82.已知点E (2,3),若抛物线的对称轴与直线AE 相交于点F ,M 为直线AE 上的任意一点,过点M 作MN//FD 交抛物线于点N ,以F ,D ,M ,N 为顶点的四边形能否为平行四边形?若能,求点M 的坐标;若不能,请说明理由;【题型12】正方形存在性问题83.(正方形)若M ,N 为抛物线上两个动点,分别过点M ,N 作直线BC 的垂线段,垂足分别为D ,E ,是否存在点M ,N 使四边形MNED 为正方形?如果存在,求正方形MNED 的边长;如果不存在,请说明理由.84.(正方形存在性)连接PB ,以PB 为向下边作正方形PBEF ,随着点P 的运动,正方形的大小,位置也随之改变.当顶点E 或F 恰好落在y 轴上,请求出点P 的坐标.85.(等腰直角三角形存在性)若P 在x 轴上方,连接PB 点F 为直线3-=x 上一点,当⊥FPB 为以点P 为直角顶点的等腰直角三角形时,请求出点P 的坐标.86.(等腰直角三角形存在性)若P 为抛物线上一点,连接PB 点F 为直线3-=x 上一点,当⊥FPB 为以点P 为直角顶点的等腰直角三角形时,请求出点P 的坐标.87.点P 是直线BC 上方的抛物线上一动点(不与C 、B 重合),连接BP ,以BP 为边作图示一侧的正方形BPMN,当它恰好有一个顶点落在抛物线对称轴上时,求出对应的P 点的坐标.【题型13】菱形存在性问题88.(菱形)M 为y 轴上一点,P 为抛物线上一点,过点P 作PN//y 轴交BC 于点N ,沿PC 折叠⊥PCN 使得N′落在y 轴上,则P 点坐标。

专题探究二次函数与定点问题方法技巧:运用韦达定理,通过设参数、消参数等手法求出定点坐标。
一、无论参数怎么变化图象都过一个定点例1.求证上:无论a(a≠0)取何值,二次函数y=ax2-2x+a-4都经过一个定点P,并求P的坐标。
例2.已知抛物线C:y=ax2+bx-4a-2b与抛物线l:y=4ax2-2bx+c的一个交点在y轴上,求抛物线l所经过的定点坐标。
二、符合几何条件的定点例3.已知抛物线y=12x2与直线y=mx+n交于点A、B,交y轴于点C,是否存在定点C,使得OA⊥OB,若存在,求C点坐标,若不存在,说明理由。
三、对称点与定点例4.过为P(1,-2)的任一直线交抛物线y=12x2-x于A、B两点,点B与点C关于对称轴对称,连AC,求证直线AC必经过一定点,并求这个定点煌坐标。
练习:1.如图,抛物线C1:y=ax2+bx+c(a≠0)过y轴上一点(0,4),C1与直线y=kx交于点E、F,P为y轴上一定点,过P的直线y=bx+n与直线y=kx交于点Q,若1OE+1OF=2OQ,求定点P的坐标。
2.如图,抛物线的顶点为(2,0),且经过点(4,1),直线y=14x与抛物线交于A、B两点。
(1)求抛物线的解析式;(2)点F为平面内一定点,M为抛物线上一动点,且点M到直线y=-1的距离与到点F的距离始终相等,求定点的坐标。
3.如图,抛物线y=12(x-1)2上任意一点P(xo,m),过点P作直线y=(x o-1)x+b与直线x=1交于点A,对于点F(1,n),恒有PF=FA,求点F的坐标。

2022年中考二次函数各省市中考真题(部分)1.(福建第10题)一支二次函数y=x 2+2x-n 与x 轴交于点A 、B 两点,抛物线y=x 2-2x-n 与x 轴交于C 、D 两点,其中n>0,若AD=2BC,则n的值为_____。
2.(杭州市第9题)已知二次函数y=x 2+ax+b (a ,b 为常数),命题①:该函数图像经过点(1,0):命题②:该函数的图像经过(3,0);命题③:该函数的图像与x 轴的焦点位于y 轴的两侧;命题④:该函数的图像的对称轴为直线x=1.如果这四个命题只有一个命题是假命题,则这个假命题是()A.命题①B.命题②C.命题③D.命题④3.(宁波市第9题)点A (m-1,y1),B (m ,y2)都在二次函数y=(x-1)2+n 的图像上。
若y1<y2,则m 的取值范围为()A. M>2B.m>23C.m<1D. 23<m<24.(温州市第9题)已知点A (a ,2),B (b ,2),C (c ,7)都在抛物线y=(x-1)2 -2上,点A 在点B 的左侧,下列选项正确的是()A.若c<0,则a<c<bB.若c<0,则a<b<cC.若c>0, 则a<c<bD.若c>0,则a<b<c5.(无锡市17题)把二次函数y=x2+4x+m 的图像向上平移1个单位长度,再向右平移3个单位长度,如果平移后所得抛物线与坐标轴有且只有一个交点,那么m 应满足条件:____。
6.(徐州市第8题)若函数y=x2-2x+b 的图像与坐标轴有三个交点,则b 的取值范围是()A.b<1且b ≠0B.b>1C.0<b<1D.b<16.(武汉市第15题)已知抛物线y=ax 2+bx+c (a ,b ,c 是常数)开口向下,过点A (-1,0),B (m ,0)两点,且1<m<2。

中考数学专题复习:二次函数与定点1.无论m为任何实数,二次函数y=x2+(2﹣m)x+m的图象总过的点是()A.(1,3)B.(1,0)C.(﹣1,3)D.(﹣1,0)2.抛物线y=(3一k)x2+(k﹣2)x+2k﹣1(k≠3)过定点,并求出定点的坐标.3.对于关于x的二次函数y=ax2﹣(2a﹣1)x﹣1(a≠0),下列说法正确的有()①无论a取何值,此二次函数图象与x轴必有两个交点;②无论a取何值,图象必过两定点,且两定点之间的距离为2;③当a>0时,函数在x<1时,y随x的增大而减小;④当a<0时,函数图象截x轴所得的线段长度必大于2.A.1个B.2个C.3个D.4个4.二次函数y=x2+bx+c满足b﹣c=2,则这个函数的图象一定经过某一个定点,这个定点是__________.5.已知二次函数y=ax2﹣(a+1)x﹣4(a为常数)(1)已知二次函数y=ax2﹣(a+1)x﹣4的图象的顶点在y轴上,求a的值;(2)经探究发现无论a取何值,二次函数的图象一定经过平面直角坐标系内的两个定点.请求出这两个定点的坐标。
6.无论m为任何实数,总在抛物线y=x2+mx+2m上的点的坐标是__________.7.对于二次函数y=x2﹣3x+2和一次函数y=﹣2x+4,把函数y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)(t为常数)称为这两个函数的“衍生二次函数”.已知不论t取何常数,这个函数永远经过某些定点,则这个函数必经过的定点坐标为__________.8.已知抛物线y=mx2+(1﹣2m)x+1﹣3m与x轴相交于不同的两点A、B。
(1)求m的取值范围;(2)证明该抛物线一定经过非坐标轴上的一点P,并求出点P的坐标;(3)当14<m≤8时,由(2)求出的点P和点A,B构成的△ABP的面积是否有最值?若有,求出该最值及相对应的m值.9.如图,直线y=kx+2k﹣1与抛物线y=kx2﹣2kx﹣4(k>0)相交于A,B两点,抛物线的顶点为P.(1)抛物线的对称轴为__________,顶点坐标为__________(用含k的代数式表示).(2)无论k取何值,抛物线总经过定点,这样的定点有几个?试写出所有定点的坐标,是否存在这样一个定点C,使直线PC与直线y=kx+2k﹣1平行?如果不存在,请说明理由;如果存在,求当直线y=kx+2k﹣1与抛物线的对称轴的交点Q与点P关于x轴对称时,直线PC的解析式.参考答案1.A.提示:原式可化为y=x2+2x﹣mx+m=x2+2x+m(1﹣x),二次函数的图象总过该点,即该点坐标与m的值无关,于是1﹣x=0,解得x=1,此时y的值为y=1+2=3,图象总过的点是(1,3).2.y=(3一k)x2+(k﹣2)x+2k﹣1(k≠3)=3x2﹣(x2﹣x﹣2)k﹣2x﹣1.∵过定点,∴x2﹣x﹣2=0,∴x=2或﹣1,∴定点的坐标为(2,7)或(﹣1,4).3.B.提示:①令y=0,即ax2﹣(2a﹣1)x﹣1=0,△=4a2+1>0,即二次函数图象与x轴必有两个交点;故本选项正确,②y=ax2﹣(2a﹣1)x﹣1=a(x﹣1)2+(x﹣1)﹣a,当x=2时,y=1,当x=0时,y=﹣1,图象必过两定点(2,1),(0,﹣1),两点之间的距离为22,故本选项错误,③二次函数y=ax2﹣(2a﹣1)x﹣1(a≠0)的对称轴为x=−1−22=1−12,当a>0时不能判断y随x的增大而减小,故本选项错误;④设函数图象与x轴的两交点为x1,x2,|x1﹣x2|=(1+2)2−412=4+12>2,故函数图象截x轴所得的线段长度必大于2,故本选项正确,故正确的有①④。

武汉市2017年中考复习-第24题⼆次函数专练A B O P y xM Nl中考第24题⼆次函数专练24、(本题满分12分)如图1,已知抛物线21:22F y x x =-+与y 轴交于点A ,顶点为B ,抛物线22:F y x ax b =++的顶点为D 在线段AB 的延长线上(不包括B 点),两抛物线相交于点C. (1)①若4a =-,求b 的值;②请⽤含a 的式⼦表达b 为;(2)如图1,若∠ACD=90°,求a 的值;(3)如图2,若抛物线2F 与直线AB 另⼀个交点为E ,连接CE ,若△CDE 的⾯积不⼩于3,求a 的取值范围.24、(本题满分12分)已知抛物线21y ax =+与x 轴交于点A 、B (点A 在B 点左侧),且与直线22y x =+仅有⼀个公共点.(1)求A 、B 两点的坐标;(2)过B 点的直线交y 轴负半轴于点P ,且交抛物线于另⼀点C ,若3APC PAB S S ??=,试求出点P 的坐标.(3)在(2)的条件下,若过点P 的另⼀条直线l 交抛物线于M 、N两点(M 在N 的左侧),且OM ⊥ON ,求直线l 的解析式.A BO CP y x124、(本题满分12分)如图,已知直线24y x =-+与两轴交于A 、B 两点,抛物线2y x bx c =++ 的顶点M 在线段AB 上,与y 轴交于点C .(1)若2b =-,求C 点的坐标;(2)若△ACM 为等腰三⾓形时,求抛物线的解析式;(3)如图2,抛物线的顶点M 与B 点重合,P 为x 轴负半轴上⼀点,过P 点作直线l交抛物线于D 、E 两点,连接BD 、BE ,试证明:对于x 轴负半轴上任意给定的⼀点P ,都存在这样的⼀条直线l ,使得△BPD 的⾯积等于△BDE 的⾯积恒成⽴.24、(本题满分12分)如图,抛物线1C :224y ax ax =++与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,M 为此抛物线的顶点,若△ABC 的⾯积为12.(1)求此抛物线的函数解析式;(2)动直线l 从与直线AC 重合的位置出发,绕点A l 与BC 交于点D ,P 是线段AD 的中点.①直接写出点P 所经过的路线长为;②点D 与B 、C 不重合时,过点D 作DE ⊥AC 于点E ,作 DF ⊥AB 于点F ,连接PE 、PF 、EF ,在旋转过程中,求 EF 的最⼩值;(3)将抛物线1C 平移得到抛物线2C ,已知抛物线2C 的顶点为N ,与直线AC 交于E 、F 两点,若EF=AC ,求直线MN 的解析式.24、(本题满分12分)点P 为抛物线222y x mx m =-+(m 为常数,0m >)上任⼀点,将抛物线绕顶点G逆时针旋转90°后得到的新图象与y 轴交于A 、B 两点(点A 在点B 的上⽅),点Q 为点P 旋转后的对应点.(1)当2m =,点P 横坐标为4时,求Q 点的坐标;(2)设点()Q a b ,,⽤含m 、b 的代数式表⽰a ;(3) 如图2,若原抛物线恰好也经过A 点,点Q 在第⼀象限内,是否存在这样的点P ,使得AQ=GQ ?若存在,请求P 点的坐标;若不存在,请说明理由.24、(本题满分12分)如图,已知抛物线223y ax ax =-+(a ≠0),与x 轴交于A 、B 两点,与y 轴交于点C ,若3OB OA =.(1)求抛物线的解析式;(2)连接BC ,点P 、点Q 是第⼀象限的抛物线上不同的两点,是否存在这样的P 点,使得BCP BCQ S S ??>恒成⽴?若存在,请求P 点的坐标;若不存在,请说明理由;(3)如图2,D 为抛物线的顶点在x 轴上的正投影,M 为线段OC上⼀点,过点M 作直线l 交抛物线于E 、F 两点,连接AE 、OE 、 BF 、DF ,若△AEO ∽△DFB ,求M 点的坐标.24、(本题满分12分)直线l 垂直x 轴于点A (4,0),点P 是直线l 上的⼀个动点,经过点P 的抛物线2y x bx=+与x 轴交于原点O 和点B ,抛物线的对称轴交OP 于点C ,交x 轴于点D ,设P 点的纵坐标为m . (1)求当点P 与点A 重合时抛物线的解析式;(2)平移直线OP ,使平移后的直线与抛物线有且只有⼀个公共点Q ,试证明:⽆论m 为何值时,△OPQ 的⾯积恒为定值,请说明理由并求其值;(3)连接BC ,试问:是否存在点P ,使得△PBC 为直⾓三⾓形?若存在,求出所有满⾜条件的点P 的坐标;若不存在,请说明理由.24、(本题满分12分)已知抛物线23y ax bx c =++(0b <)交x 轴于A 、B 两点(A 在B 点左侧),交y 轴负半轴于点C ,对称轴为直线2bx -=.(1)当4b c ==-时,求抛物线在x 轴上截得的线段长;(2)如图,过点B 的直线交y 轴于点D ,且BD ⊥AC 于点E ,若OE 平分∠AEB ,CD=2OD ,求抛物线的解析式;(3)在(2)的条件下,已知M 、N 是抛物线上两点,且以M 、N 、O 、B 为顶点的四边形是以OB 为对⾓线的平⾏四边形,求直线MN 的解析式.A OBCDEy xAOBCyx24、(本题满分12分)如图1,已知抛物线bx ax y +=2(a ≠0)经过A(3,0)、B(4,4)两点. (1)求抛物线的解析式;(2)将直线OB 向下平移m 个单位长度后,得到的直线与抛物线只有⼀个公共点D ,求m 的值及点D 的坐标;(3)如图2,若点N 在抛物线上,且∠NBO=∠ABO ,则在(2)的条件下,求出所有满⾜△POD ∽△NOB 的点P 的坐标(点P 、 O 、D 分别与点N 、O 、B 对应).24、(本题满分12分)已知等腰Rt △ABC 的顶点A 的坐标为(0,-1),顶点C 的坐标为(4,3),直⾓顶点B在第四象限,抛物线212y x bx c =-++(b c 、为常数)的顶点为P .(1)如图1,若该抛物线经过A 、B 两点,试说明抛物线的顶点P 在斜边AC 上;(2)如图2,将(1)中的抛物线的顶点P 沿AC 边所在的直线平移,设平移后的抛物线与直线AC 交于另⼀点Q ,且P 、Q 两点都在AC 边上,取边BC 的中点N ,连接NP 、BQ .当四边形BNPQ 的⾯积等于5时,求平移后抛物线的解析式;(3)将(1)中的抛物线绕点(13n n ++,)旋转180°得到⼀条新抛物线,若新抛物线与直线132y x =+有两个交点且交点在其对称轴两侧,求n 的取值范围.24、(本题满分12分)如图1,已知抛物线2y ax bx =+(0a >)的顶点为A(1,-1).(1)请直接写出:a = ,b = ;(2)若点P 在对称轴右侧的抛物线上运动,连结OP 交对称轴于点B ,点B 关于顶点A 的对称点为C 点,连接PC 、OC ,试证明:当P 点运动时,∠PCB=∠OCB 恒成⽴;(3)如图2,将抛物线沿直线OA 作n 次平移(n 为正整数,n ≤12),顶点分别为123n A A A A 、、、、,横坐标依次为1,2,…,n ,各抛物线的对称轴与x 轴的交点分别为123n D D D D 、、、、,以线段n n A D 为边向右作正⽅形n n n n A D E F ,是否存在点n F 恰好落在其中的⼀个抛物线上,若存在,求出所有满⾜条件的正⽅形边长;若不存在,请说明理由.24、(本题满分12分)如图,点P 是直线:22-=x y 上的⼀点,过点P 作直线m ,使直线m 与抛物线2xy =有两个交点,设这两个交点为A 、B.(1)如果直线m 的解析式为2+=x y ,直接写出A 、B 的坐标;(2)如果已知P 点的坐标为(2, 2),点A 、B 满⾜PA=AB ,试求直线m 的解析式;(3)设直线与y 轴的交点为C ,如果已知∠AOB =90°且∠BPC=∠OCP ,求点P 的坐标.24、(2014?孝感)如图1,矩形ABCD的边AD在y轴上,抛物线y=x2﹣4x+3经过点A、点B,与x轴交于点E、点F,且其顶点M在CD上.(1)请直接写出下列各点的坐标:A,B,C,D;(2)若点P是抛物线上⼀动点(点P不与点A、点B重合),过点P作y轴的平⾏线l与直线AB交于点G,与直线BD交于点H,如图2.①当线段PH=2GH时,求点P的坐标;②当点P在直线BD下⽅时,点K在直线BD上,且满⾜△KPH∽△AEF,求△KPH⾯积的最⼤值.24、(2014?宜昌)如图,在平⾯直⾓坐标系中,已知点P(0,4),点A在线段OP上,点B在x轴正半轴上,且AP=OB=t,0<t<4,以AB为边在第⼀象限内作正⽅形ABCD;过点C、D依次向x轴、y轴作垂线,垂⾜为M,N,设过O,C两点的抛物线为y=a x2+b x+c.(1)填空:△AOB≌△_____≌△BMC(不需证明);⽤含t的代数式表⽰A点纵坐标:A(0,);(2)求点C的坐标,并⽤含a,t的代数式表⽰b;(3)当t=1时,连接OD,若此时抛物线与线段OD只有唯⼀的公共点O,求a的取值范围;(4)当抛物线开⼝向上,对称轴是直线x=2﹣,顶点随着的增⼤向上移动时,求t的取值范围.24、(2014?鄂州)如图所⽰,在平⾯直⾓坐标系XOY 中,⼀次函数m x y +=45的图象与x 轴交于 A (-1,0),与y 轴交于点C.以直线x=2为对称轴的抛物线C 1:)0(2≠++=a c bx ax y 经过 A 、C 两点,并与x 轴正半轴交于点B.(1)求m 的值及抛物线21:(0)C y ax bx c a =++≠的函数表达式. (2)设点25(0,)12D ,若F 是抛物线21:(0)C y ax bx c a =++≠对称轴上使得△ADF 的周长取得最⼩值的点,过F 任意作⼀条与y 轴不平⾏的直线交抛物线1C 于111222(,),(,)M x y M x y 两点,试探究1211M F M F+是否为定值?请说明理由. (3)将抛物线C 1作适当平移,得到抛物线2221:(),14C y x h h =-->,若当1x m <≤时,2y x ≥-恒成⽴,求m 的最⼤值.24、(2014?黄冈)已知:如图,在四边形OABC 中,AB ∥OC ,BC ⊥x 轴于点C ,A (1,﹣1),B (3,﹣1),动点P 从点O 出发,沿着x 轴正⽅向以每秒2个单位长度的速度移动.过点P 作PQ 垂直于直线OA ,垂⾜为点Q ,设点P 移动的时间t 秒(0<t <2),△OPQ 与四边形OABC 重叠部分的⾯积为S .(1)求经过O 、A 、B 三点的抛物线的解析式,并确定顶点M 的坐标;(2)⽤含t 的代数式表⽰点P 、点Q 的坐标;(3)如果将△OPQ 绕着点P 按逆时针⽅向旋转90°,是否存在t ,使得△OPQ 的顶点O 或顶点Q 在抛物线上?若存在,请求出t 的值;若不存在,请说明理由;(4)求出S 与t 的函数关系式.24、(2014?武汉)如图,已知直线AB :42++=k kx y 与抛物线221x y =交于A ,B 两点.(1)直线AB 总经过⼀个定点C ,请直接出点C 坐标;(2)当21-=k 时,在直线AB 下⽅的抛物线上求点P ,使△ABP 的⾯积等于5;(3)若在抛物线上存在定点D 使∠ADB=90°,求点D 到直线AB 的最⼤距离.24、(2014?随州)平⾯直⾓坐标系中,四边形ABCD 是菱形,点C 的坐标为(﹣3,4),点A 在x 轴的正半轴上,O 为坐标原点,连接OB ,抛物线y=ax 2+bx+c 经过C 、O 、A 三点.(1)直接写出这条抛物线的解析式;(2)如图1,对于所求抛物线对称轴上的⼀点E ,设△EBO 的⾯积为S 1,菱形ABCD 的⾯积为S 2,当S1≤S 2时,求点E 的纵坐标n 的取值范围;(3)如图2,D (0,﹣)为y 轴上⼀点,连接AD ,动点P 从点O 出发,以个单位/秒的速度沿OB ⽅向运动,1秒后,动点Q 从O 出发,以2个单位/秒的速度沿折线O ﹣A ﹣B ⽅向运动,设点P 运动时间为 t 秒(0<t <6),是否存在实数t ,使得以P 、Q 、B 为顶点的三⾓形与△ADO 相似?若存在,求出相应的t 值;若不存在,请说明理由.。

中考第24题——二次函数综合题型一:二次函数与全等三角形1.(2019交大一模)如图,抛物线y=x2+bx+c与x轴交于点A(﹣1,0)、B两点,与y轴交于点C(0,﹣3).(1)求抛物线的函数解析式;(2)已知点P(m,n)在抛物线上,当﹣2≤m<3时,直接写n的取值范围;(3)抛物线的对称轴与x轴交于点M,点D与点C关于点M对称,试问在该抛物线上是否存在点P,使△ABP与△ABD全等?若存在,请求出所有满足条件的P点的坐标;若不存在,请说明理由.题型二:二次函数与等腰三角形1.(工大七模)如图,抛物线1C的图象与x轴交A(−3,0),B(1,0)两点,与y轴交于点C(0,3),点D为抛物线的顶点。
(1)求抛物线1C的解析式;(2)将抛物线1C关于直线1x=对称后的抛物线记为2C,将抛物线1C关于点B对称后的抛物线记为3C,点E为抛物线3C的顶点,,在抛物线2C的对称轴上是否存在点F,使得BEF∆为等腰三角形?若存在,请求出点F的坐标;若不存在,请说明理由。
题型三:二次函数与三角形面积1.(2019工大四模)已知抛物线,L :3-bx ax y 2+= 与x 轴交于 A (-1,0),B 两点,与 y 轴交于点 C ,且 抛物线 L 的对称轴为直线 x = 1。
(1)求抛物线的表达式;(2)若抛物线L ′抛物线 L 关于直线 x = m 对称,抛物线L ′与 x 轴交于点A ′,B ′两点(点A ′在点B ′左侧),要使'2△△=ABC A BC S S ,求所有满足条件的抛物线L ′的表达式2.(2019交大三模)如图,抛物线1C 的图象与x 轴交于A 、O 两点,顶点为点B (-1,-1). (1)求抛物线1C 的函数表达式.(2)将抛物线1C 绕点A 旋转180°得到抛物线2C ,设抛物线2C 的顶点为点'B ,试通过计算判断抛物线2C 是否过点B.(3)在抛物线1C 或2C 的图象上是否存在点D ,使BO B BD B S S ''△△=?若存在,请求出点D 的坐标,若不存在,请说明理由.3.(2019龙岗一模)如图,在平面直角坐标系xoy 中,抛物线c -2++=bx x y 与坐标轴交于点A 、B 、C ,已知A (-1,0),C (0,2)。

二次函数压轴之定值、定点问题1.如图,抛物线y=x2+bx+c与x轴分别交于A,B两点(点A在点B的左侧),与y轴交于点C,且OB=OC=3OA.(1)求该抛物线的函数表达式;(2)如图2,∠BAC的角平分线交y轴于点M,过M点的直线l与射线AB,AC分别于E,F,已知当直线l绕点M旋转时,11AF AE为定值,请直接写出该定值.2.如图,平面直角坐标系中,抛物线y=﹣x2+nx+4过点A(﹣4,0),与y轴交于点N,与x轴正半轴交于点B.直线l过定点A.(1)求抛物线解析式;(2)过点T(t,﹣1)的任意直线EF(不与y轴平行)与抛物线交于点E、F,直线BE、BF分别交y轴于点P、Q,是否存在t的值使得OP与OQ的积为定值?若存在,求t的值,若不存在,请说明理由.3.如图1,已知二次函数y =x 2+bx +c 的图象与x 轴交于点A (﹣1,0)和点B (3,0),与y 轴的负半轴交于点C .(1)求这个函数的解析式;(2)如图2,点T 是抛物线上一点,且点T 与点C 关于抛物线的对称轴对称,过点T 的直线TS 与抛物线有唯一的公共点,直线MN ∥TS 交抛物线于M ,N 两点,连AM 交y 轴正半轴于G ,连AN 交y 轴负半轴于H ,求OH ﹣OG4.如图1,已知抛物线的解析式为21362y x =--,直线y =kx ﹣4k 与x 轴交于M ,与抛物线相交于点A ,B (A 在B 的左侧).(1)当k =1时,直接写出A ,B ,M 三点的横坐标:x A =,x B =,x M =;(2)作AP ⊥x 轴于P ,BQ ⊥x 轴于Q ,当k 变化时,MP •MQ 的值是否发生变化?若变化,求出其变化范围;若不变,求出其值;5.如图,在正方形OABC中,AB=4,点E是线段OA(不含端点)边上一动点,作△ABE 的外接圆交AC于点D.抛物线y=ax2﹣x+c过点O,E.(1)如图1,若抛物线恰好经过点B,求此时点D的坐标;(2)如图2,AC与BE交于点F.请问点E在运动的过程中,CF•AD是定值吗?如果是,请求出这个值,如果不是,请说明理由;6.已知顶点为A的抛物线y=a(x﹣2)2(a≠0)交y轴于点B(0,2),且与直线l交于不同的两点M、N(M、N不与点A重合).(1)求抛物线的解析式;(2)若∠MAN=90°,试说明:直线l必过定点;7.如图,在直角坐标系中有Rt△AOB,O为坐标原点,OB=1,tan∠ABO=3,将此三角形绕原点O顺时针旋转90°,得到Rt△COD,二次函数y=﹣x2+bx+c的图象刚好经过A,B,C三点.(1)求二次函数的解析式及顶点P的坐标;(2)过定点Q(1,3)的直线l:y=kx﹣k+3与二次函数的图象相交于M,N两点.证明:无论k为何值,△PMN恒为直角三角形.8.已知,抛物线y=ax2+bx+c经过A(﹣1,0)、B(3,0)、C(0,3)三点,点P是抛物线上一点.(1)求抛物线的解析式;(2)如图2,当点P位于第二象限时,过P点作直线AP,BP分别交y轴于E,F两点,请问CECF的值是否为定值?若是,请求出此定值;若不是,请说明理由.9.已知点P(0,﹣4)为平面直角坐标系内一点,直线l绕原点O旋转,交经过点(0,﹣2)的抛物线y=14x2+c于M、N两点.(1)请求出该抛物线的解析式;(2)在直线l绕原点O旋转的过程中,请你研究一下(PM+MO)(PN﹣NO)是否定值?若是,请求出这个定值;若不是,请说明理由.10.如图,抛物线C:y=ax2+bx+c(a≠0)的对称轴为直线x=﹣12,且抛物线经过A、B两点,交x轴于另一点C,A(﹣2,0),B(0,2);(1)求抛物线的解析式;(2)在(1)的条件下,设对称轴直线x=﹣12与x轴交于M,点P为抛物线上对称轴左侧一点,直线PM交抛物线于另一点Q,点P关于抛物线对称轴对称点H,直线HQ交抛物线对称轴于G点,在点P运动过程中GM长是否为一定值,若为定值,请求出其值,若不为定值,请求出其变化范围.11.如图,在平面直角坐标系中,已知抛物线的顶点D为(1,﹣1),且经过点B(3,3).(1)求这个抛物线相应的函数表达式;(2)如图1,过点D且平行于x轴的直线l,与直线OB相交于点A,过点B作直线l 的垂线,垂足为C.若点Q是抛物线上BD之间的动点(不与B、D重合),连接DQ并延长交BC于点E.如图2,连接BQ并延长交CD于点F,在点Q运动的过程中,FC(AC+EC)的值是否发生变化?若不变求出该定值,若变化说明理由.12.如图,抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)与坐标轴分别交于点A(﹣3,0),B(1,0)和点C.(1)求出a与c的数量关系式;(2)如图,若抛物线y=-x2-2x+3与直线y=(2k1﹣2)x交于E,F两点,与直线y=(2k2﹣2)x交于M,N两点,且k1k2=﹣1,点P,Q分别是EF、MN的中点,求证:直线PQ必定经过一个定点,并求出该定点坐标.13.已知抛物线y=ax2+bx+5(a≠0)经过点(4,5).(1)若a+b=﹣3,求抛物线y=ax2+bx+5的解析式;(2)在(1)的条件下,经过点A(2,54)的任意直线y=mx+n(m≠0)与(1)中的抛物线交于B,C两点,那么11AB AC的值是定值吗?如果是定值,请求出这个定值,如果不是定值,请说明理由.14.如图1,抛物线C:y=ax2+bx﹣3与x轴的正半轴交于点B,与y轴交于点C,OB=OC,其对称轴为直线x=1.(1)直接写出抛物线C的解析式;(2)如图2,将抛物线C平移得到抛物线C1,使C1的顶点在原点,过点P(t,﹣1)的两条直线PM,PN,它们与y轴不平行,都与抛物线C1只有一个公共点分别为点M和点N,求证:直线MN必过定点.参考答案1.解:(1)OB=OC,C(0,c)则B(-c,0),代入抛物线解析式得c 2-bc+c=0,c-b+1=0,即当x=-1时,y =1-b+c=0,故抛物线过点(-1,0),故A(-1,0),B(3,0),C(0,-3)抛物线的解析式为y =x 2-2x -3(2)过点M 作MG||x 轴交AC 于点G ,作FP||x 轴交AM 于点P ,作CQ||x 轴,易知∆COA~∆CMG ,∆ACQ~∆AGM ,GM CG OA AC =GM AG CQ AC =,GM GM CG AG 1OA CQ AC AC+=+=即得111OA CQ GM+=,而AM 平分∠BAC ,故AC=CQ ,故111OA AC GM +=;同时CG AC GM AE =,AF GM AC CQ=即可得111AE AF GM +=,OA=1,AC=10,故11101AE AF 10+=+2.解:(1)y =-x 2-3x +4(2)存在t 的值使得OP 与OQ 的积为定值,t=-4设E(m ,-m 2-3m+4),F(n,-n 2-3n+4),设BE 的解析式为y =k (x -1),将E 点坐标代入得k =-m -4,同理k =-n -4,则OP=m+4,OQ=-n-4,故OP ∙OQ=(m+4)(-n-4)=-mn-4(m+n)-16,直线CE 的解析式为y =k 1(x-t )-1,与抛物线y =-x 2-3x +4联立得x 2+(k 1+3)x-k 1t -5=0,m+n=-k 1-3,mn =-k 1t -5,OP ∙OQ=k 1t+4k 1+1=4k 1(t+4)+1,当t=-4时,OP ∙OQ 为定值,故当t=-4时,OP ∙OQ=13.解:(1)y =x 2-2x-3(3)易知T(2,-3),设直线TS 的解析式为y=m(x-2)-3,与抛物线y =x 2-2x-3联立得x 2-(m +2)x +2m =0,有两个相等实根,m 2+4m+4-8m=0,故m=2,即TS 解析式为y =2x -7,设MN 的解析式为y =2x+h ,与抛物线联立得x 17+h ,x 27+h 故7+h ,7+h ),N(2-7+h 7+h ),直线AM 解析式为y 1=k 1x+b 1,得b 1737hh +++737hh +++,同理可得773hh ++-,OH-OG=24.解:6,6,4;(2)MP ∙MQ 的值不变.y =21362x -与y =kx -4k 联立得x 2+6kx +9-24k =0,x A +x B =6k ,x A ∙x B =9-24k ,M(4,0),MP ∙MQ=(4-x P )(4-x Q )=16-4(x A +x B )+x A x B =16+24k+9-24k=255.解:(1)易得抛物线的解析式为y =12x 2-x ,圆的直径为BE ,故∠BDE=90°,且∠BED=∠BAD=45°,作MN ⟂OA 交BC 、OA 于点M 、N ,易知∆BDM ≅∆DEN ,设DM=NE=m ,则CM=ON=m ,而OE=2,故m=1,此时D(1,3)(2)不变,CF ∙AD=16,∠DBF=∠BAD=45°,故∆ADB~∆CBF ,故CF ∙AD=AB ∙CB=166.解:(1)y =12(x -2)2(2)设直线MN 的解析式为y=kx+b ,与抛物线联立得x 2-(4+2k )x +4-2b=0,x M +x N =4+2k,x M ∙x N =4-2b ,作ME 、NF 垂直于x 轴,易知∆AME~∆NAF ,AE ME NF AF =,即有AE ∙AF=ME ∙NF ,ME=kx 1+b ,NF=kx 2+b ,AE=2-x 1,AF=x 2-2,(2-x 1)(x 2-2)=(kx 1+b)(kx 2+b),即有4+2(x 1+x 2)-x 1x 2=k 2x 1x 2+kb (x 1+x 2)+b 2,整理得2k+b =0或2k +b -2=0,即当x =2时,y =2,所以直线l 必过定点(2,2)7.解:(1)y =-x 2+2x +3,P(1,4)(2)联立y=kx-k +3和抛物线y =-x 2+2x +3得x 2+(k-2)x-k=0,x 1+x 2=k-2,x 1x 2=-k,过点M 、N 作对称轴的垂线ME 、NF ,tan ∠PME=PE ME =221111114(23)(1)111x x x x x x --++-==---,同理tan ∠PFN=211x -,(1-x)(x2-1)=1,故tan ∠PME=tan ∠FPN,∠PME=∠FPN ,故∠MPN=90°,所以无论k 为何值,∆PMN 恒为直角三角形.8.解:(1)y =-x 2+2x +3(2)CE CF 的值为定值13,设P(t,-t 2+2t+3),直线AP 的解析式为y =(3-t)x +3-t ,直线BP 的解析式为y =(-t-1)x +3t+3,故CE=-t ,CF=-3t ,故CE CF =139.(1)y =2124x -(2)(PM+MO)(PN-ON)为定值,设直线l 的解析式为y=kx ,与抛物线联立得x 2-4kx -8=0,设M(x 1,y 1),N(x 2,y 2)则有x 1x 2=-8,,y 1=kx 1,故PM=|x 1OM=|x 1,同理PN=|x 2,ON=|x 2,故+|x 1)(|x 2-|x 2)=16,故(PM+MO)(PN-ON)为定值16.10.解:(1)y=-x 2-x +2(2)连接MH ,易知AMP=CMH ,设PQ 的解析式为y=kx+b 1,MH 的解析式为y=-kx+b 2,分别代入(-12,0)得b 1=12k ,b 2=12-k ,故PM 的解析式为y=kx+12k ,MH 的解析式为y=-kx-12k 与抛物线联立得x=(1)92k -+±,所以Q((1)92k -++,292k -±),同理可得H(192k -,292k --),易知QH 的解析式为y=-x +992-当x=-12时,y=92,所以G(-12,92),所以点P 运动过程中GM 长为定值9211.解:(1)y =x 2-2x(2)FC(AC+EC)为定值,设Q(m ,m 2-2m ),易得BF 的解析式为y=(m -1)x -3m ,故点F(311m m -+,-1),D(1,-1),DE 的解析式为y=(m-1)x-m ,E(3,2m-3),FC=3-311m m -+=41m +,AC+EC=4+2m-3+1=2m+2,所以FC(AC+EC)=41m +(2m+2)=812.解:(1)c =-3a (2)联立y =-x 2-2x +3与y =(2k 1﹣2)x 得x 2+2k 1x -3=0所以x 1+x 2=-2k 1,y 1+y 2=-4k 12+4k 1,故P(-k 1,-2k 12+2k 1),同理可得Q(-k 2,-2k 22+2k 2),设直线PQ 的解析式为y=kx+b,将P 、Q 两点代入得y =(2k 1+2k 2-2)x -2,所以直线PQ 过定点(0,-2)13.解:(1)y=x 2-4x +5(3)将坐标系向右平移2个单位,向上平移1个单位,此时抛物线的解析式为y=x2,点A(0,14),设B(m,m 2),C(n,n 2),则AB=m 2+14,AC=n 2+14,故11AB AC +=AB AC AB AC +⋅=22221211()()416m n mn m n +++++,同时BC 的解析式y=kx +14,与抛物线联立得x 2-kx -14=0,m+n=k,mn =-14,故11AB AC +=414.解:(1)y =x 2-2x -3(2)平移后的抛物线的解析式为y =x 2,设M(m,m 2),N(n,n 2),直线PM 的解析式设为y=k 1(x-m)+m 2,PN 的解析式为y=k 2(x-n)+n 2,与抛物线联立得x2-k1x+k1m-m2=0,此时∆=0,即有k 1=2m ,PM 的解析式为y=2m(x-m)+m 2=2mx-m 2同理可得PN 的解析式为y=2n(x-n)+n 2=2nx-n 2,可得P(2m n +,mn ),mn =-1,MN 的解析式为y=(m+n)x +1,故MN 过定点(0,1)。

1. 如图①, 已知抛物线32++=bx ax y (a ≠0)与x 轴交于点A (1,0)和点B (-3,0),与y 轴交于点C .(1) 求抛物线的解析式;(2) 设抛物线的对称轴与x 轴交于点M ,问在对称轴上是否存在点P ,使△CMP 为等腰三角形?若存在,请直接写出所有符合条件的点P 的坐标;若不存在,请说明理由.(3) 如图②,若点E 为第二象限抛物线上一动点,连接BE 、CE ,求四边形BOCE 面积的最大值,并求此时E 点的坐标.线C 1:()522-+=x a y 的顶点为P ,与2.如图,已知抛物x 轴相交于A 、B 两点(点A 在点B 的左边),点B 的横坐标是1.(1)求P 点坐标及a 的值;(2)如图(1),抛物线C 2与抛物线C 1关于x 轴对称,将抛物线C 2向右平移,平移后的抛物线记为C 3,C 3的顶点为M ,当点P 、M 关于点B 成中心对称时,求C 3的解析式;(3)如图(2),点Q 是x 轴正半轴上一点,将抛物线C 1绕点Q 旋转180°后得到抛物线C 4.抛物线C 4的顶点为N ,与x 轴相交于E 、F 两点(点E 在点F 的左边),当以点P 、N 、F 为顶点的三角形是直角三角形时,求点Q 的坐标.yxAO BPM图1C 1C 2C 3图(1)yxAO BP N图2 C 1C 4QEF 图(2)3.如图,抛物线与y 轴交于点C (0,4),与x 轴交于点A 、B ,A 点的坐标为(4,0). (1)求该抛物线的解析式;(2)点Q 是线段AO 上的动点,过点Q 作QE ∥AC ,交BC 于点E ,连接CQ ,当△CQE 的面积最大时,求点Q 的坐标;(3)若平行于x 轴的动直线l 与该抛物线交于点P ,与直线AC 交于点F ,点D (2,0).问:是否存在这样的直线l 使得△ODF 是等腰三角形?若存在,求出P 点坐标,若不存在,说明理由.4.已知抛物线的形状与抛物线232x y -=相同,且对称轴为27-=x ,交x 轴于A 、D 两点(A 在D左边),交y 轴于B (0,-4).(1)求抛物线的解析式; (2)如图(1),E 为抛物线上在第二象限的点,连OE 、AE ,将线段OE 沿射线EA 平移,使E 与A 对应,O 与C 对应,设四边形OEAC 的面积为S ,问是否存在这样的点E ,使S=24?若存在,请求出E 点坐标,并进一步判断此时四边形OEAC 的形状;若不存在,请说明理由; (3)如图(2),在(2)的基础上,设E (x E ,y E ),C (x C ,y C ),当E 点在抛物线上运动时,下列两个结论:①C E x x +的值不变;②C E y y +的值不变,有且只有一个正确,请判断正确的结论并证明求值.O DCBAy xEQ 图(1)图(2)5.如图,拋物线y 1=ax 2-2ax +b 经过A (-1,0),C (2,23)两点,与x 轴交于另一点B ;(1) 求此拋物线的解析式;(2) 若拋物线的顶点为M ,点P 为线段OB 上一动点(不与点 B 重合),点Q 在线段MB 上移动,且∠MPQ =45︒,设线 段OP =x ,MQ =22y 2,求y 2与x 的函数关系式,并直接写出自变量x 的取值范围;(3) 在同一平面直角坐标系中,两条直线x =m ,x =n 分别与拋物线交于点E ,G ,与(2)中的函数图像交于点F ,H 。

二次函数与定点、定值问题【方法归纳】已知抛物线和满足一定条件的直线在平面直角坐标系中,直线上的线段满足一定几何条件,图中可能产生一些定点,定量关系.通常要运用几何量的关系转换成线段关系和坐标关系求解. 思路:结合二次函数,将几何向代数转化,构建方程或方程组,并归纳解题一致性.例1.已知抛物线:y =ax 2+bx +c ,顶点坐标为原点,且过(4,8),如图,若A 、B 两点在抛物线上,且OA ⊥OB ,AB 交y 轴于H 点,求H 点的坐标.易求a =21,b =0,c =0,∴y =12x 2,设A (m ,21m 2),B (n ,12n 2),设AB 的解析式y =kx +b ,联立⎪⎩⎪⎨⎧+==b kx y xy 221得x 2-2kx -2b =0,m +n =2k ,mn =-2b ,又∵OA ⊥OB ,过A 点作AC 丄x 轴,BD ⊥y 轴,垂足分别为C 、D 两点,易证△AOC ∽△OBD ,∴OC AC =BD OD ,∴A A x y =B B y x -,∴m m221=221n n -,41mn =-1,∴mn=-4,∴b =2,∴H (0,2).(2013年武汉中考压轴题的关键一步)方法总结:_________________________________________________ _________________________________________________ _________________________________________________【练1】抛物线y =21(x -1)2,顶点为M ,直线AB 交抛物线于A 、B 两点,且MA ⊥MB ,求证:直线AB 过定点.设A (x 1,y 1),B (x 2,y 2),易求M (1,0),作AE ⊥x 轴,BF ⊥x 轴,△AEM ∽△BFM ,易得EM AE =FBMF,即111x y -=221y x -,1211)1(21x x --=222)1(211--x x ,∴-21(x 1-1)2=)1(2112-x ,∴-41[x 1x 2-(x 1+x 2)+1]=1,联立⎪⎩⎪⎨⎧+=-=b kx y x y 2)1(21得,21(x -1)2=kx +b ,x 2-2x +1=2kx +2b ,x 2-(2+2k )x +1-2b =0,x 1·x 2=1-2b ,x 1+x 2=2k +2,∴(1-2b )-(2k +2)+1=-4,k +b =2,∴y =kx +b =kx +2-k =k (x -1)+2,∴AB 过定点(1,2).例2.已知抛物线y =41x 2,以M (-2,1)为直角顶点作该抛物线的内接直角三角形MAB (即M ,A ,B 均在抛物线上),求证:直线AB 过定点,并求出该定点坐标.过M 作PQ ∥x 轴,AP ⊥PQ 于P ,BQ ⊥PQ 于Q ,设AB :y =kx +b , 由⎪⎩⎪⎨⎧+==bkx y xy 241得41x 2-kx -b =0,x A +x B =4k ,x A ·x B =-4b , 由△APM ∽△MQB 得AP ·BQ =PM ·MQ ,即(y A -1)(41x B 2-1)=-(x A +2)(x B +2), ∴161(x A -2)(x B -2)=-1,x A ·x B -2(x A +x B )+4=-16, ∴-4b -8k +4=-16,b =5-2k ,∴AB :y =kx +5-2k =k (x -2)+5,过定点(2,5).【练2】(2014武汉中考)如图,已知直线AB :y =kx +2k +4于抛物线y =21x 2交于A 、B 两点. (1)直线AB 总经过一个定点C ,请直接写出点C 坐标; (2)若在抛物线上存在定点D 使∠ADB =90°,求点D 到直线AB 的最大距离.(1)C (-2,4)(2)设A (x 1,21x 12),B (x 2,21x 22),D (m ,21m 2),由⎪⎩⎪⎨⎧++==42212k kx y xy 得x 2-2kx -4k -8=0,x 1+x 2=2k ,x 1·x 2=-4k -8,过D 作EF ∥x 轴,AE ⊥EF 于E ,BF ⊥EF 于F ,由△AED ∽△DFB 得AE ·BF =DE ·DF ,即(21x 12-21m 2)(21x 22-21m 2)=(m -x 1)(x 2-m ),化简x 1x 2+m (x 1+x 2)+m 2=4,∴2k (m -2)+m 2-4=0,当m -2=0,即m =2时,点D 的坐标与k 无关,∴D (2,2),又∵C (-2,4),∴CD =25,作DM ⊥AB 于M ,则DM ≤CD =25,∴当CD ⊥AB 时,点D 到直线AB 的距离最大,最大距离为25.例3.如图,抛物线y =x 2+3顶点为P ,直线l 交抛物线于A 、B 两点,交y 轴于C 点,∠AOC =∠BOC ,求证:直线AB 过定点.设A (m ,m 2+3),B (n ,n 2+3),设直线AB 的解析式为y =kx +b ,⎩⎨⎧+=+=32x y bkx y ,∴kx +b =x 2+3,x 2-kx +3-b =0,∴mn =3-b ,∵∠AOC =∠BOC ,∴tan ∠AOC =tan ∠BOC ,∴32+m m =32+-n n,∴mn 2+3m =-m 2n -3n ,∴mn =-3,∴b =6,∴C (0,6).【练3】抛物线y =x 2-4x +5,对称轴交x 轴于P 点,直线EF 交抛物线于E 、F ,交对称轴于H ,且∠EPH =∠FPH ,求证:EF 恒过定点.E (x 1,y 1),F (x 2,y 2),⎩⎨⎧+-=+=542x x y bkx y ,∴x 2-(4+k )x +5-b =0,x 1+x 2=4+k ,x 1x 2=5-b ,tan ∠EPH =tan ∠FPH ,∴112y x -=222y x -,∴(kx 1+b)(x 2-2)=(kx 2+b )(2-x 1),∴b +2k =2,y =kx +b ,∴直线过(2,2).例4.如图,抛物线y =x 2-1交x 轴于A 、B 两点,直线y =a (a >0)交抛物线于M 、N ,点C 在抛物线上,且∠MCN =90°,点C 到MN 的距离是否为定值?若是,求出这个定值.作CH ⊥MN 于H .则∠MCH =∠CNH ,Rt △MCH ∽Rt △CNH ,CH 2=MH ·HN ,令C (x C ,t ),M (m ,m 2-1),则N (-m ,m 2-1),CH =m 2-1-t ,MH ·HN =(x C -x M )(x N -x C )=-x C 2+m 2,y C =x C 2-1=t ,故x C 2=t +1,-x C 2=-t -1,即MH ·HN =m 2-1-t ,又CH 2=MH ·HN ,∴(m 2-1-t )2=m 2-1-t ,∴m 2-1-t =0(舍去)或m 2-1-t =1,即CH =m 2-1-t =1,点C 到MN 的距离是定值,这个值为1.【练4】(2015永州改)如图,抛物线:y =41(x -1)2,R (1,1)是对称轴l 上一点,点P 为抛物线上一个动点,PM 垂直于直线y =-1于M ,求PRPM的值.设P (t ,41(t -1)2),连PR ,作PM ⊥直线y =-1于点M ,PM =41(t -1)2+1, PR =222]1)1(41[)1(--+-t t =41(t -1)2+1,∴PM =PR ,∴PRPM=1.【课后反馈】1.如图,抛物线y =x 2-1交x 轴正半轴于A (1,0),M 、N 在抛物线上,且MA ⊥NA ,试说明MN 恒过一定点,求此定点的坐标.作MP ⊥x 轴于P ,NQ ⊥x 轴于Q ,设MN :y =mx +n ,由21y mx ny x =+⎧⎪⎨=-⎪⎩得x 2-mx -n -1=0,x M +x N =m ,x M ·x N =-1-n ,tan ∠MAP =PA MP =211M M x x --=-x M -1,tan ∠ANQ =AQ NQ =211N N x x --=11Nx +.由∠MAP =∠ANQ 得-x M -1=11Nx +,即-x M ·x N -(x M +x N )-1=1,1+n -m -1=1,n =m +1,MN :y =mx +m+1=m (x +1)+1,故MN 过定点(-1,1).2.如图,抛物线y =41(x -4)2-4的顶点为P ,M ,N 均在对称轴上,且PM =PN ,延长OM 交抛物线于点A .求证:∠ANM =∠ONM .易求P (4,-4),设A (m ,41m 2-2m ),可求OA :y =(41m -2)x ,点M 在OA 上,x =4时,y =m -8,∴M (4,m -8),故N (4,-m ),tan ∠ONM =N N x y -=4m ,tan ∠ANM =4A A N x y y --=2412()4m m m m ----=41(4)4m m m --=4m ,故∠ANM =∠ONM .3.(2016六初九下2月考T24)已知抛物线y =41x 2+m 与x 轴交于A 、B 两点,与y 轴交于C 点,且OA =2OC ,直线y =kx -2k +4(k ≠0)与抛物线交于D 、E 两点. (1)求m 值及A 点坐标;(2)当k 取何值时,△ADE 的面积最小,并求面积的最小值;(3)若M 、N 为抛物线上两点,其以MN 为直径的圆始终经过A 点,求直线MN 经过的定点P 的坐标.(1)令x =0时,y =m ,∴OC =-m ,令y =0时,x =m -±2,∴OA =m -2, ∵OA =2OC ,∴m -2=2(-m ),m =-1,∴A (2,0);(2)直线y =kx -2k +4过定点(2,4),过点A 作AF ∥y 轴交DE 于F ,∴F (2,4), 设D (x 1,y 1)、E (x 2,y 2),∴S △ADE =21×4×(x 1-x 2)=2(x 1-x 2), 联立⎪⎩⎪⎨⎧-=+-=141422x y k kx y ,整理得41x 2-kx +2k -5=0,∴x 1+x 2=4k ,x 1x 2=8k -15 ∴S △ADE =2212142)(x x x x -+=84)1(2+-k ,当k =1时,S △ADE 有最小值,最小值为16; (3)设M (x 1,y 1)、N (x 2,y 2), ∵∠MAN =90°,过点M 作ME ⊥x 轴于E ,过点N 作NF ⊥x 轴于F ,∴△MEA ∽△AFN ,∴212122y x x y -=-,y 1y 2=(x 2-2)(2-x 1), 即)141)(141(2121--x x )=(x 2-2)(2-x 1),x 1x 2+2(x 1+x 2)+20=0,设直线MN 的解析式为y =kx +b ,联立⎪⎩⎪⎨⎧-=+=1412x y bkx y ,整理得x 2-4kx -4-4b =0, ∴x 1+x 2=4k ,x 1x 2=-4-4b ,∴-4-4b +2×4k +20=0,2k -b =-4, 当x =-2时,-2k +b =4,∴直线MN 必过顶点(-2,4).。

二次函数各知识点、考点、典型例题及对应练习(超全)【典型例题】题型 1 二次函数的概念例1(基础).二次函数2365y x x =--+的图像的顶点坐标是( ) A .(-1,8) B.(1,8) C (-1,2) D (1,-4) 点拨:本题主要考察二次函数的顶点坐标公式 例2.(拓展,2008年武汉市中考题,12) 下列命题中正确的是;○1若b 2-4ac >0,则二次函数y=ax 2+bx+c 的图象与坐标轴的公共点的个数是2或3○2若b 2-4ac=0,则二次函数y=ax 2+bx+c 的图象与x 轴只有一个交点,且这个交点就是抛物线顶点。
○3当c=-5时,不论b 为何值,抛物线y=ax 2+bx+c 一定过y 轴上一定点。
○4若抛物线y=ax 2+bx+c 与x 轴有唯一公共点,则方程ax 2+bx+c=0有两个相等的实数根。
○5若抛物线y=ax 2+bx+c 与x 轴有两个交点A 、B ,与y 轴交于c 点,c=4,S △ABC=6,则抛物线解析式为y=x 2-5x+4。
○6若抛物线y=ax 2+bx+c (a ≠0)的顶点在x 轴下方,则一元二次方程ax 2+bx+c=0有两个不相等的实数根。
○7若抛物线y=ax 2+bx+c (a ≠0)经过原点,则一元二次方程ax 2+bx+c=0必有一根为0。
~○8若a -b+c=2,则抛物线y=ax 2+bx+c (a ≠0)必过一定点。
○9若b 2<3ac ,则抛物线y=ax 2+bx+c 与x 轴一定没有交点。
○10若一元二次方程ax 2+bx+c=0有两个不相等的实数根,则函数y=cx 2+bx+a 的图象与x 轴必有两个交点。
○11若b=0,则抛物线y=ax 2+bx+c 与x 轴的两个交点一个在原点左边,一个在原点右边。
点拨:本题主要考查二次函数图象及其性质,一元二次方程根与系数的关系,及二次函数和一元二次方程二者之间的联系。


二次函数压轴题汇编带答案(中考真题)1.(24年安徽中考)已知物线2y x bx =-+(b 为常数)的顶点横坐标比抛物线22y x x =-+的顶点横坐标大1.(1)求b 的值;(2)点11(,)A x y 在抛物线22y x x =-+上,点11(,)B x t y h ++在抛物线2y x bx =-+上.(i)若3h t =,且10,0x t > ,求h 的值;(ii)若 11x t =-,求h 的最大值.2.(24年包头中考)如图,在平面直角坐标系中,抛物线22y x bx c =-++与x 轴相交于()1,0A ,B 两点(点A 在点B 左侧),顶点为()2,M d ,连接AM .(1)求该抛物线的函数表达式;(2)如图1,若C 是y 轴正半轴上一点,连接,AC CM .当点C 的坐标为10,2⎛⎫ ⎪⎝⎭时,求证:ACM BAM ∠=∠;(3)如图2,连接BM ,将ABM 沿x 轴折叠,折叠后点M 落在第四象限的点M '处,过点B 的直线与线段AM '相交于点D ,与y 轴负半轴相交于点E .当87BD DE =时,3ABD S △与2M BD S '△是否相等?请说明理由.3.(24年成都中考)如图,在平面直角坐标系xOy 中,抛物线()2:230L y ax ax a a =-->与x 轴交于,A B 两点(点A 在点B 的左侧),其顶点为C ,D 是抛物线第四象限上一点.(1)求线段AB 的长(2)当1a =时,若ACD ∆的面积与ABD ∆的面积相等,求tan ABD ∠的值:(3)延长CD =交x =轴于点E =,当AD DE =时,将ADB ∆沿DE 方向平移得到A EB ''∆.将抛物线L 平移得到抛物线L ',使得点A ',B '都落在抛物线L '上.试判断抛物线L '与L 是否交于某个定点.若是,求出该定点坐标;若不是,请说明理由.4.(24年重庆中考)如图,在平面直角坐标系中,抛物线()240y ax bx a =++≠经过点()1,6-,与y 轴交于点C ,与x 轴交于A B ,两点(A 在B 的左侧),连接tan 4AC BC CBA ∠=,,.(1)求抛物线的表达式(2)点P 是射线CA 上方抛物线上的一动点,过点P 作PE x ⊥轴,垂足为E ,交AC 于点D .点M 是线段DE 上一动点,MN y ⊥轴,垂足为N ,点F 为线段BC 的中点,连接AM NF ,.当线段PD 长度取得最大值时,求AM MN NF ++的最小值(3)将该抛物线沿射线CA 方向平移,使得新抛物线经过(2)中线段PD 长度取得最大值时的点D ,且与直线AC 相交于另一点K .点Q 为新抛物线上的一个动点,当QDK ACB ∠∠=时,直接写出所有符合条件的点Q 的坐标.5.(24年浙江中考)已知二次函数2y x bx c =++(b ,c 为常数)的图象经过点(2,5)A -,对称轴为直线12x =-.(1)求二次函数的表达式(1)若点(1,7)B 向上平移2个单位长度,向左平移(0)m m >个单位长度后,恰好落在2y x bx c =++的图象上,求m 的值(3)当2≤a ≤n 时,二次函数2y x bx c =++的最大值与最小值的差为94,求n 的取值范围.6.(24年呼伦贝尔中考)如图,在平面直角坐标系中,二次函数()20y ax bx c a =++≠的图像经过原点和点()4,0A .经过点A 的直线与该二次函数图象交于点()1,3B ,与y 轴交于点C .(1)求二次函数的解析式及点C 的坐标;(2)点P 是二次函数图象上的一个动点,当点P 在直线AB 上方时,过点P 作PE x ⊥轴于点E ,与直线AB 交于点D ,设点P 的横坐标为m .①m 为何值时线段PD 的长度最大,并求出最大值;②是否存在点P ,使得BPD △与AOC 相似.若存在,请求出点P 坐标;若不存在,请说明理由.7.(24年广州中考)已知抛物线232:621(0)G y ax ax a a a =--++>过点()1,2A x 和点()2,2B x ,直线2:l y m x n =+过点(3,1)C ,交线段AB 于点D ,记CDA 的周长为1C ,CDB △的周长为2C ,且122C C =+.(1)求抛物线G 的对称轴(2)求m 的值(3)直线l 绕点C 以每秒3︒的速度顺时针旋转t 秒后(045)t ≤<得到直线l ',当l AB '∥时,直线l '交抛物线G 于E ,F 两点.①求t 的值②设AEF △的面积为S ,若对于任意的0a >,均有S k ≥成立,求k 的最大值及此时抛物线G 的解析式.8.(24年绥化中考)综合与探究如图,在平面直角坐标系中,已知抛物线2y x bx c =-++与直线相交于A ,B 两点,其中点()3,4A ,()0,1B .(1)求该抛物线的函数解析式.(2)过点B 作BC x ∥轴交抛物线于点C ,连接AC ,在抛物线上是否存在点P 使1tan tan 6BCP ACB ∠=∠.若存在,请求出满足条件的所有点P 的坐标;若不存在,请说明理由.(提示:依题意补全图形,并解答)(3)将该抛物线向左平移2个单位长度得到()2111110y a x b x c a =++≠,平移后的抛物线与原抛物线相交于点D ,点E 为原抛物线对称轴上的一点,F 是平面直角坐标系内的一点,当以点B ,D ,E ,F 为顶点的四边形是菱形时,请直接写出点F 的坐标.9.(24年上海中考)在平面直角坐标系中,已知平移抛物线213y x =后得到的新抛物线经过50,3A ⎛⎫- ⎪⎝⎭和(5,0)B .(1)求平移后新抛物线的表达式(2)直线x m =(0m >)与新抛物线交于点P,与原抛物线交于点Q .①如果PQ 小于3,求m 的取值范围②记点P 在原抛物线上的对应点为P ',如果四边形P BPQ '有一组对边平行,求点P 的坐标.10.(24年乐山中考)在平面直角坐标系xOy 中,我们称横坐标、纵坐标都为整数的点为“完美点”.抛物线222y ax ax a =-+(a 为常数且0a >)与y 轴交于点A .(1)若1a =,求抛物线的顶点坐标;(2)若线段OA (含端点)上的“完美点”个数大于3个且小于6个,求a 的取值范围;(3)若抛物线与直线y x =交于M ,N 两点,线段MN 与抛物线围成的区域(含边界)内恰有4个“完美点”,求a 的取值范围.11.(24年甘肃武威中考)如图1,抛物线()2y a x h k =-+交x 轴于O,()4,0A 两点,顶点为(2,B.点C 为OB 的中点.(1)求抛物线2()y a x h k =-+的表达式;(2)过点C 作CH OA ⊥,垂足为H,交抛物线于点E .求线段CE 的长.(3)点D 为线段OA 上一动点(O 点除外),在OC 右侧作平行四边形OCFD .①如图2,当点F 落在抛物线上时,求点F 的坐标;②如图3,连接BD ,BF ,求BD BF +的最小值.12.(24年枣庄中考)在平面直角坐标系xOy 中,点()2,3P -在二次函数()230y ax bx a =+->的图像上,记该二次函数图像的对称轴为直线x m =.(1)求m 的值(2)若点(),4Q m -在23y ax bx =+-的图像上,将该二次函数的图像向上平移5个单位长度,得到新的二次函数的图像.当04x ≤≤时,求新的二次函数的最大值与最小值的和(3)设23y ax bx =+-的图像与x 轴交点为()1,0x ,()()212,0x x x <.若2146x x <-<,求a 的取值范围.13.(24年四川广安中考)如图,抛物线223y x bx c =-++与x 轴交于A ,B 两点,与y 轴交于点C ,点A 坐标为(1,0)-,点B 坐标为(3,0).(1)求此抛物线的函数解析式.(2)点P 是直线BC 上方抛物线上一个动点,过点P 作x 轴的垂线交直线BC 于点D ,过点P 作y 轴的垂线,垂足为点E ,请探究2PD PE +是否有最大值?若有最大值,求出最大值及此时P 点的坐标;若没有最大值,请说明理由.(3)点M 为该抛物线上的点,当45∠=︒MCB 时,请直接写出所有满足条件的点M 的坐标.14.(24年四川南充中考)已知抛物线2y x bx c =-++与x 轴交于点()1,0A -,()3,0B.(1)求抛物线的解析式;(2)如图1,抛物线与y 轴交于点C ,点P 为线段OC 上一点(不与端点重合),直线PA ,PB 分别交抛物线于点E ,D ,设PAD 面积为1S ,PBE △面积为2S ,求12S S 的值;(3)如图2,点K 是抛物线对称轴与x 轴的交点,过点K 的直线(不与对称轴重合)与抛物线交于点M ,N ,过抛物线顶点G 作直线l x ∥轴,点Q 是直线l 上一动点.求QM QN +的最小值.15.(24年四川泸州中考)如图,在平面直角坐标系xOy 中,已知抛物线23y ax bx =++经过点()3,0A ,与y 轴交于点B,且关于直线1x =对称.(1)求该抛物线的解析式;(2)当1x t -≤≤时,y 的取值范围是021y t ≤≤-,求t 的值;(3)点C 是抛物线上位于第一象限的一个动点,过点C 作x 轴的垂线交直线AB 于点D,在y 轴上是否存在点E,使得以B,C,D,E 为顶点的四边形是菱形?若存在,求出该菱形的边长;若不存在,说明理由.16.(24年河北中考)如图,抛物线21:2C y ax x =-过点(4,0),顶点为Q .抛物线22211:()222C y x t t =--+-(其中t 为常数,且2t >),顶点为P .(1)直接写出a 的值和点Q 的坐标.(2)嘉嘉说:无论t 为何值,将1C 的顶点Q 向左平移2个单位长度后一定落在2C 上.淇淇说:无论t 为何值,2C 总经过一个定点.请选择其中一人的说法进行说理.(3)当4t =时①求直线PQ 的解析式.②作直线l PQ ∥,当l 与2C 的交点到x 轴的距离恰为6时,求l 与x 轴交点的横坐标.(4)设1C 与2C 的交点A,B 的横坐标分别为,A B x x ,且A B x x <.点M 在1C 上,横坐标为()2B m m x ≤≤.点N 在2C 上,横坐标为()A n x n t ≤≤.若点M 是到直线PQ 的距离最大的点,最大距离为d ,点N 到直线PQ 的距离恰好也为d ,直接用含t 和m 的式子表示n.17.(24年武汉中考)抛物线215222y x x =+-交x 轴于A ,B 两点(A 在B 的右边),交y 轴于点C .(1)直接写出点A ,B ,C 的坐标(2)如图(1),连接AC ,BC ,过第三象限的抛物线上的点P 作直线PQ AC ∥,交y 轴于点Q .若BC 平分线段PQ ,求点P 的坐标(3)如图(2),点D 与原点O 关于点C 对称,过原点的直线EF 交抛物线于E ,F 两点(点E 在x 轴下方),线段DE 交抛物线于另一点G ,连接FG .若90EGF ∠=︒,求直线DE 的解析式.18.(24年四川德阳中考)如图,抛物线2y x x c =-+与x 轴交于点()1,0A -和点B ,与y 轴交于点C .(1)求抛物线的解析式;(2)当02x <≤时,求2y x x c =-+的函数值的取值范围;(3)将拋物线的顶点向下平移34个单位长度得到点M ,点P 为抛物线的对称轴上一动点,求5PA PM +的最小值.19.(24年湖北中考)如图,二次函数23y x bx =-++交x 轴于(1,0)A -和B ,交y 轴于C .(1)求b 的值.(2)M 为函数图像上一点,满足MAB ACO ∠=∠,求M 点的横坐标.(3)将二次函数沿水平方向平移,新的图像记为L ,L 与y 轴交于点D ,记DC d =,记L 顶点横坐标为n .①求d 与n 的函数解析式.②记L 与x 轴围成的图像为,U U 与ABC ∆重合部分(不计边界)记为W ,若d 随n 增加而增加,且W 内恰有2个横坐标与纵坐标均为整数的点,直接写出n 的取值范围。

1.(15年四调) 如图,在平面直角坐标系xOy 中,抛物线 293212+-=x x y 交y 轴于点E ,C 为抛物线的顶点,直线AD :y=kx+b (k >0)与抛物线相交于A ,D 两点(点D 在点A 的下方).(1)当k=2,b= 213-时,求A ,D 两点坐标;(2)当b=2-3k 时,直线AD 交抛物线的对称轴于点P ,交线段CE 于点F ,求DFPF的最小值; (3)当b=0时,若B 是抛物线上点A 的对称点,直线BD 交对称轴于点M ,求证PC=CM .2.(2016年四调)如图1,在平面直角坐标系xoy 中,抛物线M :5212+-=x y 经过点C (2,3),直线y =kx +b 与抛物线相交于A ,B 两点,∠ACB = 90°.(1)探究与猜想:①探究:取点B (6,-13)时,点A 的坐标为(-25,815),直接写出直线AB 的解析式 为________________,取点B (4,-3),直接写出AB 的解析式为________________ ②猜想:我们猜想直线AB 必经过一个定点Q ,其坐标为___________.请取点B 的横坐标为n ,验证你的猜想;友情提醒:此问如果没有解出,不影响第(2)问的解答.(2)如图2,点D 在抛物线M 上,若AB 经过原点O ,△ABD 的面积等于△ABC 的面积,试求出一个符合条件的点D 的坐标,并直接写出其余的符合条件的D 点的坐标3.(2017年四调)在平面直角坐标系中,抛物线221x y =经过点A (x 1,y 1)、C (x 2,y 2),其中x 1、x 2是方程x 2-2x -8的两根,且x 1<x 2,过点A 的直线l 与抛物线只有一个公共点 (1) 求A 、C 两点的坐标 (2) 求直线l 的解析式(3) 如图2,点B 是线段AC 上的动点,若过点B 作y 轴的平行线BE 与直线l 相交于点E ,与抛物线相交于点D ,过点E 作DC 的平行线EF 与直线AC 相交于点F ,求BF 的长4.(2017年四调)已知抛物线332++=bx ax y 与x 轴交于点A (1,0), B (3,0)两点,与y 轴交于点C .P 为抛物线的对称轴上的动点,且在x 轴的上方,直线AP 与抛物线交于另一点D .(1) 求抛物线的解析式;(2) 如图1,连接AC ,DC ,若∠ACD =60°,求点D 的横坐标;(3) 如图2,过点D 作直线3-=y 的垂线,垂足为点E ,若PD PE 2=,求点P 的坐标.5.(2019年四调)已知抛物线c bx x y ++=2经过点A (2,3-).(1)如图,过点A 分别向x 轴和y 轴作垂线,垂足分别为B ,C ,得到矩形ABOC ,且抛物线经过点C.①请直接写出该抛物线解析式;①将抛物线向左平移m (0>m )个单位,分别交线段OB ,AC 于D 、E 两点,若直线DE 刚好平分矩形ABCO 的面积,求m 的值;(2)将抛物线平移,使点A 的对应点为)3,2(1b n A -,其中1≥n .若平移后的抛物线仍然经过点A ,求平移后的抛物线定点所能达到最高点时的坐标.6.(2015年中考)已知抛物线y=x 2+c 与x 轴交于A (﹣1,0),B 两点,交y 轴于点C .(1)求抛物线的解析式;(2)点E (m ,n )是第二象限内一点,过点E 作EF ⊥x 轴交抛物线于点F ,过点F 作FG ⊥y 轴于点G ,连接CE 、CF ,若⊥CEF=⊥CFG .求n 的值并直接写出m 的取值范围(利用图1完成你的探究).(3)如图2,点P 是线段OB 上一动点(不包括点O 、B ),PM ⊥ x 轴交抛物线于点M ,① OBQ=① OMP ,BQ 交直线PM 于点Q ,设点P 的横坐标为t ,求① PBQ 的周长.7.(2016年中考)抛物线y =ax 2+c 与x 轴交于A 、B 两点,顶点为C ,点P 为抛物线上,且位于x 轴下方.(1)如图1,若P (1,-3)、B (4,0), ① 求该抛物线的解析式;② 若D 是抛物线上一点,满足∠DPO =∠POB ,求点D 的坐标;(2) 如图2,已知直线P A 、PB 与y 轴分别交于E 、F 两点.当点P 运动时,OCOFOE 是否为定值?若是,试求出该定值;若不是,请说明理由.8.(2017年中考)已知点A (﹣1,1)、B (4,6)在抛物线y=ax 2+bx 上 (1)求抛物线的解析式;(2)如图1,点F 的坐标为(0,m )(m >2),直线AF 交抛物线于另一点G ,过点G 作x 轴的垂线,垂足为H .设抛物线与x 轴的正半轴交于点E ,连接FH 、AE ,求证:FH ∥AE ;(3)如图2,直线AB 分别交x 轴、y 轴于C 、D 两点.点P 从点C 出发,沿射线CD 方向匀速运动,速度为每秒√2个单位长度;同时点Q 从原点O 出发,沿x 轴正方向匀速运动,速度为每秒1个单位长度.点M 是直线PQ 与抛物线的一个交点,当运动到t 秒时,QM=2PM ,直接写出t 的值.9.(2018年中考)抛物线L :y =-x 2+bx +c 经过点A (0,1),与它的对称轴直线x =1交于点B (1) 直接写出抛物线L 的解析式(2) 如图1,过定点的直线y =kx -k +4(k <0)与抛物线L 交于点M 、N .若△BMN 的面积等于1,求k 的值(3) 如图2,将抛物线L 向上平移m (m >0)个单位长度得到抛物线L 1,抛物线L 1与y 轴交于点C ,过点C 作y 轴的垂线交抛物线L 1于另一点D .F 为抛物线L 1的对称轴与x 轴的交点,P 为线段OC 上一点.若△PCD 与△POF 相似,并且符合条件的点P 恰有2个,求m 的值及相应点P 的坐标10.(2019年中考)已知抛物线C 1:y =(x -1)2-4和C 2:y =x 2 (1) 如何将抛物线C 1平移得到抛物线C 2?(2) 如图1,抛物线C 1与x 轴正半轴交于点A ,直线b x y +-=34经过点A ,交抛物线C 1于另一点B .请你在线段AB 上取点P ,过点P 作直线PQ ①y 轴交抛物线C 1于点Q ,连接AQ ① 若AP =AQ ,求点P 的横坐标 ① 若P A =PQ ,直接写出点P 的横坐标(3) 如图2,△MNE 的顶点M 、N 在抛物线C 2上,点M 在点N 右边,两条直线ME 、NE 与抛物线C 2均有唯一公共点,ME 、NE 均与y 轴不平行.若△MNE 的面积为2,设M 、N 两点的横坐标分别为m 、n ,求m 与n 的数量关系1、如图1,已知二次函数的图象过点O(0,0)、A(4,0)、B(2,),M是OA的中点.(1)求此二次函数的解析式;(2)设P是抛物线上的一点,过P作x轴的平行线与抛物线交于另一点Q,要使四边形PQAM是菱形,求点P的坐标;(3)将抛物线在x轴下方的部分沿x轴向上翻折,得曲线OB′A(B′为B关于x轴的对称点),在原抛物线x轴的上方部分取一点C,连结CM,CM与翻折后的曲线OB′A交于点D,若△CDA的面积是△MDA面积的2倍,这样的点C是否存在?若存在求出点C的坐标;若不存在,请说明理由.2、(武昌19年模拟24题)已知开口向下的抛物线y=ax2-2ax+3与x轴的交点为A、B两点(点A在点B的左边),与y轴的交点为C,OC=3OA(1) 请直接写出该抛物线解析式(2) 如图,D为抛物线的顶点,连接BD、BC,P为对称轴右侧抛物线上一点.若∠ABD=∠BCP,求点P的坐标(3) 在(2)的条件下,M、N是抛物线上的动点.若∠MPN=90°,直线MN必过一定点,请求出该定点的坐标3、(硚口19年模拟24题)已知抛物线y= x 2+(1+k )x +k (k <0)与x 轴交于点A 、B ,(点A在点B 左边),顶点为M . (1)如图(2P ,4、(汉阳18年五月模拟24题)如图,点A ,C 在x 轴上,点B (3,m)(m >0),且∠ACB =90°,AC =B C.线段AB 与y 轴相交于点D ,以P (1,0)为顶点的抛物线经过点B ,D . (1)求此抛物线的解析式;(2)设点Q 为抛物线上点P 至点B 之间的一动点,连结PQ 并延长交BC 于点E ,连结BQ 并延长交AC 于点F .①当BQ =DQ 时,求点Q 的坐标;②当EF ∥AB 时,求点Q 的坐标.5、(武昌19年模拟24题)已知:如图,抛物线22y ax bx a =+-与x 轴交于点A 和点B (1,0),与y 轴交于点1(0,)4C -. (1)求抛物线的解析式;(2)若点()n D ,2是抛物线上的一点,在y 轴左侧的抛物线上存在点T ,使△TAD 的面积等于△TBD 的面积,求出所有满足条件的点T 的坐标;(3)直线2y kx k =-+,与抛物线交于两点P 、Q ,如图,其中点P 在第一象限,点Q 在第二象限,P A 交y 轴于点M ,QA 交y 轴于点N ,连结BM 、BN ,试判断△BMN 的形状并证明你的结论.6、(武昌19年模拟24题)已知抛物线()221:2131C y x m x m m =--+--.(1)证明:不论m 为何值,抛物线图象的顶点M 均在某一直线l 的图象上,求此直线l 的函数解析式;(3分) (2)当2m =时,点P 为抛物线上一点,且090MOP ∠=,求点P 的坐标;(4分) (3)将(2)中的抛物线1C 沿x 轴翻折再向上平移1个单位向右平移n 个单位得抛物线2C ,设抛物线2C 的顶点为N ,抛物线2C 与x 轴相交于点A ,B (A 在B 的左边),且AM ∥BN ,求n 的值.(5分)7、(武昌19年模拟24题)如图,在平面直角坐标系xOy中,以直线x=52为对称轴的抛物线y=ax2+bx+c与直线l:y=kx+m(k>0)交于A(1,1),B两点,与y 轴交于C(0,5),直线l与y轴交于点D.(1)求抛物线的函数表达式;(2)设直线l与抛物线的对称轴的交点为F,G是抛物线上位于对称轴右侧的一点,若=34,且△BCG与△BCD面积相等,求点G的坐标;(3)若在x轴上有且仅有一点P,使∠APB=90°,求k的值.。

专题四:二次函数的图像与性质(中考15题)1.二次函数y =ax 2+bx +c (a ≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x =2,下列结论:①4a +b =0;②9a +c >3b ;③4a +2b ≥am 2+bm (m 为任意实数);④当x >﹣1时,y 的值随x 值的增大而增大;⑤若(−12,y 1),(133,y 2)是抛物线上两点,则y 1<y 2,⑥若点B (m ,y 1),C (4﹣m ,y 2)在此函数图象上,则y 1=y 2.其中正确的结论有 (填序号).第1题图 第2题图 第5题图2.如图,二次函数y =ax 2+bx +c (a ≠0)的图象与x 轴交于A (﹣1,0),对称轴为直线x =1,与y 轴的交点B 在(0,2)和(0,3)之间(不包括这两个点),下列结论:①当﹣1<x <3时,y >0;②﹣1<a <﹣.③当m ≠1时,a +b >m (am +b );④b 2﹣4ac =15a 2.其中正确的结论的序号 .3.抛物线y =ax 2+bx +c 经过点(﹣1,0),对称轴为直线x =2,与y 轴的交点在(0,﹣2)与(0,﹣3)之间(不包括这两点).下列结论:①a +b +c <0;②若点M (0.5,y 1)、N (2.5,y 2)在图象上,则y 1<y 2;③若m 为任意实数,则a (m 2﹣4)+b (m ﹣2)≥0;④﹣24≤5(a +b +c )<﹣16.其中正确结论的序号为 .4.在平面直角坐标系中,二次函数y =ax 2+bx +c (a ≠0)的图象与轴的交点分别(﹣3,0),(1,0),且函数与y 轴交点在(0,﹣1)的下方,现给以下结论:①abc <0:②关于方程a (x 2﹣1)+b (x ﹣1)+c =0始终有两个不相等的实数解;③当﹣2≤x ≤3时,y 的取值范围是﹣≤y ≤6b ;则上述说法正确的是 .(填序号)5.如图,二次函数y =ax 2+bx +c (a ≠0)的图象与x 轴交于A 、B 两点,与y 轴交于点C ,且OA =OC ,对称轴为直线x =1,则下列结论:①abc <0;②a +12b +14c =0;③当m <﹣1时,关于x 的方程ax 2+bx +c +m =0无实根;④ac ﹣b +1=0;⑤OA •OB =c a ,⑥2+c 是关于x 的一元二次方程ax 2+bx +c =0的一个根.其中正确的结论有 (填序号).6.二次函数y =ax 2+bx +c 的部分图象如图所示,对称轴为,与x 轴负半轴交点在(﹣4,0)与(﹣3,0)之间,以下结论:①3a ﹣b =0;②b 2﹣4ac >0;③5a ﹣2b +c >0;④4b +3c >0.其中一定正确的是 (填序号).7.如图,抛物线y =﹣x 2+2x +m +1(m 为常数)交y 轴于点A ,与x 轴的一个交点在2和3之间,顶点为B.以下结论:①抛物线y=﹣x2+2x+m+1与直线y=m+2有且只有一个交点;②若点M(﹣2,y1)、点N(,y2)、点P(2,y3)在该函数图象上,则y1<y2<y3;③将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为y=﹣(x+1)2+m;④点A关于直线x=1的对称点为C,点D、E分别在x轴和y轴上,当m=1时,四边形BCDE周长的最小值为.其中一定正确的是(填序号).第6题图第7题图第8题图8.二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣2,0),(x0,0),0<x0<1,与y轴正半轴相交,且交点在(0,1)的上方,下列结论:①2a<b;②(a+c)2<b2;③a(m2﹣1)+b(m+1)≤0(m 为任意实数);④b>2a+.其中一定成立的结论的序号是.9.二次函数y=ax2+bx+c的图象如图所示,给出下列结论:①abc>0;②3a﹣c>0;③若﹣1<m<n <1,则m+n<﹣;④<16,其中正确的序号是.10.如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2),且与x轴交点的横坐标分别为x1、x2,其中﹣1<x1<0,1<x2<2.下列结论:①﹣a<b<﹣2a;②b2+8a>4ac;③a<﹣1;④方程ax2+(b+c﹣2)x=0的解为x1=0,x2=1.其中正确的是.第9题图第10题图第11题图11.抛物线y=ax2+bx+c(a,b,c是常数,a≠0)的顶点坐标是(﹣2,3),与x轴的一个交点在点(﹣4,0)和点(﹣3,0)之间,其部分图象如图所示,下列结论:①4a﹣b=0;②关于x的方程ax2+bx+c=2有两个不相等实数根;③c≤3a.其中正确的序号是.12.二次函数y =ax 2+bx +c (a 、b 、c 为常数,a ≠0)中的x 与y 的部分对应值如下表:x ﹣3 01 y 4 4 n当n <0时,下列结论:①abc <0;②当x >﹣1时,y 的值随x 值的增大而减小;③a <﹣1;④n >4a ;⑤当n =−43时,关于x 的不等式ax 2+(b +43)x +c <0的解集为x <﹣3或x >1.其中一定正确的是 (填序号即可).13.二次函数y =ax 2+bx +c (a ,b ,c 是常数,a ≠0)的自变量x 与函数值y 的部分对应值如表: x … ﹣2 ﹣1 01 2 … y =ax 2+bx +c …t m ﹣2 ﹣2 n … 且当x =时,与其对应的函数值y >0,下列结论:①abc >0;②﹣2和3是关于x 的方程ax 2+bx +c=t 的两个根;③0<m +n <;④4a +c >n +2b ;其中,正确结论的是 . 14.二次函数y =ax 2+bx +c (a ,b ,c 为常数,a ≠0)中的x 与y 的部分对应值如表:x…… ﹣3 ﹣2 ﹣1 0 t …… y …… 0 m n m0 …… 下列结论中一定正确的有 .(填序号即可)①9a ﹣3b +c =0;②t =1;③关于x 的一元二次方程a (x ﹣1)2+bx +c =2a 的解是x 1=﹣2,x 2=2;④若方程ax 2+bx +c =p 有两个实数根x 1,x 2,则二次函数y =a (x ﹣x 1)(x ﹣x 2)+p 与x 轴的交点坐标是(﹣1,0),(3,0).15.定义[a 、b 、c ]为二次函数y =ax 2+bx +c (a ≠0)的特征数,下面给出特征数为[2m ,1﹣m ,﹣1﹣m ]的函数的一些结论:①当m =﹣3时,函数图象的顶点坐标是(,);②当m >0时,函数图象截x 轴所得的线段长度大于;③当m <0时,函数在x >时,y 随x 的增大而减小;④当m ≠0时,函数图象经过同一个点,正确的结论是 .16.已知,抛物线y =﹣x 2+mx +m (其中m 是常数).下列结论:①无论m 取何实数,它都经过定点P (﹣1,﹣1);②它的顶点在抛物线y =x 2+2x 上运动;③当它与x 轴有唯一交点时,m =0;④当x <﹣1时,﹣x 2+mx +m <x .其中一定正确的是 (填序号即可).17.二次函数y =(m +1)x 2﹣2mx +m ﹣2的图象与x 轴有两个交点(x 1,0)和(x 2,0),下列结论:①该函数图象过点(1,﹣1);②当m =0时,二次函数与坐标轴的交点所围成的三角形面积是2;③若该函数的图象开口向下,则m 的取值范围为﹣2<m <﹣1;④当m >0,且﹣2≤x ≤﹣1时,y 的最大值为(9m +2).其中一定正确的是 (填序号即可).18.已知二次函数y=ax2+bx+c(a>0,c<0)的图象经过点(,m),(3,n),与x轴交于点A(x1,0),点B(x2,0)(点A在点B的左侧).若7a+3b+2c=0,则有下列结论:①m<0,n>0;②x1+x2<;③<x2<3.其中一定正确的是(填序号即可).19.已知抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)的图象如图所示,下列结论:①b>a;②若﹣1<m<n<1,则m+n<﹣;③3|a|+|c|<2|b|.其中一定正确的是(填序号即可).第19题图第20题图第21题图20.数学课上老师出了这样一道题:如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣2,与x轴的一个交点在(﹣3,0)和(﹣4,0)之间,其部分图象如图所示,请同学们据此写出正确结论,每写对一个结论得20分,写错一个结论倒扣10分;小涛得到了如下结论:①c>0;②4a﹣b=0;③﹣3a+c>0;④4a﹣2b≥at2+bt(t为实数);⑤点(﹣3,y1),(﹣5,y2),(0,y3)是该抛物线的点,则y1>y3>y2.则小涛此题得分为21.如图,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)交于A,B两点,且点A的横坐标是﹣2,点B的横坐标是3,则以下结论:①抛物线y=ax2(a≠0)的图象的顶点一定是原点;②x>0时,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)的函数值都随着x的增大而增大;③AB的长度可以等于5;④△OAB有可能成为等边三角形;⑤当﹣3<x<2时,ax2+kx<b,其中一定正确的是(填序号即可).22.在平面直角坐标系xOy中,抛物线y=mx2﹣2mx+m﹣3与x轴交于点A、B.下列结论:①m的取值范围是m>0;②抛物线的顶点坐标为(1,﹣3);③若线段AB上有且只有5个点的横坐标为整数,则m的取值范围是<m≤;④若抛物线在﹣3<x<0这一段位于x轴下方,在5<x<6这一段位于x轴上方,则m的值为.其中一定正确的是(填序号即可).23.已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,3)和(0,4)之间(包含这两个点).有下列结论:①abc<0;②关于x的方程ax2+bx+c =2a有两个不等的实数根;③﹣≤a≤﹣1.其中一定正确的是(填序号即可).。
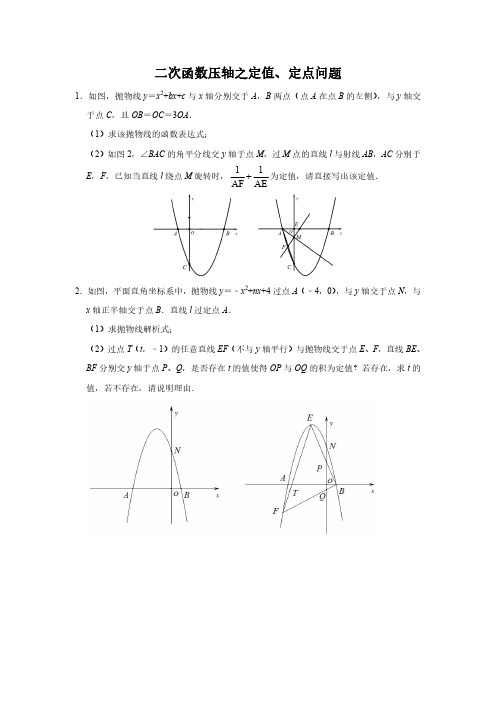
武汉中考第24题二次函数与垂直定点问题
武汉市中考第24题为二次函数的综合题,在2014年武汉市第24题第三问涉及到了直角定点问题,许多学生表示定点很难求,计算量偏大,今天笔者结合垂直问题整理了解题思路,对于这类问题做了一个小的归纳总结。
一、解题思路: 做水平和竖直辅助线得三垂直相似,如图1所示:
图1
已知AC BC ⊥,过点A 和点B 作平行于y 轴的直线,过点C 作平行于x 轴的直线,分别相交于D 和E 两点,那么由
ACD CBE ∠=∠,DAC ECB ∠=∠
可得
ACD
CBE .
所以有
AD DC
CE BE
=
进而求解题目。
二、实际例题:
例1:(2014年武汉)如图2,已知直线AB :24y kx k =++与抛物线2
12
y x =交于、A B 两点,若在抛物线上存在点D 使得90=ADB ∠°,求定点D 的坐标。
图2
作辅助线如图3所示
图3
则有
AED
DFB
则有
AE DE
DF BF
=
设()()211221,,,
2、、A x y B x y D m m ⎛⎫
⎪⎝⎭
,可得: 2
112221212
y m m x x m y m --=
-- 因为22112211
22
、y x y x =
=,所以因式分解可得: ()()121
14
m x m x ++=- 联立方程
2
2412
+y kx k y x =+=
化简可得:
22480x kx k ---=
韦达定理可得:
12122,48x x k x x k +=⋅=--
代入可得:
()2244m k m -=-
解得2m =,故()2,2D 。
例2:如图4所示,已知抛物线2
114
y x =
-与x 轴交于,A B 两点,A 在B 右侧,若,M N 为抛物线上两点,M 在N 的左侧,且以MN 为直径的圆始终经过A 点,求直线MN 经过的定点P 的坐标。
图4
作出辅助线如图5所示:
图5
则有:
MEA
AFN
则有:
ME AE
AF FN
=
设直线MN :y kx b =+,()()1122,,,M x y N x y 联立方程:
y kx b =+
2
114
y x =
- 化简可得:
24440x kx b ---=
韦达定理:
1244x x b ⋅=--、124x x k +=
已知()2,0A ,所以可得:
()
()
()
()
21
12
22
442424x
x x x
--=
--
化简可得:
()12122416x x x x +++=-
代入可得:
448416b k --++=
24b k =+
所以直线MN 的解析式为:
24y kx k =++
故过定点()2,4P -。
三、观察分析,得到猜想
例1中,动直线过定点()2,4-,抛物线上存在的定点D 使得条件成立的坐标为()2,2,例2中,抛物线上定点A 的坐标为()2,0,使得条件成立的直线过定点()2,4-,观察这几个点的坐标可以发现,两个例子中的定点的横坐标是互为相反数的,也就是两个定点到y 轴的距离是相等的,而这两个例题中的二次函数的对称轴就是y 轴,所以我们猜测,对于二次函数的垂直定点问题,可以“知一推一”,知道其中一个定点,我们可以快速求得另外一个定点的横坐标。
四、证明猜想 取特殊情况,二次函数对称轴为0。
(1)假设直线BC :()y k x m n =++,过定点(),m n -,
假设抛物线2
y ax c =+,定点A 使得90BAC ∠=°,求A 。
辅助线如图6所示:
图6
设()()1122,,,B x y C x y ()
2,,A t at c + 则由三垂直相似可得:
211
2
22y at c t x x t y at c
---=--- 化简可得
()()()()
111
222a x t x t t x x t a x t x t +--=-+-
()222212121a x x a t x x a t +++=-
联立方程:
2y kx km n y ax c
=++=+
可得:
20ax kx c km n -+--=
12c km n x x a --⋅=
、12k
x x a
+= 代入可化简:
()221a c km n akt a t --++=-
因为BC 是动直线,所以式子应该恒成立,和k 没有关系,那么可以得到: 0akm akt -+=
所以可得:t m =,证明完毕。
所以定点A 坐标为()
2,m am c +。
(2)假设直线BC 的解析式为y kx b =+,假设抛物线解析式为2
y ax c =+,抛物线上有定点A ()
2,m am c +使得90BAC ∠=°恒成立,求直线BC 过某一定点。
设()()1122,,,B x y C x y ,由三垂直相似可得
211
222y am c m x x m y am c
---=---
()()()()
111
222a x m x m m x x m a x m x m +--=-+-
化简可得:
()222212121a x x a m x x a m +++=-
联立方程:
2
y kx b y ax c
=+=+
可得:
20ax kx c b -+-=
12c b x x a -⋅=
、12k
x x a
+= 代入可得:
221ac ab akm a m -++=-
所以解得:
21b c mk am a
=+++
所以直线BC 解析式为:
21y kx c mk am a =++++
()21
y k x m c am a =++++
直线BC 过定点21,m c am a ⎛⎫
-++
⎪⎝⎭
,证明完毕。
五、由特殊到一般,得出结论 把抛物线从特殊推到一般等同于把抛物线进行平移变换,那么由相对平移我们可以固定抛物线,把对称轴和坐标轴进行平移,那么结论肯定仍然成立,读者可以自行证明。
观察两个证明,第一种证明,如果知道动直线过的定点,求抛物线上的定点的坐标就变得十分简单,直接由两点横坐标关于对称轴对称可以求出定点的横坐标,将横坐标代入解析式可以求定点的纵坐标。
第二种证明,知道抛物线过的定点坐标,也可以直接求解直线过的定点的坐标,可以由两点横坐标关于对称轴对称求出定点的横坐标,直线经过定点的纵坐标等于抛物线定点的纵坐标加上二次项系数的倒数。
即若已知动直线过定点(),M m n ,抛物线解析式为2
y ax bx c =++,那么抛物线上定
点A 坐标为1,b m n a a ⎛⎫
--
- ⎪⎝⎭
,若已知抛物线解析式为2y ax bx c =++,抛物线上定点A (),p q ,那么动直线过定点1,b M p q a a ⎛⎫
--
+ ⎪⎝
⎭。