八年级下期末考试几何难题突破
- 格式:docx
- 大小:46.05 KB
- 文档页数:2

八年级几何知识点难题解析在初中几何学习的过程中,几何知识点是必不可少的。
然而,八年级的几何知识点却是许多同学的难题。
本文将对八年级几何知识点中的难点进行解析,帮助同学们更好的掌握几何知识。
1. 圆的性质圆是八年级几何学习中必学的知识点之一。
圆有很多性质,比如弧度、切线、弦长等。
其中,最难掌握的要属弧度了。
弧度是圆心角所对的弧所对应的圆周长度与半径之比,用弧长的长度可以表示为s=rθ。
对于初学者来说,理解圆弧对应的圆心角以及计算弧长和角度之间的关系可能会较为困难。
解决这个难点的方法可以通过多画图、多练习进行巩固。
2. 三角形面积在初中阶段,三角形的面积是必修的数学知识。
对于直角三角形来说,面积等于底边乘以高。
但对于其他类型的三角形,计算面积就需要用到海龙公式、正弦公式等公式。
例如,海龙公式是根据三边求三角形面积的公式,公式为:S = √[p(p-a)(p-b)(p-c)],其中p为半周长,a、b、c为三角形的三边长。
对于初学者来说,可能较难理解公式的推导和应用。
解决这个难点的方法可以通过多练习和实例进行巩固和加深印象。
3. 平行四边形平行四边形也是八年级几何知识点中的重点之一。
其性质包括:对角线互相平分、相邻角互补、对边平行等。
其中,计算平行四边形面积、周长、对角线长度的公式也比较复杂。
例如,平行四边形的面积即为两条对角线长度的乘积乘以正弦角度。
对于初学者来说,可能需要花费较多的时间理解公式的应用方法。
解决这个难点的方法还是需要练习与实践。
4. 三角函数三角函数是高中数学的核心内容,但是在八年级的初学阶段中,三角函数也是一个较为难学的知识点。
三角函数主要包括正弦、余弦和正切等,应用十分广泛。
一些常见的性质包括角度、周期、对称轴、图像等。
对于初学者来说,难点可能在于理解三角函数的概念和性质,以及图像与周期的应用。
解决这个难点的方法是理解概念的基础上多进行练习,多画图,多做习题。
综上所述,八年级几何知识点的难点主要集中在圆的性质、三角形面积、平行四边形和三角函数等方面。

八年级下册物理期末考试高分突破必刷密卷(培优版)全解全析1.C【解析】【详解】梅西在发任意球时,能使足球由静止绕过人墙钻入球门(足球的运动状态不断变化),该现象说明力可以改变物体的运动状态,故C正确,ABD错误.2.B【解析】【详解】A.锅炉水位计和锅炉构成了一个连通器,水不流动时,液面总是相平的,通过观察水位计中水位的高低就可以知道锅炉中水的多少,故水位计是利用连通器的原理来工作的,故A错误;B.重力的方向总是竖直向下的,铅垂线是利用重力方向总竖直向下的原理来工作的,故B正确;C.钳子在使用时,动力臂大于阻力臂,故钳子是省力杠杆,故C错误;D.塑料吸盘,是利用大气压强的原理来工作的,故D错误。
故选B。
3.B【解析】【详解】将小铁块和小木块放入一盆水中.小铁块和小木块都会受到水的浮力作用.所以A说法错误.铁块沉入水底,是因为铁块受到的浮力小于它的重力.所以B说法正确.木块漂浮,所以木块受到的浮力等于木块的重力,但铁块的重力与木块的重力大小不知,所以C. D说法错误.4.C【解析】不计滑轮与轴及轻绳间的摩擦,假设物块与地面的摩擦力为f,由于第一个图中滑轮为定滑轮,使用过程不省力,故F1=f第二个图中滑轮为动滑轮,但F2处作用在动滑轮上,费2倍的力,所以F2=2f第三个图中滑轮为动滑轮,省一半的力,则31 2F f故F2>F1>F3,故C正确。
故选C 。
5.A【解析】A .平衡车的重力加上人的重力才等于地面对平衡车的支持力,不符合二力平衡的条件,故A 错误,A 符合题意;B .平衡车匀速行驶时,平衡车与车上人的位置没有发生改变,因此平衡车相对于车上的人是静止的,故B 正确,B 不符合题意;C .轮胎上的花纹,是在压力一定时,通过增大接触面的粗糙程度来增大摩擦力;故C 正确,C 不符合题意;D .关闭电机后,由于平衡车具有惯性,平衡车能继续前进,故D 正确,D 不符合题意。
故选A 。
6.B【解析】【详解】A .在容器两边分别装入不同深度的水,深度越大,压强越大,橡皮膜会向压强小的即深度浅的一边凸起,故A 错;B .两边水的深度相同,密度相同,压强相等,故橡皮膜不会凸起,故B 正确;CD .两边装有相同深度的水和盐水,盐水的密度大压强大,橡皮膜会向水的一边凸起,故C 、D 错。
P C F B Q 八年级(下)数学几何1、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F . 求证:∠DEN =∠F .2、如图,分别以△ABC 的AC 和BC 为一边,在△CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.3、 如图,以△ABC 的三边为边在BC △BCE 、△ACF ,请回答下列问题,并说明理由. (1)四边形ADEF 是什么四边形?(2)当△ABC 满足什么条件时,四边形(3)当△ABC 满足什么条件时,以A 、D 、边形不存在. 4.如图,梯形ABCD 中,AB ∥CD ,AD =BC ,AC ⊥形的高,试说明CF =21 (AB +CD), 5、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)6、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥分∠DCE .求证:PA =PF .(初二) 7、已知:△ABC 是正三角形,P 求:∠APB 的度数.(初二) 8、设P 是平行四边形ABCD 内部的一点,且∠PBA 求证:∠PAB =∠PCB .(初二)9、P 为正方形ABCD 内的一点,并且PA =a ,PB =10.图1,操作:把正方形CGEF 的对角线 如CE 放在正方形ABCD 的边BC 的延长线上(CG >取线段AE 的中点M 。
(1)(10分)探究:线段MD 、MF 的关系, 并加以证明。
DM 的延长线交CE 于点N ,且AD =NE ; ① 将正方形CGEF 绕点C 逆时针旋转45°(如图2其他条件不变;③在②的条件下且CF =2AD 。
(2)将正方形CGEF 绕点C 旋转任意角度后 (如图3),其他条件不变。
探究:线段MD 、MF 的关系,并加以证明。
M B 图111、已知:P是正方形ABCD对角线BD上一点,PE⊥DC,PF⊥BC,E、F分别为垂足,求证:AP=EF.12.如图,正方形ABCD的对角线AC、BD相交于点O①若E为AC上一点,过A作AG⊥EB于G,AG、BD交于F,求证:OE=OF②若点E在AC的延长线上,AG⊥EB交EB的延长线于G,AG的延长线交BD于点F,其他条件不变,OE=OF还成立吗?若成立,13CE上任意一点,PF⊥BDBD14.如图BAC=60°,(1)将Rt△AC'B',直线BB'探究:(2)的结论吗?为什么?。

经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)APCDB AFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 的中点,AD BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典难题(二)D 2 C 2B 2A 2 D 1C 1B 1CBDA A 1ANFECDMB1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)· ADHE M CBO· GA O DB ECQP NMP C GFBQADE 3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE 分别交于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二)经典难题(三)· O QPB DECNM · A1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .AFDECBEDACBF求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典难题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.FEP C BA OD BFAECP求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)APCBP A DCBCBDA4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.FP DE CBAAP2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.A CBPDA CBPD4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.经典难题(一)1.如下图做GH ⊥AB,连接EO 。

期末考试勾股定理与几何翻折压轴题专项训练【例题精讲】例1.(三角形翻折问题)如图,在Rt ABC △中,9086ABC AB BC ∠=︒==,,,分别在AB AC ,边上取点E F ,,将AEF △沿直线EF 翻折得到A EF '△,使得点A 的对应点A '恰好落在CB 延长线上,当60EA B '∠=︒时,AE 的长为 ,当A F AC '⊥时,AF 的长为 .【答案】 32− 407【分析】由折叠的性质可得AE A E '=,先求出30A EB '∠=︒,从而可得1122A B A E AE ''==,再由勾股定理可得BE AE =,最后由AE BE AB +=,进行计算即可;令A F '交AB 于G ,连接CG ,由折叠的性质可得:A EA F '∠=∠,AFE A FE '∠=∠,AEF A EF '∠=∠,AF A F '=,由A F AC '⊥得出90A FA A FC ''∠=∠=︒,45AFE A FE '∠=∠=︒,证明()ASA A FC AFG '≌得到CF FG =,设CF FG x ==,则10AF x =−,AG ,根据1122ACG S AC FG AG BC =⋅=⋅建立方程,解方程即可得出CF 的长,即可求解.【详解】解:由折叠的性质可得:AE A E '=,90ABC ∠=︒,18090A BE ABC '∴∠=︒−∠=︒,60EA B '∠=︒,9030A EB EA B ''∴∠=︒−∠=︒,1122A B A E AE ''∴==,BE AE∴==,AE BE AB+=,8AE AE∴=,32AE∴=−如图,令A F'交AB于G,连接CG,A F AC'⊥,90A FA A FC''∴∠=∠=︒,由折叠的性质可得:A EA F'∠=∠,AFE A FE'∠=∠,AEF A EF'∠=∠,AF A F'=,90AFE A FE'∠+∠=︒,45AFE A FE'∴∠=∠=︒,设A EA Fα'∠=∠=,则45FEB AFEα∠=∠=+︒,180135AEF FEB A EFα'∴∠=︒−∠=︒−=∠,()13545902A EB A EF BEFααα''∴∠=∠−∠=︒−−︒+=︒−,902EA B A EBα''∴∠=︒−∠=,FA C EA B EA F Aα'''∴∠=∠−∠==∠,在A FC'和AFG中,CA F AA F AFA FC AFG∠=∠⎧⎪=⎨⎪∠=∠''⎩',()ASAA FC AFG'∴≌,CF FG∴=,在Rt ABC△中,9086ABC AB BC∠=︒==,,,10AC∴,设CF FG x==,则10AF x=−,AG∴==1122ACGS AC FG AG BC=⋅=⋅,106x∴⋅=,整理得:271809000x x+−=,即29014400749x⎛⎫+=⎪⎝⎭,9012077x∴+=±,解得:307x=或30x=−(不符合题意,舍去),307CF∴=,30401077AF AC CF∴=−=−=,故答案为:32−407.【点睛】本题考查了折叠的性质、全等三角形的判定与性质、勾股定理、三角形的面积公式、等腰直角三角形的判定与性质、三角形外角的定义及性质、三角形内角和定理等知识,熟练掌握以上知识点,添加适当的辅助线是解此题的关键.例2.(坐标系中折叠问题)如图,在平面直角坐标系中,长方形ABCO的边OC OA、分别在x轴、y轴上,6AB=,点E在边BC上,将长方形ABCO沿AE折叠,若点B的对应点F 恰好是边OC的三等分点,则点E的坐标是.【答案】⎛−⎝⎭或(−【分析】本题主要考查了勾股定理与折叠问题,坐标与图形,由折叠的性质可得6AF AB==,BE EF=,90AFE B∠=∠=︒,再分当点F靠近点C时,24CF OF==,,当点F靠近点O 时,则42CF OF==,,两种情况利用勾股定理先求出OA的长,进而得到BC的长,设出CE 的长,进而得到EF的长,在Rt EFC△中,由勾股定理建立方程求解即可.【详解】解:在长方形ABCO 中,6CO AB ==,90BCO B AOC ∠=∠=∠=︒, 由折叠的性质可得6AF AB ==,BE EF =,90AFE B ∠=∠=︒,F 恰好是边OC 的三等分点,∴当点F 靠近点C 时,24CF OF ==,,在Rt AFO V中,OA =,∴BC OA ==设CE x =,则BE EF x ==,在Rt EFC △中,由勾股定理得到222EF CF CE =+,∴()2222xx =+,解得x =,∴点E的坐标是⎛− ⎝⎭; 当点F 靠近点O 时,则42CF OF ==,,在Rt AFO V中,OA ==∴BC OA ==设CE x =,则BE EF x ==,在Rt EFC △中,由勾股定理得到222CF CE =+,∴()2224x x =+,解得x =∴点E的坐标是(−;综上所述,点E的坐标是⎛− ⎝⎭或(−,故答案为:⎛− ⎝⎭或(−.例3.(四边形折叠问题)如图,已知矩形ABCD ,4AB =,5BC =,点P 是射线BC 上的动点,连接AP ,AQP △是由ABP 沿AP 翻折所得到的图形.(1)当点Q 落在边AD 上时,QC = ;(2)当直线PQ 经过点D 时,求BP 的长;(3)如图2,点M 是DC 的中点,连接MP 、MQ .①MQ 的最小值为 ;②当PMQ 是以PM 为腰的等腰三角形时,请直接写出BP 的长.【答案】(2)2BP =或8BP =(3) 2.9BP =或4BP =或10BP =【分析】(1)根据折叠的性质和勾股定理进行求解即可;(2)分点P 在线段BC 上,点P 在线段BC 的延长线上,两种情况,进行讨论求解;(3)①连接AM ,勾股定理求出AM 的长,折叠求出AQ 的长,根据MQ AM AQ ≥−,求出最小值即可;②分PM MQ =和PM PQ =两种情况,再分点P 在线段BC 上,点P 在线段BC 的延长线上,进行讨论求解即可.【详解】(1)解:当点Q 落在边AD 上时,如图所示,∵矩形ABCD ,4AB =,5BC =,∴4,5CD AB AD BC ====,90BAD B BCD ADC ∠=∠=∠=∠=︒,∵翻折,∴4,90AQ AB AQP B ==∠=∠=︒,∴1DQ AD AQ =−=,在Rt CDQ △中,CQ ==(2)当直线PQ 经过点D 时,分两种情况:当点P 在线段BC 上时,如图:∵翻折,∴4AQ AB ==,90AQP B ∠=∠=︒,BP PQ =,∴90AQD ∠=︒,∴3DQ ==,设BP PQ x ==,则:5PC BC BP x =−=−,3DP DQ PQ x =+=+,在Rt PCD △中,222DP CP CD=+,即:()()222345x x +=+−,∴2x =;∴2BP =;②当P 在线段BC 的延长线上时:∵翻折,∴4,90AQ AB Q B ==∠=∠=︒,BP PQ =,∴3DQ ==,设BP PQ x ==,则:5PC BP BC x =−=−,3DP PQ DQ x =−=−,在Rt PCD △中,222DP CP CD =+,即:()()222345x x −=+−,∴8x =;∴8BP =;综上:2BP =或8BP =;(3)①连接AM ,∵M 是CD 的中点, ∴122DM CM CD ===,∴AM =∵翻折,∴4AQ AB ==,∵MQ AM AQ ≥−,∴当,,A Q M 三点共线时,MQ 的值最小,即:4MQ AM AQ =−=4;②当PM PQ =时,如图:∵翻折,∴BP PQ PM ==,设BP x =,则:,5PM x CP BC BP x ==−=−,在Rt PCM 中,222PM CM PC =+,即:()22225x x =+−,解得: 2.9x =,即: 2.9BP =;当PM QM =,点P 在线段BC 上时,如图:∵,QM PM DM CM ==,90D C ∠=∠=︒,∴()HL MDQ MCP ≌,∴CP DQ =,点Q 在AD 上,由(1)知:1DQ =,∴1CP DQ ==,∴4BP BC CP =−=;当点P 在BC 的延长线上时:如图:此时点M 在AP 上,连接BM ,∵翻折,∴BM MQ PM ==,∵MC BP ⊥,∴210BP BC ==;综上: 2.9BP =或4BP =或10BP =.质,综合性强,难度大,属于压轴题.利用数形结合和分类讨论的思想进行求解,是解题的关键.【模拟训练】1.如图,在长方形ABCD 中,点E 是AD 的中点,将ABE 沿BE 翻折得到FBE ,EF 交BC 于点H ,延长BF DC 、相交于点G ,若8DG =,10BC =,则DC = .【答案】258【分析】本题考查了全等三角形的判定与性质,折叠的性质,勾股定理,连接EG ,根据点E 是AD 的中点得DE AE EF ==,根据四边形ABCD 是长方形得90D A ∠=∠=︒,根据将ABE 沿BE 翻折得到FBE 得90BFE D A ∠=∠=∠=︒,利用HL 证明Rt Rt EFG EDG △≌△,得8FG DG ==,设DC x =,则8CG DG DC x =−=−,8BG BF FG AB FG DC FG x =+=+=+=+,在Rt BCG V △中,根据勾股定理得,222CG BC BG +=,进行计算即可得.【详解】解:如图所示,连接EG ,∵点E 是AD 的中点,∴DE AE EF ==,∵四边形ABCD 是长方形,∴90D A ∠=∠=︒,∵将ABE 沿BE 翻折得到FBE ,∴90BFE D A ∠=∠=∠=︒在Rt EFG △和Rt EDG △中,EF ED EG EG =⎧⎨=⎩,∴()Rt Rt HL EFG EDG V V ≌,∴8FG DG ==,设DC x =,则8CG DG DC x =−=−,8BG BF FG AB FG DC FG x =+=+=+=+,在Rt BCG 中,根据勾股定理得,222CG BC BG +=,∴222(8)10(8)x x −+=+,解得258x =,故答案为:258.2.如图,在Rt ABC △中,90ACB ∠=︒,254AB =,154=AC ,点D 是AB 边上的一个动点,连接CD ,将BCD △沿CD 折叠,得到CDE ,当DE 与ABC 的直角边垂直时,AD 的长是 .【答案】154或54【分析】本题考查了勾股定理,平行四边形的判定和性质,折叠的性质,全等三角形的判定和性质,分DE BC ⊥和DE AB ⊥两种情况进行求解即可得到答案,根据题意,正确画出图形是解题的关键.【详解】解:如图,当DE BC ⊥时,延长ED 交BC 于点F ,CE 与AB 相交于点M ,∵EF BC ⊥,∴90EFC EFB ∠=∠=︒,∴90E ECF ∠+∠=︒,由折叠得,B E ∠=∠,CE CB =,MCD FCD ∠=∠,∴90B ECF ∠+∠=︒,∴90CMB ∠=︒,即C M A B ⊥,∵90ACB ∠=︒,254AB =,154=AC ,∴5BC ==, ∵1122ABC S AC BC AB CM ==△,∴11512552424CM ⨯⨯=⨯⨯,解得3CM =,∴4BM =,∵90CFD CMD FCD MCD CD CD ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩, ∴()AAS CFD CMD ≌,∴3CF CM ==,DF DM =,∴532BF BC CF =−=−=,设DF DM x ==,则4BD x =−,在Rt BFD 中,222DF BF BD +=,∴()22224x x +=−, 解得32x =, ∴35422BD =−=, ∴25515424AD AB BD =−=−=;当DE AB ⊥时,如图,设DE 与AC 相交于点M ,由折叠可得,BCD ECD ∠=∠,DE DB =,ED BD =,5EC BC ==,∵DE AB ⊥,90ACB ∠=︒,∴DE BC ∥,∴EDC BCD ∠=∠,∴EDC ECD ∠=∠,∴5ED EC ==,∴5BD ED ==, ∴255544AD AB BD =−=−=;综上,AD 的长是154或54, 故答案为:154或54.3.如图,等边三角形ABC 中,16AB BD AC =⊥,于点D ,点E F 、分别是BC DC 、上的动点,沿EF 所在直线折叠CEF △,使点C 落在BD 上的点C '处,当BEC '△是直角三角形时,BE 的值为 .【答案】24−或323【分析】本题考查了翻折变换,等边三角形的性质,折叠的性质,熟练运用折叠的性质是本题的关键.由等边三角形的性质可得30DBC ∠=︒,分9090BEC BC E ''∠=︒∠=︒,两种情况讨论,由直角三角形的性质即可求解.【详解】解:ABC 是等边三角形,BD AC ⊥,30,DBC ∴∠=︒ 由折叠的性质可得:,CE C E '=若90,BEC ∠'=︒且30,C BE ∠'=︒,2,BE E B E C C ∴='''=16,BE CE BC +==16,CE +=8,E E C C ∴'==24BE ∴=−若90,30,E C B E C B ∠'=︒='∠︒2,,BE E B C E C ∴'''=16,BE CE BC +==16,3CE E C =='∴ 32.3BE ∴=故答案为∶ 24−323.4.如图,在ABC 中,120ACB ∠=︒,8AC =,4BC =,将边BC 沿CE 翻折,使点B 落在AB 上的点D 处,再将边AC 沿CF 翻折,使点A 落在CD 的延长线上的点A '处,两条折痕与斜边AB 分别交于点E 、F ,则线段FA '的长为 .【答案】【分析】本题考查了折叠的性质,勾股定理,直角三角形的性质,添加恰当辅助线构造直角三角形是本题的关键.过点A 作AH BC ⊥交BC 的延长线于H ,由直角三角形的性质可求142HC AC ==,AH =AB 的长,由面积法可求CE 的长,由折叠的性质可求90BEC DEC ∠=∠=︒,BCE DCE ∠=∠,ACF DCF ∠=∠,然后再求解即可.【详解】解:如图,过点A 作AH BC ⊥,交BC 的延长线于H ,120ACB ∠=︒,ACB H HAC ∠=∠+∠,30HAC ∴∠=︒,142HC AC ∴==,AH ==,448BH ∴=+=,AB ∴1122ACB S BC AH AB CE =⨯⨯=⨯⨯,4CE ∴=,CE ∴,将边BC 沿CE 翻折,使点B 落在AB 上的点D 处,再将边AC 沿CF 翻折,90BEC DEC ∴∠=∠=︒,BCE DCE ∠=∠,ACF DCF ∠=∠,1602ECF ACB ∴∠=∠=︒,30CFE ∴∠=︒,EF ∴,在Rt BCE中,BE ===,AF AB EF BE ∴=−−==FA AF '∴==故答案为:5.如图,点D 是ABC 的边AB 的中点,将BCD △沿直线CD 翻折能与ECD 重合,若4AB =,2CD =,1AE =,则点C 到直线AB 的距离为 .【答案】【分析】连接BE ,延长CD 交BE 于点G ,作CH AB ⊥于点H ,如图所示,由折叠的性质及中点性质可得AEB △为直角三角形,且G 为BE 中点,从而CG BE ⊥,由勾股定理可得BE的长,再根据2ABC BDC S S =△△,即11222AB CH CD BG ⋅=⨯⋅,从而可求得CH 的长.【详解】解:连接BE ,延长CD 交BE 于点G ,作CH AB ⊥于点H ,如图所示,由折叠的性质可得:BD ED =,CB CE =,∴CG 为BE 的中垂线, ∴12BG BE =,∵点D 是AB 的中点,4AB =,2CD =,1AE =, ∴122BD AD AB ===,CBD CAD S S =,AD DE =,∴DBE DEB ∠=∠,DEA DAE ∠=∠,∵180EDA DEA DAE ∠+∠+∠=︒,即22180DEB DEA ∠+∠=︒,∴90DEB DEA ∠+∠=︒,即90BEA ∠=︒,∴BE∴12BG BE ==, ∵2ABC BDCS S =△△, ∴11222AB CH CD BG ⋅=⨯⋅,∴422CH =⨯,∴CH ,∴点C 到直线AB 的距离为.故答案为:.【点睛】本题考查翻折变换,线段中垂线的判定,等腰三角形的性质,点到直线的距离,直角三角形的判定,勾股定理,利用面积相等求相应线段的长,解题的关键是得出CG 为BE 的中垂线,2ABC BDC S S =△△.6.如图,在ABC 中,90,A AB AC ∠=︒==D 为AC 边上一动点,将C ∠沿过点D 的直线折叠,使点C 的对应点C '落在射线CA 上,连接BC ',当Rt ABC '△的某一直角边等于斜边BC '长度的一半时,CD 的长度为 .【答案】 或 【分析】由翻折得,12CD CC '=,分三种情况:①当点C '在边AC 上,且12AC BC ''=(即2BC AC ''=)时;②当点C '在CA 的延长线上,且12AC BC ''=(即2BC AC ''=)时;③当点C '在CA 的延长线上,且12AB BC '=(即2BC AB '==时,分别根据勾股定理求出AC '的长,再求出CC '的长即可 【详解】解:由翻折得,12CD CC '=,分三种情况:①当点C '在边AC 上,且12AC BC ''=(即2BC AC ''=)时,90,A AB AC ∠=︒==∴由勾股定理得,222BC AC AB ''−=,即222(2)AC AC ''−=,AC '∴=CC '∴CD ∴;②当点C '在CA 的延长线上,且12AC BC ''=(即2BC AC ''=)时,同理得AC 'CC '∴CD ∴;③当点C '在CA 的延长线上,且12AB BC '=(即2BC AB '==由勾股定理得,222AC BC AB ''=−,即22218AC '=−=,AC '∴=CC '∴CD ∴=,0>,CD AB ∴>,此时点D 不在边AC 上,不符合题意,舍去,综上,当Rt ABC '△的某一直角边等于斜边BC '长度的一半时,CD 的长度为或.故答案为:或.【点睛】本题主要考查图形的翻折变换(折叠问题),勾股定理,等腰直角三角形的性质等知识,灵活运用折叠的性质及勾股定理是解答本题的关键,同时要注意分类思想的运用.7.如图,在ABC 中,90ACB ∠=︒,3AC =,4BC =,P 为斜边AB 上的一动点(不包含A ,B 两端点),以CP 为对称轴将ACP △翻折得到A CP ',连结BA '.当A P AB '⊥时,BA '的长为 .【答案】【分析】当A P AB '⊥时,过点C 作CD AB ⊥于D ,可知125CD =,95AD =,得出PDC △为等腰直角三角形,得到PD CD =,求出PA '和BP 的长,利用勾股定理即可求出BA '的长.【详解】过点C 作CD AB ⊥于D ,在Rt ADC 中,90ACB ∠=︒,3AC =,4BC =,∴5AB = ∵1122AC BC AB CD ⨯=⨯,125CD ∴=,在Rt ADC 中,3AC =∴95AD ==,当A P AB '⊥时,如图由折叠性质可知12∠=∠,PA PA '=,又1290A PA '∠=∠+∠=︒145∠=∠2=︒∴,又2390∠+∠=︒,345∴∠=︒,23∴∠=∠,125PD CD ∴==,又PA PD AD =+,12921555PA ∴=+=,又PA PA '=,215PA '∴=,又BP AB PA =−,214555BP ∴=−=,在Rt BPA '△中,90BPA ∠='︒,222BP PA BA ∴='+,2224214575525BA ⎛⎫⎛⎫'∴=+= ⎪ ⎪⎝⎭⎝⎭,BA '∴=,故答案为:.【点睛】本题考查了勾股定理的应用,折叠问题,熟练掌握勾股定理是解题的关键.8.如图,在ABC 中,90ACB ∠=︒,AC BC =,D 为AB 上一点,连接DC ,将BDC 沿DC 翻折,得到EDC △,连接AE ,若AE CE =,4BC =,则D 到CE 的距离是 .【答案】2【分析】本题考查等腰直角三角形中的折叠问题,涉及等边三角形判定与性质,勾股定理应用、面积法等知识.设BE 交CD 于G ,过E 作EF BC ⊥交BC 延长线于F ,根据将BDC 沿DC 翻折,得到EDC △,AC BC =,AE CE =,可得ACE △是等边三角形,即知60ACE ∠=︒,而90ACB ∠=︒,故150BCE ∠=︒,30ECF ∠=︒,可得75BCD ECD ∠=∠=︒,122EF CE ==,CF =BE =15CBE ∠=︒,可得90BGC ∠=︒,即CG BE ⊥,从而12BG BE GE ===,由勾股定理得CG ,在Rt BDG △中,DG ,即得CD DG CG =+,由面积法可得D 到CE 的距离是2. 【详解】解:设BE 交CD 于G ,过E 作EF BC ⊥交BC 延长线于F ,如图:将BDC 沿DC 翻折,得到EDC △,4BC CE ∴==,BCD ECD ∠=∠,AC BC =,AE CE =,AC BC CE AE ∴===,ACE ∴是等边三角形,60ACE ∴∠=︒,90ACB ∠=︒,150BCE ∴∠=︒,30ECF ∠=︒,75BCD ECD ∴∠=∠=︒,122EF CE ==,CF =在Rt BEF △中,BE ==BCE 中,BC CE =,150BCE ∠=︒,15CBE ∴∠=︒,18090BGC BGC BCD ∴∠=︒−∠−∠=︒,即CG BE ⊥,12BG BE GE ∴==,CG ∴===,45ABC ∠=︒,15CBE ∠=︒,30DBG ∴∠=︒,在Rt BDG△中,DG =,CD DG CG ∴=+=,设D 到CE 的距离是h ,2DCE S CE h DC GE ∆=⋅=⋅,324DC GE h CE ⋅∴===,故答案为:2.9.在生活中、折纸是一种大家喜欢的活动、在数学中,我们可以通过折纸进行探究,探寻数学奥秘.【纸片规格】三角形纸片ABC ,120ACB ∠=︒,CA CB =,点D是底边AB 上一点.【换作探究】(1)如图1,若6AC =,AD =CD ,求CD 的长度;(2)如图2,若6AC =,连接CD ,将ACD 沿CD 所在直线翻折得到ECD ,点A 的对应点为点.E 若DE 所在的直线与ABC 的一边垂直,求AD 的长;(3)如图3,将ACD 沿CD 所在直线翻折得到ECD ,边CE 与边AB 交于点F ,且DE BC ∥,再将DFE △沿DF 所在直线翻折得到DFG ,点E 的对应点为点G ,DG 与CE 、BC 分别交于H ,K ,若1KH =,请直接写出AC 边的长.【答案】(1)(2)3或(3)3【分析】(1)作CE AB ⊥于E ,求得30A B ==︒∠∠,从而得出132CE AC ==,AE AC =进而得出DE AE AD =−=(2)当DE AB ⊥时,连接AE ,作CG AB ⊥于G ,依次得出45DAE DEA ∠=∠=︒,304575CAE CAD DAE ∠=∠+∠=︒+︒=︒,75CEA CAE ∠=∠=︒,30ACE ∠=︒,15ACD DCE ∠=∠=︒,45CDG CAB DAC ∠=∠+∠=︒,从而DG CG =,进一步得出结果;当ED AC ⊥时,设ED 交AC 于点W CE ,交AB 于V ,可推出90AVC ∠=︒,60ACE ∠=︒,从而30ACD DCE ∠=∠=︒,进一步得出结果;当DE BC ⊥时,可推出180ACB BCE ∠+∠=︒,从而90ACD DCE ∠=∠=︒,进一步得出结果;(3)可推出CKH 和CDH △及CHK 是直角三角形,且30HCK ∠=︒,30HDF ∠=︒,45DCH ∠=︒,进一步得出结果.【详解】(1)解:如图1,作CE AB ⊥于E ,90AEC ∴∠=︒,CA CB =,120ACB ∠=︒,30A B ∴∠=∠=︒,132CE AC ∴==,AE =,DE AE AD ∴=−==CD ∴=;(2)解:如图2,当DE AB ⊥时,连接AE ,作CG AB ⊥于G ,由翻折得:AD DE =,CAD CED =∠∠,AC CE =,45DAE DEA ∠∠∴==︒,304575CAE CAD DAE ∴∠=∠+∠=︒+︒=︒,75CEA CAE ∴∠=∠=︒,30ACE ∴∠=︒,15ACD DCE ∴∠=∠=︒,45CDG CAB DAC ∴∠=∠+∠=︒,DG CG ∴=,由(1)知:3CG =,AG =3AD AG DG ∴=−=;如图3,当ED AC ⊥时,设ED 交AC 于点W CE ,交AB 于V ,90E ACE ∴∠+∠=︒,E A ∠=∠,90A ACE ∴∠+∠=︒,90AVC ∴∠=︒,60ACE∴∠=︒,30ACD DCE∴∠=∠=︒,ACD A∴∠=∠,AD CD∴=,3CV =,CD∴=,AD CD∴==如图4,当DE BC⊥时,30E A∠=∠=︒,60BCE∴∠=︒,180ACB BCE∴∠+∠=︒,90ACD DCE∴∠=∠=︒,AD∴=,综上所述:3AD=或(3)解:如图5,∵DE BC ∥,30B C ∠=∠=︒,30BCF E ∴∠=∠=︒,30EDF B ∠=∠=︒,120ACB ∠=︒,90ACE ∴∠=︒,1452ECD ACD ACE ∴∠=∠=∠=︒,将DFE △沿DF 所在直线翻折得到DFG ,30GDF EDF ∴∠=∠=︒,60EDG ∴∠=︒,90CHK EHD ∴∠=∠=︒,DH CH ∴=1FH ∴==,1CF CH FH ∴=+,3AC ∴==.【点睛】本题考查了等腰三角形的判定和性质,直角三角形的性质等知识,解决问题的关键是正确分类,画出图形.10.如图,在ABC 中,90BAC ∠=︒,AB AC =,点D 为线段BC 延长线上一点,以AD 为腰作等腰直角DAF △,使90DAF ∠=︒,连接CF .(1)请判断CF 与BC 的位置关系,并说明理由;(2)若8BC =,4CD BC =,求线段AD 的长;(3)如图2,在(2)的条件下,将DAF △沿线段DF 翻折,使点A 与点E 重合,连接CE ,求线段CE 的长.【答案】(1)CF BC ⊥,理由见解析(2)(3)【分析】(1)证明()SAS ABD ACF △≌△,则ADB AFC ∠=∠,如图1,记AD CF 、的交点为O ,根据180FAO AFO AOF DCO CDO COD ∠+∠+∠=︒=∠+∠+∠,AOF COD ∠=∠,可得90FAO DCO ∠=∠=︒,进而可得CF BC ⊥;(2)如图2,过A 作AH BC ⊥于H ,则142BH CH AH BC ====,6DH =,由勾股定理得,AD =(3)由翻折的性质可知,DE AD =,45EDF ADF ∠=∠=︒,90ADE ∠=︒,如图3,过A 作AM BC ⊥于M ,过E 作EN BC ⊥于N ,证明()AAS ADM DEN ≌,则46DN AM EN DM ====,,6CN =,由勾股定理得,CE =计算求解即可.【详解】(1)解:CF BC ⊥,理由如下:∵等腰直角DAF △,90DAF ∠=︒,∴AD AF =,又∵90BAC ∠=︒,∴BAC CAD DAF CAD ∠+∠=∠+∠,即BAD CAF ∠=∠,∵AB AC =,BAD CAF ∠=∠,AD AF =,∴()SAS ABD ACF △≌△,∴ADB AFC ∠=∠,如图1,记AD CF 、的交点为O ,∵180FAO AFO AOF DCO CDO COD ∠+∠+∠=︒=∠+∠+∠,AOF COD ∠=∠,∴90FAO DCO ∠=∠=︒,∴CF BC ⊥;(2)解:∵8BC =,4CD BC =,∴2CD =,如图2,过A 作AH BC ⊥于H ,∵ABC 是等腰直角三角形, ∴142BH CH AH BC ====,∴6DH =,由勾股定理得,AD =∴线段AD 的长为(3)解:由翻折的性质可知,DE AD =,45EDF ADF ∠=∠=︒,∴90ADE ∠=︒,如图3,过A 作AM BC ⊥于M ,过E 作EN BC ⊥于N ,∴90AMD DNE ∠=︒=∠,同理(2)可知,4AM =,6MD =,∵90ADM EDN EDN DEN ∠+∠=︒=∠+∠,∴ADM DEN ∠=∠,∵90AMD DNE ∠=︒=∠,ADM DEN ∠=∠,AD DE =,∴()AAS ADM DEN ≌,∴46DN AM EN DM ====,,∴6CN =,由勾股定理得,CE =,∴线段CE 的长为【点睛】本题考查了全等三角形的判定与性质,三角形内角和定理,勾股定理,折叠的性质,等腰三角形的性质.熟练掌握全等三角形的判定与性质,折叠的性质是解题的关键.11.如图1,在Rt ABC △中,90C ∠=︒,5AC =,12BC =,点D 为BC 边上一动点,将ACD 沿直线AD 折叠,得到AFD △,请解决下列问题.(1)AB =______;当点F 恰好落在斜边AB 上时,CD =______;(2)连接CF ,当CBF V 是以CF 为底边的等腰三角形时,请在图2中画出相应的图形,并求出此时点F 到直线AC 的距离;(3)如图3,E 为边BC 上一点,且4,连接EF ,当DEF 为直角三角形时,CD = .(请写出所有满足条件的CD 长)【答案】(1)13,103(2)画图见解析,600169(3)52或或5或10【分析】(1)根据勾股定理可得AB 的长,再利用等积法求出CD 即可;(2)过点F 作FG AC ^,交CA 的延长线于G ,首先由等积法求出CH 的长,再根据勾股定理求出AH 的长,再次利用等积法可得FG 的长;(3)分90DEF ∠=︒或90EDF ∠=︒或90EFD ∠=︒分别画出图形,从而解决问题.【详解】(1)解:在Rt ABC △中,由勾股定理得,13AB ,当点F 落在AB 上时,由折叠知,CD DF =, ∴111222AC CD AB DF AC BC ⋅+⋅=⋅,51360CD CD ∴+=,103CD ∴=,故答案为:13,103;(2)过点F 作FG AC ^,交CA 的延长线于G ,BC BF =,AC AF =,AB ∴垂直平分CF , 由等积法得6013AC BC CH AB ⋅==,在Rt ACH 中,由勾股定理得,2513AH ===, 1122ACF S AC FG CF AH =⋅=⋅△,6025260013135169CF AH FG AC ⨯⨯⋅∴===;(3)当90DEF ∠=︒时,当点D 在CE 上时,作FH AC ⊥于H ,则4HF CE ==,5AF AC ==,3AH ∴=,2CH EF AC AH ∴==−=,设CD x =,则4DE x =−,在Rt EDF 中,由勾股定理得,222(4)2x x =−+, 解得52x =,52CD ∴=, 当点D 在EB 上时,同理可得538CH AC AH =+=+=,设CD DF x ==,则4DE x =−,在Rt EDF 中,由勾股定理得,222(4)8x x −+=,解得10x =,10CD ∴=,当90DFE ∠=︒时,由勾股定理得AE设CD DF x ==,则520x +=,x ∴,CD ∴=;当90FDE ∠=︒时,则45ADC ADF ∠=∠=︒,5CD AC ∴==,综上:52CD =或或5或10,故答案为:52或或5或10.【点睛】本题是三角形综合题,主要考查了翻折的性质,直角三角形的性质,勾股定理,等腰直角三角形的判定与性质等知识,利用等积法求垂线段的长是解题的关键.。

部编人教版八年级数学下册难点突破微专题(含解答)目录1、难点突破微专题一:勾股定理与旋转问题2、难点突破微专题二:一次函数方案设计3、难点突破微专题三:一次函数与定点、定值、定直线4、难点突破微专题四:一次函数与方程、不等式5、难点突破微专题五:一次函数与几何结合6、难点突破微专题六:借助勾股定理求最值7、难点突破微专题七:勾股定理与分类讨论8、难点突破微专题八:中点问题9、部编人教版八年级数学下册难点突破微专题九:四边形中的综合运用部编人教版八年级数学下册难点突破微专题一勾股定理与旋转问题【方法技巧】将图形旋转后得到直角三角形,再考虑用勾股定理难点突破一等边三角形为背景→旋转︒601.如图,点P为等边三角形△ABC内的一点,且PC=3,PB=4,PA=5(1)画出将△BPC绕点B逆时针方向旋转︒60后的图形;(2)求∠BPC的度数难点突破二等腰直角三角形为背景→旋转︒902.如图,在等腰直角△ABC中,∠ACB=︒45,90,点D,E在AB上,且∠DCE=︒BE=2,AD=3(1)将△BCE绕点C逆时针旋转︒90后,在图中画出旋转后的图形;(2)求DE的长难点突破三︒60(补形)→构成共顶点的两个等边三角形3.如图,在△ABC中,∠ABC=︒30,AB=6,BC=8,△ACD是等边三角形,求BD的长。
难点突破四旋转︒90(补形)→构成共顶点的两个等腰直角三角形4.如图,AB=AC,∠CAB=︒90,∠ADC=︒45,AD=4,CD=3,求BD的长。
参考答案1. 解(1)如图所示,△BQA 为△BPC 绕点B 逆时针方向旋转︒60后的图形; (2)如图,连PQ由旋转性质,△BQA ≌△BPC ,△BPQ 为等边三角形 ∴AQ =3 ,QB =4,∠BPC =∠AQB ∠BQP =︒60 又PA =5∴△PQA 为直角三角形 ∴∠AQC =︒90∴∠BPC =∠AQB =∠AQC+∠BQP =︒150134513904522901.222======中和在又===,==,==由旋转后全等性,有:)连(后的图形。
八年级数学几何解答题难题训练1,如图矩形ABCD对角线AC、BD交于O,E F分别是OA、OB的中点(1)求证△ADE ≌△BCF:(2)若AD=4cm,AB=8cm,求CF的长。
证明:(1)在矩形ABCD中,AC,BD为对角线,∴AO=OD=OB=OC∴∠DAO=∠ADO=∠CBO=∠BCO∵E,F为OA,OB中点∴AE=BF=1/2AO=1/2OB∵AD=BC, ∠DAO=∠CBO,AE=BF∴△ADE≌△BCF(2)过F作MN⊥DC于M,交AB于N∵AD=4cm,AB=8cm∴BD=4根号5∵BF:BD=NF:MN=1:4∴NF=1,MF=3∵EF为△AOB中位线∴EF=1/2AB=4cm∵四边形DCFE为等腰梯形∴MC=2cm∴FC=根号13cm。
2,如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=2DC,对角线AC⊥BD,垂足为F,过点F作EF∥AB,交AD于点E,CF=4cm.(1)求证:四边形ABFE是等腰梯形;(2)求AE的长.(1)证明:过点D作DM⊥AB,∵DC∥AB,∠CBA=90°,∴四边形BCDM为矩形.∴DC=MB.∵AB=2DC,∴AM=MB=DC.∵DM⊥AB,∴AD=BD.∴∠DAB=∠DBA.∵EF∥AB,AE与BF交于点D,即AE与FB不平行,∴四边形ABFE是等腰梯形.(2)解:∵DC∥AB,∴△DCF∽△BAF.∴CD AB =CF AF =1 2 .∵CF=4cm,∴AF=8cm.∵AC⊥BD,∠ABC=90°,在△ABF与△BCF中,∵∠ABC=∠BFC=90°,∴∠FAB+∠ABF=90°,∵∠FBC+∠ABF=90°,∴∠FAB=∠FBC,∴△ABF∽△BCF,即BF CF =AF BF ,∴BF2=CF•AF.∴BF=4 2 cm.∴AE=BF=4 2 cm.3,如图,用三个全等的菱形ABGH、BCFG、CDEF拼成平行四边形ADEH,连接AE与BG、CF分别交于P、Q,(1)若AB=6,求线段BP的长;(2)观察图形,是否有三角形与△ACQ全等?并证明你的结论解:(1)∵菱形ABGH、BCFG、CDEF是全等菱形∴BC=CD=DE=AB=6,BG∥DE∴AD=3AB=3×6=18,∠ABG=∠D,∠APB=∠AED∴△ABP∽△ADE∴BP DE =AB AD∴BP=AB AD •DE=6 18 ×6=2;(2)∵菱形ABGH、BCFG、CDEF是全等的菱形∴AB=BC=EF=FG∴AB+BC=EF+FG∴AC=EG∵AD∥HE∴∠1=∠2∵BG∥CF∴∠3=∠4∴△EGP≌△ACQ.4,已知点E,F在三角形ABC的边AB所在的直线上,且AE=BF,FH//EG//AC,FH、EC分∴∠F=∠A,∠FBH=∠ABC=∠AEP.又∵AE=BF,∴△BHF≌△EPA.∴HF=AP.∴AC=PC+AP=EG+HF.即EG+FH=AC.5,如图是一个常见铁夹的侧面示意图,OA,OB表示铁夹的两个面,C是轴,CD⊥OA 于点D,已知DA=15mm,DO=24mm,DC=10mm,我们知道铁夹的侧面是轴对称图形,请求出A、B两点间的距离.解:连接AB,同时连接OC并延长交AB于E,因为夹子是轴对称图形,故OE是对称轴,∴OE⊥AB,AE=BE,∴Rt△OCD∽Rt△OAE,∴OC:OA = CD:AE∵OC²=OD²+CD² ∴OC =26,∴AE= =15,∵AB=2AE ∴AB =30(mm).(8分)答:AB两点间的距离为30mm.6,如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上一点,且∠BFE=∠C,(1)求证:△ABF∽△EAD ;(2)若AB=5,AD=3,∠BAE=30°,求BF 的长解:(1)∵四边形ABCD是平行四边形∴AB∥CD,AD∥BC∴∠BAE=∠AED,∠D+∠C=180°且∠BFE+∠AFB=180°又∵∠BFE=∠C∴∠D=∠AFB∵∠BAE=∠AED,∠D=∠AFB∴△ABF∽△EAD(2)∵∠BAE=30°,且AB∥CD,BE⊥CD∴△ABEA为Rt△,且∠BAE=30°又∵AB=4∴AE=3分之8倍根号37,如图,AB与CD相交于E,AE=EB,CE=ED,D为线段FB的中点,GF与AB相交于点G,若CF=15cm,求GF之长。
初二下期末几何及解析1、以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,连接EB、FD,交点为G.(1)当四边形ABCD为正方形时(如图1),E B和FD的数量关系是_____________;(2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的数量关系?请加以证明;(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由;如果不变,请在图3中求出∠EGD的度数.难度一般:证全等即可(第三问,图1中就能看出是45°。
)解(1)EB=FD 。
(2)EB=FD。
证:∵△AFB为等边三角形,∴AF=AB,∠FAB=60°∵△ADE为等边三角形,∴AD=AE,∠EAD=60°,∴∠FAB+∠BAD=∠EAD+∠BAD即∠FAD=∠BAE,∴△FAD≌△BAE,∴EB=FD(3)解:∵△ADE为等边三角形,∴∠AED=∠EDA=60°∵△FAD≌△BAE,∴∠AEB=∠ADF设∠AEB为x°,则∠ADF也为x°于是有∠BED为(60-x)°,∠EDF为(60+x)°∴∠EGD=180°-∠BED-∠EDF=180°-(60-x)°-(60+x)°=60°2、已知:如图,在□ABCD中,点E是BC的中点,连接AE并延长交DC的延长线于点F,连接BF.(1)求证:△ABE≌△FCE;(2)若AF=AD,求证:四边形ABFC是矩形.简单题证明:(1)如图1.在△ABE和△FCE中,∠1=∠2,∠3=∠4,BE=CE,∴△ABE≌△FCE.FAB CDE4321EDCBAF(2)∵△ABE≌△FCE,∴AB=FC.∵AB∥FC,∴四边形ABFC是平行四边形.∵四边形ABCD是平行四边形,∴AD=BC.∵AF=AD,∴AF=BC.∴四边形ABFC是矩形.3、已知:△ABC是一等腰直角三角形纸板,∠B=90°,AB=BC=1.(1)要在这纸板上剪出一个正方形,使这个正方形的四个顶点都在△ABC的边上.小林设计出了一种剪法,如图1所示.请你再设计出一种不同于图1的剪法,并在图2中画出来.(2)若按照小林设计的图1所示的剪法来进行裁剪,记图1为第一次裁剪,得到1个正方形,将它的面积记为1S,则1S=___________;余下的2个三角形中还按照小林设计的剪法进行第二次裁剪(如图3),得到2个新的正方形,将此次所得2个正方形的面积的和.记为2S,则2S=___________;在余下的4个三角形中再按照小林设计的的剪法进行第三次裁剪(如图4),得到4个新的正方形,将此次所得4个正方形的面积的和.记为3S;按照同样的方法继续操作下去……,第n次裁剪得到_________个新的正方形,它们的面积的和.nS=______________.(题外题:把你剪出的正方形的面积与图1中的正方形面积进行比较。
专题几何中常见模型及辅助线题型大视野【例题精讲】题型一、手拉手模型例题.【2019·惠州市期末】如图,正方形ABCD的对角线AC、BD相交于点O,正方形A′B′C′D′的顶点A′与点O重合,A′B′交BC于点E,A′D′交CD于点F.(1)求证:OE=OF;(2)若正方形ABCD的边长为1,求两个正方形重叠部分的面积;(3)若正方形A′B′C′D′绕着O点旋转,EF的长度何时最小,并求出最小值.【答案】见解析.【解析】解:(1)∵四边形ABCD是正方形,四边形OB’C’D’是正方形,∴OB=OC,∠BOC=90°,∠B’OD’=90°,∠OBE=∠OCF=45°,∴∠BOE=∠FOC,∴△BOE≌△COF,∴OE=OF;(2)由(1)知,△BOE≌△COF,∴S△BOE=S△COF∴两正方形重叠部分面积=S四边形OECF=S△COF+S△OCE=S△BOE+S△OCE=S△BOC=1 4(3)由(1)知OE=OF,则△EOF是等腰直角三角形,∴EF=OE,由垂线段最短,知当OE⊥BC时,OE长度最小,最小为12,此时EF长度最小,即EF最小值为:2 2 .题型二、一线三直角模型例题.【2019·临沂市期中】如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.【答案】见解析.【解析】解:(1)结论:PB=PQ,理由:过P作PE⊥BC于E,PF⊥CD于F,∵P为正方形对角线AC上的点,∴PC平分∠DCB,∠DCB=90°,∴PF=PE,∴四边形PECF为正方形.∵∠BPE+∠QPE=90°,∠QPE+∠QPF=90°,∴∠BPE=∠QPF,∴Rt△PQF≌Rt△PBE,∴PB=PQ;(2)结论:PB=PQ.理由:过P作PE⊥BC于E,PF⊥CD于F,∵P为正方形对角线AC上的点,∴PC平分∠DCB,∠DCB=90°,∴PF=PE,∴四边形PECF为正方形,∵∠BPF+∠QPF=90°,∠BPF+∠BPE=90°,∴∠BPE=∠QPF,∴Rt△PQF≌Rt△PBE,∴PB=PQ.题型三、辅助线例1.【2019·莆田市期末】如图1,在正方形ABCD中,E、F分别是BC、AB上一点,且AF=BE,AE与DF交于点G.(1)求证:AE=DF.(2)如图2,在DG上取一点M,使AG=MG,连接CM,取CM的中点P.写出线段PD与DG之间的数量关系,并说明理由.【答案】见解析.【解析】(1)证明:∵四边形ABCD是正方形,∴AD=AB,∠DAF=∠ABE=90°,∵AF=BE,∴△DAF≌△ABE(SAS),∴AE=DF.(2)解:结论:DG PD.理由:连接GP并延长至H,使GP=PH,连接DH、CH,∵PM=PC,∠MPG=∠CPH,PG=PH,∴△MPG≌△CPH(SAS),∴∠PMG=∠PCH,GM=CH=AG,∴DF∥CH,∴∠FDC=∠DCH,∵∠DAG+∠ADG=90°,∠ADG+∠CDF=90°,∴∠DAG=∠CDG=∠DCH,∵DA=DC,∴△DAG≌△DCH(SAS),∴DG=DH,∠ADG=∠CDH,∴∠GDH=∠ADC=90°,∴△GDH是等腰直角三角形,∵GP=PH,∴PD=PG,PD⊥GH,∴DG=PD.例2.【2019·武汉市期末】在平行四边形ABCD中,E是AD上一点,AE=AB,过点E作直线EF,在EF 上取一点G,使得∠EGB=∠EAB,连接AG.(1)如图①,当EF与AB相交时,若∠EAB=60°,求证:EG=AG+BG;(2)如图②,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论.【答案】见解析.【解析】(1)证明:在EG上截取EH=BG,∵∠EAB=∠EGB,∠APE=∠BPG,∴∠ABG=∠AEH.在△ABG和△AEH中,∵AE=AB,∠ABG=∠AEH,BG=EH,∴△ABG≌△AEH,∴AH=AG,∠EAH=∠GAB,∴∠GAH=∠EAB=60°,∴△AGH是等边三角形,∴GH=AG,∴EG=AG+BG;(2)EG= AG-BG.如图,过点A作AH⊥AG,交GE的延长线于H,则∠GAH=∠EAB=90°,∴∠GAB=∠HAE.∵∠EGB=∠EAB=90°,∴∠AGH+∠AGB=∠AGH+∠H=90°.∴∠AGB=∠H,∵AB=AE,∴△ABG≌△AEH.∴BG=EH,AG=AH,∵∠GAH=∠EAB=90°,∴△AGH是等腰直角三角形.∴ AG=HG.∴EG= AG-BG.【刻意练习】1.【2018·容县期末】如图,已知△ABC中,AC=BC=5,AB=,三角形顶点在相互平行的三条直线L1,L2,L3上,且L2,L3之间的距离为3,则L1,L3之间的距离是.【答案】4.【解析】解:如图过点A作AM⊥L3于M,过点B作BN⊥L3于N.∵AC=BC=5,AB=,∴AC2+BC2=AB2,∴∠ACB=90°,∵∠AMC=∠BNC=90°,∴∠ACM+∠BCN=90°,∵∠BCN+∠CBN=90°,∴∠ACM=∠CBN,∴△ACM≌△CBN(AAS),∴AM=CN=3,在Rt△NCB中,由勾股定理得:BN=4,故答案为:4.2.【2019·长沙市雨花区期末】在正方形ABCD中,连接BD,P为射线CB上的一个动点(与点C不重合),连接AP,AP的垂直平分线交线段BD于点E,连接AE,PE.提出问题:当点P运动时,∠APE的度数,DE与CP的数量关系是否发生改变?探究问题:(1)首先考察点P的两个特殊位置:①当点P与点B重合时,如图1-1所示,∠APE=______°,用等式表示线段DE与CP之间的数量关系:______;②当BP=BC时,如图1-2所示,①中的结论是否发生变化?直接写出你的结论:______;(填“变化”或“不变化”)(2)然后考察点P的一般位置:依题意补全图2-1,2-2,通过观察、测量,发现:(1)中①的结论在一般情况下______(填“成立”或“不成立”)(3)证明猜想:若(1)中①的结论在一般情况下成立,请从图2-1和图2-2中任选一个进行证明;若不成立,请说明理由.【答案】(1)45,PC= DE;不变化;(2)成立;(3)见解析.【解析】解:(1)①当点P与点B重合时,∵四边形ABCD是正方形,∴∠APE=45°,EA=EB=ED,∴PC= DE.②当BP=BC时,①中的结论不发生变化;故答案为:45,PC= DE,不变化;(2)结论仍然成立;(3)如图,过点E作EF⊥AD于F,延长FE交BC于G,连接AC、EC,∵点E在线段AP的垂直平分线上,∴EA=EP,∵四边形ABCD是正方形,∴BD是AC的垂直平分线,∴EA=EC,∴∠EAC=∠ECA,∵BA=BC,∴∠BAC=∠BCA,∴∠EAB=∠ECB,∵EA=EP,EA=EC,∴EP=EC,∴∠EPC=∠ECP,∵∠EPC+∠EPB=180°,∴∠BAE+∠EPB=180°,∴∠ABP+∠AEP=180°,∵∠ABP=90°,∴∠AEP=90°,∴∠APE=∠PAE=45°,∵EF⊥AD,∴∠DFG=90°,∵∠BCD=∠ADC=90°,∴四边形FGCD是矩形,∴CG=FD,∠FGC=90°,∵∠BDA=45°,DE,∴FD=2∵EP=EC,∴CP=2CG=2DF DE.3.【2019·阳江市期中】(1)如图(1),在平行四边形ABCD中,DE⊥AB,BF⊥CD,垂足分别为E、F,求证:AE=CF;(2)如图(2),在平行四边形ABCD中,AC、BD是两条对角线,求证AC2+BD2=2(AB2+BC2)(3)如图(3),PQ是△PMN的中线,若PM=11,PN=13,MN=10,求出PQ的长度.【答案】见解析.【解析】解:(1)∵平行四边形ABCD中,DE⊥AB,BF⊥CD,∴AD=CB,DE=BF,∠AED=∠CFB=90°,∴Rt△AED≌Rt△CFB(HL),∴AE=CF;(2)如图,分别过A,D作AE⊥BC交CB延长线于E,DF⊥BC于F.根据勾股定理可得:AC2=AE2+(BE+BC)2①,AE2=AB2-BE2②,BD2=DF2+(BC-CF)2③,DF2=DC2-CF2④,∵四边形ABCD是平行四边形,∴AB=DC,又∵AE⊥BC,DF⊥BC,∴∠AEB=∠DFC=90°,AE=DF,∴Rt△AEB≌Rt△DFC(HL),∴BE=CF,而AB=DC,把②代入①,④代入③,可得:AC2=AB2-BE2+(BE+BC)2BD2=DC2-CF2+(BC-CF)2上面两式相加,可得:AC2+BD2=2(AB2+BC2);(3)如图,延长PQ至R,使得QR=PQ,连接RM,RN,∵PQ是△PMN的中线,∴NQ=MQ,∴四边形NPMR是平行四边形,由(2)可得,MN2+PR2=2(NP2+MP2),又∵PM=11,PN=13,MN=10,∴102+(2PQ)2=2(132+112),解得:PQ=2 .4.【2019·十堰市外国语期末】如图,已如等腰Rt△ABC和△CDE,AC=BC,CD=CE,连接BE、AD,P 为BD中点,M为AB中点、N为DE中点,连接PM、PN、MN.(1)试判断△PMN的形状,并证明你的结论;(2)若CD=5,AC=12,求△PMN的周长.【答案】见解析.【解析】解:(1)△PMN是等腰直角三角形,理由如下:延长BE交AD于F,如图所示:∵P为BD中点,M为AB中点、N为DE中点,∴PM∥AD,PM=12AD,PN∥BE,PN=12BE,∴△BCE≌△ACD(SAS),∴BE=AD,∠CBE=∠CAD,∴PM=PN,∵∠CBE+∠BEC=90°,∠AEF=∠BEC,∴∠CAD+∠AEF=∠CBE+∠BEC=90°,∴∠AFE=90°,∴BE⊥AD,∵PM∥AD,PN∥BE,∴PM⊥PN,即△PMN是等腰直角三角形;(2)∵∠ACD=90°,CD=5,AC=12,由勾股定理得:AD= =13,∴PN=PM=12AD=132,∵△PMN是等腰直角三角形,∴MN=PM=2,即△PMN的周长=PM+PN+MN=13+2.5.【2019·固始县期末】如图,在正方形ABCD中,E、F分别是边AB、BC的中点,连接AF、DE相交于点G,连接CG.(1)求证:AF⊥DE;(2)求证:CG=CD.【答案】见解析.【解析】证明:(1)∵四边形ABCD为正方形∴AB=BC=CD=AD,∠ABF=∠DAE=90°,∵E,F分别是边AB.BC的中点∴AE=12AB,BF=12BC,∴AE=BF.在△ABF与△DAE中,∵AD=AB,∠DAF=∠ABF,AE=BF,∴△DAE≌△ABF(SAS).∴∠ADE=∠BAF,∵∠BAF+∠DAG=90°,∴∠ADG+∠DAG=90°,∴∠DGA=90°,即AF⊥DE.(2)证明:延长AF交DC延长线于M,∵F为BC中点,∴CF=FB∵DM∥AB,∴∠M=∠FAB.在△ABF与△MCF中,∵∠M=∠FAB,∠CFM=∠BFA,CF=BF,∴△ABF≌△MCF(AAS),∴AB=CM.∴AB=CD=CM,∵△DGM是直角三角形,∴CG=12DM=CD.6.【2019·高阳县期中】如图,正方形ABCD的边长为2 ,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F.(1)求证:AF=BE;(2)求点E到BC边的距离.【答案】见解析.【解析】(1)证明:∵四边形ABCD为正方形,∴OA=OB,∠AOB=∠BOC=90°,∵AM⊥BE于点M,∴∠AME=90°,∴∠MAE=∠OBE,∴△AOF≌△BOE,∴AF=BE;(2)解:作EN⊥BC于N,如图,∵四边形ABCD为正方形,∴OC=22BC=2,∠OCB=45°,∵E是OC的中点,∴CE=1,在Rt△ECN中,∠ECN=45°,△CEN为等腰直角三角形,∴EN=22CE=22,即点E到BC边的距离为2.7.【2019·汕头市期中】如图,四边形ABCD和四边形CEFG都是正方形,且BC=CD,CE=CG,∠BCD=∠GCE=90°.(1)求证:△BCG≌△DCE;(2)求证:BG⊥DE.【答案】见解析.【解析】证明:(1)∵∠BCD=∠GCE=90°,∴∠BCG=∠DCE,在△BCG与△DCE中,∵BC=CD,∠BCG=∠DCE,CE=CG,∴△BCG≌△DCE(SAS);(2)∵△BCG≌△DCE,∴∠HBC=∠ODH,∵∠BHC=∠DHO,∵∠HBC+∠BHC=90°,∴∠ODH+∠DHO=90°,∴∠DOH=90°,∴BG⊥DE.8.【2019·北师大附属中学期末】如图,在▱ABCD中,BC=2AB,点E、F分别是BC、AD的中点,AE、BF交于点O,连接EF,OC.(1)求证:四边形ABEF是菱形;(2)若AB=4,∠ABC=60°,求OC的长.【答案】见解析.【解析】(1)证明:∵四边形ABCD是平行四边形,∴BC∥AD,BC=AD.∵E,F分别是BC,AD的中点,∴BE=12BC,AF=12AD,∴BE=AF.∴四边形ABEF是平行四边形.∵BC=2AB,∴AB=BE.∴平行四边形ABEF是菱形.(2)解:过点O作OG⊥BC于点G,如图所示:∵E是BC的中点,BC=2AB,∴BE=CE=AB,∵四边形ABEF是菱形,∠ABC=60°,∴BE=CE=AB=4,∠OBE=30°,∠BOE=90°.∴OE=2,∠OEB=60°.∴GE=1,OG.∴GC=GE+CE=5.在Rt△OCG中,由勾股定理得:OC=9.【2019·厦门六中月考】正方形ABCD中,点P是边CD上的任意一点,连接BP,O为BP的中点,作PE⊥BD于E,连接EO,AE.(1)若∠PBC=α,求∠POE的大小(用含α的式子表示);(2)用等式表示线段AE与BP之间的数量关系,并证明.【答案】见解析.【解析】解:(1)在正方形ABCD中,BC=DC,∠C=90°∴∠DBC=∠CDB=45°∵∠PBC=α∴∠DBP=45°-α∵PE⊥BD,且O为BP的中点∴EO=BO∴∠EBO=∠BEO∴∠EOP=∠EBO+∠BEO=90°-2α(2)连接OC,EC,在正方形ABCD中,AB=BC,∠ABD=∠CBD,BE=BE∴ΔABE≌ΔCBE∴AE=CE在RtΔBPC中,O为BP的中点∴CO=BO=12 BP∴∠OBC=∠OCB∴∠COP=2α由(1)知∠EOP=90°-2α∴∠EOC=∠COP+∠EOP=90°又由(1)知BO=EO∴EO=CO∴△EOC是等腰直角三角形∴EO2+OC2=EC2∴EC OC=22 BP即BP EC∴BP AE.10.【2018·莆田市期中】(1)如图1的正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,延长CD到点G,使DG=BE,连接EF,AG.求证:EF=FG;(2)如图2,等腰Rt△ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,求MN的长.【答案】见解析.【解析】解:(1)证明:在正方形ABCD中,∠ABE=∠ADG,AD=AB,DG=BE,∴△ABE≌△ADG(SAS),∴∠BAE=∠DAG,AE=AG,∴∠EAG=90°,∴△FAE≌△GAF(SAS),∴EF=FG;(2)解:如图,过点C作CE⊥BC,垂足为点C,截取CE,使CE=BM.连接AE、EN.∵AB=AC,∠BAC=90°,∴∠B=∠ACB=45°.∵CE⊥BC,∴∠ACE=∠B=45°.∴△ABM≌△ACE(SAS).∴AM=AE,∠BAM=∠CAE.∵∠BAC=90°,∠MAN=45°,∴∠BAM+∠CAN=45°.由∠BAM=∠CAE,得∠MAN=∠EAN=45°.∴△MAN≌△EAN(SAS).∴MN=EN.在Rt△ENC中,由勾股定理,得EN2=EC2+NC2.∴MN2=BM2+NC2.∵BM=1,CN=3,∴MN2=12+32,∴MN= .11.【2019·北师大附属中学期末】四边形ABCD是边长为4正方形,点E是边BC上一动点(含端点B,不含端点C),点F是正方形外角∠DCM的平分线上一点,且满足∠AEF=90°.(1)当点E与点B重合时,直接写出线段AE与线段EF的数量关系;(2)如图1,当点E是边BC的中点时,①补全图形;②请证明(1)中的结论仍然成立;(3)取线段CF的中点N,连接DE、NE、DN,①求证:EN=DN;②直接写出线段EN长度的取值范围.【答案】见解析.【解析】解:(1)当点与点重合时,AE=EF.(2)①如图,②如图,在AB上取AB中点H,连接HE,∵四边形ABCD是正方形∴AB=CB,且点H是AB中点,点E是BC中点,∴AH=BH=BE=CE,∴∠BEH=∠BHE=45°,∴∠AHE=135°,∵CF平分∠DCM,∴∠DCF=45°∴∠ECF=135°=∠AHE,∵∠AEF=90°∴∠AEB+∠FEC=90°,且∠AEB+∠BAE=90°,∴∠BAE=∠FEC,且AH=EC,∠AHE=∠ECF,∴△AHE≌△ECF(ASA)∴AE=EF.(3)①如图,延长DN,使HN=DN,连接FH,EH,∵CN=FN,∠DNC=∠HNF,DN=NH,∴△DCN≌△HFN(SAS)∴DC=FH,∠DCF=∠FCM=45°,∴FH∥DC,且CD⊥BC,∴FH⊥BM,∴∠FEM+∠EFH=90°,且∠FEM=∠BAE,∠BAE+∠DAE=90°,∴∠DAE=∠EFH,∵AD=CD,CD=FH,∴AD=FH,且AE=EF,∠DAE=∠EFH,∴△ADE≌△FHE,∴DE=EH,且DN=NH,∴EN=DN.②∵DE=EH,DN=NH,∴EN=DN,EN⊥DN∴DE2EN,∵点E是边BC上一动点(含端点B,不含端点C),∴4<DE2,∴2<EN≤4.12.【2019·宿迁市期末】(1)如图1,在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E 是线段OB延长线上一点,M是线段OB上一动点(不包括点O、B),作MN⊥DM,垂足为M,且MN=DM.设OM=a,请你利用基本活动经验直接写出点N的坐标______(用含a的代数式表示);(2)如果(1)的条件去掉“且MN=DM”,加上“交∠CBE的平分线与点N”,如图2,求证:MD=MN.将这个问题解决,请写出你的证明过程.(3)在(2)的条件下,如图3,请你继续探索:连接DN交BC于点F,连接FM,下列两个结论:①FM 的长度不变;②MN平分∠FMB,请你指出正确的结论,并给出证明.【答案】(1)N(2+a,a);(2)(3)见解析.【解析】(1)解:过点N作NE⊥OB于E,∵∠DMN=90°,∴∠DMO+∠NME=90°,∠NME+∠MNE=90°,∴∠DMO=∠MNE,∵DM=MN,∴△DMO≌△MNE,∴ME=DO=2,NE=OM=a,∴OE=OM+ME=2+a,∴点N坐标(2+a,a),故答案为:(2+a,a).(2)证明:在OD上截取OH=OM,连接HM,∵OD=OB,OH=OM,∴HD=MB,∠OHM=∠OMH,∴∠DHM=180°-45°=135°,∵NB平分∠CBE,∴∠NBE=45°,∴∠NBM=180°-45°=135°,∴∠DHM=∠NBM,∵∠DMN=90°,∴∠DMO+∠NMB=90°,∵∠HDM+∠DMO=90°,∴∠HDM=∠NMB,∴△DHM≌△MBN,∴DM=MN.(3)结论:MN平分∠FMB成立.理由:在BO延长线上取OA=CF,易证:△DOA≌△DCF,∴AD=DF,∠ADO=∠CDF,∵∠MDN=45°,∴∠CDF+∠ODM=45°,∴∠ADO+∠ODM=45°,∴△DMA≌△DMF,∴∠DFM=∠DAM=∠DFC,过M作MP⊥DN于P,则∠FMP=∠CDF,由(2)可知∠NMF+∠FMP=∠PMN=45°,∴∠NMB=∠MDH,∠MDO+∠CDF=45°,∴∠NMB=∠NMF,即MN平分∠FMB.13.【2019·福州市期末】如图1,点E为正方形ABCD的边AB上一点,EF⊥EC,且EF=EC,连接AF.求∠EAF的度数;如图2,连接FC交BD于M,交AD于N.求证:BD=AF+2DM.【答案】见解析.【解析】(1)解:过点F作FM⊥AB交AB的延长线于点M,∵四边形ABCD是正方形,∴∠B=∠M=∠CEF=90°,∴∠MEF+∠CEB=90°,∠CEB+∠BCE=90°,∵EC=EF,∴△EBC≌△FME,∴FM=BE,∴EM=BC∵BC=AB,∴EM=AB,∴EM﹣AE=AB﹣AE∴AM=BE,∴FM=AM,∵FM⊥AB,∴∠MAF=45°,∴∠EAF=135°.(2)证明:过点F作FG∥AB交BD于点G,由(1)可知∠EAF=135°,∵∠ABD=45°∴∠EAF+∠ABD=180°,∴AF∥BG,∵FG∥AB,∴四边形ABGF为平行四边形,AF=BG,FG=AB,∵AB=CD,∵AB∥CD,∴FG∥CD,∴∠FGM=∠CDM,∵∠FMG=∠CMD∴△FGM≌△DMC(AAS),∴GM=DM,∴DG=2DM,∴BD=BG+DG=AF+2DM.14.【2019·漯河市期中】如图1,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC',延长QC′交BA的延长线于点M.(1)试探究AP与BQ的数量关系,并证明你的结论;(2)求证:MQ=MB;(3)若AB=3,BP=2PC,求QM的长.【答案】见解析.【解析】(1)解:结论:AP=BQ.理由:∵四边形ABCD是正方形,∴AB=BC,∠ABC=∠C=90°,∴∠ABQ+∠CBQ=90°.∵BQ⊥AP,∴∠PAB+∠QBA=90°,∴∠PAB=∠CBQ.∴△PBA≌△QCB,(2)证明:∵四边形ABCD是正方形,∴DC∥AB,∴∠CQB=∠QBA.由折叠可得:∠C′QB=∠CQB,∴∠QBA=∠C′QB,∴MQ=MB.(3)解:过点Q作QH⊥AB于H,∵四边形ABCD是正方形,∴QH=BC=AB=3.∵BP=2PC,∴BP=2,PC=1,由勾股定理得:BQ=AP,BH=2.∵四边形ABCD是正方形,∴DC∥AB,∴∠CQB=∠QBA,由折叠可得:∠C′QB=∠CQB,∴∠QBA=∠C′QB,∴MQ=MB.设QM=x,则有MB=x,MH=x﹣2.在Rt△MHQ中,由勾股定理,x2=(x﹣2)2+32,解得x=13 4.∴QM的长为13 4 .15.【2019·黑龙江秋实中学期中】如图,矩形ABCD的对角线AC、BD交于点O,以BD为斜边作直角三角形BED,∠BED=90°,连结AE、CE、OE.(1)如图①,请直接写出线段OE与线段AC的数量关系;(2)如图②,延长EO交AD于H,连AG与HC,若AE=CE,求证:四边形AGCH是菱形.图1图2【答案】见解析.【解析】解:(1)AC=2OE;∵四边形ABCD是矩形,∴AC=BD,O是BD、AC的中点∵∠BED=90°,∴2OE=BD=AC;(2)由(1)知,O是AC中点,∵AE=CE,∴EH⊥AC,∵四边形ABCD是矩形,∴AD∥BC,∴∠OAH=∠OCG,在△AOH和△COG中,∵AO=OC,∠OAH=∠OCG,∠AOH=∠COG,∴△AOH≌△COG,∴AH=CG,∴四边形AGCH为平行四边形,∵EH⊥AC,∴四边形AGCH为菱形.16.【2019·禹城市期末】如图所示,四边形ABCD是正方形,M是AB延长线上一点.直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A、B重合),另一直角边与∠CBM的平分线BF相交于点F.(1)如图1,当点E在AB边得中点位置时:①通过测量DE、EF的长度,猜想DE与EF满足的数量关系是.②连接点E与AD边的中点N,猜想NE与BF满足的数量关系是,请证明你的猜想.(2)如图2,当点E在AB边上的任意位置时,猜想此时DE与EF有怎样的数量关系,并证明你的猜想.【答案】见解析.【解析】解:(1)①DE=EF;②NE=BF;理由如下:∵四边形ABCD为正方形,∴AD=AB,∠DAB=∠ABC=90°,∵N,E分别为AD,AB中点,∴AN=DN=12AD,AE=EB=12AB,∴DN=BE,AN=AE,∵∠DEF=90°,∴∠AED+∠FEB=90°,∵∠ADE+∠AED=90°,∴∠FEB=∠ADE,∵AN=AE,∴∠ANE=∠AEN,∵∠A=90°,∴∠ANE=45°,∴∠DNE=180°﹣∠ANE=135°,∵∠CBM=90°,BF平分∠CBM,∴∠CBF=45°,∠EBF=135°,∴△DNE≌△EBF,∴DE=EF,NE=BF.(2)DE=EF,理由如下:连接NE,在DA边上截取DN=EB,∵四边形ABCD是正方形,DN=EB,∴AN=AE,∴△AEN为等腰直角三角形,∴∠ANE=45°,∴∠DNE=180°﹣45°=135°,∵BF平分∠CBM,AN=AE,∴∠EBF=90°+45°=135°,∴∠DNE=∠EBF,∵∠NDE+∠DEA=90°,∠BEF+∠DEA=90°,∴∠NDE=∠BEF,∴△DNE≌△EBF,∴DE=EF.17.【2019·费县期末】在平行四边形ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.(1)在图1中证明:CE=CF;(2)若∠ABC=90°,G是EF的中点(如图2),求出∠BDG的度数;(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG的度数.【答案】见解析.【解析】解:证明:(1)∵AF平分∠BAD,∴∠BAF=∠DAF,∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,∴∠DAF=∠CEF,∠BAF=∠F,∴∠CEF=∠F.∴CE=CF.(2)连接GC、BG,∵四边形ABCD为平行四边形,∠ABC=90°,∴四边形ABCD为矩形,∵AF平分∠BAD,∴∠DAF=∠BAF=45°,∵∠DCB=90°,DF∥AB,∴∠DFA=45°,∠ECF=90°∴△ECF为等腰直角三角形,∵G为EF中点,∴EG=CG=FG,CG⊥EF,∵△ABE为等腰直角三角形,AB=DC,∴BE=DC,∵∠CEF=∠GCF=45°,∴∠BEG=∠DCG=135°∴△BEG≌△DCG,∴BG=DG,∵CG⊥EF,∴∠DGC+∠DGA=90°,又∵∠DGC=∠BGA,∴∠BGA+∠DGA=90°,∴△DGB为等腰直角三角形,∴∠BDG=45°.(3)延长AB、FG交于H,连接HD.∵AD∥GF,AB∥DF,∴四边形AHFD为平行四边形∵∠ABC=120°,AF平分∠BAD∴∠DAF=30°,∠ADC=120°,∠DFA=30°∴△DAF为等腰三角形∴AD=DF,∴CE=CF,∴平行四边形AHFD为菱形∴△ADH,△DHF为全等的等边三角形∴DH=DF,∠BHD=∠GFD=60°∵FG=CE,CE=CF,CF=BH,∴BH=GF∴△BHD≌△GFD,∴∠BDH=∠GDF∴∠BDG=∠BDH+∠HDG=∠GDF+∠HDG=60°.18.【2019·抚顺市期中】△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B,C 重合),以AD为边在AD右侧作正方形ADEF,连接CF.(1)观察猜想如图1,当点D在线段BC上时,①BC与CF的位置关系为:.②BC,CD,CF之间的数量关系为:;(将结论直接写在横线上)(2)数学思考如图2,当点D在线段CB的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.(3)拓展延伸如图3,当点D在线段BC的延长线上时,延长BA交CF于点G,连接GE.若已知AB=,CD=14 BC,请求出GE的长.【答案】见解析.【解析】解:(1)①正方形ADEF中,AD=AF,∵∠BAC=∠DAF=90°,∴∠BAD=∠CAF,∵AB=AC,∴△DAB≌△FAC,∴∠B=∠ACF,∴∠ACB+∠ACF=90°,即BC⊥CF;故答案为:垂直;②△DAB≌△FAC,∴CF=BD,∵BC=BD+CD,∴BC=CF+CD;故答案为:BC=CF+CD;(2)CF⊥BC成立;BC=CD+CF不成立,CD=CF+BC.理由如下:∵正方形ADEF中,AD=AF,∵∠BAC=∠DAF=90°,∴∠BAD=∠CAF,∵AB=AC,∴△DAB≌△FAC,∴∠ABD=∠ACF,∵∠BAC=90°,AB=AC,∴∠ACB=∠ABC=45°.∴∠ABD=180°﹣45°=135°,∴∠BCF=∠ACF﹣∠ACB=135°﹣45°=90°,∴CF⊥BC.∵CD=DB+BC,DB=CF,∴CD=CF+BC.(3)解:过A作AH⊥BC于H,过E作EM⊥BD于M,EN⊥CF于N,∵∠BAC=90°,AB=AC,∴BC AB=4,AH=12BC=2,∴CD=14BC=1,CH=12BC=2,∴DH=3,由(2)得BC⊥CF,CF=BD=5,∵四边形ADEF是正方形,∴AD=DE,∠ADE=90°,∵BC⊥CF,EM⊥BD,EN⊥CF,∴四边形CMEN是矩形,∴NE=CM,EM=CN,∵∠AHD=∠ADE=∠EMD=90°,∴∠ADH+∠EDM=∠EDM+∠DEM=90°,∴∠ADH=∠DEM,∴△ADH≌△DEM,∴EM=DH=3,DM=AH=2,∴CN=EM=3,EN=CM=3,∵∠ABC=45°,∴∠BGC=45°,∴△BCG是等腰直角三角形,∴CG=BC=4,∴GN=1,由勾股定理得:EG。
P C
G F
B
Q A D
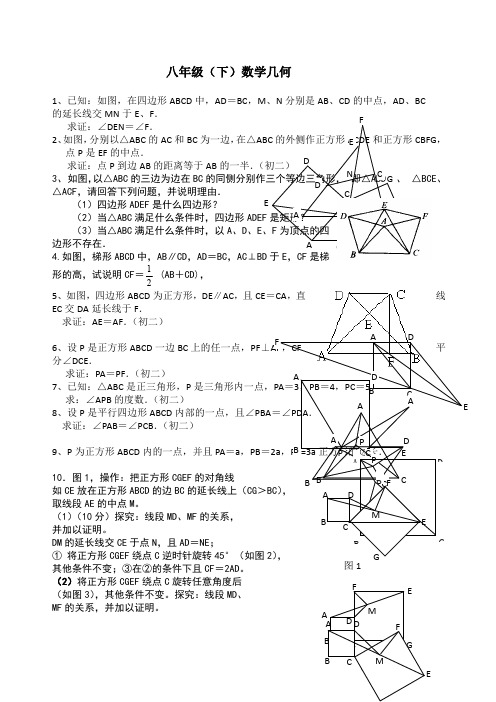
E 八年级(下)数学几何
1、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .
求证:∠DEN =∠F . 2、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的
中点.
求证:点P 到边AB 的距离等于AB 的一半.(初二)
3、 如图,以△ABC 的三边为边在BC 的同侧分别作三个等边三角形,•即△ABD•、•△BCE 、△ACF ,请
回答下列问题,并说明理由. (1)四边形ADEF 是什么四边形?
(2)当△ABC 满足什么条件时,四边形ADEF 是矩形? (3)当△ABC 满足什么条件时,以A 、D 、E 、F 为顶点的四边形不存在. 4.如图,梯形ABCD 中,AB ∥CD ,AD =BC ,AC ⊥BD 于E ,CF 是梯形的高,试说明CF =
2
1
(AB +CD), 5、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .
求证:AE =AF .(初二)
6、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE . 求证:PA =PF .(初二)
7、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.
求:∠APB 的度数.(初二)
8、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二) 9、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC=3a 正方形的边长.
10.图1,操作:把正方形CGEF 的对角线
如CE 放在正方形ABCD 的边BC 的延长线上(CG >BC ), 取线段AE 的中点M 。
(1)(10分)探究:线段MD 、MF 的关系, 并加以证明。
DM 的延长线交CE 于点N ,且AD =NE ;
① 将正方形CGEF 绕点C 逆时针旋转45°(如图2), 其他条件不变;③在②的条件下且CF =2AD 。
(2)将正方形CGEF 绕点C 旋转任意角度后 (如图3),其他条件不变。
探究:线段MD 、 MF 的关系,并加以证明。
11、已知:P 是正方形ABCD 对角线BD 上一点,PE ⊥DC ,PF ⊥BC ,E 、F 分别为
垂足, 求证:AP =EF .
A N F
E C
D
M B E
D
A C
B
F
D A
E P
C B A
A P
C
B
P
A
D C B A C
B
P D
A B
C
D
F
G
E
M
图1 图2 B
A C E
D F
G
M F M
E
C G A
D B
图3
12.如图,正方形ABCD 的对角线AC 、BD 相交于点O
①若E 为AC 上一点,过A 作AG ⊥EB 于G ,AG 、BD 交于F , 求证:OE=OF
②若点E 在AC 的延长线上,AG ⊥EB 交EB 的延长线于G ,AG 的延长线交BD 于点F ,其他条件不变,OE=OF 还成立吗?若成立,请给予证明,若不成立请说明理由。
13、如图,已知E 是正方形ABCD 的对角线BD 上一点, 且BE =BC ,P 是CE 上任意一点,PF ⊥BD 于F ,PG ⊥BC 于G 。
求证: PF+PG =
2
1
BD 14.如图2-1,在Rt △ABC 中,∠ACB=90°,∠BAC=60°, (1)将Rt △ABC 绕点A 逆时针旋转90°,得到Rt △AC'B',直线BB'交直线CC'于
点D ,连接AD.
探究:AD 与BB'之间的关系,并说明理由。
(2)如图2-2,若将Rt △ABC 绕点A 逆时针旋转任意角度,其他条件不变,
还有(1)的结论吗?为什么?。