多普勒效应及应用

多普勒效应的应用
多普勒效应是指当波源和观察者相对运动时，观察者所接
收到的波的频率发生变化的现象。

多普勒效应的应用十分
广泛，下面列举一些常见的应用场景：
1. 天文学：多普勒效应用于天文学中，可以测量星体的运
动速度和远离或靠近地球的速度。

2. 超声波成像：医学上常用超声波成像设备，利用多普勒
效应可以测量血流速度，用于检测血管狭窄和心脏病等疾病。

3. 雷达测速仪：交通警察使用雷达测速仪测量车辆的速度。

通过测量接收到的车辆发射的无线电波的频率变化，即可
得出车辆的速度。

4. 太阳系的远距离测量：科学家利用多普勒效应测量太阳
系中行星的运动速度和距离。

5. 银行滞留款式识别：将红外传感器放置在自动提款机(ATM)网格上方，可以通过检测人员接近时红外波的频率变化，来判断用户是否具有正当使用ATM的权限，以不同频率变化代表是否试图伪造卡片密码或干扰机器进行恶意攻击。

总之，多普勒效应在天文学、医学、交通管理等领域都有重要的应用，它为我们提供了测量和判断物体运动速度的重要手段。

多普勒效应及其应用1. 简介多普勒效应（Doppler Effect）是指当观察者和发射源相对运动时，观察者接收到的波的频率会发生变化的现象。

这个现象最早由奥地利物理学家克里斯琴·多普勒（Christian Doppler）在1842年提出。

多普勒效应不仅在物理学中有着广泛的应用，还涉及到声学、光学、无线电波等多个领域。

2. 多普勒效应的原理2.1 基本原理多普勒效应分为两种：一种是波源相对于观察者运动，另一种是观察者相对于波源运动。

根据这两种情况，多普勒效应又可以分为两种类型：正多普勒效应和负多普勒效应。

当波源相对于观察者远离时，观察者接收到的波的频率会变低，这种现象称为负多普勒效应；当波源相对于观察者靠近时，观察者接收到的波的频率会变高，这种现象称为正多普勒效应。

2.2 数学表达多普勒效应的数学表达式为：[ f’ = f ]•( f’ ) 是观察者接收到的波的频率；•( f ) 是波源发出的原始频率；•( v ) 是波在介质中的传播速度；•( v_0 ) 是观察者和波源之间的相对速度；•( v_s ) 是波源相对于介质的运动速度。

当观察者和波源相向而行时，取加号；当观察者和波源远离时，取减号。

3. 多普勒效应的应用3.1 声学在声学中，多普勒效应广泛应用于测量物体的速度和距离。

例如，多普勒雷达就是利用多普勒效应测量物体速度的一种装置。

它通过发射一定频率的雷达波，然后接收反射回来的雷达波，根据接收到的频率变化来计算物体的速度。

此外，多普勒效应在医学领域也有重要应用。

例如，多普勒超声波就是利用多普勒效应来检测血流速度的一种技术。

通过检测血流速度，可以判断出是否存在血栓、血管狭窄等疾病。

3.2 光学在光学中，多普勒效应的应用主要有激光雷达和光纤通信等方面。

激光雷达利用多普勒效应来测量目标物体的速度和距离，广泛应用于自动驾驶、无人机等领域。

光纤通信中，多普勒效应会导致光信号的相位变化，从而影响信号的传输质量。

多普勒效应生活中的例子多普勒效应是一种物理现象，它描述了当一个物体在运动时，它所发出的声波或电磁波的频率会发生变化。

这种现象在我们的日常生活中随处可见，下面是一些例子：1. 警笛声：当警车向我们靠近时，警笛声的频率会变高，当警车远离我们时，警笛声的频率会变低。

这是因为警车的运动引起了声波的多普勒效应。

2. 雷达测速：雷达测速仪利用多普勒效应来测量车辆的速度。

当雷达向车辆发射电磁波时，车辆的运动会导致电磁波的频率发生变化，从而可以计算出车辆的速度。

3. 天文学：天文学家利用多普勒效应来测量星系和星际物质的速度。

当星系或星际物质向我们靠近时，它们所发出的光的频率会变高，当它们远离我们时，光的频率会变低。

4. 航空飞行：当飞机向地面靠近时，它所发出的声波的频率会变高，当飞机远离地面时，声波的频率会变低。

这种现象对于飞行员来说非常重要，因为它可以帮助他们判断飞机的高度和速度。

5. 超声波检测：医生利用多普勒效应来检测胎儿的心跳和血流速度。

当超声波穿过人体组织时，它们会受到组织的运动影响，从而产生多普勒效应。

6. 气象学：气象学家利用多普勒雷达来测量风速和降雨量。

当雷达向降雨区域发射电磁波时，降雨的运动会导致电磁波的频率发生变化，从而可以计算出降雨的速度和量。

7. 汽车制动器：当汽车制动时，制动器会产生高频率的振动，这种振动会引起声波的多普勒效应，从而产生刺耳的噪音。

8. 音乐演奏：当乐器演奏者向听众靠近时，乐器所发出的声波的频率会变高，当演奏者远离听众时，声波的频率会变低。

这种现象对于乐器演奏者来说非常重要，因为它可以帮助他们控制音乐的节奏和速度。

9. 交通信号灯：当交通信号灯向车辆发出红色或绿色的光时，光的频率会保持不变。

但是当交通信号灯向车辆发出黄色的光时，光的频率会发生变化，从而提醒驾驶员注意减速。

10. 电视和无线电广播：当电视或无线电广播信号穿过大气层时，它们会受到大气层的运动影响，从而产生多普勒效应。

什么是多普勒效应
多普勒效应是一种物理现象，描述了当光源或声源相对于观察者发生相对运动时，观察者所感知到的频率或波长的变化。

多普勒效应分为多普勒频移和多普勒波长变化两种形式，分别用于描述光学和声学的情况。

多普勒频移（Doppler Frequency Shift）：
1. 光学多普勒效应：
•描述：当光源或观察者相对于彼此运动时，观察者测量到的光频率会有所改变。

•频率变化：如果光源和观察者相向运动，光频率升高（蓝移）；如果它们远离彼此，光频率降低（红移）。

•应用：光学多普勒效应在天文学中广泛应用，用于测量星体的运动速度和方向。

多普勒波长变化（Doppler Wavelength Shift）：
1. 声学多普勒效应：
•描述：当声源或听者相对于彼此运动时，听者感知到的声音波长会发生变化。

•波长变化：声源和听者相向运动时，听者感知到的声音波长缩短；相远离运动时，波长延长。

•应用：声学多普勒效应在实际生活中广泛应用，例如警车、救护车的声音变化。

数学表达：
多普勒效应的数学表达式取决于具体情境，但一般可以用下面的公式来表示频率变化：
f′=v∓vsf(v±v0)
其中：
•f′ 是观察者测量到的频率，
• f 是光源或声源的固有频率，
• v 是波在介质中的传播速度，
• v0 是观察者相对于介质的速度（正表示远离，负表示相向运动），
• vs 是光源或声源相对于介质的速度（正表示远离，负表示相向运动）。

多普勒效应的重要性在于它使我们能够测量和理解运动物体的速度，同时也应用于通信、雷达技术等领域。

生活中有哪些应用了多普勒效应一、声波的多普勒效应在日常生活中，我们都会有这种经验：当一列鸣着汽笛的火车经过某观察者时，他会发现火车汽笛的声调由高变低. 为什么会发生这种现象呢?这是因为声调的高低是由声波振动频率的不同决定的，如果频率高，声调听起来就高;反之声调听起来就低.这种现象称为多普勒效应，它是用发现者克里斯蒂安多普勒(ChristianDoppler,1803-1853)的名字命名的，多普勒是奥地利物理学家和数学家.他于1842年首先发现了这种效应.为了理解这一现象，就需要考察火车以恒定速度驶近时，汽笛发出的声波在传播时的规律.其结果是声波的波长缩短，好象波被压缩了.因此，在一定时间间隔内传播的波数就增加了，这就是观察者为什么会感受到声调变高的原因;相反，当火车驶向远方时，声波的波长变大，好象波被拉伸了. 因此，声音听起来就显得低沉.定量分析得到f1=(u+v0)/(u-vs)f ，其中vs为波源相对于介质的速度，v0为观察者相对于介质的速度，f表示波源的固有频率，u表示波在静止介质中的传播速度. 当观察者朝波源运动时，v0取正号;当观察者背离波源(即顺着波源)运动时，v0取负号. 当波源朝观察者运动时vs前面取负号;前波源背离观察者运动时vs 取正号. 从上式易知，当观察者与声源相互靠近时，f1f ;当观察者与声源相互远离时。

f1二、光波的多普勒效应具有波动性的光也会出现这种效应，它又被称为多普勒-斐索效应. 因为法国物理学家斐索(1819-1896)于1848年独立地对来自恒星的波长偏移做了解释，指出了利用这种效应测量恒星相对速度的办法.光波与声波的不同之处在于，光波频率的变化使人感觉到是颜色的变化. 如果恒星远离我们而去，则光的谱线就向红光方向移动，称为红移;如果恒星朝向我们运动，光的谱线就向紫光方向移动，称为蓝移.三、光的多普勒效应的应用20世纪20年代，美国天文学家斯莱弗在研究远处的旋涡星云发出的光谱时，首先发现了光谱的红移，认识到了旋涡星云正快速远离地球而去.1929年哈勃根据光普红移总结出著名的哈勃定律：星系的远离速度v与距地球的距离r成正比，即v=Hr,H为哈勃常数.根据哈勃定律和后来更多天体红移的测定，人们相信宇宙在长时间内一直在膨胀，物质密度一直在变小. 由此推知，宇宙结构在某一时刻前是不存在的，它只能是演化的产物. 因而1948年伽莫夫(G. Gamow)和他的同事们提出大爆炸宇宙模型. 20世纪60年代以来，大爆炸宇宙模型逐渐被广泛接受，以致被天文学家称为宇宙的"标准模型" .多普勒-斐索效应使人们对距地球任意远的天体的运动的研究成为可能，这只要分析一下接收到的光的频谱就行了. 1868年，英国天文学家W. 哈金斯用这种办法测量了天狼星的视向速度(即物体远离我们而去的速度)，得出了46 km/s 的速度值。

多普勒效应的作用
多普勒效应是一种物理现象，当发射者和接收者相对运动时，波的频率和波长会发生变化。

多普勒效应在多个领域中具有重要的应用，包括：
1. 天文学：多普勒效应被用于确定星体的速度和运动方向。

通过测量天体的频率变化，可以推断出星体向我们移动或远离我们的速度。

2. 遥感技术：多普勒效应被应用于雷达测距和速度测量中。

通过测量目标物体反射回来的信号频率变化，可以确定目标物体的相对速度和距离。

3. 医学影像：多普勒效应被用于超声波成像中。

通过测量回声波的频率变化，可以获得人体内部组织或血流的速度和方向信息，用于诊断和监测疾病。

4. 交通监测：多普勒效应被应用于交通雷达和测速摄像机中。

通过测量行驶车辆反射回来的信号频率变化，可以判断车辆的速度，用于交通监测和执法。

5. 宇航技术：多普勒效应被用于航天器与地面通信中。

当航天器以高速运动时，信号的频率会发生变化，需要调整接收器来保持通信稳定。

总之，多普勒效应在物理学、天文学、遥感技术、医学影像、交通监测和宇航技术等领域中具有广泛的应用。

多普勒的应用和原理一、多普勒效应的原理多普勒效应是描述当波源和观测者相对运动时，波的频率和波长发生变化的现象。

该现象可以用于测量物体的速度、方向和距离。

1.1 波的频率和波长的变化当波源和观测者相向而行时，波源发出的波的频率相对于观测者来说会增加，波长则会缩短。

而当波源和观测者背离而行时，波的频率相对于观测者来说会减小，波长则会延长。

1.2 多普勒频移公式多普勒频移公式可以描述多普勒效应的量化关系：f' = f * (v + vr) / (v - vs)其中，f'是观测者接收到的频率，f是波源发出的频率，v是波的速度，vr是观测者的速度，vs是波源的速度。

二、多普勒效应的应用2.1 多普勒测速仪多普勒测速仪是利用多普勒效应测量物体的速度的一种设备。

通过测量接收到的频率与波源发出的频率之间的差异，可以计算物体的速度。

2.2 多普勒雷达多普勒雷达常用于测量目标的速度和距离。

利用多普勒效应，通过观测回波频率与发射频率之间的差异，可以计算出目标物体的速度。

2.3 医学应用多普勒效应在医学领域有广泛的应用。

例如，超声多普勒技术可以用于测量血流速度，对心脏、血管等器官进行检测和诊断。

2.4 多普勒流量计多普勒流量计是一种用于测量液体或气体流速的设备。

通过使用多普勒效应，它可以非侵入性地测量液体或气体的速度和流量。

2.5 遥感技术多普勒效应在遥感技术中也有应用。

利用多普勒频移公式，可以通过分析卫星接收到的微波信号的频率变化，来获得地球表面的运动信息和物体的速度。

三、总结多普勒效应是一种广泛应用于各个领域的物理现象。

它的原理是当波源和观测者相对运动时，波的频率和波长发生变化。

利用多普勒效应，我们可以测量物体的速度、方向和距离。

多普勒效应在多个领域都有重要的应用，如测速仪、雷达、医学、流量计和遥感技术等。

这些应用使得多普勒效应成为一项重要的技术，对各个领域的研究和应用产生了积极的影响。

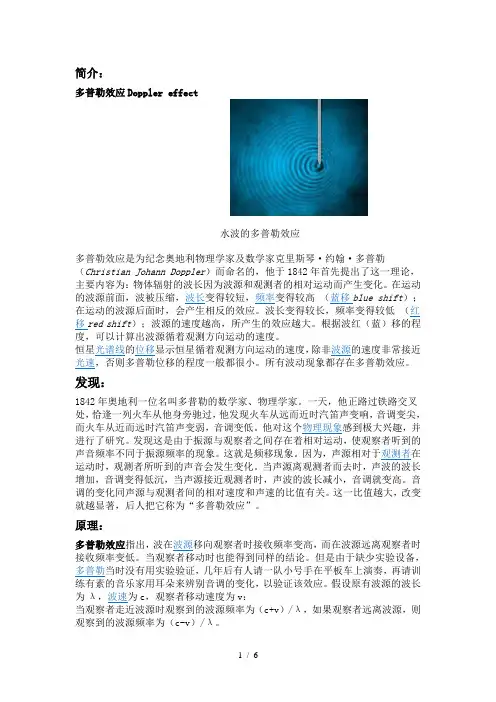
简介：多普勒效应Doppler effect水波的多普勒效应多普勒效应是为纪念奥地利物理学家及数学家克里斯琴·约翰·多普勒（Christian Johann Doppler）而命名的，他于1842年首先提出了这一理论，主要内容为：物体辐射的波长因为波源和观测者的相对运动而产生变化。

在运动的波源前面，波被压缩，波长变得较短，频率变得较高（蓝移blue shift）；在运动的波源后面时，会产生相反的效应。

波长变得较长，频率变得较低（红移red shift）；波源的速度越高，所产生的效应越大。

根据波红（蓝）移的程度，可以计算出波源循着观测方向运动的速度。

恒星光谱线的位移显示恒星循着观测方向运动的速度，除非波源的速度非常接近光速，否则多普勒位移的程度一般都很小。

所有波动现象都存在多普勒效应。

发现：1842年奥地利一位名叫多普勒的数学家、物理学家。

一天，他正路过铁路交叉处，恰逢一列火车从他身旁驰过，他发现火车从远而近时汽笛声变响，音调变尖，而火车从近而远时汽笛声变弱，音调变低。

他对这个物理现象感到极大兴趣，并进行了研究。

发现这是由于振源与观察者之间存在着相对运动，使观察者听到的声音频率不同于振源频率的现象。

这就是频移现象。

因为，声源相对于观测者在运动时，观测者所听到的声音会发生变化。

当声源离观测者而去时，声波的波长增加，音调变得低沉，当声源接近观测者时，声波的波长减小，音调就变高。

音调的变化同声源与观测者间的相对速度和声速的比值有关。

这一比值越大，改变就越显著，后人把它称为“多普勒效应”。

原理：多普勒效应指出，波在波源移向观察者时接收频率变高，而在波源远离观察者时接收频率变低。

当观察者移动时也能得到同样的结论。

但是由于缺少实验设备，多普勒当时没有用实验验证，几年后有人请一队小号手在平板车上演奏，再请训练有素的音乐家用耳朵来辨别音调的变化，以验证该效应。

假设原有波源的波长为λ，波速为c，观察者移动速度为v：当观察者走近波源时观察到的波源频率为（c+v）/λ，如果观察者远离波源，则观察到的波源频率为（c-v）/λ。