小升初奥数冲刺合集

小升初奥数题必考100道及答案(完整版)题目1：有一个两位数，十位上的数字是个位上数字的2 倍，如果把十位上的数字与个位上的数字交换，就得到另外一个两位数，把这个两位数与原两位数相加，和是132。

求原两位数。

答案：设原两位数个位上的数字为x，则十位上的数字为2x。

原两位数为20x + x = 21x，交换后的两位数为10x + 2x = 12x。

根据题意可得：21x + 12x = 132，33x = 132，x = 4。

所以原两位数为84。

题目2：小明从家到学校，如果每分钟走50 米，就要迟到3 分钟；如果每分钟走70 米，则可提前5 分钟到校。

小明家到学校的路程是多少米？答案：设小明按时到校要x 分钟。

50(x + 3) = 70(x - 5)，50x + 150 = 70x - 350，20x = 500，x = 25。

路程为50×(25 + 3) = 1400（米）题目3：甲乙两数的和是180，甲数的1/4 等于乙数的1/5，甲乙两数各是多少？答案：设甲数为x，则乙数为180 - x。

1/4 x = 1/5 (180 - x)，5x = 4×(180 - x)，5x = 720 - 4x，9x = 720，x = 80，乙数为100。

题目4：某工厂有三个车间，第一车间的人数占三个车间总人数的25%，第二车间人数是第三车间的3/4，已知第一车间比第二车间少40 人，三个车间一共有多少人？答案：设三个车间总人数为x 人。

第一车间人数为0.25x，第二车间和第三车间人数之和为0.75x。

第二车间人数为0.75x×3/7 = 9/28 x。

0.25x + 40 = 9/28 x，9/28 x - 7/28 x = 40，2/28 x = 40，x = 560 人。

题目5：一桶油，第一次用去2/5 ，第二次用去10 千克，这时剩下的油正好是整桶油的一半。

这桶油有多少千克？答案：设这桶油有x 千克。

小升初数学冲刺奥数题100道附答案(完整版)1. 某班有40 名学生，期中数学考试，有两名同学因故缺考，这时班级平均分为89 分，缺考的同学补考各得99 分，这个班期中考试平均分是多少？答案：89.5 分思路：班级总分(40 - 2)×89 = 3382 分，加上补考同学的分数3382 + 99×2 = 3580 分，平均分3580÷40 = 89.5 分。

2. 修一条路，第一天修了全长的1/4 ，第二天修了余下的1/3 ，还剩120 米没修，这条路全长多少米？答案：240 米思路：设全长为x 米，第一天修了1/4x 米，余下3/4x 米，第二天修了3/4x×1/3 = 1/4x 米，可列方程x - 1/4x - 1/4x = 120 ，解得x = 240 米。

3. 一个长方体，如果高增加2 厘米，就变成一个正方体，这时表面积比原来增加56 平方厘米，原来长方体的体积是多少？答案：441 立方厘米思路：增加的表面积是4 个同样的长方形的面积和，一个面的面积为56÷4 = 14 平方厘米，长方形的长即正方体的棱长为14÷2 = 7 厘米，原长方体高为7 - 2 = 5 厘米，体积为7×7×5 = 245 立方厘米。

4. 甲、乙两车同时从A、B 两地相向而行，在距A 地80 千米处相遇，相遇后两车继续前进，甲车到达B 地、乙车到达A 地后均立即按原路返回，第二次在距A 地60 千米处相遇。

A、B 两地相距多少千米？答案：150 千米思路：第一次相遇时，甲乙合走一个全程，甲走了80 千米。

第二次相遇时，甲乙合走三个全程，甲走了80×3 = 240 千米。

此时距离A 地60 千米，所以两个全程为240 + 60 = 300 千米，全程为150 千米。

5. 有一批零件，甲单独做要12 天完成，乙单独做要15 天完成，两人合作3 天后，剩下的由乙单独做，还要几天完成？答案：5 天思路：甲每天完成1/12 ，乙每天完成1/15 ，两人合作 3 天完成(1/12 + 1/15)×3 = 9/20 ，剩下11/20 ，乙单独做需要11/20÷1/15 = 8.25 天，约为5 天。

小升初奥数题集锦及答案(全面)1、某市小学数学竞赛，不低于80分的人数比80分以下的人数的4倍还多2人，及格的人数比不低于80分的人数多22人，恰是不及格人数的6倍。

求参赛的总人数。

解：设不低于80分的人数为4x+2，80分以下的人数为x，及格的人数为4x+24，不及格的人数为x/6.因为总人数为不低于80分的人数加上80分以下的人数，即4x+2+x=5x+2，所以总人数为5x+2.又因为及格的人数比不低于80分的人数多22人，即4x+24=5x+2+22，解得x=44.所以总人数为5x+2=222.2、一张电影票原价为x元，根据题意可列出方程：(x-3)*1.5=1.2x，解得x=15，所以一张电影票原价为15元。

3、设乙的存款为y元，则甲的存款为9600-y元。

根据题意可列出方程：9600*0.6-120=(9600-y)*0.6，解得y=3600，所以乙的存款为3600元。

4、设原混合糖中有奶糖x颗，巧克力糖y颗。

根据题意可列出方程组：y+10=0.6(x+10+y)y+30=0.75(x+10+y)解得x=60，y=90，所以原混合糖中有60颗奶糖，90颗巧克力糖。

5、设XXX原有玻璃球为x个，则XXX原有玻璃球为3x/4，根据题意可列出方程：x/6=(3x/4+2)-x，解得x=24，所以XXX原有玻璃球24个。

6、设丙帮助甲的时间为x小时，帮助乙的时间为y小时，则可列出方程组：10/x+12/y=110/(x+y)+12/(x+y)+15/(x+y)=1解得x=20，y=30，所以丙帮助甲10小时，帮助乙12小时。

7、设全部工作需要的时间为x天，则可列出方程组：1/72)+(1/72+1/48)*2+(1/72+1/48+1/28)*4/3=1/31/72)+(1/72+1/48)*3+(1/72+1/48+1/28)*4/3+8=(5/6)*x1/72+1/48+1/28)*2/3=(1/72+1/48+1/28+1/x)*1/6解得x=72，所以余下的工作由丙单独完成需要36天。

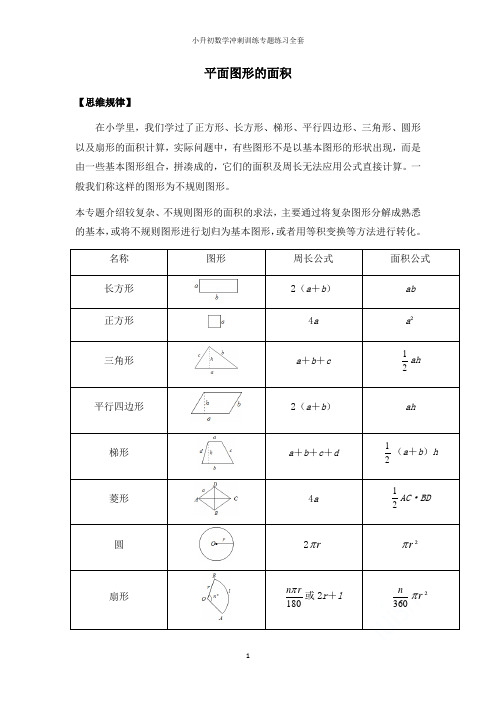
平面图形的面积【思维规律】在小学里，我们学过了正方形、长方形、梯形、平行四边形、三角形、圆形以及扇形的面积计算，实际问题中，有些图形不是以基本图形的形状出现，而是由一些基本图形组合，拼凑成的，它们的面积及周长无法应用公式直接计算。

一般我们称这样的图形为不规则图形。

本专题介绍较复杂、不规则图形的面积的求法，主要通过将复杂图形分解成熟悉的基本，或将不规则图形进行划归为基本图形，或者用等积变换等方法进行转化。

名称 图形周长公式 面积公式长方形 2（a ＋b ）ab 正方形4aa ²三角形a ＋b ＋c12ah 平行四边形2（a ＋b ） ah梯形a ＋b ＋c ＋d12（a ＋b ）h 菱形4a12AC ·BD 圆2r π r π²扇形180n rπ或2r ＋l 360nr π²【重点点拨】例1、甲和乙都是正方形。

甲的边长为4厘米，乙的边长为6厘米，求阴影部分的面积。

思考：如果只知道甲的边长为4厘米，是否还可以求出阴影部分的面积？例2、如右图，正方形ABCD的边长为6厘米，△ABE、△ADF与四边形AECF的面积彼此相等，求△AEF的面积。

例3、如右图，A为△CDE的DE边上的中点，3BC＝CD，若△ABC（阴影部分）面积为5平方厘米，求△ABD及△ACE的面积。

例4、如下图，已知ABCD是平行黑眼圈这形，AC是对角线，AC＝3CG，AE＝EF ＝FB，△EFG的面积是6平方厘米，求平行四边形ABCD的面积。

例5、如图，△ABC的面积是1平方厘米，DC＝2BD，AE＝3ED，则△ACE的面积是平方厘米。

例6、如图，长方形ABCCD中，△ABP的面积为20平方厘米，△CDQ的面积为35平方厘米，则阴影四边形的面积等于________厘米。

例7、如图，长方形被其内的一些直线划分了若干块，已知边上有3块面积分别是13、35、49.那么图中阴影部分的面积是多少？例8、有四条线段的长度已知知道，还有两个角是直角，那么四边形（阴影部分）的面积是多少？例9、在各图中，ABCD是长方形，三长线段贩长度如图所示，M是线段DE的中点，求边开边ABMD（阴影部分）的面积。

小升初数学常考奥数题100道附答案(完整版)1. 计算：1+2-3-4+5+6-7-8+9+10-11-12+...+2017+2018-2019-2020答案：-2020思路：每4 个数的计算结果为-4，2020÷4 = 505，所以结果为-4×505 = -20202. 某数除以4 余3，除以5 余2，除以6 余1，这个数最小是多少？答案：57思路：满足除以4 余3 的数有3、7、11、15、19...；满足除以5 余2 的数有2、7、12、17、22...；满足除以6 余1 的数有1、7、13、19、25...。

所以这个数最小是573. 鸡兔同笼，鸡比兔多15 只，共有脚180 只，鸡兔各有多少只？答案：鸡45 只，兔30 只思路：设兔有x 只，则鸡有x + 15 只。

4x + 2×(x + 15) = 180，解得x = 30，鸡有45 只4. 一个数减去7 的差再乘以7，所得的结果与它减去13 的差再乘以13 的结果相同，这个数是多少？答案：20思路：设这个数为x，(x - 7)×7 = (x - 13)×13，解得x = 205. 甲乙两人同时从A、B 两地相向而行，第一次在离A 地75 千米处相遇，相遇后继续前进，到达目的地后又立即返回，第二次在离 B 地55 千米处相遇，A、B 两地相距多少千米？答案：170 千米思路：第一次相遇时，甲走了75 千米，两人共走了一个全程；第二次相遇时，两人共走了三个全程，所以甲走了75×3 = 225 千米，此时甲走了一个全程多55 千米，所以全程为225 - 55 = 170 千米6. 一个长方体，如果高增加2 厘米，就变成一个正方体，这时表面积比原来增加56 平方厘米，原来长方体的体积是多少？答案：441 立方厘米思路：增加的表面积是4 个相同的长方形的面积，一个面的面积为56÷4 = 14 平方厘米，长方形的长（即正方体的棱长）为14÷2 = 7 厘米，原长方体高为7 - 2 = 5 厘米，体积为7×7×5 = 245 立方厘米7. 有三根铁丝，一根长54 米，一根长72 米，一根长36 米，要把它们截成同样长的小段，不许剩余，每段最长是多少米？答案：18 米思路：求54、72、36 的最大公因数，为188. 一个最简分数，分子、分母的和是50，如果把这个分数的分子、分母都减去5，所得分数的值是2/3，原来的分数是多少？答案：21/29思路：设分子为x，则分母为50 - x，(x - 5) / (50 - x - 5) = 2 / 3，解得x = 21，分数为21/299. 小明买了3 支铅笔和2 支钢笔，共用去22 元，钢笔的单价是铅笔的6 倍，钢笔和铅笔的单价各是多少元？答案：钢笔12 元，铅笔2 元思路：设铅笔单价为x 元，则钢笔单价为6x 元，3x + 2×6x = 22，解得x = 2，钢笔单价12 元10. 一桶油，第一次用去1/5，第二次比第一次多用去20 千克，还剩16 千克，这桶油有多少千克？答案：60 千克思路：设这桶油有x 千克，x - 1/5x - 1/5x - 20 = 16，解得x = 6011. 某工厂有三个车间，第一车间人数占总人数的1/4，第二车间人数是第三车间人数的3/4，第一车间比第三车间少40 人，三个车间共有多少人？答案：560 人思路：设总人数为x 人，第三车间人数为3/7×(3/4x + x)，则3/7×(3/4x + x) - 1/4x = 40，解得x = 56012. 学校组织数学竞赛，按参赛人数的1/5 颁奖，分设一、二、三等奖，已知获二等奖的人数比一等奖多20 人，且获二等奖的人数是三等奖的4/5，一共有多少人参赛？答案：1500 人思路：设参赛总人数为x 人，二等奖人数为1/5x×4/9，一等奖人数为1/5x×1/9，1/5x×4/9 - 1/5x×1/9 = 20，解得x = 150013. 有一堆糖果，其中奶糖占45%，再放入16 块水果糖后，奶糖就只占25%，这堆糖中有奶糖多少块？答案：9 块思路：设原来糖果总数为x 块，45%x = 25%(x + 16)，解得x = 20，奶糖有45%×20 = 9 块14. 修一条路，已修的和未修的长度比是1∶3，再修300 米后，已修的和未修的长度比是1∶2，这条路全长多少米？答案：3600 米思路：设已修的长度为x 米，未修的长度为3x 米，(x + 300) / (3x - 300) = 1 / 2，解得x = 900，全长4x = 3600 米15. 甲、乙两仓库存货吨数比为4∶3，如果从甲库中取出8 吨放到乙库中，则甲、乙两仓库存货吨数比为4∶5，两仓库原存货总吨数是多少吨？答案：63 吨思路：设甲仓库原存货4x 吨，乙仓库原存货3x 吨，(4x - 8) / (3x + 8) = 4 / 5，解得x = 9，总吨数7x = 63 吨16. 在一个底面半径是10 厘米的圆柱形杯中装水，在水中放一底面半径为5 厘米的圆锥形铝锤，使铝锤全部被水淹没，当铝锤从杯中取出后，杯里水面下降了 5 毫米，求铝锤的高是多少厘米？答案：6 厘米思路：下降的水的体积等于圆锥形铝锤的体积，3.14×10×10×0.5 = 1/3×3.14×5×5×h，解得h = 6 厘米17. 一辆汽车从甲地开往乙地，如果把车速提高20%，可以比原定时间提前1 小时到达，如果以原速行驶120 千米后，再将速度提高25%，则可提前40 分钟到达，那么甲、乙两地相距多少千米？答案：270 千米思路：设原速度为v，原时间为t，vt = 1.2v×(t - 1)，解得t = 6 小时。

小升初奥数题集锦及答案1、某市举行小学数学竞赛，结果不低于80分的人数比80分以下的人数的4倍还多2人，及格的人数比不低于80分的人数多22人，恰是不及格人数的6倍，求参赛的总人数？解：2、电影票原价每张若干元,现在每张降低3元出售,观众增加一半,收入增加五分之一,一张电影票原价多少元？3、甲乙在银行存款共9600元，如果两人分别取出自己存款的40%，再从甲存款中提120元给乙。

这时两人钱相等，求乙的存款4、由奶糖和巧克力糖混合成一堆糖，如果增加10颗奶糖后，巧克力糖占总数的60%。

再增加30颗巧克力糖后，巧克力糖占总数的75%,那么原混合糖中有奶糖多少颗？巧克力糖多少颗？5、小明和小亮各有一些玻璃球，小明说：“你有球的个数比我少1/4！”小亮说：“你要是能给我你的1/6，我就比你多2个了。

”小明原有玻璃球多少个？6、搬运一个仓库的货物，甲需要10小时，乙需要12小时，丙需要15小时.有同样的仓库A和B，甲在A仓库、乙在B仓库同时开始搬运货物，丙开始帮助甲搬运，中途又转向帮助乙搬运.最后两个仓库货物同时搬完.问丙帮助甲、乙各多少时间？7、一件工作,若由甲单独做72天完成,现在甲做1天后,乙加入一起工作,合作2天后,丙也一起工作,三人再一起工作4天,完成全部工作的1/3,又过了8天,完成了全部工作的5/6,若余下的工作由丙单独完成,还需要几天?8、股票交易中，每买进或卖出一种股票都必须按成交易额的1％和2％分别交纳印花税和佣金（通常所说的手续费）。

老王10月8日以股票10.65元的价格买进一种科技股票3000股，6月26日以每月13.86元的价格将这些股票全部卖出，老王卖出这种股票一共赚了多少钱？9、某书店老板去图书批发市场购买某种图书，第一次购书用100元，按该书定价2.8元出售，很快售完。

第二次购书时，每本的批发价比第一次增多了0.5元，用去150元，所购数量比第一次多10本，当这批书售出4/5时出现滞销，便以定价的5折售完剩余图书。

小升初奥数冲刺1.平均数问题 (2)2.差倍问题 (3)3.归一问题 (4)4.归总问题 (4)5.植树问题 (5)6.年龄问题 (7)7.鸡兔问题 (9)8.行程问题 (10)1)直线上的相遇与追及 (11)2)火车过人、过桥与错车问题 (12)3)多个对象间的行程问题 (14)4)环形问题与时钟问题 (14)9.流水行船行程问题 (14)10.盈亏问题 (17)11.工程问题 (19)12.百分数与纳税问题 (21)13.时钟问题—钟面追及问题、快慢表问题 (23)1)钟面追及问题 (23)2)快慢表问题 (24)14.图形问题 (26)15.牛吃草问题 (35)16.浓度与配比 (39)17.约数与倍数 (45)18.质数与合数 (46)19.抽屉原理 (48)1.平均数问题1、李明在期中考试中语文、外语和自然的平均分是74分，数学成绩公布后，四门成绩的平均分提高了3分。

李明数学数学考多少分？【解答】74×3=222分74+3=77分77×4=308分308-222=86分2、这学期，王平前四个单元测验的平均成绩是85分，他想使前五个单元的平均成绩上升到87分，第五个单元必须考多少分？【解答】85×4=340分87×5=435分435-340=95分3、李明在期中考试中语文、外语和自然的平均分是95分，数学成绩公布后四门成绩的平均分减少了2分。

你知道李明的数学得了几分吗？【解答】95×3=285分95-2=93分93×4=372分372-285=87分4、甲地到乙地的全程是120千米。

小红骑车从甲地到乙地每小时行30千米，从乙地返回甲地每小时行20千米。

求小红往返甲乙两地的平均速度。

【解答】120÷30=4小时120÷20=6小时120＋120=240千米4＋6=10小时240÷10=24千米此题需要注意，求平均速度，一定要用总路程除以总时间。

小升初奥数精讲精练500题100题精讲（一）数论------100题数论（1）例题1：（第7题）一个三位数是3的倍数，去掉它的个位数字后，所得的两位数是17的倍数。

这个三位数最大是____。

例题2：（第8题）将被11除余1，被15除余12的自然数按从小到大的顺序排成一列：a1，a2，a3，……，则a1=____；若a m-1＜2011＜a m，则m=_____。

例题3：（第15题）请选择一个你喜欢的两位数，将它连续写5遍组成一个十位数（如：两位数12连续写5遍成为1212121212），将这个十位数除以这个两位数，所得到的商再除以9，所得的余数是_____。

例题4：（第18题）六年级1班有30多人，个子最高的小明发现，放学站队时无论是2人、还是3人或者4人站成一排，他都只能自己单独站在最后，没有人与他站一排。

则六年级1班共有_____人。

例题5：（第46题）如果现在是上午的10点21分，那么经过2879……９（共20个9）分钟之后的时间是____点____分。

100题精讲（一）数论------ 100题数论（2）例题1：（第49题）一个六位数的末位数字是2，如果将2移到首位，则原数就是新数的3倍。

原数是_____。

例题2：（第53题）有一个两位数，如果用它除以它的个位数字，商9余6；如果用它除以个位数字与十位数字的和，商5余3。

这个两位数是_____。

例题3：（第54题）一串数的前4项分别是2、0、1、0，从第5项开始，每一项都是它前面4项数字和的个位数字，那么该数列中_____（填“会”或“不会”）出现2、0、1、1连续4项。

例题4：（第64题）有三箱螺帽，其中第一个箱子里有303只螺帽，第二个箱子里的螺帽是全部螺帽的，第三个箱子里的螺帽是全部螺帽的7（n是自然数）。

则第三个箱子里有螺帽_____只。

例题5：（第74题）由2011个9组成的多位数999……99除以74所得余数是_____。

100题精讲（一）数论------ 100题数论（3）例题1：（第75题）小萌在超市买了3种糖果，其中红色糖果每粒8分，绿色糖果每粒1角，黄色糖果每粒2角，她共付了1元2角2分。

小升初最常考奥数题100道及答案(完整版)1. 一桶水可灌3/4 壶水，1 壶水可以冲2 杯水，1 桶水可以冲几杯水？答案：3/4×2 = 3/2 = 1.5（杯）2. 小明看一本书，第一天看了全书的1/4，第二天看了全书的2/5，第二天比第一天多看了21 页，这本书一共有多少页？答案：21÷（2/5 - 1/4）= 21÷3/20 = 140（页）3. 有一批货物，第一天运走了总数的2/5，第二天运走的货物比总数的1/4 多4 吨，这时还剩17 吨，这批货物共有多少吨？答案：（17 + 4）÷（1 - 2/5 - 1/4）= 21÷7/20 = 60（吨）4. 某工厂有三个车间，第一车间的人数占三个车间总人数的25%，第二车间人数是第三车间的3/4，已知第一车间比第二车间少40 人，三个车间一共有多少人？答案：40÷[(1 - 25%)×3/(3 + 4) - 25%] = 40÷[3/7 - 1/4] = 560（人）5. 师徒两人合做一批零件，徒弟做了总数的2/7，比师傅少做21 个，这批零件有多少个？答案：21÷（1 - 2/7 - 2/7）= 21÷3/7 = 49（个）6. 仓库里有一批化肥，第一次取出总数的2/5，第二次取出总数的1/3 少12 袋，这时仓库里还剩24 袋，两次共取出多少袋？答案：（24 - 12）÷（1 - 2/5 - 1/3）= 12÷4/15 = 45（袋），45 - 24 = 21（袋）7. 甲、乙、丙三个数的和是110，甲与乙的比是3:2，乙与丙的比是4:1，乙数是多少？答案：甲:乙= 3:2 = 6:4，乙:丙= 4:1，所以甲:乙:丙= 6:4:1，乙数：110×4/(6 + 4 + 1) = 408. 一辆汽车从甲地开往乙地，行了全程的3/8，离乙地还有135 千米，两地之间的公路长多少千米？答案：135÷（1 - 3/8）= 216（千米）9. 修一条路，已修的与未修的比是1:5，又修了490 米后，已修的与未修的比是3:1，这时还有多少米未修？答案：490÷（3/4 - 1/6）×1/4 = 180（米）10. 某校有学生465 人，其中女生的2/3 比男生的4/5 少20 人，男、女生各有多少人？答案：设男生有x 人，4/5 x - 2/3×(465 - x) = 20 ，解得x = 225，女生人数：465 - 225 = 240（人）11. 水果店里卖出的梨的重量是苹果的5/7，梨比苹果少卖30 千克，梨卖了多少千克？答案：30÷（1 - 5/7）×5/7 = 75（千克）12. 一筐苹果卖掉1/5 后，又卖掉6 千克，这时卖出的重量正好是剩下的1/2，这筐苹果原来有多少千克？答案：6÷（1/3 - 1/5）= 45（千克）13. 甲、乙两班共有84 人，甲班人数的5/8 与乙班人数的3/4 共有58 人，甲、乙两班各有多少人？答案：设甲班有x 人，5/8 x + 3/4×(84 - x) = 58 ，解得x = 40，乙班：84 - 40 = 44（人）14. 学校买来两种图书共220 本，取出甲种图书的1/4 和乙种图书的1/5 共50 本借给五年级（1）班同学阅读，问甲、乙两种图书各买来多少本？答案：设甲种图书有x 本，1/4 x + 1/5×(220 - x) = 50 ，解得x = 120，乙种图书：220 - 120 = 100（本）15. 某工厂第一车间有工人150 人，第二车间有工人90 人，要使第一车间人数是第二车间的2 倍，需要从第二车间调多少人到第一车间？答案：(150 + 90)÷(2 + 1) = 80（人），90 - 80 = 10（人）16. 甲、乙两堆煤共180 吨，甲堆煤的1/3 比乙堆煤的2/3 多18 吨，甲、乙两堆煤各有多少吨？答案：设甲堆煤有x 吨，1/3 x - 2/3×(180 - x) = 18 ，解得x = 138，乙堆煤：180 - 138 = 42（吨）17. 学校图书馆有科技书和文艺书共3200 本，科技书的本数是文艺书的4/5，科技书和文艺书各有多少本？答案：文艺书：3200÷（1 + 4/5）= 16000/9 ≈1778（本），科技书：3200 - 1778 = 1422（本）18. 一辆汽车从甲地到乙地，已经行了全程的1/5，再向前行50 千米，就比全程的2/3 少6 千米，求甲乙两地的距离。

小升初奥数冲刺题大全汇总1、（归一问题）工程队计划用60人5天修好一条长4800米的公路，实际上增加了20人，每人每天比计划多修了4米，实际修完这条路少用了几天？4800÷5÷60=16(米) 计划每人每天修16米4800÷【（60+20）×(16+4)】=3（天）实际3天完成5-3=2（天）少用2天2、（相遇问题）甲、乙两辆汽车同时从东西两地相向开出，甲车每小时行56千米，乙车每小时行48千米。

两车距中点40千米处相遇。

东西两地相距多少千米？40×2=80（千米）相遇时，甲车比乙车多走80千米80÷（56-48）=10（小时）甲乙两车开车时间都是10小时（56+48）×10=1040（千米）东西两地相距1040千米3、（追及问题）大客车和小轿车同地、同方向开出，大客车每小时行60千米，小轿车每小时行84千米，大客车出发2小时后小轿车才出发，几小时后小轿车追上大客车？84－60=24千米小轿车每小时比大客车多走24千米60×2÷24=5小时 5小时小轿车能追上大客车（小轿车把大客车多走的路补回来，就追上了的大客车）4、（过桥问题）列车通过一座长2700米的大桥，从车头上桥到车尾离桥共用了3分钟。

已知列车的速度是每分钟1000米，列车车身长多少米？分析：要想列车完全通过桥，则列车要走的距离=桥的长度+列车的长度1000×3=3000米列车3分钟走了3000米，即桥的长度+列车的长度=3000米3000-2700=300米列车车身长300米5、（错车问题）一列客车车长280米，一列货车车长200米，在平行的轨道上相向而行，从两个车头相遇到车尾相离经过20秒。

如果两车同向而行，货车在前，客车在后，从客车头遇到货车尾再到客车尾离开货车头经过120秒。

客车的速度和货车的速度分别是多少？分析：客车相对货车走的距离，两次都是两车的车身长之和，只不过行驶方向不一样，造成用时不一样的结果（280+200）÷20=24（米／秒）两车速度之和为24米／秒（280+200）÷120=4（米／秒）客车速度每秒比货车快4米（24-4）÷2=10（米／秒）货车速度为10米／秒24-10=14（米／秒）客车速度为14米／秒6、（行船问题）客轮和货轮从甲、乙两港同时相向开出，6小时后客轮与货轮相遇，但离两港中点还有6千米。

小升初数学必考奥数题100道附答案(完整版)题目1：有四个小朋友，他们的年龄一个比一个大一岁，四个人的年龄乘积是360。

他们中年龄最大的是多少岁？答案：将360 分解因数，360 = 2×2×2×3×3×5 = 3×4×5×6，所以年龄最大的是6 岁。

题目2：计算：1 + 2 - 3 - 4 + 5 + 6 - 7 - 8 + 9 +…+ 2014 - 2015 - 2016 + 2017 + 2018答案：原式= (1 + 2 - 3 - 4) + (5 + 6 - 7 - 8) +…+ (2013 + 2014 - 2015 - 2016) + 2017 + 2018 = 2017 + 2018 = 4035题目3：一项工程，甲单独做10 天完成，乙单独做15 天完成。

甲乙合作，几天可以完成？答案：甲每天完成工程的1/10，乙每天完成工程的1/15，两人合作每天完成1/10 + 1/15 = 1/6，所以合作需要6 天完成。

题目4：在一个比例中，两个外项互为倒数，其中一个内项是2.5，另一个内项是多少？答案：两个外项互为倒数，乘积为1。

根据比例的性质，两个内项的积也为1，所以另一个内项是1÷2.5 = 0.4题目5：一个数除以8 余5，除以9 余6，这个数最小是多少？答案：这个数加上3 就能被8 和9 整除，8 和9 的最小公倍数是72，所以这个数最小是72 - 3 = 69题目6：一个圆形花坛的周长是25.12 米，在它的周围加宽1 米，加宽后的面积比原来增加了多少平方米？答案：原来花坛的半径为25.12÷3.14÷2 = 4 米，加宽后的半径为5 米。

增加的面积为3.14×(5²- 4²) = 28.26 平方米题目7：一个长方体的棱长总和是120 厘米，长、宽、高的比是3:2:1，这个长方体的体积是多少立方厘米？答案：120÷4 = 30 厘米，3 + 2 + 1 = 6，长为15 厘米，宽为10 厘米，高为5 厘米，体积为750 立方厘米题目8：甲乙两车同时从A、B 两地相对开出，4 小时后相遇。

小升初名校冲刺方案奥数知识大集结1 、一个杯子最大的容量是500毫升，甲将杯子装满水，喝了部分后又加入了杯子容量的水，之后甲又将杯子里一半的水用来浇花。

这时，杯子里还剩下200毫升水。

则甲喝了（）毫升水。

A.100B.150C.200D.2502 、某部队组织新兵从甲地到乙地进行长途拉练。

去的时候第一天走25公里，以后每天都比前一天多走5公里，结果最后一天只走25公里便到达了目的地。

回程时，第一天走35公里，以后还是每天比前一天多走5公里，结果最后一天只走30公里便回到出发地。

则甲乙两地相距（）公里。

A.175B.200C.225D.2503 、某书店按阶梯价格出售一批书，原价每本15元，10本以下部分按原价计算，第11本至第20本按原价九折计算，第21本至第30本部分按原价八折计算，折扣以此类推，但最低只能为五折。

则用1000元最多可以买（）本书。

A.66B.95C.103D.1114、某单位前台有两个窗口，办理业务的人员要先到1号窗口审核资料，审核通过的才可以到2号窗口缴费。

已知平均一份资料的审核时间为1.5分钟，且审核通过率仅有，而一份资料的缴费时间仅为50秒。

假设前台共有10名工作人员，且各窗口的人员数量固定，则1号窗口应安排（）人，才能使得前台运作效率最高。

A.9B.8C.7D.65 、一小偷藏匿于某商场，三名保安甲、乙、丙分头行动搜查商场的100家商铺。

已知甲检查过80家，乙检查过70家，丙检查过60家，则三人都检查过的商铺至少有（）家。

A.5B.10C.20D.306 、小王的旅行箱密码为3位数，且三个数字全是非0的偶数，而且这个三位数恰好是小王今年年龄的平方数。

则小王今年（）岁。

A.17B.20C.22D.347 、如下图所示，在一个边长为8米的正方形与一个直径为8米的半圆形组成的花坛中，阴影部分栽种了新引进的郁金香，则郁金香的栽种面积为（）平方米。

A.4＋4πB.4＋8πC.8＋8πD.16＋8π8 、参加奥运开幕式表演的某方阵正在彩排，如果减少一行和一列，人数减少319人。

小升初名校冲刺方案奥数知识大集结1 、货车A由甲城开往乙城，货车B由乙城开往甲城，它们同时出发并以各自恒定的速度行驶，在途中第一次相遇时，它们离甲城为35千米。

相遇后两车继续以原来的速度行驶至目的地城市后立即折返，途中再一次相遇，这时它们离乙城为25千米。

则甲乙两城相距（）千米。

A.80B.85C.90D.952 、甲乙两人在玩一个沙盘游戏，比赛的规则是：在一个分为50个单位的区域上，每人轮流去划定这些区域作为自己的领地，每次可以划定1到5个单位，谁作为最后划定区域的人则为胜利者，如果由甲划定，那么甲一开始要划定（）个单位，才能保证自己获胜。

A.1B.2C.3D.43 、上一个虎年老王和小赵的年龄和为54岁，上上个虎年老王年龄是小赵年龄的6倍多，如两人年龄均按出生的阴历年份计算且出生的当个阴历年为0岁，则老王出生于：A.鼠年B.虎年C.龙年D.马年4 、某城市准备在公园里建一个矩形的花园，长比宽多40米，同时在花园周围建一条等宽的环路。

路的外周长为280米，路的面积为1300平方米，则路的宽度为多少米？A.3B.4C.5D.65 、某工厂4个车间的工人都出生在1985到1988年间，如果统计任意2个车间的人数和，分别得到54、63、75、78、90、99这6个不同的结果。

则人数最多的车间至少有多少工人出生于同一年？A.14B.15C.16D.176 、某公司面试员工，其中五分之二的应聘者获得了职位，最终录取者的平均分比录取线高7分，落选者的平均分比录取线低13分，所有应聘者的平均分为58分，则该公司的招聘录取线是多少分？A.60B.63C.65D.697 、有一批汽车零件由A和B负责加工，A每天比B少做3个零件。

如果A和B两人合作需要18天才能完成，现在让A先做12天，然后B再做17天，还剩这批零件的没有完成，这批零件共有多少个？A.300B.250C.240D.2708 、甲、乙和丙三种不同浓度、不同规格的酒精溶液，每瓶重量分别为3公斤、7公斤和9公斤，如果将甲乙各一瓶、甲丙各一瓶和乙丙各一瓶分别混合，得到的酒精浓度分别为50%，50%和60%。

小升初奥数高频考点历年真题总汇（一）1 、某杂志为每篇投稿文章安排两位审稿人,若都不同意录用则弃用；若都同意则录用；若两人意见不同,则安排第三位审稿人,并根据其意见录用或弃用,如每位审稿人录用某篇文章的概率都是60%,则该文章最终被录用的概率是：A.36%B.50.4%C.60%D.64.8%2 、生产一件甲产品消耗4份原料A、2份原料B、3份原料C,可获得1.1万元利润；生产一件乙产品3份原料A、5份原料B,可获得1.3万元利润。

现有40份原料A、38份原料B、15份原料C用于生产,问最多可获得多少万元利润？A.10.2B.12.0C.12.2D.12.83 、某企业在软件园区的分公司有甲、乙2个开发团队。

现从乙团队调走25人,此时甲、乙团队人数比为4∶3。

然后又从甲团队调走42人,此时甲、乙团队人数之比2∶5。

问两次调动之前,甲、乙团队人数比为：A.3∶4B.6∶7C.1∶2D.2∶54 、某高校向学生颁发甲、乙两项奖学金共10万元。

已知每份甲等、乙等奖学金的金额分别为3000元和1000元,每人只能最多获得一项奖学金,获得乙等奖学金的人数在获得甲等奖学金人数的2倍到3倍之间。

问最多可能有多少人获得奖学金？A.62B.64C.66D.685 、一个位于O点的雷达探测半径为25千米。

某日该雷达探测到一辆车沿直线驶过探测区,行驶过程中途经距离雷达20千米外的P点。

如该车在雷达探测区内行驶的距离为X千米,为X的最大值和最小值相差多少？A.15B.16C.20D.256 、蔬菜摊贩某日花费x元购进蔬菜,上午、下午、傍晚分别按进货单价的150%、130%、120%卖掉占总进货价值50%、20%、25%的蔬菜,并将剩下未卖的蔬菜送给养殖场。

如摊位成本为0.06x,则该摊贩当日盈利为：A.0.2xB.0.25xC.0.3xD.0.35x7 、甲、乙两条生产线同时接到羽毛球拍、网球拍两种球拍的生产任务。

已知甲要生产的球拍总数和乙相同。

苏教版小升初奥数题100道附答案(完整版)1. 计算：2+4+6+8+…+100答案：2550思路：这是一个等差数列求和，首项是2，末项是100，公差是2，项数是50，根据等差数列求和公式可得（2+100）×50÷2=2550。

2. 某数加上5，乘以5，减去5，除以5，结果还是5，这个数是多少？答案：1思路：从后往前推，除以5 之前是5×5=25，减去5 之前是25+5=30，乘以5 之前是30÷5=6，加上5 之前是6-5=1。

3. 鸡兔同笼，有20 个头，54 条腿，鸡兔各有多少只？答案：鸡13 只，兔7 只思路：设鸡有x 只，兔有y 只，可列出方程组x+y=20，2x+4y=54，解得x=13，y=7。

4. 一个数除以3 余2，除以5 余3，除以7 余2，这个数最小是多少？答案：23思路：除以 3 余 2 和除以7 余 2 的最小数是23，且23 除以 5 余3，所以这个数最小是23。

5. 小明从一楼到三楼用了6 分钟，照这样计算，他从一楼到六楼要用多少分钟？答案：15思路：从一楼到三楼走了2 层楼梯用了6 分钟，每层用时6÷2=3 分钟，从一楼到六楼走5 层楼梯，要用3×5=15 分钟。

6. 一块长方形草地，长100 米，宽80 米，在草地周围每隔10 米种一棵树，一共要种多少棵树？答案：36思路：长方形周长为（100+80）×2=360 米，每隔10 米种一棵树，所以树的数量为360÷10=36 棵。

7. 一个正方体棱长总和是48 厘米，它的表面积是多少平方厘米？答案：96思路：正方体有12 条棱，每条棱长度相等，所以棱长为48÷12=4 厘米，表面积为6×4×4=96 平方厘米。

8. 一桶油连桶重10 千克，倒出一半油后，连桶重5.5 千克，桶重多少千克？答案：1思路：一半油重10-5.5=4.5 千克，油重4.5×2=9 千克，桶重10-9=1 千克。

小升初突击训练系列试卷一一、计算题：（每题５分，共１０分）1、（111×66-185×8)÷37=______.２、1997+4+1993+1992…-2+1=_______．二、填空题:（每题５分，共25分）１、某地区水电站规定，如果每月用电不超过24度，则每度收9分；如果超过24度，则多出度数按每度2角收费．若某月甲比乙多交了角（甲、乙都是整数），则甲交了______角______分2、乒乓球单打决赛在甲、乙、丙、丁四位选手中进行，赛前，有些人预测比赛结果，A说：甲第4；B说：乙不是第2，也不是第4；C说：丙的名次在乙的前面；D说：丁将得第1．比赛结果表明，四个人中只有一人预测错了．那么，甲、乙、丙、丁四位选手的名次分别为：_______．3、41位数55…5□99…9（其中5和9各有20个）能被7整除，那么中间方格内的数字是_____．4、如图，一长方形被一条直线分成两个长方形，这两个长方形的宽的比为1∶3，若阴影三角形面积为1平方厘米，则原长方形面积为______平方厘米．5．字母A、B、C代表三个不同的数字，其中A比B大，B比C大，如果用数字A、B、C组成的三个三位数相加的和为777，其竖式如右，那么三位数ABC是______．三、解答题：（1~7题每题5分，8，9，10题每题10分，共65分）1．一列快车和一列慢车相向而行，快车的车长是280米，慢车的车长是385米．坐在快车上看见慢车驶过的时间是11秒，那么坐在慢车上看见快车驶过的时间是多少秒？2．一堆苹果，2个2个地数剩1个，3个3个地数剩2个，4个4个地数剩3个，5个5个地数剩4个，6个6个地数剩5个，求这堆苹果至少有多少个？3．甲、乙、丙三人去完成植树任务，已知甲植一棵树的时间，乙可以然后丙休息了8天，乙休息了3天，甲没休息，最后一起完成任务．问：从开始植树算起，共用了多少天才完成任务？5．原计划有420块砖让若干学生搬运，每人运砖一样多，后来增加一个学生，这样每个学生就比原计划少搬2块．那么原来有学生多少人？6．六年级学生和一年级学生共120人一起给树浇水，六年级学生一人提两桶水，一年级学生两人抬一桶水，两个年级一次浇水180桶，问有一年级学生多少人？7、小红有一只手表和一只小闹钟，走时总有点差别，小闹钟走半小时，手表要多走36秒，又知在半小时的标准时间里，小闹钟少走了36秒，问：这只手表准不准？每小时差多少？8、甲、乙、丙三个小孩分别带了若干块糖，甲带的最多，乙带的较少，丙带的最少．后来进行了重新分配，第一次分配，甲分给乙、丙，各给乙、丙所有数少4块，结果乙有糖块最多；第二次分配，乙给甲、丙，各给甲、丙所有数少4块，结果丙有糖块最多；第三次分配，丙给甲、乙，各给甲、乙所有数少4块，经三次重新分配后，甲、乙、丙三个小孩各有糖块44块，问：最初甲、乙、丙三个小孩各带糖多少块？9、外表相同的18个小球中，有9克和10克的两种重量，从18个球中取出两个球放在天平左边以作比较，另外16个球分成8对，依次放在天平的右边与这两个球比较重量，发现有5对比那两个球重，有2对比那两个球轻，有一对与那两个球重量相等，这18个球的总重量是多少？10、A s shown below, the area of the parallelogram ABCD is 54 cm2, E, F trisect CA and BA, the area of the shadow is _________.小升初突击训练系列试卷二一、计算题：（每题５分，共１０分）1、114×+36÷45+×２、二、填空题:（每题５分，共２５分）１、和式2007200620052004321A 2008200720062005432＝－＋－＋＋－＋与1进行比较，则A ＿＿＿1。

小升初数学择校考（自主招生考）附加题（奥数）考前集训专题1、 =⨯-⨯202020202019201920202019201920202、 估计下面四个算式的计算结果，最大的是（ ）A. )201911(2019+⨯B. )201911(2019-⨯ C. )201911(2019+÷ D.)201911(2019-÷ 3、有15个同学合影留念，每人要一张照片，最初三张照片和一张底片共收成本费2.70元，以后加印一张照片收费0.40元。

平均每人应付 元。

4、数字M 介于11~19之间，那么8，12和M 这三个数的平均数可能是（ ）。

A ．15或11B ．14或12C ．12或15D ．11或125、求在8点几分时，时针与分针重合在一起？6、某校把2019名学生按0001到2019的顺序编号，在新年联欢会上，编号为5的倍数或6的倍数的同学将得到一张贺卡，且每人最多得一张，大会共需多少张贺卡？7、某市水文站8月1日~8月6日，每日下午2时发布的汛情公告如下：8月1日：水位32米；8月2日：水位32．9米；8月3日：水位32．4米；8月4日：水位32．6米；8月5日：水位32．2米；8月6日水位：31．8米。

（警戒水位为32米，历史最高水位为32．6米）⑴根据上面的数据，完成下面的折线统计图。

某市8月1日~8月6日汛情统计图⑵从图中你得到了哪些信息？8、六个小朋友围成一圈，每人心里想好一个数，并把这个数告诉左、右相邻的两个人，然后每个人把左、右两个相邻人告诉自己的数的平均数亮出来。

如图所示，问：亮出11的人原来心中想的数是多少？9、为保护水资源，某市规定：每人每月用水量不超过2吨，每吨水费1.1元；超过2吨部分，每吨水费2元。

赵伟家五口人，四月份交水费23元。

他家四月份用水多少吨？10、贝贝家每天都喝3袋牛奶，7月份按零售价买了5天牛奶共花了16.5元，八月份按批发价预订了全月每天的牛奶，共付了88.35元。

小升初常考的奥数题100道附答案(完整版)1. 有红、黄、白三种颜色的球，红球和黄球一共有21 个，黄球和白球一共有20 个，红球和白球一共有19 个。

三种球各有多少个？答案：三种球的总数：(21 + 20 + 19)÷2 = 30（个）白球：30 - 21 = 9（个）红球：30 - 20 = 10（个）黄球：30 - 19 = 11（个）2. 在一个减法算式里，被减数、减数与差的和等于120，而减数是差的3 倍，那么差等于多少？答案：被减数= 减数+ 差被减数+ 减数+ 差= 120所以被减数= 60差：60÷(3 + 1) = 153. 某班学生去划船，如果增加一条船，那么每条船正好坐6 人；如果减少一条船，那么每条船就要坐9 人。

问：学生有多少人？答案：设原来有x 条船。

6(x + 1) = 9(x - 1)x = 5学生人数：6×(5 + 1) = 36（人）4. 老师把一些苹果分给小朋友。

如果每人分一个，还剩下8 个苹果；如果每人分2 个，那么还少2 个苹果。

一共有多少个小朋友？答案：设小朋友有x 个。

x + 8 = 2x - 2x = 105. 甲、乙两数的和是180，甲数的1/4 等于乙数的1/5，甲、乙两数各是多少？答案：甲：乙= 4 : 5甲：180×4/(4 + 5) = 80乙：180 - 80 = 1006. 一个长方形，如果长增加2 厘米，宽增加5 厘米，那么面积就增加60 平方厘米，这时恰好是一个正方形。

原来长方形的面积是多少平方厘米？答案：设正方形边长为x 厘米。

(x - 2)(x - 5) + 60 = x²x = 10原长方形长8 厘米，宽 5 厘米，面积40 平方厘米。

7. 一筐苹果分给甲、乙、丙三人，甲分得全部苹果的1/5 加5 个苹果，乙分得全部苹果的1/4 加7 个苹果，丙分得其余苹果的1/2，最后剩下的苹果正好等于一筐苹果的1/8。