中心投影与平行投影

2023中心投影与平行投影contents •引言•中心投影•平行投影•中心投影与平行投影的比较•实际应用与展望目录01引言投影是二维图形或三维形体在某个平面或空间上表现出来的形象。

投影定义根据投影线是否汇聚于一点，投影分为中心投影和平行投影。

投影分类投影的定义与分类中心投影光线从一个点出发，经过物体，投射到另一个平面上的中心点，形成的投影称为中心投影。

平行投影光线从一个点出发，经过物体，投射到另一个平面上，光线相互平行且汇聚于同一点，形成的投影称为平行投影。

中心投影与平行投影的概述中心投影与平行投影的基本概念和性质。

两种投影在工程、艺术、设计等领域的应用。

如何运用投影知识解决实际问题。

本文的讨论重点02中心投影定义光线从一点出发，把物体投影到投影面上，形成中心投影。

性质中心投影的光源为灯泡、火炬等点光源，投影面为各种曲面的透明或半透明材料。

中心投影的定义与性质手影表演、皮影戏、夜晚的路灯下，人和物体的影子都是中心投影。

例子建筑设计、城市规划、室内设计等领域中，利用中心投影原理来制造三维立体模型，模拟实际场景。

应用中心投影的例子和应用优点直观性强，易于理解；可以产生生动的光影效果，增强视觉冲击力；在夜晚或暗光环境下，能够提供更好的照明效果。

缺点立体感较差，不易掌握；受光源位置影响大，光源位置不对则难以取得好的效果；会产生影子、遮挡物等限制因素。

中心投影的优缺点03平行投影平行投影的定义将物体放在无限远处，在投影面上得到的投影称为平行投影。

平行投影的性质物体与投影面平行，投影线与投影面垂直，投影反映物体的真实大小，但无立体感。

平行投影的定义与性质太阳光线可以看作是互相平行的，将物体放在太阳光下可以得到物体的平行投影。

平行投影的例子在建筑、城市规划、工程设计中广泛运用，通过平行投影可以获得建筑物的平面图和立面图等。

平行投影的应用平行投影的例子和应用平行投影的优点易于绘制和计算，可以真实反映物体的形状和大小，适用于大规模的工程和建筑项目。

中心投影与平行投影
1. 中心投影
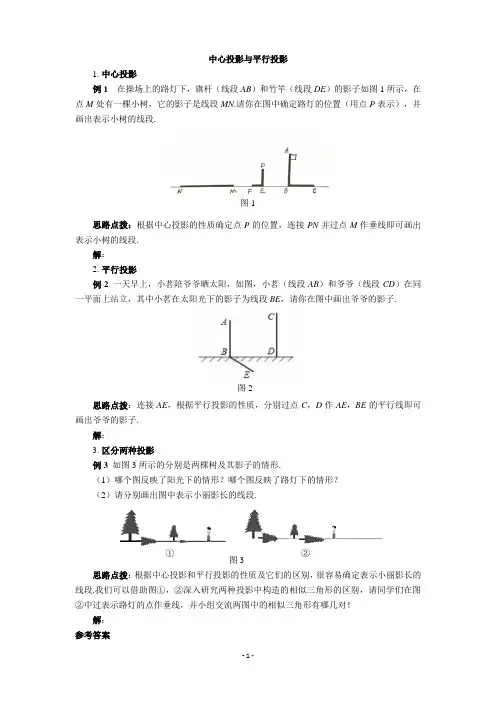
例1 在操场上的路灯下，旗杆（线段AB ）和竹竿（线段DE ）的影子如图1所示，在点M 处有一棵小树，它的影子是线段MN .请你在图中确定路灯的位置（用点P 表示），并画出表示小树的线段.
思路点拨：根据中心投影的性质确定点P 的位置，连接PN 并过点M 作垂线即可画出表示小树的线段.
解：
2. 平行投影
例2 一天早上，小茗陪爷爷晒太阳，如图，小茗（线段AB ）和爷爷（线段CD ）在同一平面上站立，其中小茗在太阳光下的影子为线段BE ，请你在图中画出爷爷的影子.
思路点拨：连接AE ，根据平行投影的性质，分别过点C ，D 作AE ，BE 的平行线即可画出爷爷的影子.
解：
3. 区分两种投影
例3 如图3所示的分别是两棵树及其影子的情形.
（1）哪个图反映了阳光下的情形？哪个图反映了路灯下的情形？
（2）请分别画出图中表示小丽影长的线段.
思路点拨：根据中心投影和平行投影的性质及它们的区别，很容易确定表示小丽影长的线段.我们可以借助图①，②深入研究两种投影中构造的相似三角形的区别，请同学们在图②中过表示路灯的点作垂线，并小组交流两图中的相似三角形有哪几对！
解：
参考答案
①
②
图3 图2 图1
例1 如图1，点P 即为所求，线段HM 为表示小树的线段.
例2 如图2，线段DF 即为所求.
例3 （1）图①反映了阳光下的情形，图②反映了路灯下的情形.
（2）如图3，线段AB ，CD 是表示小丽影长的线段. 图 1
图2
①
② 图3。

中心投影与平行投影教案章节一：中心投影1.1 学习目标了解中心投影的定义及特点。

学会运用中心投影进行图形绘制。

1.2 教学内容中心投影的定义：通过一个点（称为中心）向平面上的图形发射光线，形成的投影称为中心投影。

中心投影的特点：投影线相交于一点，投影角度随距离的增加而减小。

1.3 教学活动引入中心投影的概念，展示图片，让学生观察并描述中心投影的特点。

讲解中心投影的原理，并通过实际操作演示中心投影的绘制过程。

学生分组讨论，每组设计一个中心投影的图形，并绘制出来。

1.4 作业布置让学生利用中心投影绘制一个简单的物体，如房屋、树木等，并观察投影的变化。

章节二：平行投影2.1 学习目标了解平行投影的定义及特点。

学会运用平行投影进行图形绘制。

2.2 教学内容平行投影的定义：通过一组平行的光线从一个方向照射平面上的图形，形成的投影称为平行投影。

平行投影的特点：投影线平行，投影角度不变。

2.3 教学活动引入平行投影的概念，展示图片，让学生观察并描述平行投影的特点。

讲解平行投影的原理，并通过实际操作演示平行投影的绘制过程。

学生分组讨论，每组设计一个平行投影的图形，并绘制出来。

2.4 作业布置让学生利用平行投影绘制一个简单的物体，如建筑物、车辆等，并观察投影的变化。

章节三：中心投影与平行投影的比较3.1 学习目标掌握中心投影与平行投影的区别和联系。

能够根据实际情况选择合适的投影方式。

3.2 教学内容中心投影与平行投影的比较：中心投影的特点是投影线相交于一点，投影角度随距离的增加而减小；平行投影的特点是投影线平行，投影角度不变。

选择合适的投影方式：根据实际需求，选择中心投影或平行投影进行图形绘制。

3.3 教学活动引导学生通过观察已绘制的中心投影和平行投影图形，总结两者的区别和联系。

讲解在实际应用中如何选择合适的投影方式，例如在建筑设计中，可以根据建筑物的高度和角度选择平行投影或中心投影。

学生分组讨论，每组设计一个场景，选择合适的投影方式进行绘制。

汇报人：2023-11-22contents •投影的定义与分类•平行投影•中心投影•两种投影方式的比较•实际应用案例分析•总结与展望目录01投影的定义与分类投影面投影1. 正平行投影：投影线平行于投影面且垂直于投射中心。

2. 斜中心投影：投影线汇聚于一条直线上。

平行投影：投影线相互平行且垂直于投影面。

1. 正中心投影：投影线汇聚于一点。

01020304050602平行投影定义在平行投影中，投射线都是相互平行的，投影线与投射线也是平行的。

描述图形变化平行性视觉效果真实性工程制图建筑设计机械制图03020103中心投影01020304定义光源位置图形形状投影面唯一性相似性角度变化光源位置影响建筑绘图机械制图艺术创作04两种投影方式的比较中心投影在摄影、电影制作等领域中广泛应用，通过中心投影可以得到物体的真实图像。

中心投影平行投影平行投影中心投影投影的优缺点比较05实际应用案例分析建筑设计中的平行投影与中心投影平行投影在建筑设计领域，平行投影是一种常用的技术，用于将三维建筑模型转化为二维平面图。

这种方法能够准确反映建筑物的尺寸和形状，以及其在空间中的相对位置。

平行投影在建筑设计中具有重要作用，因为它能够提供一种标准化的沟通方式，使设计师、工程师和承包商都能够准确理解建筑物的设计和规划。

中心投影中心投影是一种将三维物体投影到二维平面的方法，其特点是投影线汇聚于一点，也称交汇投影。

在建筑设计中，中心投影通常用于绘制透视图，以表现建筑物的外观和内部空间效果。

透视图是一种具有强烈立体感的图像，能够直观地展示建筑物的空间关系和设计细节。

在机械制图领域，平行投影同样是一种常用的技术，用于将三维零件或装配体转化为二维平面图。

这种方法能够准确反映零件或装配体的尺寸、形状和相对位置，是进行机械设计和制造过程中的重要环节。

平行投影在机械制图中的应用非常广泛，包括零件图、装配图、钣金展开图等。

中心投影在机械制图中，中心投影通常用于绘制轴测图。

空间几何的投影在几何学中，投影是一种常见的概念，它可以帮助我们理解空间中物体的形状和位置。

投影是指将一个三维物体在二维平面上的映射，通过投影可以得到物体在平面上的影子或者投影图像。

在空间几何中，投影有不同的种类，包括平行投影、中心投影和斜投影等。

本文将介绍空间几何中的投影概念以及如何计算投影，以帮助读者更好地理解和应用投影的知识。

一、平行投影平行投影是指将三维物体投影到一个平行于某个平面的平面上。

在平行投影中，物体的大小和形状在投影过程中保持不变。

平行投影可以简化物体的表达和计算，常用于工程、建筑和计算机图形学等领域。

例如，日常生活中我们常见的地图就是使用平行投影的方式将地球的表面投影到平面上。

计算平行投影的方法通常通过确定投影中心、投影平面和投影方向来实现。

具体步骤包括：1. 确定投影中心：根据物体和投影平面的相对位置，确定一个点作为投影中心，该点将成为投影光线的起点。

2. 确定投影平面：确定一个平行于某个平面的平面作为投影平面，物体在该平面上的投影将呈现出物体的形状和大小。

3. 确定投影方向：确定物体在投影平面上的投影方向，以确定投影光线的方向和长度。

通过以上步骤，我们可以得到物体在平行投影中的投影图像，从而更好地理解物体在平面上的形状和尺寸。

二、中心投影中心投影是指将三维物体投影到一个以投影中心为原点的球面上。

在中心投影中，物体的大小和形状在投影过程中会发生变化，物体离投影中心越远，投影的大小会越小。

中心投影常用于天文学和地理学中，用来表达地球、星球和宇宙物体等的形状和位置关系。

计算中心投影的方法也常通过确定投影中心、投影平面和投影方向来实现。

不同的是，在中心投影中，投影平面为一个与投影中心相切的球面，投影方向为从投影中心到物体上各个点的方向。

通过确定投影中心和投影平面，再绘制出所有的投影线，可以得到物体在球面上的投影图像。

三、斜投影斜投影是指将三维物体投影到一个与物体不平行的平面上。

在斜投影中，物体的形状和大小在投影过程中会发生变化，投影结果可能会失真或拉伸，但可以更真实地表达物体在空间中的位置和形态。

中心投影与平行投影教案一、教学目标1. 让学生了解中心投影和平行投影的定义及特点。

2. 培养学生运用投影知识解决实际问题的能力。

3. 提高学生对几何图形的认识和空间想象能力。

二、教学内容1. 中心投影：a. 定义：光线从一点发出，照射到一个平面上的投影。

b. 特点：光线为放射状，投影为向中心聚拢的形状。

2. 平行投影：a. 定义：光线从多个方向平行照射到一个平面上的投影。

b. 特点：光线为平行状，投影为相同大小的形状。

三、教学重点与难点1. 教学重点：中心投影和平行投影的定义及特点。

2. 教学难点：如何运用投影知识解决实际问题。

四、教学方法1. 采用问题驱动法，引导学生探究中心投影和平行投影的特点。

2. 利用几何画板或实物模型，直观展示投影现象。

3. 设计实践环节，让学生动手操作，加深对投影知识的理解。

五、教学过程1. 导入：a. 引导学生回顾之前学过的投影知识。

b. 提问：什么是中心投影？什么是平行投影？2. 新课讲解：a. 讲解中心投影的定义及特点。

b. 讲解平行投影的定义及特点。

3. 实例分析：a. 分析生活中常见的中心投影和平行投影现象。

b. 引导学生运用投影知识解决实际问题。

4. 实践操作：a. 学生分组，利用几何画板或实物模型进行投影实验。

b. 总结实验结果，巩固对中心投影和平行投影的理解。

5. 课堂小结：a. 回顾本节课所学内容。

b. 强调中心投影和平行投影的特点及应用。

6. 作业布置：a. 请学生运用投影知识，解决一些实际问题。

b. 绘制中心投影和平行投影的示意图，加深对投影现象的理解。

六、课程拓展1. 引导学生思考：除了中心投影和平行投影，还有其他类型的投影吗？2. 介绍正投影和斜投影的概念，让学生了解投影的分类。

七、课堂互动1. 提问：中心投影和平行投影在日常生活中有哪些应用？2. 学生分享实例，如建筑物的影子、路灯下的影子等。

八、思维训练1. 设计一道有关投影的思维训练题，如：一个长方体在一个斜面上的投影是什么形状？2. 学生独立思考，小组讨论，得出答案。

初中数学投影有哪些种类投影在数学中有多种类型，包括平行投影、中心投影、透视投影等。

下面我们将逐一介绍这些类型的投影。

1. 平行投影：平行投影是指将三维物体的每个点沿着平行于某个方向的直线投射到一个平行于该方向的平面上。

在平行投影中，被投影物体的大小和形状在投影平面上保持不变。

常见的平行投影包括正交投影和斜投影。

-正交投影：正交投影是指将三维物体的每个点沿着垂直于投影平面的直线投射到投影平面上。

在正交投影中，投影线与投影平面垂直，被投影物体在投影平面上的大小和形状与实际物体相同。

正交投影常用于制图和工程设计中。

-斜投影：斜投影是指将三维物体的每个点沿着与投影平面不垂直的直线投射到投影平面上。

在斜投影中，投影线与投影平面不垂直，被投影物体在投影平面上的大小和形状与实际物体不同。

斜投影常用于绘画和计算机图形学中。

2. 中心投影：中心投影是指将三维物体的每个点沿着射线投射到一个平面上。

在中心投影中，投影线都通过一个中心点，被投影物体的大小和形状会随着距离的增加而发生变化，从而呈现出透视效果。

中心投影常用于绘画、摄影和计算机图形学中，以模拟人眼观察物体的效果。

3. 透视投影：透视投影是指将三维物体的每个点沿着射线投射到一个平面上。

在透视投影中，被投影物体的大小和形状会随着距离的增加而发生变化，从而呈现出透视效果。

透视投影常用于绘画、摄影和计算机图形学中，以模拟人眼观察物体的效果。

除了以上几种常见的投影类型，还有其他特殊类型的投影，如等轴投影、鸟瞰投影、鸟瞰投影等。

这些投影类型在不同的领域和应用中有着特定的用途和意义。

总结起来，投影在数学中有多种类型，包括平行投影、中心投影、透视投影等。

不同类型的投影在几何学、物理学、计算机图形学等领域中具有广泛的应用，对于理解和研究物体的形状、光线的传播以及生成逼真的图像等方面都起着关键作用。

中心投影与平行投影知识点一中心投影与平行投影1、投影：光线通过物体，向选定的面（投影面）投射，并在该面上得到图形的方法。

2、中心投影：投射线交于一点的投影称为中心投影。

其投影的大小随物体与投影中心间距离的变化而变化，所以其投影不能反映物体的实形.3、平行投影：投射线相互平行的投影称为平行投影。

平行投影的投影线是平行的。

在平行投影中，投影线正对着投影面时，叫做正投影，否则叫做斜投影。

在平行投影下，与投影面平行的平面图形留下的影子与这个平面图形全等；4、中心投影与平行投影的区别与联系(1)中心投影后的图形与原图形相比虽然改变较多，但直观性强，看起来与人的视觉效果一致，最像原来的物体，画实际效果图时，一般用中心投影法；(2)平行投影形成的直观图则能比较精确地反映原来物体的形状和特征。

画立体几何中的直观图形时一般用平行投影法。

例1、判断下列命题是否正确（1）直线的平行投影一定为直线（2）一个圆在平面上的平行投影可以是圆或椭圆或线段（3）矩形的平行投影一定是矩形（4）两条相交直线的平行投影可以平行知识点二三视图1、概念：视图是指将物体按正投影向投影面投射所得到的图形。

线自物体由前向后投射所得投影称为主视图或正视图。

光线自物体由上向下投射所得投影称为俯视图。

光线自物体由左向右投射所得投影称为左视图。

2、三视图画法规则高平齐：主视图与左视图的高要保持平齐长对正：主视图与俯视图的长应对正宽相等：俯视图与左视图的宽度应相等例2、画出下列几何体的三视图分析：一般先画主视图，其次画俯视图，最后画左视图。

画的时候把轮廓线要画出来，被遮住的轮廓线要画成虚线。

解：这二个几何体的三视图如下例3、如图，设所给的方向为物体的正前方，试画出它的三视图（单位：cm）变式1、如图，E、F分别为正方形的面ADD1A1、BCC1B1的中心，则四边形BFD1E在该正方体的面上的正投影不可能为回顾与反思变式2、三视图如下，试判断该几何体的形状变式3、个物体由几块相同的正方体组成，其三视图如图所示，试据图回答下列问题：(1)该物体有多少层？ (2)该物体的最高部分位于哪里？(3)该物体一共由几个小正方体构成？【解】(1)该物体一共有两层，从正视图和侧视图都可以看出来．(2)该物体最高部分位于左侧第一排和第二排．(3)从侧视图及俯视图可以看出，该物体前后一共三排，第一排左侧2个，右侧1个；第二排左侧2个，右侧没有；第三排左侧1个，右侧1个．该物体一共由7个小正方体构成.知识点三 直观图----斜二测画法基本步骤如下：1、建系：在已知图形中取互相垂直的x 轴和y 轴，得到直角坐标系xoy ，直观图中画成斜坐标系'''x o y ，两轴夹角为45︒.2、平行不变：已知图形中平行于x 轴或y 轴的线段，在直观图中分别画成平行于x ’或y ’轴的线段.3、长度规则：已知图形中平行于x 轴的线段，在直观图中保持长度不变；平行于y 轴的线段，长度为原来的一半. 例4、（1）画水平放置的一个直角三角形的直观图；（2）画棱长为4cm 的正方体的直观图. 解：（1）画法：如图，按如下步骤完成. 第一步，在已知的直角三角形ABC 中取直角边CB 所在的直线为x 轴，与BC 垂直的直线为y 轴，画出对应的x '轴和y '轴，使45x O y '''∠=o .第二步，在x '轴上取''O C BC =，过'C 作'y 轴的平行线，取1''2C A CA =.第三步，连接''A O ，即得到该直角三角形的直观图.（2）画法：如图，按如下步骤完成.第一步，作水平放置的正方形的直观图ABCD ，使45,BAD ∠=o 4,2AB cm AD cm ==. 第二步，过A 作z '轴，使90BAz '∠=o . 分别过点,,B C D 作z '轴的平行线，在z '轴及这组平行线上分别截取4AA BB CC DD cm ''''====.第三步，连接,,,A B B C C D D A ''''''''，所得图形就是正方体的直观图. 点评：直观图的斜二测画法的关键之处在于将图中的关键点转化为坐标系中的水平方向与垂直方向的坐标长度，然后运用“水平长不变，垂直长减半”的方法确定出点，最后连线即得直观图. 注意被遮挡的部分画成虚线.变式1、下列图形表示水平放置图形的直观图，画出它们原来的图形.变式2、如下图所示，梯形1111A B C D 是一平面图形ABCD 的直观图. 若111//A D O y ，1111//A B C D ，1111223A B C D ==，111'1A D O D ==. 请画出原来的平面几何图形的形状，并求原图形的面积.解：如图，建立直角坐标系xOy ，在x 轴上截取1'1OD O D ==；1'2OC O C ==.在过点D 的y 轴的平行线上截取1122DA D A ==.在过点A 的x 轴的平行线上截取112AB A B ==. 连接BC ，即得到了原图形.由作法可知，原四边形ABCD 是直角梯形，上、下底长度分别为2,3AB CD ==，直角腰长度为2AD =，所以面积为23252S +=⨯=.变式3、利用斜二测画法得到的 ①三角形的直观图一定是三角形； ②正方形的直观图一定是菱形；③等腰梯形的直观图可以是平行四边形； ④菱形的直观图一定是菱形. 以上结论正确的是 （ B ） A ．①② B ． ① C ．③④ D ． ①②③④巩固练习一：1、两条相交直线的平行投影是（ ） A 、 两条相交直线 B 、 一条直线C 、 一条折线D 、 两条相交直线或一条直线2、如果一个三角形的平行投影仍是一个三角形，则下列结论中正确的是（ ） A 、 内心的平行投影还是内心 B 、 重心的平行投影还是重心 C 、 垂心的平行投影还是垂心 D 、 外心的平行投影还是外心3、下列说法正确的是（ ）A 、 矩形的平行投影一定是矩形B 、 梯形的平行投影一定是梯形或线段C 、 正方形的平行投影一定是矩形D 、 正方形的平行投影一定是菱形 4、当图形中的直线或线段不平行于投射线时，下列说法中不正确的是（ ） A 、 直线或线段的平行投影仍是直线或线段 B 、 平行直线的平行投影仍是平行的直线C 、 与投射面平行的平面图形，它的投影与这个图形全等D 、 在同一直线或平行直线上，两条线段平行投影的比等于这两条线段的比5、从投影的角度来看，正等测画法和斜二测画法画出的直观图都是在平行投影下画出来的空间图形6、矩形的平行投影一定是矩形7、梯形的平行投影一定是梯形8、平行四边形的投影可能是正方形9、两条相交直线的投影可能平行 10、当直线或线段不平行于投射线时，直线或线段的平行投影仍是直线或线段 11、平行直线的平行投影仍是平行的直线12、与投影面平行的平面图形，它的投影与这个图形全等13、在同一直线或平行线上，两条线段平行投影的比等于这两条线段的比14、如果一个三角形的平行投影仍是三角形，那么它的中位线的平行投影，一定是这个三角形的平行投影的对应的中位线。

中心投影与平行投影教案第一章：中心投影概念介绍1.1 了解中心投影的定义：中心投影是指由一点（称为投影中心）向一个平面（称为投影面）发出的光线，将物体上的点投影到投影面上的图形。

1.2 学习中心投影的特点：1）中心投影的光线是平行的，且投影中心是光线汇聚的点。

2）在中心投影中，物体的形状和大小在投影面上保持不变。

1.3 探究中心投影的规律：1）物体上的点在投影面上的位置与投影中心的位置有关。

2）物体上的点在投影面上的位置与物体到投影中心的距离有关。

第二章：中心投影的应用2.1 学习中心投影在几何中的应用：通过中心投影，我们可以将三维空间中的点、线、面投影到二维平面上的点、线、面。

2.2 掌握中心投影在艺术设计中的应用：中心投影可以用来绘制三维效果的艺术作品，如绘画、雕塑等。

2.3 练习中心投影的实际应用：利用中心投影的知识，解决实际问题，如设计建筑物的立面图、绘制电路板等。

第三章：平行投影概念介绍3.1 了解平行投影的定义：平行投影是指由一组平行光线（称为投影线）向一个平面（称为投影面）发出的光线，将物体上的点投影到投影面上的图形。

3.2 学习平行投影的特点：1）平行投影的光线是平行的，且投影线与投影面垂直。

2）在平行投影中，物体的大小和形状在投影面上保持不变，但物体在投影面上的位置会发生变化。

3.3 探究平行投影的规律：1）物体上的点在投影面上的位置与投影线的位置有关。

2）物体上的点在投影面上的位置与物体到投影线的距离有关。

第四章：平行投影的应用4.1 学习平行投影在几何中的应用：通过平行投影，我们可以将三维空间中的点、线、面投影到二维平面上的点、线、面。

4.2 掌握平行投影在艺术设计中的应用：平行投影可以用来绘制三维效果的艺术作品，如绘画、雕塑等。

4.3 练习平行投影的实际应用：利用平行投影的知识，解决实际问题，如设计建筑物的立面图、绘制电路板等。

第五章：中心投影与平行投影的比较相同点：都能将三维空间中的点、线、面投影到二维平面上的点、线、面。