生活中平行投影和中心投影的例子

平行投影的例子
平行投影是把一个形体的三维量投射成一个平面上的图像的方法，它与现实接近，并且可以被用于透视投影、变形投影、多面体投影和三维平行投影等应用程序。

平行投影的例子可以帮助我们更好地理解这个概念。

一个最常见的例子是通过把一个立方体投射到一个平面上，可以在平面上呈现出公立立方体的形状。

当将一个立方体投射到一个垂直于立方体某一侧的影平面我们可以在投影平面上呈现出一个正方形，它正好是立方体四个侧面垂直于投影平面的投影组合成的图案。

另一个例子是将一个椎体投射到一个平面上，会得到一个椎体形状的投影，椎体上的六个面的投影组合成的图案正好是一个正六边形。

此外，还可以通过多面体的投影，将多面体投射到一个平面上，由投射后的邻边多边形的图案组成的投影称为多面体的投影，这是一种根据多面体的角落和边长来投射到平面上的图形，此外还可以将三维物体投射到二维平面上，使人们可以很好地清楚地欣赏三维形体动态投影到二维平面上时的效果，这种平行投影也常常被用于动画、建筑设计、城市规划以及游戏等的视觉展示上。

总的来说，平行投影的例子比较多，上述仅仅是其中的一部分，但是其中的技术原理和应用可以帮助我们更好地理解平行投影，从而能够更好地使用这种技术。

- 1 -。

实际生活中的投影河北 欧阳庆红投影问题在日常生活中随处可见，解答这类题时要注意分清本质（即是中心投影还是平行投影问题）及每种投影的特征.例1:图1是一天中四个不同时刻两个建筑物的影子：将它们按时间先后顺序进行排列，正确的是（ ）A 、③④②①B 、②④③①C 、③④①②D 、③①②④分析：太阳光是平行光,因而投影是平行投影,太阳光早上与地面夹角较小,到中午左右最大;即物体的投影先最长,然后变短,最后又变长;其次,,太阳是从东方升起,物体的投影的方向正好相反,不同高度的物体的投影的长度也不相同,高的物体的投影也较长,图③中物体的投影最长,其方向是西方,因此表示的时间是早上;图④中物体的投影较短,其方向是西北方向,太阳在东南边,因此表示的时间是上午;图①中物体的投影较短,其方向是东北方向,太阳在西南边,因此表示时间是下午;图②中物体投影较长,其方向是东方,因此太阳在西边,因此表示的时间是下午近傍晚时.故选C 、反思:⑴在平行投影中,高的物体的投影也较长;⑵要注意方向,如光线从东边照过来,投影就在西边;⑶太阳光是特殊的平行光,要注意随着时间的推移,太阳光的方向及其投影的变化规律.例2:(05河北)如图2，晚上，小亮在广场上乘凉．图2中线段AB 表示站立在广场上的小亮，线段PO 表示直立在广场上的灯杆，点P 表示照明灯． （1）请你在图中画出小亮在照明灯（P ）照射下的影子；（2）如果灯杆高PO ＝12m ，小亮的身高AB ＝1.6m ，小亮与灯杆的距离BO ＝13m ，请求出小亮影子的长度．分析:根据中心投影的特征,先确定A 点的投影,从而画出小亮的影子,再将这一问题转化为数学问题,用相似三角形的知识求解.解：（1）如图3，连接PA 并延长交地面于点C,线段BC 就是小亮在照明灯(P)照射下的影子.（2）在△CAB 和△CPO 中，∵ ∠C =∠C ，∠ABC =∠POC =90°，图2图1∴ △CAB ∽△CPO ．∴COCBPO AB =． ∴ BCBC+=13126.1． ∴ BC =2．∴ 小亮影子的长度为2m ．例3:某校墙边有两根木杆.⑴某一时刻甲木杆在阳光下的影子如图4所示,你能画出乙木杆的影子吗?(用线段表示影子) ⑵在图4中,当乙木杆移动到什么位置时,其影子刚好不落在墙上? ⑶在你所画的图中有相似三角形吗?为什么?分析:所要画出的乙木杆的影子与甲木杆形成的影子是同一时刻,根据同一时刻两物体的高度比等于其影长的比,同时,在同一时刻太阳光线是互相平行的,平行移动乙杆,使其杆顶端的影长恰好抵达墙角.解:(1)如图5,过E 点作直线D D '的平行线,交D A '所在直线于E ',则E B '为乙木杆的影子. (2)平移由乙杆、乙杆的影子和太阳光线所构成的图形（即E BE '∆），直到其影子的顶端E '抵达墙角.（3）D AD '∆与E BE '∆相似.反思:由一物体及其影长,画出同一时刻另一物体的影子,其作法是:⑴过已知物体的顶端及其影长的端点作一直线,再过另一物体的顶端作之前所作的直线的平行线,交已知物体的影子所在直线于一点,则该点到该物体的底部的线段即为影长.但应注意以下两点:①两物体必须在同一平面内;②所求物体必须在已知的影子所在的直线上. ⑵在同一时刻,不同物体的底部中点、顶端的中心及影子的端点所构成的三角形是相似三角形.D '甲E BDA乙图4D '甲 E B DA乙 图5 E 'ED '甲 BDA乙 图6EE '。

中心投影的应用当我们晚上漫步在两旁有路灯的城市街道时，细心的同学会发现一个有趣的现象：离开路灯愈远，我们影子就越长．这是为什么呢（如图1，用AB表示路灯的高度，CD，EF表示同一个人的不同位置，则DF，FG就表示人相应位置的影长）事实上，当人在路灯下行走时，在每一时刻，路灯发出的光线与人的身体、身影构成一个直角三角形，根据勾股定理，人的身高是一定的，因而从头顶到地面的光线的长越长，则他的影长就越长．我们把路灯、台灯、手电筒的光线看成是从一个点发出的，像这样，在点光源的照射下，物体产生的影称为中心投影．中心投影有一个重要的性质：形成中心投影的光线是不平行的，即光线是相交的，而交点就是光源的位置．利用灯、物体、影子之间的关系我们可以解决如下的三类问题．一、已知灯的位置，可以确定物体的影子例1 如图2，晚上小明在灯下散步，在小明由A处走到B处这一过程中，他在地上的影子（）．（A）逐渐变短（B）逐渐变长（C）先变短，再变长（D）先变长，再变短．析解：路灯的光线可以看成是从一个点发出的，物体所产生的投影为中心投影，过灯所在的位置点及小明头顶作射线与地面相交，交点到小明脚根的距离就是影长．如图3，根据画出每个位置的影长容易发现：小明从A到B的影子变化可分为两个阶段：A→M影子越来越短，M→B 影子越来越长，因此从A→B先变短，再变长，故选（C）．二、已知两物体及两物体的影子可以确定灯的位置例2 在同一直线上的三根旗杆直立在地面上，第一、第二根旗杆在同一灯光下的影子如图4，请在图中画出光源的位置，并画出第三根旗杆在该灯光下的影子．解题过程请同学们自己完成．三、已知灯的位置及物体和物体影子的高度，确定灯的高度与灯之间的距离例3 如图5，有一路灯杆AB（底部B不能直接到达），在灯光下，小明在点D处测得自己的影长DF=3m，沿BD方向到达点F处再测得自己的影长FG=4m，如果小明的身高为，求路灯杆AB的高度．解题过程请同学们自己完成．参考答案：AB的高度为．例4 如图6，王华同学在晚上由路灯AC走向路灯BD，当他走到点到达Q点时，发现身前他影子的顶部刚好接触到路灯BD的底部，已知王华同学的身高是，两个路灯的高度都是．（1）求两个路灯之间的距离；（2）当王华同学走到路灯BD处时，他在路灯AC下的影子长是多少解题过程请同学们自己完成．参考答案：（1）两路灯之间的距离为18ｍ；（2）AC的影子长是ｍ．评注：本题创设了以灯光和影子为实际背景的相似三角形的性质的实际应用问题，要想正确解决问题，首先要审清题意，画出图形，尤其是要找出影子，然后再综合应用所学知识．。

投影与视图知识点总结在我们的日常生活和学习中，投影与视图是一个重要的数学概念，它不仅在数学领域有着广泛的应用，在工程、建筑、设计等实际领域也发挥着关键作用。

接下来，让我们一起深入了解投影与视图的相关知识点。

一、投影投影是光线（投射线）通过物体，向选定的面（投影面）投射，并在该面上得到图形的方法。

1、中心投影由同一点（点光源）发出的光线形成的投影叫做中心投影。

比如，夜晚路灯下的人影就是中心投影的例子。

其特点是：等长的物体平行于地面放置时，在灯光下，离点光源越近的物体的影子越短，离点光源越远的物体的影子越长。

2、平行投影由平行光线（太阳光线）形成的投影称为平行投影。

平行投影又分为正投影和斜投影。

正投影是指投射线垂直于投影面的平行投影。

在平行投影中，同一时刻，不同物体的物高和影长成比例。

二、视图视图是将物体按正投影向投影面投射所得到的图形。

1、三视图三视图包括主视图、俯视图和左视图。

主视图：从物体的前面向后面投射所得的视图。

俯视图：从物体的上面向下面投射所得的视图。

左视图：从物体的左面向右面投射所得的视图。

三视图的位置关系：主视图在上方，俯视图在主视图的正下方，左视图在主视图的正右方。

三视图的大小关系：长对正、高平齐、宽相等。

即主视图与俯视图的长相等，主视图与左视图的高相等，俯视图与左视图的宽相等。

2、常见几何体的三视图（1）正方体：三视图都是正方形。

（2）长方体：主视图、左视图是长方形，俯视图是长方形。

（3）圆柱：主视图、左视图是长方形，俯视图是圆。

（4）圆锥：主视图、左视图是三角形，俯视图是圆及圆心。

（5）球：三视图都是圆。

三、根据视图还原几何体根据三视图还原几何体时，要先分别根据主视图、俯视图和左视图想象几何体的前面、上面和左面的形状，然后综合起来考虑整体形状。

四、投影与视图的应用1、在建筑设计中，设计师需要通过绘制三视图来准确表达建筑物的形状和尺寸，以便施工人员能够按照设计进行施工。

2、在机械制造中，工程师需要根据零件的三视图来制造零件，确保零件的精度和质量。

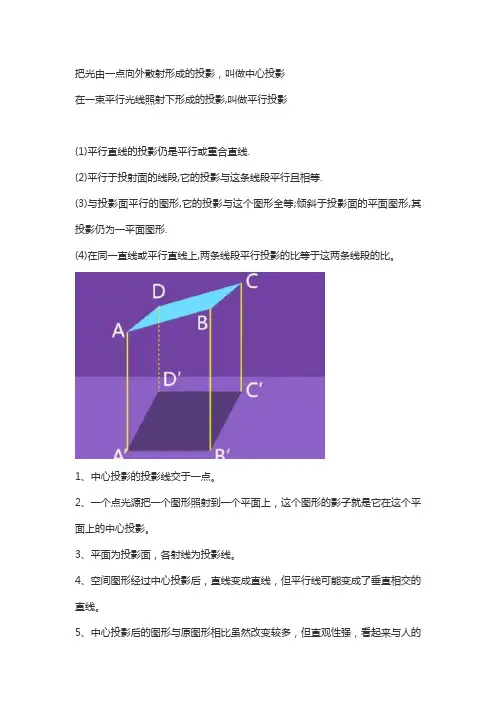
把光由一点向外散射形成的投影，叫做中心投影
在一束平行光线照射下形成的投影,叫做平行投影
(1)平行直线的投影仍是平行或重合直线.
(2)平行于投射面的线段,它的投影与这条线段平行且相等.
(3)与投影面平行的图形,它的投影与这个图形全等;倾斜于投影面的平面图形,其投影仍为一平面图形.
(4)在同一直线或平行直线上,两条线段平行投影的比等于这两条线段的比。

1、中心投影的投影线交于一点。

2、一个点光源把一个图形照射到一个平面上，这个图形的影子就是它在这个平面上的中心投影。

3、平面为投影面，各射线为投影线。

4、空间图形经过中心投影后，直线变成直线，但平行线可能变成了垂直相交的直线。

5、中心投影后的图形与原图形相比虽然改变较多，但直观性强，看起来与人的
视觉效果一致。

6、最像原来的物体，所以在绘画时，经常使用这种方法，但在立体几何中很少用中心投影原理来画图。

7、如果一个平面图形所在的平面与投射面平行，那么中心投影后得到的图形与原图形也是平行的，并且中心投影后得到的图形与原图形相似。

空间几何的投影在几何学中，投影是一种常见的概念，它可以帮助我们理解空间中物体的形状和位置。

投影是指将一个三维物体在二维平面上的映射，通过投影可以得到物体在平面上的影子或者投影图像。

在空间几何中，投影有不同的种类，包括平行投影、中心投影和斜投影等。

本文将介绍空间几何中的投影概念以及如何计算投影，以帮助读者更好地理解和应用投影的知识。

一、平行投影平行投影是指将三维物体投影到一个平行于某个平面的平面上。

在平行投影中，物体的大小和形状在投影过程中保持不变。

平行投影可以简化物体的表达和计算，常用于工程、建筑和计算机图形学等领域。

例如，日常生活中我们常见的地图就是使用平行投影的方式将地球的表面投影到平面上。

计算平行投影的方法通常通过确定投影中心、投影平面和投影方向来实现。

具体步骤包括：1. 确定投影中心：根据物体和投影平面的相对位置，确定一个点作为投影中心，该点将成为投影光线的起点。

2. 确定投影平面：确定一个平行于某个平面的平面作为投影平面，物体在该平面上的投影将呈现出物体的形状和大小。

3. 确定投影方向：确定物体在投影平面上的投影方向，以确定投影光线的方向和长度。

通过以上步骤，我们可以得到物体在平行投影中的投影图像，从而更好地理解物体在平面上的形状和尺寸。

二、中心投影中心投影是指将三维物体投影到一个以投影中心为原点的球面上。

在中心投影中，物体的大小和形状在投影过程中会发生变化，物体离投影中心越远，投影的大小会越小。

中心投影常用于天文学和地理学中，用来表达地球、星球和宇宙物体等的形状和位置关系。

计算中心投影的方法也常通过确定投影中心、投影平面和投影方向来实现。

不同的是，在中心投影中，投影平面为一个与投影中心相切的球面，投影方向为从投影中心到物体上各个点的方向。

通过确定投影中心和投影平面，再绘制出所有的投影线，可以得到物体在球面上的投影图像。

三、斜投影斜投影是指将三维物体投影到一个与物体不平行的平面上。

在斜投影中，物体的形状和大小在投影过程中会发生变化，投影结果可能会失真或拉伸，但可以更真实地表达物体在空间中的位置和形态。

空间几何的投影问题在空间几何学中，投影是一个重要的概念，它用来描述一个物体在垂直于某个方向的平面上所形成的影像。

投影问题在实际生活中有着广泛的应用，比如建筑设计、计算机图形学等领域。

本文将重点讨论空间几何中的投影问题，探讨其原理、方法和应用。

一、投影的原理投影可以看作是一种几何变换，它将三维空间中的实体映射到二维平面上。

在投影中，我们需要确定两个关键要素：视点和投影面。

视点是观察者所处的位置，而投影面则是物体投影到的平面。

通过选择不同的视点和投影面，我们可以得到不同的投影效果。

根据视点和投影面的位置关系，投影可以分为正投影和斜投影两种形式。

正投影是指视点位于无穷远处，即光线是平行投射的情况。

斜投影是指视点位于有限距离处，即光线呈斜线投射的情况。

二、投影的方法在空间几何中，我们可以利用几何分析和代数方法来求解投影问题。

下面介绍几种常见的投影方法：1. 平行投影：平行投影是指在视点无穷远处，光线平行于投影面的投影方式。

在平行投影中，物体在投影面上的尺寸保持不变，只有位置发生了变化。

平行投影常用于建筑设计和制图等领域。

2. 中心投影：中心投影是指在视点有限距离处，光线从视点发出且垂直于投影面的投影方式。

在中心投影中，物体在投影面上的尺寸和位置都会发生变化，呈现出近大远小的效果。

中心投影常用于透视画和计算机图形学等领域。

3. 斜投影：斜投影是指在视点有限距离处，光线不垂直于投影面的投影方式。

在斜投影中，物体在投影面上的尺寸和位置都会发生变化，但它与中心投影不同的是，斜投影不呈现出近大远小的效果。

斜投影常用于工程制图和计算机图形学等领域。

三、投影的应用投影问题在现实生活和工程实践中有着广泛的应用。

下面列举几个例子，来说明投影在不同领域的具体应用：1. 建筑设计：在建筑设计中，投影被用于创建建筑物的平面图和立体图。

通过正投影和斜投影等方法，设计师可以将三维建筑物的形状和结构映射到平面上，方便进行设计和施工。

空间几何中的投影问题在我们的日常生活和学习中，空间几何的概念无处不在。

而其中的投影问题，更是具有重要的意义和应用价值。

从简单的物体在阳光下的影子，到复杂的工程设计和建筑规划，投影问题都发挥着关键的作用。

那么，什么是空间几何中的投影呢？简单来说，投影就是将一个空间中的物体或者图形，通过某种方式映射到一个平面上所得到的图像。

就好像我们用手电筒照射一个物体，在墙上形成的影子就是这个物体的一种投影。

投影的类型多种多样，常见的有平行投影和中心投影。

平行投影就像是太阳光直直地照射下来，光线是平行的，所得到的投影大小和形状不会因为物体与投影面的距离变化而改变。

比如，我们在教室里使用的投影仪，它所投射出的图像就是平行投影。

而中心投影则是以一个点为中心，光线向四周发散，这样形成的投影会随着物体与投影中心的距离变化而改变大小和形状。

比如我们晚上在路灯下看到自己的影子，就是中心投影。

在解决空间几何中的投影问题时，我们首先要明确投影的类型，因为这会直接影响到我们的解题思路和方法。

比如，对于平行投影，我们通常可以利用相似三角形的性质来计算投影的长度、面积等；而对于中心投影，可能需要考虑角度和距离的关系。

为了更好地理解投影问题，让我们来看一个具体的例子。

假设有一个边长为 2 的正方体，我们要计算它在水平面上的平行投影的面积。

由于正方体的六个面都是正方形，且平行于水平面的面在水平面上的投影不变，所以正方体在水平面上的投影仍然是一个正方形。

而这个正方形的边长就是正方体的棱长 2，那么投影的面积就是 2×2 ＝ 4。

再来看一个稍微复杂一点的例子。

有一个圆锥，底面半径为 3，高为 4，我们要计算它在垂直于圆锥轴的平面上的中心投影的面积。

首先，我们需要求出圆锥的母线长，根据勾股定理，母线长为 5。

然后，根据中心投影的性质，我们可以知道投影是一个等腰三角形，其底边长就是圆锥的底面直径 6，高可以通过相似三角形的性质求出。

假设投影三角形的高为 h，根据相似比可得：h/4 ＝ 5/3，解得 h ＝ 20/3。

空间几何中的投影问题在我们的日常生活和学习中，空间几何是一个充满魅力和挑战的领域。

而其中的投影问题，更是理解空间物体形态和位置关系的关键所在。

首先，让我们来明确一下什么是投影。

简单地说，投影就是将一个三维的物体在某个平面上留下的影子或者痕迹。

比如说，当阳光照射在一个建筑物上，地面上出现的建筑物的轮廓就是一种投影。

在空间几何中，投影可以分为平行投影和中心投影。

平行投影就像是一束平行的光线照射在物体上所产生的投影。

这时候，不管物体离投影面有多远，投影的大小和形状都不会改变。

就好比我们用幻灯片投影在屏幕上的图像，无论幻灯片离屏幕的距离怎么变化，只要光线是平行的，投影的样子就基本不变。

中心投影则有所不同。

它就像是我们拿着手电筒照射一个物体，光线从一个点出发，所以物体离光源越远，投影就越小；离光源越近，投影就越大。

这种投影在我们生活中也很常见，比如晚上路灯下人的影子，就会随着人离路灯的距离变化而变化。

了解了投影的基本类型，接下来我们看看投影在解决空间几何问题中的应用。

比如说，在计算一个几何体的表面积或者体积时，通过对其进行投影，可以将复杂的三维问题转化为相对简单的二维问题。

假设我们有一个不规则的立体图形，要计算它的表面积。

我们可以分别从不同的方向对其进行投影，得到几个平面图形。

然后计算这些平面图形的面积，再根据投影的关系进行适当的调整和计算，就能较为准确地得出立体图形的表面积。

再来说说投影在确定空间位置关系中的作用。

比如判断两条直线是否相交，如果我们能从不同的角度对这两条直线进行投影，观察投影后的直线是否相交，就能在一定程度上帮助我们判断原空间中两条直线的位置关系。

在投影的学习中，还有一个重要的概念——三视图。

三视图包括主视图、左视图和俯视图。

主视图是从物体的正面观察得到的投影，左视图是从物体的左面观察得到的投影，俯视图则是从物体的上面观察得到的投影。

通过三视图，我们可以非常直观地了解一个物体的形状和结构。