- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
为了解决这一问题,应该对短期债券赋予较高的权重,而对长期 债券赋予较低的权重,从而允许长期债券存在较高的误差。在Bolder和 Streliski (1999)的论文中,设定了如下的权重系数:
wj
1/ Durj 1/ Durj
而将参数
的估计过程定义为:
ˆ*
arg min
n
w2j
D10
(s)
a3
b3s
c3 s 2
d3s3
s [0, 5] s [5,10] s [10,30]
其中,函数必须满足以下的7个约束条件:
D(i) 0
D5i
(5)
D(i) 5
(5)
(10) D10i (10)
D0
(0)
1
i 0,1, 2
从而,我们可以将互相独立的参数缩减到5个:
0
1
1
exp(
1
)
2
1
exp(
1
)
exp
1
1
1
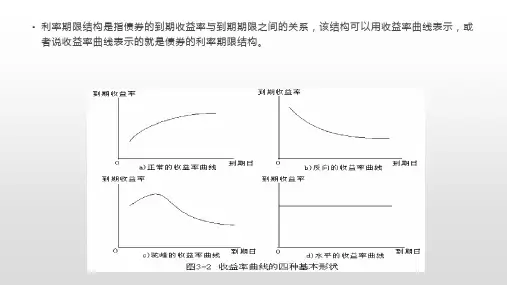
这就是Nelson-Siegel模型的基本表达形式。当固定 0 时,通过 1和2 的不同组合,利用这个模型,可以推出四种不同形状的零
s
推导出的附息债券理论价格。
显然,债券样本中长期品种的价格波动性应大于短期品种,而由此带来 的结果是:以上述方法中表示长期债券的定价误差往往大于短期债券。 这就是在进行收益率曲线拟合时无法避免的样本异方差特征,导致的结 果往往是收益率曲线在远端出现“过度拟合”(Over fitting)的情况, 而在近端则无法很好地表现短期债的实际情况。
静态利率期限结构模型
静态利率期限结构模型概述
静态利率期限结构模型以当天市场的债券价格信息为基础,构 造利率曲线函数,利用所构造的利率曲线得到理论价格来逼近债券 的市场价格,从而得出符合当天价格信息的利率期限结构。
静态利率期限结构模型最为常见的有样条函数模型和节约型模 型,样条函数模型主要包括多项式样条法、指数样条法和B样条法, 节约型模型的主要代表是Nelson-Siegel模型及其扩展模型。
选择样条函数的分段数量和取样条分界点在指数样条法中也同样 十分重要,其方法可以参见多项式样条法。并且,指数样条模型 也容易导致远期利率曲线不稳定。不同于多项式样条法的是,其 参数估计必须采用非线性最优化。
0
Nelson-Siegel模型及其扩展形式
Nelson-Siegel模型可以由一个公式来说明,该公式的形式与那些描述 动态利率的普通微分方程的解的表达式十分类似。该公式为:
(Ti
)
Di21
(Ti
)
其中 D(1) (Ti ), D(2) (Ti )分别为D(Ti ) 的一阶导数和二阶导数。
例如,考虑30年期的贴现率函数,可以用三次多项式分段 拟合如下:
D(
s)
D0
D5
(s) (s)
a1 a2
b1s c1s2 d1s3 b2s c2s2 d2s3
2
exp( 2
)
于是,可以得到:
R(0,
)
0
1
1
exp( 1
)
2
1
exp(
Pˆt j Fs( j) f (s t; ) s
于是,假想出贴现函数 B(t, s) f (s t; 1) 或零息票债券利率
R(t, s t) g(s t; 2)的具体形式,其中 1 和 2 为参数向量。然后
利用假想出的具体形式,来推导附息债券的理论价格,当推导出的
s 0,5 s 5,10
s 10,30
指数样条法
指数样条函数是Vasicek and Fong (1982)提出的。与在多项式样条函数 部分所述的原因相同,也采用三阶指数形式样条函数,其形式为:
D(s)
D1
(
s)
D2
(s)
a1 b1eus c1e2us d1e3us
零息票收益曲线(zero-coupon yield curve), (常用): R(t, ) 或 Rˆ (t, ) ; 远期利率曲线(forward rates curve): T F(t, s,T s)
瞬时远期利率期限结构(instantaneous forward term structure),(常用):s f (t, s) 。
R(t, ) 起息日为时间t,剩余到期期限为 年的连续复合利率。有:
B(t,t ) exp[ R(t, )]
F(t, s,T s) 在时间t计算的,起息日为时间s,剩余到期期限为T-s的远 期利率。有:
B f (t, s,T ) B(t,T ) exp[(T s)F (t, s,T s)] B(t, s)
利率期限结构(term structure of interest rates),又称收益率 曲线(yield curve),是指在相同风险水平下,利率与到期期限 之间的关系,或者说是理论上的零息债券利率曲线。
常见的利率期限结构有以下四种:
贴现因子曲线(discount factor curve): B(t,t ) ;
D0(s) Nhomakorabea
1
b1s
c1s 2
d1s3
D(s)
D5
(s)
1
b1s
c1s 2
d1
s3
s
53
d2
D10
(s)
1
b1s
c1s 2
d1
s3
s
5 3
s
-
5 3
d2
s
-
53
s
103
d3
s
-10 3
f
(0,
)
0
1
exp(
1
)
2
1
exp(
1
)
其中,f (0, ) 表示即期计算的,在未来时间 时发生的瞬间远期利
率。 0 , 1, 2以及1均为待估参数。利用
R(0, ) 1
f (0, s)ds
0
可以得到:
R(0,
)
利率期限结构模型
静态模型
样条函数模型 节约型模型
多项式样条法(McCulloch,1971,1975) 指数样条法(Vasicek&Fong,1982) B样条法,(Steeley,1991)
Nelson-Siegel模型(Nelsen &Siegel,1987) Svensson扩展模型(Svensson,1994)
注意,对于即期贴现率函数 D(s) 来说,显然有 D(0) 1 。另外,为 了保证分段函数的平滑性以及在分段点的平滑过渡,必须保证贴现函 数在整个定义域内连续且一、二阶可导,还需要满足如下约束条件:
Di (Ti ) Di1(Ti )
Di1
(Ti
)
Di11 (Ti
)
Di2
ln B(t,T )
rt T
|T t
Rt 起息日为时间t,剩余到期期限为 t 年的连续复合利率。有:
Rt R(t, t)
(t,T ) 贴现债券价格 B(t,T ) 在时间t的预期瞬间收益。
(t,T ) 贴现债券价格 B(t,T ) 在时间t的瞬时波动。 W ,Wˆ 标准布朗运动。 (t,T ) 瞬间远期利率 f (t,T ) 的波动。有:
理论价格与给定的市场价格最为接近时,就可以估计出由 1 和 2
构成的参数向量,即:
n
ˆ *
arg min
(Pt j
j 1
Pˆt j )2
其中,Pˆt j 是从模型
或模型
Pˆt j Fs( j) f (s t; ) s
Pˆt j Fs( j) exp[(s t)g(s t; )]
u lim f (0, s) s
即,u可以被认为是当前的起息日为未来无限远时的瞬间远期利率。
同样,指数样条法也必须满足如下约束条件:
D(0) 1
Di
(Ti
)
Di 1 (Ti
)
Di1
(Ti
)
Di11 (Ti
)
Di
2
(Ti
)
Di21
(Ti
)
其中,D(1) (Ti ), D(2) (Ti )分别为D(Ti ) 的一阶导数和二阶导数。
a2
b2eus
c2e2us
d
e3us
2
D3 (s) a3 b3eus c3e2us d3e3us
...........
s [0,T1] s [T1,T2 ] s [T2 ,T3 ]
模型中,除了 ai , bi , ci , di外,u也是一个参数,并且有明显的经济含 义。Vasicek and Fong (1982)证明了如下等式:



![21利率期限结构模型[金融计算与建模].pptx](https://uimg.taocdn.com/75509ca0f12d2af90342e659.webp)





